Inne miary ryzyka

i współczynnik beta

Omawiane zagadnienia

Inne miary ryzyka wykorzystywane w
modelu Markowitza
Model Sharpe’a – oparty na
współcznynniku beta

Czy ryzyko dla inwestora to:

a) Każde

odchylenie rzeczywistej stopy dochodu od stopy

oczekiwanej?

Czy raczej:

b) Ujemne

odchylenie rzeczywistej stopy dochodu od stopy

oczekiwanej?

Jeżeli przyjąć rozumienie ryzyka

jako zjawiska

negatywnego

, tzn. ujemnego odchylenia wartości rzeczywistej

stopy dochodu od jej średniej oczekiwanej, to miarami
wspomagającymi proces decyzyjny mogą być:

-

semiwariancja stopy zwrotu

-

semiodchylenie standardowe stopy zwrotu

1. semiwariancja stopy zwrotu (

SV)

jest

ważoną sumą kwadratów ujemnych
odchyleń możliwych stóp zwrotu od
oczekiwanej stopy zwrotu

:

∑

=

=

n

i

i

i

d

p

SV

1

2

gdzie:

gdzie:

⎪⎩

⎪

⎨

⎧

≥

−

<

−

−

=

−

−

−

,

0

,

0

,

0

k

k

gdy

k

k

gdy

k

k

d

i

i

i

i

1. Semiodchylenie standardowe stopy
zwrotu (

SS)

jest pierwiastkiem

kwadratowym semiwariancji

:

∑

=

=

n

i

i

i

d

p

SS

1

2

Semiwariancja i semiodchylenie standardowe stopy zwrotu

odpowiadają

wariancji i odchyleniu standardowemu

tej stopy przy założeniu, że ryzyko

rozumiane jest w kategoriach zagrożenia, co oznacza, iż bierze się pod uwagę
tylko ujemne odchylenia od oczekiwanej stopy zwrotu.

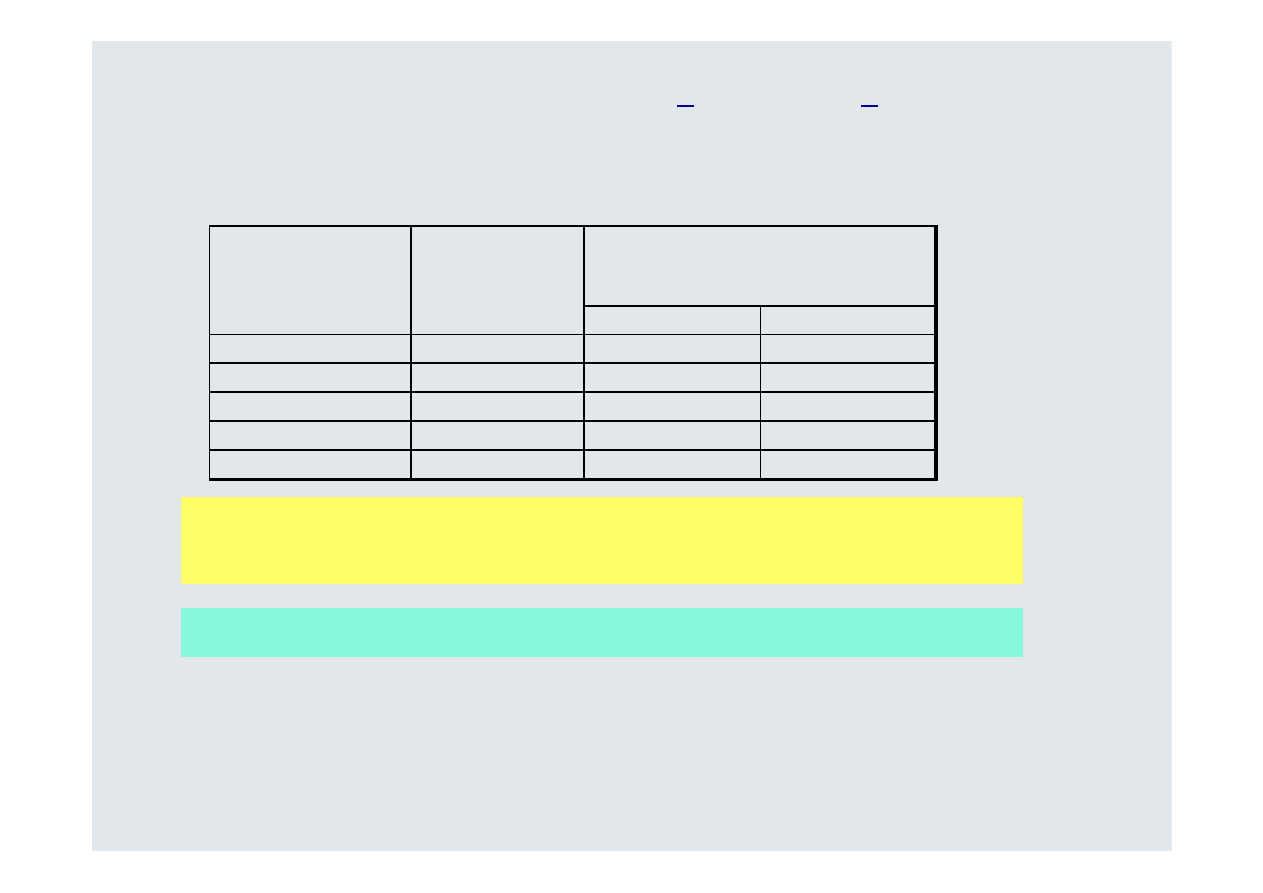
SV

A

= 0,1 x (4 - 8,5)

2

+ 0,2 x (6 - 8,5)

2

+ 0,2 x (8 - 8,5)

2

+ 0,1 x

(5 - 8,5)

2

= =0,585

SV

B

= 0,1 x (2 - 10,0)

2

+ 0,2 x (6 - 10,0)

2

=1,28

A

B

Głęboka recesja

0,1

4%

2%

Łagodna recesja

0,2

6%

6%

Stagnacja

0,4

12%

10%

Łagodny wzrost

0,2

8%

14%

Szybki wzrost

0,1

5%

18%

Stan koniunktury

Praw dopodobień-

stw o w ystąpienia

Stopa dochodu z inwestycji

Dla podanego przykładu – (k

A

= 8,5%, k

B

= 10%)

A. semiwariancja:

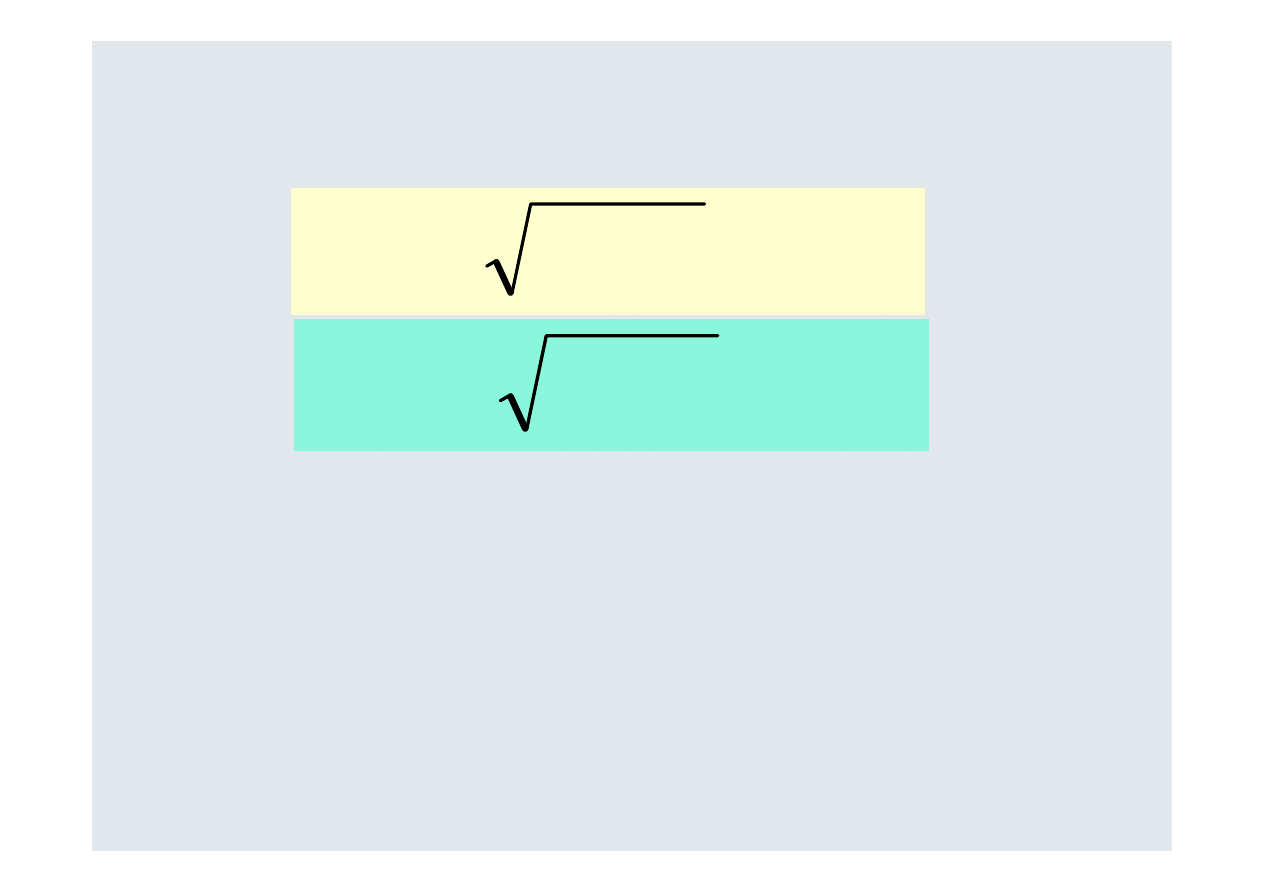
B. Semiodchylenie standardowe stopy zwrotu

76

,

0

585

,

0

=

=

A

SS

Można również zastosować uogólniony sposób, w

którym zamiast ujemnych odchyleń od oczekiwanej
stopy zwrotu uwzględnia się ujemne odchylenia od stopy
zwrotu określonej przez inwestora. Podejście to można
stosować, gdy inwestor chce uniknąć osiągnięcia stóp
zwrotu niższych niż ta, którą uważa za
satysfakcjonującą.

13

,

1

280

,

1

=

=

B

SS

INNE MIARY RYZYKA

I. Odchylenie przeciętne stopy zwrotu:

Przy mierzeniu

odchylenia standardowego

stopy zwrotu

odchylenia możliwych stóp zwrotu od oczekiwanej stopy zwrotu
podnosi się do kwadratu, co powoduje, iż jednorazowe duże
odchylenie podniesione do kwadratu może zawyżyć wielkość
ryzyka. Wady tej pozbawione jest

odchylenie przeciętne stopy

zwrotu,

obliczane za pomocą wzoru:

∑

−

−

−

=

n

i

i

i

k

k

p

d

1

Gdzie:

d – odchylenie przeciętne stopy zwrotu

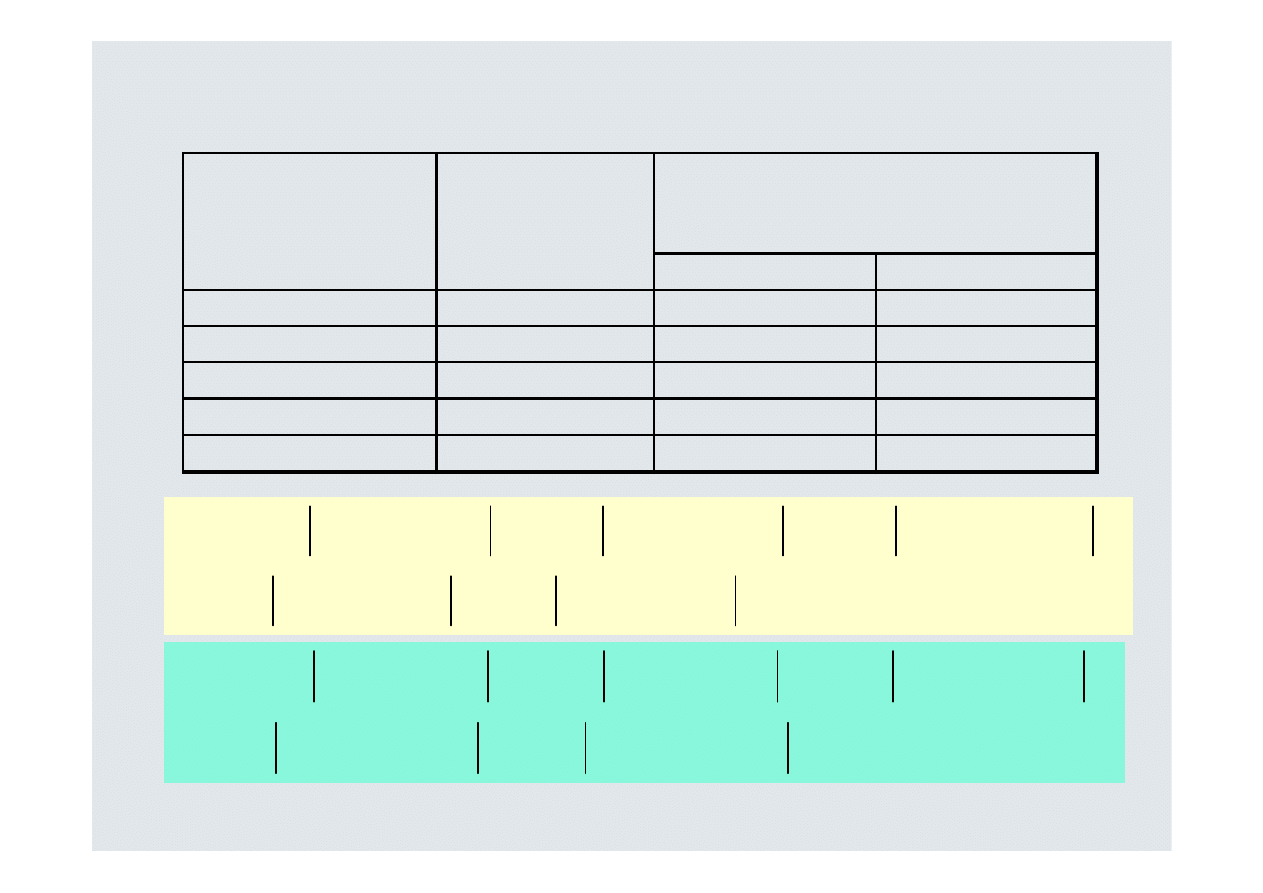
A

B

Głęboka recesja

0,1

4%

2%

Łagodna recesja

0,2

6%

6%

Stagnacja

0,4

12%

10%

Łagodny wzrost

0,2

8%

14%

Szybki wzrost

0,1

5%

18%

Stan koniunktury

Prawdopodo -

bieństwo

wystąpienia

Stopa dochodu z inwestycji

%

8

,

2

%

5

,

8

%

5

1

,

0

%

5

,

8

%

8

2

,

0

%

5

,

8

%

12

4

,

0

%

5

,

8

%

6

2

,

0

%

5

,

8

%

4

1

,

0

=

−

⋅

+

−

⋅

+

+

−

⋅

+

−

⋅

+

−

⋅

=

a

d

%

2

,

3

%

5

,

8

%

18

1

,

0

%

5

,

8

%

14

2

,

0

%

10

%

10

4

,

0

%

10

%

6

2

,

0

%

10

%

2

1

,

0

=

−

⋅

+

−

⋅

+

+

−

⋅

+

−

⋅

+

−

⋅

=

b

d

Dla podanego przykładu – (k

A

= 8,5%, k

B

= 10%)

INNE MIARY RYZYKA

II. Semiodchylenie przeciętne stopy zwrotu:

Jeżeli ryzyko rozumiane jest jedynie w kategoriach

negatywnych to odpowiednikiem

odchylenia przeciętnego

stopy

zwrotu jest

semiodchylenie przeciętne stopy zwrotu,

obliczane za

pomocą wzoru:

∑

−

=

n

i

i

i

d

p

sd

1

gdzie:

⎪⎩

⎪

⎨

⎧

≥

−

<

−

−

=

−

−

−

,

0

,

0

,

0

k

k

gdy

k

k

gdy

k

k

d

i

i

i

i

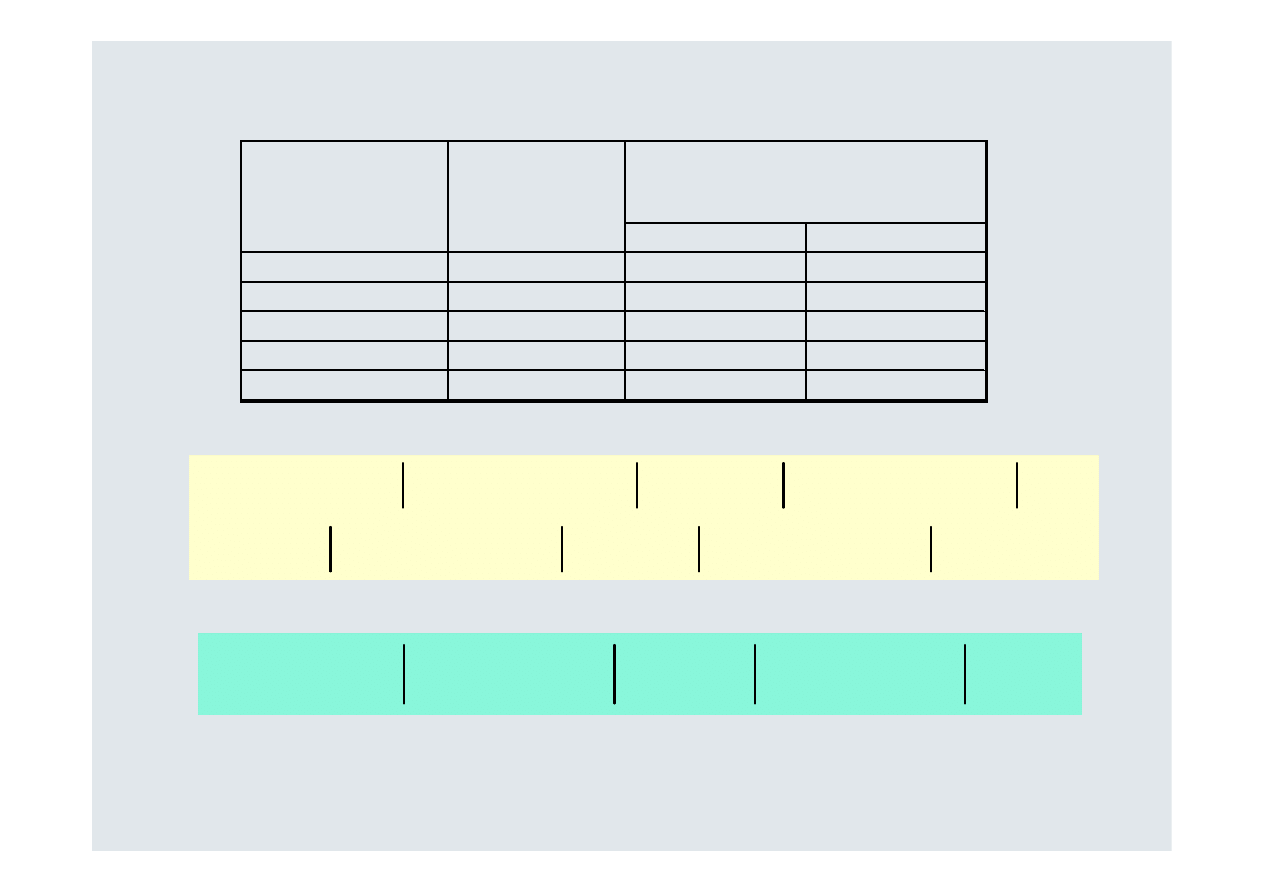
Semiodchylenie przeciętne stopy zwrotu:

A

B

Głęboka recesja

0,1

4%

2%

Łagodna recesja

0,2

6%

6%

Stagnacja

0,4

12%

10%

Łagodny wzrost

0,2

8%

14%

Szybki wzrost

0,1

5%

18%

Stan koniunktury

Prawdopodo -

bieństwo

wystąpienia

Stopa dochodu z inwestycji

%

4

,

1

%

5

,

8

%

5

1

,

0

%

5

,

8

%

8

2

,

0

%

5

,

8

%

6

2

,

0

%

5

,

8

%

4

1

,

0

=

−

⋅

+

−

⋅

+

+

−

⋅

+

−

⋅

=

A

sd

6

,

1

%

10

%

6

2

,

0

%

10

%

2

1

,

0

=

−

⋅

+

−

⋅

=

B

sd

MODEL

SHARPE’A

ZARYS PROBLEMU

Założenie:

Pakiet

m

jest tzw.

pakietem rynkowym

, tzn. że jeżeli na rynku

znajduje się określona liczba

n

akcji, to w skład pakietu

m

będzie wchodzić każda z tych akcji w takich proporcjach,
w jakich występują one na rynku.

Gdy rynek kapitałowy znajduje się w stanie równowagi,

jedynie pakiet rynkowy jest pakietem efektywnym

.

W przypadku zachwiania równowagi np.:

•

wzrost/spadek ceny jednej/części akcji

•

wzrost/spadek dochodu z akcji

•

wzrost/spadek ryzyka w jednej/części akcji

rozpoczyna się proces dostosowawczy, przywracający stan

równowagi:

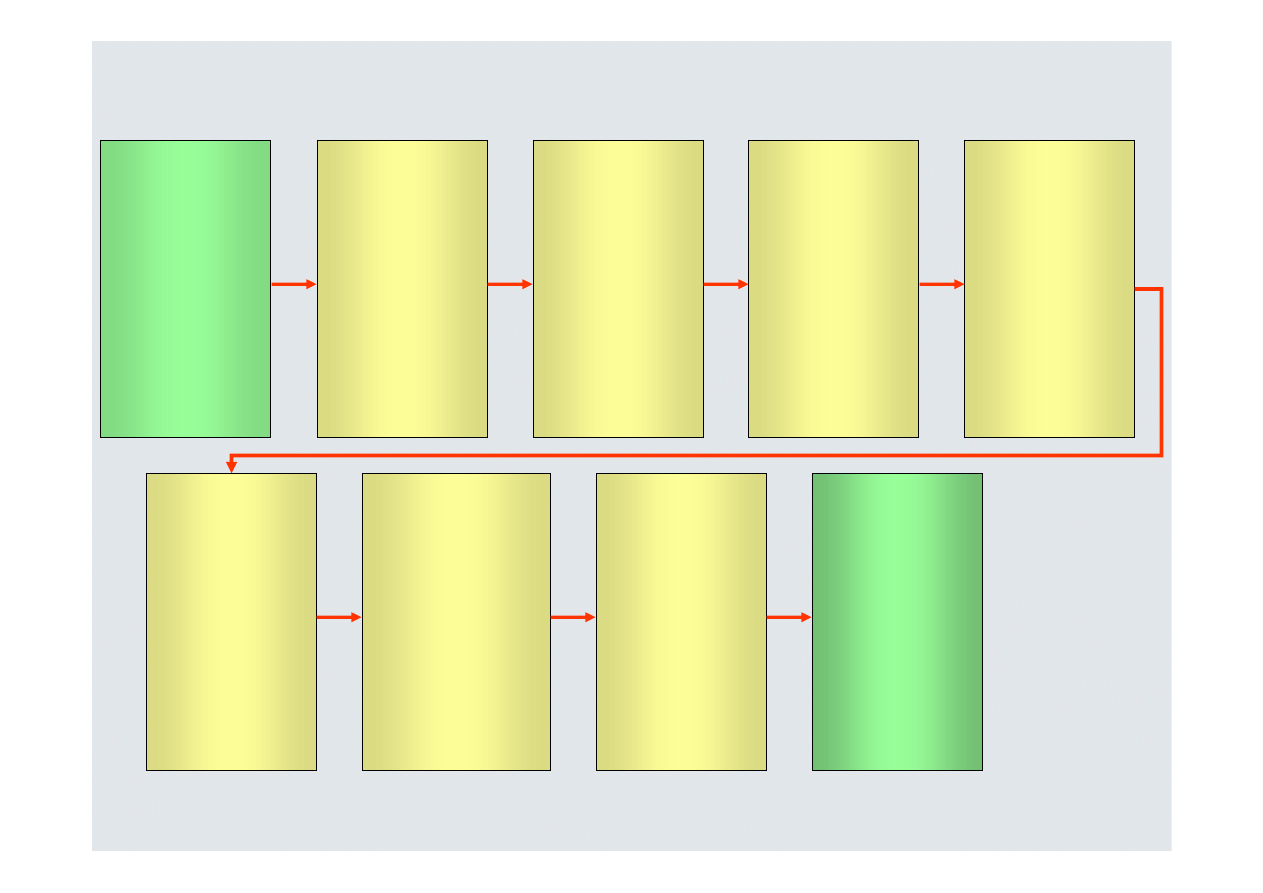
Zachwianie

równowagi

rynku

kapitałowego

Dążenie do

przywrócenia

stanu

równowagi

Oferty kupna

i sprzedaży

papierów

wartościowy

ch

Wszyscy

składają

podobne

oferty:

pojawia się

niedobór

jednych i

nadmiar

drugich

papierów

Zmiana cen

akcji

znajdujących

się na rynku

Zmiana

poziomu

oczekiwanych

stóp dochodu

i ryzyka

Nowy układ

równowagi

Pakietem

efektywnym

jest znowu

pakiet

rynkowy

Stan

równowagi
– pakietem

efektywnym

jest pakiet

rynkowy

Ogólne ryzyko akcji można podzielić na dwie części:

1.

część, którą można wyeliminować odpowiednio kształtując

strukturę portfela

2.

część, której wyeliminować nie można.

Zestawienie efektywnego pakietu złożonego z bardzo znacznej ilości

akcji wg dotychczas przedstawionej metodologii jest bardzo trudne
i wymaga znajomości:

1. oczekiwanych stóp dochodu z poszczególnych akcji,

2. odchyleń standardowych tych stóp dochodu,

3. współczynników korelacji pomiędzy oczekiwanymi stopami

dochodów każdej z możliwych par akcji wchodzących w skład

pakietu.

Zadanie to można bardzo uprościć gdy:

zamiast korelacji pomiędzy poszczególnymi parami akcji

wykorzystamy korelację pomiędzy tymi akcjami a składającym się
z nich pakietem

lub też ogólnym wskaźnikiem charakteryzującym

stan koniunktury

.

Twierdzenie:

zmiany ogólnego stanu koniunktury dotykają w podobny sposób

wszystkie przedsiębiorstwa.

Jednak:

- jakkolwiek stopy dochodu poszczególnych akcji będą wykazywały
wahania o wspólnym kierunku, to skala tych wahań będzie
zróżnicowana, gdyż:

- sprzedaż i zyski różnych przedsiębiorstw nie są jednakowo wrażliwe

na zmiany ogólnego staniu koniunktury,

- wahania stóp dochodu uzależnione są również od specyficznych cech

przedsiębiorstwa (np. jakości zarządzania).

Zatem:

☯

część całkowitej zmienności stóp dochodu

poszczególnych akcji

można przypisać czynnikom o

charakterze ogólnym,

☯

część zaś

czynnikom specyficznym

, wpływającym na

stopę dochodu danego przedsiębiorstwa, a w

konsekwencji i jego akcji.

Wg

W. Sharpe’a

– całkowite ryzyko poszczególnych

akcji można podzielić na dwie części:

1.

część, która jest skorelowana ze zmianami ogólnej

sytuacji gospodarczej, czyli tzw.

ryzyko

systematyczne,

2.

część rezydualna – czyli

ryzyko specyficzne

.

Zależność między oczekiwanymi stopami dochodu pojedynczych akcji a

oczekiwana stopą dochodu pakietu składającego się z tych akcji można wyrazić

za pomocą następującego równania regresji:

e

specyficzn

ryzyko

-

pakietu

dochodu

stopa

oczekiwana

-

x

akcji

dochodu

stopa

oczekiwana

-

y

:

gdzie

)

(

ε

ε

+

=

x

f

y

W ramach pakietów ukształtowanych w racjonalny sposób zmienność
rezydualna stopy dochodu (ryzyko specyficzne)

może być wyeliminowana

całkowicie

- będzie się wzajemnie znosić (gorsze wyniki jednych firm

rekompensowane będą lepszymi wynikami innych firm).

Inwestorzy nie będą

zatem żądać z jego powodu dodatkowego wynagrodzenia

(wyższej

oczekiwanej stopy dochodu).

Zatem:

W warunkach efektywnego rynku kapitałowego tylko ryzyko systematyczne
będzie decydować o poziomie stopy dochodu żądanej przez inwestorów, czyli
wycenie aktywów o zmiennej stopie dochodu!

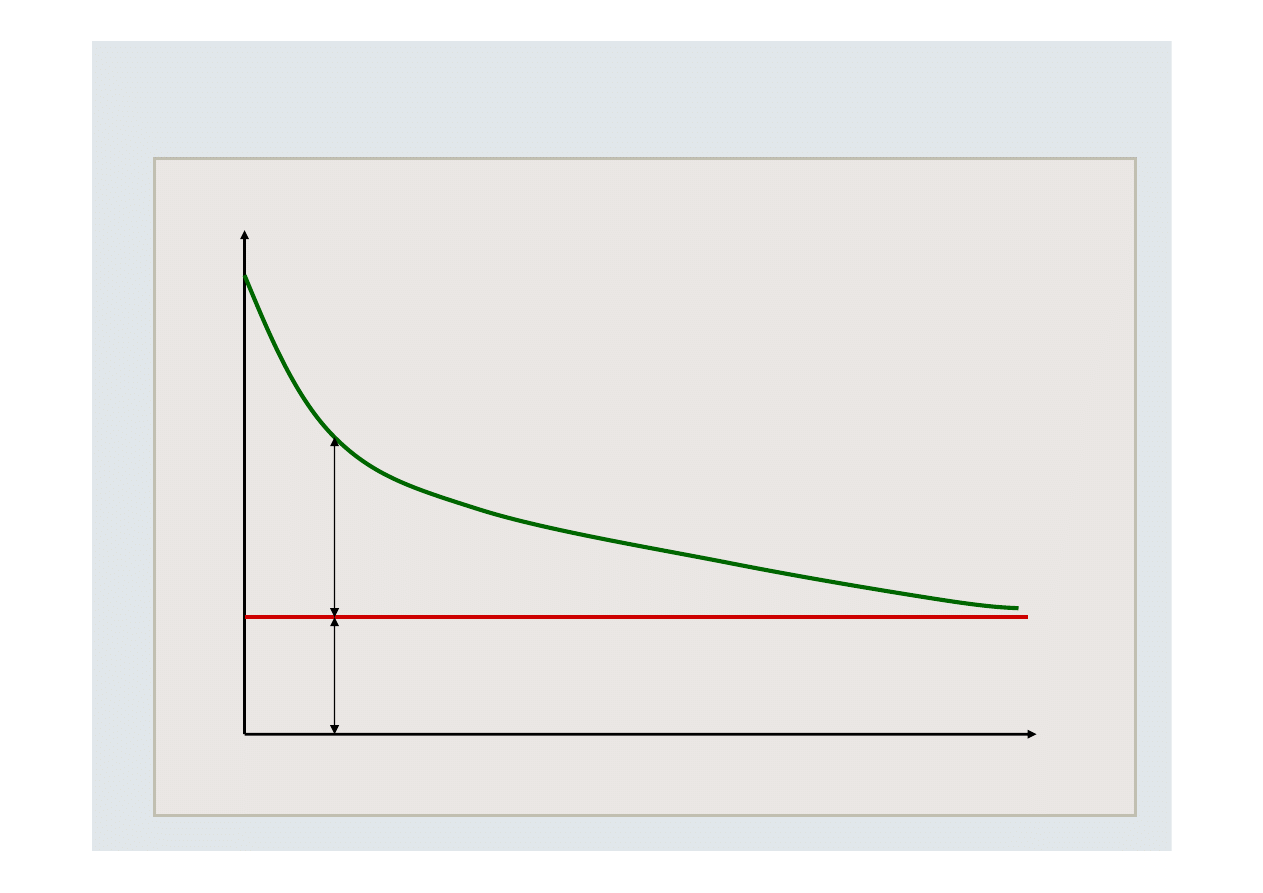
Ryzyko portfela i liczba papierów wartościowych

Ryzyko portfela i liczba papierów wartościowych

:

:

Liczba papierów wartościowych

W

ar

ia

n

cj

a

st

op

y

zw

ro

tu

z

p

or

tf

el

a

Ryzyko systematyczne

Ryzyko specyficzne

Współczynnik regresji β można wyrazić jako:

im

m

i

r

σ

σ

β

=

Współczynnik β wyraża relacje pomiędzy zmianami oczekiwanej stopy

dochodu pakietu rynkowego a zmianami stóp dochodu poszczególnych

akcji wchodzących w jego skład

, przy czym:

a) oczekiwane stopy dochodu akcji, dla których

β = 1

, wykazują taką samą

zmienność jak stopa dochodu pakietu rynkowego,

b) oczekiwane stopy dochodu akcji, dla których

β < 1

, są mniej wrażliwe na

zmiany ogólnej sytuacji gospodarczej,

c) akcje, dla których

β > 1

, są obarczonym większym ryzykiem niż pakiet

rynkowy, a zatem oczekiwania co do ich stopy dochodu będą wyższe.

Jeżeli rynek kapitałowy jest w stanie
równowagi, to oczekiwana stopa
dochodu oraz ryzyko (zmienność
oczekiwanej stopy dochodu mierzona
odchyleniem standardowym)
odpowiadają współrzędnym punktów
leżących na prostej

sml.

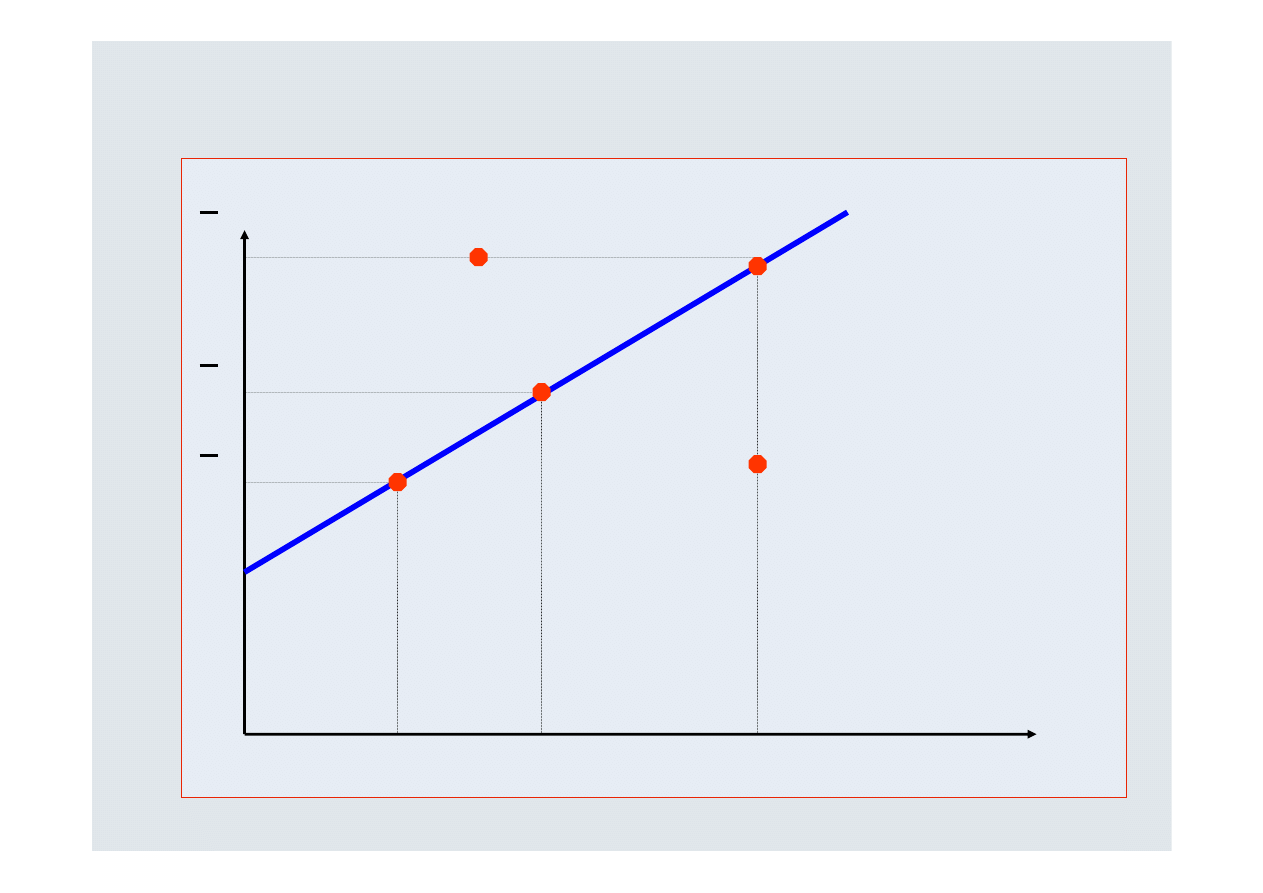
Wykorzystując powyższe obliczenia można przedstawić wykres obrazujący
zależności między analizowanymi zmiennymi

:

0 0,6 1,0 1

0 0,6 1,0 1

,4

,4

k

B

k

m

k

A

R

f

A

m

B

β

Dochód

C

D

sml

Współczynniki

β

i

zostały zdefiniowane jako miary ryzyka

systematycznego poszczególnych akcji (aktywów).

Współczynnik

β

p

portfela

składającego się z różnych akcji (różnych aktywów)

jest średnia ważoną współczynników

β

i

poszczególnych aktywów

(akcji):

∑

=

=

n

i

i

i

p

x

1

β

β

Jeżeli firmę potraktować jako zbiór wyodrębnionych
grup aktywów, to używając powyższych zależności
możemy obliczyć wpływ projektów inwestycyjnych
na współczynnik

β

firmy, a tym samym na:

•

ryzyko systematyczne,

•

koszt kapitału własnego, i

•

średni ważony koszt kapitału.