1

CEL ĆWICZENIA

1

1

Cel ćwiczenia

Celem ćwiczenia jest poznanie własności układów generacyjnych oraz praktyczne zastosowanie wyników nieliniowej
teorii generatorów drgań harmonicznych

2

Przebieg ćwiczenia

2.1

Badanie generatora z regulacją punktu pracy tranzystora

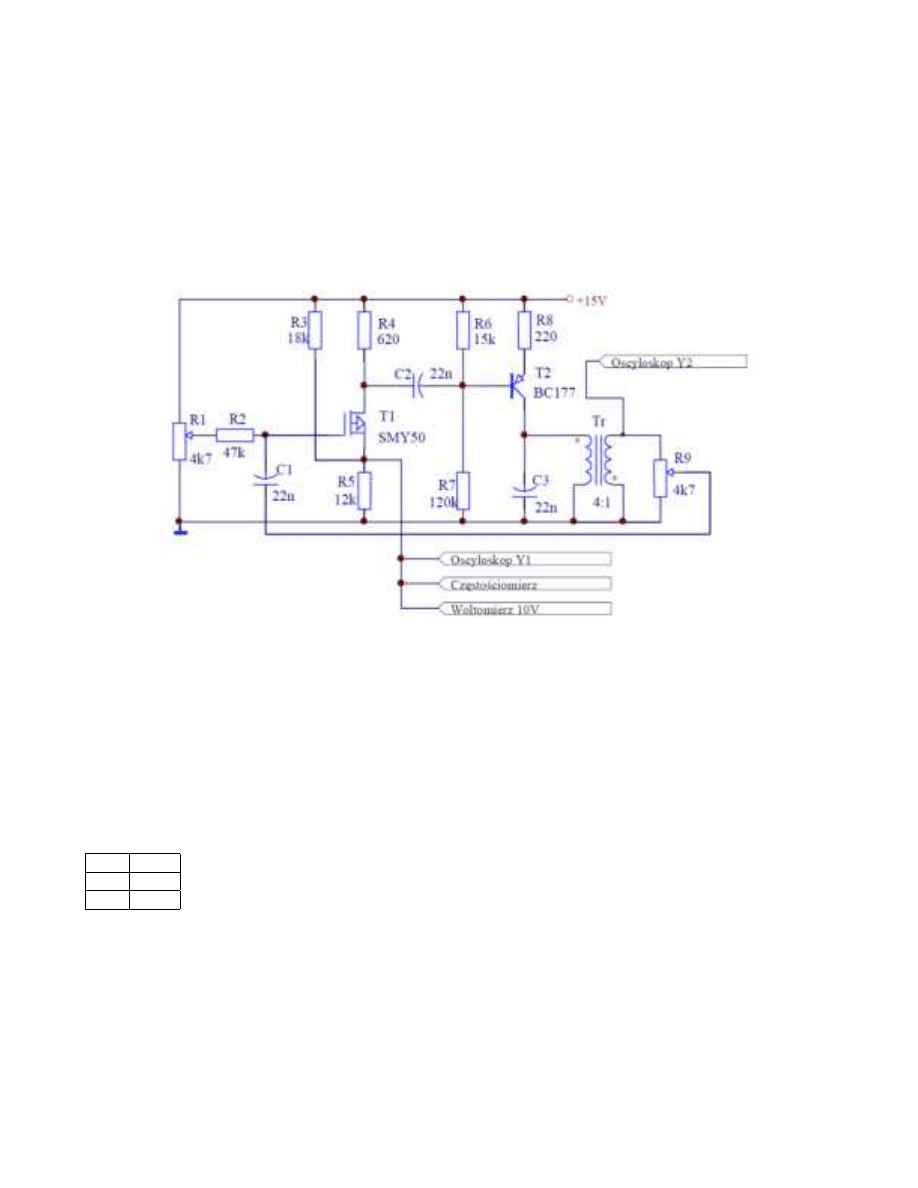
Rysunek 1: generator z regulacja punktu pracy tranzystora R

1

i wzmicnienia w pętli sprzężenia zwrotnego R

9

2.1.1

Badanie wpływu punktu pracy tranzystora na amplitudę drgań generatora.

Po podłączeniu układu jak na rys. 1 ustawiliśmy napięcie zasilania U

z

=10V i dokonaliśmy pomiaru maksymal-

nej i minimalnej wartości napięcia na rezystorze R

5

. Następnie regulując potecionometrem R

1

ustawiamy wartość

napięcia równej średniej arytmetycznej uprzednio pomierzonych napięć i zmieniając położenie potencjometru R1
zmierzyliśmy oscyloskopem napięcie wyjściowe generatora w zależności od napięcia U

R5

(odkładające się na rezy-

storze R

5

.)

Tabela 1:

U

R5

U

W Y

1

6.5

4,5

5

2.1.2

Obserwacja wpływu punktu pracy tranzystora na amplitudę drgań generatora.

Poprzez regulacje wzmocnienia w pętli generatora uzyskaliśmy wzbudzenie, przy zachowaniu niewielkich odkształceń
oscylogramów napięcia. Zmieniając położenie potencjometru R

1

obserwowaliśmy na oscyloskopie napięcie wyjściowe

generatora uzależnione od napięcia U

R5

.

2

PRZEBIEG ĆWICZENIA

2

Tabela 2:

U

R5

[V]

U

W Y

[V]

4

3,8

4,2

7,1

4,8

11,2

5,4

12,6

6,0

11,3

6,4

10,1

7

8,3

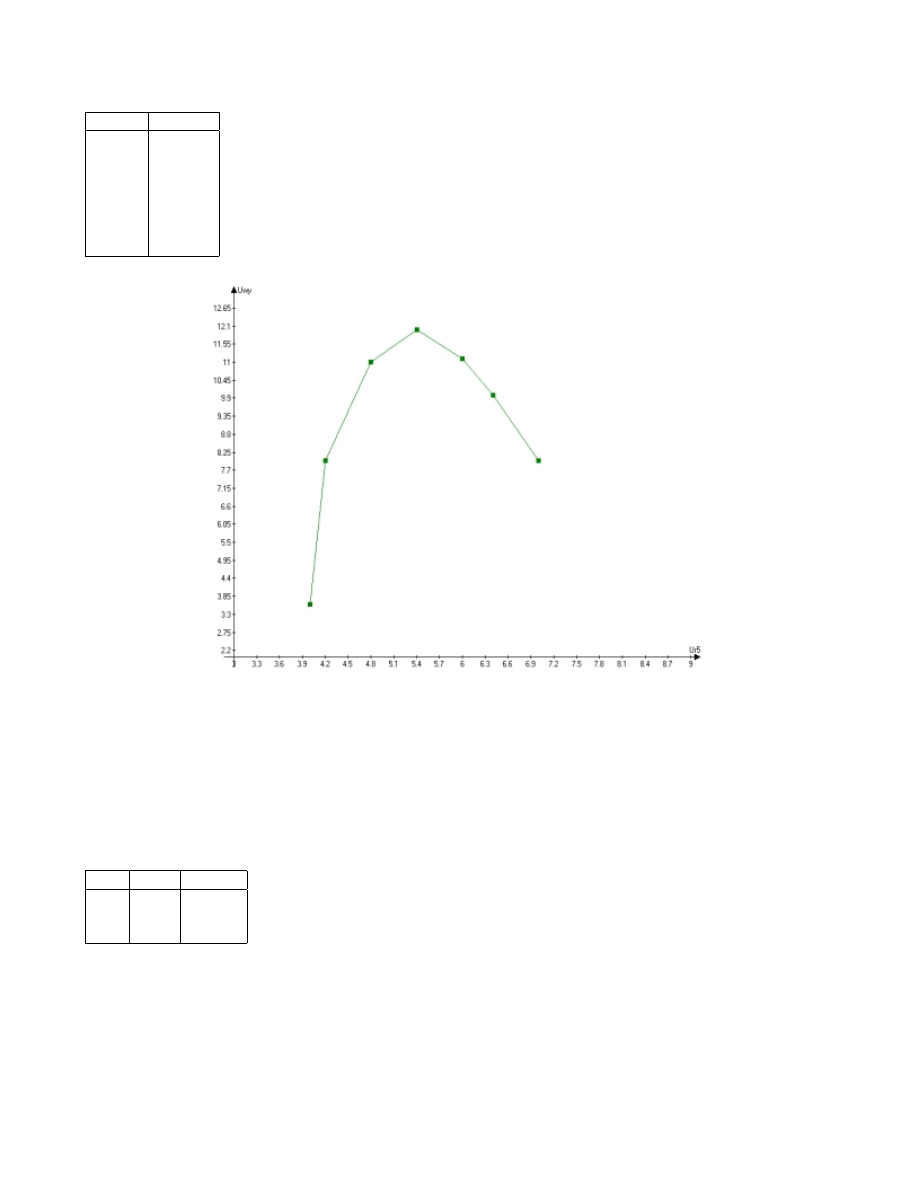
Rysunek 2: Zależność pomiędzy napięciami U

R5

i U

W Y

2.1.3

Badanie wpływu wzmocnienia w pętli sprzężenia zwrotnego na pracę generatora.

Ustawiliśmy układ tak, ażeby generator pracował z maksymalną amplitudą bez dużych zniekształceń. Przy zmianach
wartości dodatniego sprzężenia zwrotnego pomierzyliśmy napięcie U

R5

i napięcie wyjściowe generatora U

W Y

, oraz

częstotliwość f

Tabela 3:

U

R5

U

W Y

f[kHz]

1,5

10

109.515

3,5

18

108.694

5,9

17,5

108.521

2.1.4

Badanie wpływu wzmocnienia w pętli sprzężenia zwrotnego na stałość częstotliwości genera-
tora.

Ustawiliśmy generator w stanie granicznego wzbudzenia i dokonaliśmy pomiaru częstotliwości dla 2 napięć U

z

=8,9

i 10 V.

2

PRZEBIEG ĆWICZENIA

3

Tabela 4:

f

8

[kHz]

f

9

[kHz]

f

10

[kHz]

∆f

f

[%]

108,194

108,382

108,525

0,13

106,298

107,102

107,404

0,17

2.2

Badanie generatora z ujemną rezystancją.

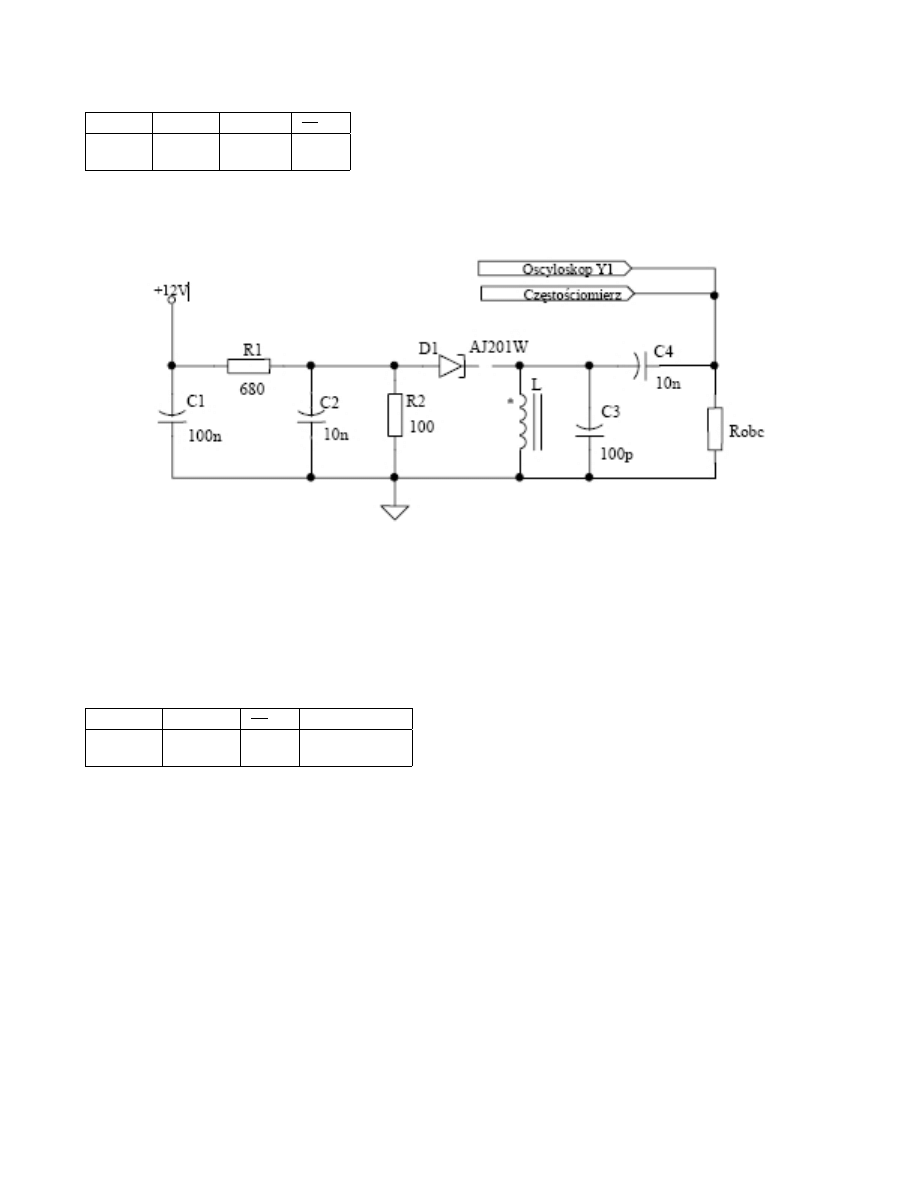
Rysunek 3: Generator z diodą tunelową.

2.2.1

Badanie stałości częstotliwości generatorów

Dokonaliśmy pomiaru częstotliwość generatora przy napięciu zasilania 10V i 9V dla obciążenia rezystorem R

obc

=

1kΩ jak i bez obciążenia. Tabela zawiera wartości średnie częstotliwości.

Tabela 5:

f

9

[M Hz]

f

10

[MHz]

∆f

f

[%]

2,418

2,501

3,43

z obciążeniem

2,439

2,518

3,23

bez obciążenia

2

PRZEBIEG ĆWICZENIA

4

2.3

Generator z dzieloną pojemnością (Colpitts’a)

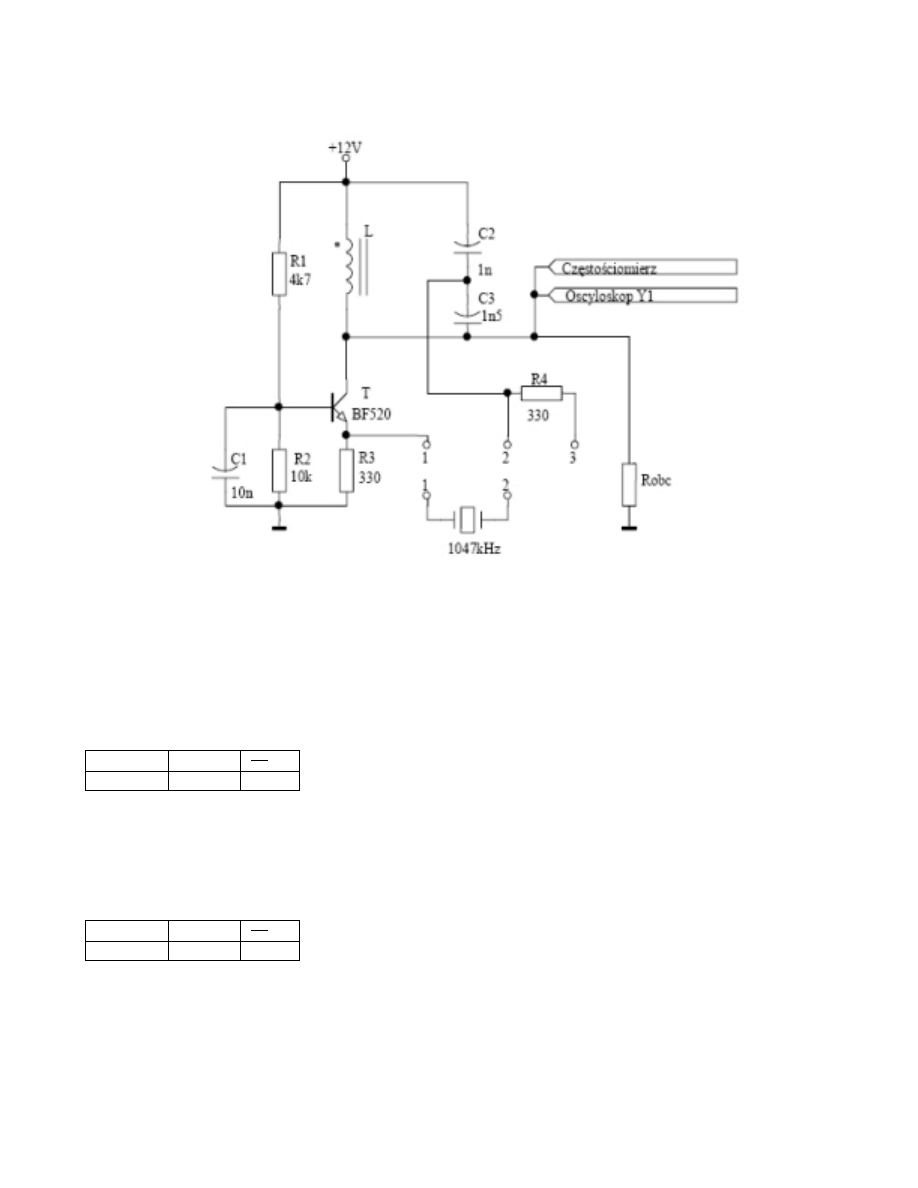
Rysunek 4: Generator z dzieloną pojemnością

2.3.1

Badanie generatora z silnym sprzężeniem.

Połączyliśmy układ jak na rys. 2. i następnie zwarliśmy zaciski 1-2. Dla napięć wejściowych 9V i 10V pomierzyliśmy
częstotliwości generatora. Tabela zawiera wartości średnie częstotliwości.

Tabela 6:

f

10

[M Hz]

f

9

[MHz]

∆f

f

[%]

1,14677

1,14013

0,58

2.3.2

Badanie generatora ze słabym sprzężeniem

Powtórzyliśmy powyższy krok dla zwartych zacisków 1-3. Tabele zawiera wartości średnie częstotliwości.

Tabela 7:

f

10

[M Hz]

f

9

[MHz]

∆f

f

[%]

1,11618

1,11374

0.21

2.3.3

Badanie generatora z rezonatorem kwarcowym.

2

PRZEBIEG ĆWICZENIA

5

Tabela 8: dla zwartych zacisków 1-2

f

10

[M Hz]

f

9

[MHz]

∆f

f

[%]

1,15541

1,15541

0

1,15542

1,15541

0

Tabela 9: dla zwartych zacisków 1-3

f

10

[M Hz]

f

9

[MHz]

∆f

f

[%]

1,14449

1,14602

-0,13

2.4

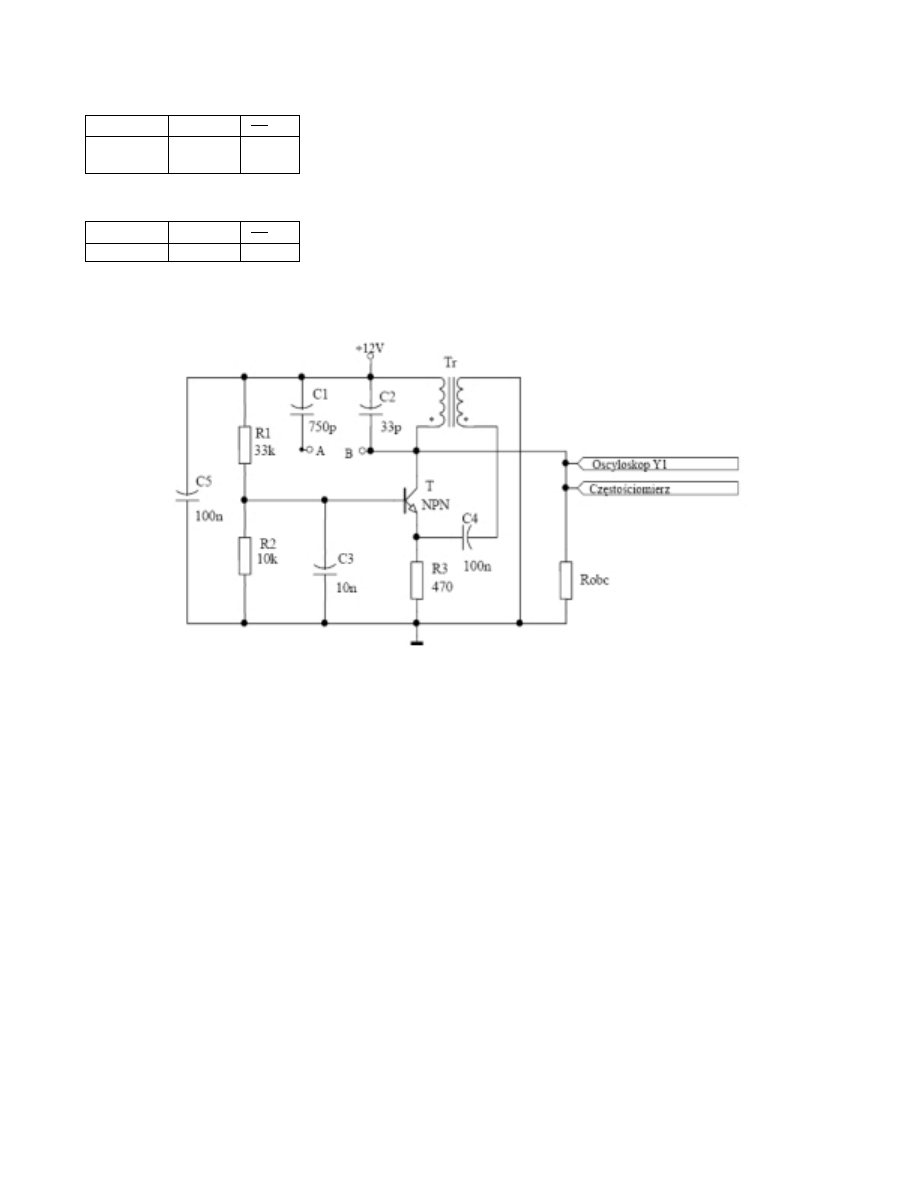
Badanie generatora ze sprzężeniem transformatorowym (Meissnera).

Rysunek 5: Generator ze sprzężeniem transformatorowym

2.4.1

Badanie wpływu pojemności obwodu rezonansowego na stałość częstotliwości generatora.

Połączyliśmy układ jak na rys. 3. Dla napięcia zasilania 9V i 10V zmierzyliśmy częstotliwości generatora.

3

WNIOSKI

6

Tabela 10:

f

10

[kHz]

f

9

[kHz]

∆f

f

[%]

3,139

3,153

-0,44

3

Wnioski

W przeprowadzony ćwiczeniu wykorzystaliśmy następujące generatory: –z transformatorem realizującym sprzęże-
nie zwrotne. Jest to generator sygnału sinusoidalnego. Na oscylogramach można zaobserwować, wpływ na wartości
generowanego przebiegu, zmiana wartości napięcia zasilania, jak i wartości wzmocnienia w pętli sprzężenia zwrotne-
go. –z ujemną rezystancją. Dla diody tunelowej pracującą w punkcie pracy zapewniającym jej ujemną rezystancję
dynamiczną; Zachodzi równanie różniczkowe obwodu, którego rozwiązanie liniowe pozwala sformułować wniosek, że
gdy straty mocy w obwodzie rezonansowym są kompensowane przez ujemna rezystancja - to mamy do czynienia z
drganiami niegasnącymi. –Colpittsa który to składa się z jednostopniowego wzmacniacza pracującego w konfiguracji
wspólnego emitera z pętlą sprzężenia zwrotnego (obwód rezonansowy), –Meissnera w którym to sprzężenie zwrotne
zostało realizowane poprzez transformator (przesunięcie fazy - 180). Uzwojenie wtórne tworzy obwód rezonansowy.
Parametry tego obwodu (L i C) definiują częstotliwość drgań.

Analizując otrzymane wyniki pod kątem wpływu zmiany częstotliwości pod wpływem zmiany napięcia, zaobserwo-
waliśmy że najmniejsza zmiana zachodzi dla generatora Colpittsa w którym został wykorzystany rezonator kwar-
cowy. Jest to zgodne z oczekiwaniami - rezonator kwarcowy wykorzystywany jest jako stabilizator częstotliwości.

Wykres zależności pomiędzy napięciami U

R5

i U

W Y

, jest zbliżony do teoretycznego przebiegu tej, że charakte-

rystyki. Prawdopodobnie otrzymalibyśmy większe podobieństwo gdybyśmy dysponowali większa ilością pomiarów
(wygładzenie charakterystyki)

Rysunek 6: przykładowy oscylogram - napięcie bez zakłóceń