HYDROLOGIA,

METEOROLOGIA

I KLIMATOLOGIA

Cz. II – HYDROLOGIA

W 6 – Wody podziemne 3

M. Nawalany

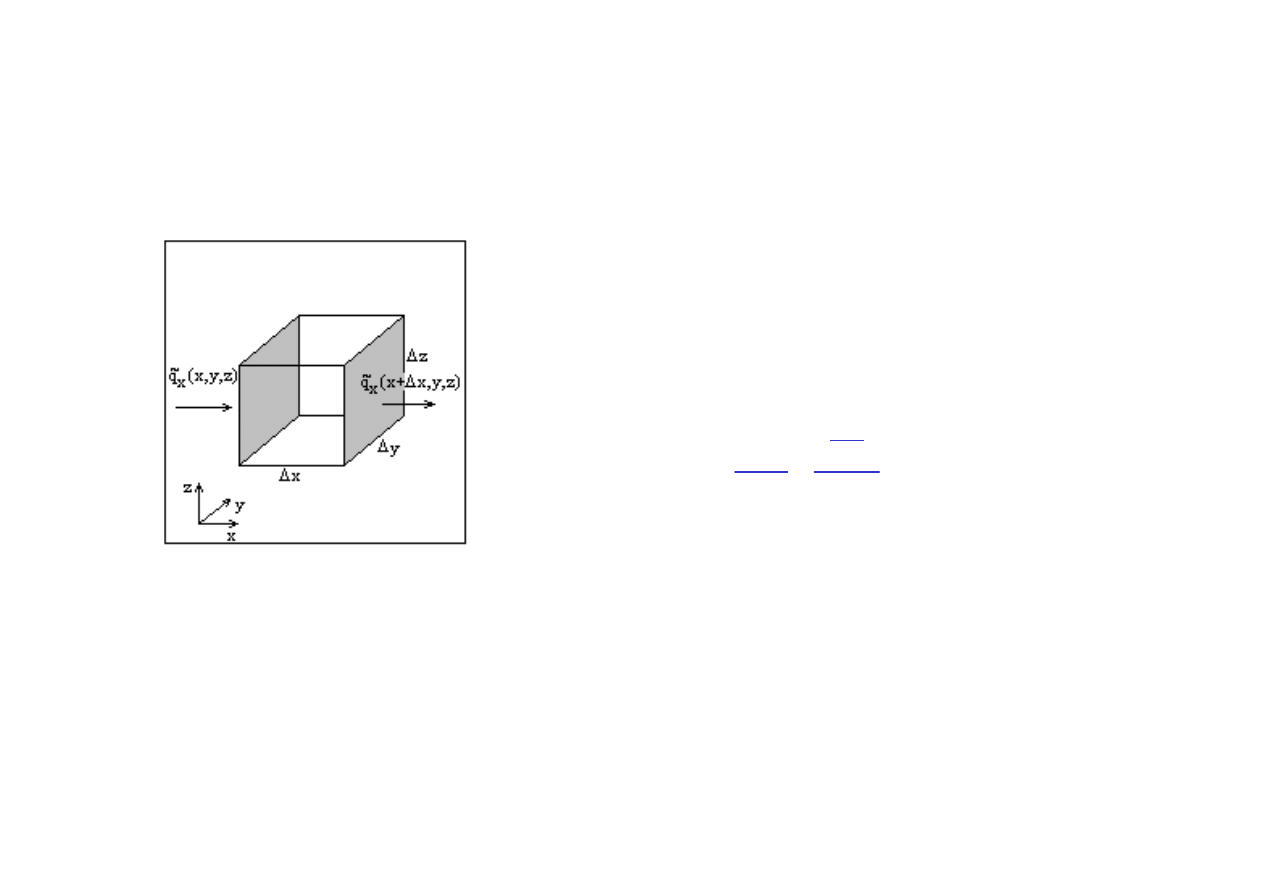
Prawo zachowania masy

Objętość kontrolna, stan ustalony:

- składowa x strumienia masy wody

x

q~

⎥

⎦

⎤

⎢

⎣

⎡

=

2

~

m

S

M

q

s

kg

gdzie:

M [kg/s]

– wydatek (przepływ) masowy

S [m

2

]

– pole powierzchni przez którą

przepływa wydatek M

Prawo zachowania masy – c.d.

Związek pomiędzy strumieniem masowym a strumieniem
objętościowym q :

q~

ρ

q

q~

⋅

=

gdzie:

ρ

[kg/m

3

] – gęstość cieczy.

Prawo ciągłości dla ośrodków porowatych ma postać:

( )

( )

q~

div

t

n

−

=

∂

ρ

∂

Z postaci tej widać, że woda może być gromadzona w ośrodku albo
wskutek zmiany gęstości, albo wskutek zmiany geometrii ośrodka, czyli
zmiany wartości n.

Przypadki prawa ciągłości

1. Płyn nieściśliwy (

ρ

= const.), brak zmian geometrii ośrodka:

czyli:

2. Przypadek ogólny:

( )

0

q

div

=

0

z

q

y

q

x

q

z

y

x

=

∂

∂

+

∂

∂

+

∂

∂

( )

( )

q~

div

t

n

−

=

∂

ρ

∂

Człon

reprezentuje nadmiar masy wpływającej nad masą

wypływająca z elementarnej objętości w jednostce czasu.

( )

q

div ~

−

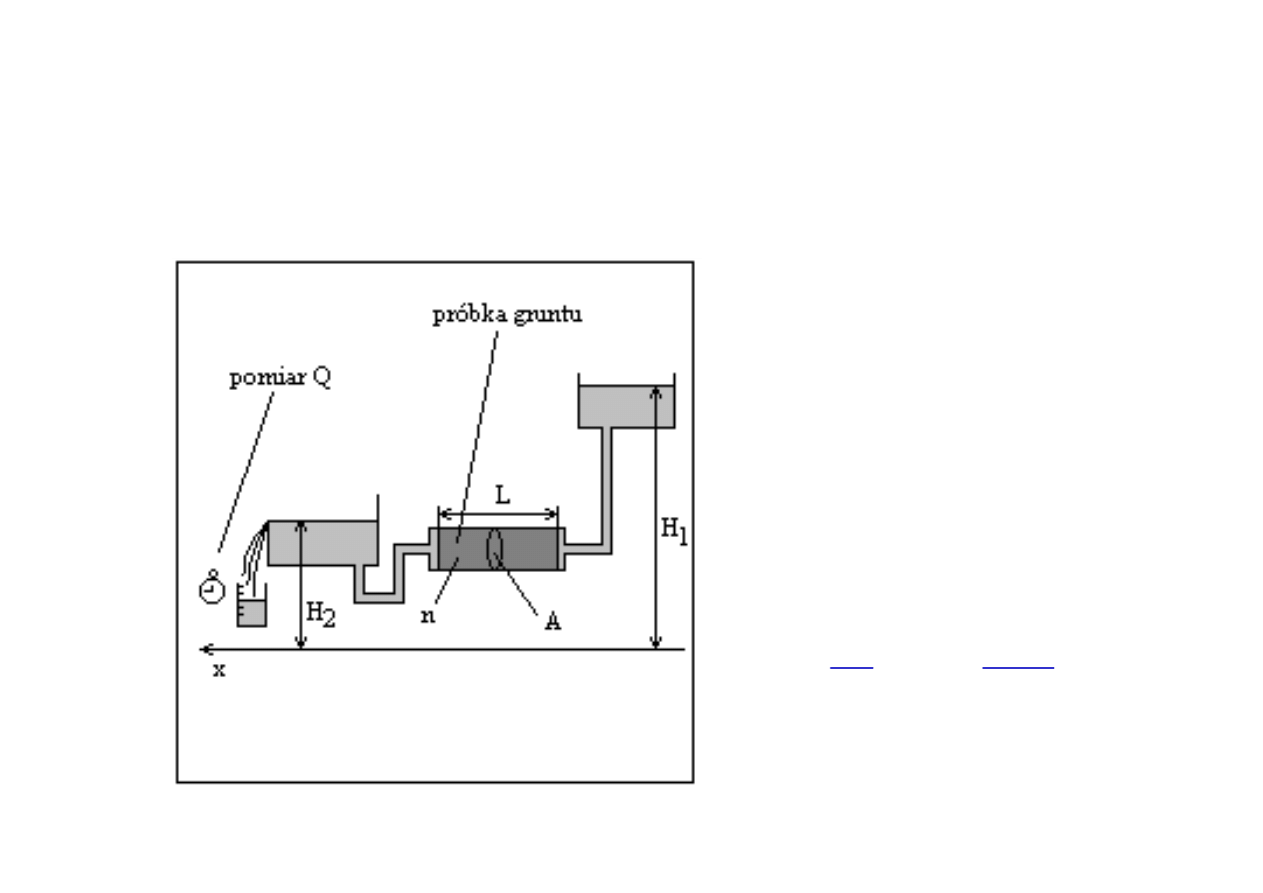
Prawo Darcy

Eksperyment Darcy:

W doświadczeniu
zaobserwowano, że:

Q ~ A,

Q ~

∆H = H

2

– H

1

,

Q ~ 1/L

Wynika stąd, że:

L

H

k

A

Q

q

∆

∆

−

=

=

Prawo Darcy – c.d.

Prawo Darcy w najprostszej postaci :

z

k

q

z

z

∂

Φ

∂

−

=

x

k

q

x

x

∂

Φ

∂

−

=

y

k

q

y

y

∂

Φ

∂

−

=

Równanie przepływu wód podziemnych

Po wstawieniu prawa Darcy do prawa ciągłości otrzymuje się
trójwymiarowe równanie przepływu dla wód podziemnych:

⎟

⎠

⎞

⎜

⎝

⎛

∂

Φ

∂

∂

∂

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

Φ

∂

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

Φ

∂

∂

∂

=

∂

Φ

∂

z

k

z

y

k

y

x

k

x

t

S

z

y

x

S

Dwuwymiarowe przybliżenie płaskie przepływu wód podziemnych:

)

(

)

(

~

~

~

2

1

z

q

z

q

y

T

y

x

T

x

t

S

z

z

y

x

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

Φ

∂

∂

∂

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

Φ

∂

∂

∂

=

∂

Φ

∂

gdzie:
S [-]

– współczynnik wodopojemności sprężystej: S = S

S

l

,

T

i

[m

2

/s]

– współczynnik przewodności hydraulicznej: T

i

= k

i

l

(

)

(

)

∫

Φ

=

Φ

2

1

z

z

dz

t

,

z

,

y

,

x

~

l

1

t

,

y

,

x

~

–

wysokość hydrauliczna uśredniona po

miąższości warstwy wodonośnej

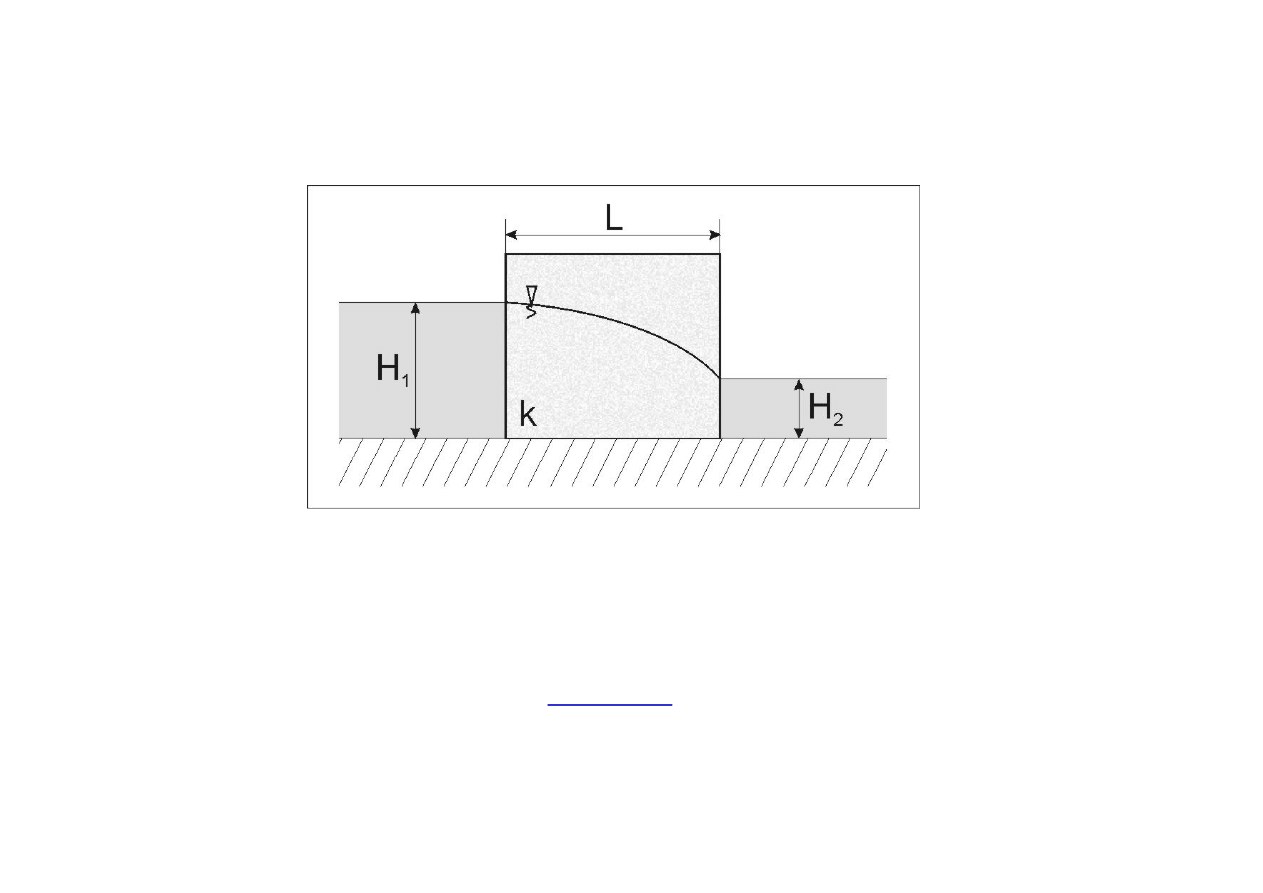
Przykład – dopływ do rowu

Dla przepływu ze swobodnym zwierciadłem T = k H. Ustalony przepływ
swobodny jednowymiarowy w jednorodnej warstwie wodonośnej przy braku
zasilania infiltracyjnego oraz podsiąku opisany jest prostym równaniem Laplace’a.

0

x

)

x

(

H

2

2

2

=

∂

∂

Przykład – dopływ do rowu – c.d.

C

Bx

x

H

+

=

)

(

2

Rozwiązanie ogólne ma postać:

Dla rozpatrywanego równania i warunków brzegowych H(0) = H

1

, H(L)

= H

2

- parametry B oraz C wynoszą odpowiednio:

,

2

1

2

2

L

H

H

B

−

=

2

1

H

C

=

Stąd rozwiązanie szczególne:

2

1

2

1

2

2

2

)

(

H

x

L

H

H

x

H

+

−

=

Rozwiązanie to nazywa się PARABOLĄ DUPUITA.

Dopływ do rowu wyznaczony z paraboli Dupuita wynosi:

x

x

H

Dk

x

x

H

x

DkH

Q

x

∂

∂

−

=

∂

∂

−

=

)

(

2

1

)

(

)

(

~

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

L

H

H

kD

Q

x

2

2

2

1

2

~

Równanie transportu masy w strumieniu wód podziemnych

Mechanizmy transportu masy wyrażone jako strumienie masy (kg/m

2

/s):

1.

Transport adwekcyjny

2.

Transport dyfuzyjny

3.

Transport dyspersyjny

VC

J

adw

=

x

C

D

J

dyf

x

dyf

∂

∂

−

=

y

C

D

J

dyf

y

dyf

∂

∂

−

=

z

C

D

J

dyf

z

dyf

∂

∂

−

=

x

C

D

J

dysp

xx

x

dysp

∂

∂

−

=

,

y

C

D

J

dysp

yy

y

dysp

∂

∂

−

=

,

z

C

D

J

dsp

zz

z

dysp

zz

∂

∂

−

=

,

,

Po podstawieniu sumy trzech strumieni do prawa zachowania masy:
równanie transportu masy w wodach podziemnych.

r

C

V

z

C

V

y

C

V

x

z

C

D

z

y

C

D

y

x

C

D

x

t

C

z

y

x

zz

yy

xx

+

∂

∂

−

∂

∂

−

∂

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

=

∂

∂

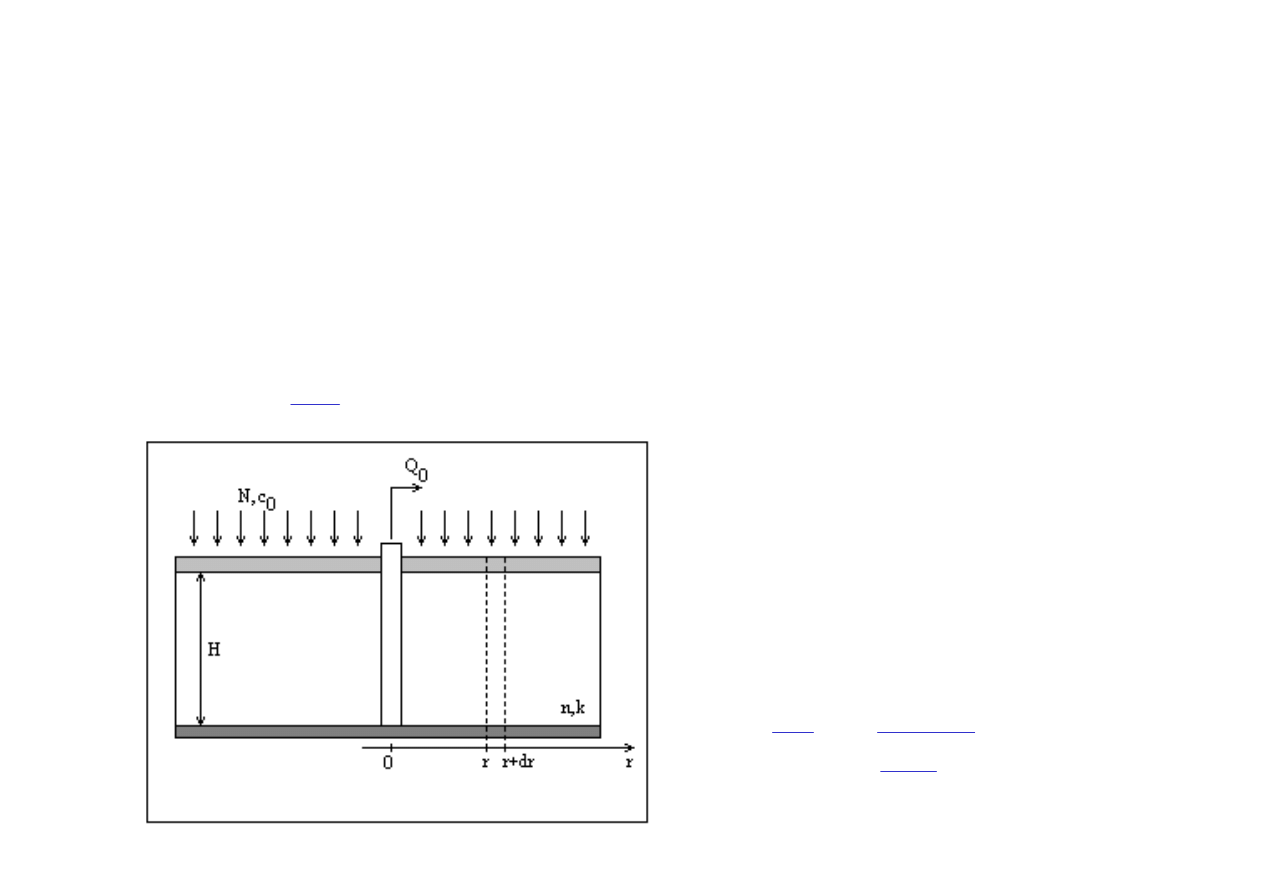
Przykład – dopływ zanieczyszczeń do studni

Dana jest studnia zupełna ujmująca wodę w obszarze rolniczym z warstwy
wodonośnej o zwierciadle napiętym. Warstwa wodonośna jest jednorodna i
izotropowa. Zasilanie pochodzi z wód opadowych. Wody te infiltrując wymywają
z powierzchni pestycydy używane do ochrony roślin. W warstwie wodonośnej
pestycydy ulegają biodegradacji zgodnie z prawem rozpadu:

( )

t

exp

C

)

t

(

C

0

λ

−

=

Czyli:

5

.

0

2

ln

T

=

λ

gdzie: - okres

połowicznego rozpadu.

5

.

0

T

Dane są: H, n, k, T

0.5

, Q

0

, c

0

.

Poszukuje się stężenia wody
pobieranej przez studnię przy
założeniu, że jedynym
mechanizmem transportu masy
pestycydu jest adwekcja.

1

N

Hn

1

c

Q

M

c

0

0

w

+

λ

=

=

Stężenie pestycydu w wodzie
pobieranej w studni wynosi:

[kg/m

3

]