WYDZIAŁ ETI PG

Katedra Systemów Elektroniki Morskiej

Technika obliczeniowa i symulacyjna

- laboratorium

MATLAB i SPICE jako narzędzia do obliczania

prądów, napięć i mocy

w obwodzie elektrycznym prądu sinusoidalnego

Numeryczne rozwiązywanie równań liniowych

Materiały do ćwiczenia nr 7

Opracował: Czesław Stefański

m. in na podstawie

materiałów dra W. Szkudlińskiego

Gdańsk 2015

C. Stefański

2/11

Ostatnia modyfikacja: maj 2016

1. Wstęp

Niniejsze ćwiczenie jest ostatnim, które jest poświęcone wdrożeniu umiejętności obliczania prądów i napięć w ob-

wodzie przy wykorzystaniu narzędzia MATLAB z jego algorytmami numerycznego rozwiązywania układów równań linio-
wych oraz nabyciu sprawności w korzystaniu z symulacyjnego narzędzia Micro̵CAP (jedna z „odmian” SPICE’a)

1

. Jednak

tym razem będziemy starali się zastosować zdobyte już umiejętności do analizy obwodów pobudzanych przebiegami
sinusoidalnymi. Wykorzystamy w tym celu wszystkie dotąd stosowane podejścia, łącznie z metodą tableau z poprzed-
niego ćwiczenia

2

.

Po raz ostatni przypominamy, że przy tworzeniu algorytmów analizy automatycznej (komputerowej) wygodnie

jest trzymać się zasady, że każdy dwójnik ma „swój” prąd i „swoje” napięcie, przeciwnie względem siebie zastrzałkowane (czyli sto-
sujemy tzw. strzałkowanie skojarzone). Przez to algorytmy stają się bardziej jednorodne i dzięki temu zwykle są szybsze mimo większej
niż przy strzałkowaniu „chaotycznym” liczby niewiadomych.

Przypominamy, że na rysunkach 1 mamy do czynienia z tzw. skojarzonym strzałkowaniem prądów i napięć – polega ono na tym,

że zwrot spadku napięcia na każdym z elementów obwodu jest przeciwny do kierunku przepływającego przez ten element prądu.

i

0

i

1

i

2

i

3

E

0

R

1

R

2

R

3

u

0

u

2

u

3

u

1

J

5

u

5

i

5

i

1

i

2

i

3

i

4

E

1

R

2

R

3

R

4

u

1

u

3

u

4

u

2





t

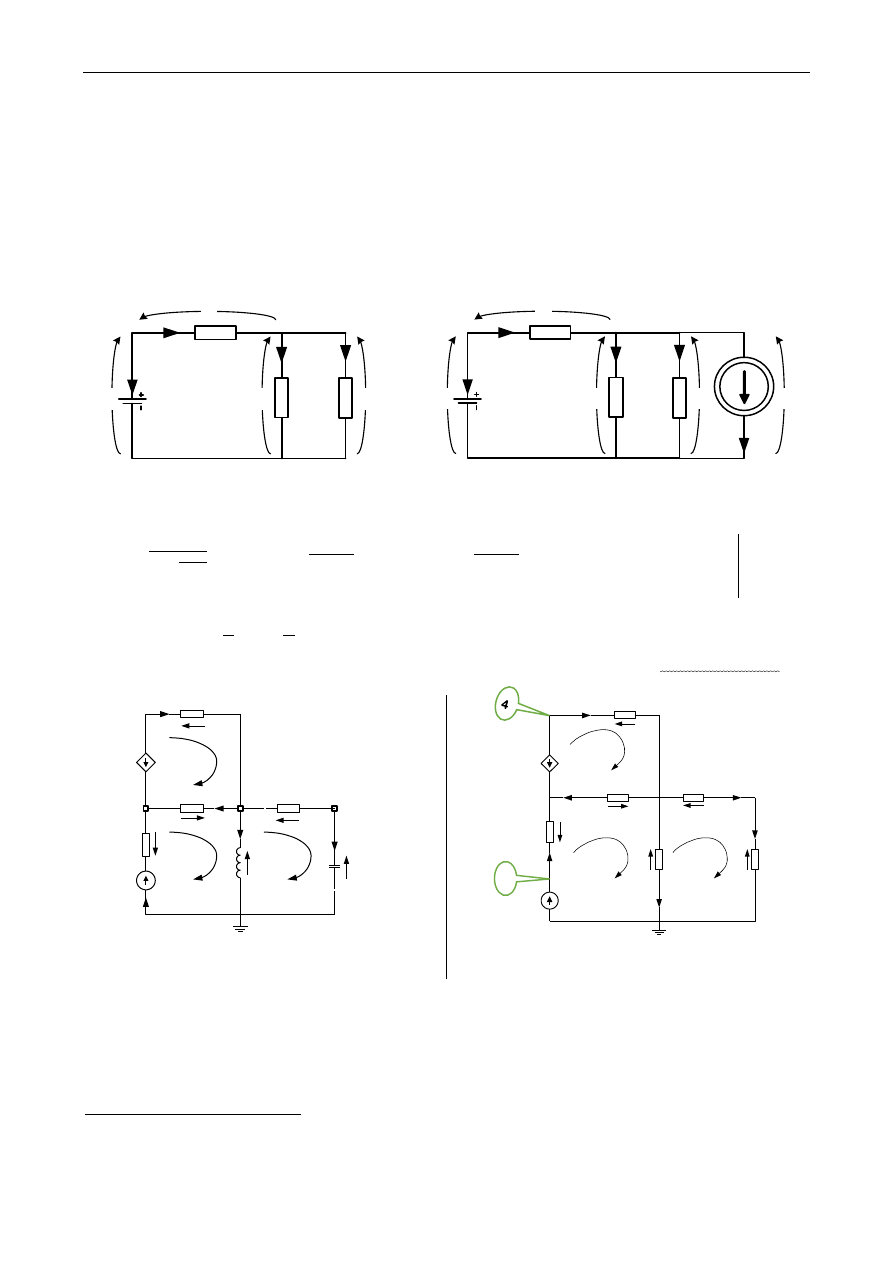
Rys. 1a. Prosty obwód prądu stałego

Rys. 1b. Przykład strzałkowania skojarzonego

Dla obwodu z rys. 1a, opierając się na naszej dotychczasowej wiedzy dotyczącej analizy stałoprądowej otrzymujemy prądy oraz

napięcia:

𝑖

1

=

𝐸

𝑅

1

+

1

𝐺

2

+𝐺

3

,

𝑖

2

=

𝐺

2

𝐺

2

+ 𝐺

3

⋅ 𝑖

1

,

𝑖

3

=

𝐺

3

𝐺

2

+ 𝐺

3

⋅ 𝑖

1

,

𝑖

0

= −𝑖

1

,

(1)

𝑢

1

= 𝑅

1

⋅ 𝑖

1

,

𝑢

2

= 𝑅

2

⋅ 𝑖

2

,

𝑢

3

= 𝑅

3

⋅ 𝑖

3

,

𝑢

0

= 𝐸,

gdzie

𝐺

2

=

1

𝑅

2

i 𝐺

3

=

1

𝑅

3

.

2. Poszukiwanie prądów, napięć i mocy w rozbudowanym obwodzie elektrycznym prądu zmiennego

1

s

e

)

(t

e

1

R

2

R

4

R

3

R

5

L

6

C

)

(

1

t

i

o

)

(

2

t

i

o

)

(

3

t

i

o

)

(

1

t

i

)

(

2

t

i

)

(

3

t

i

)

(

4

t

i

)

(

5

t

i

)

(

4

1

t

i

r

e

s





t

E

t

e

e

m



cos

)

(









)

(

1

t

u

)

(

2

t

u

)

(

3

t

u

)

(

4

t

u

)

(

6

t

u

)

(

5

t

u

Rys. 2. Badany obwód prądu sinusoidalnie zmiennego

.

1

R

2

R

3

R

4

R

5

Z

.

.

6

Z

1

I

m

E

1

s

E

2

I

3

I

4

I

01

I

5

I

6

I

02

I

03

I

3

R

U

1

R

U

2

U

4

U

5

U

6

U

1

2

3

Rys. 3. Model obwodu z rys. 2 dla zespolonych ampli-

tud prądów i napięć

3

Najpierw analizować będziemy obwód o strukturze jak na rysunku 2. Zmiana jego klasyfikacji nie polega jedynie na

tym, że mamy w nim cewkę indukcyjną i kondensator, ale wynika przede wszystkim z charakteru przebiegu napięcia
wytwarzanego przez jedyne w tym obwodzie źródło niezależne. W obwodzie prądu sinusoidalnego, znajdującego się
w stanie ustalonym, przedstawione w (1) związki między prądem i napięciem przyjmują postać wyrażeń wiążących wiel-
kości zespolone:

1

Narzędzie to, po „narysowaniu” obwodu w jego oknie graficznym przez użytkownika, potrafi automatycznie, acz bez ujawniania ich użytkownikowi,

utworzyć odpowiednie równania opisujące obwód, rozwiązać je (podobnymi jak MATLAB algorytmami) i udostępnić rozwiązania między innymi we
wspomnianym oknie z obwodem.

2

podejście z gałęzią uogólnioną, jako wymagające przekształcenia obwodu (dlaczego? ZNSP) pozostawiamy Czytelnikowi do samodzielnej realizacji,

natomiast tu, w dalszej części wykorzystamy pewną sztuczkę w postaci podejścia iteracyjnego

3

Węzły 4 i 5, dodatkowo zaznaczone, zostaną wykorzystane w metodzie tableau.

5

C. Stefański

3/11

Ostatnia modyfikacja: maj 2016

𝑈̂

𝑘

= 𝑍

𝑘

⋅ 𝐼̂

𝑘

lub równoważnie

𝐼̂

𝑘

= 𝑌

𝑘

⋅ 𝑈̂

𝑘

(2)

gdzie

𝑍

𝑘

= 𝑅

𝑘

dla 𝑘 = 1, 2, 3, 4, 𝑍

5

= 𝐣𝜔

𝑒

𝐿

5

, 𝑌

6

= 𝐣𝜔

𝑒

𝐶

6

, 𝑌

𝑘

=

1

𝑍

𝑘

dla 𝑘 = 1, 2, 3, 4, 5, 6.

𝑍

5

i 𝑍

6

nazywamy impedancjami odpowiednio cewki 𝐿5 i kondensatora 𝐶6, w takim sensie 𝑍

𝑘

jest impedancją opornika

𝑅𝑘 dla 𝑘 = 1, 2, 3, 4. Natomiast 𝑌

𝑘

=

1

𝑍

𝑘

jest admitancją elementu 𝑘. Jednostką impedancji jest om (Ω), a jednostką

admitancji jest simens (S). Wielkości „daszkowane” są nazywane amplitudami zespolonymi przebiegów sinusoidalnych
lub wskazami tych przebiegów. Niosą one informację o amplitudzie (moduł wskazu) i fazie (argument wskazu) sinusoi-
dalnego przebiegu czasowego, z którym są „spowinowacone”. W dalszej części instrukcji, powodowani wygodą nota-
cyjną, pomijamy daszki nad oznaczeniami wskazów.

Zakładając, że w obwodzie występuje stan ustalony, możemy w miejsce rys. 2 wprowadzić do rozważań model dla

zespolonych amplitud prądów i napięć, przedstawiony na rys. 3.

Metoda oczkowa

Na podstawie rys. 3, można zapisać układ równań oczkowych dla wielkości zespolonych

[

𝑅

1

+ 𝑅

2

+ 𝑍

5

−𝑍

5

−𝑅

2

−𝑍

5

𝑅

4

+ 𝑍

5

+ 𝑍

6

0

−𝑅

2

𝑟

𝑅

2

+ 𝑅

3

] ⋅ [

𝐼

𝑜1

𝐼

𝑜2

𝐼

𝑜3

] = [

𝐸

𝑚

0
0

]

(3)

gdzie 𝐼

𝑜1

, 𝐼

𝑜2

, 𝐼

𝑜3

to amplitudy zespolone sinusoidalnych prądów 𝑖

𝑜1

(𝑡), 𝑖

𝑜2

(𝑡), 𝑖

𝑜3

(𝑡).

Metoda potencjałów węzłowych

1

W odniesieniu do analizy wskazowej klasyczna, niezmodyfikowana metoda potencjałów węzłowych „nienawidzi”

sytuacji, gdy w obwodzie występują inne elementy, niż w tym zdaniu wymienione, czyli: niezależne źródła prądowe,
źródła prądowe sterowane napięciem oraz impedancje. Wprowadzenie pojęcia gałęzi uogólnionych rozszerza zakres
stosowania tej metody o niezależne źródła napięciowe, o ile znajdą się w dobrym towarzystwie (sąsiedztwie).

Otóż uogólniona gałąź obwodu to grupa elementów tworząca strukturę – dwójnik złożony pokazany na rysunku 4.

Taki dwójnik złożony utworzony jest w ogólności ze źródła prądu, źródła napięcia oraz elementu 𝐵

𝑘

. Jednak konkretna

uogólniona gałąź obwodu może równie dobrze składać się z trzech, dwóch lub tylko z jednego z elementów pokazanych
na rysunku 4. Gałąź uogólnioną stosujemy po to, by graf obwodu wskazowego, którego definicja, analogiczna do grafu
obwodu stałoprądowego, jest nieco dalej podana, zawierał mniej gałęzi, a macierze opisu sieci miały mniejsze rozmiary,
ale także po to, by – bez dodatkowego przekształcania obwodu – można było metodą węzłową analizować sieci zawie-
rające niezależne źródła napięciowe.

~

k

U

k

I

~

k

I

k

U

k

J

k

E

.

.

k

B

Rys. 4. Uogólniony dwójnik (gałąź o numerze 𝒌) obwodu

Element 𝐵

𝑘

widoczny na rysunku 4, to na ogół po prostu impedancja 𝑍

𝑘

, ale może być to również źródło prądowe

𝐼

𝑘

= 𝑦

𝑘𝑙

⋅ 𝑈

𝑙

sterowane napięciem wskazowym 𝑈

𝑙

występującym na elemencie 𝐵

𝑙

gałęzi uogólnionej o numerze 𝑙.

Wszystko jest analogiczne do przypadku stałoprądowego opisanego w instrukcjach do ćwiczeń 3 i 4, przeto tam

odsyła się Czytelnika.

Dla obwodu o 𝑏 gałęziach uogólnionych oraz (𝑛 + 1) węzłach węzły numerujemy tak, by węzeł odniesienia (masy)

miał numer zero, a pozostałe węzły numery od 1 do 𝑛. Wtedy napięcia (wskazowe) i prądy (wskazowe) w takich gałę-
ziach można przedstawić w formie następujących wektorów kolumnowych:

𝑼

̃ = col(𝑈̃

1

, 𝑈̃

2

, … , 𝑈̃

𝑏

),

𝑼 = col(𝑈

1

, 𝑈

2

, … , 𝑈

𝑏

),

𝑬 = col(𝐸

1

, 𝐸

2

, … , 𝐸

𝑏

)

(4)

𝑰̃ = col(𝐼̃

1

, 𝐼̃

2

, … , 𝐼̃

𝑏

),

𝑰 = col(𝐼

1

, 𝐼

2

, … , 𝐼

𝑏

),

𝑱 = col(𝐽

1

, 𝐽

2

, … , 𝐽

𝑏

),

𝑽 = col(𝑉

1

, 𝑉

2

, … , 𝑉

𝑛

),

gdzie 𝑽, to wektor potencjałów węzłowych czyli potencjałów 𝑛 węzłów w odniesieniu do potencjału węzła odniesienia
(czyli węzła o numerze zero).

Do rozważań będzie nam potrzebna także kwadratowa macierz admitancji gałęziowych 𝒀

𝑏×𝑏

wiążąca prądy 𝐼

𝑘

ele-

mentów 𝐵

𝑘

z napięciami 𝑈

𝑙

elementów 𝐵

𝑙

obwodu następującym równaniem:

1

Zagadnienie opracowane przez dra Witolda Szkudlińskiego na podstawie pracy L.O. Chua, Pen-Min Lin : Komputerowa analiza układów elektronicz-

nych, WNT 1981.

C. Stefański

4/11

Ostatnia modyfikacja: maj 2016

𝑰 = 𝒀

𝑏×𝑏

⋅ 𝑼 .

(5a)

Ta macierz o wielu elementach zerowych ma wymiary macierzy 𝑏×𝑏 i zawiera na głównej przekątnej admitancje dwój-
ników 𝑌

𝑘

= 1/𝑍

𝑘

oraz poza główną przekątną, elementy 𝑦

𝑘𝑙

, czyli parametry źródeł sterowanych. Przykładowo dla ob-

wodu z rysunku 3 mamy

𝒀

6×6

=

[

𝐺

1

0

0

0

0

0

0

𝐺

2

0

0

0

0

0

0

𝐺

3

0

0

0

0

0

0

𝐺

4

0

0

0

0

0

0

𝑌

5

0

0

0

0

0

0 𝑌

6

]

,

(5b)

o ile do problemu podejdziemy iteracyjnie, to znaczy przyjmiemy, że źródło sterowane 𝐸𝑠1 w kolejnych krokach traktu-
jemy jako niezależne, o wartości 𝐸𝑠1[𝑘] = 𝑟 ⋅ 𝐼

4

[𝑘 − 1], gdzie 𝑘 jest numerem kroku obliczeniowego.

Zwykła obserwacja struktury z rysunku 4, prowadzi do następujących zapisów macierzowych dla całego obwodu złożo-
nego z 𝑏 gałęzi (𝑘 = 1, 2, … . , 𝑏):

𝑼

̃ = 𝑼 − 𝑬 , 𝑰̃ = 𝑰 − 𝑱 .

(6)

Wektory 𝑬 oraz 𝑱 dla przykładowego obwodu z rys. 2 (b=6) są następujące:

𝑬[𝑘] = col[𝐸

1

, 0, −𝑟 ⋅ 𝐼̃

4

[𝑘 − 1], 0, 0, 0],

(6a)

𝑱[𝑘] = col[ 0, 0, 0, 0, 0, 0],

(6b)

bo, jak widać ze wzorów (6) i (6b), w każdym kroku 𝐼

4

= 𝐼̃

4

. Ponadto założymy 𝐼

4

[0] = 0.

Pewne uproszczenie i jednocześnie ułatwienie spojrzenia na właściwości strukturalne obwodu daje nam przedstawienie struktury w
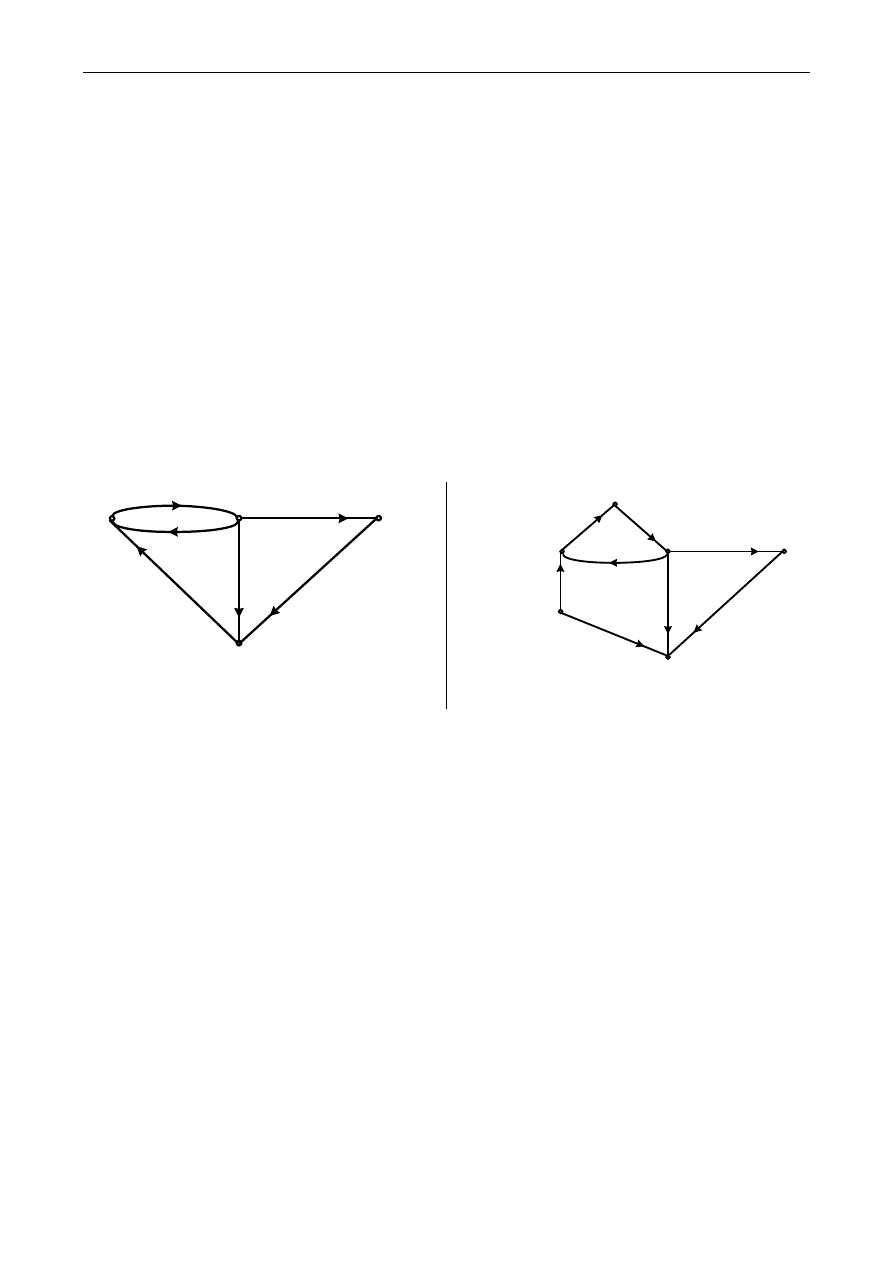
postaci grafu; graf obwodu z rys. 2 jest przedstawiony na rysunku 5 poniżej.

j

k

⓪

l

3

2

5

6

4

1

Rys. 5. Graf prądowy obwodu z rys. 3

(przy gałęziach uogól-

nionych)

j

k

⓪

l

3

2

5

6

4

1

7

8

m

n

Rys. 6. Graf prądowy obwodu z rys. 3

(bez gałęzi uo-

gólnionych; 𝐼

7

= 𝐼(𝐸

𝑠1

), 𝐼

8

= 𝐼(𝐸

𝑚

))

Graf ten odzwierciedla połączenie sześciu gałęzi (typu jak na rysunku 4) w czterech węzłach obwodu. Konkretny wierzchołek grafu
odpowiada wzajemnie jednoznacznie konkretnemu węzłowi obwodu, zaś konkretna krawędź grafu odpowiada wzajemnie jedno-
znacznie konkretnej uogólnionej gałęzi obwodu. Relacja incydencji wierzchołków i krawędzi grafu jest identyczna jak między ich od-
powiednikami w obwodzie. Wreszcie kierunki krawędzi grafu są identyczne jak przyjęte za dodatnie kierunki przepływu prądów 𝐼̃

𝑘

przez gałęzie obwodu.
Grafy prądowe można przedstawiać graficznie, jak na rysunku 5, ale można też zapisywać je równoważnie w postaci macierzy incy-
dencji. Częściej wykorzystuje się tzw. zredukowaną macierz incydencji, którą otrzymuje się z pełnej macierzy incydencji przez skreśle-
nie jednego wiersza macierzy pełnej (w analizie obwodów ten skreślany wiersz odpowiada węzłowi odniesienia). Ze zredukowanej
macierzy incydencji można bez trudu odtworzyć macierz pełną (jak?), zatem obie macierze niosą tę samą informację o grafie prądo-
wym.

Graf z rysunku 5, przy założeniu, że węzeł  obwodu jest węzłem odniesienia, stanowi podstawę do zapisania jego zredukowa-

nej macierzy incydencji 𝑨 (dalej nazywanej krótko macierzą incydencji)

"

A

= [

−1 -1

1

0 0 0

0

1 −1

1 1

0

0

0

0 −1 0 1

] .

(7)

gdzie:

𝑎

𝑘𝑙

= 1 w przypadku, gdy prąd w gałęzi o numerze „𝑙” wypływa z węzła „𝑘”,

𝑎

𝑘𝑙

= −1 w przypadku, gdy prąd w gałęzi o numerze „𝑙” wpływa do węzła „𝑘”,

𝑎

𝑘𝑙

= 0 w przypadku, gdy gałąź o numerze „𝑙” nie łączy się z węzłem „𝑘”.

Jednocześnie, prądy i napięcia we wszystkich gałęziach obwodu złożonego z 𝑏 gałęzi (na przykład o postaci jak na rysunku 4) oraz

𝑛 węzłów niezależnych i węzła odniesienia, podlegają prawom Kirchhoffa, które można przedstawić za pomocą następujących zapi-
sów macierzowych

𝑨 ⋅ 𝑰̃ = 𝟎

(8)

𝑼

̃ = 𝑨

𝑻

⋅ 𝑽

gdzie 𝑨

𝑻

to transponowana macierz incydencji .

Stosunkowo krótkie przekształcenia w obrębie wzorów (6-7) dają w efekcie

𝒀

𝒏×𝒏

⋅ 𝑽 = 𝑱

𝒏

(9)

gdzie:

C. Stefański

5/11

Ostatnia modyfikacja: maj 2016

𝒀

𝒏×𝒏

= 𝑨 ⋅ 𝒀

𝒃×𝒃

⋅ 𝑨

𝑻

,

𝑱

𝒏

= 𝑨 ⋅ 𝑱 − 𝑨 ⋅ 𝒀

𝒃×𝒃

⋅ 𝑬.

Rozwiązaniem układu równań (9) są potencjały wszystkich (niezależnych) 𝑛 węzłów obwodu i prądów dwójniko-

wych. Powrót do drugiego z równań (8) pozwala z kolei na otrzymanie wszystkich napięć na gałęziach uogólnionych
obwodu. Natomiast napięcia na elementach „admitancyjnych” (czyli na elementach typu 𝐵

𝑘

) obwodu uzyskamy na pod-

stawie równania (6).

Metoda tableau

W metodzie tableau przyjmujemy, że każdy dwójnik jest rozpięty pomiędzy parą węzłów (nie korzystamy z gałęzi

uogólnionych). Dlatego wykorzystamy numerację węzłów od zerowego (odniesienia/masy) do piątego z rysunku 3.
Wtedy graf prądowy dla sytuacji z tego rysunku może wyglądać jak na rysunku 6, pod warunkiem, że problemu podej-
dziemy iteracyjnie, to znaczy przyjmiemy, że źródło sterowane 𝐸𝑠1 (gałąź 7 grafu) w kolejnych krokach traktujemy
jako niezależne, o wartości 𝐸𝑠1[𝑘] = 𝑟 ⋅ 𝐼

4

[𝑘 − 1], gdzie 𝑘 jest numerem kroku obliczeniowego.

Graf z rysunku 6, przy założeniu, że węzeł  obwodu jest węzłem odniesienia, stanowi podstawę do zapisania jego

zredukowanej macierzy incydencji 𝑨 (dalej nazywanej krótko macierzą incydencji)

"

A

=

[

-1 -1

0

0 0 0 1 0

0

1 -1

1 1 0 0 0

0

0

0 -1 0 1 0 0

0

0

1

0 0 0 1 0

1

0

0

0 0 0 0 1]

.

(8)

Dla obwodu o 𝑏 gałęziach oraz (𝑛 + 1) węzłach [dla obwodu z rysunku 3 mamy 𝑏 = 8 i 𝑛 = 5] węzły numerujemy

tak, by węzeł odniesienia (masy) miał numer zero, a pozostałe węzły numery od 1 do 𝑛. Wtedy napięcia i prądy w takich
gałęziach można przedstawić w formie następujących wektorów kolumnowych:

𝑼 = col(𝑈

1

, 𝑈

2

, … , 𝑈

𝑏

),

(9)

𝑰 = col(𝐼

1

, 𝐼

2

, … , 𝐼

𝑏

),

𝑽 = col(𝑉

1

, 𝑉

2

, … , 𝑉

𝑛

),

gdzie 𝑽, to wektor potencjałów węzłowych czyli potencjałów 𝑛 węzłów w odniesieniu do potencjału węzła odniesienia
(czyli węzła o numerze zero).

Prądy (wskazowe) i napięcia (wskazowe) we wszystkich gałęziach obwodu złożonego z 𝑏 gałęzi (na przykład o po-

staci jak na rysunku 3) oraz 𝑛 węzłów niezależnych i węzła odniesienia, podlegają prawom Kirchhoffa, które można
przedstawić za pomocą następujących zapisów macierzowych

𝑨 ⋅ 𝑰 = 𝟎

(10)

𝑼 = 𝑨

𝑻

⋅ 𝑽

gdzie 𝑨

𝑻

to transponowana macierz incydencji.

Do pełnego opisu obwodu brakuje równań opisujących zachowanie się elementów; dla oporników są to równania prawa
Ohma, dla niezależnych idealnych źródeł napięciowych równania postaci 𝑈

𝐸

= 𝐸, itd. Takich równań powinno być łącz-

nie 𝑏. W zapisie macierzowym można im nadać formę

𝑴 ⋅ 𝑰 + 𝑵 ⋅ 𝑼 = 𝑬𝒙𝒄,

(11)

gdzie 𝑴 = [𝑚

𝑖𝑗

]

𝑏×𝑏

, 𝑵 = [𝑛

𝑖𝑗

]

𝑏×𝑏

, 𝑬𝒙𝒄 = col(𝑒𝑥

1

, 𝑒𝑥

2

, … , 𝑒𝑥

𝑏

).

Na przykład, gdy element o numerze 𝑘 jest opornikiem o oporze 𝑅

𝑘

, to 𝑚

𝑘𝑘

= 𝑅

𝑘

, 𝑛

𝑘𝑘

= −1, 𝑒𝑥

𝑘

= 0, co odpo-

wiada (pod warunkiem, że 𝑚

𝑘𝑗

= 𝑛

𝑘𝑗

= 0 dla 𝑗 ≠ 𝑘) zapisowi prawa Ohma dla tego elementu w postaci

𝑅

𝑘

⋅ 𝐼

𝑘

− 𝑈

𝑘

= 0.

Podobnie, gdy element o numerze 𝑙 jest źródłem prądowym o SPM 𝐽

𝑙

, to 𝑚

𝑙𝑙

= 1, 𝑛

𝑙𝑙

= 0, 𝑒𝑥

𝑘

= 𝐽

𝑙

, co odpowiada

(pod warunkiem, że 𝑚

𝑙𝑗

= 𝑛

𝑙𝑗

= 0 dla 𝑗 ≠ 𝑙) zapisowi definicyjnego równania dla tego elementu w postaci

1 ⋅ 𝐼

𝑙

− 0 ⋅ 𝑈

𝑙

= 𝐽

𝑙

(założono, że strzałki 𝐼

𝑙

oraz 𝐽

𝑙

są zgodne).

Ponieważ mogą występować w analizie wskazowej impedancje indukcyjności oraz admitancje pojemności, więc rozsze-
rzamy zakres tego, co może się mieścić pod współczynnikami macierzy 𝑴 oraz 𝑵.

Na przykład, gdy element o numerze 𝑘 jest induktorem o impedancji 𝑍

𝑘

, to 𝑚

𝑘𝑘

= 𝑍

𝑘

, 𝑛

𝑘𝑘

= −1, 𝑒𝑥

𝑘

= 0, co od-

powiada (pod warunkiem, że 𝑚

𝑘𝑗

= 𝑛

𝑘𝑗

= 0 dla 𝑗 ≠ 𝑘) zapisowi (na wskazach) prawa Ohma dla tego elementu w po-

staci

𝑍

𝑘

⋅ 𝐼

𝑘

− 𝑈

𝑘

= 0.

podobnie, gdy element o numerze 𝑘 jest kondensatorem o admitancji 𝑌

𝑙

, to 𝑚

𝑙𝑙

= −1, 𝑛

𝑙𝑙

= 𝑌

𝑙

, 𝑒𝑥

𝑘

= 0, co odpo-

wiada (pod warunkiem, że 𝑚

𝑙𝑗

= 𝑛

𝑙𝑗

= 0 dla 𝑗 ≠ 𝑙) zapisowi (na wskazach) prawa Ohma dla tego elementu w postaci

𝑌

𝑙

⋅ 𝑈

𝑙

− 𝐼

𝑙

= 0.

Powyższe równania macierzowe dają się zapisać w postaci

[

𝑨

𝟎

𝟎

𝟎

𝑨

𝑇

−𝟏

𝑴 𝟎

𝑵

] ⋅ [

𝑰

𝑽

𝑼

] = [

𝟎
𝟎
𝑬𝒙𝒄

] .

(12)

Macierz kwadratowa z ostatniego równania nosi nazwę macierzy tableau.
Powyższe równanie może być łatwo przekształcone do postaci

C. Stefański

6/11

Ostatnia modyfikacja: maj 2016

[𝑨

𝟎

𝑴 𝑵⋅𝑨

𝑇

] ⋅ [𝑰

𝑽

] = [𝟎

𝑬𝒙𝒄

] .

(13)

Rozwiązaniem układu równań (13) są potencjały wszystkich (niezależnych) 𝑛 węzłów obwodu i prądów dwójniko-

wych. Powrót do drugiego z równań (10) pozwala z kolei na otrzymanie wszystkich napięć na gałęziach obwodu.

Wbrew pozorom, procedury rozwiązywania układów równań postaci (3), (9), czy (13) nie różnią się w zasadniczy

sposób od przypomnianych w rozdziale 3 reguł postępowania wcześniej stosowanych dla układów równań ze współ-
czynnikami i zmiennymi rzeczywistymi. Przypomniano je w punkcie 3. Rezultatem rozwiązania będzie wektor liczb ze-
spolonych. Każda z tych liczb jest amplitudą zespoloną pewnego sygnału kosinusoidalnego. Każdą z otrzymanych zespo-
lonych amplitud wykorzystamy w ten sposób, że jej moduł będzie stanowił amplitudę kosinusoidalnego prądu o często-
tliwości kątowej (pulsacji) 𝜔

𝑒

, zaś faza jest jednocześnie przesunięciem fazowym kosinusoidy prądu w relacji do kosinu-

soidalnego napięcia 𝑒(𝑡).

Moc w obwodach prądu sinusoidalnego

Jeżeli w każdym elemencie obwodu natężenie prądu i napięcie są sinusoidalne o następującej ogólnej postaci:

𝑢(𝑡) = 𝑈

𝑚

cos(𝜔𝑡 + 𝜑

𝑢

)

𝑖(𝑡) = 𝐼

𝑚

cos(𝜔𝑡 + 𝜑

𝑖

)

(14)

to, jak wiemy, zapisane powyżej przebiegi mogą być reprezentowane przez następujące, niezależne od czasu, wielkości
zespolone zwane wskazami

𝑈 = 𝑈

𝑚

𝐞

𝐣𝜑

𝑢

𝐼 = 𝐼

𝑚

𝐞

𝐣𝜑

𝑖

(16)

Oprócz prądu i napięcia, z każdym elementem obwodu (o impedancji 𝑍) jest związane pojęcie mocy, które dla obwodu
sinusoidalnego można rozpisać na następujące składowe:

 moc czynną 𝑃

𝑐

:

𝑃

𝑐

= Re(𝑃

𝑧

) =

1
2

𝐼

𝑚

2

⋅ Re(𝑍) =

1
2

𝑈

𝑚

2

⋅ Re(𝑌

∗

) [W],

(16)

 moc bierną 𝑃

𝑏

:

𝑃

𝑏

= Im(𝑃

𝑧

) =

1
2

𝐼

𝑚

2

⋅ Im(𝑍) =

1
2

𝑈

𝑚

2

⋅ Im(𝑌

∗

) [var],

(16)

gdzie

𝑃

𝑧

oznacza moc zespoloną:

𝑃

𝑧

=

1
2

𝑈 ⋅ 𝐼

∗

= 𝑃

𝑐

+ 𝐣𝑃

𝑏

[VA].

(17)

Definiuje się też moc pozorną

𝑃

𝑝

= abs(𝑃

𝑧

) = √𝑃

𝑐

2

+ 𝑃

𝑏

2

[VA]

1

.

(18)

Moc czynna jest równa mocy średniej za okres 𝑇 sinusoidy napięcia , czy też prądu:

𝑃

𝑐

= 𝑝(𝑡)

̅̅̅̅̅̅ =

1
𝑇

∫

𝑢(𝑡) ⋅ 𝑖(𝑡)

𝑡

𝑜

+𝑇

𝑡

𝑜

.

(19)

Warto też dodać, że występujące w żelazku zjawisko zamiany energii elektrycznej na ciepło jest wynikiem niezero-

wej mocy czynnej dla rezystancyjnej spirali grzejnej (idealne kondensatory i cewki indukcyjne się nie rozgrzewają).

Bilans mocy w obwodzie prądu sinusoidalnego

Spójrzmy na zagadnienie bilansu najpierw ogólnie, pamiętając, że dla prądów i napięć gałęzi obwodu wskazowego

mieliśmy zależności (patrz wzory (10)):

𝑨 ⋅ 𝑰 = 𝟎, 𝑼 = 𝑨

𝑻

⋅ 𝑽.

Wykorzystamy je w następujących rachunkach:

2 ⋅ ∑𝑃

𝑧

= 𝑼

𝑇

⋅ 𝑰

∗

= (𝑨

𝑻

⋅ 𝑽)

𝑇

⋅ 𝑰

∗

= (𝑽

𝑻

⋅ 𝑨) ⋅ 𝑰

∗

= 𝑽

𝑻

⋅ (𝑨 ⋅ 𝑰

∗

) = 𝑽

𝑻

⋅ (𝑨 ⋅ 𝑰)

∗

= 𝑽

𝑻

⋅ 𝟎

∗

= 0 ,

(20a)

∑𝑃

𝑧

= ∑(𝑃

𝑐

+ 𝐣𝑃

𝑏

) = ∑𝑃

𝑐

+ 𝐣∑𝑃

𝑏

= 0 ⇒ ∑𝑃

𝑐

= 0 oraz ∑𝑃

𝑏

= 0.

(20b)

Zatem w obwodzie prądu sinusoidalnego bilans mocy ma miejsce dla mocy czynnej, biernej i zespolonej. Nie ma podstaw
do bilansowania mocy pozornej.

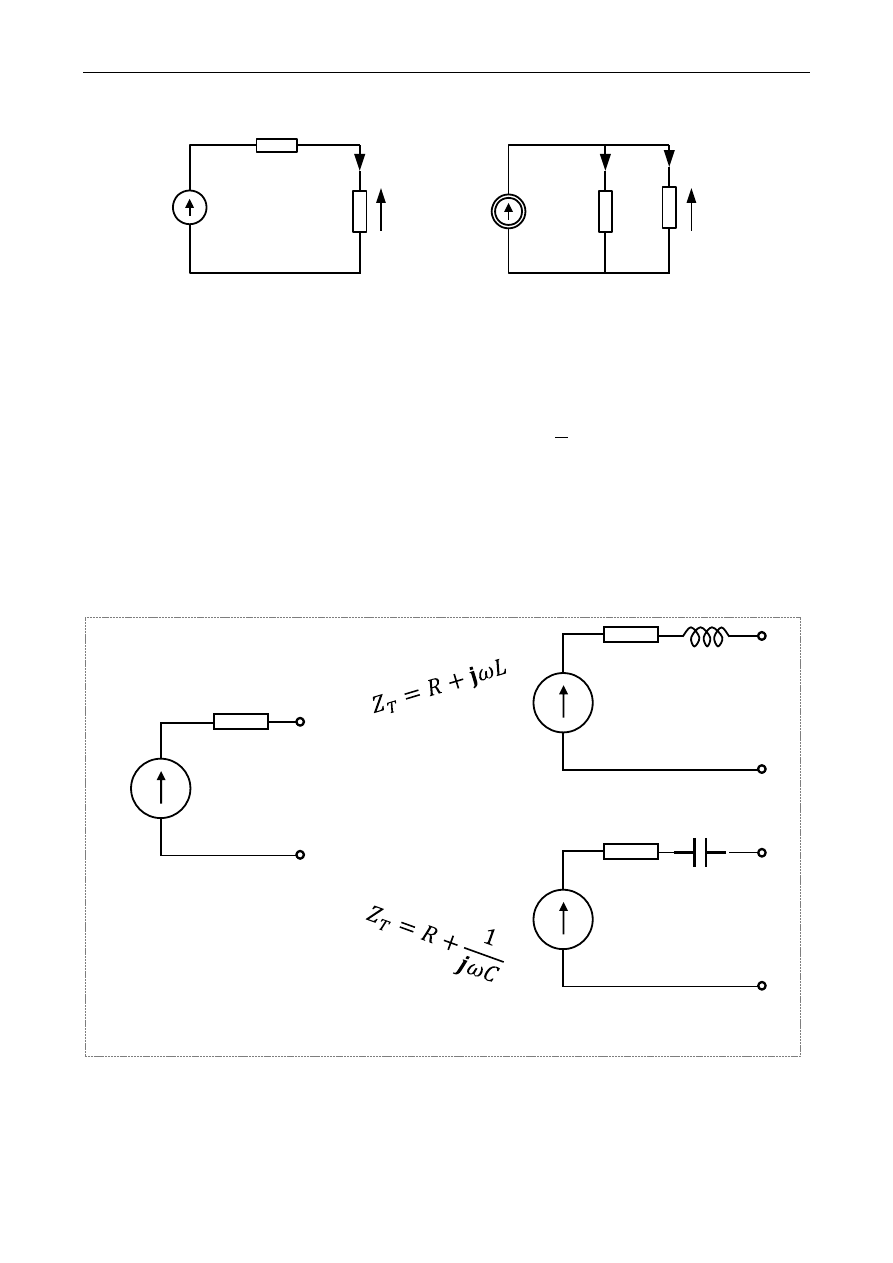
Koncepcja źródeł zastępczych Thevenina i Nortona dla przypadku pobudzeń sinusoidalnych

Jeżeli nasze potrzeby ograniczają się do znalezienia prądu (napięcia, mocy) tylko w kilku tworzących dwójnik ele-

mentach obwodu (w skrajnym, ale i najczęstszym przypadku w jednym elemencie), to całą pozostałą część struktury
możemy zastąpić tzw. źródłem Thevenina lub źródłem Nortona. Przyjmując, że wybranym ważnym elementem jest im-
pedancja 𝑍

5

, możemy zgodnie z powyższą koncepcją wieloelementowy obwód wskazowy zredukować do jednej z przed-

stawionych na rys. 7 postaci.

1

Jednostka mocy pozornej [VA] jest identyczna jak jednostka mocy czynnej [W] i jednostka mocy biernej [var]. Każda z tych jednostek jest iloczynem

wolta i ampera. Różny jest jednak sens fizyczny każdej z tych wielkości. Nazwa war (wolt amper reaktancyjny) wywodzi się z angielskiego Volt Ampere
Reactive, gdzie reactive power oznacza moc bierną.

C. Stefański

7/11

Ostatnia modyfikacja: maj 2016

N

R

5

R

)

(

5

I

I

N



5

I

)

b

N

I

T

E

T

R

5

R

5

I

)

a

5

U

5

U

Rys. 7. Wskazowe obwody zastępcze: a) Thevenina, b) Nortona

Poza 𝑍

5

, parametry pozostałych elementów z rys. 7 muszą zostać dopiero obliczone na tej podstawie, że przez

dwójnik o impedancji 𝑍

5

winien przepływać taki sam wskazowy prąd 𝐼

5

, jaki przepływał przez ten element w ramach

obwodu z rys. 3.

Wprowadzone przez Thevenina oraz Nortona definicje dają nam następujące zapisy, które odnoszą się do rysunku 3

i rysunków 7:

𝐸

𝑇

= 𝑈

5

|

𝑍

5

→∞

, 𝐽

𝑁

= 𝐼

5

|

𝑍

5

=0

, 𝑍

𝑇

= 𝑍

𝑁

=

𝐸

𝑇

𝐽

𝑁

.

(21)

Rysunek 7 przedstawia sytuację w obwodzie wskazowym, będącym modelem obwodu prądu sinusoidalnie zmiennego
dla amplitud zespolonych (analogicznie jak obwód z rysunku 3 jest takim modelem dla obwodu z rysunku 2). Oczywiście
zastąpienie w obwodzie wskazowym jego części źródłem zastępczym, np. źródłem Thevenina (wskazowym) może być
jednoznacznie skojarzone z zamianą odpowiedniej części obwodu prądu sinusoidalnego przez źródło Thevenina sinuso-
idalne. Sinusoidalne źródło Thevenina złożone jest z idealnego generatora napięcia sinusoidalnego 𝑒

𝑇

(𝑡) =

𝐸

𝑇𝑚

cos(𝜔𝑡 + 𝜑

𝑇

) [V] połączonego szeregowo ze strukturą elementów R, L, C, której impedancja na pulsacji 𝜔 wynosi

𝑍

𝑇

. Najczęściej wybieramy pośród struktur jak najprostszych, co prowadzi do tworu będącego szeregowym bądź rów-

noległym połączeniem opornika R i induktora L, albo opornika R i kondensatora C.

3. Wspomagane programem MATLAB rozwiązywanie układu równań liniowych

Przypomnimy teraz krótko to, co zostało bardziej szczegółowo omówione w instrukcji do poprzednich ćwiczeń, a co dotyczyło rozwiązywania

układu równań liniowych wspomaganego narzędziami typu MATLAB (lub mu podobnymi, jak OCTAVE, czy SciLab). Układ równań można zapisywać
w formie „klamrowej”:

{

𝑎

11

𝑥

1

+ 𝑎

12

𝑥

2

+ ⋯ 𝑎

1𝑛

𝑥

𝑛

= 𝑏

1

𝑎

21

𝑥

1

+ 𝑎

22

𝑥

2

+ ⋯ 𝑎

2𝑛

𝑥

𝑛

= 𝑏

2

… … … … … … … … … … .

𝑎

𝑛1

𝑥

1

+ 𝑎

𝑛2

𝑥

2

+ ⋯ 𝑎

𝑛𝑛

𝑥

𝑛

= 𝑏

𝑛

(22)

lub w postaci macierzowej

E

T

Z

T

e

T

(t)

R

L

e

T

(t)

R

C

Rys 8. Realizacja zastępczego źródła Thevenina w strukturze szeregowej w obwodzie prądu sinusoidalnego

(prawa część rysunku) i odpowiadające mu wskazowe źródło Thevenina w obwodzie wskazowym (lewa
część rysunku)

𝑒

𝑇

(𝑡) = |𝐸

𝑇

|cos(𝜔𝑡 + arg(𝐸

𝑇

))

𝑍

𝑇

𝑍

5

𝐽

𝑁

𝑍

𝑁

𝐽

𝑁

− 𝐼

5

𝑍

5

C. Stefański

8/11

Ostatnia modyfikacja: maj 2016

[

𝑎

11

𝑎

12

𝑎

13

… . 𝑎

1𝑁

𝑎

21

𝑎

22

𝑎

23

… . 𝑎

2𝑁

𝑎

31

𝑎

32

𝑎

33

… 𝑎

3𝑁

…

…

…

…

…

𝑎

𝑁1

𝑎

𝑁2

𝑎

𝑁3

… 𝑎

𝑁𝑁

]

⋅

[

𝑥

1

𝑥

2

𝑥

3

…

𝑥

𝑁

]

=

[

𝑏

1

𝑏

2

𝑏

3

…

𝑏

𝑁

]

.

(23)

Skrócony zapis (przy notacji bez nawiasów kwadratowych) równania (23) wygląda następująco:

𝑨 ∙ 𝒙 = 𝒃

(24)

W tym przypadku rozwiązanie jest w naszym zasięgu nawet bez wspomagania komputerowego, przy czym często korzystamy z przejrzystych

zapisów metody Cramera

𝒙

𝟏

=

𝜟

𝟏

𝜟

, 𝒙

𝟐

=

𝜟

𝟐

𝜟

, 𝒙

𝟑

=

𝜟

𝟑

𝜟

, 𝒙

𝟒

=

𝜟

𝟒

𝜟

, 𝜟 ≠ 𝟎 .

(25)

gdzie Δ jest wyznacznikiem macierzy 𝑨, zaś każdy z Δ

𝑛

to wyznacznik macierzy powstałej z 𝑨 przez zastąpienie w niej wektorem 𝒃 kolumny o numerze

„𝑛-tym”.

Współcześnie, spośród wielu opracowanych metod numerycznego rozwiązywania układów równań liniowych, duże znaczenie mają różne wa-

rianty metody eliminacji Gaussa. Algorytm tej metody dla równania (23) jest następujący (eliminacja niewiadomych w wyrażeniu (23) przebiega
następująco):



W pierwszym kroku od wierszy 2, 3, … . , 𝑁 odejmujemy wiersz pierwszy pomnożony przez taki współczynnik, który zapewnia jako
wynik odejmowania nowy wiersz nie zawierający już niewiadomej 𝑥

1

.

Po pierwszym kroku (krok 𝑠 = 1; ang.: step) otrzymujemy

[

𝑎

11

𝑎

12

𝑎

13

… 𝑎

1𝑁

0 𝑎

22

(1)

𝑎

23

(1)

… 𝑎

2𝑁

(1)

0 𝑎

32

(1)

𝑎

33

(1)

… 𝑎

3𝑁

(1)

… …

…

… …

0 𝑎

𝑁2

(1)

𝑎

𝑁3

(1)

… 𝑎

𝑁𝑁

(1)

]

⋅

[

𝑥

1

𝑥

2

𝑥

3

…

𝑥

𝑁

]

=

[

𝑏

1

𝑏

2

(1)

𝑏

3

(1)

…

𝑏

𝑁

(1)

]

(26a)

gdzie

𝑎

𝑖𝑘

(1)

= 𝑎

𝑖𝑘

− 𝑙

𝑖1

⋅ 𝑎

1𝑘

,

𝑏

𝑖

(1)

= 𝑏

𝑖

− 𝑙

𝑖1

⋅ 𝑏

1

, przy 𝑙

𝑖1

=

𝑎

𝑖1

𝑎

11

oraz 𝑖, 𝑘 = 2, 3, … , 𝑁



W drugim kroku od wierszy 3, 4, … . , 𝑁 odejmujemy wiersz drugi pomnożony przez taki współczynnik, który zapewnia jako wynik
odejmowania nowy wiersz nie zawierający już niewiadomej 𝑥

2

.

Po drugim kroku (krok 𝑠 = 2) otrzymujemy

[

𝑎

11

𝑎

12

𝑎

13

… 𝑎

1𝑁

0 𝑎

22

(1)

𝑎

23

(1)

… 𝑎

2𝑁

(1)

0 0

𝑎

33

(2)

… 𝑎

3𝑁

(2)

… …

…

… …

0 0

𝑎

𝑁3

(2)

… 𝑎

𝑁𝑁

(2)

]

⋅

[

𝑥

1

𝑥

2

𝑥

3

…

𝑥

𝑁

]

=

[

𝑏

1

𝑏

2

(1)

𝑏

3

(2)

…

𝑏

𝑁

(2)

]

(26b)

gdzie

𝑎

𝑖𝑘

(2)

= 𝑎

𝑖𝑘

(1)

− 𝑙

𝑖2

⋅ 𝑎

2𝑘

(1)

,

𝑏

𝑖

(2)

= 𝑏

𝑖

(1)

− 𝑙

𝑖2

⋅ 𝑏

2

(1)

, przy 𝑙

𝑖2

=

𝑎

𝑖2

(1)

𝑎

22

(1)

oraz 𝑖, 𝑘 = 3, 4, … , 𝑁



Powyższe postępowanie stosujemy do otrzymanego w drugim kroku równania (26b) i kolejno w następnych krokach do następnych
równań ze zwiększającą się ilością zer pod przekątną główną przetwarzanej macierzy; po (N-1) krokach otrzymujemy

[

𝑎

11

𝑎

12

𝑎

13

… 𝑎

1𝑁

0

𝑎

22

(1)

𝑎

23

(1)

… 𝑎

2𝑁

(1)

0

0

𝑎

33

(2)

… 𝑎

3𝑁

(2)

…

…

…

… …

0

0

0

… 𝑎

𝑁𝑁

(𝑁−1)

]

⋅

[

𝑥

1

𝑥

2

𝑥

3

…

𝑥

𝑁

]

=

[

𝑏

1

𝑏

2

(1)

𝑏

3

(2)

…

𝑏

𝑛

(𝑁−1)

]

(26)

gdzie

𝑎

𝑖𝑘

(𝑠)

= 𝑎

𝑖𝑘

(𝑠-1)

− 𝑙

𝑖𝑠

⋅ 𝑎

𝑠𝑘

(𝑠-1)

, 𝑏

𝑖

(𝑠)

= 𝑏

𝑖

(𝑠-1)

− 𝑙

𝑖𝑠

⋅ 𝑏

𝑠

(𝑠-1)

,

przy 𝑙

𝑖𝑠

=

𝑎

𝑖𝑠

(𝑠-1)

𝑎

𝑠𝑠

(𝑠-1)

, 𝑠 = 1, 2, … , 𝑁-1, 𝑖 = 𝑠+1, 𝑠+2, … , 𝑁, 𝑘 = 𝑖-1, 𝑖, … 𝑁 (przy czym 𝑎

𝑝𝑞

(0)

= 𝑎

𝑝𝑞

).

Przykład obliczeń według tego algorytmu był podany w instrukcji do ćwiczenia drugiego – warto z nim ponownie zapoznać się.
Poniżej przypominamy też pewien wariant metody Gaussa noszący nazwę metody LU. Polega ona na przyjęciu lewostronnej macierzy ze wzoru

(9) jako macierzy 𝑼 (trójkątnej górnej) i utworzeniu dodatkowej macierzy 𝑳 (trójkątnej dolnej) zbudowanej ze współczynników 𝑙

𝑖𝑠

. Przykładowo dla

przypadku macierzy o wymiarach 4x4 (𝑁 = 4) otrzymujemy

𝑼 =

[

𝑎

11

𝑎

12

𝑎

13

𝑎

14

0

𝑎

22

(1)

𝑎

23

(1)

𝑎

24

(1)

0

0

𝑎

33

(2)

𝑎

34

(2)

0

0

0

𝑎

44

(3)

]

, 𝑳 =

[

1

0

0

0

𝑙

21

1

0

0

𝑙

31

𝑙

32

1

0

𝑙

41

𝑙

42

𝑙

43

1]

(27)

Macierze te, dla 𝑁 ≥ 2, mają następujące pożyteczne właściwości

𝑳 ∙ 𝑼 = 𝑨, |𝑳| = 1, |𝑨| = |𝑼|

(28)

Wzory (27) i (28) wskazują na korzystniejszy od tradycyjnego sposób obliczania wyznacznika macierzy 𝑨; dodajmy, sposób wykorzystywany w

operacji det(A) MATLAB-a.

C. Stefański

9/11

Ostatnia modyfikacja: maj 2016

Poszukiwanie wektora rozwiązań 𝒙 możemy teraz przedstawić w postaci

𝑳 ∙ 𝑼 ∙ 𝒙 = 𝒃 ,

(29)

𝒚 = 𝑳

−𝟏

∙ 𝒃 ,

𝒙 = 𝑼

−𝟏

∙ 𝒚 ,

gdzie 𝒚 to pomocniczy wektor kolumnowy w procedurze (29).

Eliminację Gaussa prowadzącą do otrzymania macierzy LU można także zastosować nie do oryginalnego układu równań (23), tylko do układu

równań z przestawionymi wierszami. Najbardziej oczywista potrzeba przestawienia wierszy może w ramach algorytmu eliminacji wynikać z potrzeby
ominięcia sytuacji dzielenia przez zero, ale możemy także w ten sposób zwiększać dokładność obliczeń.

Wspomnianą optymalizację dokładności obliczeń w odniesieniu do układu równań (23) otrzymujemy w MATLAB-ie po zastosowaniu do dekom-

pozycji funkcji lu MATLAB-a z argumentami wyjściowymi 𝑳, 𝑼, 𝑷:

[L,U,P] = lu(A).

(30)

Funkcja ta w miejsce macierzy 𝑨 zwraca nam trzy macierze, które możemy podstawić do równania (24). Po podstawieniu, zapis tego równania przyj-
muje postać

𝑷 ∙ 𝑳 ∙ 𝑼 ∙ 𝒙 = 𝒃

.

(31)

Zawierająca informację o przestawieniach wierszy macierz 𝑷 ma następujące właściwości

𝑷 = 𝑷

−𝟏

,

|𝑷| = 1 .

(32)

Stąd rozwiązanie równania (24) możemy w tym przypadku uzyskać na podstawie wyrażenia

𝑳 ∙ 𝑼 ∙ 𝒙 = 𝒃

𝒑

(33)

gdzie

𝒃

𝒑

= 𝑷 ∙ 𝒃.

Sposób zamiany kolejności wierszy daje się odczytać z macierzy 𝑷. Ściśle rzecz biorąc, niezerowy wyraz 𝑝

𝑖𝑗

= 1 tej macierzy informuje nas, że

nowym 𝑖-tym równaniem w zapisie (23) ma być stare 𝑗-te równanie tego zapisu.

Realizując poleceniem lu(A)opisaną powyżej procedurę stosujemy optymalizowaną dekompozycję [L, U, P] w sposób jawny, ale oprócz

tego dekompozycja taka jest automatycznie wykonywana niejawnie w ramach następujących poleceń Matlaba:



w przypadku równania postaci (24), gdy je rozwiązujemy poleceniem

x=A\b

(34)



w przypadku obliczania wyznacznika macierzy A

DA = det(A)

(35)

4. Pliki MATLABA do wspomagania analizy obwodów

function [x]=cramer(A,b)

%Metoda Cramera rozwiązywania układów równań liniowych
%Zapis układu równań A*x=y
N=rank(A);
for k=1:N
K=A(:,k); % Kolumna o numerze k w macierzy A na starcie
A(:,k)=b; % Macierze A

1

, A

2

,…,A

m

DK(k)=det(A); % Wyznaczniki D

1

, D

2

,…,D

m

A(:,k)=K; %Powrót do startowej postaci macierzy A
end
D=det(A); % Wyznacznik główny
x=DK./D; % Tablicowe dzielenie wyznaczników
%Koniec cramer.m

function [LA,UA]=dekompozycja(A)

% Dekompozycja (rozkład) macierzy A na dwie macierze
%„trójkątną-dolną” LA i „trójkątną- górną” UA
N=rank(A); % Określa liczbę niezależnych równań
el=eye(N); % Generuje macierz z "jedynkami" na głównej przekątnej
a=zeros(N); % Generuje macierz wypełnioną zerami
a=A; % Przepisuje elementy macierzy
for s=1:(N-1) % Litera s oznacza liczbę kroków w metodzie Gaussa

% Litery i oraz k oznaczają numery wiersza i kolumny

for i=n:N

el(i,s)=a(i,s)/a(s,s)

for k=1:N

a(i,k)=a(i,k)-el(i,s)*a(s,k);

end

end
end
LA=el; % Macierz trójkątna dolna
UA=a; % Macierz trójkątna górna
% Koniec dekompozycja.m

%Cw7_1.m

%***Obliczanie prądów oczkowych dla obwodu z rys. 2***
format short eng;
N=input('N=');
R1=100; R2=100; R3=100;R4=N;L5=N *1e-3; C6=N/10 *1e-6; r7=N/100; E8m=N; fe=N/10 *1e3;
Z5=j*2*pi*fe*L5;Z6=-j/(2*pi*fe*C6);
Zoo=[R1+R2+Z5, -Z5,-R2 ;
-Z5,R4+Z5+Z6, 0 ;

C. Stefański

10/11

Ostatnia modyfikacja: maj 2016

-R2, r7, R2+R3];
E=[E8m,0,0]';

Io_cramer=cramer(Zoo,E).';

[LZoo,UZoo]=dekompozycja(Zoo);
y=(LZoo^(-1))*E;
Io_gauss_lu=(UZoo^(-1))*y;

Io_lup=Zoo\E;
[Io_cramer Io_gauss_lu Io_lup]

%Cw7_2.m

%***Program wspomagający poszukiwanie napięć węzłowych***
%
N=input('N=');N=abs(N)+(N==0);N;
LI=input('Podaj, ile wykonac iteracji - LI=');
format short eng;
R1=100; R2=100; R3=100;R4=N;L5=N *1e-3; C6=N/10 *1e-6; r7=5*N; E8m=N; fe=N/10 *1e3;
Z5=j*2*pi*fe*L5;Z6=-j/(2*pi*fe*C6);
Z=[R1, R2, R3, R4, Z5, Z6];E1=E8m; % dane
% obwodu (opory,źródła)
A=

[ -1,-1, 1, 0, 0, 0;

0, 1, -1, 1, 1, 0;
0, 0, 0,-1, 0, 1];
Y=(1)./Z;
Ybb=diag([Y]);
J=zeros(6,1);
Ynn=A*Ybb*A';
E=zeros(6,1);E(1,1)=E1;E(3,1)=0;
for licznik=1:LI
Jn=A*J-A*Ybb*E;
V=Ynn\Jn;
Uu=(A')*V;U=Uu+E;
I=Ybb*U;
E(3,1)=-r7*I(4);
endfor

Modul_V=abs(V)
Faza_V=(180/pi)*angle(V)


PzB=1/2*U.*conj(I);display("PzB'=");display(PzB.');
sumPzB=sum(PzB)
PzE=-1/2*E.*conj(I);display("PzE'=");display(PzE.');
sumPzE=sum(PzE)
sumPz=sumPzB+sumPzEMod_V=abs(V)

5. Symulacja obwodu elektrycznego za pomocą programu SPICE

W programie SPICE poszukiwanie rozwiązania układu równań liniowych jest oparte na tej samej metodzie numerycznej LU, która

jest opisana w rozdziale 3. Jednak w odróżnieniu od właściwości programu MATLAB, nie ma w programie SPICE dla WINDOWS po-
trzeby zewnętrznego formułowania równań opisujących obwód. W edytorze programu tworzymy wirtualny obwód złożony: ze źródeł
niezależnych, źródeł sterowanych, rezystorów, cewek indukcyjnych i kondensatorów i w miarę potrzeby z innych elementów pocho-
dzących z banku elementów SPICE’a. W ten sposób SPICE – w zewnętrznym oglądzie – raczej symuluje właściwości obwodu niż wspo-
maga poszukiwanie rozwiązań równań opisujących taki obwód.

Z wielu wariantów SPICE’a w laboratorium jest do dyspozycji program Micro-Cap (MC). Obwód prądu stałego z rys. 2, wpro-

wadzony do MC wygląda jak na rys. 8.

Rysunki 2 i 8 różnią się przede wszystkim dodatkowymi fragmentami, które pojawiły się z tego względu, że w banku
elementów MC mamy rysunki źródeł sterowanych w postaci czwórnikowej. Edytor nie pozwala na wygodny sposób
określania kierunków odniesienia dla przepływu prądów w gałęziach oraz nadawania numerów porządkowych węzłów.
We wprowadzonym do edytora programu obwodzie można poprzez kliknięcie myszką w obrębie wybranego elementu
zmienić w otwierającym się wtedy okienku wartość liczbową parametru (E, J, g, R1, R2,…, R8) (na rys. 9 mamy przykła-
dowo R1=100[Ω], r= r7[Ω]

1

).

Jeżeli z kilku wariantów badania obwodu DC (prądu stałego) wybierzemy Dynamic DC otrzymamy napięcia węzłowe (V1,
V2, …, V5), czyli potencjały każdego z ponumerowanych węzłów względem napięcia odniesienia (masa, ziemia) oraz
prądy gałęziowe (I1, I2, …, I8).

Obwód prądu sinusoidalnie zmiennego z rys. 2 wprowadzony element po elemencie do edytora graficznego Mi-

cro∙Cap-a i poddany analizie Dynamic AC jest przedstawiony na rys. 9.

1

r [Ω] to parametr zwany transrezystancją ZNSP oznaczonego na rysunku 3 przez Es1 rozpiętego między węzłami (3, 5) – wejście i (2, 4) – wyjście

(uwaga: węzeł 0, to węzeł masy).

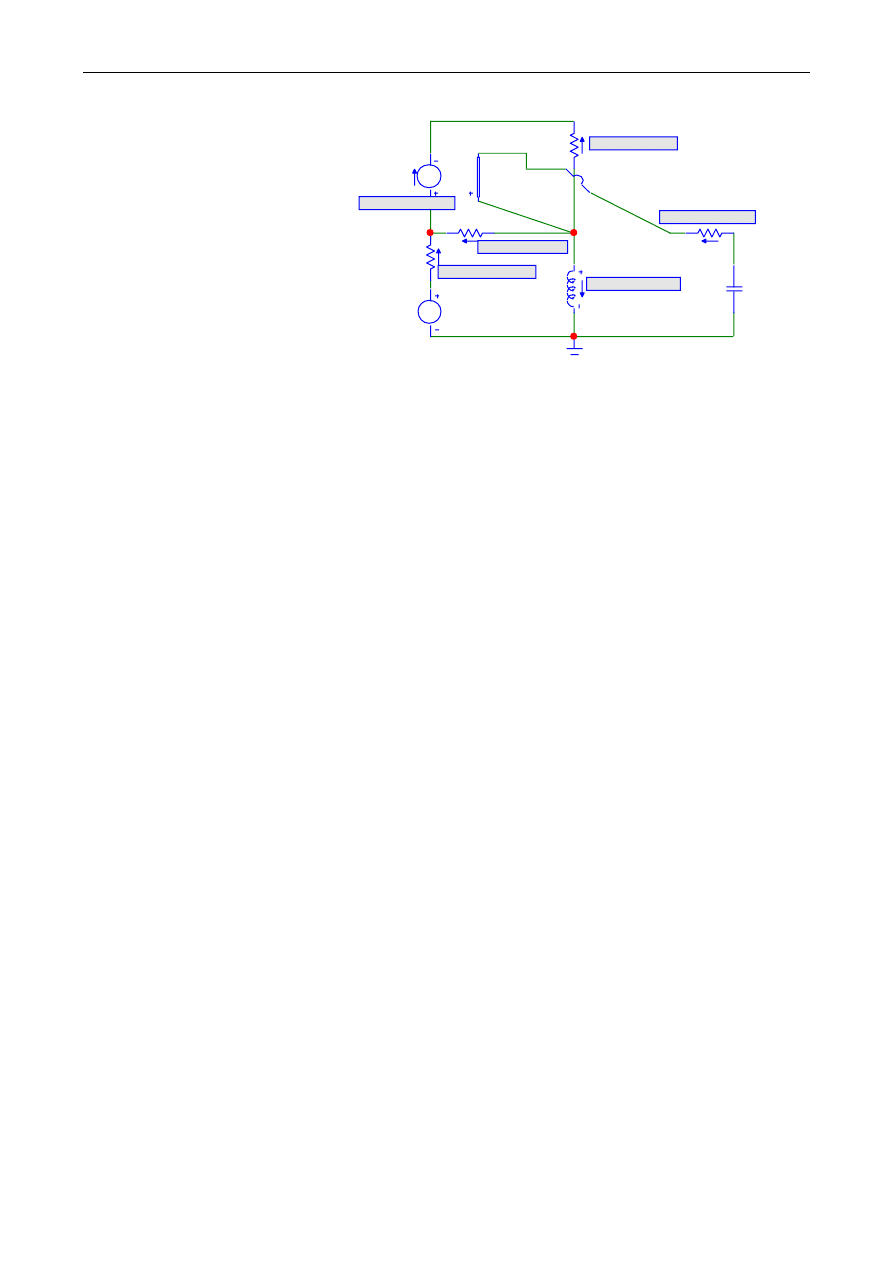
C. Stefański

11/11

Ostatnia modyfikacja: maj 2016

Rys. 9. Obwód prądu sinusoidalnie zmiennego poddany analizie Dynamic AC (𝒇

𝒆

= 𝟓 [kHz])

Na schemacie z rys. 9 uwidoczniono jednocześnie parametry sinusoidalnych prądów gałęziowych, otrzymane w wyniku
analizy AC obwodu. Każda z pierwszych liczb zamieszczonych w prostokątnych obwódkach oznacza amplitudę sinusoi-
dalnego prądu płynącego przez daną gałąź w stanie ustalonym. Druga z liczb jest dla danego prądu przesunięciem fazo-
wym (w stopniach) w odniesieniu do sinusoidy napięcia wytwarzanego w źródle E8.

Pytania kontrolne

1) Wymień znane Tobie metody bezpośredniego rozwiązywania układu równań liniowych. Omów jedną z nich.

Porównaj ją z pozostałymi (podając jej przewagi, bądź niedoskonałości w stosunku do pozostałych).

2) Co to jest macierz incydencji obwodu? Narysuj graf o zredukowanej macierzy incydencji

𝐴 = [

1 −1 −1

0 0 0

0

1

0 −1 1 0

0

0

1

1 0 1

].

3) Podaj cel i szczegóły tworzenia tzw. źródła Thevenina dla wieloelementowego obwodu liniowego (zilustruj

problem na niezbyt złożonym, ale też i nietrywialnym przykładzie).

4) Podaj cel i szczegóły tworzenia tzw. źródła Nortona dla wieloelementowego obwodu liniowego (zilustruj pro-

blem na niezbyt złożonym, ale też i nietrywialnym przykładzie).

5) Czym w ogólnym przypadku różni się tzw. obwód prądu stałego (DC) od obwodu typu AC?
6) Na liniowym dwójniku D, przy strzałkowaniu skojarzonym, prąd i napięcie są sinusoidalne oraz odpowiednio

𝑖(𝑡) = 𝐼

𝑚

cos(𝜔𝑡) [A] i 𝑢(𝑡) = 𝑈

𝑚

cos(𝜔𝑡 + 𝜑) [V]. Oblicz moc czynną, bierną, pozorną i zespoloną na D

oraz podaj jednostki stosowane przy tych mocach. Ile wynosi impedancja i admitancja dwójnika D?

7) Na czym polega strzałkowanie skojarzone? Jakie są jego zalety? Czy Micro∙Cap stosuje ten sposób strzałkowa-

nia?

8) Objaśnij działanie ciągu komend MATLAB-a: a=-5:-1; b=1:5; diag(a'.*b')-diag(a.*b);

ans. Podaj wynik (czyli zapisz, co zostanie wyświetlone na ekranie).

9) Objaśnij jak jest rozumiane MATLAB-owe „dzielenie” A\b oraz objaśnij czym są (macierze, wektory, wymiary)

poszczególne elementy (A, b, wynik) tego działania.

10) Opisz metodę tableau analizy obwodów. Porównaj ją (przewagi, niedostatki) z metodami: potencjałów węzło-

wych i prądów oczkowych.

R1

100

R2 100

Es1

r7

R3

100

R4

N

L5

N*1m

C6

N/10*1u

E8

AC {E8m} 0

Dane do programu EJRGZY (skasowac znak mnożenia

po wklejeniu do tabeli połączeń - np. zamiast 2*i ma być 2i):

R1=100.000000000

R2=100.000000000

R3=100.000000000

R4=50.000000000

Z5=0.000000000+1570.796326795*i

Y6=0.000000000+0.157079633*i

E7=0.000000000

E8=50.000000000

.define E8m N

.define r7 5*N

.define fe N/10 *1k

.define N 50

Es1=r7*i(R4)

UWAGA. Pamiętać o ustawieniu

(sprawdzeniu) w polach parametrów

analizy Dynamic AC częstotliwości fe

153.497m,365.421u

-269.19m,-6.792m

-115.692m,-6.426m

115.692m,6.426m

-153.953m,-5.287m

-455.647u,-4.922m