Wydział ETI PG

Katedra Systemów Elektroniki Morskiej

Przybliżone rozwiązywanie

równań nieliniowych

- wykorzystanie programów MATLAB i SPICE

w stałoprądowej analizie i symulacji

obwodu z tranzystorem bipolarnym

Opracował:

Czesław Stefański

Gdańsk, 2015

~ 2 ~

Wstęp

Podstawy teoretyczne potrzebne do wykonania ćwiczenia pt. Przybliżone rozwiązywanie (układów)

równań nieliniowych - wykorzystanie programów MATLAB i SPICE w stałoprądowej analizie i symulacji
obwodów z tranzystorem bipolarnym są obszerne. Obejmują zarówno zagadnienia z dziedziny metod
numerycznych, czy podstawową umiejętność użycia programów MATLAB i SPICE, jak i wybraną wiedzę
dotyczącą modeli tranzystora npn, czy wreszcie podstawy analizy obwodów (w szczególności topologiczne
podejście do tworzenia węzłowych równań opisu sieci). Najpierw bardzo krótko przedstawimy lub
przypomnimy te podstawy (wyjątkiem użycie MATLAB-a; o nim wspomnimy na końcu), by w efekcie
sformułować i rozwiązać możliwie prosty przykład przybliżonego wyznaczania pierwiastków układu równań
nieliniowych. Jednym z zadań studentów wykonujących ćwiczenie będzie zapis przedstawionych przykładów
dla konkretnych danych, rozwiązanie ich „sposobem inżynierskim”, przy użyciu przedstawionych procedur
i programu MATLAB oraz w programie symulacyjnym SPICE, a także porównanie uzyskanych rozwiązań.
Niektóre zagadnienia (przedstawione zmniejszoną czcionką), były już prezentowane w materiale do
poprzednich ćwiczeń, ale są tu powtórzone dla porządku wywodu oraz wygody Czytelnika.

1. Metody przybliżonego rozwiązywania układów równań nieliniowych. Omówienie

metody Newtona-Raphsona

Jak już wiemy, wzory dokładne na rozwiązania równań, bądź układów równań istnieją tylko dla bardzo szczególnych

typów równań, na przykład dla układów równań liniowych czy dla równań algebraicznych do stopnia czwartego włącznie
(dla przypadku ogólnego)

[1]

. Co więcej, w bardzo wielu zagadnieniach napotykamy na równania bądź układy równań

nieliniowych, dla których potrafimy znaleźć tylko rozwiązania przybliżone. Różne sposoby przybliżonego rozwiązywania
równań nieliniowych omówiono w skrypcie

[2]

. Tu tylko nadmieniamy, że omówiono tam metody bisekcji, siecznych, regula

falsi i stycznych oraz sugerujemy zapoznanie się z opisem tych metod. Warto wspomnieć, że metody graficzne też bywają
przydatne.

Dla układów równań nieliniowych podstawową rolę w wyznaczaniu rozwiązań przybliżonych odgrywa algorytm

(metoda) iteracji prostej

[2]

. Ze względu na swoje zalety jest on stosowany bardzo często. Metoda Newtona-Raphsona

może być przedstawiana z jednej strony jako szczególny przypadek metody iteracji prostej (punktu stałego

[3]

), a z drugiej

strony jako uogólnienie, na przypadek układu równań nieliniowych, metody stycznych. Poniżej krótko zostanie omówiony
rodowód algorytmu Newtona-Raphsona.

1.1.

Algorytm Newtona-Raphsona (N-R)

1.1.1. Przypadek pojedynczego równania (ujęcie intuicyjne; przypomnienie)

Chcemy rozwiązać równanie

𝑓(𝑥) = 0,

(1.1)

przy czym o funkcji 𝑓(𝑥) zakładamy, że jest ciągła
i wielokrotnie różniczkowalna w otoczeniu punktu 𝑥

∗

,

będacego rozwiązaniem badanego równania.

Niech 𝑥

(𝑗)

będzie wartością 𝑥 w j-tym kroku

iteracji (możemy założyć, że 𝑥

(𝑗)

nie jest

rozwiązaniem; gdyby było, nasze zadanie byłoby
zakończone). Rozwińmy funkcję 𝑓(𝑥) w szereg
Taylora wokół punktu 𝑥 = 𝑥

(𝑗)

:

𝑓(𝑥) = 𝑓(𝑥

(𝑗)

) +

𝑑𝑓(𝑥)

𝑑𝑥

|

𝑥=𝑥

(𝑗)

(𝑥 − 𝑥

(𝑗)

) +

𝑑2𝑓(𝑥)

𝑑𝑥2

|

𝑥=𝑥

(𝑗)

(𝑥 − 𝑥

(𝑗)

)

2

+ … .

Jeśli 𝑥 = 𝑥

(𝑗+1)

będzie następną wartością 𝑥 (w

kolejnej iteracji), powyższe równanie przyjmie postać:

𝑓(𝑥

(𝑗+1)

) = 𝑓(𝑥

(𝑗)

) +

𝑑𝑓(𝑥)

𝑑𝑥

|

𝑥=𝑥

(𝑗)

(𝑥

(𝑗+1)

− 𝑥

(𝑗)

) +

𝑑2𝑓(𝑥)

𝑑𝑥2

|

𝑥=𝑥

(𝑗)

(𝑥

(𝑗+1)

− 𝑥

(𝑗)

)

2

+ … .

Gdyby wartość początkowa 𝑥 = 𝑥

(0)

została

przyjęta dostatecznie blisko rozwiązania dokładnego 𝑥

∗

, to niechybnie 𝑥

(𝑗+1)

− 𝑥

(𝑗)

byłoby małe, a to pozwoliłoby

pominąć pochodne wyższych rzędów w ostatniej równości i przyjąć przybliżenia:

0 ≈ 𝑓(𝑥

(𝑗+1)

) ≈ 𝑓(𝑥

(𝑗)

) +

𝑑𝑓(𝑥)

𝑑𝑥

|

𝑥=𝑥

(𝑗)

(𝑥

(𝑗+1)

− 𝑥

(𝑗)

),

[1]

Wacław

Sierpiński

: Zasady algebry wyższej, "Monografie Matematyczne" Tom 11, Rozdział 10. Plik

pdf

jest dostępny z serwisu

Biblioteka

Wirtualna Nauki

[2]

Andrzej Szatkowski, Jacek Cichosz: Metody numeryczne. Podstawy teoretyczne. WPG, Gdańsk 2002

[3]

Leon O. Chua, Pen-Min Lin: Komputerowa analiza układów elektronicznych. Algorytmy i metody obliczeniowe. WNT Warszawa 1981.

x* x

(2)

x

(1)

x

(0)

f(x

(0)

)

f(x

(1)

)

f(x

(2)

)

𝒇

(

𝒙

(

𝟏

)

)

−𝟎

𝒙

(𝟏)

−𝒙

(𝟐)

=𝒇

′

(

𝒙

(

𝟏

)

) ⟹

𝒙

(𝟐)

=𝒙

(𝟏)

−

𝒇

(

𝒙

(

𝟏

)

)

𝒇

′

(

𝒙

(

𝟏

)

)

𝑥

𝑓(𝑥)

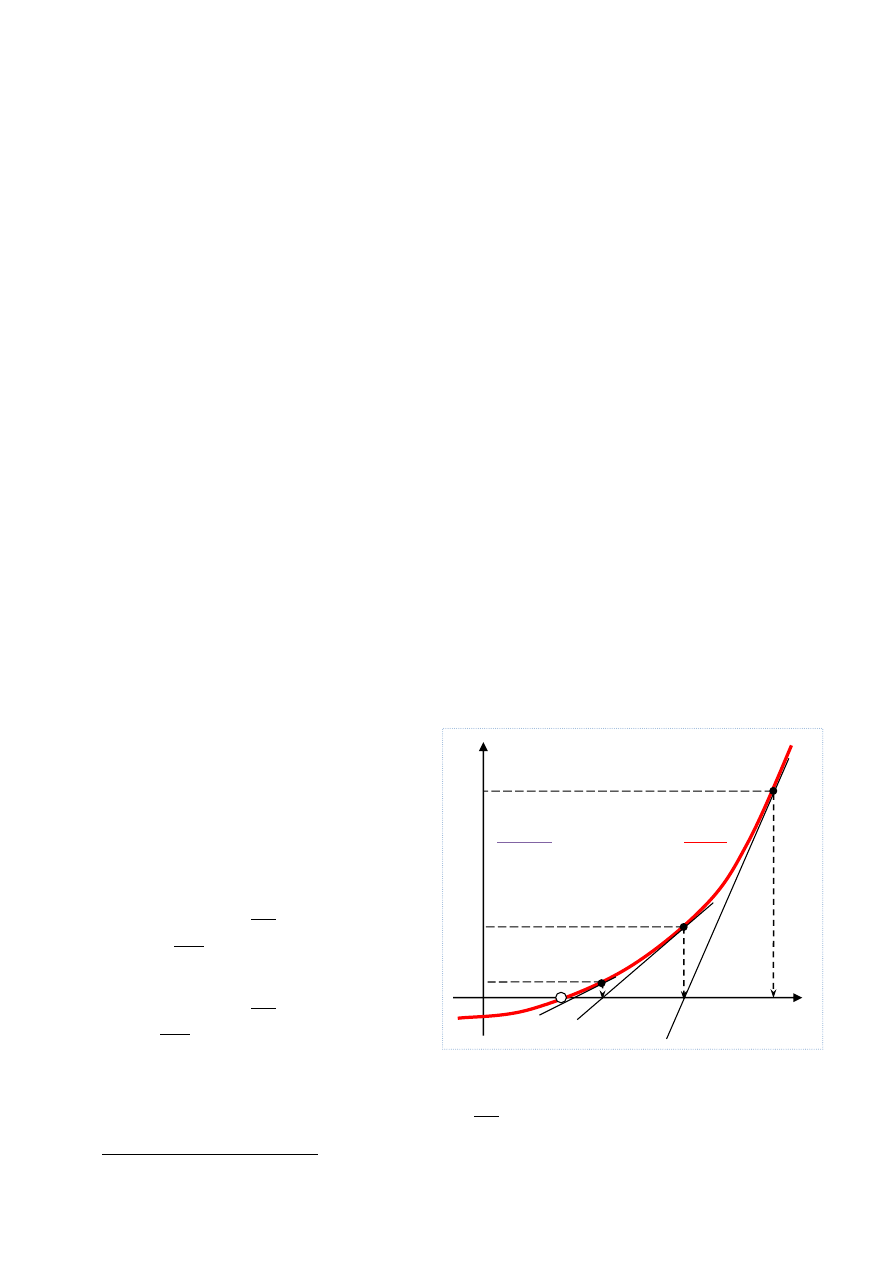
Rysunek 1.1.1

~ 3 ~

skąd już uzyskalibyśmy regułę iteracyjną:

𝑥

(𝑗+1)

= 𝑥

(𝑗)

−

1

𝑑𝑓(𝑥)

𝑑𝑥 |𝑥=𝑥(𝑗)

𝑓(𝑥

(𝑗)

) .

(1.2)

Interpretację tej reguły iteracyjnej dla j=2 pokazano na rysunku 1.1.1 (metoda N-R w przypadku jednowymiarowym

jest często nazywana metodą stycznych, a ostatni rysunek stanowi przekonujące uzasadnienie dla takiej nazwy).

1.1.2. Przypadek układu równań (ujęcie intuicyjne)

Chcemy rozwiązać następujący układ 𝑛 równań nieliniowych z 𝑛 niewiadomymi

𝑓

𝑖

(𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

) = 0, 𝑖 = 1,2, … , 𝑛.

(1.3)

Niech 𝒙

(𝑗)

= 𝑐𝑜𝑙(𝑥

1

(𝑗)

, 𝑥

2

(𝑗)

, … , 𝑥

𝑛

(𝑗)

) będzie wartością 𝒙 = 𝑐𝑜𝑙(𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

) w j-tym kroku iteracji.

Rozwińmy funkcje 𝑓

𝑖

(𝒙), 𝑖 = 1, 2, … , 𝑛 (są to funkcje wielu zmiennych) w szereg Taylora wokół punktu 𝒙

(𝑗)

:

𝑓

𝑖

(𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

) = 𝑓

𝑖

(𝑥

1

(𝑗)

, 𝑥

2

(𝑗)

, … , 𝑥

𝑛

(𝑗)

) +

𝜕𝑓(𝒙)

𝜕𝑥

1

|

𝒙=𝒙

(𝑗)

(𝑥

1

− 𝑥

1

(𝑗)

) +

𝜕𝑓(𝒙)

𝜕𝑥

2

|

𝒙=𝒙

(𝑗)

(𝑥

2

− 𝑥

2

(𝑗)

) + … +

𝜕𝑓(𝒙)

𝜕𝑥

𝑛

|

𝒙=𝒙

(𝑗)

(𝑥

𝑛

− 𝑥

𝑛

(𝑗)

) +

+wyrazy wyższych rzędów zawierające czynniki (𝑥

𝑖

− 𝑥

𝑖

(𝑗)

)

𝑚

,

𝑚 > 1, 𝑖 = 1, 2, … , 𝑛.

Niech 𝒙 = 𝒙

(𝑗+1)

będzie wartością 𝒙 w (𝑗 + 1) iteracji; wstawiając je do powyższego równania otrzymujemy

𝑓

𝑖

(𝑥

1

(𝑗+1)

, 𝑥

2

(𝑗+1)

, … , 𝑥

𝑛

(𝑗+1)

) = 𝑓

𝑖

(𝑥

1

(𝑗)

, 𝑥

2

(𝑗)

, … , 𝑥

𝑛

(𝑗)

) +

𝜕𝑓(𝒙)

𝜕𝑥

1

|

𝒙=𝒙

(𝑗)

(𝑥

1

(𝑗+1)

− 𝑥

1

(𝑗)

) +

𝜕𝑓(𝒙)

𝜕𝑥

2

|

𝒙=𝒙

(𝑗)

(𝑥

2

(𝑗+1)

− 𝑥

2

(𝑗)

) + … +

𝜕𝑓(𝒙)

𝜕𝑥

𝑛

|

𝒙=𝒙

(𝑗)

(𝑥

𝑛

(𝑗+1)

− 𝑥

𝑛

(𝑗)

) +

+wyrazy wyższych rzędów zawierające czynniki (𝑥

𝑖

(𝑗+1)

− 𝑥

𝑖

(𝑗)

)

𝑚

,

𝑚 > 1, 𝑖 = 1, 2, … , 𝑛.

Oczywiście, jak w przypadku jednowymiarowym zakładamy, że punkty

𝒙

(𝑗)

wyznaczane w kolejnych iteracjach

są bliskie rozwiązaniu 𝒙

∗

, przeto każda składowa wektora 𝒙

(𝑗+1)

− 𝒙

(𝑗)

jest mała i możemy pominąć

w ostatnim wzorze wyrazy rzędu wyższego niż pierwszy. Ponadto ponieważ 𝒙

(𝑗+1)

jest, w naszym mniemaniu

bliskie 𝒙

∗

, więc 𝒇(𝒙

(𝑗+1)

) ≈ 𝒇(𝒙

∗

) = 𝟎 , gdzie 𝒇(𝒙) = 𝑐𝑜𝑙(𝑓

1

(𝒙), … , 𝑓

𝑛

(𝒙)) . W efekcie możemy napisać:

𝑓

𝑖

(

𝒙

(𝑗)

) +

𝜕𝑓(𝒙)

𝜕𝑥

1

|

𝒙=𝒙

(𝑗)

(𝑥

1

(𝑗+1)

− 𝑥

1

(𝑗)

) +

+

𝜕𝑓

𝑖

(𝒙)

𝜕𝑥

2

|

𝒙=𝒙

(𝑗)

(𝑥

2

(𝑗+1)

− 𝑥

2

(𝑗)

) + … +

𝜕𝑓

𝑖

(𝒙)

𝜕𝑥

𝑛

|

𝒙=𝒙

(𝑗)

(𝑥

𝑛

(𝑗+1)

− 𝑥

𝑛

(𝑗)

) = 0,

𝑖 = 1,2, … , 𝑛

Ten układ równań może być zapisany w postaci macierzowej następująco:

𝑴

𝑱

(𝒙

(𝑗)

)(𝒙

(𝑗+1)

− 𝒙

(𝑗)

) = −𝒇(𝒙

(𝑗)

),

gdzie macierz Jacobiego 𝑴

𝑱

(𝒙) funkcji 𝒇(𝒙) jest liczona w punkcie 𝒙

(𝑗)

:

𝑴

𝑱

(𝒙

(𝑗)

) = [𝑀

𝑱

𝑘𝑙

(𝒙

(𝑗)

)]

𝑛×𝑛

i 𝑀

𝑱

𝑘𝑙

(𝒙

(𝑗)

) =

𝜕𝑓𝑘(𝒙)

𝜕𝑥𝑙

|

𝒙=𝒙

(𝑗)

.

(1.4)

Ostatecznie uzyskujemy wzór rekurencyjny algorytmu N-R dla przypadku układu równań

𝒇(𝒙) = 𝟎

:

𝒙

(𝑗+1)

= 𝒙

(𝑗)

− 𝑖𝑛𝑣 (𝑴

𝑱

(𝒙

(𝑗)

)) ∙ 𝒇(𝒙

(𝑗)

),

(1.5)

przy czym 𝑖𝑛𝑣(𝑴) oznacza macierz odwrotną do 𝑴.

Podobnie, jak dla przypadku jednowymiarowego wykazuje się, że jeśli punkt startowy 𝒙

(0)

algorytmu leży

dostatecznie blisko rozwiązania 𝒙

∗

, to algorytm jest zbieżny. Wybór właściwego punktu startowego może

stanowić osobny problem w praktyce obliczeniowej.

2. Model tranzystora bipolarnego npn

Wprowadzenie modelu obwodowego tranzystora jest niezbędne, aby zrozumieć przedstawiony w dalszej

części instrukcji matematyczny opis przykładowego obwodu nieliniowego z tranzystorem. Ograniczymy się do
stałoprądowych modeli Ebersa-Molla tego elementu

[3]

. W pewnych sytuacjach w obliczeniach zgrubnych,

[3] Leon O. Chua, Pen-Min Lin: Komputerowa analiza układów elektronicznych. Algorytmy i metody obliczeniowe. WNT Warszawa 1981.

~ 4 ~

ręcznych, elektronicy wykorzystują dużo prostszy model tranzystora. Ten prostszy model też objaśnimy nieco
dalej i od razu tam wykorzystamy przy obliczaniu punktu startowego algorytmu rozwiązania przykładowego
obwodu z tranzystorem.
2.1.

Stałoprądowy model tranzystora bipolarnego npn

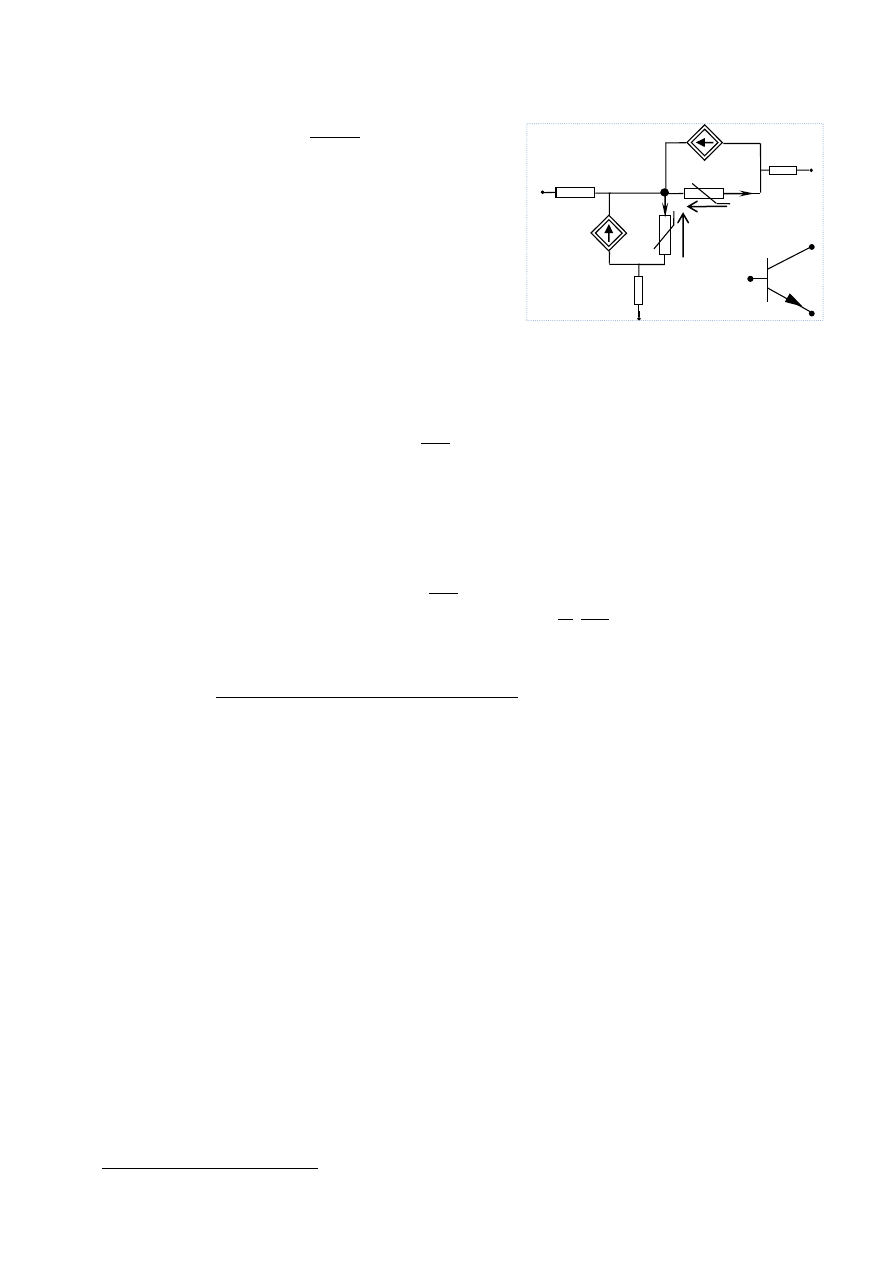
Na rysunku 2.2.1 pokazano pewien stałoprądowy model
tranzystora bipolarnego npn. Występuje w nim siedem
elementów. Oto ich opis:

R

E

– rezystancja kontaktów i objętościowa emitera

(typowa wartość: 0<R

E

<10),

R

B

– rezystancja kontaktów, objętościowa i rozproszona

bazy (typowa wartość: 0<R

B

<100),

R

C

– rezystancja kontaktów i objętościowa kolektora

(typowa wartość: 0<R

C

<10),

β

R



β

R







CF

– źródło prądowe sterowane prądem kolektora

(przy czym:

β

R

– parametr beta układu wspólnej bazy w połączeniu inwersyjnym (typowa

wartość:

β

R

=1), I

CF

– prąd złącza kolektorowego),

β

F



β

F





I

EF

– źródło prądowe sterowane prądem emitera (przy czym:

β

F

– parametr beta układu wspólnej

bazy w połączeniu normalnym (typowa wartość:

β

F

=100), I

EF

– prąd złącza emiterowego),

R

de

– nieliniowa rezystancja złącza emiter-baza opisana zależnością

𝐼

𝐸𝐹

= 𝐼

𝑆𝐸

(1 + 𝛽

𝐹

)

(

exp (

𝑞𝑒 𝑈1𝐸

𝑁𝐸𝑘𝑇

) − 1

)

(2.2)

(przy czym: I

SE

– prąd nasycenia złącza emiter-baza (typowa wartość: 10

-17

< I

SE

< 10

-9

A dla krzemu

i 10

-11

< I

SE

< 10

-5

A dla germanu), q

e

– ładunek elektronu=1.6∙10

-19

C, k – stała Boltzmanna=

1.38∙10

-23

J/K, T – temperatura bezwzględna złącz w kelwinach, N

E

– stała emisji złącza emiter-baza

(współczynnik korekcji zwiększający rezystancję dynamiczną emitera i napięcie złącza w porównaniu
do wartości idealnych określonych przez q

e

U

1E

/kT; typowa wartość: 1< N

E

<2.5 ) ),

R

dc

– nieliniowa rezystancja złącza kolektor-baza opisana zależnością

𝐼

𝐶𝐹

= 𝐼

𝑆𝐶

(1 + 𝛽

𝑅

)

(

exp

(

𝑞𝑒 𝑈2𝐶

𝑁𝐶𝑘𝑇

)

− 1

)

(2.3)

(przy czym: I

SC

– prąd nasycenia złącza kolektor-baza (I

SC

≈I

SE

∙

𝛽𝐹

𝛽𝑅

∙

1+𝛽𝑅

1+𝛽𝐹

), N

C

– stała emisji złącza kolektor-

baza (współczynnik korekcji zwiększający rezystancję dynamiczną kolektora i napięcie złącza
w porównaniu do wartości idealnych określonych przez q

e

U

2C

/kT; typowa wartość: 1< N

C

<2.5 )).

Ten model jest nieco uproszczonym

1

modelem Ebersa-Molla tranzystora npn.

3. Topologiczne podejście do macierzowego opisu z potencjałami węzłowymi

Podobnie jak w poprzednim ćwiczeniu z diodą, znowu zamierzamy wykorzystać pewien zalgorytmizowany

sposób tworzenia opisu sieci w prezentowanym dalej przykładowym obwodzie nieliniowym. Dlatego
konieczne jest krótkie przypomnienie tego sposobu.

3.1.

Macierz incydencji, a prądowe równania Kirchhoffa

Przypominamy, że struktura obwodu może być wizualizowana poprzez graf strukturalny. Gdy przyporządkujemy krawędziom

grafu orientację zgodną z założonym zwrotem prądów w obwodzie, uzyskamy graf prądowy. Graf ten możemy nie tylko narysować, ale
również „zakodować” w wygodnej dla komputera postaci macierzy zwanej (zredukowaną) macierzą incydencji, najczęściej oznaczanej
jako 𝑨.

Załóżmy, że wierzchołki grafu oznaczono liczbami 1, 2, .., 𝑛, a krawędzie liczbami 1, 2, …, 𝑏. Pełną macierz incydencji tego grafu 𝑨

𝒂

definiujemy następująco:

𝑨

𝒂

= [𝑎

𝑘𝑙

]

𝑛×𝑏

,

(3.1)

przy czym:

𝑎

𝑘𝑚

= 0, gdy krawędź k-ta nie jest incydentna

2

z m-tym wierzchołkiem,

𝑎

𝑘𝑚

= 1,

gdy krawędź k-ta jest incydentna z m-tym wierzchołkiem i skierowana od tego wierzchołka,

𝑎

𝑘𝑚

= −1,

gdy krawędź k-ta jest incydentna z m-tym wierzchołkiem i skierowana do tego wierzchołka.

Zredukowaną macierz incydencji uzyskamy z macierzy incydencji poprzez usunięcie dowolnego z jej wierszy.

Na rysunku 3.1.1 pokazano przykładowy graf (prądowy). Gdyby w tym grafie wybrać jako wierzchołek odniesienia wierzchołek 

i w związku z tym usunąć czwarty wiersz pełnej macierzy incydencji, to uzyskalibyśmy następującą (zredukowaną) macierz incydencji:

𝑨 = [

0 −1 −1 −1

1

0

0

0

0

1

0

0

0 −1

0

0

0

1

0

0

0

0

0 −1 −1 −1 −1

].

1

Nie jest to model globalny, gdyż nie uwzględniono upływności złącz BE i BC; w modelu globalnym te upływności są modelowane pr zez rezystory –

o megaomowych rezystancjach – podłączone równolegle do R

de

i R

dc

.

2

krawędź k jest incydentna z wierzchołkiem m wtedy i tylko wtedy, gdy wierzchołek m jest jednym z końców krawędzi k

C

R

B

B

E

R

dc

R

de



F

(1+



F

)

-1

I

EF



R

(1

+



R

)

-1

I

CF

I

CF

I

EF

U

2C

U

1E

R

C

R

E

C

B

E

R

ys

. 2

.2

.1

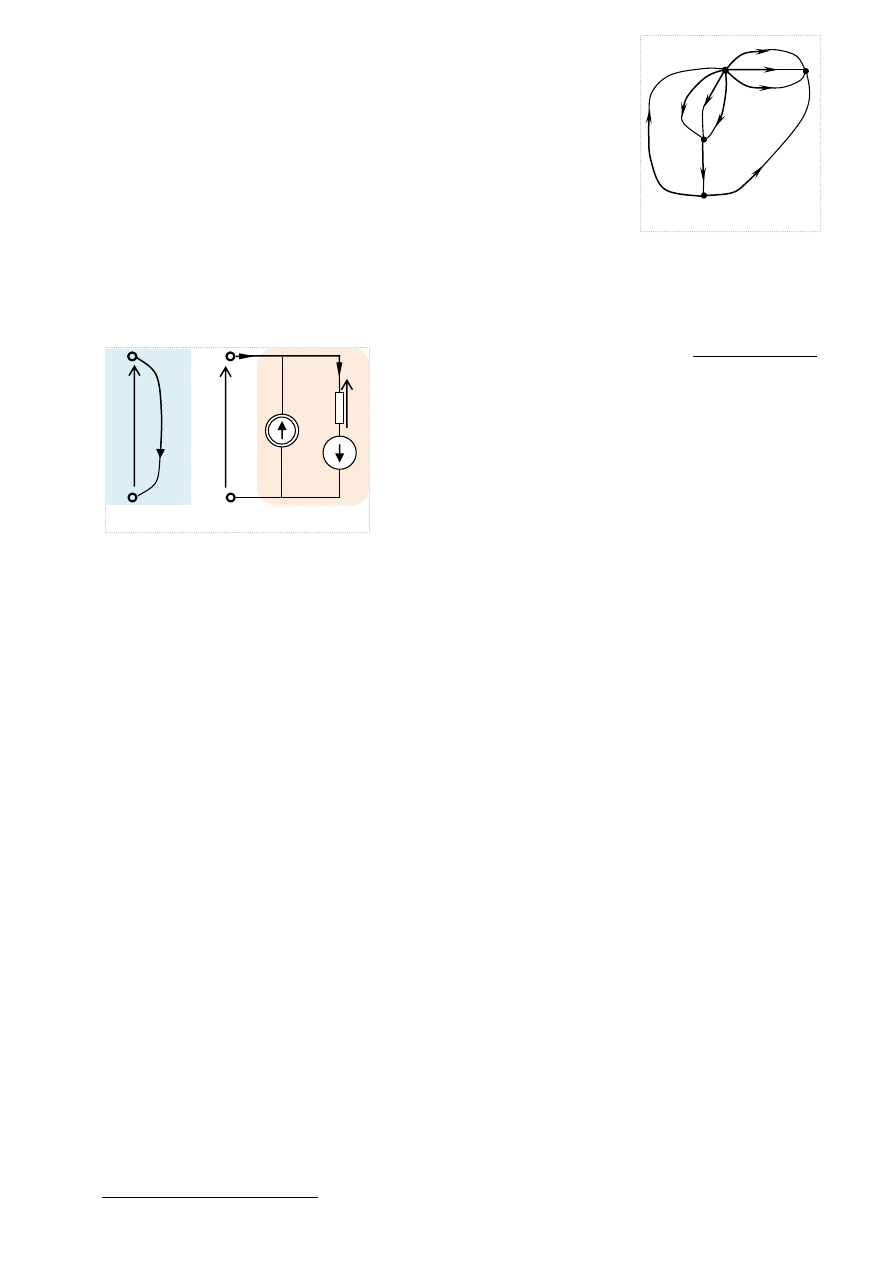
~ 5 ~

Oznaczamy prąd gałęzi obwodu odpowiadającej krawędzi 𝑘-tej grafu przez 𝑖̃

𝑘

. Te prądy

gałęziowe tworzą wektor prądów 𝑖̃ = 𝑐𝑜𝑙(𝑖̃

1

, 𝑖̃

2

, … , 𝑖̃

𝑏

). Wtedy zapis

𝑨 ∙ 𝒊̃ = 𝟎

(3.2)

jest macierzowym zapisem pełnego układu niezależnych równań PPK rozważanego obwodu (są
to równania PPK zapisane dla 𝑛-1 (spośród 𝑛) węzłów obwodu).

Graf napięciowy sieci dwójnikowej może być uzyskany z grafu prądowego przez zmianę

zwrotów wszystkich krawędzi. Niech 𝑢̃

𝑘

oznacza napięcie gałęzi sieci odpowiadającej krawędzi

𝑘 grafu napięciowego. Ponadto niech 𝒖

̃ = 𝑐𝑜𝑙(𝑢̃

1

, 𝑢̃

2

, … , 𝑢̃

𝑏

).

Przyjmijmy, że w sieci (o grafie prądowym z rysunku powyżej) przyjęto węzeł 4 jako węzeł

odniesienia i potencjały węzłowe węzłów 1, 2 i 3 względem węzła 4 wynoszą 𝑣

1

, 𝑣

2

i 𝑣

3

. Możemy

napisać, że

𝑢̃

1

= 𝑣

2

, 𝑢̃

2

= −𝑣

1

, 𝑢̃

3

= −𝑣

1

, 𝑢̃

4

= −𝑣

1

, 𝑢̃

5

= 𝑣

1

− 𝑣

2

, 𝑢̃

6

= −𝑣

3

, 𝑢̃

7

= −𝑣

3

, 𝑢̃

8

=

−𝑣

3

, 𝑢̃

9

= 𝑣

2

− 𝑣

3

.

Gdybyśmy oznaczyli przez 𝒗 wektor potencjałów węzłowych 𝑣

1

, 𝑣

2

i 𝑣

3

(tzn. 𝒗 = 𝑐𝑜𝑙(𝑣

1

,𝑣

2

, 𝑣

3

) ) i napisali

𝒖

̃ = 𝑨

𝑇

∙ 𝒗,

(3.3)

to byłby to macierzowy zapis wcześniejszych wyrażeń na napięcia 𝑢̃

𝑘

, 𝑘 = 1,2, … 9.

Przypominamy, że ostatnia równość jest słuszna w przypadku dowolnej sieci dwójnikowej i nosi nazwę transformacji węzłowej.

3.2.

Tworzenie równań węzłowych dla sieci rezystancyjnych

Warto po raz kolejny prześledzić, w jaki sposób można wykorzystać komputer do
utworzenia układu równań węzłowych dla sieci liniowych i nieliniowych. W tym
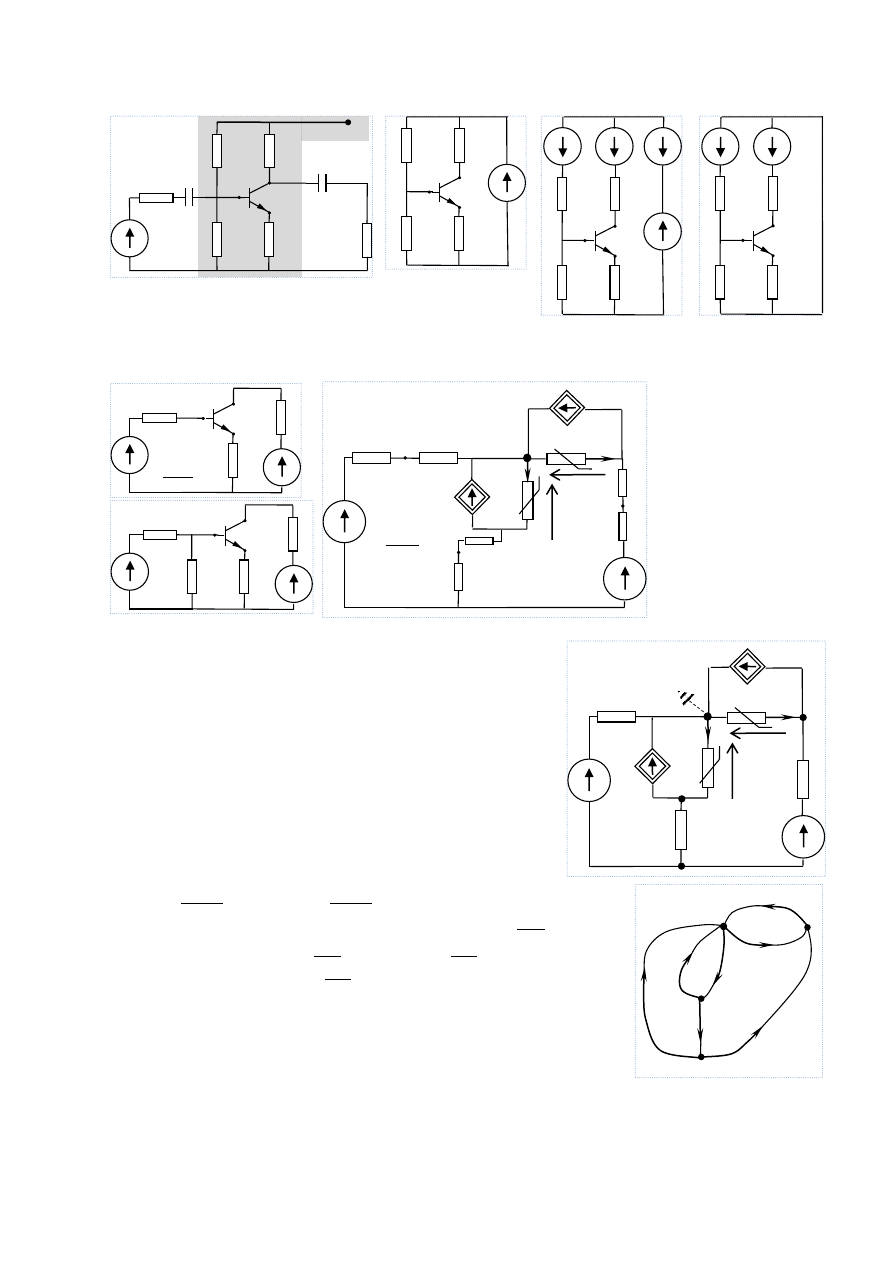
celu dogodnie jest przyjąć, że każda krawędź grafu sieci reprezentuje gałąź złożoną
sieci pokazaną na rysunku 3.2.1. Gałąź złożona może się składać ze źródeł nieza-
leżnych: prądowego 𝐽

𝑘

i napięciowego 𝐸

𝑘

oraz elementu 𝑏

𝑘

– może nim być

uzależniony napięciowo

1

rezystor 𝑅

𝑘

, bądź źródło prądowe sterowane napięciem

z innego elementu z grupy „𝑏

𝑘

”. Uprasza się o zwrócenie uwagi (bo to ważne) na

założone wzajemne usytuowanie zwrotów prądów i napięć elementów gałęzi
złożonej.

Rozważmy teraz sieć o grafie 𝑛 wierzchołkowym i 𝑏 krawędziowym. Załóżmy

numerację krawędzi od 1 do 𝑏, a numerację węzłów albo od 0 do 𝑛-1, albo od 1 do
𝑛. Nie tracąc nic z ogólności możemy założyć, że wierzchołkiem odniesienia jest

wierzchołek oznaczony numerem spoza zbioru {1, …, 𝑛-1} (przy numeracji wierzchołków od 0 do 𝑛-1 będzie to wierzchołek 0, a przy
numeracji od 1 do 𝑛 będzie nim wierzchołek 𝑛). Zdefiniujmy wektory napięć i prądów:

𝒖

̃ = 𝑐𝑜𝑙(𝑢̃

1

, . . , 𝑢̃

𝑏

) , 𝒖 = 𝑐𝑜𝑙(𝑢

1

, . . , 𝑢

𝑏

), 𝑬 = 𝑐𝑜𝑙(𝐸

1

, … , 𝐸

𝑏

),

𝒊̃ = 𝑐𝑜𝑙(𝑖̃

1

, . . , 𝑖̃

𝑏

) , 𝒊 = 𝑐𝑜𝑙(𝑖

1

, . . , 𝑖

𝑏

), 𝑱 = 𝑐𝑜𝑙(𝐽

1

, … , 𝐽

𝑏

).

(3.4)

Z rysunku 3.2.1 widać, że

𝒖

̃ = 𝒖 − 𝑬, 𝒊̃ = 𝒊 − 𝑱.

(3.5)

Prąd 𝑖

𝑘

zależy albo od napięcia 𝑢

𝑘

(rezystor), albo od napięcia powiedzmy 𝑢

𝑗

(źródło sterowane). Zatem możemy napisać:

𝒊 = 𝒈(𝒖) = 𝑐𝑜𝑙 (𝑔

1

(𝑢

𝑝

1

), 𝑔

2

(𝑢

𝑝

2

), … , 𝑔

𝑏

(𝑢

𝑝

𝑏

)),

(3.6)

gdzie {𝑝

1

,𝑝

2

, … , 𝑝

𝑏

} ⊂ {1, 2, … , 𝑏}.

(Widać, że 𝑏

𝑘

nie może być zwarciem, bo prąd elementu 𝑏

𝑘

ma być uzależniony od napięcia.)

W przypadku liniowym zachodzi oczywiście 𝑔

𝑗

(𝑢

𝑝

𝑗

) = 𝑔̅

𝑗

⋅ 𝑢

𝑝

𝑗

(𝑔̅

j

jest konduktancją lub transkonduktancją i jest mierzone w simensach) i wtedy

zapis 𝒊 = 𝒈(𝒖) można przedstawić jako 𝒊 = 𝑮

𝑏×𝑏

⋅ 𝒖, gdzie macierz 𝑮

𝑏×𝑏

nosi nazwę macierzy konduktancji gałęziowych (jest to inna macierz, niż

macierz konduktancji węzłowych!!!).

Wcześniej już zapisaliśmy, że 𝑨 ⋅ 𝒊̃ = 𝟎 i 𝒊̃ = 𝒊 − 𝑱. Stąd i z zależności 𝒊 = 𝒈(𝒖) wynika, że

𝑨 ⋅ 𝒈(𝒖) = 𝑨 ⋅ 𝑱.

Ponadto skoro 𝒖

̃ = 𝒖 − 𝑬 i 𝒖

̃ = 𝑨

𝑇

𝒗, to

𝒖 = 𝑨

𝑇

∙ 𝒗 + 𝑬.

Zatem

𝑨 ⋅ 𝒈(𝑨

𝑇

∙ 𝒗 + 𝑬) = 𝑨 ⋅ 𝑱.

(3.7)

W przypadku liniowym ostatnia zależność przekształca się następująco:

𝑨 ⋅ 𝑮

𝑏×𝑏

∙ (𝑨

𝑇

∙ 𝒗 + 𝑬) = 𝑨 ⋅ 𝑱,

(𝑨 ⋅ 𝑮

𝑏×𝑏

∙ 𝑨

𝑇

) ∙ 𝒗 = 𝑨 ⋅ (𝑱 − 𝑮

𝑏×𝑏

∙ 𝑬),

𝑮

𝑛

∙ 𝒗 = 𝑱

𝑛

.

Ostatnie równanie jest macierzowym zapisem równań węzłowych. Widać, że zarówno macierz konduktancji węzłowych 𝑮

𝑛

, jak i wektor

węzłowych wydajności prądowych 𝑱

𝑛

mogą być łatwo wyznaczone w programie komputerowym na podstawie macierzy incydencji A, macierzy

konduktancji gałęziowych 𝑮

𝑏×𝑏

i wektorów źródeł niezależnych J i E.

Wykorzystanie zależności 𝑨 ⋅ 𝒈(𝑨

𝑇

∙ 𝒗 + 𝑬) = 𝑨 ⋅ 𝑱 do „automatyzacji” tworzenia matematycznego opisu sieci

zilustrujemy w przykładzie obwodu z tranzystorem.

4. Przykładowe stałoprądowe obwody nieliniowe i ich rozwiązywanie metodami

przybliżonymi

4.1.

Układ z jednym tranzystorem bipolarnym – wyznaczenie punktu pracy

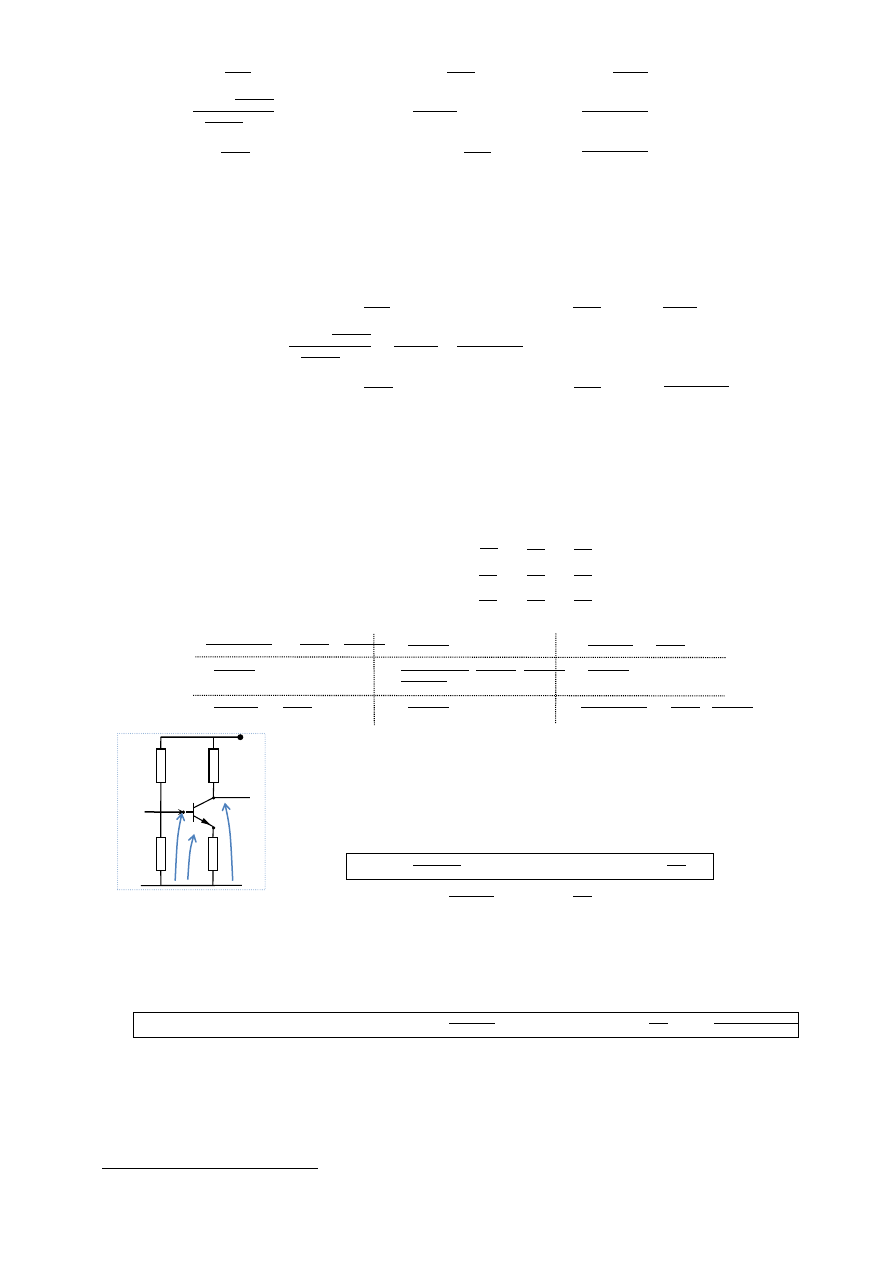
Układ, w którym zamierzamy wyznaczyć punkt pracy elementu nieliniowego (tranzystora) ma postać jak

na rysunku 4.1a). Przy wyznaczaniu punktu pracy interesują nas tylko prądy i napięcia stałe. Dzięki kondensa-

1

Jeżeli prąd rezystora jest funkcją napięcia na tym rezystorze, to mówimy, że ten rezystor jest uzależniony napięciowo

1

9

5





7

6

8

4



3

2



Rys. 3.1.1.

𝑢̃

𝑘

𝑖̃

𝑘

E

k

J

k

𝑢̃

𝑘

𝑖̃

𝑘

b

k

i

k

Rys. 3.2.1.

𝑢

𝑘

~ 6 ~

torom prąd stały nie popłynie przez nieopisane elementy układu. Do analizy stałoprądowej pozostaje zaciem-
niony fragment układu równoważny układowi pokazanemu na rysunku 4.1b). Źródło napięciowe można
przesunąć, a następnie układ dalej przekształcić (żadne z tych przekształceń nie zmieni napięć między
końcówkami tranzystora). Ciąg tych przekształceń jest pokazany na rysunkach 4.1c-f).

Gdy w schemacie 4.1f) zastąpimy tranzystor jego modelem dla prądów stałych, uzyskamy obwód

pokazany na rysunku 4.1g). Gdybyśmy znali napięcia U

1E

i U

2C

, potrafilibyśmy z obwodu 4.1g) wyznaczyć

pozostałe prądy i napięcia, dlatego ustalimy uwagę na wyznaczeniu tych napięć.

Dla ułatwienia zapisów
uprościmy oznaczenia,
tak jak zostało pokazane
na

schemacie

4.1h).

Przyjęto nadto, że węzeł
wskazany przez groty
napięć U

1E

i U

2C

będzie

węzłem odniesienia. Je-
go graf prądowy, przy
założeniu, że wykorzy-
stujemy gałęzie złożone,
ma postać pokazaną na

rysunku 4.1i).
Na tej podstawie piszemy macierze i wektory: incydencji A,
potencjałów węzłowych V, SPM J, SEM E, napięć dwójnikowych u,
prądów dwójnikowych i:

𝑨 = [

0 1 −1

1 0

0

0

1 0

0 −1 0

0

1

0 0

0

0 1 −1 −1

], 𝑽 = [

𝑣

1

𝑣

2

𝑣

3

],

𝑱 = 𝟎,

𝑬 = 𝑐𝑜𝑙(𝐸

1

, 0,0,0,0,0, 𝐸

7

),

𝒖 = 𝑐𝑜𝑙(𝑢

1

, … , 𝑢

7

)=𝑨

𝑇

𝑽 + 𝑬

=𝑐𝑜𝑙(𝑣

2

+ 𝐸

1

, 𝑣

1

, −𝑣

1

, 𝑣

1

− 𝑣

2

, 𝑣

3

, −𝑣

3

, 𝑣

2

− 𝑣

3

+ 𝐸

7

)

,

𝒊 = 𝑐𝑜𝑙(𝑖

1

, … , 𝑖

7

) = 𝒈(𝒖)

= 𝑐𝑜𝑙(𝑔

1

(𝑢

1

), 𝑔

2

(𝑢

6

), 𝑔

3

(𝑢

3

), 𝑔

4

(𝑢

4

), 𝑔

5

(𝑢

3

), 𝑔

6

(𝑢

6

), 𝑔

7

(𝑢

7

)),

gdzie:

𝐸

1

= 𝑈

𝐶𝐶

∙

𝑅12

𝑅11+𝑅12

, 𝐸

7

= 𝑈

𝐶𝐶

, 𝑅

1

=

𝑅11𝑅12

𝑅11+𝑅12

+ 𝑅

𝐵

, 𝑅

4

= 𝑅

14

+ 𝑅

𝐸

, 𝑅

7

= 𝑅

13

+ 𝑅

𝐶

,

𝑔

𝑘

(𝑢

𝑘

) = 𝑢

𝑘

/𝑅

𝑘

dla 𝑘 ∈ {1,4,7}, 𝑔

3

(𝑢

3

) = 𝐼

𝑆𝐸

(1 + 𝛽

𝐹

) (exp (

𝑞𝑒 𝑢3

𝑀𝐸𝑘𝑇

) − 1),

𝑔

6

(𝑢

6

) = 𝐼

𝑆𝐶

(1 + 𝛽

𝑅

) (exp (

𝑞𝑒 𝑢6

𝑀𝐶𝑘𝑇

) − 1), 𝑔

2

(𝑢

6

) =

𝛽𝑅

1+𝛽𝑅

𝑔

6

(𝑢

6

), 𝑔

5

(𝑢

3

) =

𝛽𝐹

1+𝛽𝐹

𝑔

3

(𝑢

3

).

Ponieważ dla 𝑘-tej gałęzi złożonej zachodzi

𝑖̃

𝑘

= 𝑖

𝑘

− 𝐽

𝑘

(macierzowo 𝒊̃ = 𝒊 − 𝑱; w naszym przykładzie dodatkowo 𝑱 = 𝟎) oraz zapisane
macierzowo równania PPK dla prądów 𝑖̃

𝑘

gałęzi złożonych mają postać

𝑨 ∙ 𝒊̃ = 0, więc możemy napisać, że

𝑨𝒊 = 𝑨𝑱 = 𝟎, czyli 𝑨𝒈(𝒖) = 𝟎,

(4.1)

albo w formie równoważnego układu równań:

{

𝑔

2

(𝑢

6

) − 𝑔

3

(𝑢

3

) + 𝑔

4

(𝑢

4

) = 0

𝑔

1

(𝑢

1

) − 𝑔

4

(𝑢

4

) + 𝑔

7

(𝑢

7

) = 0

𝑔

5

(𝑢

3

) − 𝑔

6

(𝑢

6

) − 𝑔

7

(𝑢

7

) = 0

R

11

R

12

R

13

R

14

U

CC

C

e(t)

B

E

Rys. 4.1a)

R

11

R

12

R

13

R

14

U

CC

C

B

E

R

ys

. 4

.1

b)

R

11

R

12

R

13

R

14

U

CC

C

B

E

U

CC

U

CC

U

CC

R

ys

.

4.

1c

)

R

11

R

12

R

13

R

14

C

B

E

U

CC

U

CC

R

ys

.

4.

1d

)

R

11

R

12

R

13

R

14

C

B

E

U

CC

U

CC

Rys. 4.1e)

R

11

||R

12

R

13

R

14

C

B

E

U

CC

𝑈

𝐶𝐶

𝑅

12

𝑅

11

+𝑅

12

Rys. 4.1f)

R

11

||R

12

R

13

R

14

C

U

CC

𝑈

𝐶𝐶

𝑅

12

𝑅

11

+𝑅

12

R

B

B

E

R

dc

R

de



R

(1

+



R

)

-1

I

CF

I

CF

I

EF

U

2C

U

1E

R

C

R

E

Rys. 4.1g)



F

(1+



F

)

-1

I

EF

R

1

R

7

R

4



E

7

E

1



R

6

R

3



F

(1+



F

)

-1

I

3

I

6

I

3

U

2C

U

1E



Rys. 4.1h)



R

(1

+



R

)

-1

I

6

1

5





7

6

4



3

2



Rys. 4.1i)

~ 7 ~

Uwzględnienie wcześniejszych wyrażeń na 𝒊, 𝒖, 𝑬 w ostatnim układzie równań prowadzi do układu równań

1

:

{

𝐼

𝑆𝐶

𝛽

𝑅

(

exp (

−𝑞𝑒𝑣3

𝑀𝐶𝑘𝑇

) − 1

)

−

𝐼

𝑆𝐸

(

1 + 𝛽

𝐹

) (

exp

(

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

)

− 1

)

+

𝑣1−𝑣2

𝑅14+𝑅𝐸

= 0

𝑣

2

+

𝑈

𝐶𝐶

∙

𝑅12

𝑅11+𝑅12

𝑅11𝑅12

𝑅11+𝑅12

+𝑅𝐵

−

𝑣

1

−𝑣

2

𝑅

14

+𝑅

𝐸

+

𝑣

2

−𝑣

3

+𝑈

𝐶𝐶

𝑅

13

+𝑅

𝐶

= 0

𝐼

𝑆𝐸

𝛽

𝐹

(

exp (

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

) − 1

) −

𝐼

𝑆𝐶

(

1 + 𝛽

𝑅

) (

exp

(

−𝑞𝑒𝑣3

𝑀𝐶𝑘𝑇

)

− 1

) −

𝑣

2

−𝑣

3

+𝑈

𝐶𝐶

𝑅

13

+𝑅

𝐶

= 0

(4.1a)

Uzyskaliśmy równanie

𝒇(𝑽) = 𝟎,

(4.2)

przy czym

𝒇(𝑽) = 𝒇(𝑐𝑜𝑙(𝑣

1

, 𝑣

2

, 𝑣

3

)) = [

𝑓

1

(𝑣

1

, 𝑣

2

, 𝑣

3

)

𝑓

2

(𝑣

1

, 𝑣

2

, 𝑣

3

)

𝑓

3

(𝑣

1

, 𝑣

2

, 𝑣

3

)

]=

=

[

𝐼

𝑆𝐶

𝛽

𝑅

(

exp (

−𝑞𝑒𝑣3

𝑀𝐶𝑘𝑇

) − 1

) −

𝐼

𝑆𝐸

(

1 + 𝛽

𝐹

) (

exp

(

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

)

− 1

)

+

𝑣1−𝑣2

𝑅14+𝑅𝐸

𝑣

2

+

𝑈

𝐶𝐶

∙

𝑅12

𝑅11+𝑅12

𝑅11𝑅12

𝑅11+𝑅12

+𝑅𝐵

−

𝑣

1

−𝑣

2

𝑅

14

+𝑅

𝐸

+

𝑣

2

−𝑣

3

+𝑈

𝐶𝐶

𝑅

13

+𝑅

𝐶

𝐼

𝑆𝐸

𝛽

𝐹

(

exp (

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

) − 1

) −

𝐼

𝑆𝐶

(

1 + 𝛽

𝑅

) (

exp

(

−𝑞𝑒𝑣3

𝑀𝐶𝑘𝑇

)

− 1

) −

𝑣

2

−𝑣

3

+𝑈

𝐶𝐶

𝑅

13

+𝑅

𝐶

]

.

(4.2a)

Równanie to rozwiążemy metodą Newtona-Raphsona, czyli wyliczając 𝑽 w kolejnych krokach według
algorytmu (por. wzór 1.5):

𝑽

(𝑗+1)

= 𝑽

(𝑗)

− [𝑴

𝑱

(𝑽

(𝑗)

)]

−1

𝒇(𝑽

(𝑗)

);

(4.3)

tak naprawdę szybciej będzie rozwiązywać następujący równoważny układ równań liniowych z niewiadomą
𝑽

(𝑗+1)

metodą Gaussa (unikamy odwracania macierzy Jacobiego 𝑴

𝑱

(𝑽

(𝑗)

)):

𝑴

𝑱

(𝑽

(𝑗)

) ∙ 𝑽

(𝑗+1)

= 𝑴

𝑱

(𝑽

(𝑗)

) ∙ 𝑽

(𝑗)

− 𝒇(𝑽

(𝑗)

)

(4.3a)

Pozostała do wyznaczenia macierz Jacobiego 𝑴

𝑱

(𝑽) = [

𝑑

𝑑𝑣1

𝑓

1

𝑑

𝑑𝑣2

𝑓1

𝑑

𝑑𝑣3

𝑓1

𝑑

𝑑𝑣1

𝑓2

𝑑

𝑑𝑣2

𝑓2

𝑑

𝑑𝑣3

𝑓2

𝑑

𝑑𝑣1

𝑓3

𝑑

𝑑𝑣2

𝑓3

𝑑

𝑑𝑣3

𝑓3

]. Elementarne obliczenia dają:

𝑴

𝑱

(𝑽) =

[

(1+𝛽𝐹)𝑞𝑒𝐼𝑆𝐸

𝑀𝐸𝑘𝑇

exp(

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

)+

1

𝑅14+𝑅𝐸

−

1

𝑅14+𝑅𝐸

−

𝛽𝑅𝑞𝑒𝐼𝑆𝐶

𝑀𝐶𝑘𝑇

exp(

−𝑞𝑒 𝑣3

𝑀𝐶𝑘𝑇

)

−

1

𝑅14+𝑅𝐸

1

𝑅11𝑅12

𝑅11+𝑅12

+𝑅𝐵

+

1

𝑅13+𝑅𝐶

+

1

𝑅14+𝑅𝐸

−

1

𝑅13+𝑅𝐶

−

𝛽𝐹𝑞𝑒𝐼𝑆𝐸

𝑀𝐸𝑘𝑇

exp(

−𝑞𝑒 𝑣1

𝑀𝐸𝑘𝑇

)

−

1

𝑅13+𝑅𝐶

(1+𝛽𝑅)𝑞𝑒𝐼𝑆𝐶

𝑀𝐶𝑘𝑇

exp(

−𝑞𝑒 𝑣3

𝑀𝐶𝑘𝑇

)+

1

𝑅13+𝑅𝐶

]

.

(4.3b)

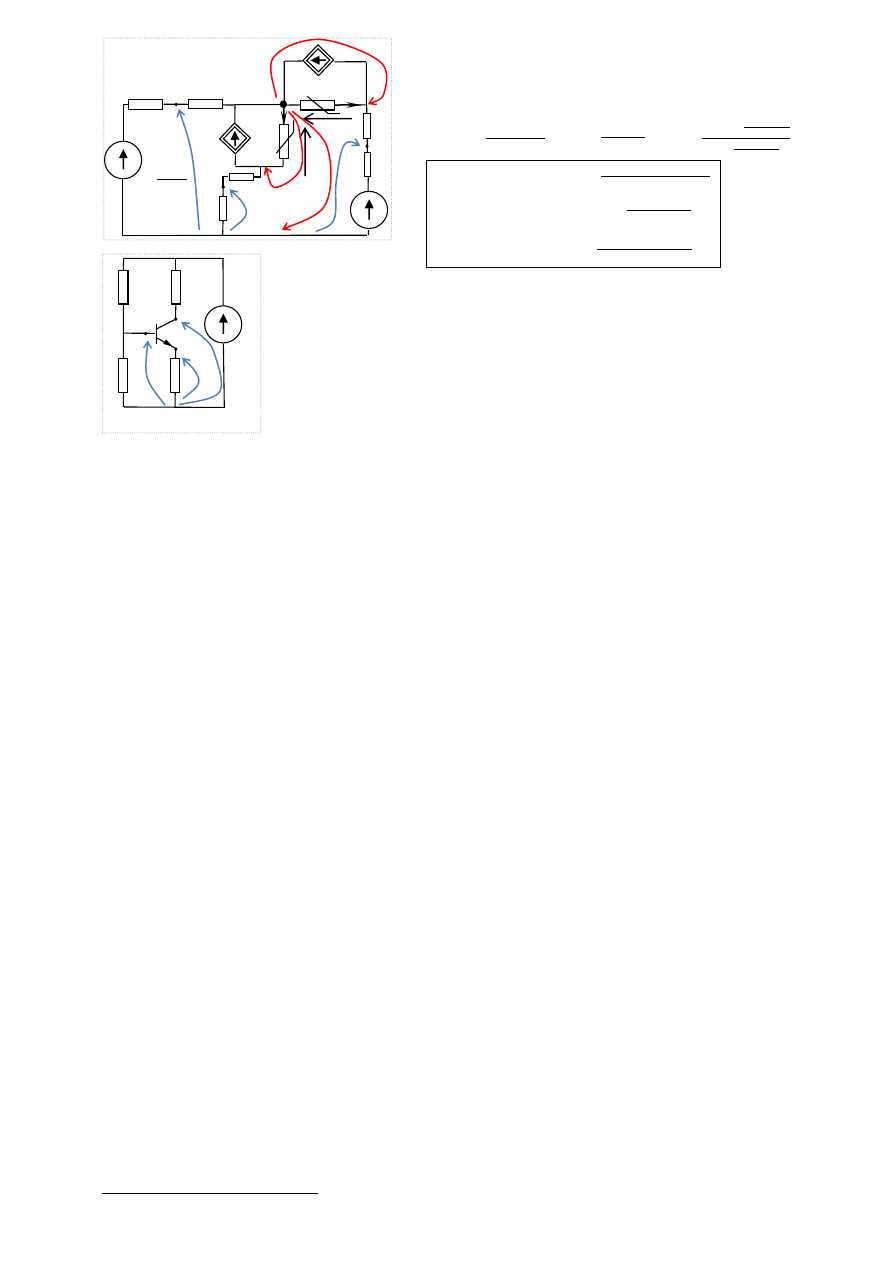
Aby uzyskać zbieżność algorytmu trzeba trafnie obrać punkt startowy algorytmu.
Wskazówką może być „inżynierskie” podejście do wyznaczania punktu pracy
tranzystora. Zakłada się w obliczeniach zgrubnych, że

w warunkach przewodzenia

tranzystora

napięcie emiter-baza wynosi (około) 0,7V oraz, że prąd bazy jest

praktycznie zerowy (czyli prąd kolektora ≅ prąd emitera: 𝐼

𝑅13

≅ 𝐼

𝑅14

). Wtedy (por.

rys. 4.1j):

𝑣

𝐵

= 𝑈

𝐶𝐶

𝑅12

𝑅11+𝑅12

, 𝑣

𝐸

≅ 𝑣

𝐵

− 0.7, 𝑣

𝐶

≅ 𝑈

𝐶𝐶

−

𝑣𝐸

𝑅14

∙

𝑅

13

(4.4)

(oraz 𝑈

𝐶𝐸

≅ 𝑈

𝐶𝐶

− (𝑈

𝐶𝐶

𝑅12

𝑅11+𝑅12

− 0,7) (1

+

𝑅13

𝑅14

)).

Jeżeli uwzględnimy, że w przybliżeniu

𝑅

𝐵

≅ 0, 𝑅

𝐶

≅ 0, 𝑅

𝐸

≅ 0,

czyli

𝑈

𝑅𝐵

≅ 0, 𝑈

𝑅𝐶

≅ 0, 𝑈

𝑅𝐸

≅ 0,

to (porównaj rys. 4.1k):

𝑣

1

≅ 𝑣

𝐸

− 𝑣

𝐵

≅ −0.7V, 𝑣

2

≅ −𝑣

𝐵

≅ −𝑈

𝐶𝐶

𝑅12

𝑅11+𝑅12

, 𝑣

3

≅ 𝑣

𝐶

− 𝑣

𝐵

≅ 0.7

𝑅13

𝑅14

+ 𝑈

𝐶𝐶

𝑅11𝑅14−𝑅12𝑅13

(𝑅11+𝑅12)𝑅14

.

(4.5)

Taką właśnie będziemy zakładać wartość startowego wektora 𝑽

(0)

= 𝑐𝑜𝑙(𝑣

1

(0)

, 𝑣

2

(0)

, 𝑣

3

(0)

).

1

Czytelnik łatwo zauważy, że te trzy równania bilansu prądów dla węzłów 1, 2 i 3 można „napisać od ręki”, bez przedstawionej tu procedury. Niestety

komputer schematu „nie widzi”, więc zadajemy mu problem stosownie do jego możliwości, a on „odwdzięcza się” automatycznym tworzeniem równań
oraz ich rozwiązywaniem.

R

11

R

12

R

13

R

14

U

CC

C

B

E

R

ys

.

4.

1j)

v

C

v

E

v

B

I

B

=0

~ 8 ~

Gdy już wyznaczymy wektor potencjałów węzłowych 𝑽, możemy
przystąpić do wyznaczania potencjałów v

E

, v

B

i v

C

liczonych

względem dolnego węzła. Z rysunku 4.1k odczytujemy
(zakładamy zwroty prądów w prawo i ku dołowi):

𝐼

𝑅𝐶

=

𝑣3−𝑣2−𝑈𝐶𝐶

𝑅𝐶+𝑅13

, 𝐼

𝑅𝐸

=

𝑣

1

−𝑣

2

𝑅

𝐸

+𝑅

14

, 𝐼

𝑅 𝐵

=

𝑣2+𝑈𝐶𝐶∙

𝑅12

𝑅11+𝑅12

𝑅𝐵+

𝑅11𝑅12

𝑅11+𝑅12

,

𝑣

𝐶

= 𝑣

3

− 𝑣

2

− 𝐼

𝑅 𝐶

𝑅

𝐶

=

(𝑣

3

−𝑣

2

)𝑅

13

+𝑈

𝐶𝐶

𝑅

𝐶

𝑅

𝐶

+𝑅

13

,

𝑣

𝐸

= 𝑣

1

− 𝑣

2

− 𝐼

𝑅𝐸

𝑅

𝐸

=

(𝑣

1

−𝑣

2

)𝑅

14

𝑅

𝐸

+𝑅

14

,

𝑣

𝐵

= −𝑣

2

+ 𝐼

𝑅𝐸

𝑅

𝐵

=

𝑈

𝐶𝐶

𝑅

11

−1

𝑅

𝐵

−𝑣

2

(𝑅

11

−1

+𝑅

12

−1

)𝑅

𝐵

+1

.

(4.6)

Po wyznaczeniu wartości potencjałów bazy, emitera i kolektora możemy wyznaczyć
napięcia i prądy na elementach układu polaryzującego tranzystor. Wynoszą one
(prądy strzałkowane ku dołowi; rys. 4.1l):

𝑈

𝑅11

= 𝑈

𝐶

− 𝑣

𝐵

, 𝐼

𝑅11

= 𝑈

𝑅11

/𝑅

11

, 𝑈

𝑅12

= 𝑣

𝐵

, 𝐼

𝑅12

= 𝑈

𝑅12

/𝑅

12

,

𝑈

𝑅13

= 𝑈

𝐶

− 𝑣

𝐶

, 𝐼

𝑅13

= 𝑈

𝑅13

/𝑅

13

, 𝑈

𝑅14

= 𝑣

𝐸

, 𝐼

𝑅14

= 𝑈

𝑅14

/𝑅

14

,

𝐼

𝑈 𝐶𝐶

= −(𝐼

𝑅11

+ 𝐼

𝑅13

).

(4.7)

Wyznaczymy jeszcze moce, jakie są wydzielane na elementach obwodu. Uzyskujemy:

𝑃

𝑅𝑗

= 𝑈

𝑅

𝑗

𝐼

𝑅

𝑗

, 𝑃

𝑈𝐶𝐶

= 𝑈

𝑈

𝐶𝐶

𝐼

𝑈

𝐶𝐶

, 𝑃

tranz

= (𝑣

𝐵

− 𝑣

𝐸

)𝐼

𝑅14

+ (𝑣

𝐶

− 𝑣

𝐵

)𝐼

𝑅13

.

(4.8)

5. Rozwiązywanie równań i układów równań nieliniowych - wybrane narzędzia

MATLAB-a. Zapewnienie zbieżności w programie SPICE

W tym punkcie zarysujemy podstawy wykorzystania MATLAB-a do rozwiązywania nieliniowych równań

algebraicznych jednej bądź wielu zmiennych i bardzo krótko skomentujemy, jak radzi sobie z ewentualną
niezbieżnością algorytmu Newtona-Raphsona program SPICE. Niekiedy jest to powtórzenie lub rozszerzenie
tego, co zawierała instrukcja do poprzedniego ćwiczenia.

5.1.

Definiowanie funkcji w MATLAB-ie

Warto rozpocząć od sposobów definiowania funkcji matematycznych w MATLAB-ie. Oprócz funkcji wbudowanych,

można korzystać z funkcji definiowanych przez Użytkownika. Te ostatnie zazwyczaj tworzy się albo wykorzystując
polecenie inline, albo poprzez utworzenie m-pliku w edytorze MATLAB-a [5].

5.1.1. Polecenie inline

Dla prostych przypadków, szczególnie dla funkcji jednolinijkowych, tworzenie funkcji poleceniem inline jest po

prostu wygodne. Na przykład, aby utworzyć funkcję 𝑓(𝑥) = 2 cos

3

(𝑥) + 5𝑥

2

− 𝑥 + 2 wystarczy napisać (po znaku

zachęty; tu „cs>>”):

cs>> f=inline(‘2*(cos(x))^3+5*x^2-x+2’)

Od tego momentu można korzystać ze zdefiniowanej funkcji, na przykład wyznaczyć jej wartość w punkcie x=π .

5.1.2. M-plik. Użycie edytora MATLAB-a do tworzenia funkcji

Dzięki edytorowi użytkownik może pisać funkcje dowolnej złożoności/długości. Wskazane jest postępować

następująco:

1. ustawić bieżący folder roboczy na swój zasób dyskowy (np. na

D:\ZasobyStudenckie, poprzez

cd D:\ZasobyStudenckie)

2. a) wpisać polecenie „edit fun.m” w linii zachęty, albo

b) wybrać „File”, „New”, „M-File”

i wpisać:

function y=fun(x)
y=2*(cos(x))^3+5*x^2-x+2
endfunction

3. zapisać plik w folderze roboczym pod nazwą fun.m.

[5] Salamon R.: MATLAB. Podstawy i zastosowania. PG WETI KSEM Gdańsk 2008

R

11

||R

12

R

13

R

14

C

U

CC

𝑈

𝐶𝐶

𝑅

12

𝑅

11

+𝑅

12

R

B

B

E

R

dc

R

de



F

(1+



F

)

-1

I

EF



R

(1

+



R

)

-1

I

CF

I

CF

I

EF

U

2C

U

1E

R

C

R

E

v

1

v

2

v

3

v

B

v

E

v

C

Rys. 4.1k)

R

11

R

12

R

13

R

14

U

CC

C

B

E

v

E

v

C

v

B

Rys. 4.1l)

~ 9 ~

Uwaga. Ponieważ nazwa funkcji i m-pliku, w którym ta funkcja jest zapisana muszą być identyczne, ważne jest, by

edytowaną zawartość zapisać pod nazwą nazwa_funkcji.m (czyli w powyższym przykładzie pod nazwą fun.m).

5.2.

Wyznaczanie rozwiązań równań w MATLAB-ie

5.2.1. Funkcja fzero MATLAB-a

Można wykorzystać funkcję fzero do równania nieliniowego o postaci f(x)=0. Lewa strona równania musi być

wpierw zapisana jako funkcja (inline lub m-plik).
Oto jak wyglądałoby rozwiązanie równania 2*(cos(x))^3+5*x^2-x+2=0 przy użyciu inline i fzero:

cs>> f=inline(‘2*(cos(x))^3+5*x^2-x+2’);

cs>> fzero(f,4)
ans =

0.22919

cs>>

To samo przy użyciu m-pliku definiującego funkcję fun wyglądałoby następująco:

cs>>x=fzero(fun,4)

x=

0.22919

cs>>

Funkcja fzero wykorzystuje podejście podziału przedziału w celu lokalizacji pierwiastków.

5.2.2. Funkcja roots MATLAB-a
Jeżeli układ nieliniowych równań algebraicznych składa się z równań wielomianowych, można użyć procedury
roots w celu znalezienia zer wielomianu. Rozważmy wielomian 𝑤(𝑥) = 𝑥

3

− 5𝑥

2

− 𝑥 + 2. Użytkownik

powinien utworzyć wektor współczynników wielomianu (w kolejności malejących potęg zmiennej), a
następnie użyć polecenia roots:

cs>>w=[1 -5 -1 2]; roots(w)

ans=

5.1190

-0.6874

0.5684

cs>>

Jeszcze tylko sprawdzimy, czy te liczby są pierwiastkami rozważanego wielomianu:

cs>> p=inline('w(1)*x.^3+w(2)*x.^2+w(3)*x+w(4)'); p(roots(w))

ans=

3.7303e-014

-4.4409e-016

4.4409e-016

cs>>

Widać, że przybliżonymi pierwiastkami są.

Uwaga. Przy zapisywaniu wektora współczynników wielomianu należy wpisywać wszystkie (również
zerowe!!!) współczynniki (np., gdy 𝑤(𝑥) = 𝑥

4

+ 3𝑥

2

+ 1, to w=[1 0 3 0 1])

5.2.3. Funkcja fsolve MATLAB-a
Do rozwiązywania układów równań nieliniowych stosuje się w MATLAB-ie procedurę fsolve wykorzystującą
metody quasi-Newtona [6]. Zadaniem Użytkownika jest dostarczenie procedury wyznaczania (wektora
wartości) funkcji. Dla przykładu rozwiążmy następujący układ równań

{

𝑓

1

(𝑥

1

, 𝑥

2

) = 0

𝑓

2

(𝑥

1

, 𝑥

2

) = 0

z niewiadomymi 𝑥

1

i 𝑥

2

i wyrażeniami po lewych stronach równości:

𝑓

1

(𝑥

1

, 𝑥

2

) = 𝑥

1

− 10𝑥

2

2

+ cos(𝑥

1

+ 𝑥

2

) , 𝑓

2

(𝑥

1

, 𝑥

2

) = 𝑥

1

+ 5𝑥

1

2

+ exp (𝑥

1

− 𝑥

2

)

M-plik i funkcję MATLAB-a realizującą wyżej przedstawione wyrażenia nazwiemy Funef.m i Funef:

function f=Funef(x)

f(1)=x(1)-10*x(2)*x(2)+cos(x(1)+x(2));

f(2)=x(1)+5*x(2)*x(2)+exp(x(1)-x(2));

endfunction

(Oczywiście powyższy skrypt funkcji zapisujemy w pliku Funef.m.) Przyjmiemy punkt startowy algorytmu
x0=[0;0] (wektor kolumnowy) i uruchamiamy obliczenia. Zapis w MATLAB-ie i wyniki są następujące:

cs>>x0=[0;0];

cs>>fsolve('Funef',x0)

ans =

-0.63683

-0.10140

[6] http://www.mathworks.com/access/helpdesk/help/toolbox/optim/

~ 10 ~

5.2.3.1. Funkcja fsolve z pakietu OCTAVE

W pakiecie GNU Octave, który jest w wysokim stopniu zgodnym odpowiednikiem MATLAB-a, ale jest

rozpowszechniany w ramach powszechnej licencji publicznej (GNU), także dostępne są procedury
rozwiązywania układów równań. Ich nazwy są na ogół identyczne jak w MATLABIE, zaś stosowanie i działanie
podobne. Tu ograniczymy się do przedstawienia funkcji fsolve.
Oto opis funkcji fsolve z pakietu OCTAVE:
- sposób wywołania:

[x, fval, info] = fsolve (fcn, x0);

- oznaczenia:

fcn

- nazwa funkcji postaci f(x)

x0

- warunek początkowy.

- komentarz:

jeżeli fcn jest dwuelementową tablicą łańcuchów lub dwuelementową macierzą klatkową zawierającą
albo nazwę funkcji albo inline lub uchwyt do funkcji, to pierwszy element nazywa funkcję, a drugi nazywa
(definiuje) jakobian j(x) postaci

𝒋(𝒙) = [𝑗

𝑘𝑙

(𝒙)] , gdzie 𝑗

𝑘𝑙

(𝒙) =

𝜕

𝜕𝑥𝑙

𝑓

𝑘

(𝒙)

.

W Octave jest również dostępna funkcja

fsolve_options (opt, val).

Ta funkcja, gdy jest wywoływana z dwoma parametrami, pozwala ustawić wartości opcji dla funkcji fsolve,
a gdy z jednym wtedy „odczytuje” odpowiednią opcję, wreszcie gdy zostanie wywołana bez parametrów,
wtedy „wyświetla” dostępne opcje i ich aktualne wartości.

Jedną z opcji jest

„tolerance”

określająca nieujemną tolerancję względną.

Oto pełny przykład użycia funkcji fsolve z pakietu Octave. Aby rozwiązać układ równań:

−2𝑥

2

+ 3𝑥𝑦 + 4 𝑠𝑖𝑛(𝑦) = 6

3𝑥

2

− 2𝑥𝑦

2

+ 3 𝑐𝑜𝑠(𝑥) = −4

najpierw musimy napisać m-funkcję, która oblicza wartości danej funkcji matematycznej. Tu na przykład
mógłby to być następujący zapis:

function y = f(x)

y(1) = -2*x(1)^2 + 3*x(1)*x(2) + 4*sin(x(2)) - 6;

y(2) = 3*x(1)^2 - 2*x(1)*x(2)^2 + 3*cos(x(1)) + 4;

endfunction

Następnie wywołujemy fsolve

z warunkiem początkowym, aby znaleźć pierwiastki układu równań. Dla

wyżej zdefiniowanej funkcji f mogłoby to wyglądać następująco:

[x, info] = fsolve(@f, [1; 2])

W efekcie takiego wywołania uzyskalibyśmy:

x =
0.57983
2.54621
info = 1

Komunikat

info = 1

oznacza, że proces iteracyjny był zbieżny.

Jeżeli w danych nie podano macierzy Jacobiego (tak jak w powyższym przykładzie), to jest ona przybliżana
numerycznie. Wymaga to wielu obliczeń wartości funkcji i spowalnia proces rozwiązania układu równań.
W powyższym przykładzie można było obliczyć macierz Jacobiego analitycznie. Efekt obliczeń zapisano w
postaci m-funkcji:

function MJ = JacobiMatrix(x)

MJ(1,1) = 3*x(2) - 4*x(1);

MJ(1,2) = 4*cos(x(2)) + 3*x(1);

MJ(2,1) = -2*x(2)^2 - 3*sin(x(1)) + 6*x(1);

MJ(2,2) = -4*x(1)*x(2);

endfunction

Użycie tej macierzy Jacobiego w funkcji fsolve wygląda następująco:

[x, info] = fsolve({@f,@JacobiMatrix},[1;2]);

Rezultat tego użycia funkcji

fsolve

jest identyczny z wcześniejszym.

5.3. Uwagi. Inne przydatne procedury

Podsumujmy - w MATLAB-ie (i w Octave) możemy rozwiązać układ równań nieliniowych postaci

~ 11 ~

𝒇(𝒙) = 𝟎

używając funkcji fsolve. Funkcja ta wykorzystuje techniki iteracyjne, przeto wymaga podania punktu
startowego obliczeń, a to ma również czasem i taki skutek, że wystąpi rozbieżność algorytmu, mimo istnienia
rozwiązania układu równań. O zbieżności algorytmu mówi trzeci parametr wyniku wywołania funkcji fsolve.

Ponadto przy znajdowaniu rozwiązań układów równań nieliniowych mogą być pomocne inne procedury

MATLAB-a, na przykład: polyder, która umożliwia wyznaczenie pochodnej wielomianu, polyval umożli-
wiająca wyznaczenie wartości wielomianu w podanym punkcie, feval wyznaczająca wartość funkcji w
punkcie, fminsearch znajdująca minimum funkcji wielu zmiennych, fminbnd umożliwiająca wyznaczenie
wartości argumentu funkcji jednej zmiennej, dla którego ta funkcja osiąga minimum, fplot , która konstruuje
wykres, ezplot konstruująca wykres funkcji dwóch zmiennych, czy optimset pozwalająca utworzyć lub
zmodyfikować strukturę opcji optymalizacji – to polecenie wykorzystywane jest jako argument wejściowy
funkcji: fsolve, fminbnd, fminsearch, fzero, lsqnonneg. W razie potrzeby Czytelnik znajdzie opis
tych procedur w literaturze, bądź bezpośrednio w pomocy MATLAB-a.

5.4. Środki zaradcze w programie SPICE na wypadek niezbieżności algorytmu Newtona-Raphsona

Gdy w programie Micro-Cap 9 (jedna z wersji SPICE-a) wybierzemy Analysis - Dynamic AC, a następnie

Dynamic AC – Operating Point Methods, to pojawi się okienko z dostępnymi metodami wyznaczania punktu
pracy (Standard Newton-Raphson, Diagonal Gmin Stepping, Junction Gmin Stepping, Source Stepping,
Pseudo Transient). Pierwsza z nich to omawiana wcześniej metoda Newtona-Raphsona. Jest ona niezawodna,
ale tylko wtedy, gdy punkt startowy algorytmu leży dostatecznie blisko rozwiązania dokładnego. Niestety
bywa, że nie leży i proces staje się rozbieżny. Wobec niezbieżności obliczeń mających na celu znalezienie
statycznego punktu pracy układu klasyczną metodą Newtona-Raphsona stosuje się specjalną procedurę
obliczeń. Jej idea jest następująca: w układzie, w którym wszystkie niezależne źródła napięciowe i prądowe
mają wydajność równą zeru wszystkie potencjały węzłowe również są równe zeru. Jeżeli powiększymy
wydajność źródeł do kilku procent ich wydajności nominalnej to należy się spodziewać, że stosując zwykły
algorytm Newtona-Raphsona i zaczynając iteracje od zerowych wartości potencjałów węzłowych łatwo
znajdziemy punkt pracy układu. Otrzymany punkt pracy może posłużyć dalej jako punkt początkowy do
obliczania punktu pracy po dalszym powiększeniu wydajności źródeł. Jeżeli na każdym etapie tej procedury
jesteśmy w stanie znaleźć statyczny punkt pracy to w momencie, gdy źródła osiągną swoją wydajność
nominalną obliczony punkt pracy jest właściwym punktem pracy układu. Ta metoda „kroczących źródeł”
nazywana jest przez Izydorczyka [7] metodą parametryzacji źródeł, a przez Porębskiego i Korohodę [8] metodą
kontynuacji (ang.: source stepping). Jest to „sztuczka”, która w istotny sposób polepsza zbieżność obliczeń
statycznego punktu pracy układu i w wielu przypadkach jest bardzo użyteczna. Czytelnika zainteresowanego
pozostałymi „sztuczkami” zachęcamy do samodzielnych poszukiwań.

Pytania kontrolne

1. Co to jest macierz Jacobiego? Oblicz macierz Jacobiego 𝐽(𝑥

1

, 𝑥

2

) dla funkcji 𝒇(𝑥

1

, 𝑥

2

) = 𝑐𝑜𝑙(𝑓

1

, 𝑓

2

) = 𝑐𝑜𝑙(𝑥

1

2

, 𝑥

2

3

) .

2. Wzór rekurencyjny algorytmu N-R dla układu równań 𝒇(𝒙) = 𝟎 ma postać 𝒙

(𝑗+1)

= 𝒙

(𝑗)

− 𝑖𝑛𝑣 (𝑴

𝑱

(𝒙

(𝑗)

)) ∙ 𝒇(𝒙

(𝑗)

). Objaśnij

oznaczenia występujące w tym wzorze. Rozszyfruj skrót N-R. Co wiesz o zbieżności algorytmu N-R?

3. Z ilu elementów składa się - przedstawiony w tej instrukcji - nieco uproszczony stałoprądowy model Ebersa-Molla tranzystora

npn? Jaką rolę spełniają w tym modelu stałe emisji M

E

i M

C

?

4. Co to jest macierz incydencji grafu? Narysuj graf o (zredukowanej) macierzy incydencji 𝑨 = [

1

0 −1

−1 1

0

].

5. Zapisz i objaśnij równość nazywaną transformacją węzłową (w szczególności objaśnij użyte w tej równości oznaczenia).
6. Co to jest gałąź złożona sieci dwójnikowej? Narysuj ją i objaśnij, dlaczego idealne źródło napięciowe nie może być samodzielnie

reprezentowane taką gałęzią, a idealne źródło prądowe może.

7. Dla sieci dwójnikowej utworzono graf prądowy wykorzystując koncepcję gałęzi złożonych. Macierz incydencji tego grafu to

𝑨 = [

1

0 −1

−1 1

0

], wektor napięć źródłowych sieci wynosi 𝑬 = 𝑐𝑜𝑙(𝐸

1

, 0,0), a wektor prądów źródłowych to

𝑱 = 𝑐𝑜𝑙(0,0, 𝐽

3

), wreszcie prądy uzależnionych napięciowo dwójników 𝑔

𝑘

sieci są zdefiniowane następująco:

𝒊 = 𝑐𝑜𝑙(𝐺

1

𝑢

1

, 𝐺

2

𝑢

2

, 𝑔

3

(𝑢

3

)). Zapisz równania węzłowe tej sieci oraz narysuj ją.

8. Podaj twierdzenie Thevenina bądź Nortona i skonstruuj prosty przykład objaśniający zastosowanie podanego przez Ciebie

twierdzenia.

9. Na czym polega uproszczone, „inżynierskie” podejście do wyznaczania punktu pracy tranzystora?
10. Podaj przykład definiowania funkcji przy pomocy polecenia inline.
11. Podaj ciąg poleceń MATLAB-a , dzięki którym, przy wykorzystaniu procedury roots, zostaną obliczone pierwiastki funkcji

𝑥

6

− 2𝑥

3

+ 𝑥 + 1.

12. Opisz krótko „sztuczkę” wykorzystywaną w programie SPICE w celu zaradzenia możliwej niezbieżności algorytmu N-R przy

wyznaczaniu polaryzacji w układzie z elementami nieliniowymi.

~ 12 ~

Literatura

[1]Wacław

Sierpiński

: Zasady algebry wyższej, "Monografie Matematyczne" Tom 11, Rozdział 10.

Plik

pdf

jest dostępny z serwisu

Biblioteka Wirtualna Nauki

[2] Andrzej Szatkowski, Jacek Cichosz: Metody numeryczne. Podstawy teoretyczne. WPG, Gdańsk 2002
[3] Leon O. Chua, Pen-Min Lin: Komputerowa analiza układów elektronicznych. Algorytmy i metody obliczeniowe. WNT

Warszawa 1981.

[4] Jerzy Osiowski, Jerzy Szabatin: Podstawy teorii obwodów, WNT Warszawa
[5]Roman Salamon: MATLAB. Podstawy i zastosowania. PG WETI KSEM Gdańsk 2008
[6] http://www.mathworks.com/access/helpdesk/help/toolbox/optim/
[7] Jacek Izydorczyk: PSpice – komputerowa symulacja układów elektronicznych. Wydawnictwo Helion 1993

Zob. też wersja elektroniczna na http://ftp.pei.prz.rzeszow.pl/PSpice-Izydorczyk/

[8] Jan Porębski J., Przemysław Korohoda: SPICE – program analizy nieliniowej układów elektronicznych. PWN

Warszawa 1993