Cyfrowe przetwarzanie sygnałów

Transformaty ortogonalne (05)

Sławomir Kulesza

Wykład fakultatywny dla studentów

III r. spec. Informatyka ogólna

Rok akademicki 2012/2013

Transformaty skończone

●

Każde przekształcenie skończonego w sensie

czasu trwania sygnału z dyskretnym czasem na

sygnał o tej samej długości zależny od innej

wielkości nazywamy transformatą.

●

Transformata mapuje sygnał z dziedziny czasu

na przeciwdziedzinę (np. częstości).

●

Transformata odwrotna mapuje sygnał z

przeciwdziedziny z powrotem na dziedzinę

czasu.

Para transformat

●

Niech x[n] będzie sygnałem z dyskretnym
czasem (o długości N), zaś X[k] niech będzie
N-punktowym ciągiem współczynników jego
transformaty, wówczas prostą transformatę:

nazywamy równaniem analizy sygnału

X [k ]=

∑

n=0

N −1

x [n] Ψ

∗

[

k , n]

Para transformat

●

Analogicznie, transformatę odwrotną:

określa się mianem równania syntezy
sygnału.

●

Występujący w obu transformatach sygnał
Ψ[k,n] nazywany jest bazą transformaty.

x [n]=

1

N

∑

n=0

N −1

X [ k ] Ψ [k , n]

Transformaty ortogonalne

●

Spośród licznych transformat skończonych,
wyróżnioną grupę stanowią transformaty
ortogonalne spełniające warunek:

●

Transformaty ortogonalne zbudowane są
zatem w oparciu o ortogonalne sygnały
bazowe

1

N

∑

n=0

N −1

Ψ [

k , n] Ψ

∗

[

l , n]=

{

1⇔l=k
0⇔l≠k

Zachowanie energii

●

Transformaty ortogonalne zachowują energię
sygnału:

Jest to tzw. równość Parsevala

∑

n=0

N −1

∣

x [n]∣

2

=

∑

n=0

N −1

x [n] x

∗

[

n]=

1

N

∑

n=0

N −1

∣

X [k ]∣

2

Dyskretna transformata Fouriera

●

N-punktowa dyskretna transformata Fouriera
(Discrete Fourier Transform – DFT) jest
zdefiniowana jako:

●

Gdzie sygnał bazowy zespolonym ciągiem
wykładniczym:

X [k ]=

∑

n=0

N −1

x [n]e

−

j2 π kn/ N

, k =0,1 ,... N −1

Ψ [

k , n]=e

j2 π k n/ N

Ortogonalność sygnałów bazowych

●

Sprawdźmy ortogonalność sygnałów
bazowych DFT:

●

Podstawmy:

1

N

∑

n=0

N −1

Ψ [

k , n] Ψ

∗

[

l , n]=

1

N

∑

n=0

N −1

e

j 2 π(k−l )n/ N

S

N −1

=

∑

n=0

N −1

e

j 2 π(k−l )n/ N

=

∑

n=0

N −1

u

n

Ortogonalność sygnałów bazowych

●

Suma szeregu wynosi:

●

Po podstawieniu:

S

N −1

=

1−u

N

1−u

S

N −1

=

1−e

j 2 π(k−l )

1−e

j 2 π(k−l )/ N

=

{

1⇔l=k +r ℤ
0⇔l≠k

Dyskretna Transformata Fouriera

●

Podstawiając:

●

DFT można zapisać jako:

●

Transformata odwrotna iDFT ma postać:

w

N

=

e

−

j 2 π/ N

X [k ]=

∑

n=0

N −1

x [n]w

N

kn

, k =0,1 ,... , N −1

x [n]=

1

N

∑

k=0

N −1

X [ k ] w

N

−

kn

, k =0,1 ,... , N −1

Szybka Transformata Fouriera

●

Aby ograniczyć złożoność obliczeniową DFT
opracowano algorytmy rzędu N(log

2

N), które

określane są mianem szybkiej transformaty
Fouriera (Fast Fourier Transform – FFT).

●

FFT jest identyczna z DFT, tyle że prowadzi do
wyniku w krótszym czasie, zwłaszcza gdy
N=2

k

.

Związki między DTFT a DFT

●

DTFT sygnału z dyskretnym czasem jest dana
jako:

●

Próbkując widmo DTFT w równoodległych
częstościach:

X (e

j ω

)=

∑

n=0

∞

x [n]e

−

j ω n

=

∑

n=0

N −1

x [n]e

−

j ω n

ω

k

=

2 π k

N

, k =0,1 ,... , N −1

Związki między DTFT a DFT

●

Próbkowaną DTFT można zapisać jako:

●

Przez porównanie widać, że N-punktowa DFT
X[k] jest ciągiem próbek transformaty DTFT
X(e

jω

) zebranych w N-równooldległych

punktach widma ω

k

.

X (e

j ω

)∣

ω

k

=

∑

n=0

N −1

x [n]e

−

j 2 π k n/ N

Zero-padding

●

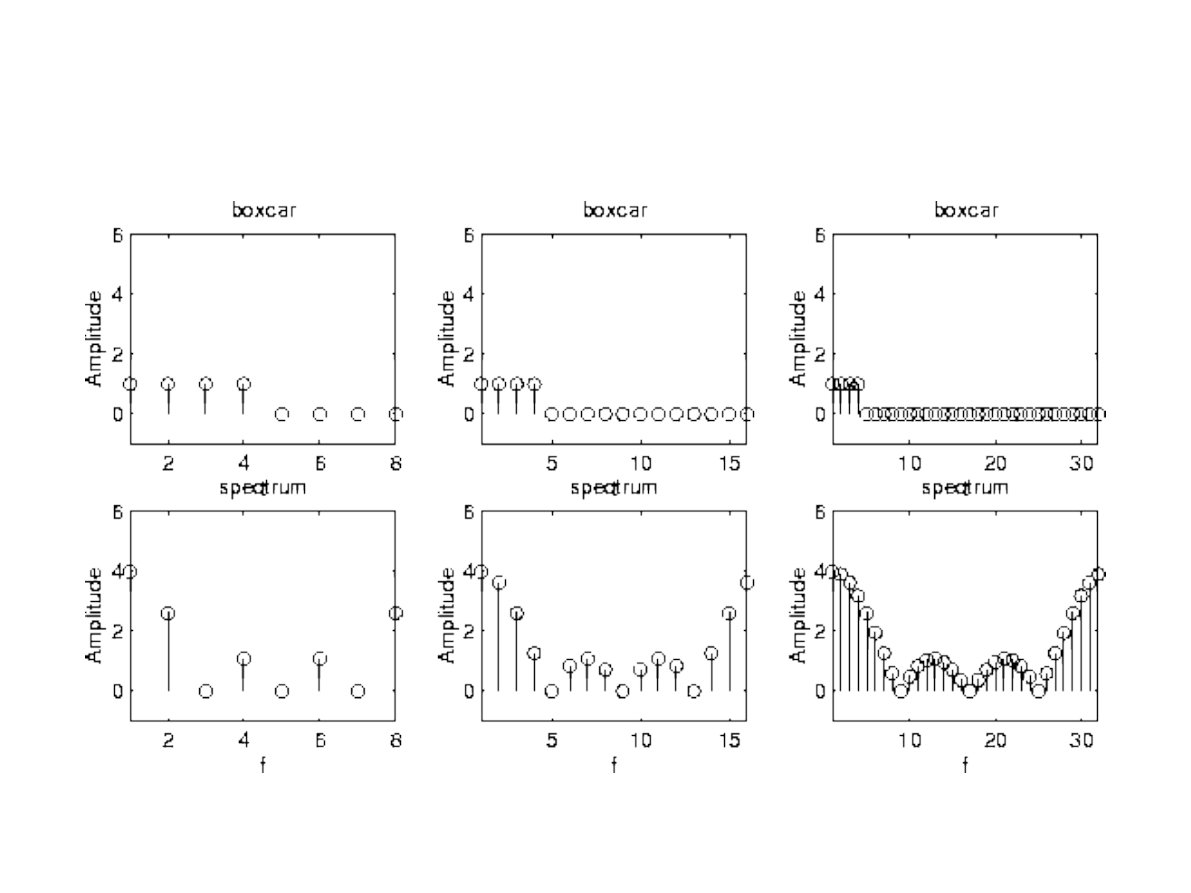
Jeśli chcemy obliczyć transformatę DTFT na
gęstej siatce M-punktów dla sygnału N-
punktowego, możemy ten sygnał uzupełnić
(M-N)-zerami (zero padding):

●

Wówczas:

x [n]→ x

p

[

n]=[ x ,0 ,0,0 ,0 ,0]

X (e

j ω

k

)=

∑

n=0

N −1

x [n]e

−

j 2 π k n/ M

=

∑

n=0

M −1

x

p

[

n]e

−

j 2 π kn / M

Zero-padding

Kołowe przesunięcie sygnału

●

Ponieważ własności DFT wykorzystują
przesuwanie sygnału w dziedzinie i
przeciwdziedzinie, należy zdefiniować te
operacje.

●

Jeśli wyjściowy sygnał x[n] jest N-punktowy
(0≤n≤N-1), to jego przesunięta kopia nie może
wyjść poza ten zakres. Wykorzystuje się w tym
celu operację modulo, definiując przesunięcie
kołowe (circular shift).

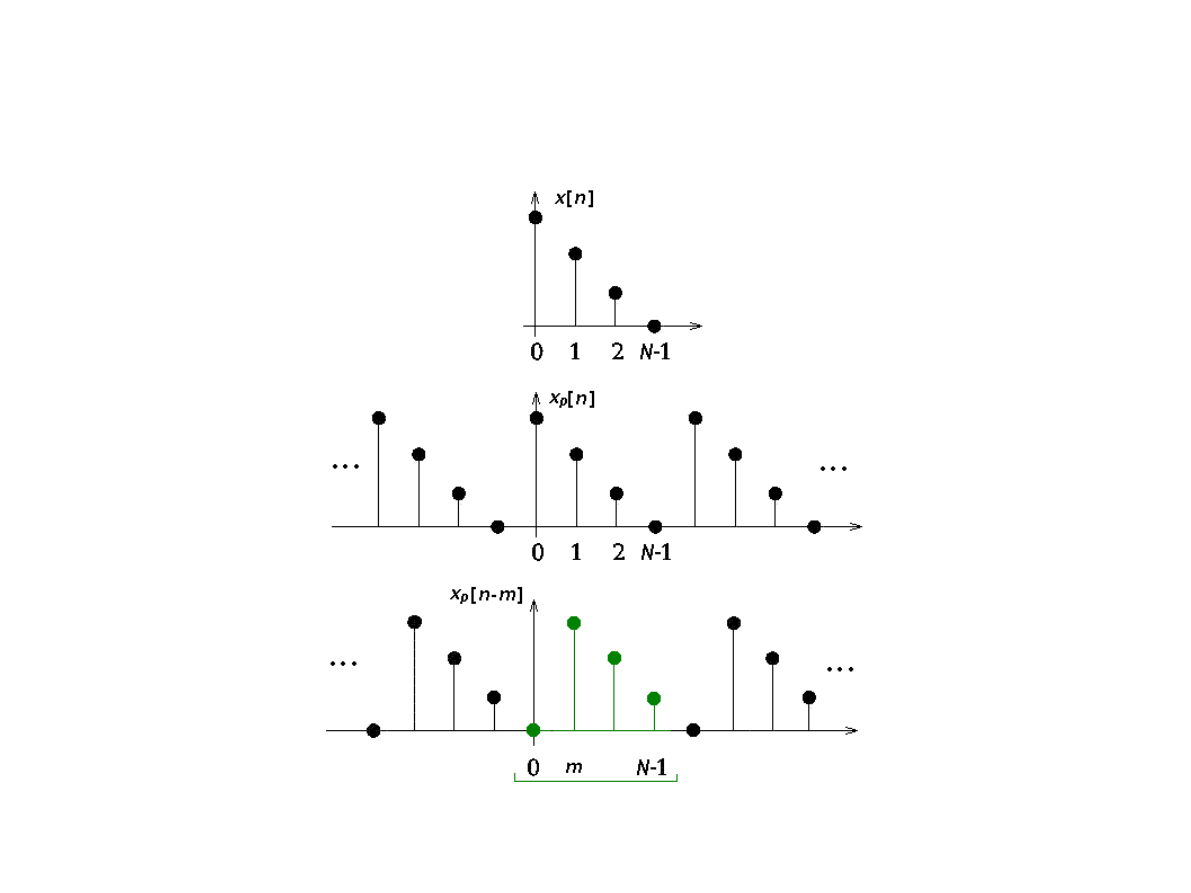
Kołowe przesunięcie sygnału

Kołowe przesunięcie sygnału

●

Zauważmy przy tym, że:

●

Tak więc przesunięcie w prawo o n

0

-próbek

jest tożsame przesunięciu w lewo o (N-n

0

)-

próbek.

x

s

[

n]= x [(n−n

0

)

N

]=

x [(n−N +n

0

)

N

]

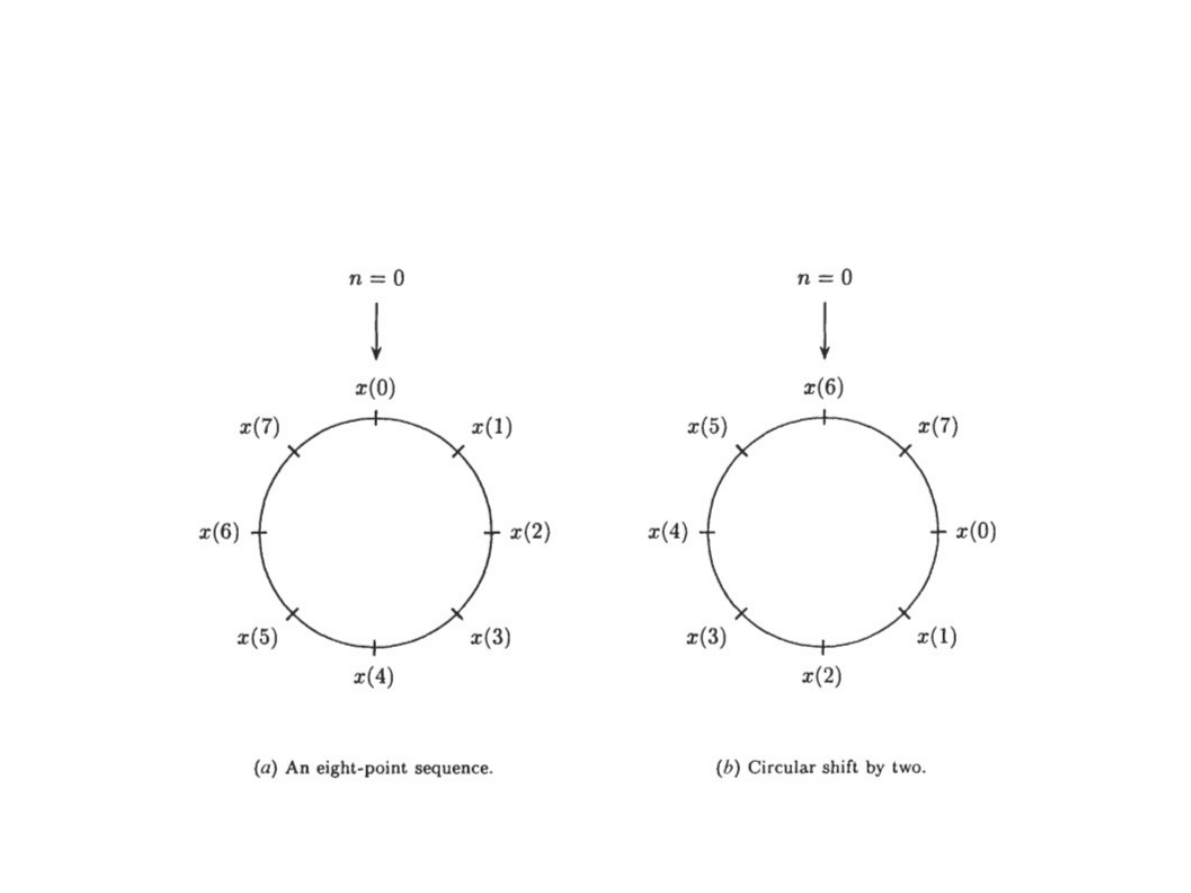
Kołowe przesunięcie sygnału

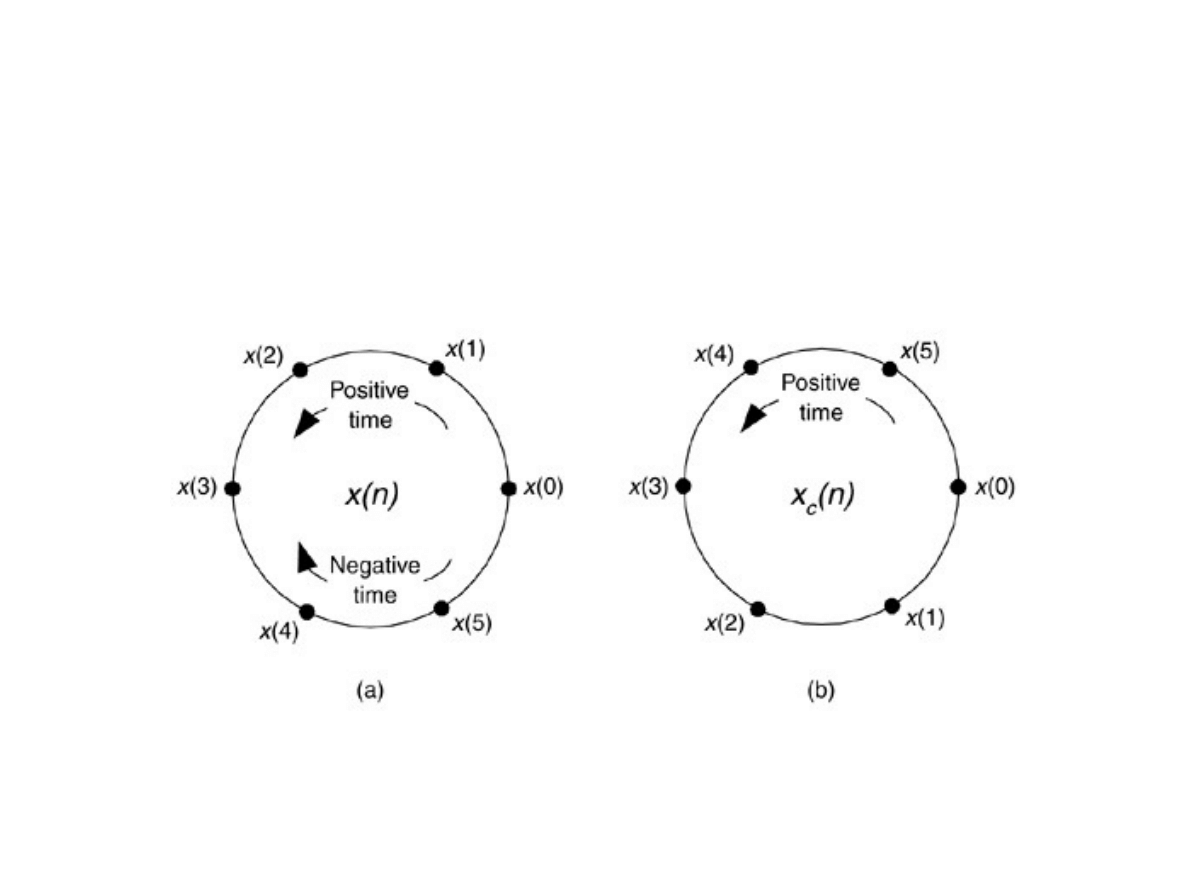
Kołowe zawinięcie sygnału

Splot kołowy

●

Przypomnijmy, że splot dwóch N-punktowych
sygnałów x[n] oraz h[n] ma postać:

●

Aby jednak zachować długość ciągu
wynikowego, musimy operację splotu
zdefiniować wykorzystując operację kołowego
przesunięcia i odbicia sygnału.

y

L

[

n]=x⊗h=

∑

m=0

N −1

x [m] h[n−m] , 0≤n≤2N−2

Splot kołowy

●

Splot kołowy zdefiniowany jest jako:

●

Splot kołowy jest zawsze ciągiem N-
punktowym.

y

c

[

n]=

∑

m=0

N −1

x [n]h[(n−m)

N

]=

x ∘ h

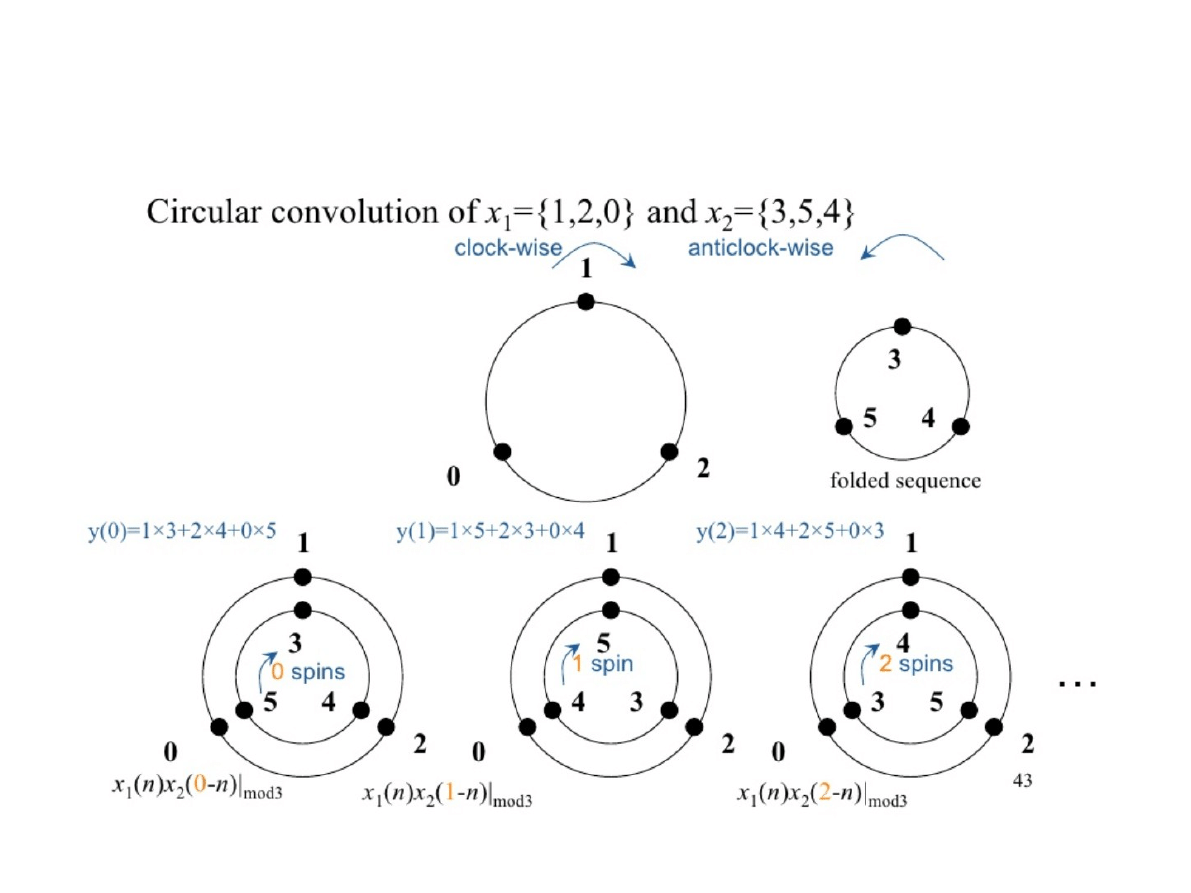
Obliczanie splotu kołowego

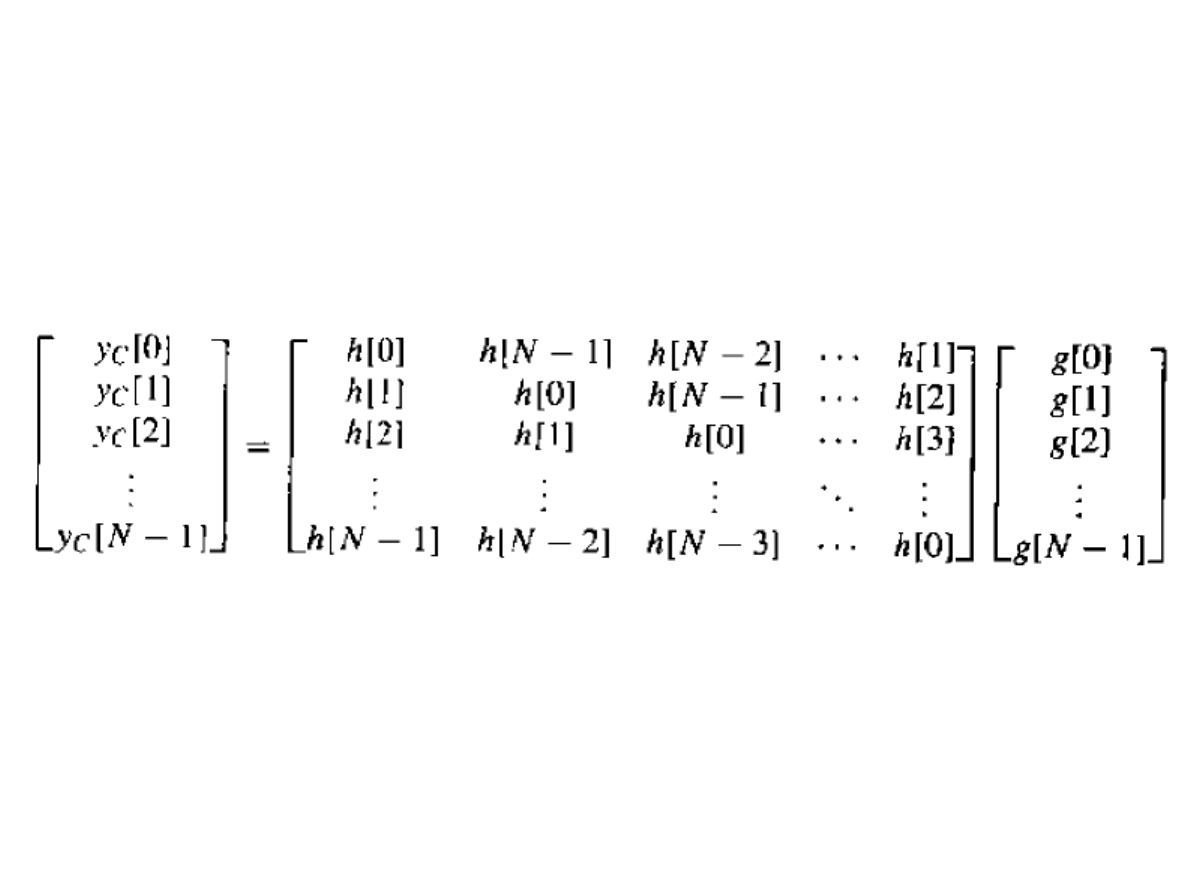
Obliczanie splotu kołowego

●

Metoda macierzowa

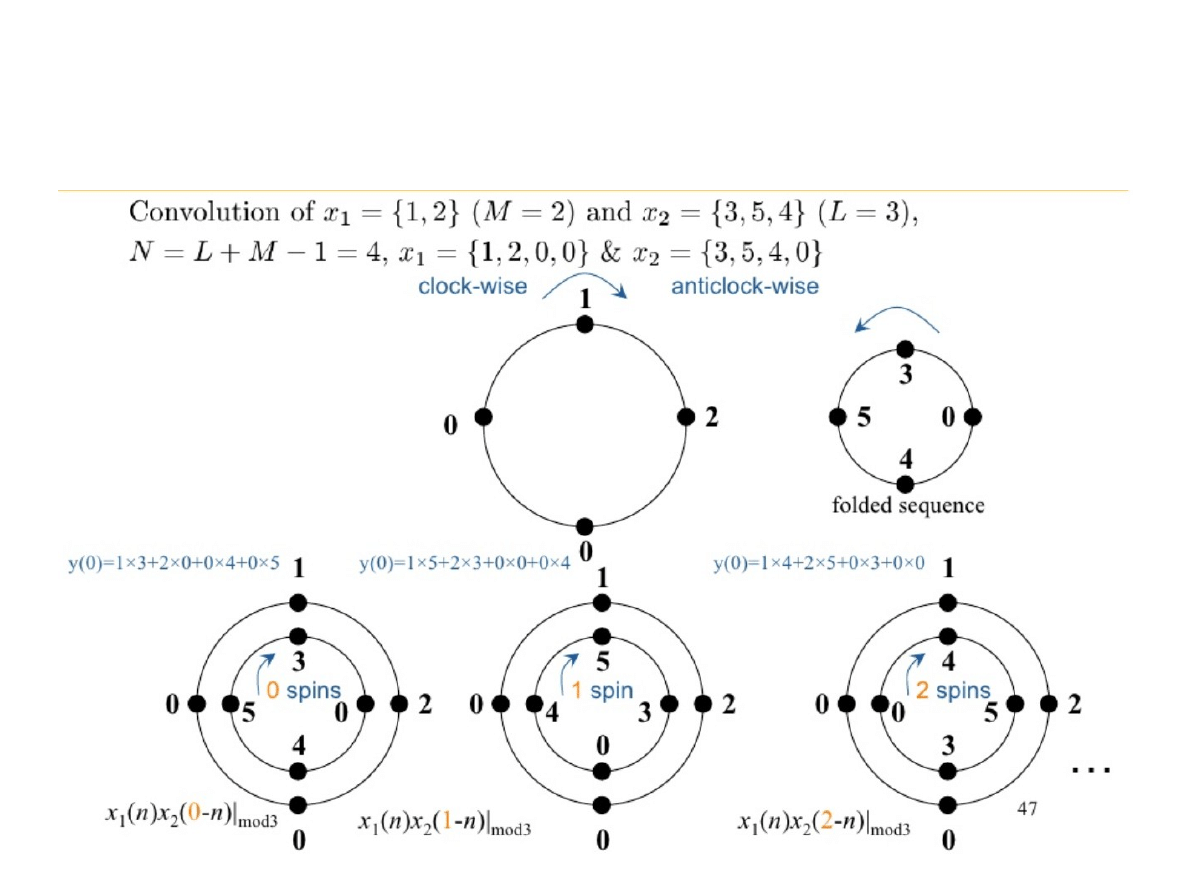
Obliczanie splotu liniowego przy

pomocy splotu kołowego

Filtracja sygnałów

●

Mając wydajne algorytmy obliczania DFT –
Fast Fourier Transform (FFT) możemy szybko
liczyć transformaty dowolnych sygnałów i
transformaty odwrotne.

●

Mając możliwość liczenia splotu liniowego jako
splotu kołowego sygnału uzupełnionego
zerami możemy zbudować wydajne filtry
cyfrowe.

Podział sygnałów N-punktowych

●

Każdy sygnał czasu dyskretnego można
przedstawić jako sumę składowych
sprzężonych kołowo: symetrycznej x

cs

[n] oraz

antysymetrycznej x

ca

[n]:

x [n]= x

cs

[

n]+ x

ca

[

n]

x

cs

[

n]=

1
2

(

x [n]+ x

∗

[(−

n)

N

])

x

ca

[

n]=

1

2

(

x [n] ax

∗

[(−

n)

N

])

Sygnały parzyste i nieparzyste

●

N-punktowy sygnał rzeczywisty czasu
dyskretnego rozkłada się według powyższego
wzoru na dwie składowe rzeczywiste: parzystą
(zespoloną symetryczną) oraz nieparzystą
(zespoloną antysymetryczną).

Symetrie geometryczne

●

N-punktowy sygnał x[n] jest symetryczny, gdy:

●

N-punktowy sygnał x[n] jest antysymetryczny,
gdy:

x [n]= x [ N −1−n]

x [n]=−x [ N −1−n]

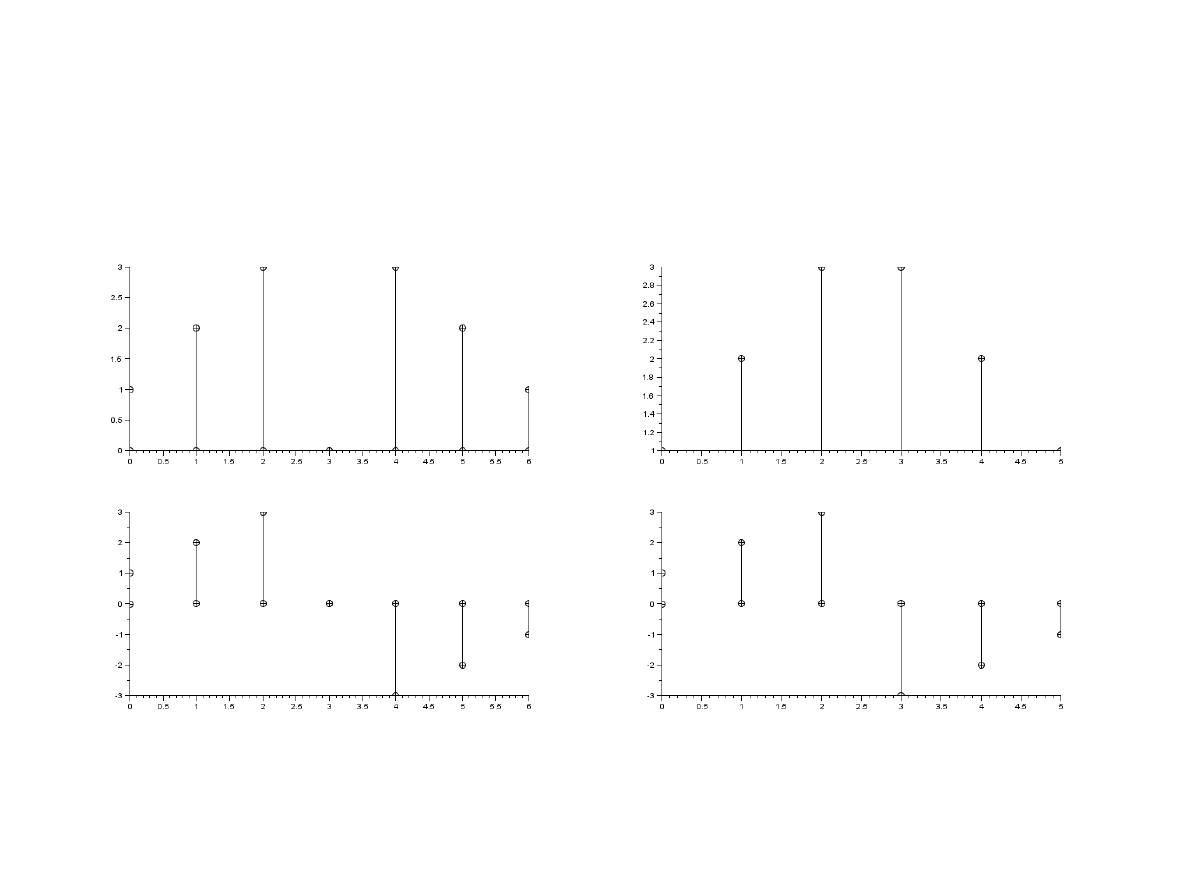
Symetrie geometryczne

Związki DFT z symetriami

●

W ogólności, DFT jest sygnału z dyskretnym
czasem jest sygnałem zespolonym postaci:

gdzie poszczególne składowe liczy się ze
wzorów:

X [k ]= X

ℜ

[

k ]= X

ℑ

[

k ]

X

ℜ

[

k ]=

1

2

(

X [k ]+ X

∗

[

k ])

X

ℑ

[

k ]=

1
2

(

X [k ]− X

∗

[

k ])

Związki DFT z symetriami

●

W ogólności, DFT jest sygnału z dyskretnym
czasem jest sygnałem zespolonym postaci:

gdzie poszczególne składowe liczy się ze
wzorów:

X [k ]= X

ℜ

[

k ]= X

ℑ

[

k ]

X

ℜ

[

k ]=

1

2

(

X [k ]+ X

∗

[

k ])

X

ℑ

[

k ]=

1
2

(

X [k ]− X

∗

[

k ])

Symetrie DFT dla sygnałów

zespolonych

Symetrie DFT dla sygnałów

rzeczywistych

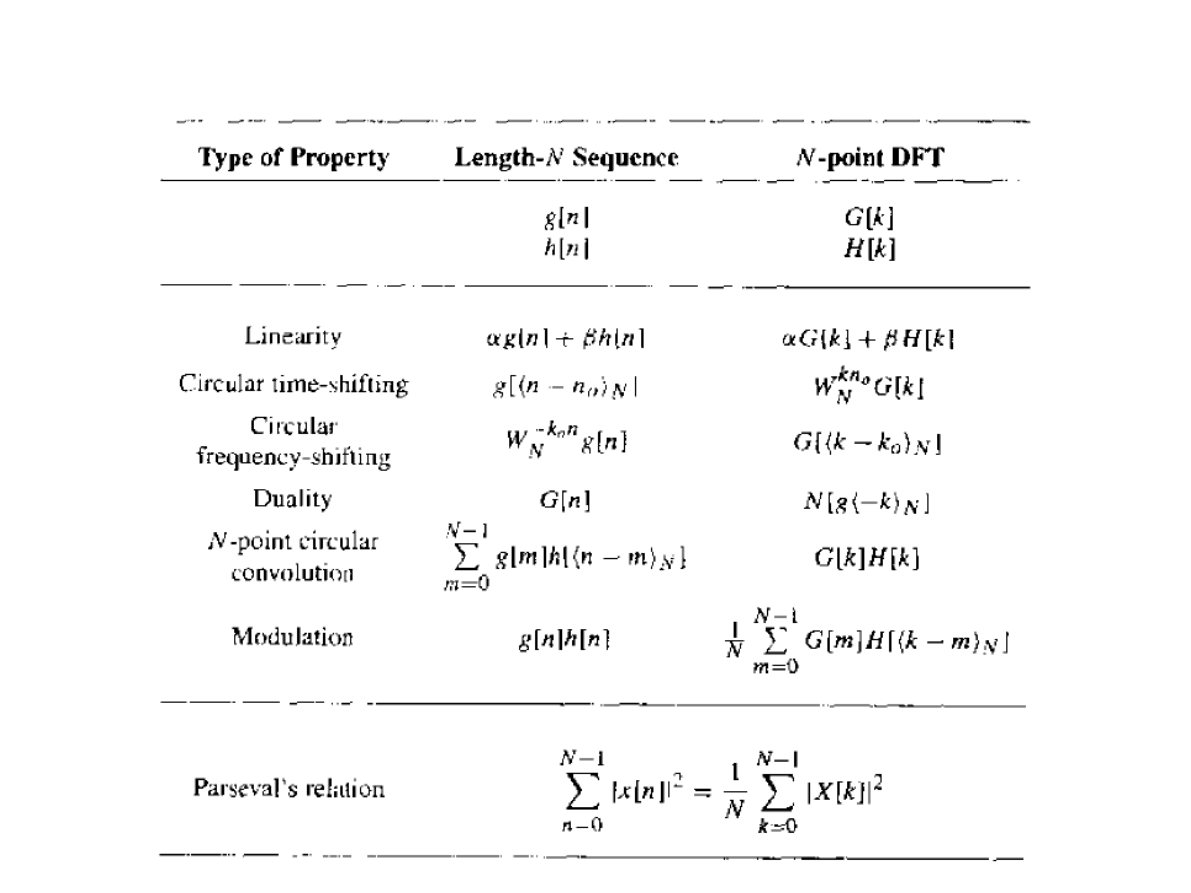
Własności DFT

Nadmiarowość DFT

●

Pamiętamy, że N-punktowa DFT sygnału
rzeczywistego jest sygnałem zespolonym
spełniającym warunek symetrii:

●

Dla parzystego N, próbki X[0] oraz X[(N-2)/2]
są rzeczywiste, zaś pozostałe (N-2)-próbki są
zespolone, jednak tylko połowa z nich jest
różna od reszty.

X [k ]= X

∗

[(−

k )

N

]

Nadmiarowość DFT

●

Dla nieparzystego N, X[0] jest próbką
rzeczywistą, a pozostałe (N-1) – zespolone,
jednak tylko połowa z nich jest odmienna od
reszty dzięki symetrycznemu sprzężeniu.

●

Świadczy to o nadmiarowości sygnału
(redundancy).

Przedłużanie sygnału

●

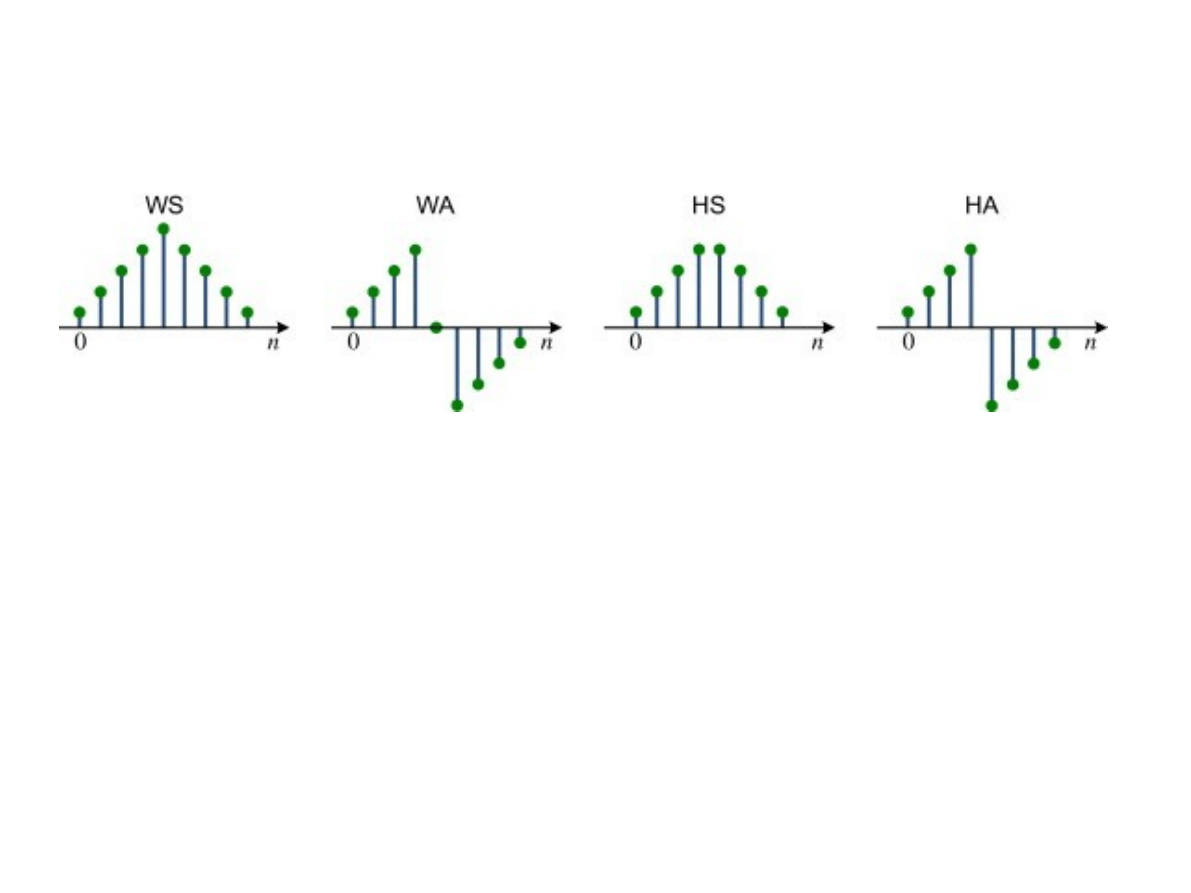
4 możliwe schematy przedłużania sygnału:

–

WS – whole-sample symmetry

–

WA – whole-sample antisymmetry

–

HS – half-sample symmetry

–

HA – half-sample antisymmetry

●

Po przedłużeniu obu końców sygnału
dostajemy 16 możliwych schematów
przedłużania, z czego 8 symetrycznych
stanowi bazę DCT, zaś 8 antysymetrycznych –
bazę DST

Przedłużanie sygnału

●

Jeśli sygnał wyjściowy ma postać: x[n] =
[a,b,c,d], to jego okresowy, przedłużony
odpowiednik ma postać:

●

x

WSWS

[n] = [a,b,c,d,c,b] – typ I

●

x

HSHS

[n] = [a,b,c,d,d,c,b,a] – typ II

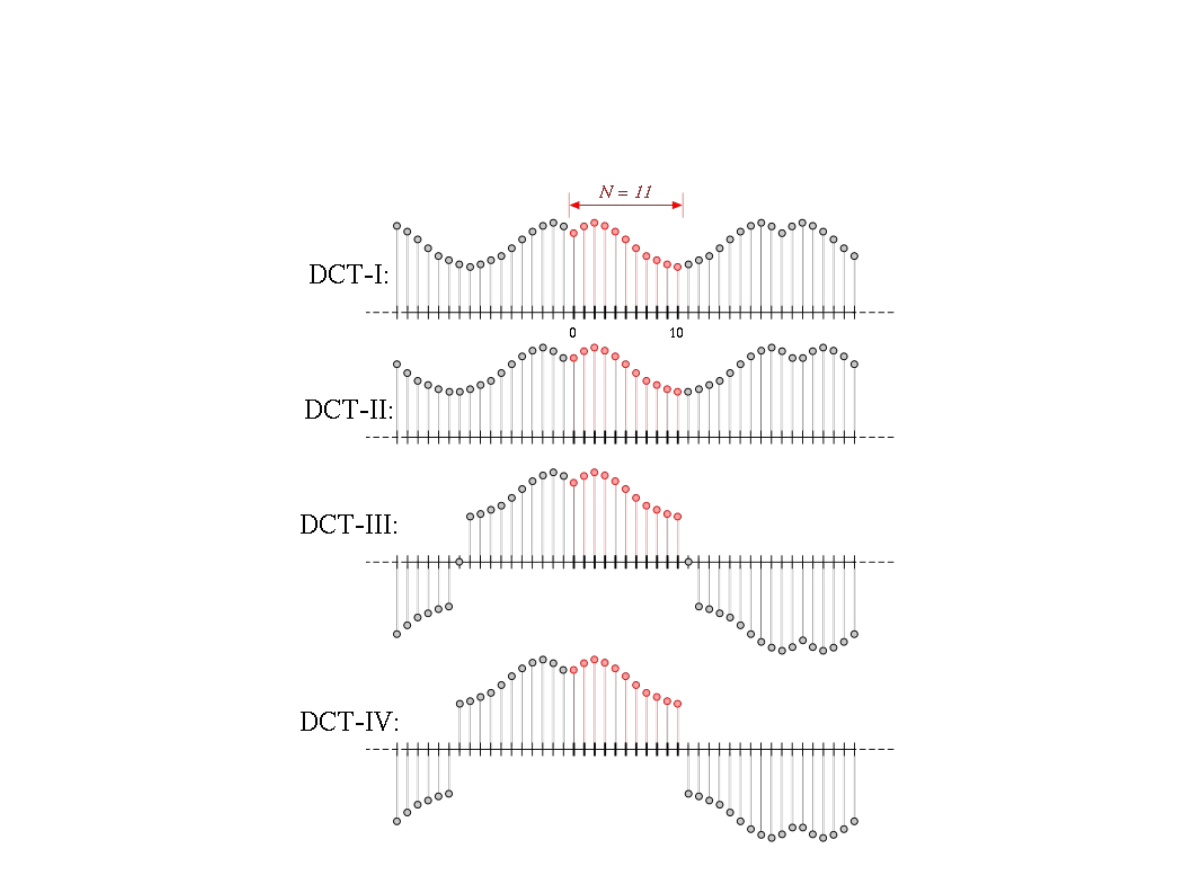
Przedłużanie sygnału

DCT typ II

●

Standardem używanym do kodowania JPEG,
MPEG oraz H.261 jest transformata
kosinusowa bazująca na przedłużaniu typu II.

●

Ta transformata jest nazywana także parzystą,
symetryczną DCT.

DCT typu II

●

Niech dany jest N-punktowy sygnał x[n].

●

Najpierw sygnał ten jest uzupełniany zerami:

●

Następnie tworzy się sygnał symetryczny typu
II y[n]:

x

zp

[

n]=

{

x [n]⇔0≤n≤ N −1

0⇔ N ≤n≤2N−1

y [n]=x

zp

[

n]+ x

zp

[

2N−1−n]=…

…

{

x [n]⇔0≤n≤N −1

x [2N−1−n]⇔ N ≤n≤2N−1

DCT typu II

●

Powstały sygnał spełnia warunek symetrii:

●

2N-punktowa transformata DFT tego sygnału
ma postać:

y [n]= y [2N−1−n]

Y [k ]=

∑

n=0

2N−1

y [n]w

2N

kn

, k =0,1 ,... , 2N−1

DCT typu II

●

Po przekształceniach:

●

N-punktowa transformata DCT typu II powstaje

przez wybranie pierwszych N-próbek powyższej

transformaty DFT i przemnożenie ich przez w

2N

k/2

Y [k ]=w

2N

−

k /2

∑

n=0

N −1

2x [n]cos

(

π

k (2n+1)

2N

)

,…

0≤k ≤2N−1

DCT typu II

●

DCT typu II ma ostatecznie postać:

●

Zauważmy, że dla rzeczywistego x[n], X

DCT

jest

także rzeczywiste.

X

DCT

[

k ]=

∑

n=0

N −1

2 x [n]cos

(

π

k (2n+1)

2N

)

, 0≤k ≤ N −1

iDCT

●

Odwrotna transformata kosinusowa N-
punktowego DCT ma postać:

●

Gdzie:

x [n]=

1

N

∑

k=0

N −1

α[

k ] X

DCT

[

k ]cos

(

π

k (2n+1)

2N

)

,0≤n≤ N −1

α [

k ]=

{

1

2

⇔

k =0

1⇔1≤k ≤N −1

Własności DCT

●

Liniowość DCT:

●

Symetria DCT:

●

Zachowanie energii:

α

g [n]+β h[n] ⇔

DCT

α

G

DCT

[

k ]+β H

DCT

[

k ]

g

∗

[

n] ⇔

DCT

G

DCT

∗

[

k ]

∑

n=0

N −1

∣

g [n]∣

2

=

1

2N

∑

k=0

N −1

α[

k ]∣G

DCT

[

k ]∣

2

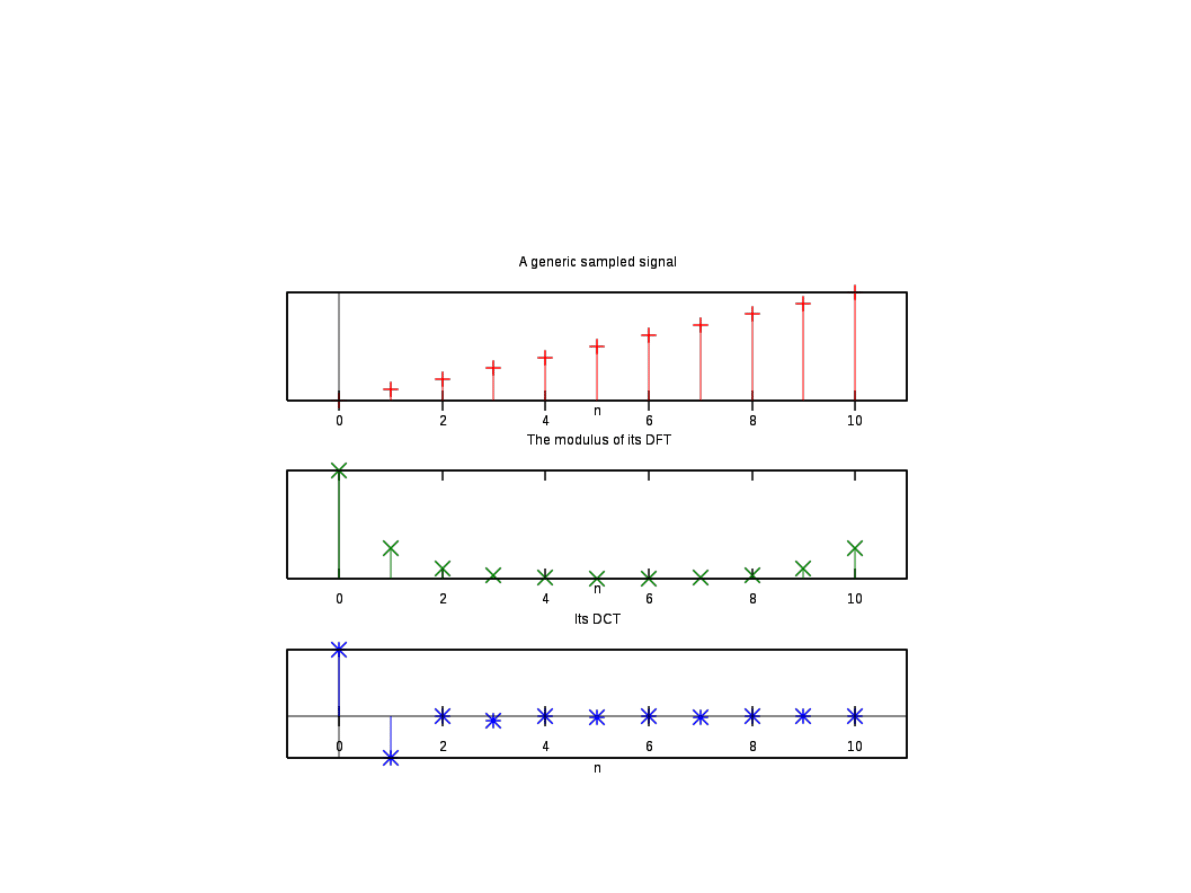
Kompaktowość DCT

Transformata Haara

●

Transformata Haara bazuje na sygnałach
powstałych ze spróbkowania ciągłych w
przedziale 0 ≤ t ≤ 1 funkcji Haara.

●

Zbiór funkcji Haara h

k

(t) zawiera N elementów,

k=0,1,...,N-1 (N jest potęgą 2).

●

Opisujący daną funkcję indeks k jest
jednoznacznie wyznaczony przez parę liczb p
oraz q takich, że:

k =2

p

+

q−1

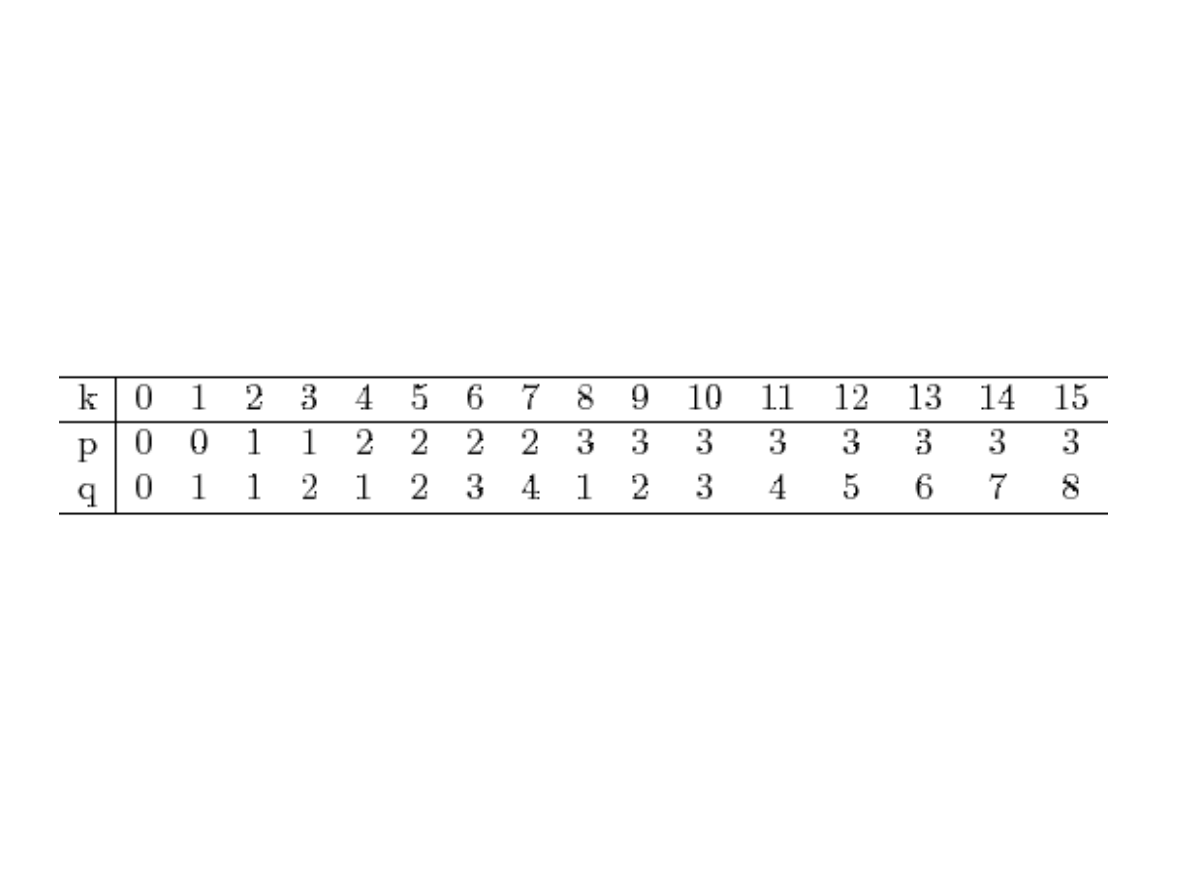
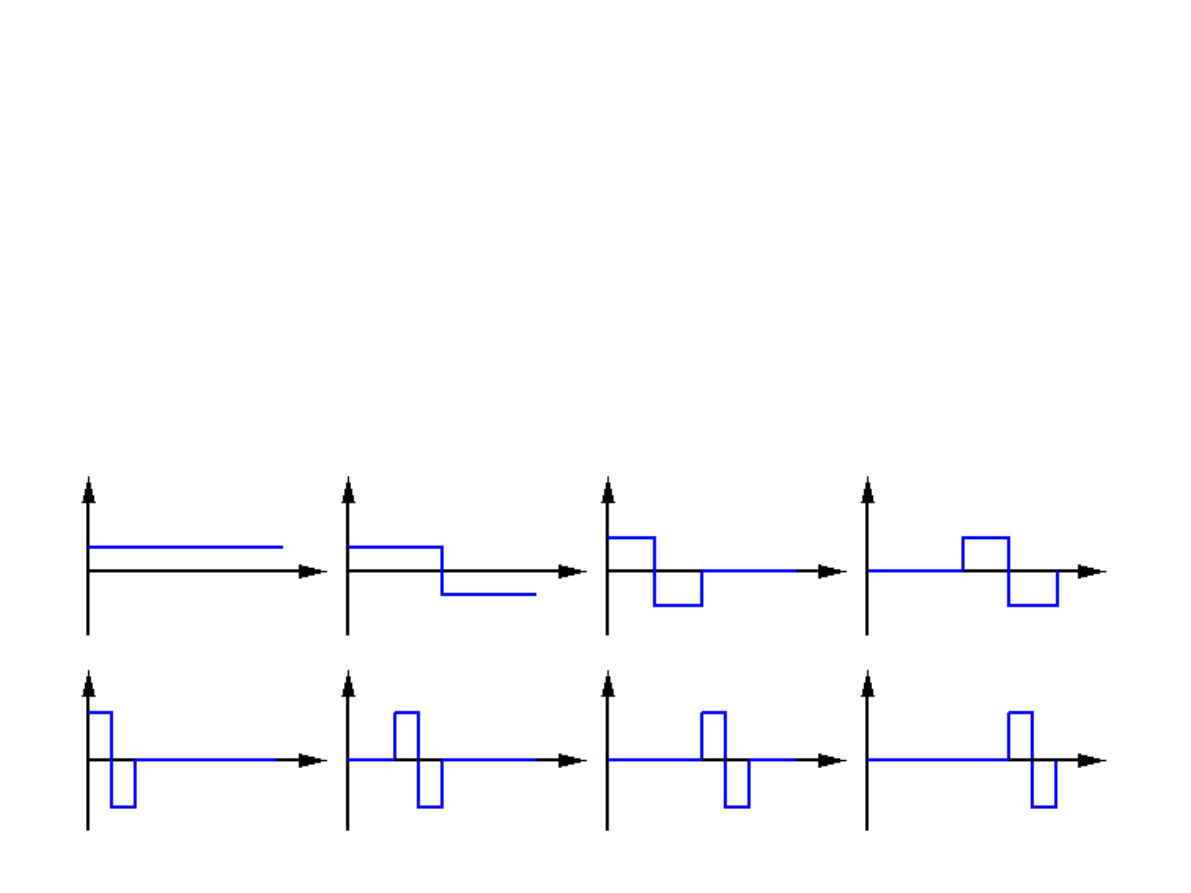
Indeksowanie funkcji Haara

●

Dla N=16:

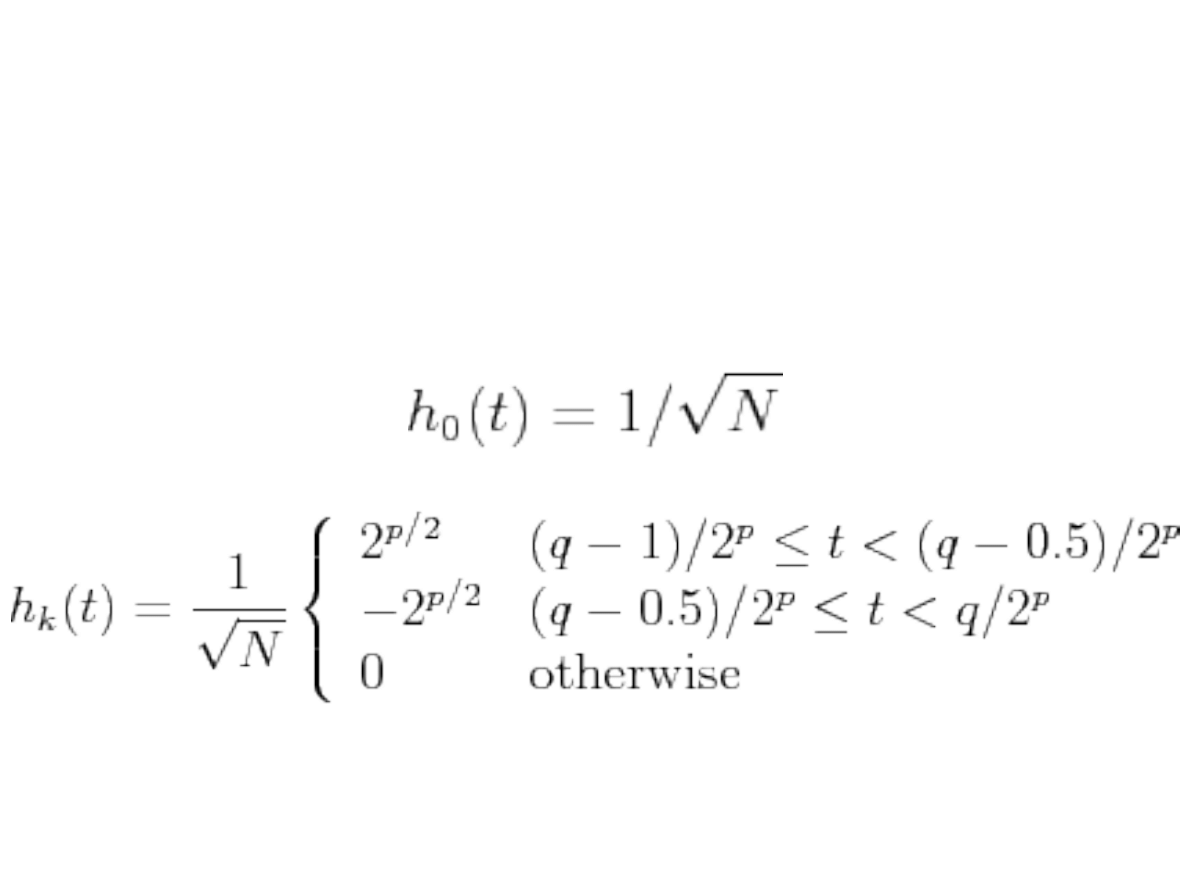
Znormalizowane funkcje Haara

●

Znormalizowane funkcje Haara zdefiniowane
są jako:

Macierz transformaty Haara

●

Macierzą transformaty Haara H

N

nazywamy

dyskretną funkcję Haara spróbkowaną w
punktach t=n/N, n=0,1,...,N-1.

●

Dla N=8:

Transformata Haara

●

N-punktowa transformata Haara ma postać:

●

O ile współczynniki transformat DFT oraz DCT
były powiązane ze specyficznymi
częstościami, transformata Haara (i inne
transformaty falkowe) odzwierciedla różne
położenia i skale składowych sygnału.

X

Haar

=

H

N

⋅

x [n]

Własności transformaty Haara

●

Ortogonalność:

wynika stąd łatwość liczenia transformaty
odwrotnej:

H

N

−

1

=

1

N

H

N

t

x [n]=

1

N

H

N

t

X

Haar

Własności transformaty Haara

●

Zachowanie energii sygnału:

∑

n=0

N −1

∣

x [n]∣

2

=

1

N

∑

k=0

N −1

∣

X

Haar

[

k ]∣

2

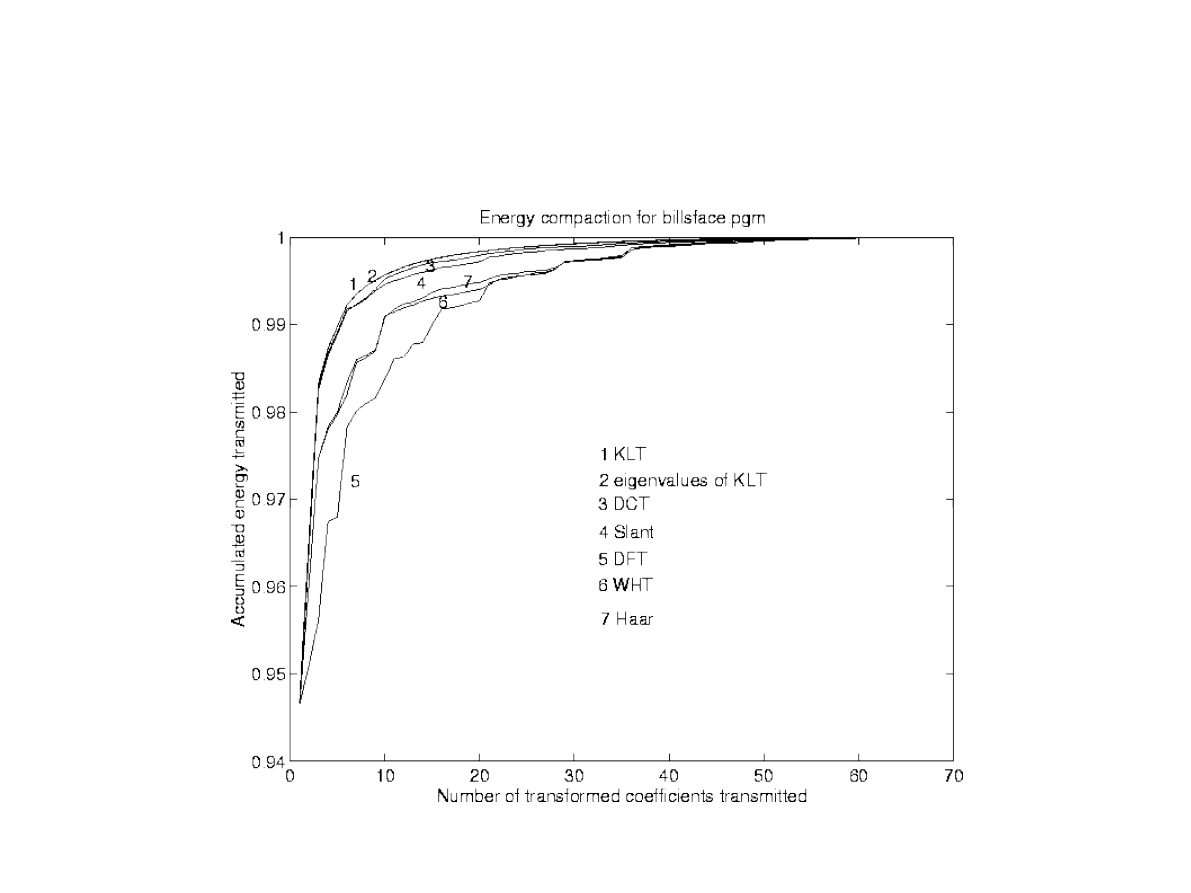
Kompaktowość transformat