Cyfrowe przetwarzanie sygnałów

z-transformata (06)

Sławomir Kulesza

Wykład fakultatywny dla studentów

III r. spec. Informatyka ogólna

Rok akademicki 2012/2013

z-transformata

●

Istnieją sygnały czasu dyskretnego, które nie
są zbieżne w sensie DTFT, a więc nie
posiadają transformat DTFT, np.:

●

Aby badać własności tych sygnałów w
dziedzinie innej niż czas należy zdefiniować
odpowiednią transformatę - z-transformatę.

x [n]=u[n]

x [n]=sin (ω n)

x [n]=(0.5)

n

u[−n]

z-transformata

●

Z-transformatą sygnału czasu dyskretnego
x[n] nazywamy funkcję:

gdzie: z – jest zmienną zespoloną.

●

Z-transformatę oznaczamy symbolicznie:

X ( z)=

∑

n=−∞

∞

x [n] z

−

n

z [n]⇔

ℤ

−

1

ℤ

X (z)

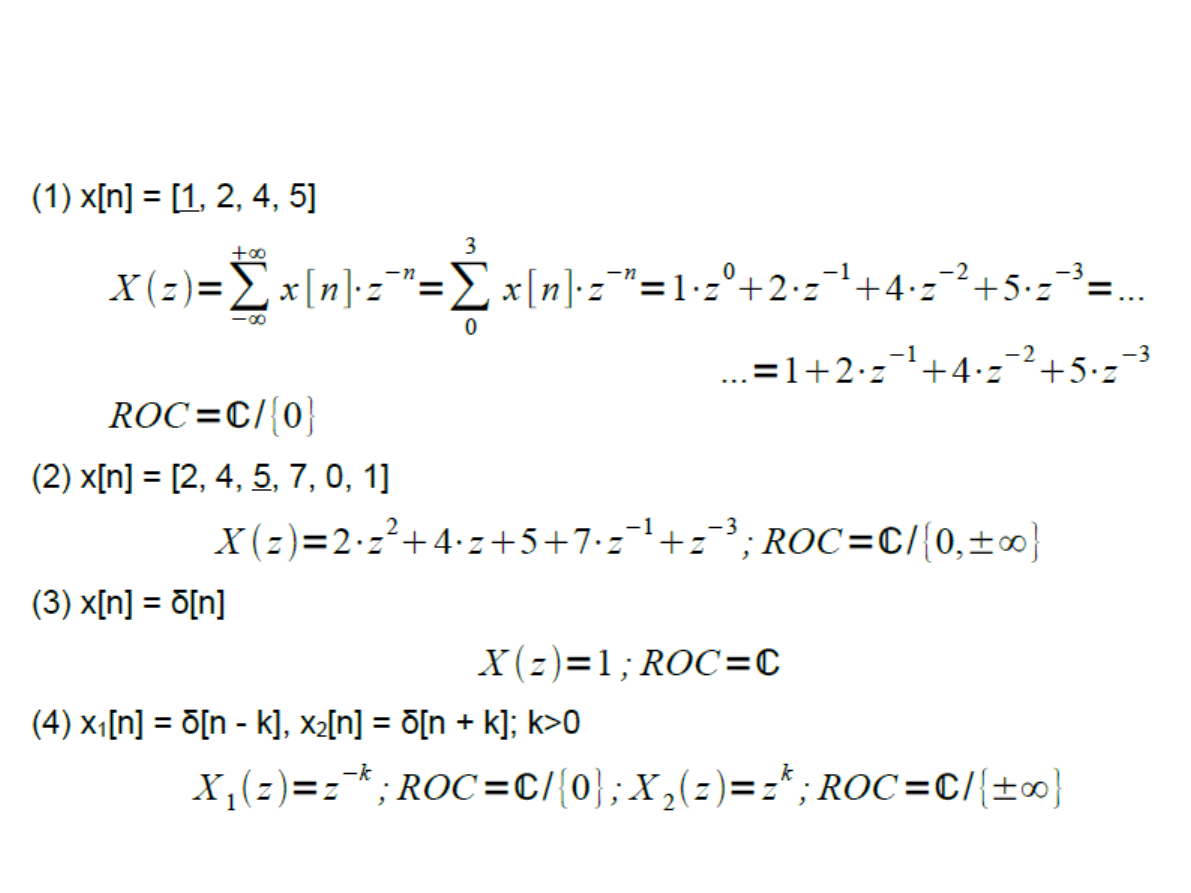
Przykłady

Z-transformata a DTFT

●

Wyraźmy zmienną z w postaci wykładniczej:

●

Wówczas z-transformata przyjmie postać:

●

Dla porównania, DTFT ma postać:

z=r e

j ω

Z (r e

j ω

)=

∑

n=−∞

∞

x [n] r

−

n

e

−

j ω n

X (e

j ω

)=

∑

n=−∞

∞

x [n]e

−

j ω n

Z-transformata a DTFT

●

Z porównania DTFT oraz z-transformaty
widać, że ta ostatnia jest tożsama DTFT
zmodyfikowanego sygnału x[n]:

̃x [n]= x [n]⋅r

−

n

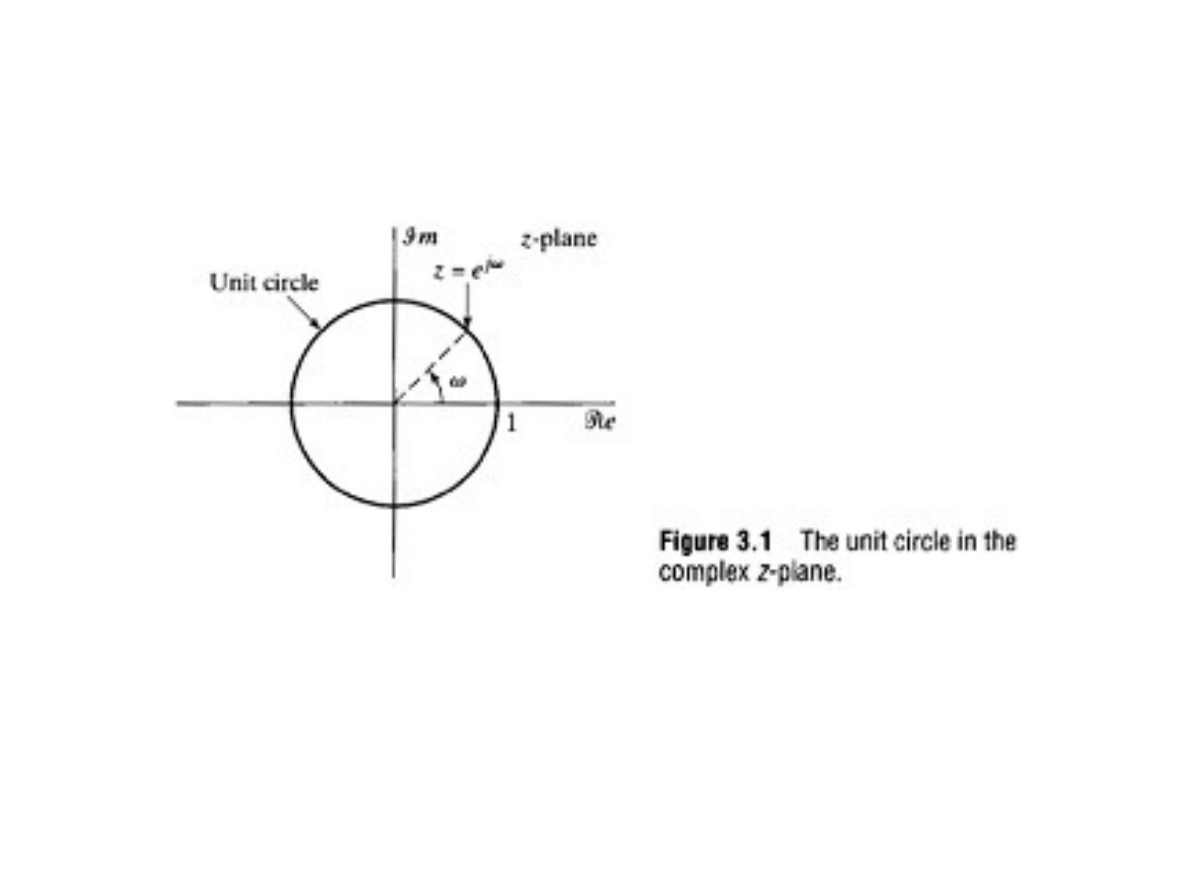
Interpretacja geometryczna

●

DTFT sygnału x[n] jest zbieżna wtedy i tylko
wtedy, gdy ROC jego z-transformaty zawiera
okrąg jednostkowy.

Zbieżność z-transformaty

●

Z-transformata jest bezwzględnie sumowalna
wtedy i tylko wtedy, gdy:

●

Może zatem zajść sytuacja, że dla pewnych
wartości parametru r z-transformata sygnału
x[n] będzie zbieżna, a jego DTFT – nie.

●

Zbiór wszystkich wartości r, dla których z-
transformata jest zbieżna nazywa się obszarem
zbieżności – ROC (Region of Convergence).

∑

n=−∞

∞

∣

x [n] r

−

n

∣

<∞

Zbieżność z-transformaty

●

Zauważmy, że:

∣

X (z)∣=

∑

n=−∞

∞

∣

x [n]∣⋅∣r

−

n

∣=

∑

n=−∞

−

1

∣

x [n] r

−

n

∣+

∑

n=0

∞

∣

x [n]

r

n

∣

=

...

...=

∑

n=1

∞

∣

x [−n]r

n

∣+

∑

n=0

∞

∣

x [n]

r

n

∣

Zbieżność z-transformaty

Zbieżność

∑

n=1

∞

∣

x [−n]⋅r

n

∣

Zbieżność

∑

n=0

∞

∣

x [n]

r

n

∣

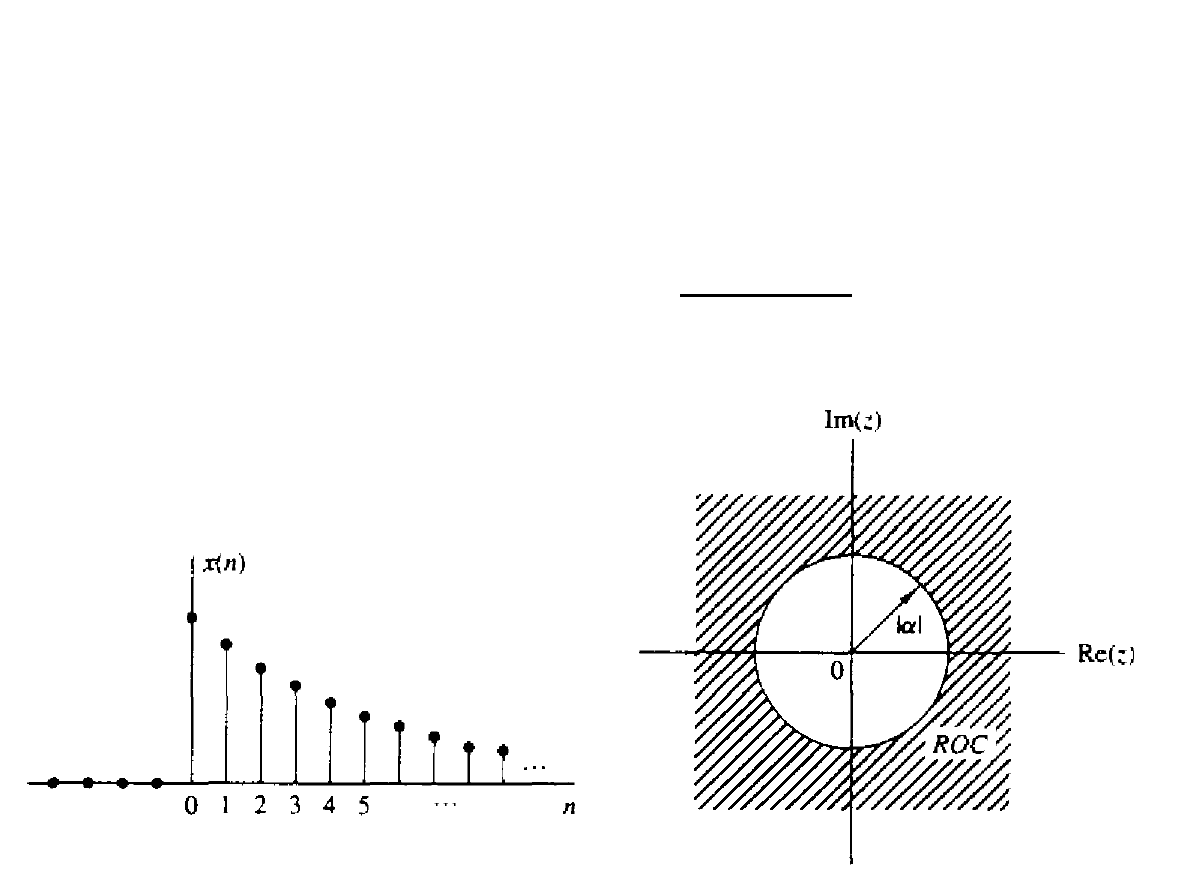
Przykład

●

Wyznaczyć z-transformatę sygnału: x [n]=a

n

⋅

u [n]

X ( z)=

∑

n=0

∞

a

n

⋅

z

−

n

=

∑

n=0

∞

(

a⋅z

−

1

)

n

=

1

1−a⋅z

−

1

; ROC :∣z∣>∣a∣

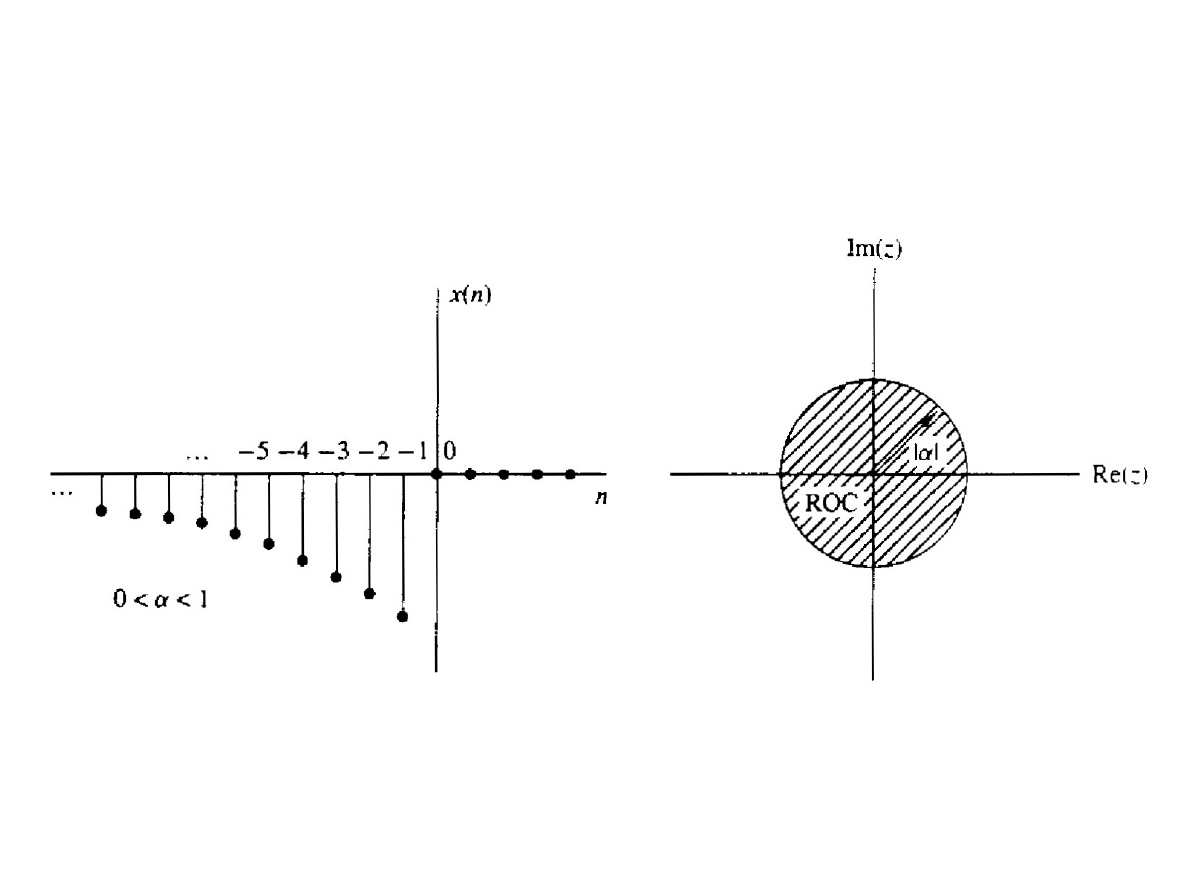
Przykład

●

Wyznaczyć z-transformatę sygnału:

x [n]=−a

n

⋅

u [−n−1]

X ( z)=

∑

n=−∞

−

1

(−

a

n

)⋅

z

−

n

=−

∑

n=1

∞

(

a

−

1

⋅

z)

n

=−

a

−

1

⋅

z

1−a

−

1

⋅

z

=

...

...=

1

1−a⋅z

−

1

; ROC :∣z∣<∣a∣

Przykład (cd.)

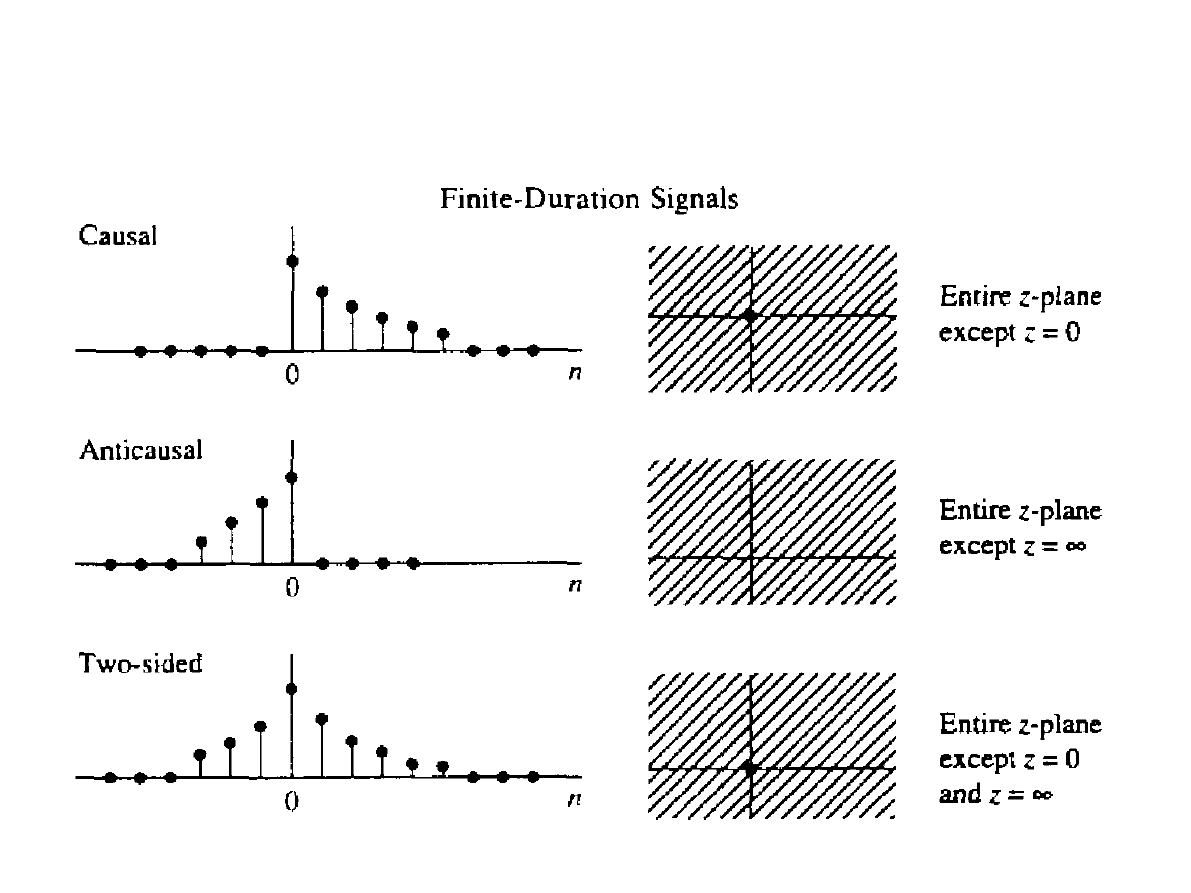
Jednoznaczność z-transformaty

●

Istnieją sygnały posiadające identyczną z-
transformatę, np. przyczynowy sygnał u[n]
oraz antyprzyczynowy sygnał u[-n-1]:

●

Zamknięta postać z-transformaty nie pozwala
jednoznacznie odtworzyć sygnału w dziedzinie
czasu – wymagana jest także znajomość
ROC.

Z (u [n])=Z (u [−n−1])=

1

1−z

−

1

Jednoznaczność z-transformaty

●

Sygnały czasu dyskretnego x[n] są określone
jednoznacznie poprzez podanie ich z-
transformaty X(z) oraz obszaru zbieżności
ROC.

●

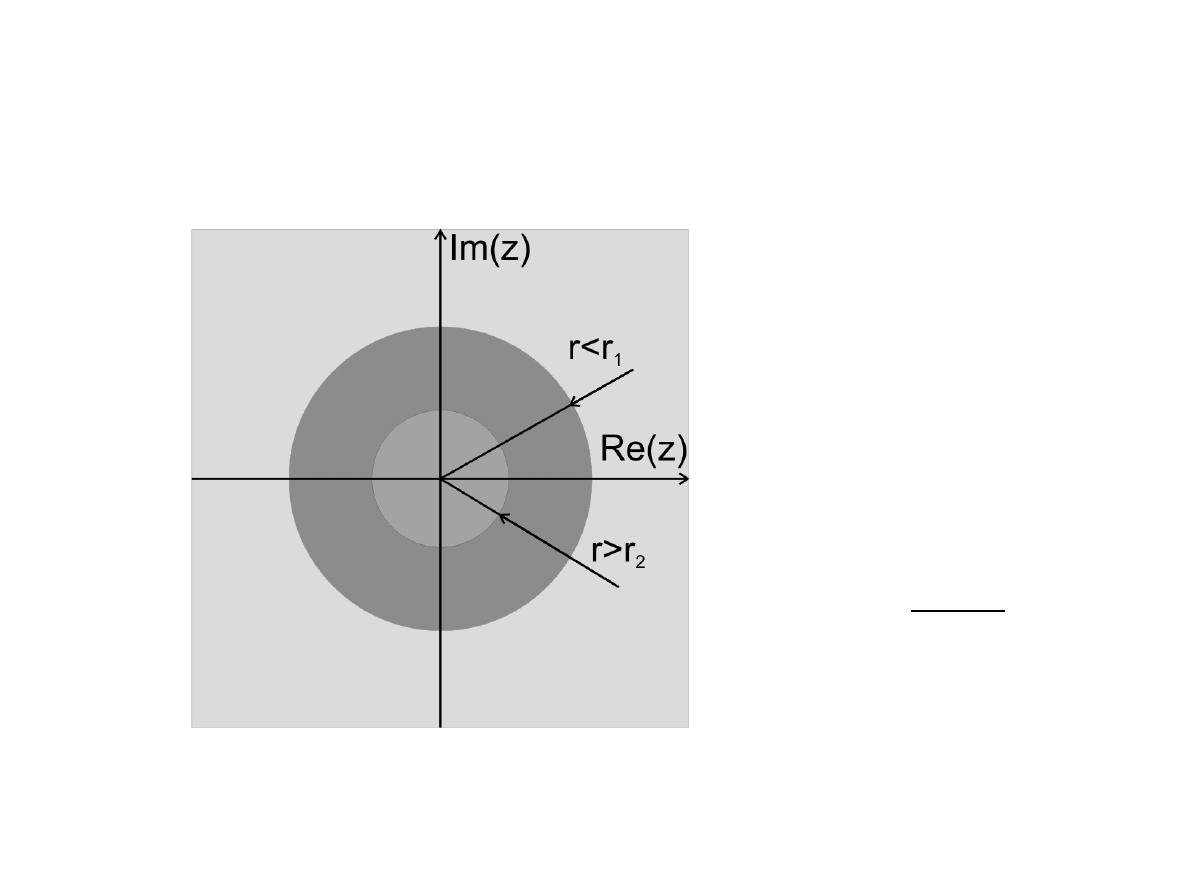
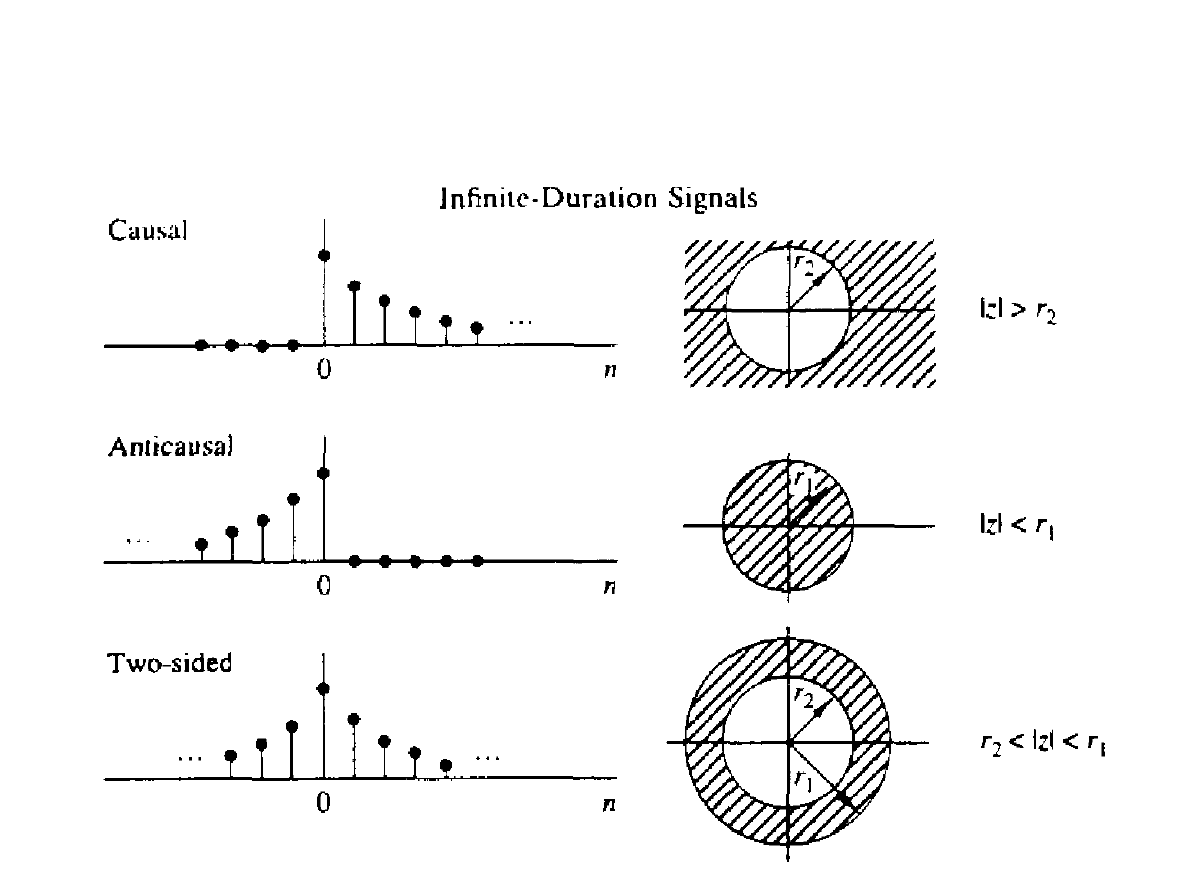
ROC sygnałów antyprzyczynowych leży
wewnątrz okręgu o promieniu r

1

, zaś ROC

sygnałów przyczynowych leży poza okręgiem
o promieniu r

2

.

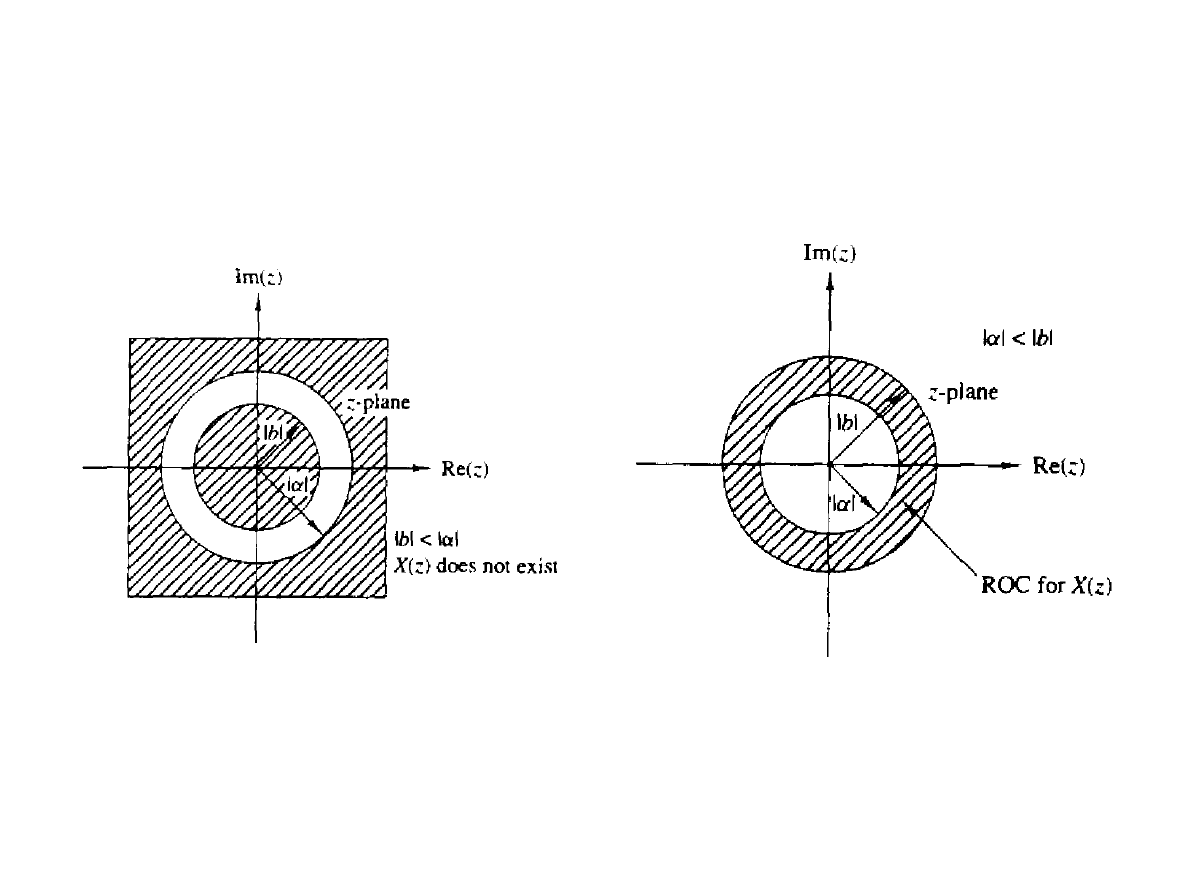
Przykład

●

Wyznaczyć z-transformatę sygnału:

●

Rozpatrzmy 2 przypadki:

●

|b| < |a|: obszary nie przekrywają się, więc X[z]
nie istnieje,

●

|b| > |a|:

x [n]=a

n

u [n]+b

n

u [−n−1]

X ( z)=

∑

n=0

∞

(

a⋅z

−

1

)

n

+

∑

n=1

∞

(

b

−

1

⋅

z)

n

; ROC :∣z∣>∣a∣,∣z∣<∣b∣

X [ z ]=

1

1−a⋅z

−

1

−

1

1−b⋅z

−

1

=

b−a

a+b− z−a⋅b⋅z

−

1

; ROC :∣a∣<∣z∣<∣b∣

Przykład

Przykład

Przykład

Pary z-transformat

Wymierna z-transformata

●

Wymierna z-transformata opisywana jest
wyrażeniem postaci:

gdzie: M – jest stopniem wielomianu P(z), zaś
N – stopniem wielomianu D(z)

H (z)=

P ( z)

D( z)

=

p

0

+

p

1

z

−

1

+…+

p

M

z

−

M

d

0

+

d

1

z

−

1

+…+

d

N

z

−

N

Wymierna z-transformata

●

Alternatywna postać wymiernej z-transformaty
opisywana jest wyrażeniem:

Lub w postaci iloczynowej:

H (z)=z

(

N −M )

p

0

z

M

+

p

1

z

M −1

+…+

p

M

d

0

z

N

+

d

1

z

N −1

+…+

d

N

H (z)=z

(

N −M )

p

0

d

0

∏

k=1

M

(

z−α

k

)

∏

k=1

N

(

z−β

k

)

Zera i bieguny wymiernej

z-transformaty

●

Zauważmy, że z-transformata w postaci
iloczynowej:

w punktach α

k

przyjmuje wartość zero, zaś w

punktach β

k

dąży do nieskończoności.

●

Wartości α

k

to zera z-transformaty (zeros -

(o)), zaś wartości β

k

– jej bieguny (poles - (x)).

H (z)=z

(

N −M )

p

0

d

0

∏

k=1

M

(

z−α

k

)

∏

k=1

N

(

z−β

k

)

Zera i bieguny z-transformaty

●

Z postaci iloczynowej:

wynika także, że z-transformata posiada (N-M)
zer w początku układu (z=0).

●

Wymierna z-transformata jest całkowicie
reprezentowana przez podanie wzmocnienia
p

0

/d

0

oraz lokalizację biegunów β

k

i zer α

k

.

H (z)=z

(

N −M )

p

0

d

0

∏

k=1

M

(

z−α

k

)

∏

k=1

N

(

z−β

k

)

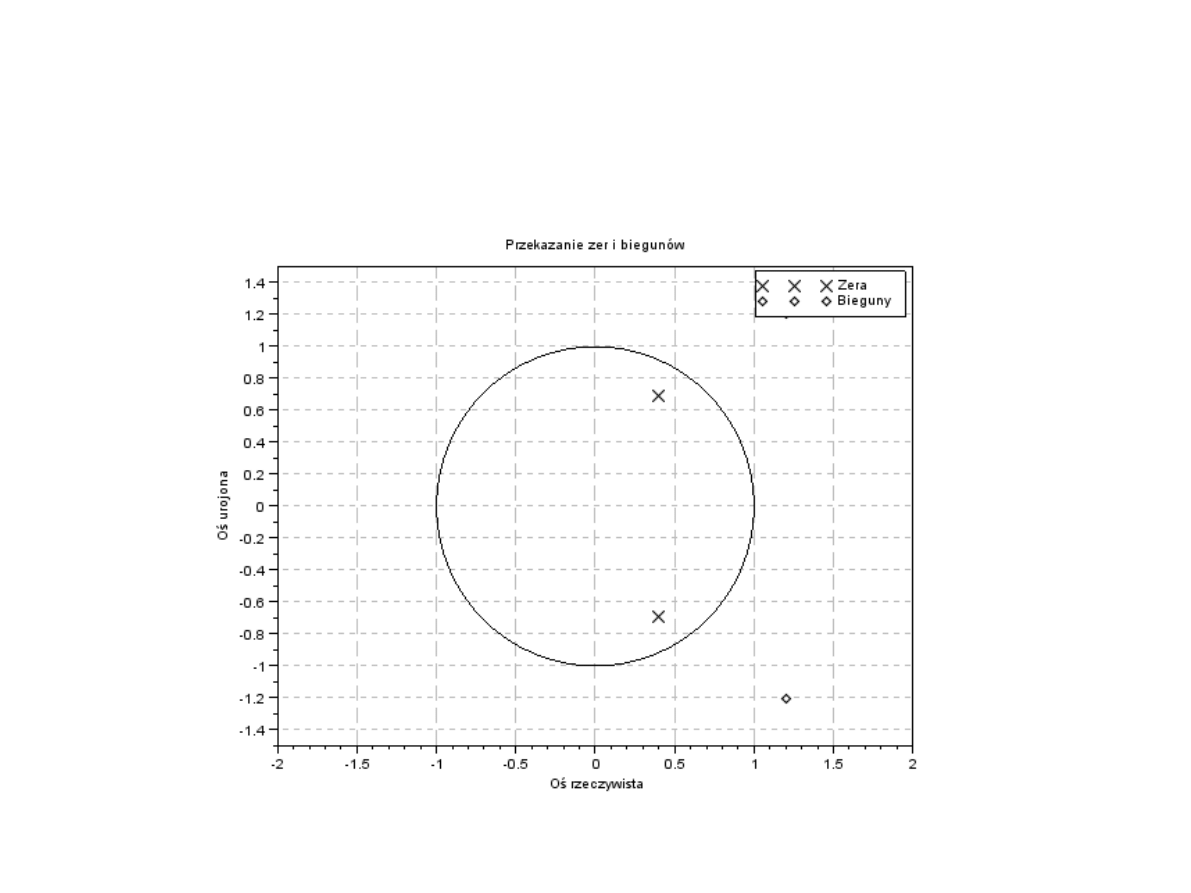
Przykład

●

Wyznaczanie zer i biegunów z-transformaty
postaci:

zera: α = 1.2 ± j1.2
bieguny: β = 0.4 ± j0.69

H (z)=

1−2.4 z

−

1

+

2.88 z

−

2

1−0.8 z

−

1

+

0.64 z

−

2

Przykład

Wymierna z-transformata o

współczynnikach rzeczywistych

●

Zera i bieguny wymiernej z-transformaty o
współczynnikach rzeczywistych są liczbami
zespolonymi parami sprzężonymi:

Fakt ten wykorzystuje się przy projektowaniu
filtrów cyfrowych metodą zer i biegunów z-
transformaty.

(

z−(a+ jb)

)

⋅

(

z−(a− jb)

)

=…

…=

z

2

−

2az+a

2

+

b

2

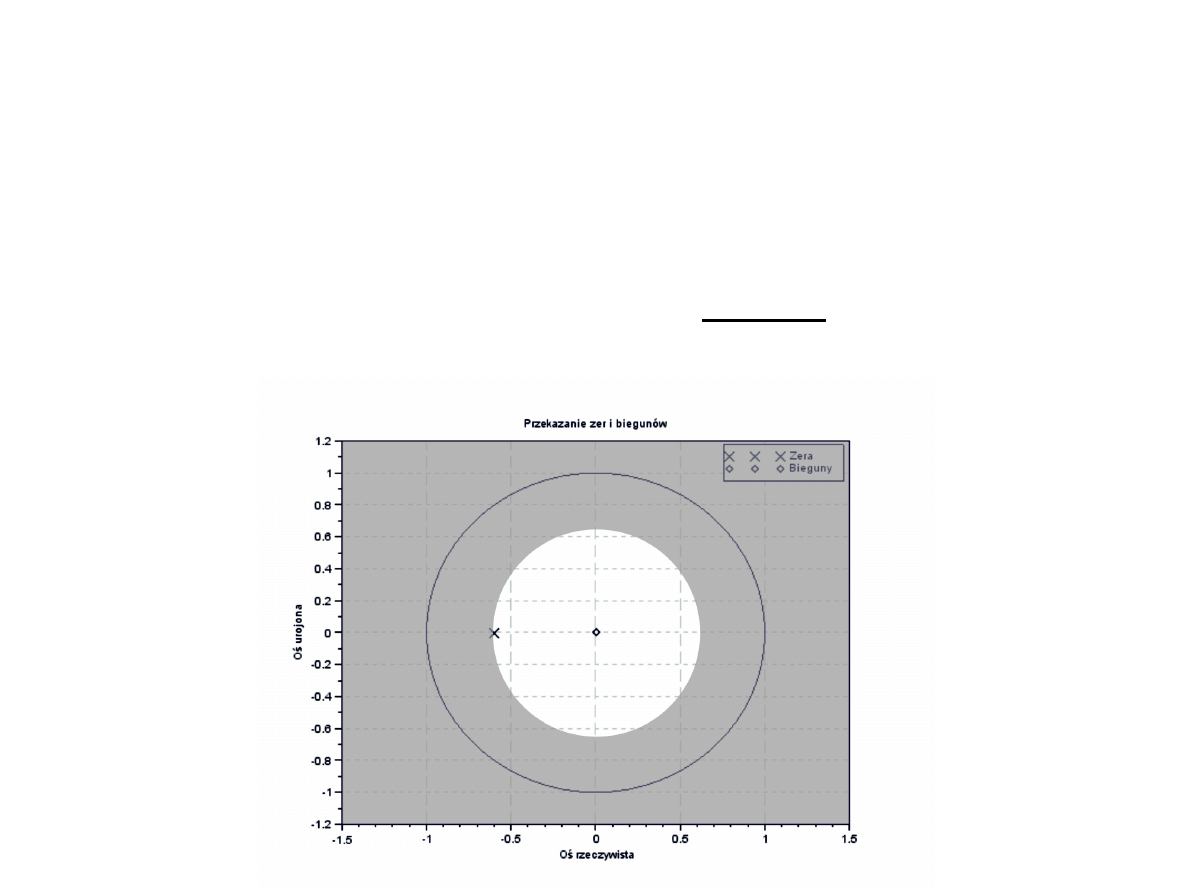
Obszar zbieżności

wymiernej z-transformaty

●

Określmy ROC z-transformaty sygnału:

h[n]=(−0.6)

n

u [n] , H ( z)=

z

z +0.6

⇔

|z|>0.6

ROC wymiernej z-transformaty

●

ROC z-transformaty sygnału prawostronnego
postaci:

jest określona warunkiem:

●

ROC z-transformaty sygnału lewostronnego:

●

Jest określona warunkiem:

x [n]=

(

a (α)

n

+

b(β)

n

)

u [n− N

0

]

,∣α∣<∣β∣

∣β∣<∣

z∣<∞

x [n]=

(

a (α)

n

+

b(β)

n

)

u [−n− N

0

]

,∣α∣<∣β∣

0≤∣z∣<∣α∣

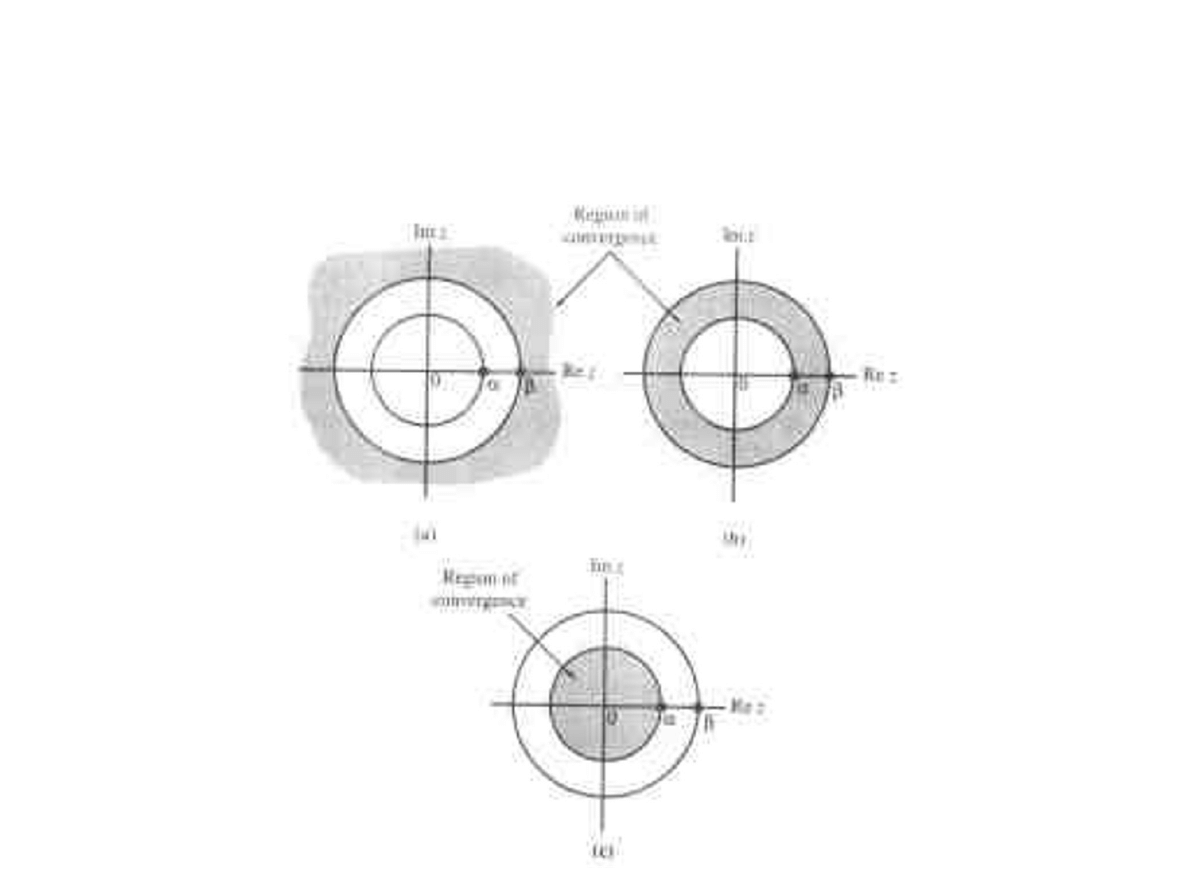
ROC wymiernej z-transformaty

Własności z-transformaty

Odwrotna z-transformata

●

W wielu aspektach technicznych związanych z
przetwarzaniem sygnału istotnego znaczenia
nabiera problem odwracania z-transformaty,
czyli przejścia od X(z) do x[n].

●

Odwracanie z-transformaty odbywa się
zasadniczo metodami:

–

całek Cauchy'ego,

–

tablicową,

–

rozkładu na ułamki proste,

–

długiego dzielenia.

Metoda całek Cauchy'ego

Metoda całek Cauchy'ego

Metoda tablicowa

●

Najprostszą metodą jest doprowadzenie danej z-
transformaty do postaci ujętej w tablicach i
skorzystanie z gotowego wyrażenia na odwrotną
z-transformatę funkcji.

●

Ponieważ z-transformata jest przekształceniem
liniowym, wystarczy przedstawić ją jako
kombinację liniową z-transformat elementarnych.

Tablica par z-transformat

Przykład

●

Znaleźć odwrotną z-transformatę funkcji:

●

Przekształćmy powyższe wyrażenie do postaci:

●

Porównując z danymi z tabeli znajdujemy, że:

H (z)=

0.5z

z

2

−

z+0.25

∣

z∣>0.5

H (z)=

0.5z

−

1

(

1−0.5z

−

1

)

2

h[n]=n(0.5)

n

u [n]

Metoda rozkładu na ułamki proste

●

Obszarem zbieżności wymiernej z-transformaty
H(z) sygnału przyczynowego h[n] jest obszar
leżący na zewnątrz koła.

●

Metoda rozszerzania ułamków częściowych
polega rozbijaniu funkcji H(z) na sumę
prostszych wyrazów, których odwrotne z-
transformaty można znaleźć np. metodą
tablicową.

Rozkładanie na ułamki proste

●

Wymierna z-transformata dana jest wyrażeniem:

●

Jeśli M≥N, wówczas funkcja wymierna H(z) jest
ułamkiem niewłaściwym.

●

Można w takiej sytuacji dokonać dzielenia
wielomianu P(z) przez D(z) i zapisać wynik w
postaci zawierającej ułamek właściwy P

1

/D:

H (z)=

∑

k=0

M −N

α

k

z

−

k

+

P

1

(

z)

D( z)

H (z)=

P ( z)

D( z)

=

p

0

+

p

1

z

−

1

+…+

p

M

z

−

M

d

0

+

d

1

z

−

1

+…+

d

N

z

−

N

Przykład

●

Dany jest ułamek niewłaściwy postaci:

●

Dokonując długiego dzielenia wielomianów
otrzymamy ostatecznie, że:

H (z)=

2+0.8 z

−

1

+

0.5 z

−

2

+

0.3 z

−

3

1+0.8 z

−

1

+

0.2 z

−

2

H (z)=−3.5+1.5 z

−

1

+

5.5+2.1 z

−

1

1+0.8z

−

1

+

0.2z

−

2

Wydzielanie ułamka właściwego

1.5 z

−

1

−

3.5

0.3 z

−

3

+

0.5 z

−

2

+

0.8 z

−

1

+

2: 0.2 z

−

2

+

0.8 z

−

1

+

1

−(

0.3 z

−

3

+

1.2 z

−

2

+

1.5 z

−

1

)

= −

0.7 z

−

2

−

0.7 z

−

1

+

2

−

0.7 z

−

2

−

2.8 z

−

1

−

3.5

=

2.1 z

−

1

+

5.5

Reszta z dzielenia

Odwrotna

kolejność!!!

Część wydzielona

Bieguny pojedyncze

●

Gdy H(z) jest ułamkiem właściwym z
pojedynczymi, rozdzielonymi biegunami λ

k

,

można ją wówczas przedstawić w postaci
sumy ułamków prostych:

●

Stałe r

k

w powyższym wzorze to tzw. residua

funkcji H(z).

H (z)=

∑

k=1

N

r

k

1−λ

k

z

−

1

Residua

●

Wartości residuów obliczamy ze wzoru:

●

Ponieważ zakładamy przyczynowość
badanych sygnałów (ROC: |z| > |λ

k

|), zatem:

r

k

=(

1−λ

k

z

−

1

)⋅

H ( z)∣

z=λ

k

H (z)=

∑

k=1

N

r

k

1−λ

k

z

−

1

⇒

Z

−

1

g [n]=

∑

k=1

N

r

k

(λ

k

)

n

u [n]

Przykład

●

Znaleźć odwrotną z-transformatę funkcji:

●

Funkcja ma dwa rozdzielone bieguny: -0.6, 0.2

●

Dokonujemy rozkładu na ułamki proste:

H (z)=

1+2z

−

1

(

1−0.2z

−

1

)(

1+0.6z

−

1

)

H (z)=

r

1

1−0.2z

−

1

+

r

2

1+0.6z

−

1

Przykład

●

Obliczamy wartości residuów:

●

Poszukiwana odwrotna z-transformata ma
więc postać:

r

1

=(

1+0.6z

−

1

)

H ( z)∣

z=−0.6

=

1+2z

−

1

1−0.2z

−

1

∣

z=−0.6

=−

1.75

r

2

=(

1−0.2z

−

1

)

H (z)∣

z=0.2

=

1+2z

−

1

1+0.6z

−

1

∣

z=0.2

=

2.75

h[n]=−1.75(−0.6)

n

u [n]+2.75(0.2)

n

u [n]

Przykład

●

Wartości residuów można także obliczyć
doprowadzając sumę ułamków prostych z
powrotem do postaci wyjściowej i porównując
wartości powstałych wyrażeń:

H ( z)=

r

1

1−0.2z

−

1

+

r

2

1+0.6z

−

1

=…

…=

(

r

1

+

r

2

)+(−

0.2 r

1

+

0.6 r

2

)

z

−

1

(

1−0.2z

−

1

)(

1+0.6z

−

1

)

=

1+2z

−

1

(

1−0.2z

−

1

)(

1+0.6z

−

1

)

{

r

1

+

r

2

=

1

−

0.2 r

1

+

0.6 r

1

=

2

⇒

{

r

1

−

1.75

r

2

=

2.75

Bieguny wielokrotne

●

Gdy H(z) jest ułamkiem właściwym z L-krotnym
biegunem λ

1

, i pozostałymi biegunami

pojedynczymi, należy ją wówczas przedstawić w
postaci:

H (z)=

∑

k=1

L

β

k

(

1−λ

1

z

−

1

)

k

+

∑

k=2

N − L+1

r

k

1−λ

k

z

−

1

Bieguny wielokrotne

●

Stałe β

k

w powyższym wzorze (nie będące

residuami dla k>1) oblicza się ze wzoru:

●

Użyteczny wzór dla biegunów podwójnych:

β

k

=

1

(

L−k )! (−λ

1

)

L−k

d

L−k

d ( z

−

1

)

L−k

(

(

1−λ

1

z

−

1

)

L

H (z)

)

∣

z=λ

1

H (z)=

1

(

1−λ z

−

1

)

2

⇔

Z

h [n]=(n+1)(λ)

n

u [n]

Przykład

●

Dana jest funkcja H(z) postaci:

H ( z)=

1

(

1−

1

2

z

−

1

)(

1+

1

3

z

−

1

)

2

=

...

...=

r

1

1−

1

2

z

−

1

+

β

1

1+

1

3

z

−

1

+

β

2

(

1+

1
3

z

−

1

)

2

=

...

...=

0.36

1−

1

2

z

−

1

+

0.24

1+

1

3

z

−

1

+

0.4

(

1+

1
3

z

−

1

)

2

Metoda długiego dzielenia

wielomianów

●

Istotą tej metody jest przedstawienie funkcji
wymiernej w postaci szeregu potęgowego z

-k

,

gdy sygnał jest przyczynowy, i z

k

, gdy sygnał

jest antyprzyczynowy.

●

Z własności z-transformaty wynika, że
współczynnik stojący przy wyrazie z

-k

jest

jednocześnie poszukiwaną k-tą próbką
sygnału h[n].

●

Metoda długiego dzielenia prowadzi zwykle do
nieskończonych szeregów potęgowych
zmiennej z

-k

.

Przykład

●

Wyznaczyć odwrotną z-transformatę funkcji
metodą długiego dzielenia wielomianów:

H (z)=

z

−

1

1−2z

−

1

+

z

−

2

,∣z∣>1

Przykład

z

−

1

+

2 z

−

2

+

3 z

−

3

+…

z

−

1

:1−2 z

−

1

+

z

−

2

−(

z

−

1

−

2 z

−

2

+

z

−

3

)

=

2 z

−

2

−

z

−

3

−(

2 z

−

2

−

4 z

−

3

+

2 z

−

4

)

=

3 z

−

3

−

2z

−

4

H (z)=0+ z

−

1

+

2 z

−

2

+

3 z

−

3

+…

h[n]=[0 ,1, 2, 3,…]

Funkcja przenoszenia

●

Funkcja odpowiedzi częstotliwościowej H(e

jω

)

układu LTI jest transformatą DTFT jego
odpowiedzi impulsowej h[n].

●

Funkcja odpowiedzi częstotliwościowej zawiera
kompletną informację o zachowaniu się układu w
dziedzinie częstotliwości, jednak z uwagi na
zespoloną postać, trudno nią manipulować przy
kształtowaniu charakterystyk filtrów.

●

Z drugiej strony, z-transformata jest wielomianem
zmiennej z

-1

i dla rzeczywistych h[n] jest

wielomianem o współczynnikach rzeczywistych.

Funkcja przenoszenia

●

Wiemy, że:

●

Funkcja przenoszenia H(z) dana jest jako:

●

Jest to więc funkcja wymierna zmiennej z

y [n]=

∑

k=−∞

∞

x [n] h[n−k ]

Y (z)= X ( z) H ( z)

H (z)=

Y ( z)

X ( z)

Funkcja przenoszenia filtrów FIR

●

W przypadku filtrów FIR ich odpowiedź
impulsowa zawiera skończoną liczbę próbek,
a odpowiedź układu ma postać:

●

Funkcja przenoszenia ma zatem postać:

y [n]=

∑

k=N

1

N

2

x [k ] h[n−k ]

H (z)=

∑

k=N

1

N

2

h[k ] z

−

k

Funkcja przenoszenia filtrów IIR

●

Filtry IIR opisywane są równaniami
różnicowymi o stałych współczynnikach:

●

Po zastosowaniu z-transformaty, otrzymujemy
wyrażenie:

∑

k=0

N

a

k

y [n−k ]=

∑

k=0

M

b

k

x [n−k ]

∑

k=0

N

a

k

z

−

k

Y ( z)=

∑

k=0

M

b

k

z

−

k

X ( z)

Funkcja przenoszenia filtrów IIR

●

Stąd, po przekształceniach funkcja przenoszenia
ma postać:

●

Ponieważ odpowiedź jest sygnałem
przyczynowym, ROC tej funkcji spełnia warunek:

H (z)=

Y ( z)

X ( z)

=

∑

k=0

M

b

k

z

−

k

∑

k=0

N

a

k

z

−

k

∣

z∣>max

k

∣λ

k

∣

Stabilność filtrów

●

Filtry z odpowiedzią impulsową h[n] są
stabilne wtedy, gdy:

●

Często trudno jednak sprawdzić ten warunek
wprost, zatem kryterium stabilności
wyprowadza się w oparciu o położenie
biegunów funkcji przenoszenia H(z).

∑

k=−∞

∞

∣

h[n]∣<∞

Stabilność filtrów

●

Jeśli ROC funkcji przenoszenia filtru LTI
zawiera koło jednostkowe, filtr jest stabilny w
sensie BIBO.

●

Wszystkie bieguny stabilnej funkcji
przenoszenia H(z) filtra przyczynowego
muszą leżeć wewnątrz koła jednostkowego.

●

Wszystkie bieguny stabilnej funkcji
przenoszenia H(z) filtra antyprzyczynowego
muszą leżeć na zewnątrz koła
jednostkowego.