1

Wykład 6

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

KINEMATYKA PUNKTU MATERIALNEGO

2

1.1. Ogólna klasyfikacja

MECHANIKA – dział fizyki poświęcony badaniu ruchów i stanów

równowagi ciał. Obejmuje statykę, kinematykę
i dynamikę

Statyka

– dział mechaniki badający prawa równowagi

ciał będących pod działaniem sił

Kinematyka – dział mechaniki zajmujący się opisem ruchu

ciał bez uwzględnienia jego przyczyn oraz
cech fizycznych ciał.

Dynamika

– dział mechaniki badający ruch ciał
materialnych pod wpływem działających
na nie sił

Statyka

– dział mechaniki badający prawa równowagi

ciał będących pod działaniem sił

Dynamika

– dział mechaniki badający ruch ciał
materialnych pod wpływem działających
na nie sił

Część 1

Równania ruchu punktu

4

1.1. Układy odniesienia

Układ odniesienia

– rzeczywiste lub umowne ciało sztywne, względem

którego

opisuje się ruch innych ciał. Z układem odniesienia jest

związany

układ współrzędnych

x

y

z

x

y

z

5

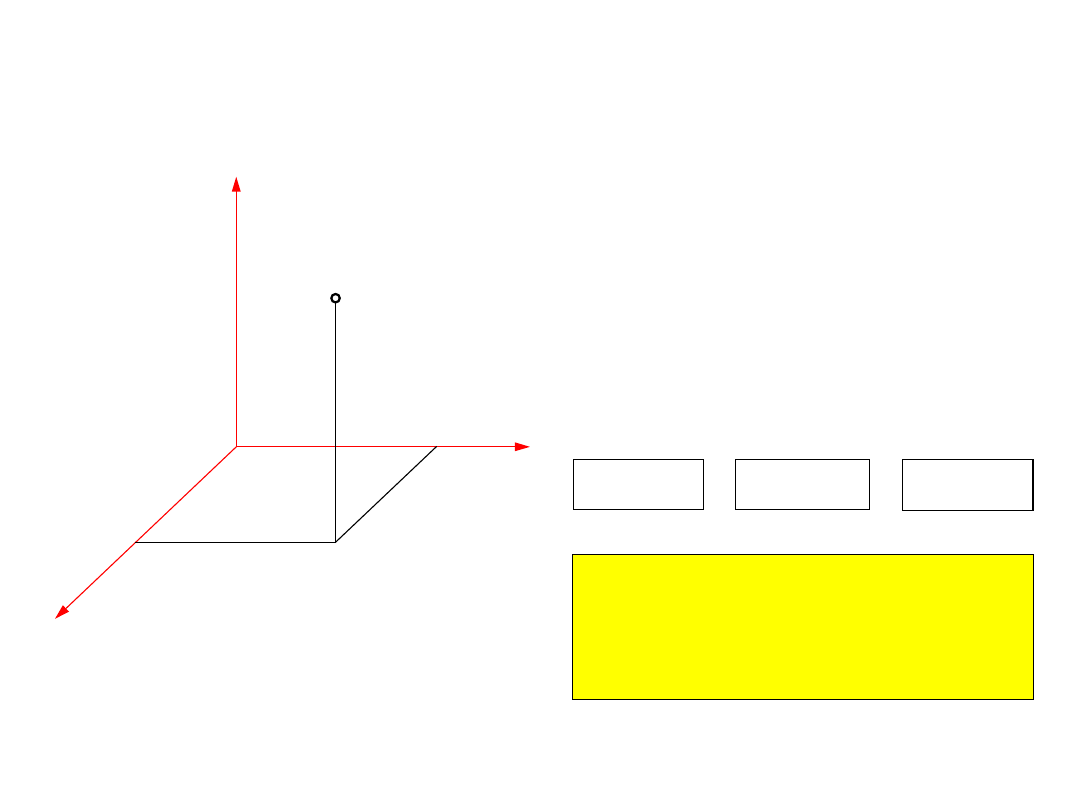
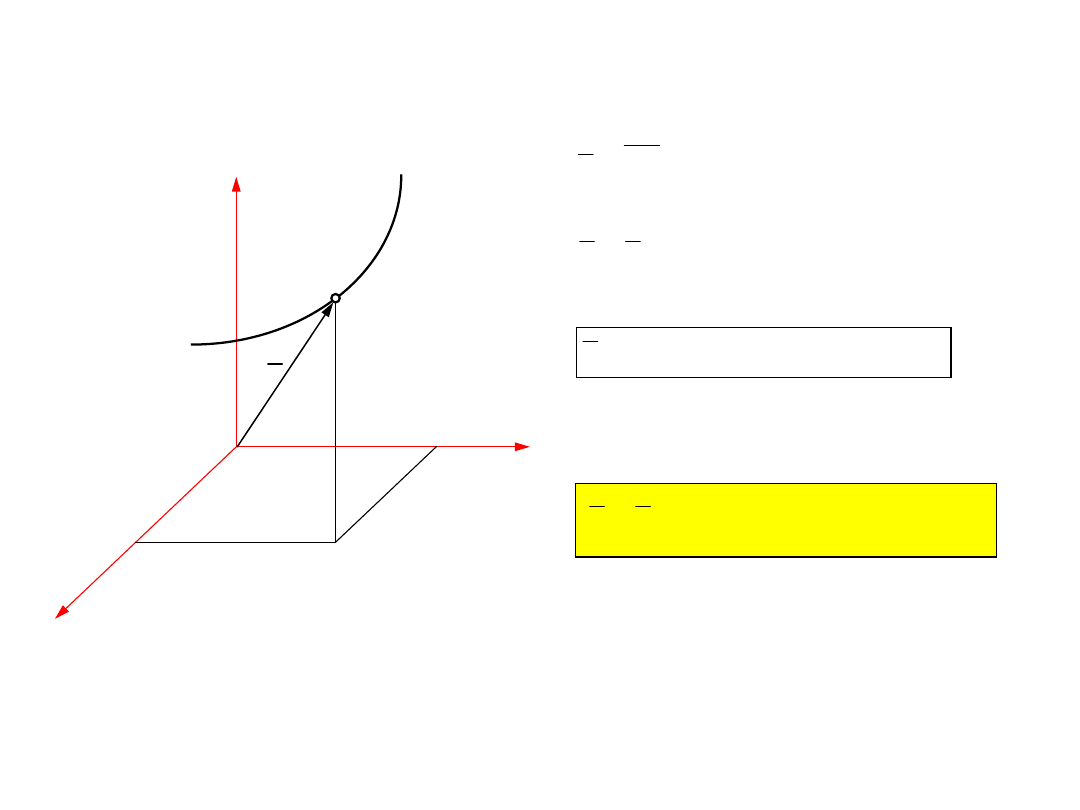
1.2. Równania ruchu w prostokątnym układzie

współrzędnych

x

y

z

A

x

A

y

A

z

A

O

A

A

A

x , y , z

- współrzędne punktu

A

w prostokątnym
układzie współrzędnych

Gdy punkt

A

zmienia swoje

położenie w czasie to

x

A

, y

A

, z

A

są

pewnymi funkcjami czasu

( )

A

x

f t

=

1

( )

A

y

f t

=

2

( )

A

z

f t

=

3

Powyższe równania są równaniami
ruchu punktu

A

w prostokątnym

układzie współrzędnych.

Jest to tzw. skalarny opis ruchu

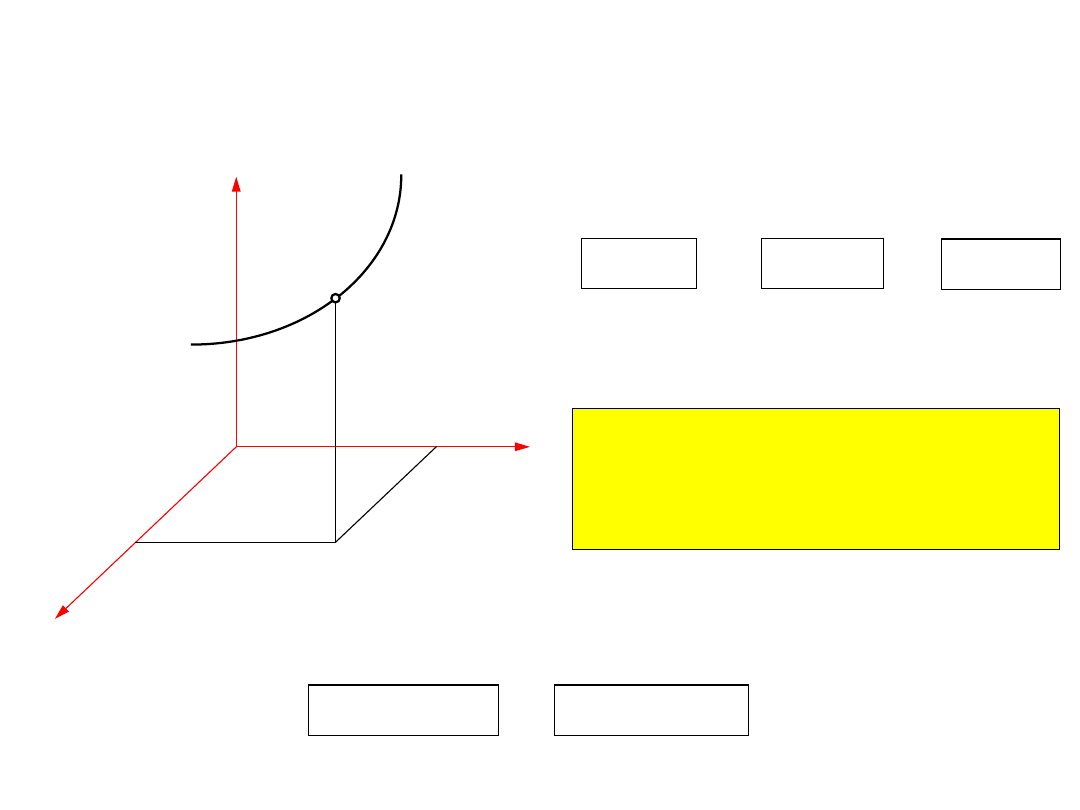
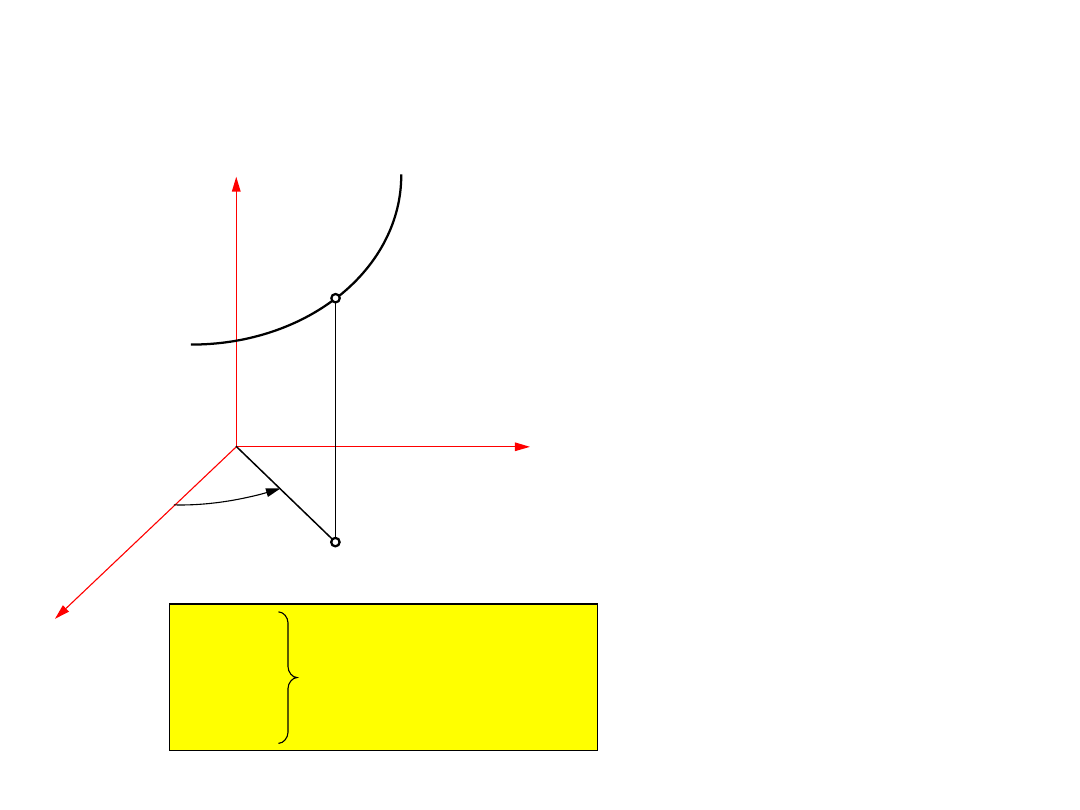
6

x

y

z

A

x

A

y

A

z

A

O

Jeśli założy się, że

t

jest parametrem

to równania:

( )

x f t

=

1

( )

y f t

=

2

( )

z f t

=

3

są równaniami toru punktu

A

Tor punktu

jest to zbiór wszystkich chwilowych
położeń punktu w trakcie trwania
ruchu

Po wyrugowaniu czasu z równań parametrycznych otrzymuje
się układ dwóch równań, które są równaniem krawędziowym
toru:

(

)

F x, y, z =

1

0

(

)

F x, y, z =

2

0

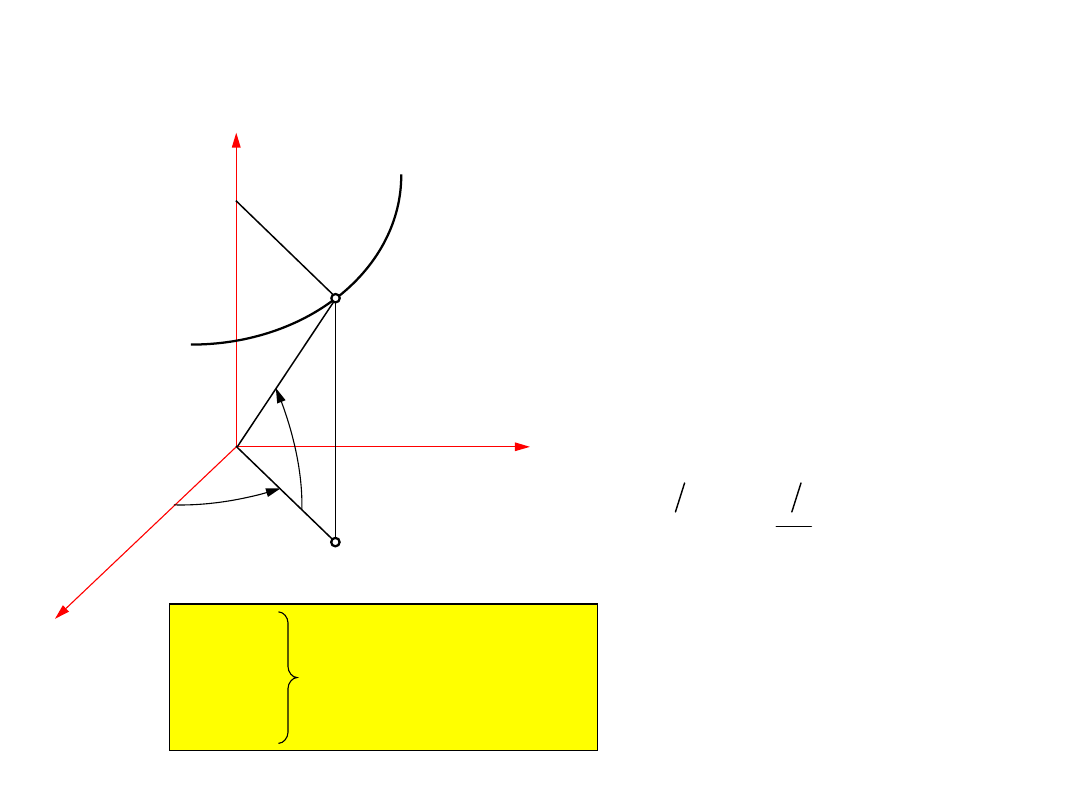
7

x

y

z

A

x

A

y

A

z

A

O

r

- wektor wodzący punktu A

( )

( )

( )

r

f t i f t j f t k

=

�+

�+

�

1

2

3

r OA

=

( )

r r t

=

- funkcja wektorowa

( )

r r t

=

- wektorowy opis
ruchu

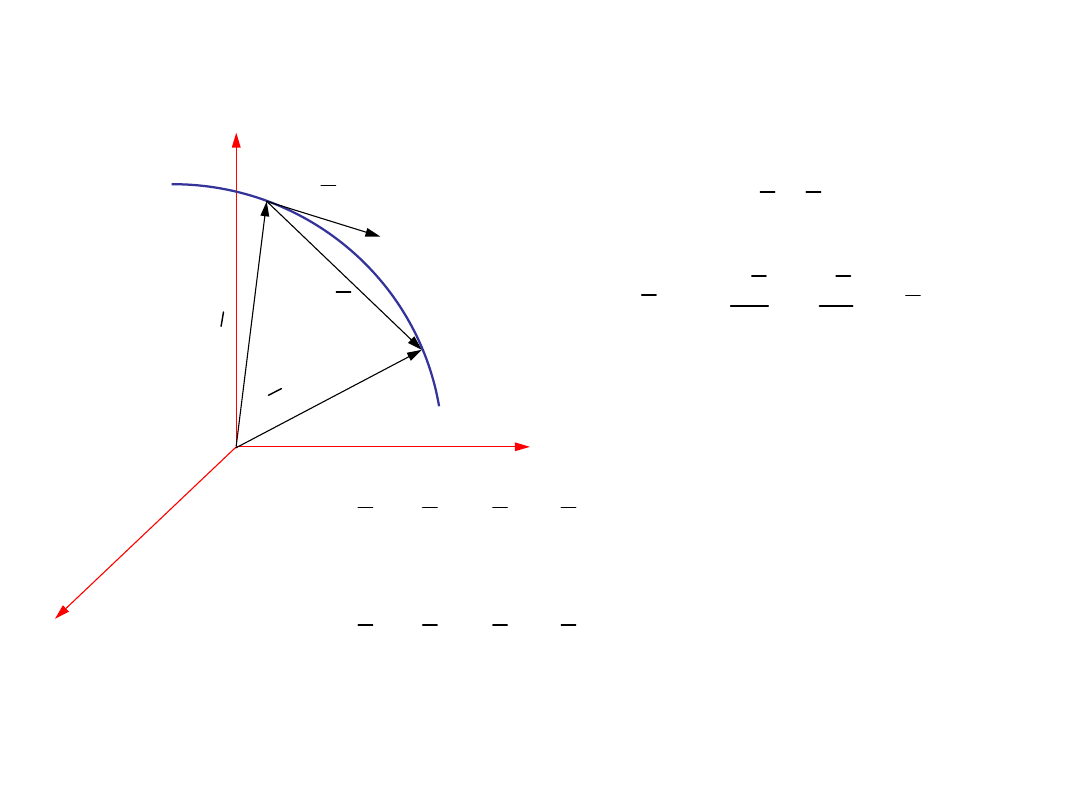
8

x

y

z

z

A

O

r

( )

r r t

=

- opis skalarny ruchu

we współrzędnych
walcowych

φ

( )

φ φ t

=

( )

z z t

=

A'

r

φ

z

- odległość rzutu punktu

A

na płaszczyznę

Oxy

od

początku
układu współrzędnych

- miara kąta pomiędzy płaszczyzną

Oxz

a płaszczyzną przechodzącą przez

punkty

A

i oś

Oz

- współrzędna

z

w

prostokątnym
układzie współrzędnych

φ

π

� <

0

2

r �0

x rcosφ

=

z z

=

y rsinφ

=

1.3. Równania ruchu we współrzędnych walcowych

9

x

y

z

z

A

O

( )

r r t

=

- opis skalarny ruchu

we współrzędnych

sferycznych

φ

( )

φ φ t

=

( )

θ θ t

=

A'

r

φ

θ

- odległość punktu

A

od punktu

O

- miara kąta pomiędzy płaszczyzną
przechodzącą przez punkt

A

i oś

Oz

a płaszczyzną

Oxz

- miara kąta pomiędzy
płaszczyzną

Oxy

a promieniem

r

θ

r

φ

π

� <

0

2

r �0

π

θ π

-

� �

2

2

z

θ

gdy OA

Oz

>

��

0

z

A

x rcosφcosθ

=

z rsinθ

=

y rsinφcosθ

=

1.4. Równania ruchu w sferycznym układzie

współrzędnych

Część 2

Prędkość i przyspieszenie punktu

11

2.1. Prędkość punktu w opisie wektorowym i

skalarnym

x

y

z

O

t

A

tΔt

A

+

Δr

x

y

z

r xe

ye

ze

=

+

+

df

Δt

Δr

υ lim

Δt

�

=

0

dr

dt

=

( )

x f t

=

1

( )

y f t

=

2

( )

z f t

=

3

r

= &

Jeśli

to

- prędkość punktu w opisie
wektorowym

x

y

z

υ

x υ

y υ

z

=

=

=

&

&

&

x

y

z

υ xe

ye

ze

=

+

+

&

&

&

gdzie

- składowe prędkości

w prostokątnym
układzie
współrzędnych

( )

v t





r t

Δt





r

t

( )

r r t

=

Dany jest wektorowy opis
ruchu:

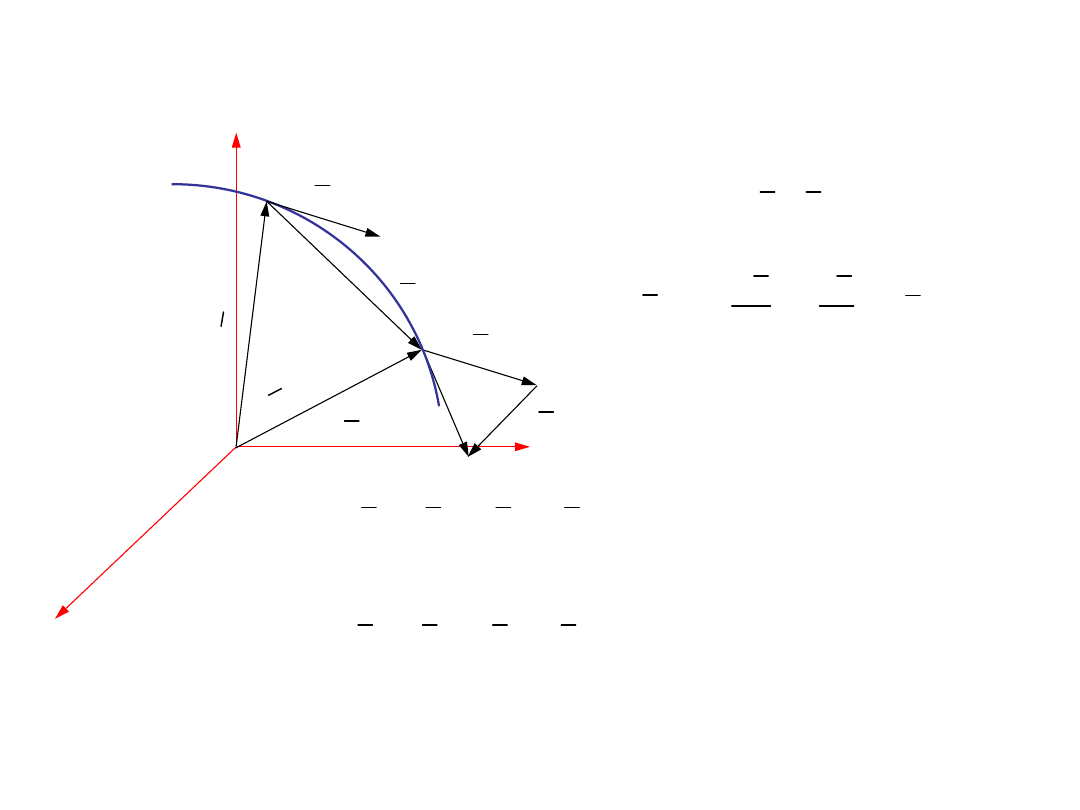
12

2.2. Przyspieszenie punktu w opisie wektorowym i

skalarnym

x

y

z

O

(

)

v tΔt

+

Δr

x

y

z

r xe

ye

ze

=

+

+

df

Δt

Δυ

a lim

Δt

�

=

0

dυ

dt

=

( )

x f t

=

1

( )

y f t

=

2

( )

z f t

=

3

r

=&&

Jeśli

to

- przyspieszenie punktu w
opisie
wektorowym

x

y

z

a

x a

y a

z

=

=

=

&&

&&

&&

x

y

z

a xe

ye

ze

=

+

+

&&

&&

&&

gdzie

- składowe
przyspieszenia
w prostokątnym
układzie
współrzędnych

( )

v t





r t

Δt





r

t

Δv

( )

v t

( )

r r t

=

Dany jest wektorowy opis
ruchu:

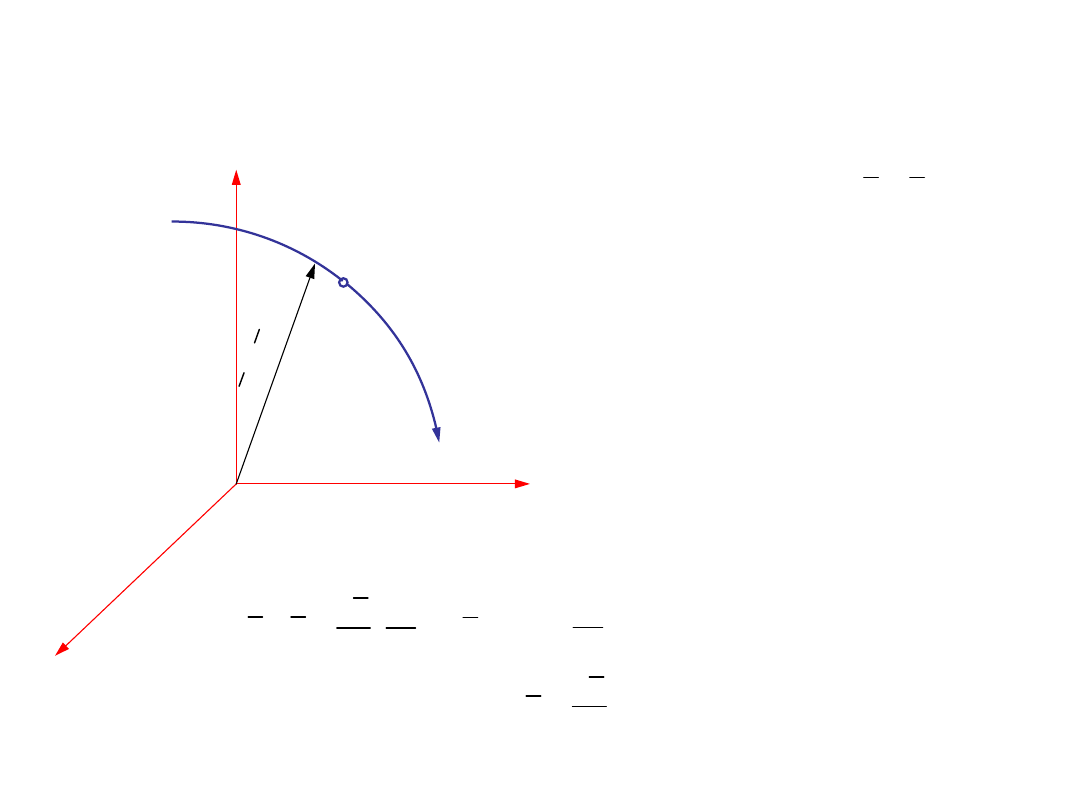
13

2.3. Prędkość i przyspieszenie punktu w opisie

naturalnym

x

y

z

O

3. Punkt początkowy toru

s <0

( )

s s t

=





r

r

s



Ω

0

s

s <0

Naturalny opis ruchu:

4. Równanie ruchu

2. Orientacja toru

Ω

0

( )

r r s

=

1. Równanie toru

dr

τ

ds

=

dr ds

υ r

sτ

ds dt

= =

� =

&

&

- wektor kierunku
stycznego do toru

ds

s

dt

=

&

- prędkość skalarna

Prędkość punktu w opisie naturalnym

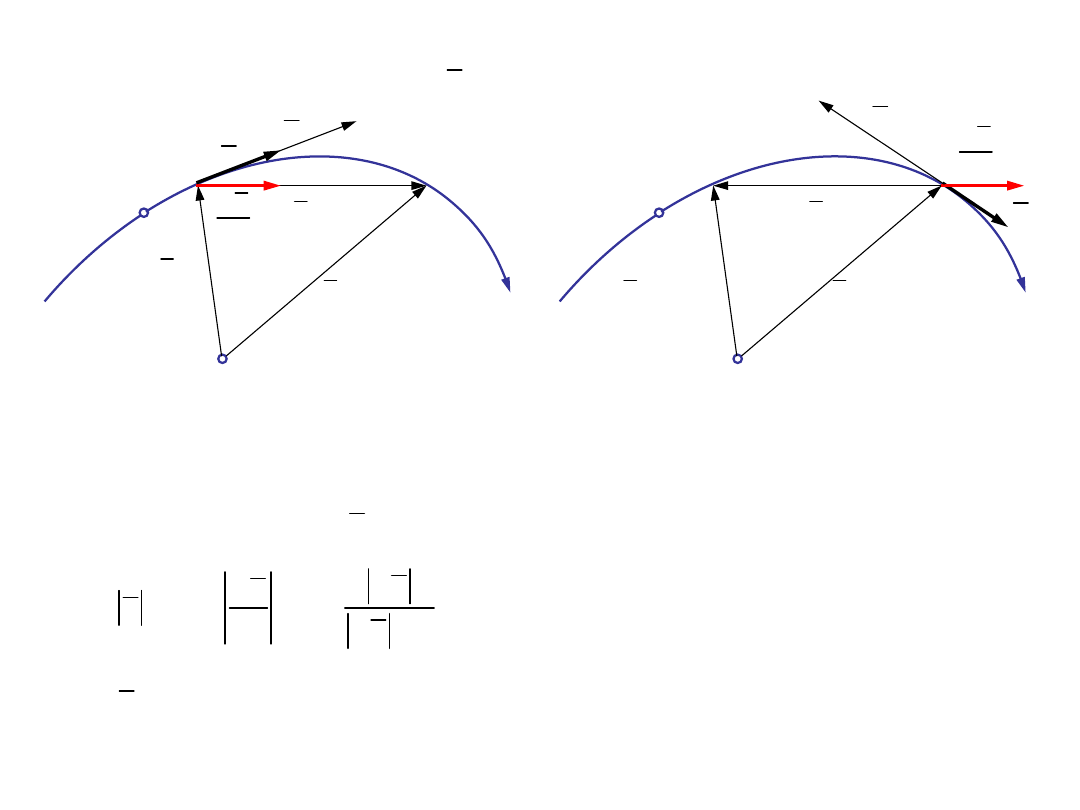
14

( )

r t

(

)

r tΔt

+

Δr

Δs

Ω

0

τ

Δr

s

Δs <0

O

( )

r t

(

)

r tΔt

+

Δr

Δs

Ω

0

τ

Δr

s

Δs >0

O

υ

υ

Zwrot wektora kierunku stycznego do
toru jest zawsze zgodny z orientacją toru

t

A

tΔt

A

+

t

A

tΔt

A

+

Wartość wektora

τ

Δs

ξ

Δr

Δr

τ

lim

lim

Δs

Δr ξ

�

�

=

=

=

+

0

0

1

Ustalenie zwrotu wektora

τ

τ

jest wersorem kierunku stycznego do toru

15

τ τ

^&

( )

d

aυ

sτ

sτ sτ

dt

= =

=

+

&

&

&

&& &

n

dτ

dτ ds

dτ dα

dτ

a

s

s

s

sκ

s κν

dt

ds dt

dα ds

dα

=

=

� =

� =

=

2

2

2

&

&

&

&

&

- przyspieszenie normalne do toru

Przyspieszenie punktu w opisie
naturalnym

d

τ

τ

τ τ

dt

=

=

=

2

2

1

2

0

&

s

sτ a

=

&&

- przyspieszenie styczne do toru

n

sτ a

=

&

&

s

n

a a a

= +

df

dα

κ

ds

=

- krzywizna krzywej (zakłada się, że
przyrosty
drogi i kąta są tego samego znaku)

ds

ρ

dα κ

=

=

1

- promień krzywizny

ν

- wektor współliniowy z a więc normalny do toru

τ&

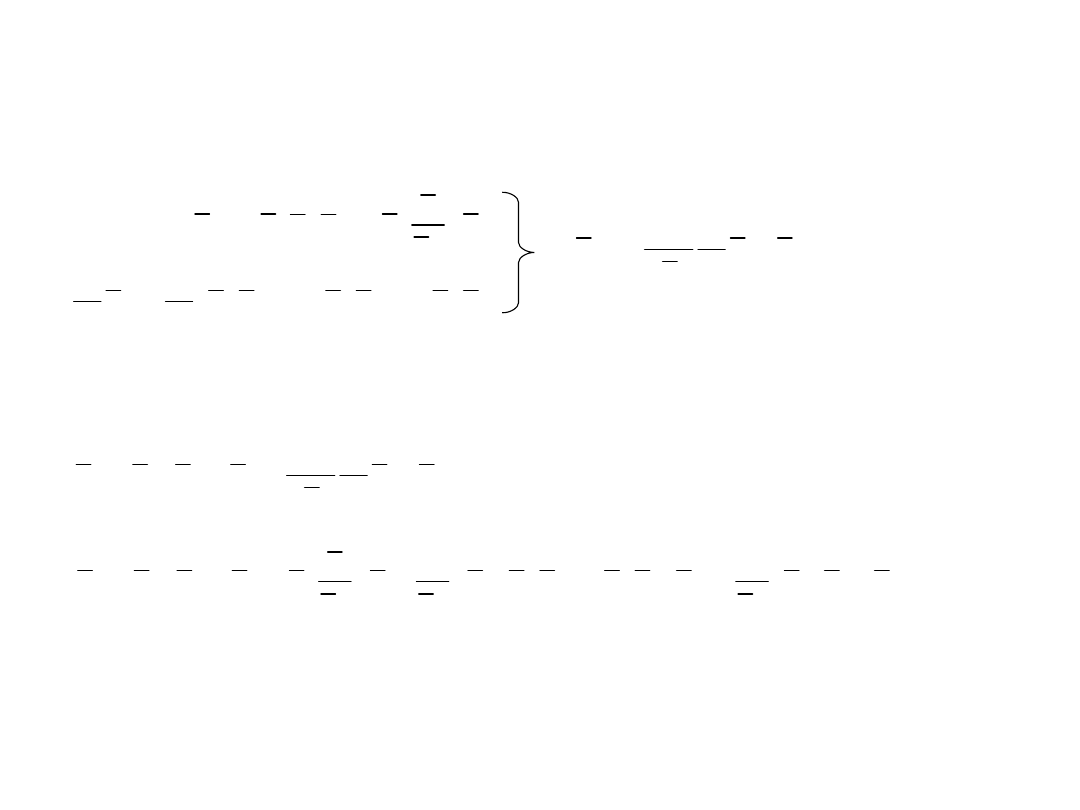
16

(

)

s

υ

a

aτ τ

a

υ

υ

�

�

= �

= �

�

�

�

�

2

(

)

d

d

υ

υ υ

υ υ

a υ

dt

dt

=

� = �� = ��

2

2

2

&

s

d

aυ υ

dt

υ

�

�

=�

�

�

�

2

2

1

2

n

s

d

a

a a

aυ υ

dt

υ

�

�

= -

= - �

�

�

�

2

2

1

2

(

) (

)

(

)

n

s

υ

a

a a

a

aυ

a υ υ

a υ υ

υ a υ

υ

υ

υ

�

�

= -

= -

�

=

� � -

� � =

� �

�

�

�

�

�

�

�

�

2

2

2

1

1

Przyspieszenie normalne można wyznaczyć z zależności

Przyspieszenie styczne do toru jest rzutem przyspieszenia całkowitego na
kierunek styczny

17

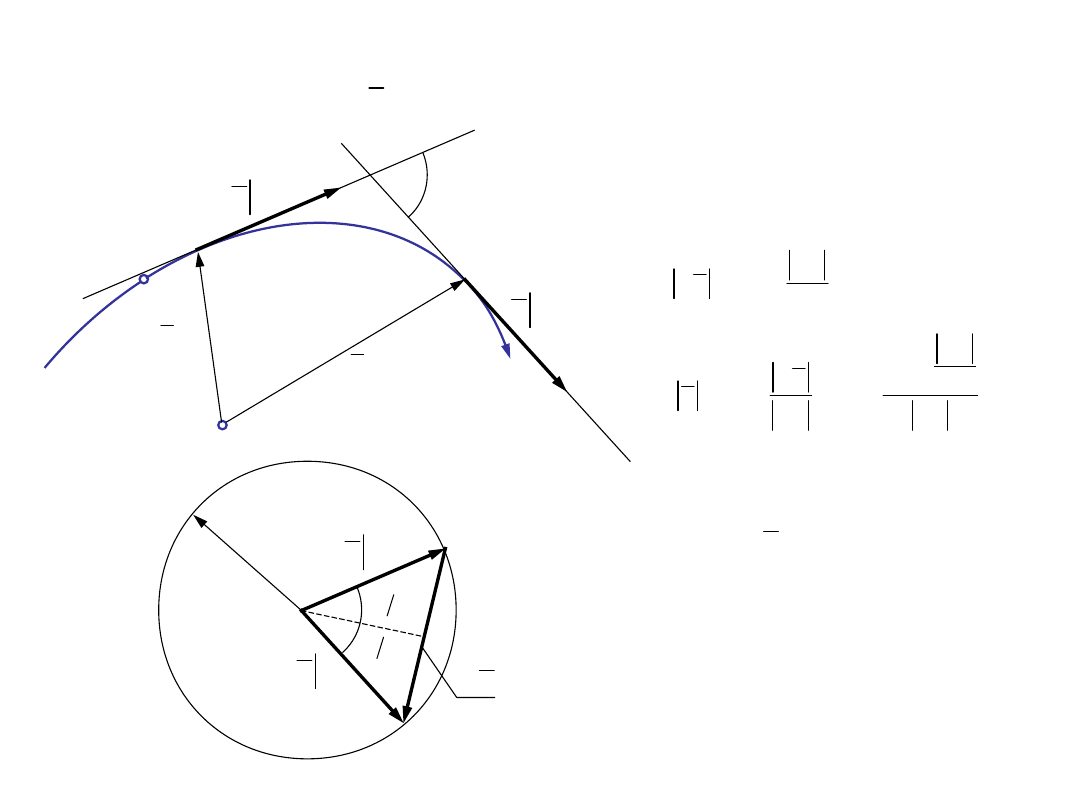
Własności
wektora

ν

( )

r t

(

)

r tΔt

+

Δα

Δτ

sin

=2

2

Ω

0

tΔt

τ

+

s

O

Δτ

t

A

tΔt

A

+

t

τ

Δα

Δα 2

Δα 2

t

τ

tΔt

τ

+

r =1

Δα

Δα

Δα

sin

Δτ

ν

lim

lim

Δα

Δα

�

�

=

=

=

0

0

2

2

1

Wektor jest wersorem

ν

18

( )

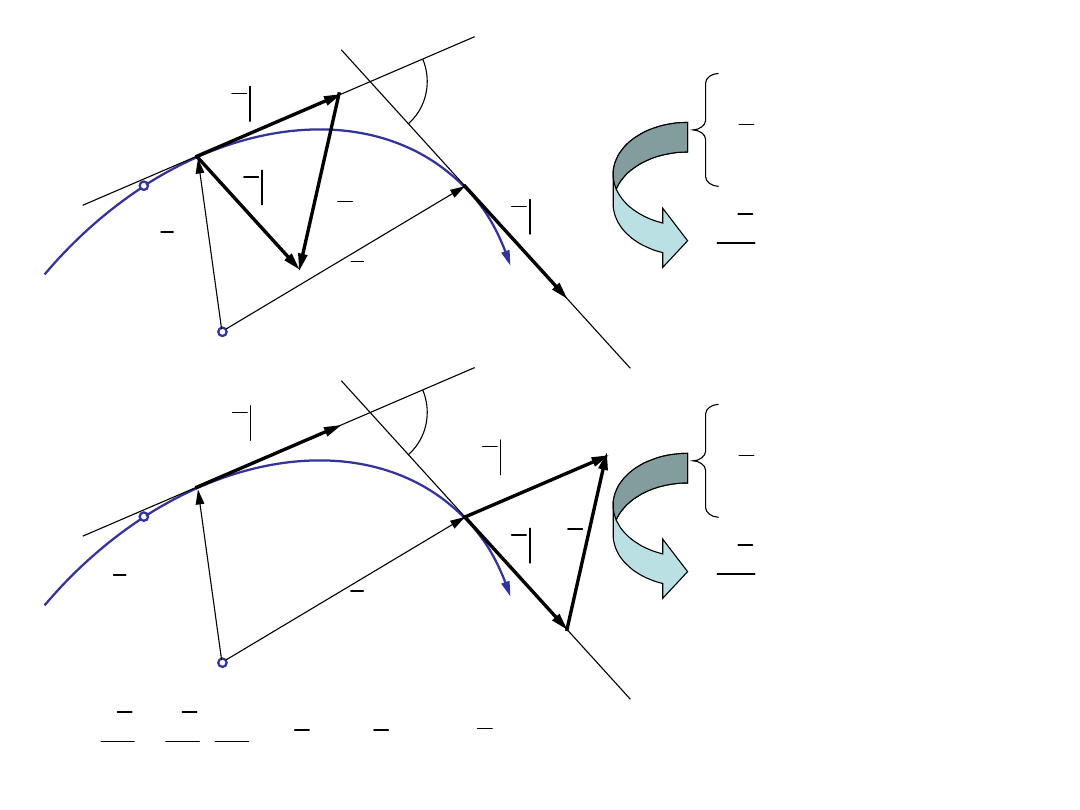
r t

(

)

r tΔt

+

Ω

0

s

O

t

A

tΔt

A

+

t

τ

Δα

tΔt

τ

+

Δτ

Δs <0

Δs <0

Δτ

skierowany w obszar
po stronie wklęsłej toru

Δτ

Δs

skierowany w obszar
po stronie wypukłej
toru

( )

r t

(

)

r tΔt

+

Ω

0

tΔt

τ

+

s

O

t

A

tΔt

A

+

t

τ

Δα

tΔt

τ

+

Δτ

Δs >0

Δs >0

Δτ

skierowany w obszar
po stronie wklęsłej toru

Δτ

Δs

skierowany w obszar
po stronie wklęsłej toru

tΔt

τ

+

jest skierowany do środka
krzywizny

dτ

dτ dα

κν

ν

ds dα ds

=

� =

��

ν

19

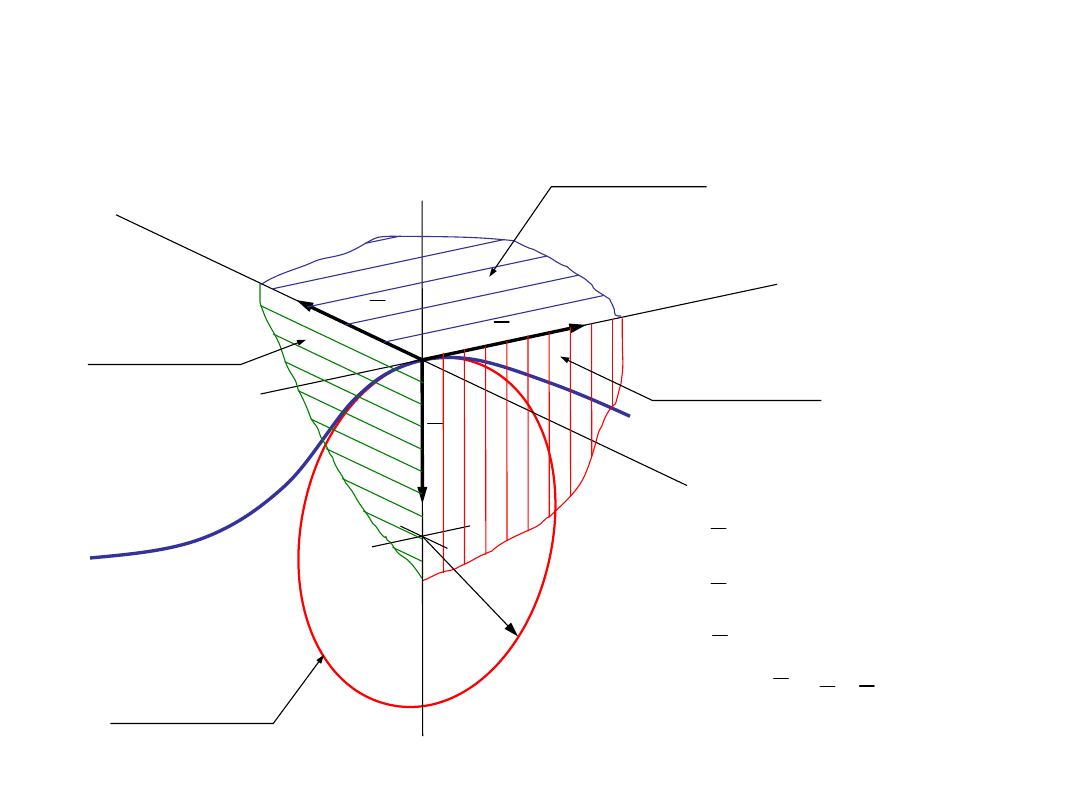
2.4. Trójścian Freneta

τ

ν

b

styczn

a

n

o

rm

a

ln

a

g

łó

w

n

a

bino

rmaln

a

płaszczyzna
ściśle styczna

płaszczyzn
a
normalna

okrąg
ściśle styczny

płaszczyzna
prostująca

ρ

τ

ν

b

- wersor binormalny

- wersor styczny

- wersor normalny

bτ ν

= �

20

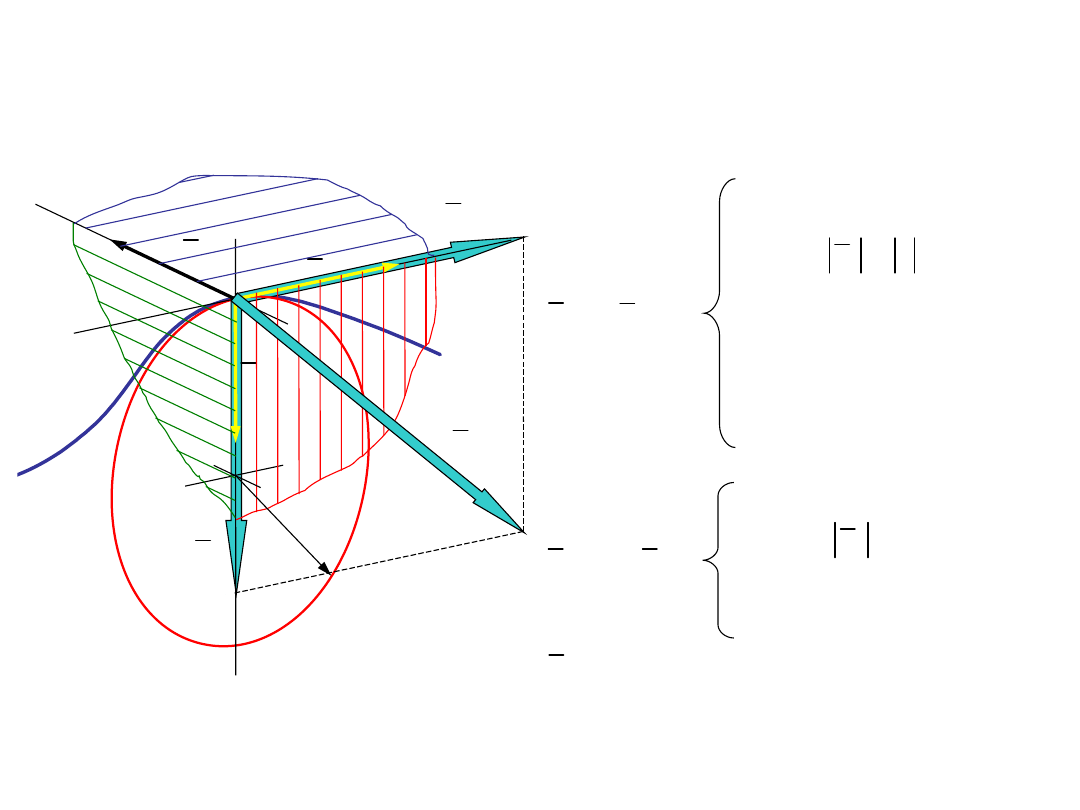
Przyspieszenie w lokalnej bazie
Freneta

τ

ν

b

ρ

przeciwny do orientacji
toru
gdy

kierunek styczny
do toru

moduł

s

a

n

a

a

0

b

a =

s

a

sτ

=

�

&&

s

a

s

= &&

0

s <

&&

zwrot zależny od znaku
zgodny z orientacją toru
gdy

0

s >

&&

s&&

kierunek normalnej
głównej

moduł

zwrot zawsze do środka
krzywizny toru

2

2

n

a

sκ υ κ

=

=

&

Wektor przyspieszenia leży
w płaszczyźnie ściśle
stycznej

2

n

a

sκν

=

�

&

Część 3

Ruch po okręgu

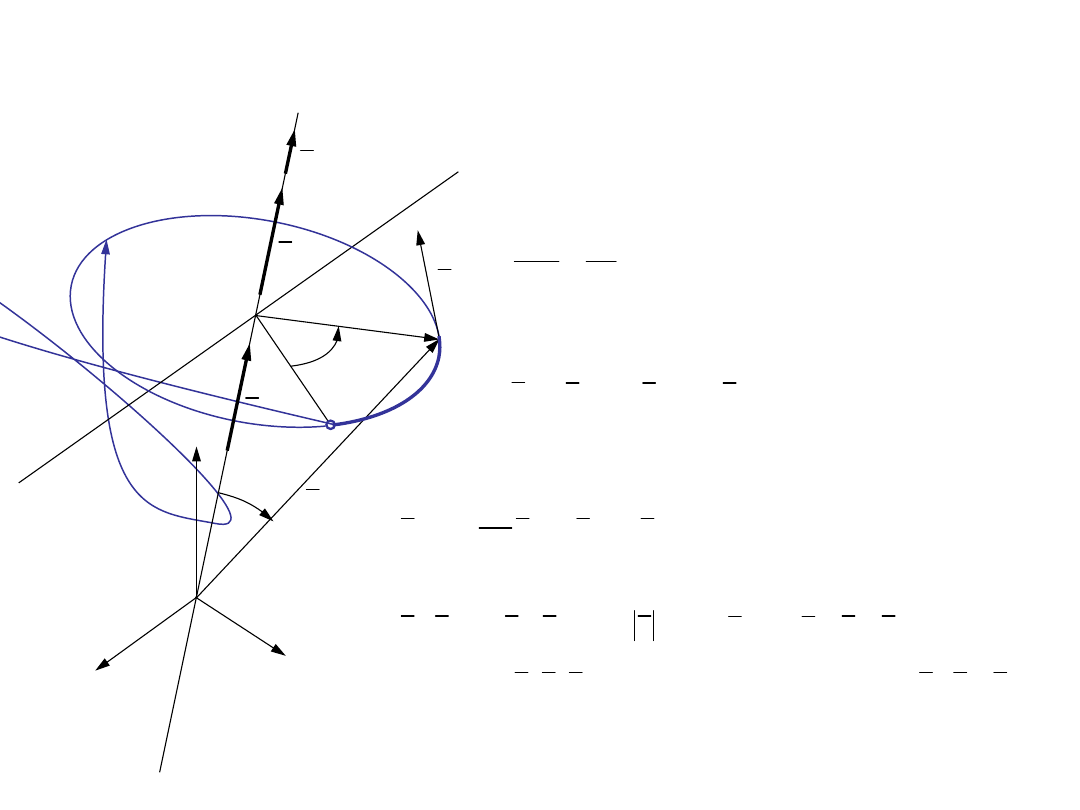
22

A

Ω

0

r

υ

R

φ

α

s

x

y

z

l

e

ε

O

ś

o

b

ro

tu

O

2

2

sφ

s Rφ

πR

π

=

�

=

υ sτ Rφτ Rωτ

=

=

=

&

&

df

ω φ

=&

- skalarna prędkość kątowa

0

df

l

l

l

Δt

Δφ

ω lim

e φe ωe

Δt

�

=

=

=

&

- wektor prędkości kątowej

3.1. Prędkość w ruchu po okręgu

gdzie

- zależność pomiędzy
drogą s a drogą kątową
φ

Punkt porusza się po okręgu o promieniu
R
i środku w punkcie O

Prędkość w ruchu po okręgu

1

l

ω r ω e r ω

r sinα τ Rωτ υ r

===����=״=�

&

ω, r, υ

Wektory związane są
zależnością

ω r υ

� =

ω

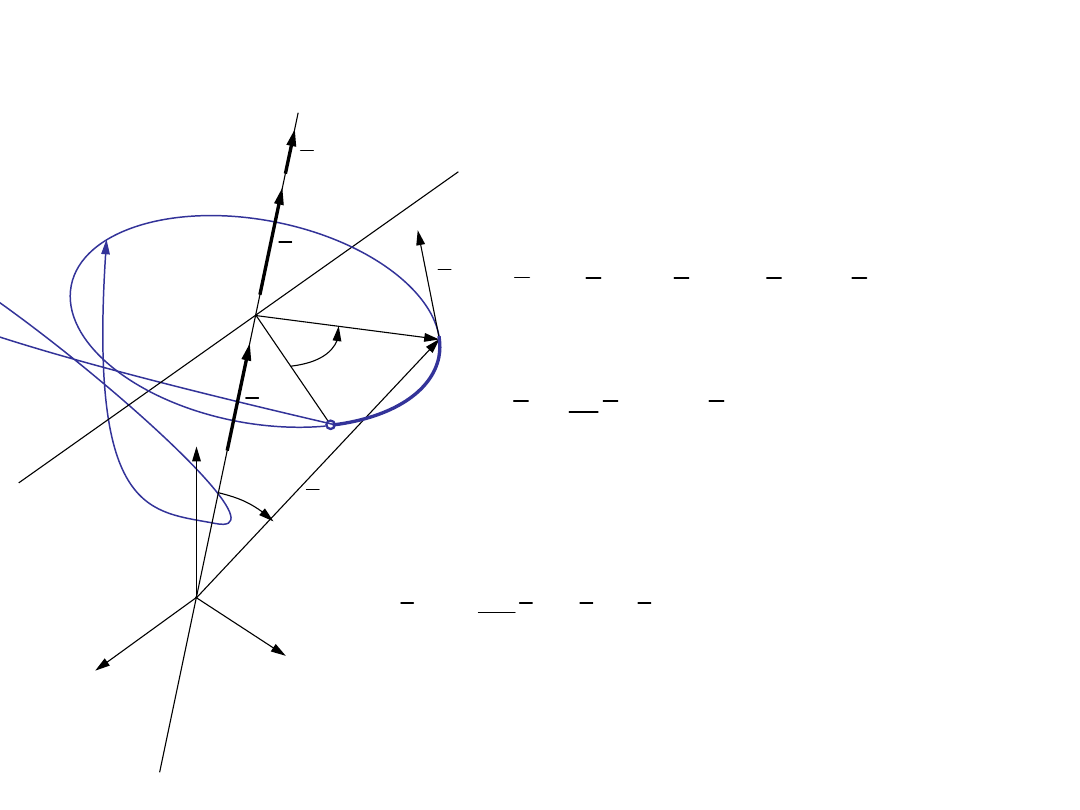
23

A

Ω

0

r

υ

R

φ

α

s

x

y

z

l

e

ω

O

ś

o

b

ro

tu

O

0

df

l

l

l

Δt

Δω

ε lim

e φe

εe

Δt

�

=

=

=

&&

- wektor przyspieszenia
kątowego

3.2. Przyspieszenie w ruchu po okręgu (opis

naturalny)

Przyspieszenie normalne do toru

s

a

sτ Rφτ Rωτ Rετ

=

=

=

=

&&

&&

&

Przyspieszenie styczne do toru

2

2

n

s

aν Rω ν

R

=

=

&

df

ε φ

=&&

- skalarne przyspieszenie kątowe

gdzie

ε

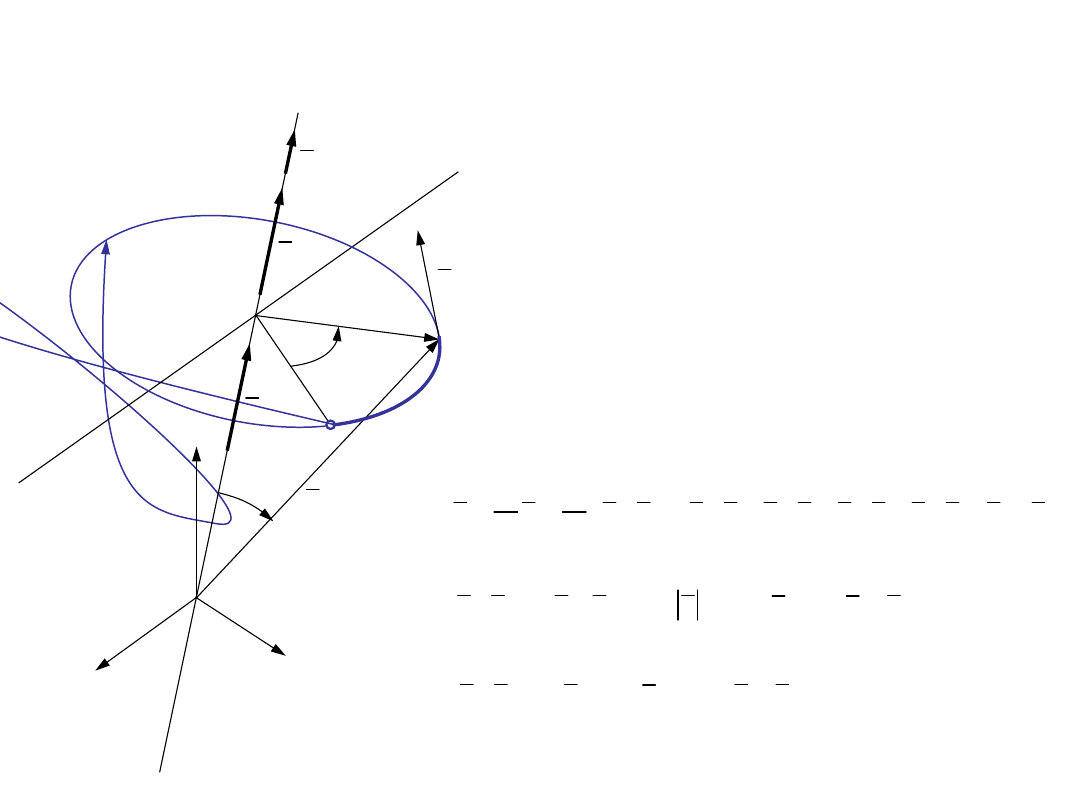
24

(

)

s

n

d

d

aυ

ω r

ω r ω r ε r ω υ a

a

dt

dt

=

=

� = � + � = � + � = +

&

&

1

l

s

ε r ε e r ε

r sinα τ Rετ a

==����=״=�

2

l

n

ω υ ω e Rωτ Rω ν a

==״=�

A

Ω

0

r

υ

R

φ

α

s

x

y

z

l

e

ω

O

ś

o

b

ro

tu

O

ε

3.3. Przyspieszenie w ruchu po okręgu (opis

wektorowy)