Wyk

ł

ad 5

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

1

Wyk

ł

ad 5

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciąg

ł

ych

Instytut Mechaniki Budowli
Wydzia

ł

Inżynierii Lądowej

RODZAJE OBCIĄŻEŃ

REDUKCJA – PODSUMOWANIE DZIA

Ł

U

Część 1

RODZAJE OBCIĄŻEŃ

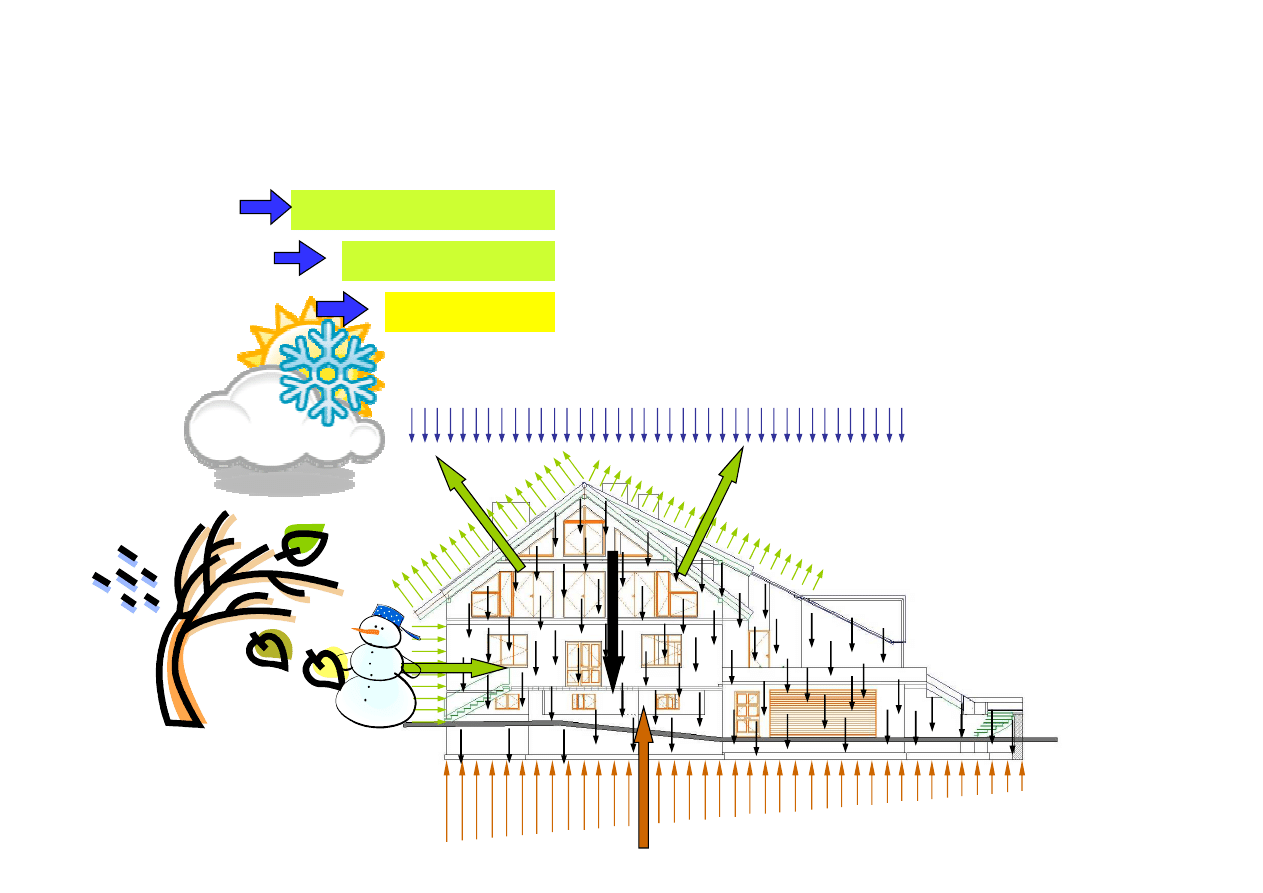
2.1. Klasyfikacja si

ł

def: działa na ka

ż

dy element obj

ę

to

ś

ci (masy)

ciała.

Przykłady:
- siły grawitacji
- siły bezwładno

ś

ci

def: działa tylko na jeden punkt ciała;

zast

ę

puje siły rozło

ż

one.

Warto

ść

siły skupionej oraz jej miejsce

przyło

ż

enia musz

ą

by

ć

takie, aby efekt działania

siły skupionej był identyczny z działaniem siły

SIŁA

POWIERZCHNIOWA

MASOWA

SKUPIONA

def.: dzia

ł

a na każdy element powierzchni cia

ł

a.

Przyk

ł

ady

- dzia

ł

anie gruntu na p

ł

ytę fundamentową

- dzia

ł

anie śniegu na dach

- dzia

ł

anie wiatru na powierzchnię budynku

3

siły skupionej był identyczny z działaniem siły
rozło

ż

onej na powierzchni lub w obj

ę

to

ś

ci

4

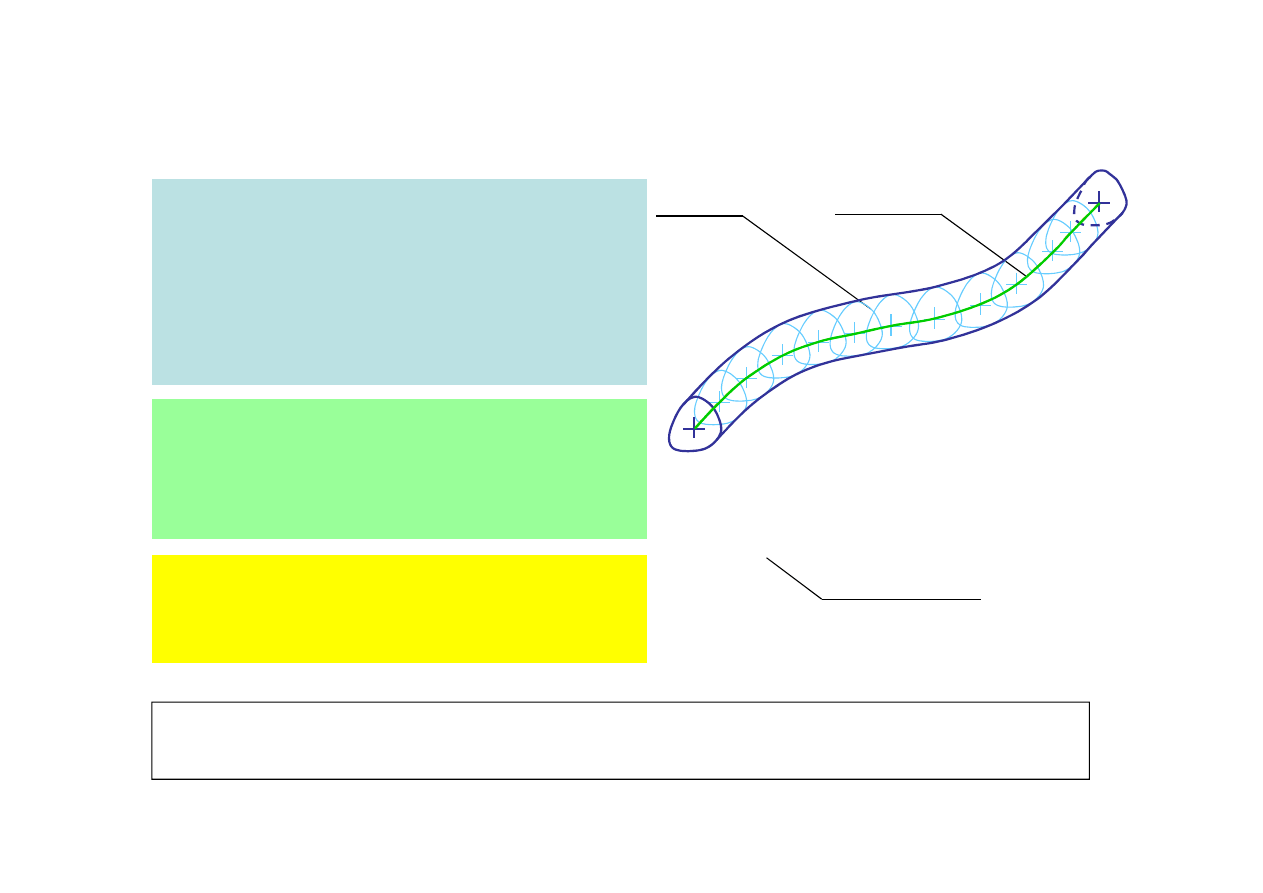
2.2. Obciążenia w uproszczonych modelach ustrojów budowlanych

Pręt
Pod

ł

użny element ustroju

budowlanego, w którym jeden
wymiar (d

ł

ugość) jest znacznie

większy od dwóch pozosta

ł

ych

(szerokość i wysokość)

Oś pręta
Linia, na której leżą środki

Pręt

Oś pręta

a) Model pręta wraz z uk

ł

adem obciążeń

5

Linia, na której leżą środki
geometryczne wszystkich
przekrojów pręta

Ze względu na zaniechanie wymiarów przekroju poprzecznego pręta
punktom osi przypisuje się charakterystyki geometryczne przekroju

Model pręta
W mechanice modelem pręta jest
linia pokrywająca się z osią pręta

Model pręta

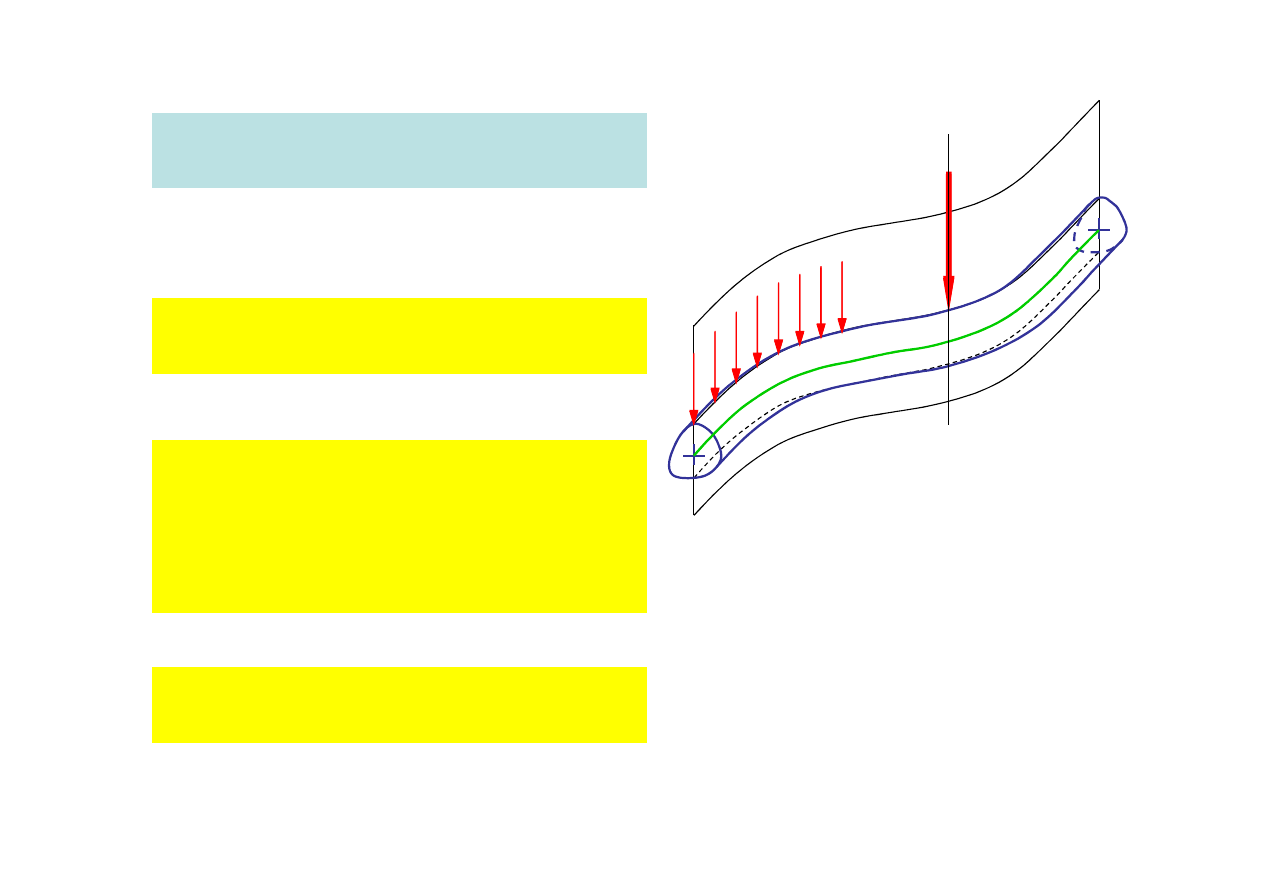
Za

ł

ożenia odnośnie obciążeń

przy

ł

ożonych do pręta

1. Kierunki dzia

ł

ania si

ł

skupionych

przecinają się z osią pręta.

6

2. Si

ł

y powierzchniowe i masowe

przy

ł

ożone do pręta zamienia się

na obciążenia liniowe dzia

ł

ające

wzd

ł

uż tworzących powierzchni

walcowej zawierającą oś pręta

3. W modelu pręta si

ł

y skupione

i liniowe są przy

ł

ożone do jego osi

Obciążenia w modelu pręta

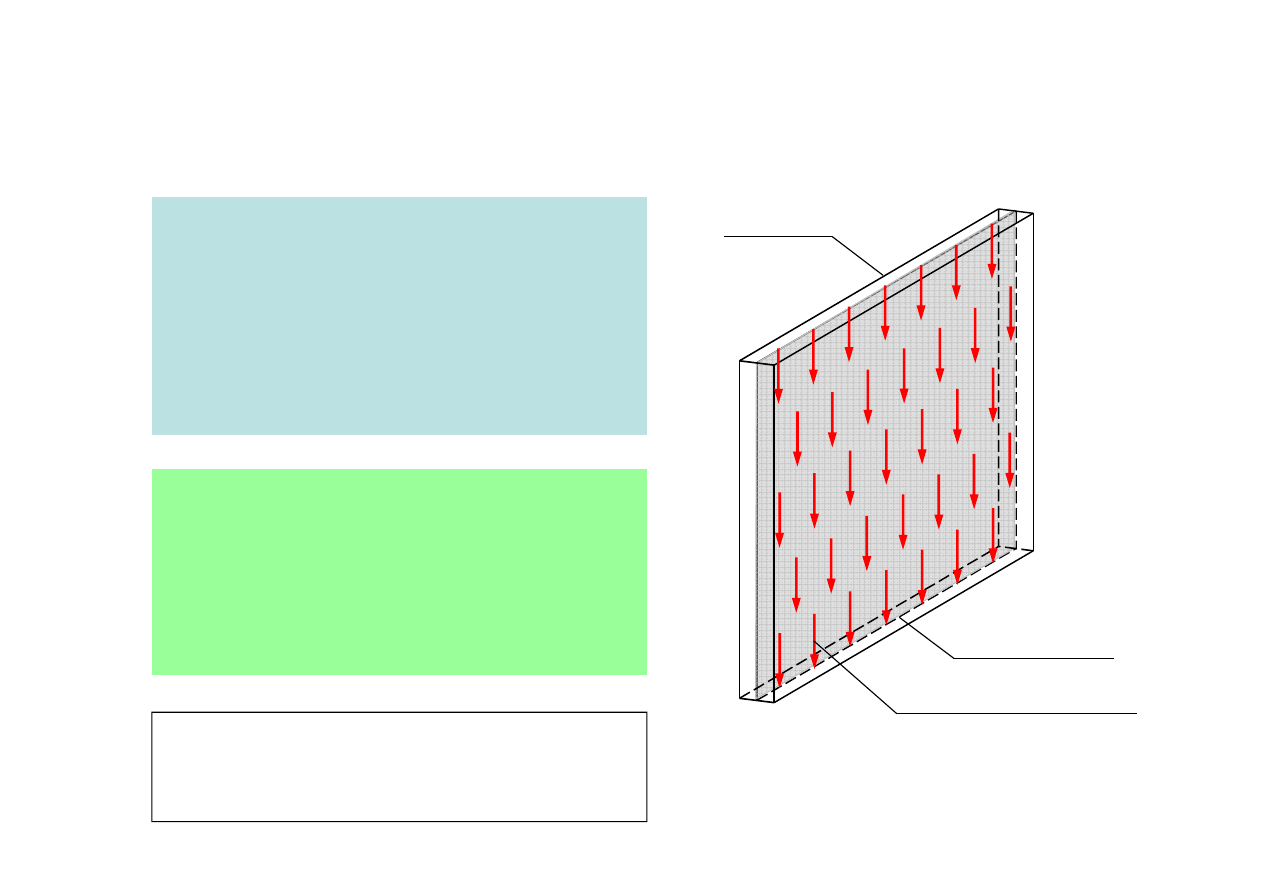
Tarcza
P

ł

aski element ustroju

budowlanego, w którym dwa
wymiary są znacznie większe od
trzeciego a kierunki dzia

ł

ania

wszystkich obciążeń są równoleg

ł

e

do p

ł

aszczyzny tarczy

Tarcza

b) Model tarczy wraz z uk

ł

adem obciążeń

7

Model tarczy
W mechanice modelem tarczy jest
p

ł

aszczyzna w po

ł

owie grubości

tarczy. Przyjmuje się, że w tej
p

ł

aszczyźnie zawierają się kierunki

dzia

ł

ania wszystkich obciążeń

Model tarczy

Obciążenie

w płaszczyźnie tarczy

Obciążenia masowe tarczy zamie-
nia się na obciążenia powierzchnio-
we dzia

ł

ające w p

ł

aszczyźnie tarczy

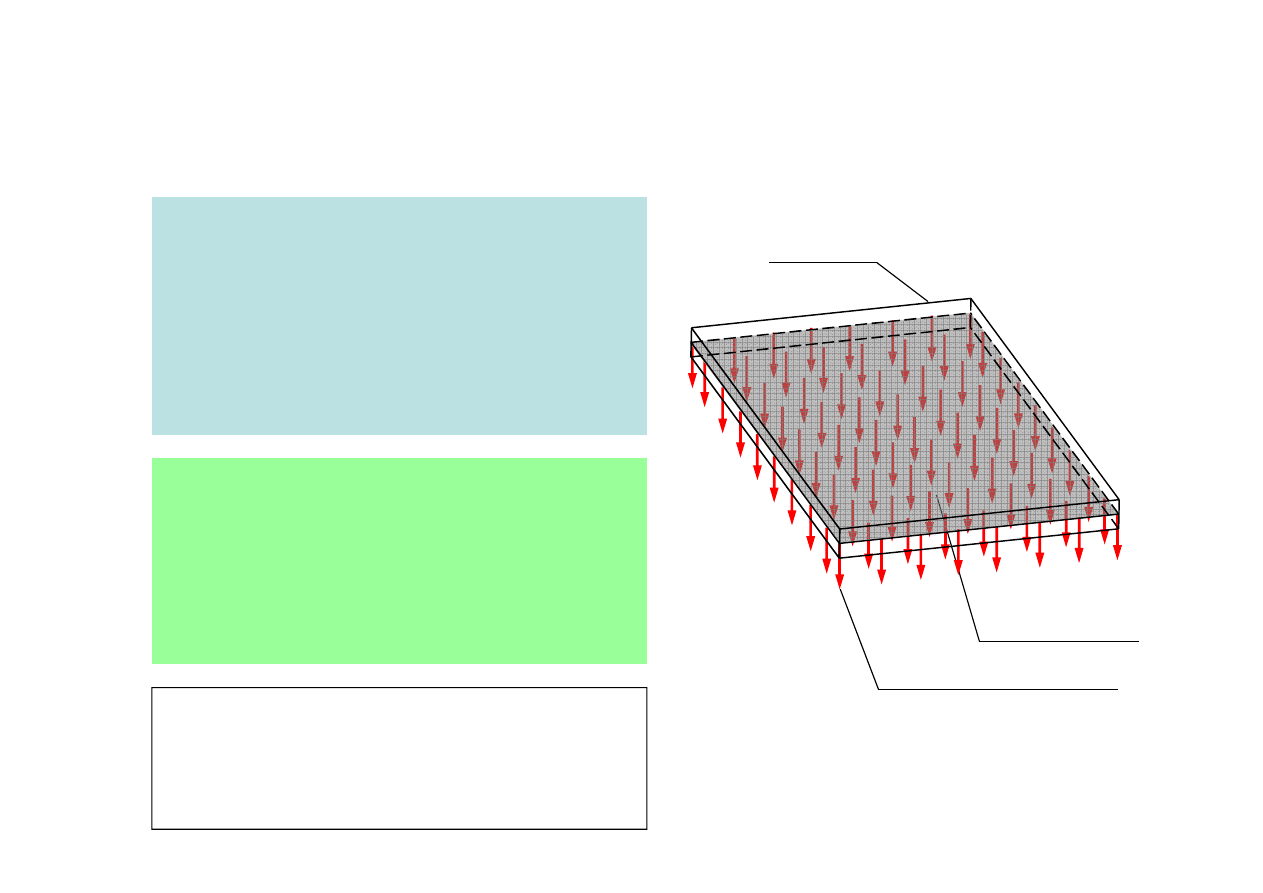
P

ł

yta

P

ł

aski element ustroju

budowlanego, w którym dwa
wymiary są znacznie większe od
trzeciego a kierunki dzia

ł

ania

wszystkich obciążeń są prostopad

ł

e

do p

ł

aszczyzny p

ł

yty

c) Model p

ł

yty wraz z uk

ł

adem obciążeń

Płyta

8

Model p

ł

yty

W mechanice modelem p

ł

yty jest

p

ł

aszczyzna w po

ł

owie grubości

p

ł

yty. Przyjmuje się, że kierunki

dzia

ł

ania wszystkich obciążeń są

prostopad

ł

e do tej p

ł

aszczyzny

Model płyty

Obciążenie

w płaszczyźnie płyty

Obciążenia masowe p

ł

yty zamienia

się na obciążenia powierzchniowe
dzia

ł

ające w kierunku prostopad

ł

ym

do p

ł

yty

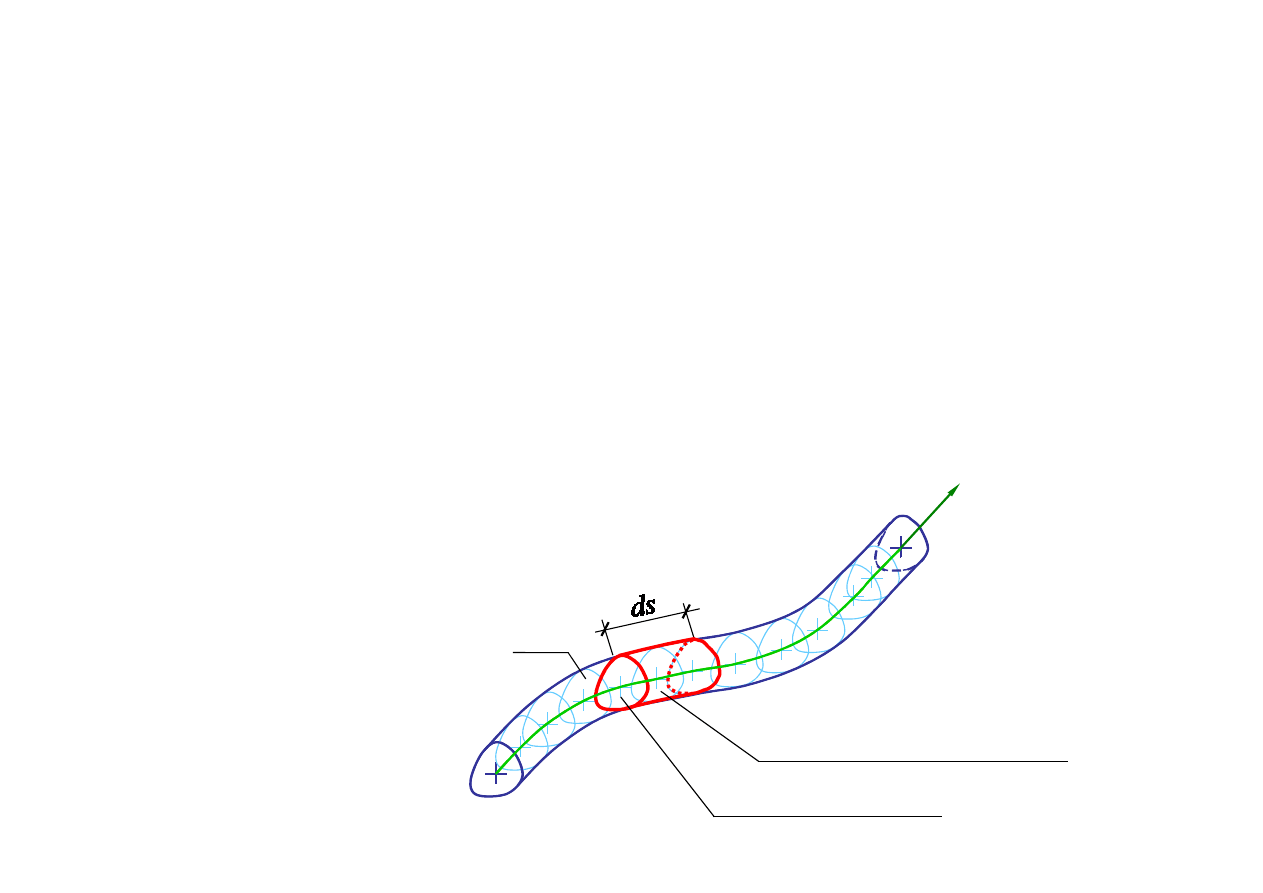
2.3. Obliczanie obciążeń

a) Przeliczenie obciążenia masowego pręta (ciężaru w

ł

asnego)

na równoważne obciążenie liniowe

( )

( )

( ) ( )

( ) ( ) ( )

q s

ds

γ s

dV

γ s

A s

ds

q s

γ s

A s

⋅ =

⋅

=

⋅

⋅

→

=

⋅

( )

γ s

[N/m

3

]

- obciążenie masowe (ciężar w

ł

aściwy)

d s

[m]

- d

ł

ugość elementarnego odcinka pręta

s

[m]

- wspó

ł

rzędna

ł

ukowa

9

( )

q s

[N/m]

- obciążenie roz

ł

ożone wzd

ł

uż osi pręta

( )

A s

[m

2

]

- pole przekroju

d s

[m]

- d

ł

ugość elementarnego odcinka pręta

s

γ

(

s)

elementarny odcinek pręta

Pole przekroju

( )

A s

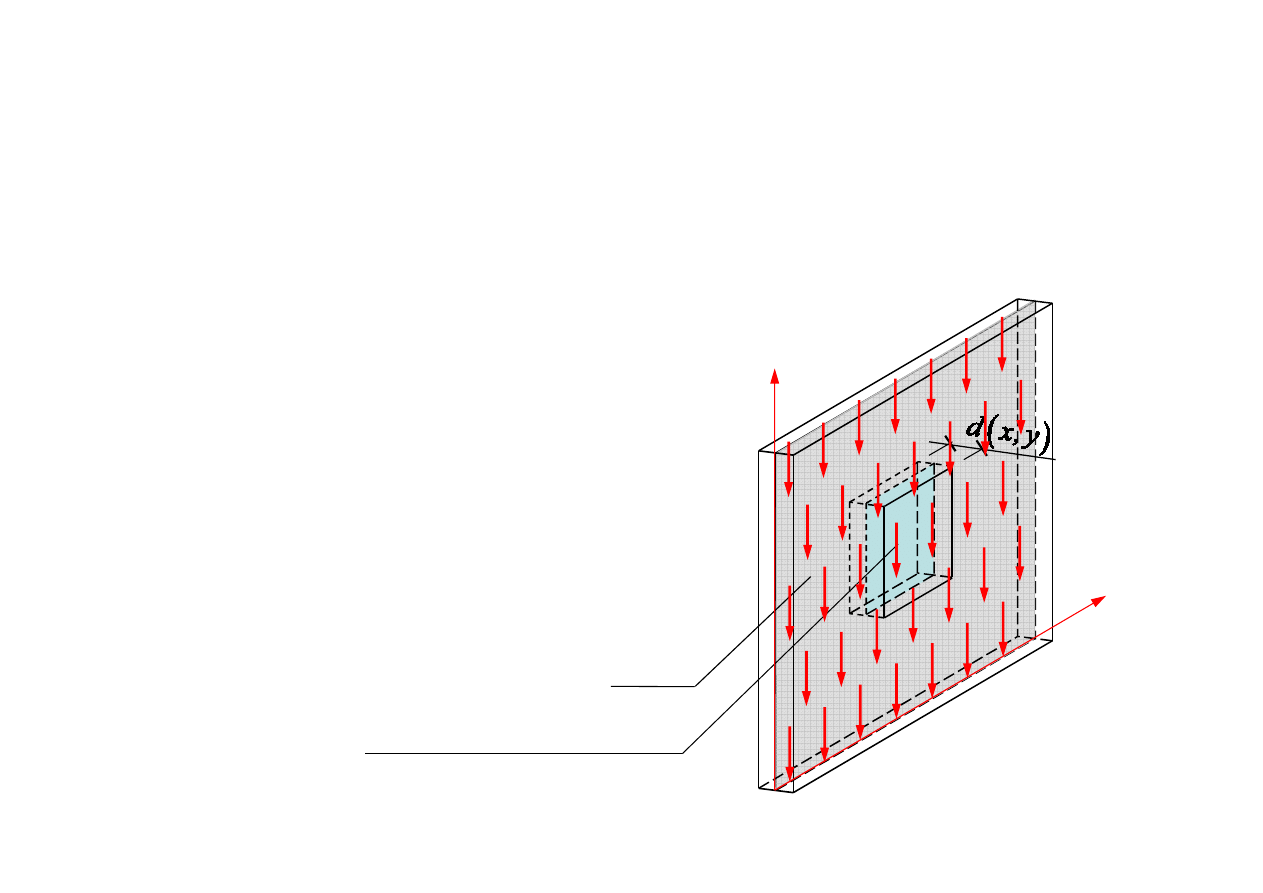
b) Przeliczenie obciążenia masowego tarczy (ciężaru w

ł

asnego)

na równoważne obciążenie powierzchniowe

( )

( )

( ) ( )

( ) ( ) ( )

p x, y

dA

γ x, y

dV

γ x, y

d x, y

dA

p x, y

γ x, y

d x, y

⋅

=

⋅

=

⋅

⋅

→

=

⋅

( )

γ x, y

[N/m

3

]

- obciążenie masowe

(ciężar w

ł

aściwy)

x, y

[m]

- wspó

ł

rzędne

y

10

( )

p x, y

[N/m

2

]

- obciążenie powierzchniowe

( )

d x, y

[m]

- grubość tarczy

dA

[m

2

]

- powierzchnia elementarnego

wycinka tarczy

elementarny wycinek tarczy

γ

(

x, y)

x

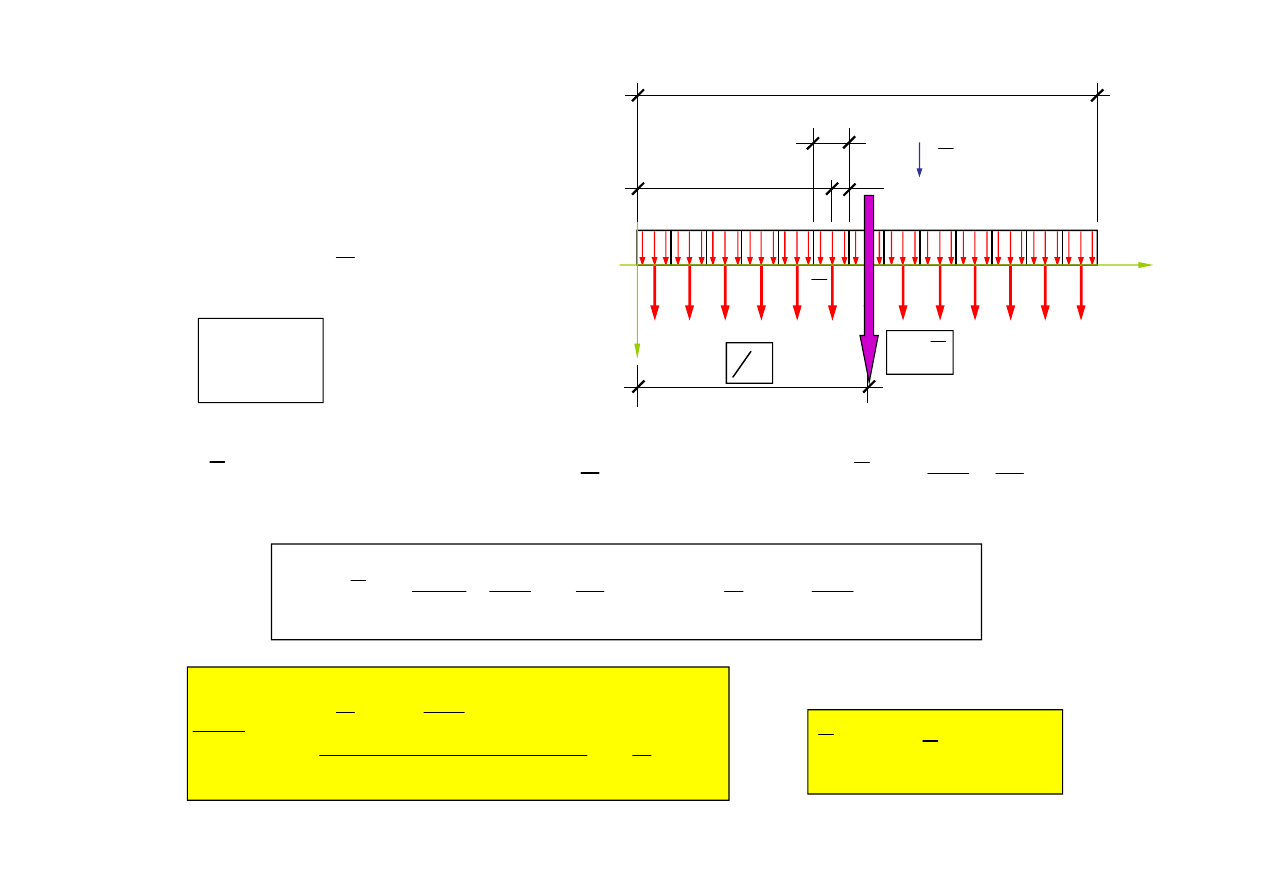
2.3. Redukcja obciążenia ciąg

ł

ego

i

∆x

i

x

l

i

F

(

)

e

=

1 0

x

y

i

i

l

F

q∆x

q

n

=

=

(

) (

)

l





ql

ql





2

n

i

i

F

ql

=

=

∑

1

δ

q

l

1

2

ql e

⋅

a) Obciążenie równomiernie

roz

ł

ożone

11

(

) (

)

i

i

i

l

r

x

i

∆

x

δ

i

δ

n





=

=

−

=

−









0

0

0

i

i

ql

ql

F r

i

δ

n

n





⋅ =

−









2

2

0

n

i

i

i

n

ql

ql

ql

F r

n

n

δ

ql

qlδ

n

n

n

=



 



+

⋅ =

−

=

+

−



 





 



∑

2

2

2

2

1

1

1

0

0

2

2

2

*

n

ql

ql

qlδ

n

OO

lim

l

ql

→∞





+

−













=

=









2

2

1

0

2

2

1

0

2

(

)

n

i

i

F

F e

ql

=

=

=

∑

1

0

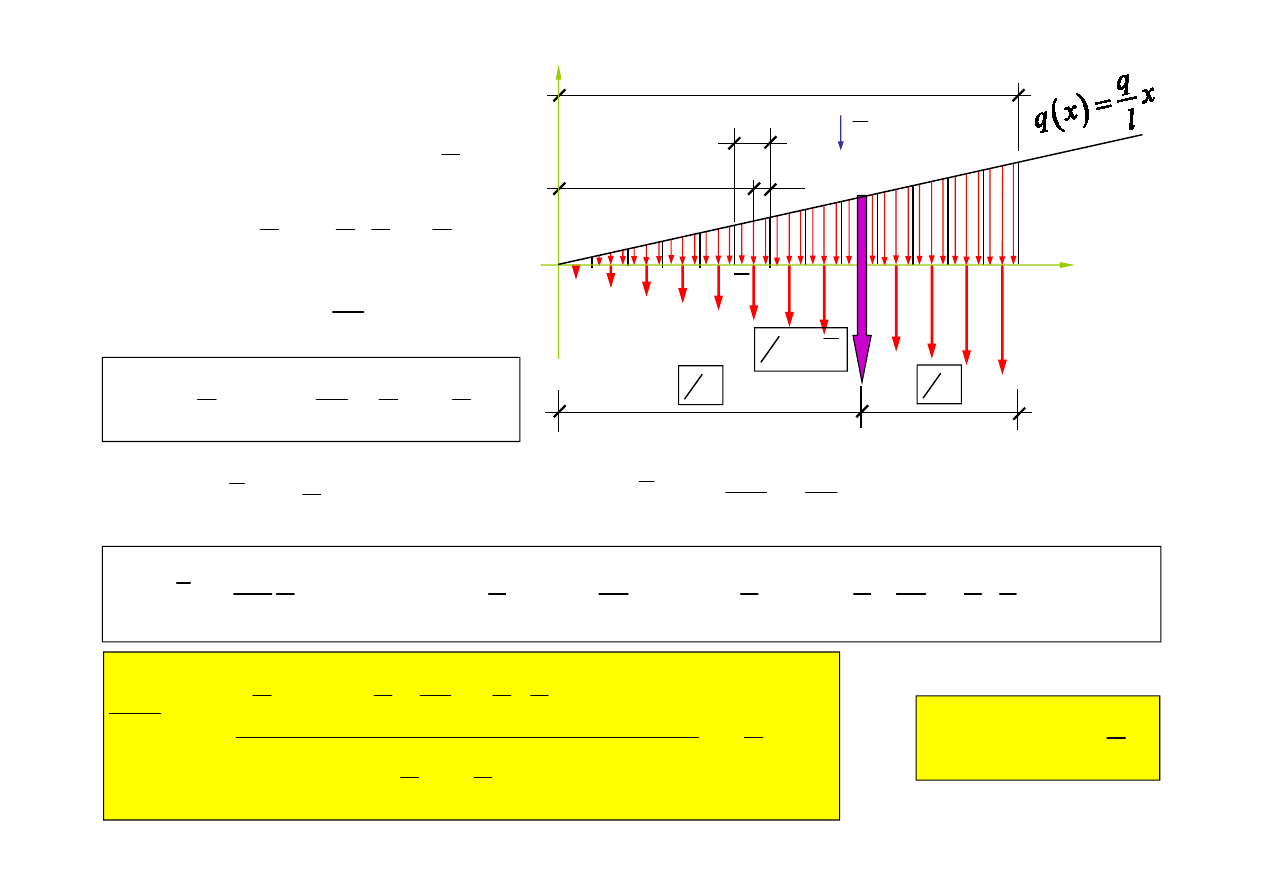
i

∆x

i

x

l

i

F

(

)

e

= −

1 0

x

y

( )

i

i

i

F

q x ∆x

=

δ

q

l

2

3

ql e

⋅

1

2

l

1

3

( )

i

i

q

q l

q

q x

x

i

i

l

l n

n

=

=

=

i

ql

F

i

n

=

2

(

)

n

i

i

ql

F

n n

ql

n

n

=





=

+

=

+









∑

2

1

1

1

1

1

1

2

2

i

l

∆x

n

=

b) Obciążenie trójkątne

12

(

)

(

)

n

i

i

i

ql

ql

F r

n

n

n

n n

δ

ql

qlδ

n

n

n

n

n

=



 











⋅ =

+

+ −

+

=

+ +

−

+



 



























∑

2

3

2

2

3

2

2

1

1

1

1

3

1

1 1

2

3

1

0

2

1

0

6

2

6

2

i

l

r

i

δ

n





=

−









0

i

i

ql

ql

F r

i

i

δ

n

n





⋅ =

−









2

2

3

2

0

*

n

ql

qlδ

n

n

n

OO

lim

l

ql

n

→∞













+ +

−

+





























=

=













+









2

2

1

3

1

1 1

2

1

0

6

2

2

0

1

1

3

1

2

n

i

n

i

F

lim

F

ql

→∞ =

=

=

∑

1

1

2

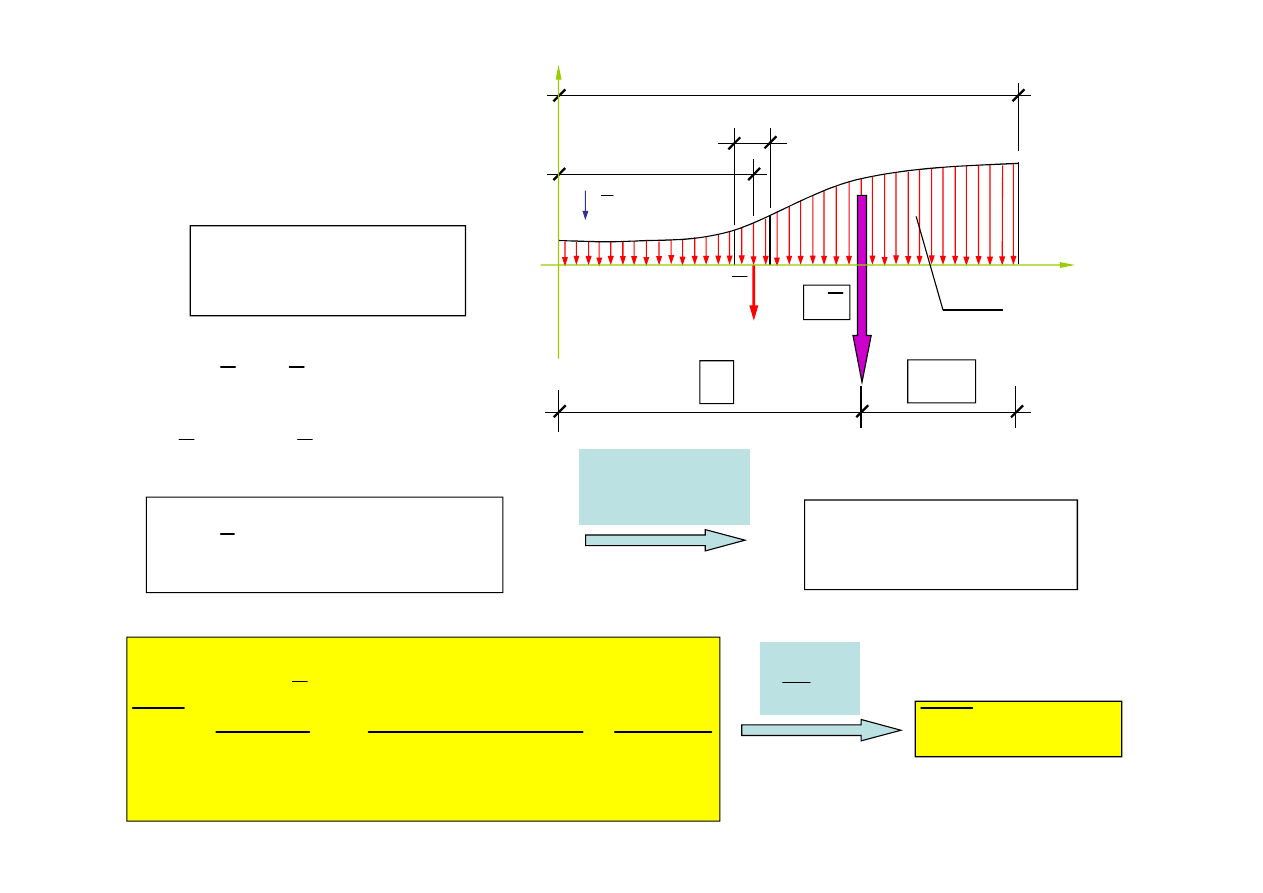
dx

x

l

dF

(

)

e

= −

1 0

x

y

( )

i

F

dF

f x dx

→

=

( )

q

f x

=

c

x

Pe

c

l

x

−

( )

l

n

i

i

F

f x dx

P

=

→

=

∑

∫

1

0

(

)

i

r

r

x

→ =

0

( )

(

)

F r

dF r

f x xdx

⋅ →

⋅ =

0

c) Obciążenie

q = f(x)

P

13

( )

l

n

i

i

i

F r

f x xdx

=





⋅ →









∑

∫

1

0

0

( )

(

)

i

i

F r

dF r

f x xdx

⋅ →

⋅ =

0

( )

l

df

y

f x xdx

S

=

∫

0

( )

(

)

l

y

f x xdx

S

=

∫

0

0

( )

( )

(

)

l

n

i

y

*

i

l

n

i

i

f x xdx

F r

S

OO

P

F

f x dx

=

=









⋅





=

→

=













∫

∑

∑

∫

0

1

1

0

0

0

df

y

C

S

x

P

=

(

)

*

C

OO

x

==

0

Część 2

TEORIA RÓWNOWAŻNOŚCI UK

Ł

ADÓW SI

Ł

podsumowanie dzia

ł

u

podsumowanie dzia

ł

u

Uwaga 1
Dzia

ł

rachunku wektorowego, który opisuje równoważność uk

ł

adów

wektorów jako obiektów matematycznych bez względu na to, jakie
fizyczne wielkości wektorowe są przez nie reprezentowane.

3.1. Teoria równoważności uk

ł

adów wektorów – uwagi

Uwaga 2
Teoria równoważności uk

ł

adów wektorów znajduje zastosowanie tylko

w tych zagadnieniach fizyki, w których dwa równoważne, zgodnie z tą

15

Uwaga 3
W wys

ł

uchanych wyk

ł

adach rozważano równoważność uk

ł

adów

wektorów, w odniesieniu do których, tylko ze względu na charakter
kierunku studiów przyjęto, że wektory reprezentują si

ł

y.

w tych zagadnieniach fizyki, w których dwa równoważne, zgodnie z tą
teorią, uk

ł

ady wektorów wywo

ł

ują w tym zagadnieniu ten sam skutek.

Uwaga 4
Teorię równoważności uk

ł

adów wektorów w mechanice stosuje się m.

in. do opisu zagadnień związanych z równowagą uk

ł

adów materialnych.

Każdy uk

ł

ad si

ł

jest równoważny uk

ł

adowi z

ł

ożonemu z wektora

równego sumie, zaczepionego w dowolnym punkcie i pary si

ł

o momencie równym momentowi uk

ł

adu si

ł

względem tego punktu.

3.2. Twierdzenie o redukcji

Jeżeli parę si

ł

wyznaczymy w taki sposób, by jedna z nich by

ł

a

zaczepiona w punkcie redukcji a następnie dodamy ją do wektora

16

Każdy uk

ł

ad si

ł

można zastąpić uk

ł

adem równoważnym z

ł

ożonym

z dwóch wektorów, z których jeden jest zaczepiony w dowolnie
wybranym punkcie.

zaczepiona w punkcie redukcji a następnie dodamy ją do wektora
równego sumie to:

O

ś

ś

ro

d

k

o

w

a

M

B

M

B

O

M

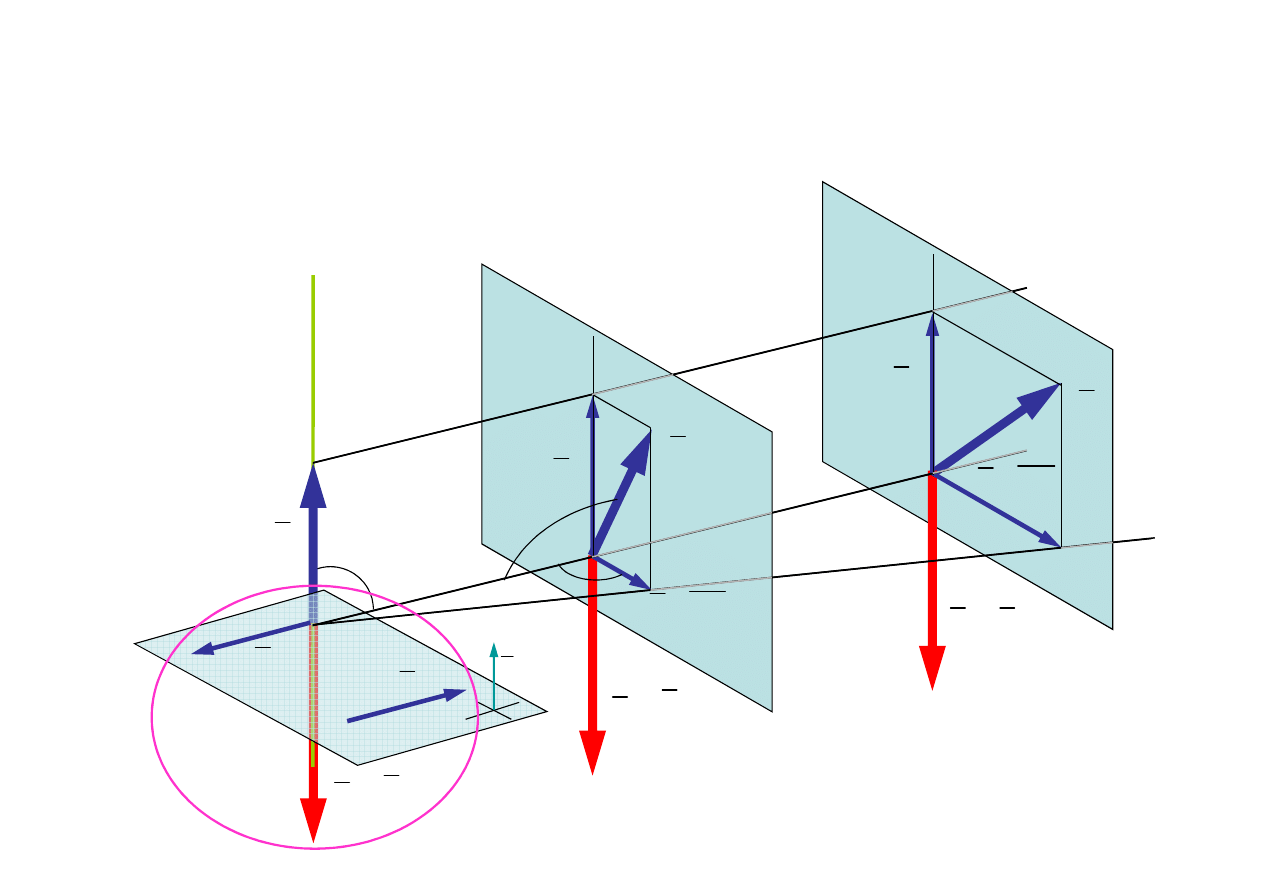
3.3. Przypadek ogólny

K

≠

0

- w

ł

asności wektorów zredukowanych

17

A

π

B

π

O

M

O

w

S

=

o

a

S

=

b

S

=

A

M

A

B

O

M

n

S

OA

×

F

F

−

o

o

S

OB

×

Skrętnik

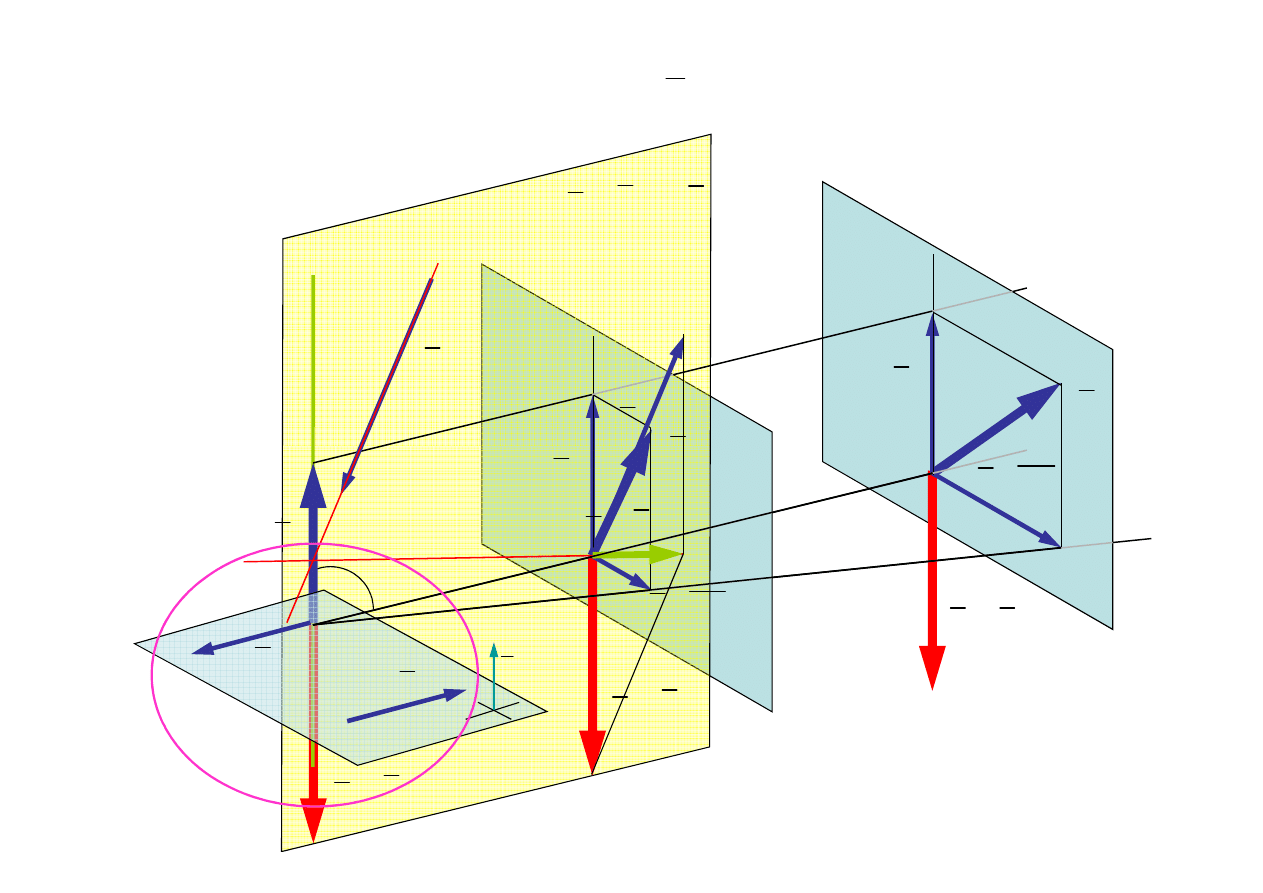
O

ś

ś

ro

d

k

o

w

a

B

M

B

M

O

M

3.4. Przypadek szczególny

K

S

=

∩

≠

0

0

- redukcja do wypadkowej

W punkcie O prostej dzia

ł

ania wypadkowej uk

ł

ad si

ł

redukuje się do jednego wektora

w

S

M

= ∩

=

0

F

F

−

18

A

π

B

π

O

w

S

=

o

a

S

=

b

S

=

A

B

O

M

n

S

OA

×

A

M

O

M

F

F

−

S

OB

×

a

F

+

Wypadkowa

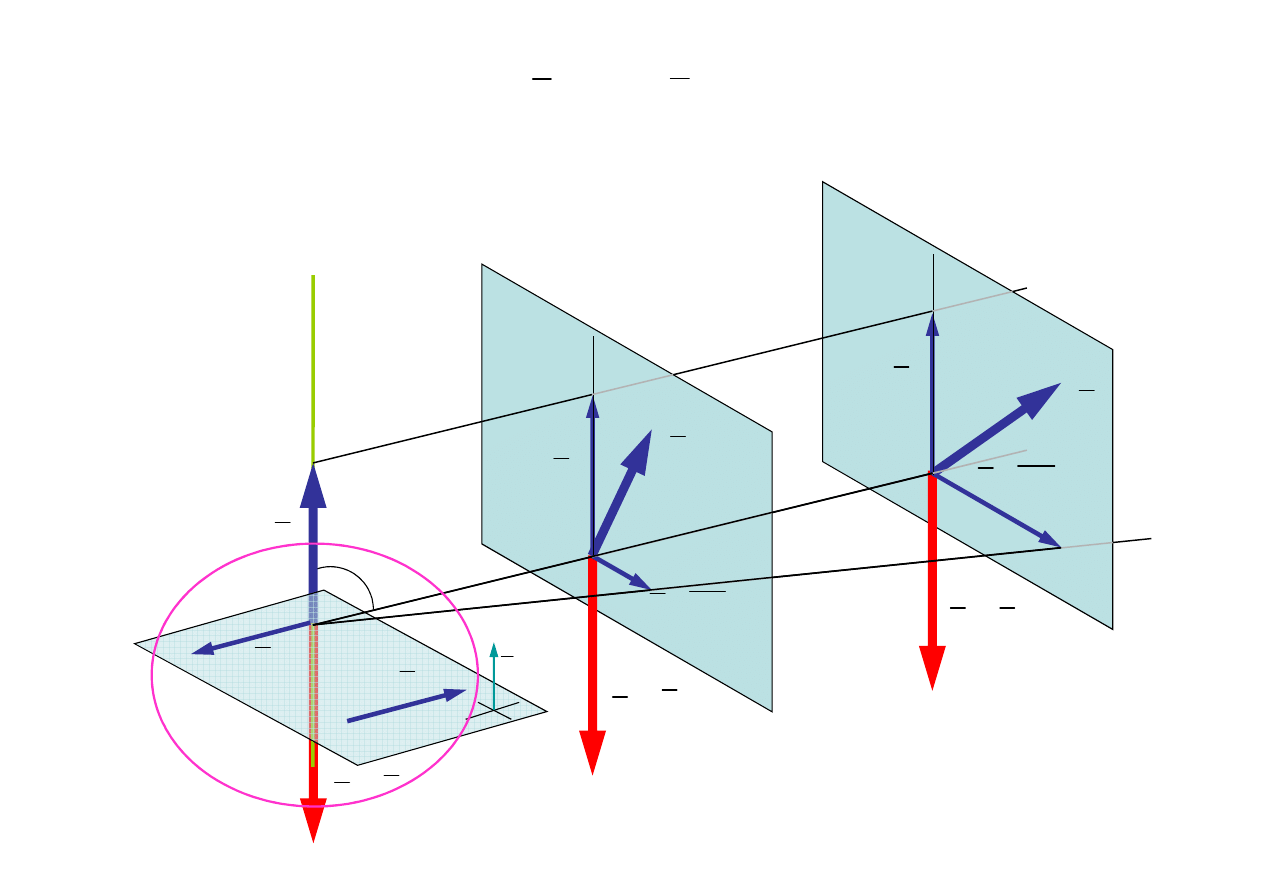
O

ś

ś

ro

d

k

o

w

a

B

M

B

M

O

M

3.4. Przypadek szczególny

M

S

≠

∩

=

0

0

- redukcja do pary si

ł

W dowolnym punkcie przestrzeni uk

ł

ad si

ł

redukuje się do pary si

ł

19

A

π

B

π

O

w

S

=

o

a

S

=

b

S

=

A

B

O

M

n

S

OA

×

A

M

O

M

F

F

−

S

OB

×

Para si

ł

3.5. Przypadki redukcji - podsumowanie

Cztery przypadki redukcji

do najprostszej postaci

Cztery przypadki redukcji

w punkcie

Uk

ł

ad zerowy

1.

S

M

= ∩

=

0

0

2.

S

M

= ∩

≠

0

0

Uk

ł

ad zerowy

1.

S

M

= ∩

=

0

0

2.

S

M

= ∩

≠

0

0

20

Para si

ł

2.

S

M

= ∩

≠

0

0

Skrętnik

4.

K

≠

0

Wektor i para si

ł

(lub dwa wektory)

4.

S

M

≠ ∩

≠

0

0

Para si

ł

2.

S

M

= ∩

≠

0

0

Jeden wektor

3.

S

M

≠ ∩

=

0

0

Wypadkowa

3.

S

K

≠ ∩

=

0

0