Wyk

ł

ad 10

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Wyk

ł

ad 10

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciąg

ł

ych

Instytut Mechaniki Budowli
Wydzia

ł

Inżynierii Lądowej

ZASADA PRAC WIRTUALNYCH

WARUNKI RÓWNOWAGI SI

Ł

Część 1

Więzy

Więzy

– ograniczenia na

ł

ożone na cia

ł

o materialne

1.1. Definicja

Ruch swobodny (przy ca

ł

kowitym

braku więzów)

3

Ograniczenie na

ł

ożone na jeden

punkt bry

ł

y sztywnej:

1

A

( )

A

r t

const

=

Ograniczenie na

ł

ożone na wszystkie

punkty bry

ł

y sztywnej:

( )

0

z t

z

≥

Kinematyczne (nieholonomiczne):

Geometryczne (holonomiczne):

(

)

1

1

1

n

n

n

f x , y ,z , ... , x , y ,z ,t

warunek na

ł

o

ż

ony na funkcj

ę

(

)

1

1

1

1

1

1

n

n

n

n

n

n

f x , y ,z , ... , x , y ,z , x , y ,z , ... , x , y ,z ,t

& &

& &

&

&

warunek na

ł

o

ż

ony na funkcj

ę

1.2. Rodzaje więzów

4

(

)

1

1

1

1

1

1

n

n

n

n

n

n

f x , y ,z , ... , x , y ,z , x , y ,z , ... , x , y ,z ,t

& &

& &

&

&

Stacjonarne (skleronomiczne,
nie zależne jawnie od czasu):

Niestacjonarne (reonomiczne,
zależne jawnie od czasu):

(

)

1

1

1

1

1

1

n

n

n

n

n

n

f x , y ,z , ... , x , y ,z , x , y ,z , ... , x , y ,z

& &

& &

&

&

warunek na

ł

o

ż

ony na funkcj

ę

warunek na

ł

o

ż

ony na funkcj

ę

(

)

1

1

1

1

1

1

n

n

n

n

n

n

f x , y ,z , ... , x , y ,z , x , y ,z , ... , x , y ,z , t

& &

& &

&

&

Szorstkie (chropowate):

Rodzaje więzów (cd.)

G

ł

adkie (idealne):

wi

ę

zy, których praca reakcji jest równa 0

wi

ę

zy, których praca reakcji jest ró

ż

na od 0

5

Dwustronne (równościowe):

Jednostronne (nierównościowe):

warunek na

ł

o

ż

ony na ruch w postaci równo

ś

ci

warunek na

ł

o

ż

ony na ruch w postaci nierówno

ś

ci

Rodzaje więzów (cd.)

Geometryczne

Kinematyczne

Stacjonarne

Niestacjonarne

6

G

ł

adkie

Szorstkie

Jednostronne

Dwustronne

( )

A

r t

const

=

( )

( )

( )

1

2

3

0

0

0

A

x

A

y

A

z

f : x

t

C

f : y

t

C

f : z

t

C

−

=

−

=

−

=

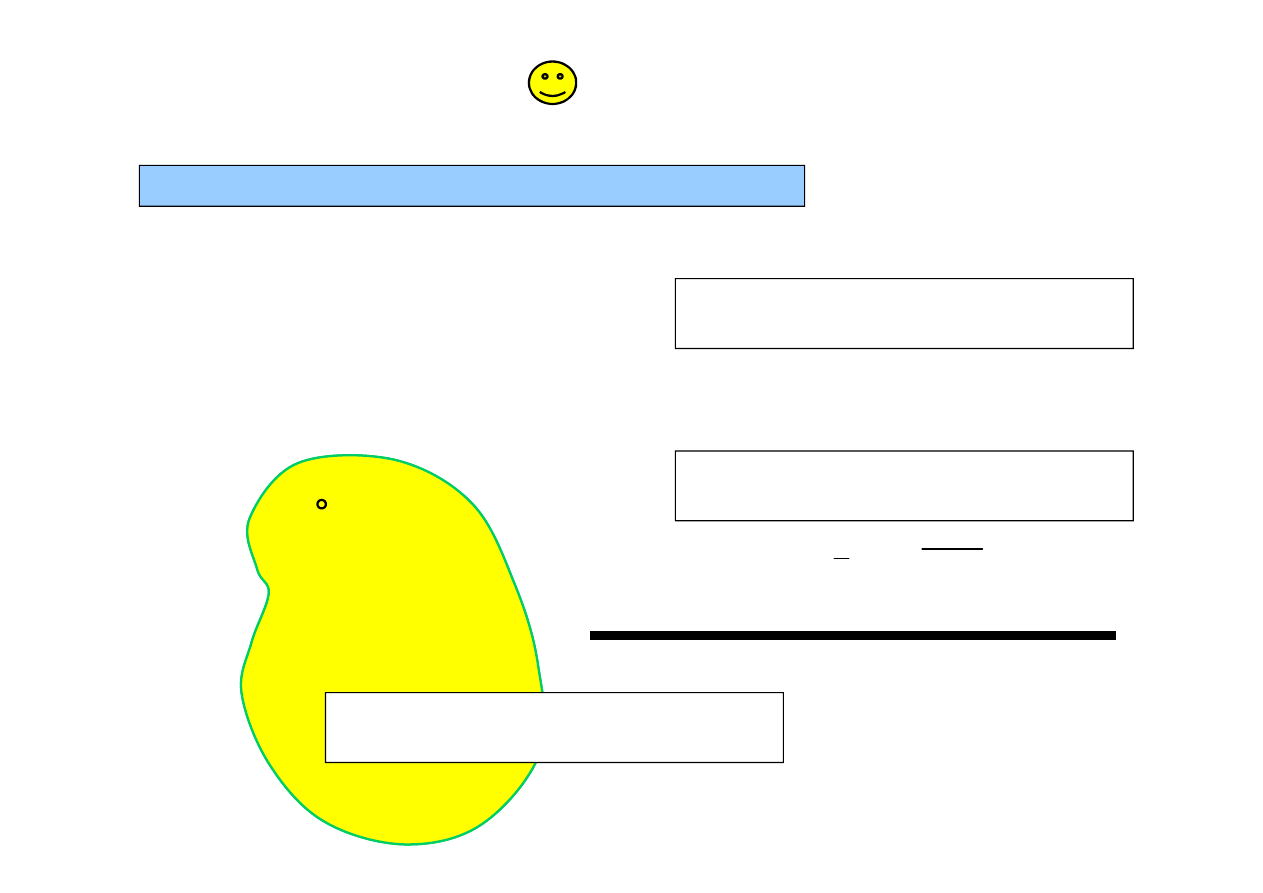
Przyk

ł

ad 1:

Ruch bry

ł

y sztywnej wokó

ł

punktu

o ustalonym po

ł

ożeniu bez strat energii

1.3. Przyk

ł

ady ruchu z więzami

7

A

geometryczne

stacjonarne

dwustronne

g

ł

adkie

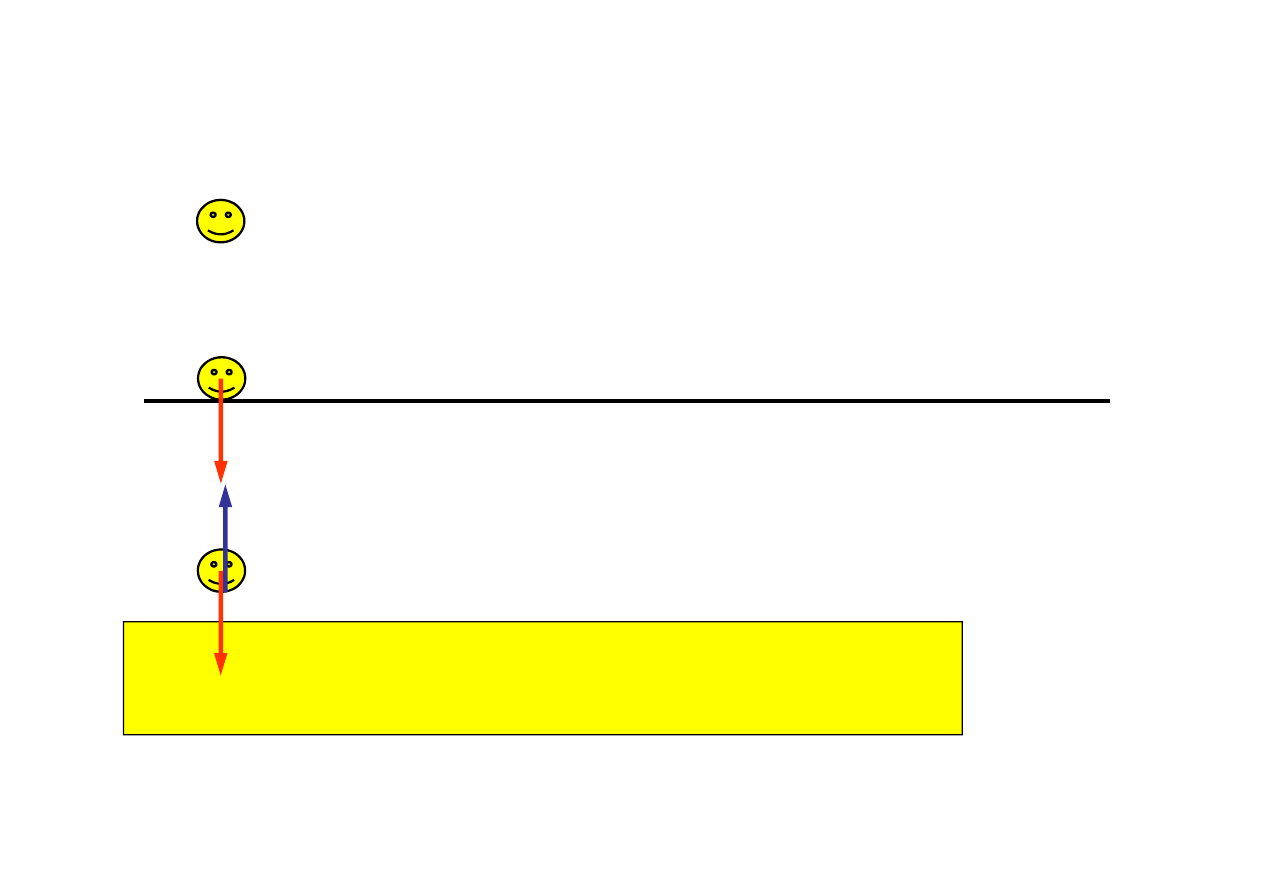
Przyk

ł

ad 2:

Ruch swobodny punktu materialnego
w polu grawitacyjnym ze zderzeniem
sprężysto-plastycznym z szorstką
powierzchnią

( )

0

A

z

t

z

≥

( )

1

0

0

A

f : z

t

z

− ≥

8

geometryczne

stacjonarne

jednostronne

szorstkie

Praca wi

ę

zów jest ró

ż

na od 0

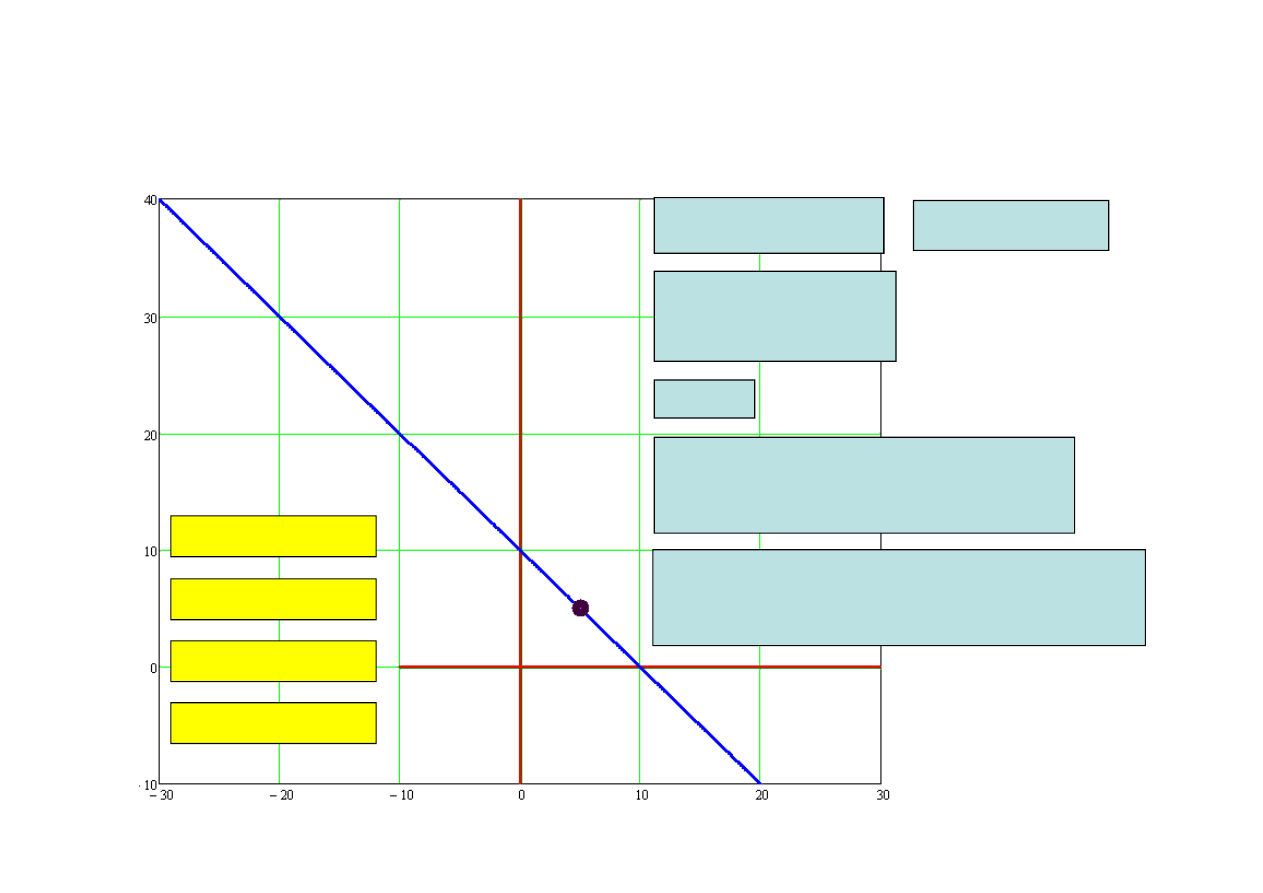
Przyk

ł

ad 3:

Ruch punktu materialnego w polu grawitacyjnym bez tarcia po prostej
poruszającej się w p

ł

aszczyźnie Oxy równoleg

ł

ej do linii si

ł

pola

( )

( ) ( )

(

)

ρ t

ξ t , η t

=

φ

ω t

= ⋅

cos φ

sin φ

α

sin φ cos φ





=





−





%

( )

( )

x t

ξ t

cos ωt

sin ωt









−





( )

( )

10

η t

ξ t

=

−

9

( )

( )

( )

( )

x t

ξ t

cos ωt

sin ωt

y t

η t

sin ωt

cos ωt









−





=

⋅

























( )

( )

( )

( )

( )

( )

1

2

0

0

f : x t

cos ωt ξ t

sin ωt η t

f :

y t

sin ωt ξ t

cos ωt η t

−

⋅

+

⋅

=

−

⋅

−

⋅

=

geometryczne

niestacjonarne

dwustronne

g

ł

adkie

Ruch swobodny, gdy na punkt materialny nie dzia

ł

ają żadne si

ł

y

Ruch po poziomej powierzchni (bez tarcia) w polu grawitacyjnym

10

Aksjomat o więzach

W ruchu cia

ł

a nieswobodnego nic się nie zmieni, gdy więzy myślowo

zostaną usunięte i ich dzia

ł

anie zostanie zastąpione si

ł

ami reakcji

Ruch w polu grawitacyjnym pod dzia

ł

aniem si

ł

y grawitacji i reakcji więzów

Część 2

Zasada prac wirtualnych

11

2.1. Przemieszczenie wirtualne

Przemieszczenie rzeczywiste

– wektor

ł

ączący dwa rzeczywiste po

ł

ożenia

cia

ł

a. Jest zależne od więzów i dzia

ł

ających si

ł

Przemieszczenie wirtualne

– wektor

ł

ączący dwa możliwe po

ł

ożenia

cia

ł

a. Jest zależne wy

ł

ącznie od więzów

12

Przemieszczenie wirtualne jest wspó

ł

liniowe z prędkością możliwą, na jaką pozwalają

więzy

{ }

0

s

ˆ

δ

k υ , k

R

= ⋅

∈ −

Problem

1. Uk

ł

ad materialny jest zdefiniowany za pomocą n punktów materialnych

2. Więzy opisane są przez m niezależnych równań

3. Więzy są geometryczne, stacjonarne, g

ł

adkie

Jaki warunek musi spe

ł

niać przemieszczenie wirtualne punktu i

gdzie:

( )

( )

( )

1

x

x t , y

y t , z

z t

i

, ..., n

=

=

=

=

(

)

1

1

1

0

1

j

n

n

n

f

x , y ,z , ... , x , y ,z

j

, ...,m

=

=

Równanie więzów:

13

gdzie:

(

)

1

1

1

0

1

j

n

n

n

d

f

x , y ,z , ... , x , y ,z

j

, ...,m

dt





=

=





( )

( )

( )

1

i

i

i

i

i

i

x

x t , y

y t , z

z t

i

, ..., n

=

=

=

=

Różniczkowanie po t:

1

0

1

n

j

j

j

i

i

i

i

i

i

i

f

f

f

x

y

z

j

, ...,m

x

y

z

=

∂

∂

∂





+

+

=

=





∂

∂

∂





∑

&

&

&

1

1

1

1

1

1

0

1

j

j

j

j

j

j

n

n

n

n

n

n

f

f

f

f

f

f

dx

dy

dz

dx

dy

dz

...

j

, ...,m

x dt

y dt

z dt

x

dt

y

dt

z

dt

∂

∂

∂

∂

∂

∂

+

+

+ +

+

+

=

=

∂

∂

∂

∂

∂

∂

1

0

1

n

j

j

j

i

i

i

i

i

i

i

f

f

f

x

y

z

j

, ...,m

x

y

z

=

∂

∂

∂





+

+

=

=





∂

∂

∂





∑

&

&

&

Przesunięcie wirtualne punktu A

i

:

(

)

(

)

si

i

i

i

i

xi

yi

zi

δ

k υ

kx , ky , kz

δ , δ , δ

= ⋅ =

=

&

&

&

k

⋅

1

0

1

n

j

j

j

xi

yi

zi

i

i

i

i

f

f

f

δ

δ

δ

j

, ...,m

x

y

z

=

∂

∂

∂





+

+

=

=





∂

∂

∂





∑

14

1

i

i

i

i

x

y

z

=

∂

∂

∂





j

j

j

i

j

i

i

i

f

f

f

grad f

,

,

x

y

z

∂

∂

∂





=





∂

∂

∂





1

0

n

si

i

j

i

grad f

δ

=

⋅

=

∑

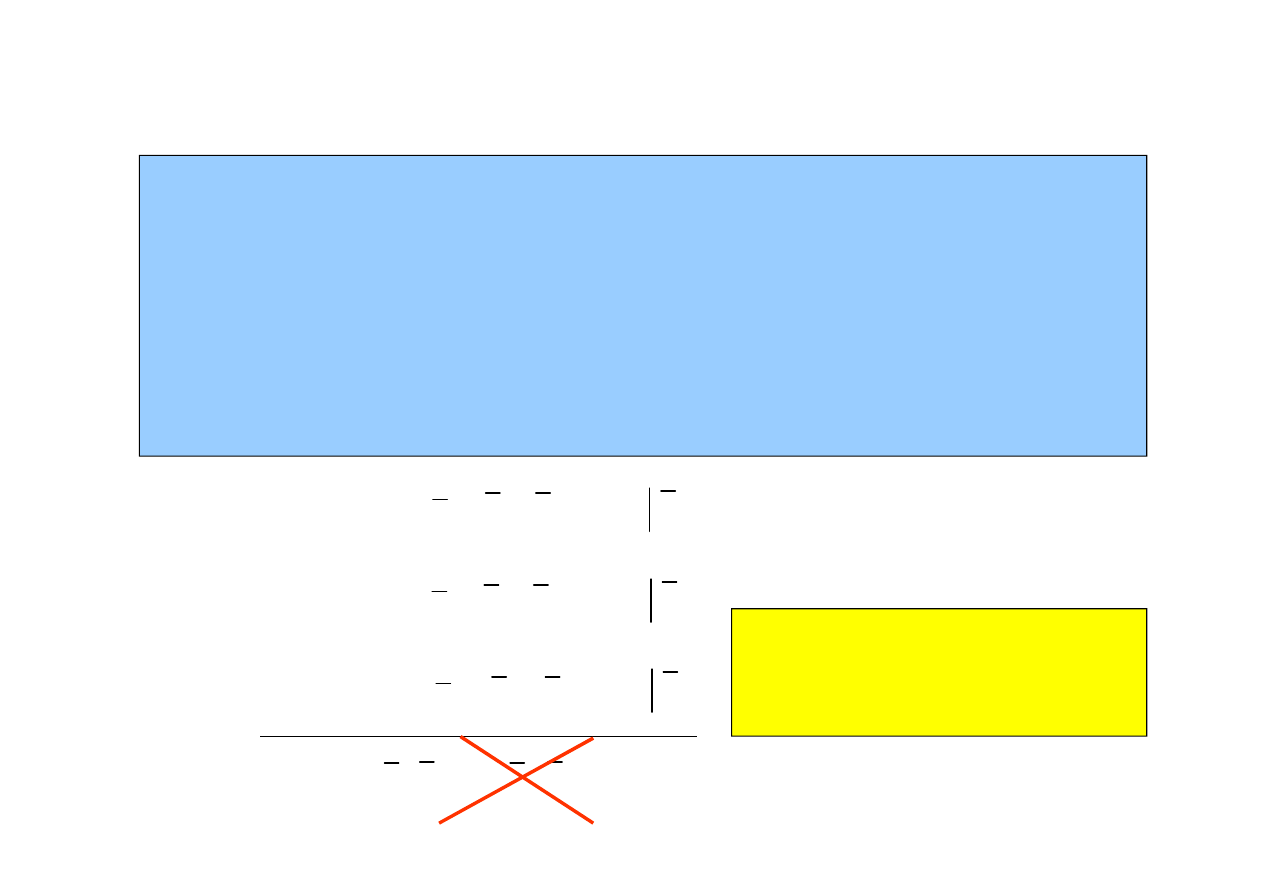
Problem

1. Uk

ł

ad materialny jest zdefiniowany za pomocą n punktów materialnych

2. Więzy opisane są przez m niezależnych równań

3. Więzy są geometryczne, stacjonarne, g

ł

adkie i dwustronne

4. Uk

ł

ad materialny jest obciążony uk

ł

adem si

ł

czynnych i reakcji więzów

5. Uk

ł

ad materialny znajduje się w spoczynku

Jaki warunek musi spe

ł

niać uk

ł

ad si

ł

aby uk

ł

ad materialny pozostawa

ł

w równowadze

2.2. Zasada prac wirtualnych

15

Jaki warunek musi spe

ł

niać uk

ł

ad si

ł

aby uk

ł

ad materialny pozostawa

ł

w równowadze

Zerowanie się pracy si

ł

czynnych

na przemieszczeniach wirtual-
nych jest warunkiem koniecznym
równowagi uk

ł

adu materialnego

1

1

1

1

0

0

0

i

i

i

i

n

n

n

n

m r

F

R

...

m r

F

R

...

m r

F

R

⋅ = +

=

⋅ = + =

⋅ =

+

=

&&

&&

&&

Równania ruchu:

1

s

δ

⋅

si

δ

⋅

sn

δ

⋅

1

1

0

n

n

i

si

i

si

i

i

δL

F δ

R δ

−

−

=

⋅ +

⋅

=

∑

∑

Problem

1. Uk

ł

ad materialny jest zdefiniowany za pomocą n punktów materialnych

2. Więzy opisane są przez m niezależnych równań

3. Więzy są geometryczne, stacjonarne, g

ł

adkie i dwustronne

4. Uk

ł

ad materialny jest obciążony uk

ł

adem si

ł

czynnych i reakcji więzów

5. Uk

ł

ad materialny znajduje się w ruchu rzeczywistym

Jaki warunek spe

ł

nia teraz uk

ł

ad si

ł

?

16

Iloraz różnicowy:

(

) ( )

i

i

i

r t

∆t

r t

r

∆t

+

−

≈

&

(

) ( )

( )

2

0

i

i

i

i

∆r

r t

∆t

r t

r ∆t

∆ t

=

+

−

=

+

&

( )

(

)

2

1

1

1

0

n

n

n

i

i

i

i

i

si

i

i

i

δL

F ∆r

F

r ∆t

∆ t

F δ

∆L

=

=

=

=

⋅

=

⋅

+

=

⋅ +

∑

∑

∑

&

W ruchu rzeczywistym:

0

δL

≠

Zasada prac wirtualnych

Warunkiem koniecznym i wystarczającym równowagi uk

ł

adu si

ł

dzia

ł

ających na uk

ł

ad materialny swobodny lub nieswobodny

o więzach geometrycznych, stacjonarnych, dwustronnych i g

ł

ad-

kich jest, by suma prac wirtualnych wszystkich si

ł

czynnych, na

wszystkich przemieszczeniach wirtualnych, by

ł

a równa 0

17

1

0

n

i

si

si

i

δL

F δ

,

δ

−

=

⋅

=

∀

∑

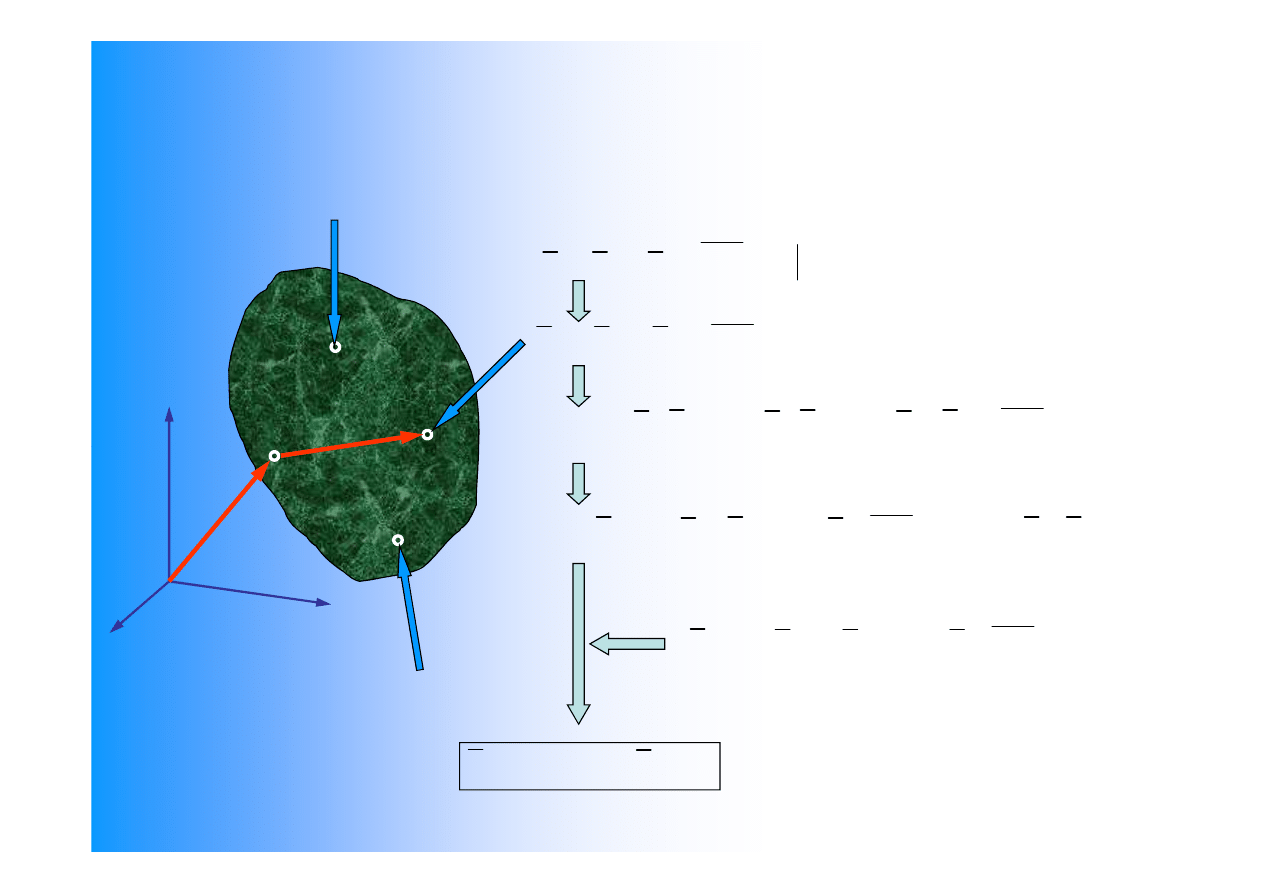
2.3. Równania równowagi

i

A

A

i

υ

υ

ω

AA

= +

×

{ }

0

k ,

k

R

⋅

∈ −

si

sA

ωA

i

δ

δ

δ

AA

=

+

×

(

)

n

n

n

i

si

i

sA

i

ωA

i

δL

F δ

F δ

F

δ

AA

=

⋅

=

⋅

+

⋅

×

∑

∑

∑

Warunki równowagi si

ł

dzia

ł

ających na cia

ł

o sztywne swobodne

z

F

1

F

i

A

i

A

1

A

18

(

)

1

1

1

i

si

i

sA

i

ωA

i

i

i

i

=

=

=

∑

∑

∑

(

)

1

1

0

n

n

sA

i

ωA

i

i

sA

ωA

i

i

δL

δ

F

δ

F

A A

δ ,δ

=

=

=

⋅

+

⋅

×

=

∀

∑

∑

(

)

1

1

n

n

i

A

i

i

i

i

S

F , M

F

A A

=

=

=

=

×

∑

∑

0

0

A

S

M

=

∩

=

O

x

y

r

A

F

n

A

n

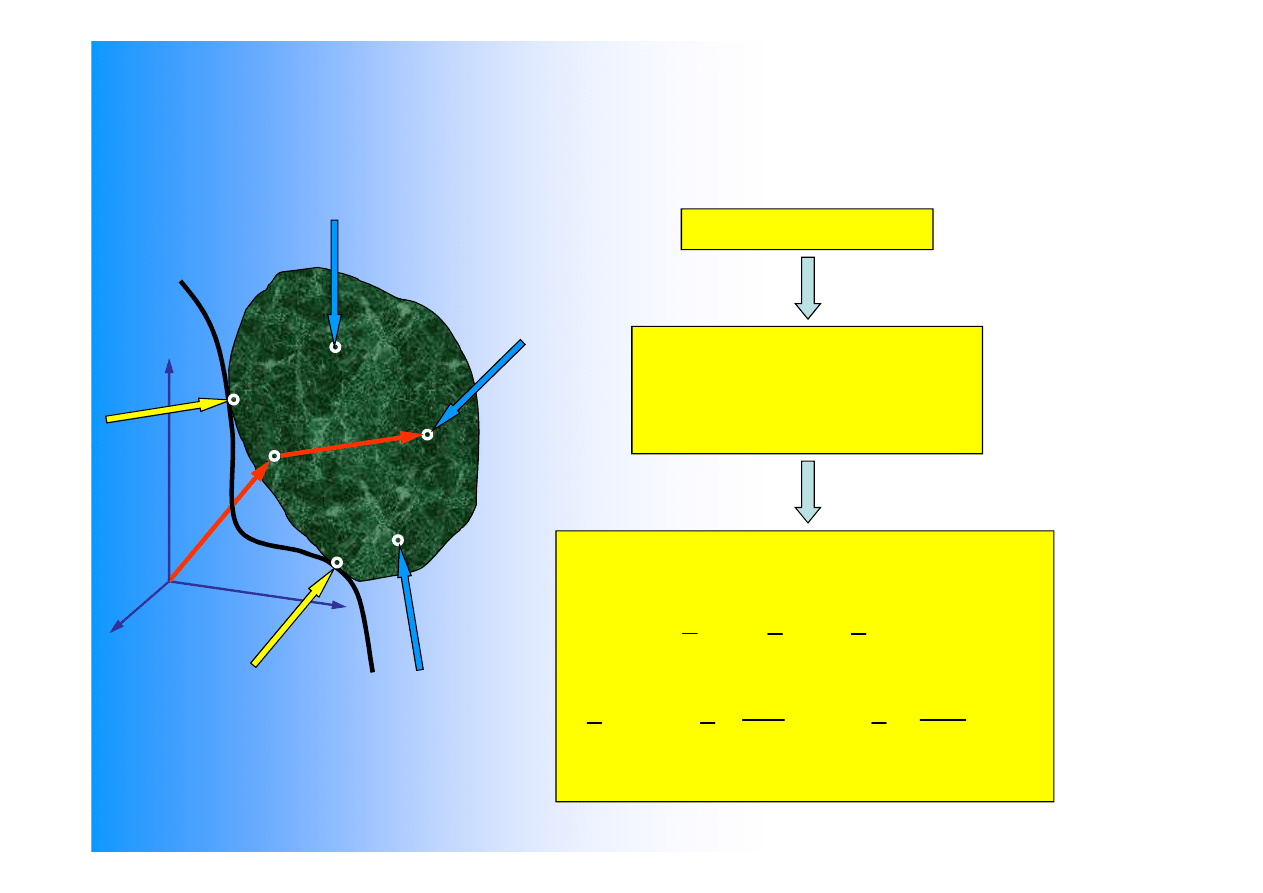
Warunki równowagi si

ł

dzia

ł

ających na cia

ł

o sztywne nieswobodne

A

A

i

A

1

z

F

1

F

i

R

1

B

1

Postulat o więzach

Cia

ł

o zostaje oswobodzone

z więzów, jednocześnie

poddane jest dzia

ł

aniu

uk

ł

adu si

ł

czynnych i reakcji

19

A

n

O

x

y

r

A

F

n

R

1

R

j

B

j

uk

ł

adu si

ł

czynnych i reakcji

(

) (

)

1

1

1

1

0

0

n

m

i

j

i

j

n

m

A

i

i

j

j

i

j

S

F

R

M

F

A A

R

B A

=

=

=

=

=

+

=

=

×

+

×

=

∑

∑

∑

∑

Warunki równowagi cia

ł

a swobodnego

1

1

1

1

0

0

0

0

0

0

n

m

x

ix

jx

i

j

n

m

y

iy

jy

i

j

n

m

S

F

R

S

F

R

S

F

R

=

=

=

=

= ⇔

+

=

= ⇔

+

=

= ⇔

+

=

∑

∑

∑

∑

∑

∑

Równania równowagi – postać ogólna

20

( )

( )

( )

( )

( )

( )

1

1

1

1

1

1

1

1

0

0

0

0

0

0

0

0

z

iz

jz

i

j

n

m

Ax

Ax

i

Ax

j

i

j

n

m

Ay

Ay

i

Ay

j

i

j

n

m

Az

Az

i

Az

j

i

j

S

F

R

M

M

F

M

R

M

M

F

M

R

M

M

F

M

R

=

=

=

=

=

=

=

=

= ⇔

+

=

= ⇔

+

=

= ⇔

+

=

= ⇔

+

=

∑

∑

∑

∑

∑

∑

∑

∑

0

0

0

x

y

Az

S

S

M



=



=





=



0

0

0

0

Az

Bz

Cz

M

M

AB AC

M

=





=

×

≠





=





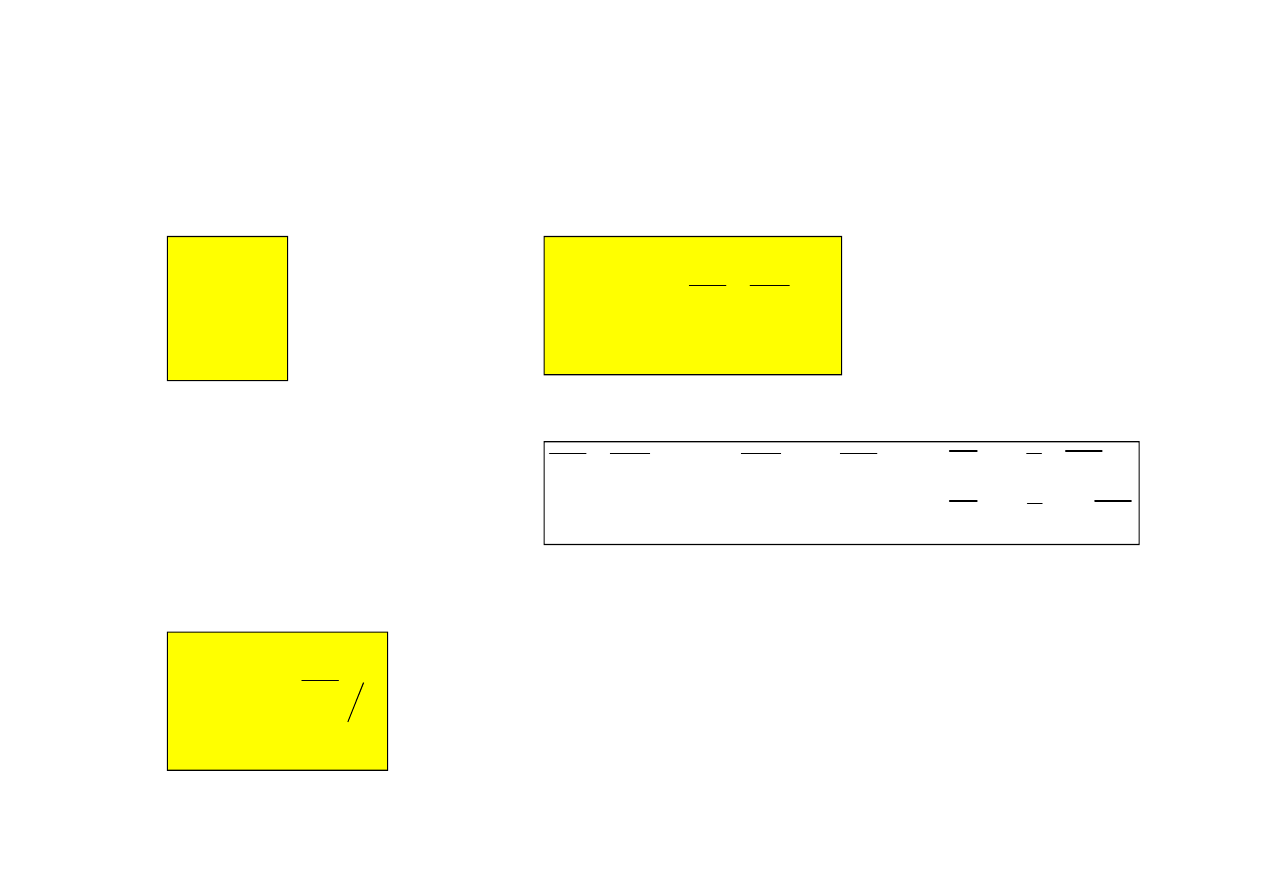
Uzasadnienie warunku nie wspó

ł

liniowości punktów

Uk

ł

ad 1

Uk

ł

ad 2

2.3. Równania równowagi w odniesieniu do uk

ł

adów p

ł

askich

21

0

0

0

l

Az

Bz

S

M

AB

l

M

=





=

⊥





=



0

0

0

B

C

Az

Bz

M

S

AB

AB AC

AC

λ AB

M

M

M

S

λ AB





= ×

×

=

⇒

= ⋅





⇒





= ∩

=



= × ⋅







Gdy A, B, C wspó

ł

liniowe to jedno z równań jest zależne

Uzasadnienie warunku nie prostopad

ł

ości prostej l i wektora AB

0

l

S

=

Jeśli punkty A i B leżą na prostej dzia

ł

ania wypadkowej (uk

ł

ad nie

jest w równowadze) oraz prosta l jest prostopad

ł

a do AB to:

Bez sformu

ł

owanego warunku uk

ł

ad równań 3 nie stanowi

jednoznacznego warunku równowagi uk

ł

adu si

ł

Uk

ł

ad 3

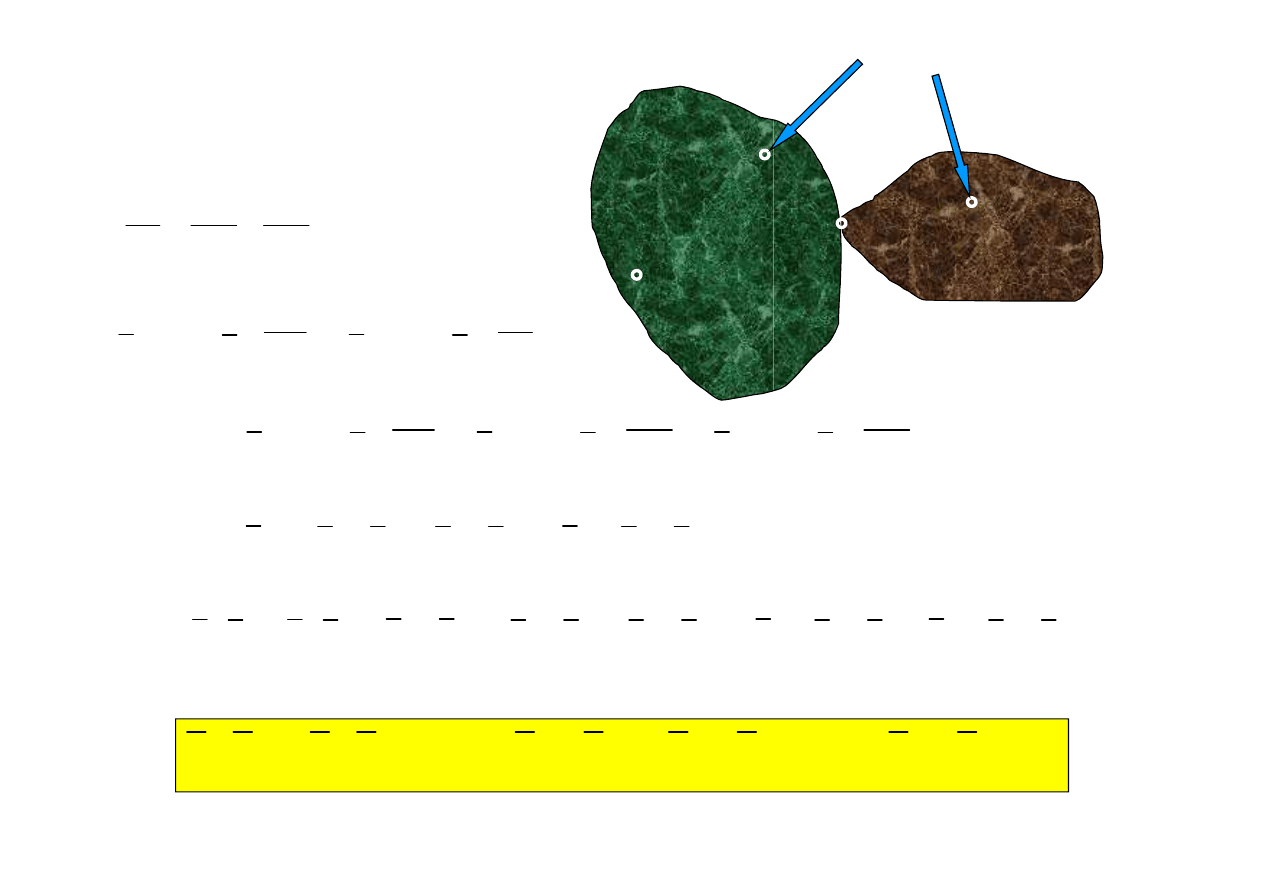
2.4. Równania równowagi dwóch tarcz po

ł

ączonych przegubem

A

A

i

B

B

j

F

i

F

j

i

A

A

i

υ

υ

ω

AA

= +

×

j

B

B

j

υ

υ

ω

BB

= +

×

B

A

A

υ

υ

ω

AB

= +

×

j

A

ωA

ωB

j

δ

δ

δ

AB δ

BB

=

+

×

+

×

22

i

A

ω

A

i

δ

δ

δ

AA

=

+

×

(

)

(

)

(

)

i

A

i

ωA

i

j

A

j

ωA

j

ωB

j

i

i

j

j

j

δL

F δ

F

δ

AA

F δ

F

δ

AB

F

δ

BB

=

⋅ +

⋅

×

+

⋅ +

⋅

×

+

⋅

×

∑

∑

∑

∑

∑

i

j

A

ωA

i

i

ωA

j

ωB

j

j

i

j

i

j

j

δL

F

F

δ

δ

F

A A

δ

F

BA

δ

F

B B

















=

+

⋅

+

⋅

×

+

⋅

×

+

⋅

×

































∑

∑

∑

∑

∑

i

i

j

j

i

j

δL

F δ

F δ

=

⋅ +

⋅

∑

∑

A

A

i

B

B

j

F

i

F

j

ωA

i

i

ωA

j

i

j

δ

F

A A

δ

F

BA

δ

F

A A

δ

F

B A

δ

F

B B









⋅

×

+

⋅

×

=





























=

⋅

×

+

⋅

×

−

⋅

×













∑

∑

∑

∑

∑

j

j

BA

B A B B

=

−

23

ω

A

i

i

ω

A

j

j

ω

A

j

j

i

j

j

δ

F

A A

δ

F

B A

δ

F

B B

=

⋅

×

+

⋅

×

−

⋅

×

























∑

∑

∑

( )

( )

( )

ωA

A

i

A

j

ωA

B

j

δ

M

F

M

F

δ

M

F





=

⋅

+

−

⋅





( )

( )

( )

( )

( )

( )

0

i

j

A

ωA

A

i

A

j

ωA

B

j

ωB

B

j

δL

S F

S F

δ

δ

M

F

M

F

δ

M

F

δ

M

F









=

+

⋅ +

⋅

+

−

⋅

+

⋅

=









( )

( )

( )

( )

( )

0

0

0

i

j

A

i

A

j

B

j

S F

S F

, M

F

M

F

, M

F

+

=

+

=

=