
Wyk
ł
ad 8,9
MECHANIKA TEORETYCZNA
Studia stacjonarne I stopnia – rok akademicki 2013/14
Wyk
ł
ad 8,9
Autor:
Henryk Laskowski
Katedra Podstaw Mechaniki Ośrodków Ciąg
ł
ych
Instytut Mechaniki Budowli
Wydzia
ł
Inżynierii Lądowej
KINEMATYKA BRY
Ł
Y SZTYWNEJ

Część 1
Sposoby opisu ruchu cia
ł
a sztywnego
Cia
ł
o sztywne
– model fizyczny cia
ł
a o masie roz
ł
ożonej w pewnej przestrzeni,
której elementy nie mogą się względem siebie przemieszczać.
Punkt materialny jest szczególnym przypadkiem cia
ł
a sztywnego.
α, β, γ
Tymi wektorami mogą być
wersory uk
ł
adu wspó
ł
rzędnych
związanego z cia
ł
em sztywnym
1
2
3
r
α r
β r
γ r
= ⋅ + ⋅ + ⋅
- liczby
rzeczywiste
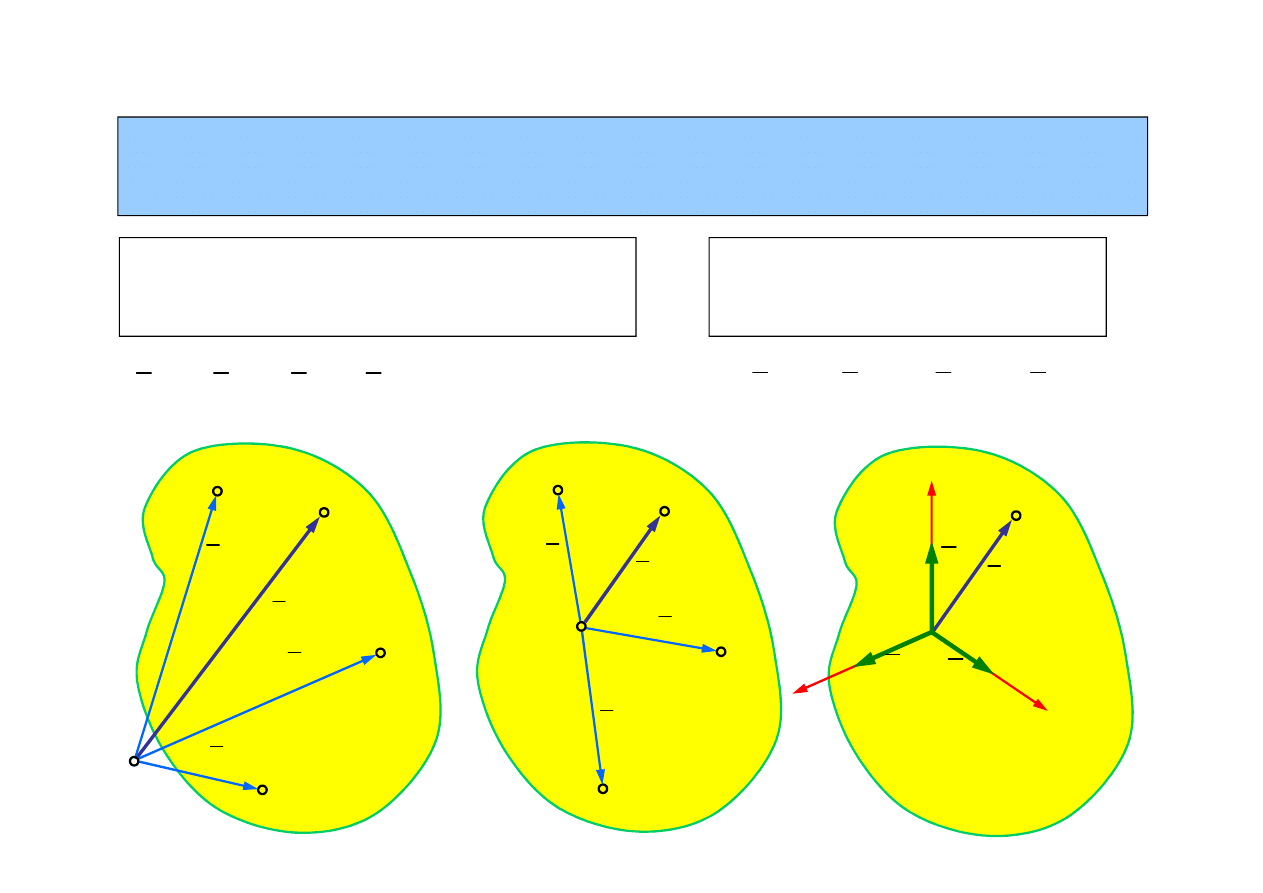
Dowolny wektor w przestrzeni można
przedstawić w postaci kombinacji liniowej
trzech niekomplanarnych wektorów.
ξ
ξ
η
η
ζ
ζ
ρ
ρ e
ρ e
ρ
e
=
⋅ + ⋅ + ⋅
1.1. Opis cech geometrycznych cia
ł
a sztywnego
3
O
1
A
2
A
3
A
A
1
r
2
r
3
r
r
1
A
2
A
3
A
A
1
ρ
2
ρ
3
ρ
ρ
O
ξ
ζ
η
A
ρ
ξ
e
ζ
e
η
e
O
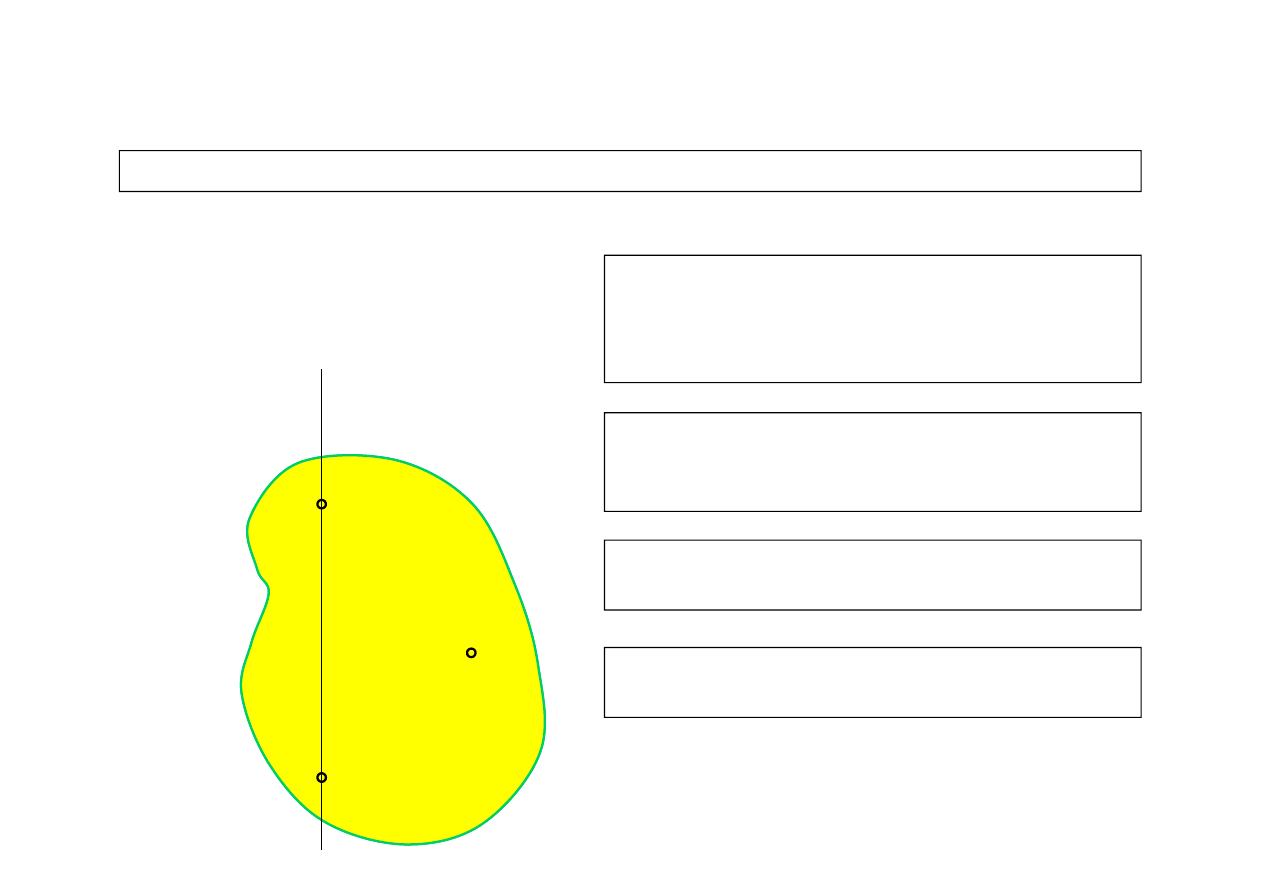
1.2. Opis po
ł
ożenia cia
ł
a sztywnego
Pytanie: Ile punktów bry
ł
y należy unieruchomić, aby unieruchomić ca
ł
ą bry
ł
ę?
1 punkt – bry
ł
a obraca się w dowolnym
kierunku wokó
ł
dowolnej osi
przechodzącej przez ustalony
punkt
2 punkty – bry
ł
a obraca się w dowolnym
4
1
A
2
A
3
A
Aby unieruchomić bry
ł
ę sztywną, trzeba
unieruchomić trzy niewspó
ł
liniowe punkty
2 punkty – bry
ł
a obraca się w dowolnym
kierunku wokó
ł
osi przechodzą-
cej przez dwa ustalone punkty
3 punkty – bry
ł
a jest ca
ł
kowicie
unieruchomiona
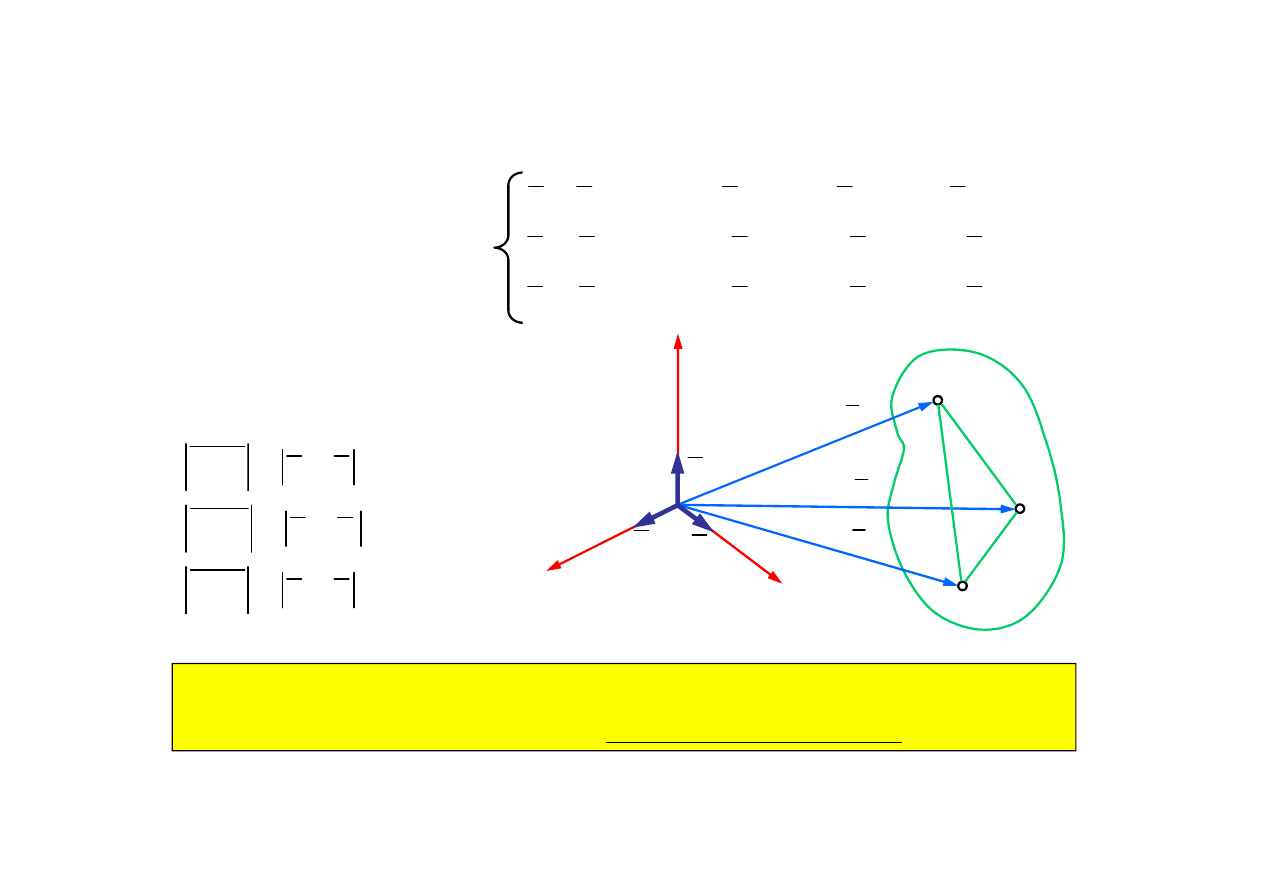
1.3. Opis ruchu cia
ł
a sztywnego przez podanie równań ruchu
trzech nie wspó
ł
liniowych punktów
( )
( )
( )
( )
2
2
2
2
2
x
y
z
r
r t
x t e
y
t e
z
t e
=
=
+
+
( )
( )
( )
( )
3
3
3
3
3
x
y
z
r
r t
x t e
y
t e
z
t e
=
=
+
+
( )
( )
( )
( )
1
1
1
1
1
x
y
z
r
r t
x t e
y t e
z t e
=
=
+
+
=
− =
=
Równania ruchu trzech
niewspó
ł
liniowych punktów
(9 skalarnych funkcji czasu):
Warunki sta
ł
ych odleg
ł
ości
(3 równania algebraiczne):
1
A
1
r
z
d
5
Po
ł
ożenie bry
ł
y sztywnej w każdej chwili można określić za pomocą dziewięciu
skalarnych funkcji czasu które powinny spe
ł
niać trzy warunki sztywności. Sześć
niezależnych funkcji (9 – 3 = 6) nazywamy wspó
ł
rzędnymi uogólnionymi
1
2
2
1
1
2
3
3
2
2
1
3
3
1
3
A A
r
r
d
const
A A
r
r
d
const
A A
r
r
d
const
=
− =
=
=
−
=
=
=
− =
=
2
A
3
A
2
r
3
r
x
O
y
x
e
y
e
z
e
1
d
2
d
3
d
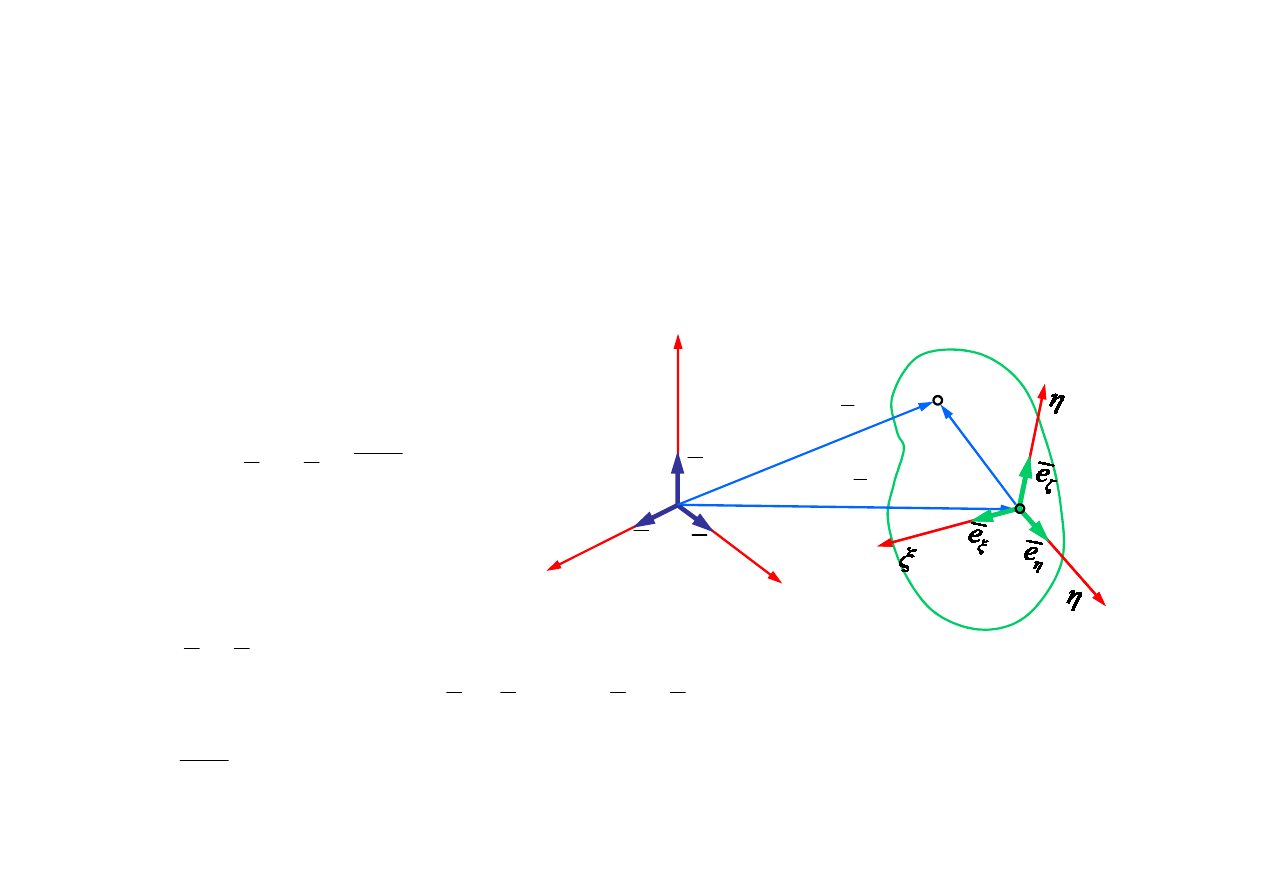
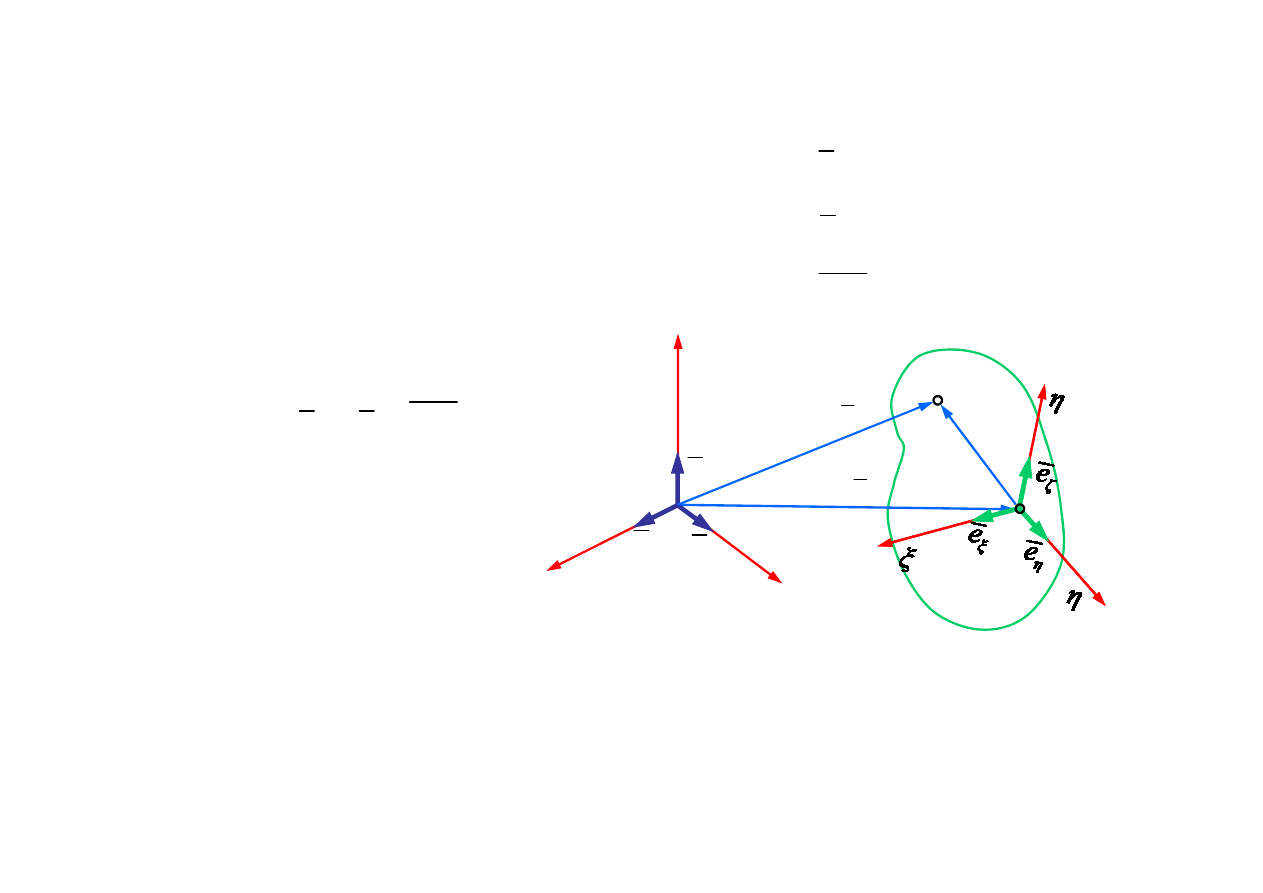
1.4. Opis ruchu cia
ł
a sztywnego we wspó
ł
rzędnych
przestrzennych i materialnych
Uk
ł
ad
Αξηζ
– uk
ł
ad wspó
ł
rzędnych materialnych Lagrange’a
(niezależnych od czasu)
Związek wektorowy pomiędzy
opisem przestrzennym i materialnym
M
M
r
z
Uk
ł
ad Oxyz – uk
ł
ad wspó
ł
rzędnych przestrzennych Eulera
6
M
A
r
r
AM
= +
A
r
x
O
y
x
e
y
e
z
e
A
- wektor zdefiniowany we wspó
ł
rzędnych materialnych
niezależnych od czasu
AM
M
A
r , r
( )
( )
A
A
M
M
r
r t ,
r
r
t
=
=
- wektory zdefiniowane we wspó
ł
rzędnych przestrzennych
M
A
r
r
AM
= +
w zapisie macierzowym:
Związek
(
)
A
A
A
A
r
x
y
z
=
(
)
M
r
x
y
z
=
(
)
AM
ξ
η
ζ
=
M
M
r
z
7
( )
( )
( )
( )
( )
( )
( )
( )
( )
A
A
A
ξ
cos x,ξ
c os y,ξ
cos z,ξ
x
x
η
cos x,η
cos y,η
cos z,η
y
y
ζ
cos x,ζ
cos y,ζ
cos z,ζ
z
z
−
=
⋅ −
−
( )
( )
( )
( )
( )
( )
( )
( )
( )
A
A
A
x
x
cos x,ξ
cos x,η
cos x,ζ
ξ
y
y
cos y,ξ
cos y,η
cos y,ζ
η
z
z
cos z,ξ
cos z,η
cos z,ζ
ζ
−
−
=
⋅
−
A
A
A
ξ
x
x
η
α
y
y
ζ
z
z
−
= ⋅ −
−
%
A
T
A
A
x
x
ξ
y
y
α
η
z
z
ζ
−
−
=
⋅
−
%
A
r
x
O
y
x
e
y
e
z
e
A
W
ł
asności macierzy przejścia:
Elementy macierzy przejścia
kosinusy kierunkowe osi uk
ł
adu wspó
ł
rzędnych przestrzennych w uk
ł
adzie wspó
ł
rzędnych
materialnych i materialnych w uk
ł
adzie wspó
ł
rzędnych przestrzennych
( )
( )
( )
cos x,ξ
c os y,ξ
cos z,ξ
Wiersze macierzy przejścia
wspó
ł
rzędne wersorów uk
ł
adu
materialnego we wspó
ł
rzędnych
przestrzennych
x
e
↓
y
e
↓
z
e
↓
ξ
e
←
Macierz przejścia opisuje rotację cia
ł
a
8
Iloczyn skalarny dwóch wierszy (kolumn) jednoimiennych jest równy 1
Kolumny macierzy przejścia
wspó
ł
rzędne wersorów uk
ł
adu
przestrzennego we wspó
ł
rzędnych
materialnych
Macierz przejścia zawiera 9 elementów, jednak tylko trzy są niezależne, ponieważ te
9 elementów powinno spe
ł
niać 6 niezależnych warunków
( )
( )
( )
( )
( )
( )
( )
( )
( )
cos x,ξ
c os y,ξ
cos z,ξ
α
cos x,η
cos y,η
cos z,η
cos x,ζ
cos y,ζ
cos z,ζ
=
%
ξ
e
←
η
e
←
ξ
e
←
Iloczyn skalarny dwóch wierszy (kolumn) różnoimiennych jest równy 0
( )
( )
( )
2
2
2
1
ξ
ξ
e e
cos
x,ξ
c os
y,ξ
cos
z,ξ
⋅ =
+
+
=
( )
( )
( )
2
2
2
1
η
η
e e
cos
x,η
c os
y,η
cos
z,η
⋅ =
+
+
=
( )
( )
( )
2
2
2
1
ζ
ζ
e
e
cos
x,ζ
c os
y,ζ
cos
z,ζ
⋅ =
+
+
=
( )
( )
( )
( )
( )
( )
0
ξ
η
e e
cos x,ξ
cos x,η
c os y,ξ
c os y,η
cos z,ξ
cos z,η
⋅ =
⋅
+
⋅
+
⋅
=
( )
( )
( )
( )
( )
( )
0
η
ζ
e e
cos x,η cos x,ζ
c os y,η c os y,ζ
cos z,η cos z,ζ
⋅ =
⋅
+
⋅
+
⋅
=
( )
( )
( )
( )
( )
( )
0
ξ
ζ
e e
cos x,ξ
cos x,ζ
c os y,ξ
c os y,ζ
cos z,ξ
cos z,ζ
⋅ =
⋅
+
⋅
+
⋅
=
Związki pomiędzy elementami macierzy przejścia:
9
( )
( )
( )
( )
( )
( )
0
ξ
ζ
e e
cos x,ξ
cos x,ζ
c os y,ξ
c os y,ζ
cos z,ξ
cos z,ζ
⋅ =
⋅
+
⋅
+
⋅
=
( )
( )
( )
2
2
2
1
x
x
e e
cos
x,ξ
c os
x,η
cos
x,η
⋅ =
+
+
=
( )
( )
( )
2
2
2
1
y
y
e e
cos
y,ξ
c os
y,η
cos
y,ζ
⋅ =
+
+
=
( )
( )
( )
2
2
2
1
z
z
e e
cos
z,ξ
c os
z,η
cos
z,ζ
⋅ =
+
+
=
( )
( )
( )
( )
( )
( )
0
x
y
e e
cos x,ξ
cos y,ξ
c os x,η c os y,η
cos x,ζ
cos y,ζ
⋅ =
⋅
+
⋅
+
⋅
=
( )
( )
( )
( )
( )
( )
0
y
z
e e
cos y,ξ
cos z,ξ
c os y,η c os z,η
cos y,ζ
cos z,ζ
⋅ =
⋅
+
⋅
+
⋅
=
( )
( )
( )
( )
( )
( )
0
x
z
e e
cos x,ξ
cos z,ξ
c os x,η c os z,η
cos x,ζ
cos z,ζ
⋅ =
⋅
+
⋅
+
⋅
=
( )
A
A
r
r t
=
Jednoznaczny opis ruchu cia
ł
a sztywnego we wspó
ł
rzędnych przestrzennych i materialnych
sprowadza się do opisu ruchu ustalonego punktu bry
ł
y sztywnej, z którym jest związany uk
ł
ad
wspó
ł
rzędnych Lagrange’a
( )
( )
( )
( )
( )
( )
( )
( )
( )
cos x,ξ
c os y,ξ
cos z,ξ
α
cos x,η
cos y,η
cos z,η
cos x,ζ
cos y,ζ
cos z,ζ
=
%
oraz zdefiniowania dziewięciu kątów kierunkowych jako funkcji czasu występujących w
elementach macierzy przejścia z uk
ł
adu Lagrange’a do uk
ł
adu Eulera.
10
Znajomość kątów kierunkowych pozwala na jednoznaczne wyznaczenie macierzy
przejścia a odwrotne dzia
ł
anie nie daje jednoznacznego wyniku
Zdefiniowanie wektora jest równoznaczne ze zdefiniowaniem trzech niezależnych
skalarnych funkcji czasu
( )
( )
( )
( )
(
)
A
A
A
A
r t
x
t
y
t
z
t
=
( )
A
r t
( )
( )
( )
Spośród dziewięciu kątów kierunkowych tylko trzy są niezależne ponieważ wszystkie,
poprzez elementy macierzy przejścia, są związane sześcioma niezależnymi warunkami.
Jednak te warunki nie pozwalają na jednoznaczne wyznaczenie sześciu niewiadomych
kątów w przypadku, gdy tylko trzy są ściśle określone.
z'
z'
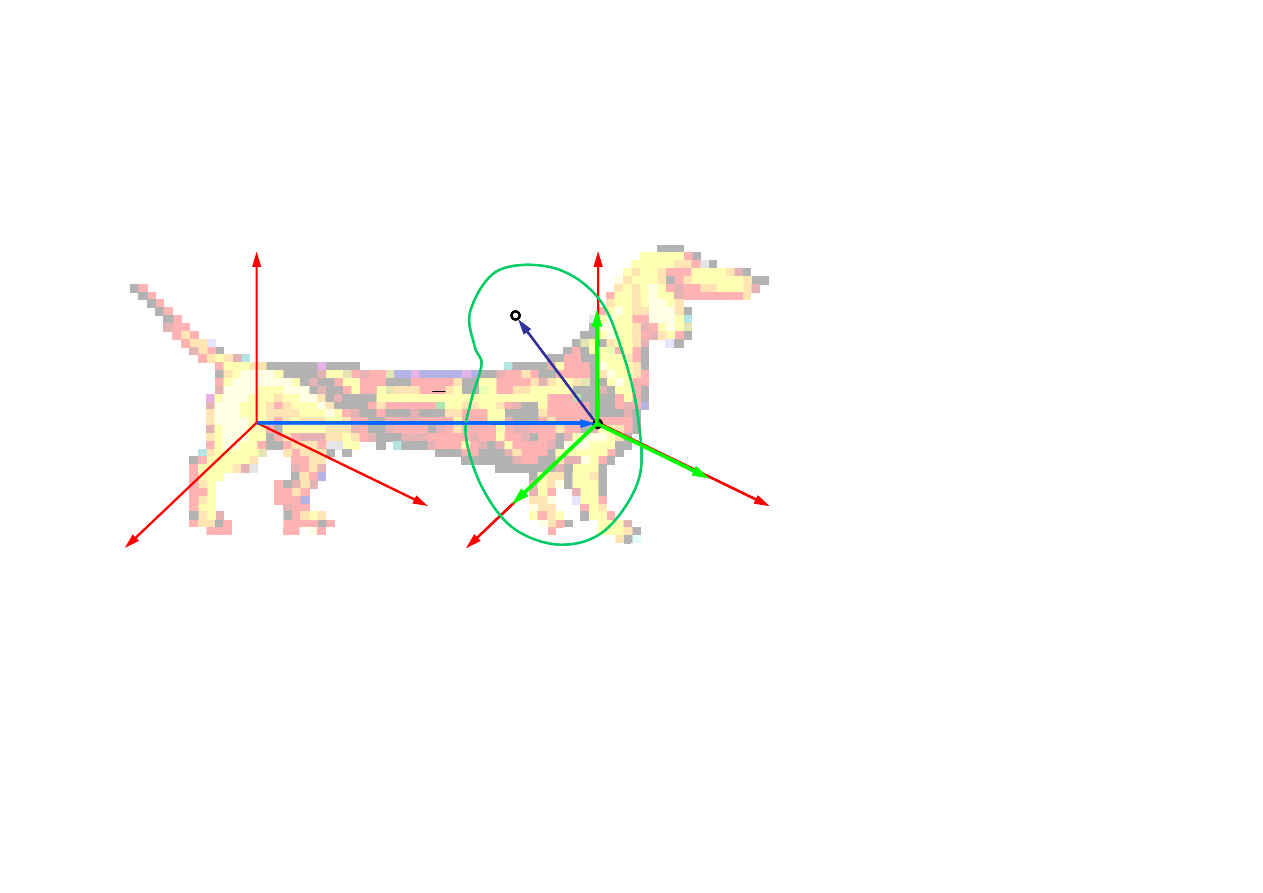
1.5. Opis ruchu cia
ł
a sztywnego za pomocą kątów Eulera
Każdy ruch bry
ł
y sztywnej można przedstawić jako z
ł
ożenie ruchu postępowego
pewnego ustalonego punktu oraz ruchu obrotowego bry
ł
y wokó
ł
tego punktu
A
r
z
O
M
A
ζ
M
A
ζ
11
x'
y'
x'
y'
x
y
ξ
η
ξ
η
Opis ruchu
- opis ruchu postępowego punktu A w uk
ł
adzie przestrzennym Oxyz za pomocą
wektora r
A
- opis po
ł
ożenia punktu M w uk
ł
adzie materialnym
Αξηζ
za pomocą wektora
ΑΜ
- opis ruchu obrotowego uk
ł
adu materialnego
Αξηζ
w uk
ł
adzie Ax’y’z’, przesuniętym
równolegle względem uk
ł
adu Oxyz
,
za pomocą kątów Eulera
O
z
θ
ζ
η
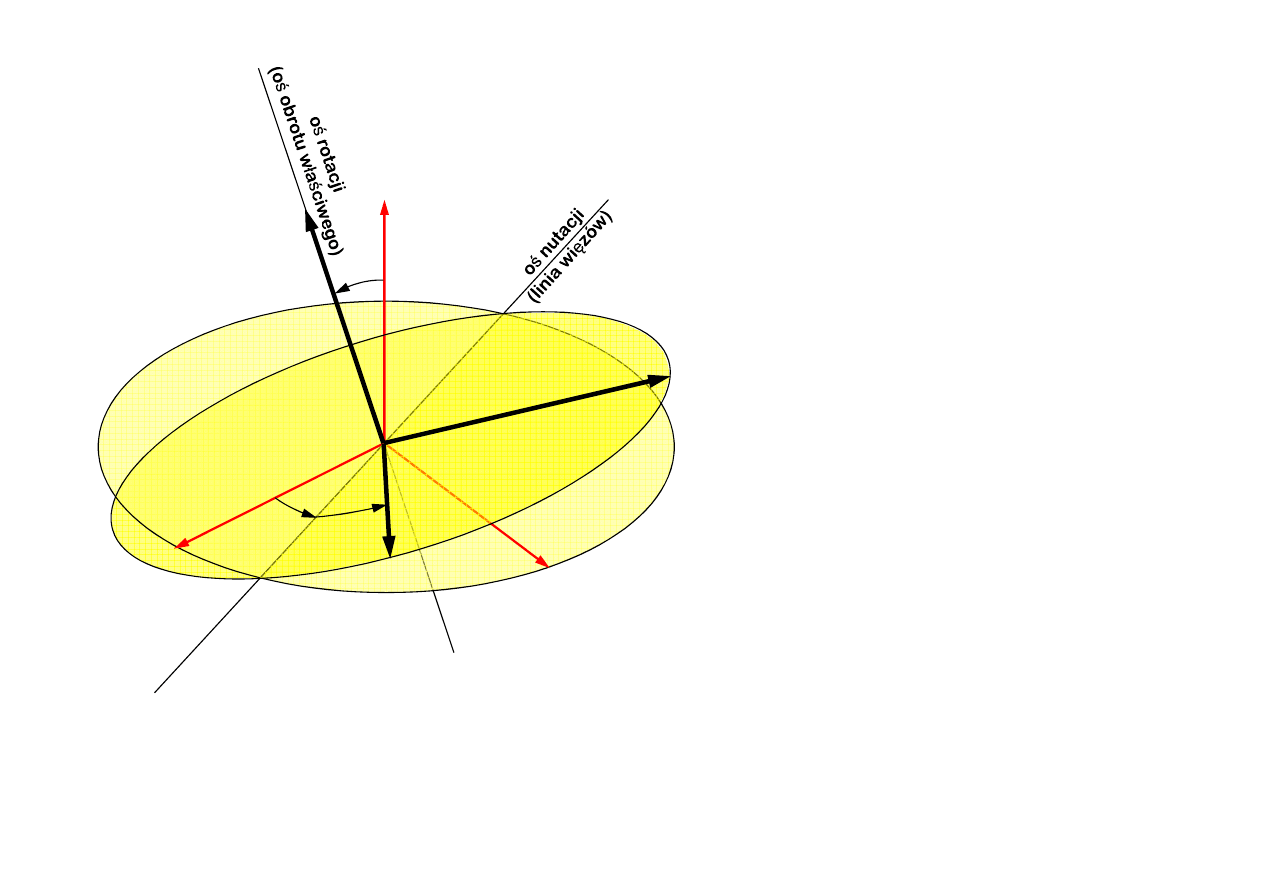
Definicja kątów Eulera
Kąt nutacji
ψ
zawarty pomiędzy osią Ox a osią nutacji
leżącą w p
ł
aszczyźnie Oxy
Kąt precesji
θ
zawarty pomiędzy osią Oz a osią
Οζ
12
O
x
y
ξ
φ
Kąt rotacji φ (kąt obrotu w
ł
aściwego)
zawarty pomiędzy osią nutacji a osią
Οξ
zawarty pomiędzy osią Oz a osią
Οζ
ψ
1
ζ
O
z
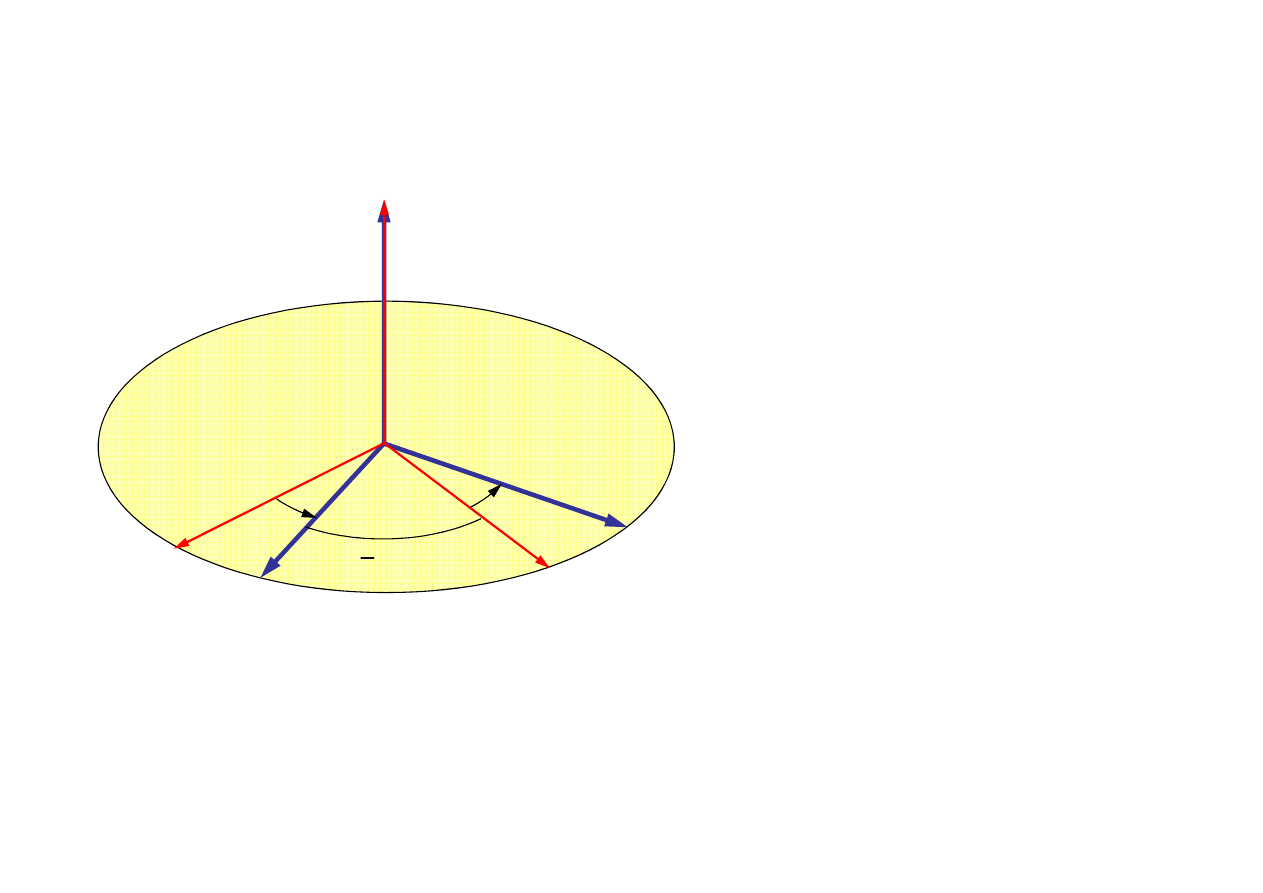
Obrót wokó
ł
osi Oz o kąt
ψ
(precesja, kąt precesji)
(
)
(
)
(
)
(
)
1
1
1
1
1
0
0
0
0
1
cos x,ξ
c os y,ξ
α
cos x,η
cos y,η
=
%
1
0
0
cos ψ
sinψ
α
sinψ
cos ψ
= −
%
13
1
ξ
1
η
2
π
ψ
−
ψ
ψ
O
x
y
1
1
1
0
0
0
0
1
ξ
cos ψ
sinψ
x
η
sinψ
cos ψ
y
ζ
z
= −
⋅
1
0
0
0
1
α
sinψ
cos ψ
= −
%
1
1
1
ξ
x cos ψ
y sinψ
η
x sinψ
y cos ψ
ζ
z
=
+
= −
+
=
1
ζ
O
z
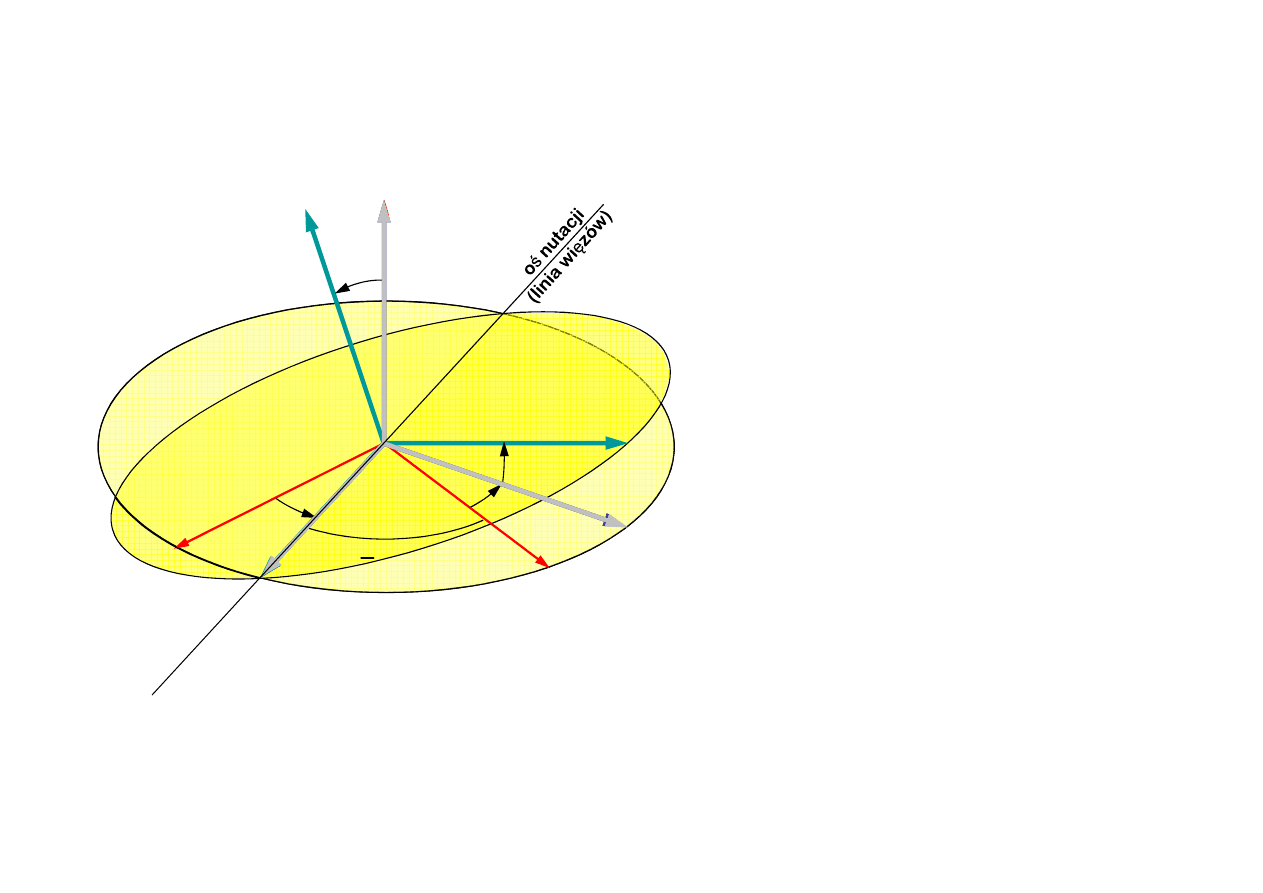
Obrót wokó
ł
osi O
ξ
1
o kąt
θ
(nutacja, kąt nutacji)
(
)
(
)
(
)
(
)
2
1
2
1
2
1
2
1
2
1
0
0
0
0
α
cos η ,η
c os ζ ,η
cos η ,ζ
cos ζ ,ζ
=
%
2
1
0
0
0
α
cos θ
sin θ
=
%
η
2
ζ
θ
14
1
ξ
1
η
2
π
ψ
−
ψ
ψ
O
x
y
2
1
2
1
2
1
1
0
0
0
0
ξ
ξ
η
cos θ
sin θ
η
ζ
sin θ
cos θ
ζ
=
⋅
−
2
0
0
α
cos θ
sin θ
sin θ
cos θ
=
−
%
2
1
2
1
1
2
1
1
ξ
ξ
x cos ψ
y sinψ
η
η cos θ
ζ sin θ
x cos θ sinψ
y cos θ cos ψ
z sin θ
ζ
η sin θ
ζ cos θ
x sin θ sinψ
y sin θ cos ψ
z cos θ
= =
+
=
+
= −
+
+
= −
+
=
−
+
2
ξ
2
η
θ
1
ζ
O
z
Obrót wokó
ł
osi O
ζ
2
o kąt
ϕ
(rotacja, kąt rotacji)
η
2
ζ
θ
η
ζ
φ
(
)
(
)
(
)
(
)
2
2
3
2
2
0
0
0
0
1
cos ξ ,ξ
c os η ,ξ
α
cos ξ ,η
cos η ,η
=
%
3
0
0
cos φ
sin φ
α
sin φ
cos φ
= −
%
15
1
ξ
1
η
ψ
ψ
O
x
y
(
) (
)
(
) (
)
2
2
2
2
2
1
1
ξ
ξ cos φ η sin φ
x cos φ cos ψ
sin φ cos θ sinψ
y cos φ sinψ
sin φ cos θ cos ψ
z sin φ sin θ
η
ξ sin φ η cos φ
x
sin φ cos ψ
cos φ cos θ sinψ
y
sin φ sin ψ
cos φ cos θ cos ψ
z cos φ sin θ
ζ
ξ
η sin θ
ζ cos θ
x sin θ sinψ
y sin θ cos ψ
z cos θ
=
+
=
−
+
+
+
= −
+
= −
−
+ −
+
+
=
= −
+
=
−
+
2
ξ
2
η
θ
ξ
φ
2
2
2
0
0
0
0
1
ξ
cos φ
sin φ
ξ
η
sin φ cos φ
η
ζ
ζ
= −
⋅
3
0
0
0
1
α
sin φ cos φ
= −
%

cos φ cos ψ
sin φ cos θ sinψ
cos φ sinψ
sin φ cos θ cos ψ
sin φ sin θ
α
sin φ cos ψ
cos φ cos θ sinψ
sin φ sinψ
cos φ cos θ cos ψ
cos φ sin θ
sin θ sinψ
sin θ cos ψ
cos θ
−
+
= −
−
−
+
−
%
Związek macierzowy pomiędzy wspó
ł
rzędnymi Eulera i Lagrange’a w opisie ruchu
obrotowego za pomocą kątów Eulera
Macierz przejścia z uk
ł
adu Oxyz do uk
ł
adu obróconego, opisanego za pomocą kątów Eulera
16
ξ
cos φ cos ψ
sin φ cos θ sinψ
cos φ sinψ
sin φ cos θ cos ψ
sin φ sin θ
x
η
sin φ cos ψ
cos φ cos θ sinψ
sin φ sinψ
cos φ cos θ cos ψ
cos φ sin θ
y
ζ
sin θ sinψ
sin θ cos ψ
cos θ
z
−
+
= −
−
−
+
⋅
−
obrotowego za pomocą kątów Eulera

Część 2
Prędkości i przyspieszenia punktów cia
ł
a sztywnego
w ruchu dowolnym
w ruchu dowolnym
( )
( )
A
r t
r t
AM
=
+
- wektor wodzący początku uk
ł
adu ruchomego
( )
A
r t
2.1. Prędkość punktów cia
ł
a sztywnego w ruchu dowolnym
( )
r t
- wektor wodzący w uk
ł
adzie nieruchomym
AM
- wektor wodzący w uk
ł
adzie ruchomym
(niezależny od czasu)
( )
( ) ( )
A
r t
r t
ρ t
=
+
- wektorowy opis ruchu punktu materialnego
w ruchu wzgl
ę
dnym
18
- prędkość unoszenia punktów cia
ł
a sztywnego
w ruchu dowolnym równa prędkości bezwzględnej
u
A
b
υ
r
ω AM
υ
= + ×
=
&
AM
(niezależny od czasu)
b
υ
- prędkość bezwzględna
0
w
υ
=
- prędkość względna
A
w
w
u
b
r
r
ρ
ω ρ
υ
υ
υ
= +
+ × = + =
&
&
&
- pr
ę
dko
ść
w ruchu wzgl
ę
dnym
A
u
b
w
d
r
r
AM
ω ρ
υ
υ
dt
= +
+ × = =
&
&
0
w
w
a
ρ
=
&&
- przyspieszenie względne w ruchu względnym
(
)
A
w
w
w
w
c
u
b
r
r
ρ
ω ρ
ω ρ
ω
ρ
ω ρ
a
a
a
a
= +
+ ×
+ × + ×
+ ×
=
+ +
=
&&
&&
&&
&
&
&
- przyspieszenie Coriolisa w ruchu względnym
2
a
ω ρ
=
×
&
2.2. Przyspieszenie punktów cia
ł
a sztywnego w ruchu dowolnym
2
2
0
w
d
a
AM
dt
=
=
19
- przyspieszenie Coriolisa w ruchu względnym
2
c
w
a
ω ρ
=
×
&
- przyspieszenie unoszenia w ruchu względnym
(
)
u
A
a
r
ω ρ
ω
ω ρ
= + × + × ×
&&
&
2
0
c
d
a
ω
AM
dt
=
×
=
(
)
u
A
b
a
r
ω AM
ω
ω AM
a
= + ×
+ × ×
=
&&
&
- przyspieszenie punktów cia
ł
a sztywnego
w ruchu dowolnym równe przyspieszeniu
bezwzględnemu
z
l
2.3. Twierdzenia o rozk
ł
adzie prędkości punktów cia
ł
a sztywnego
w ruchu dowolnym
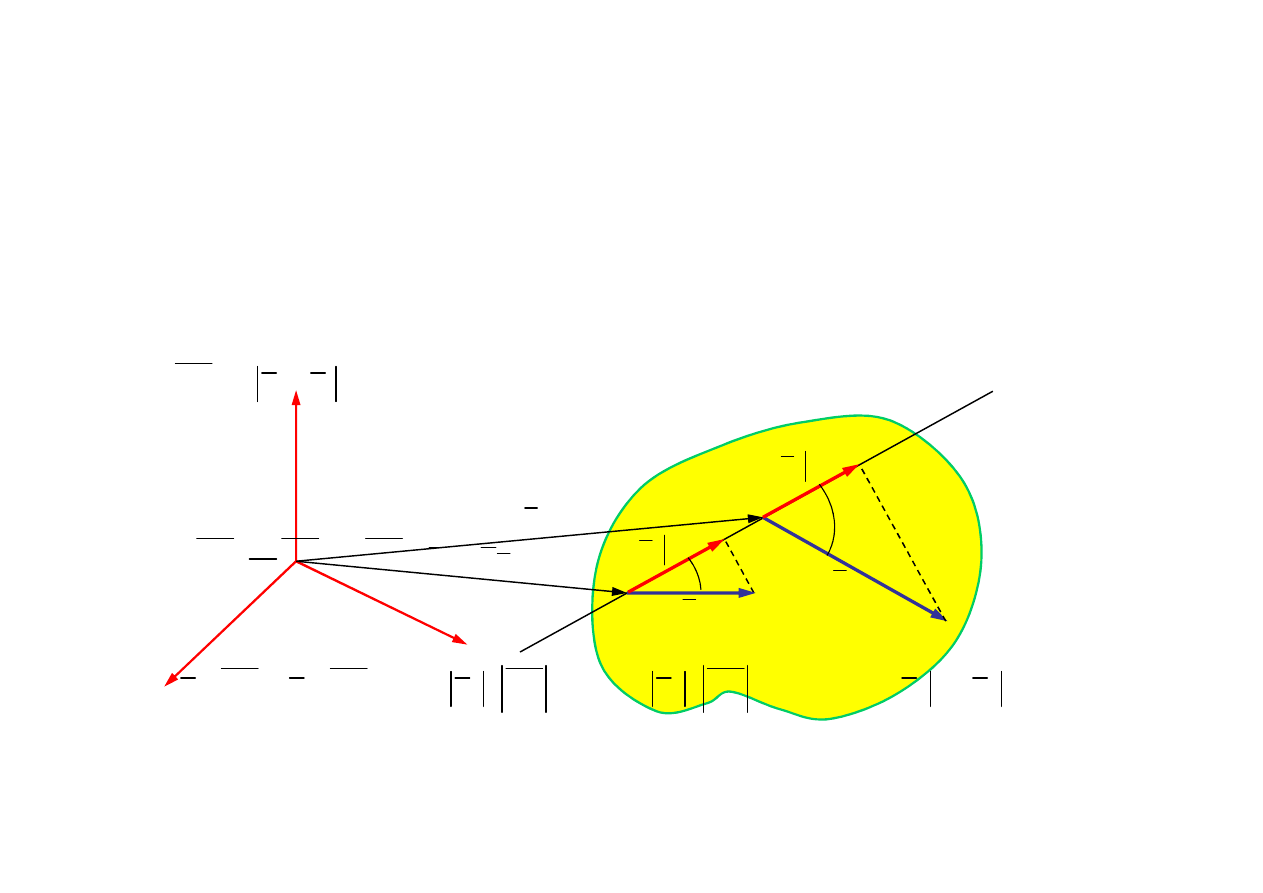
Twierdzenie 1
W ruchu dowolnym bry
ł
y sztywnej rzuty prędkości punktów leżących na
prostej na tę prostą są równe
20
x
O
y
A
B
r
A
r
B
B
υ
A
υ
B l
υ
A l
υ
α
β
z
l
Dowód twierdzenia 1
2
2
B
A
AB
r
r
const
=
−
=
Z za
ł
ożenia o sztywności
cia
ł
a
21
x
O
y
A
B
r
A
r
B
B
υ
A
υ
B l
υ
A l
υ
α
β
(
)
2
2
0
B
A
d
AB
AB
AB υ
υ
dt
⋅
=
⋅
−
=
B
A
B
A
B
A
l
l
υ
AB
υ
AB
υ
AB cos α
υ
AB cos β
υ
υ
⋅
= ⋅
⇔
⋅
⋅
=
⋅
⋅
⇔
=
Różniczkowanie po czasie
Wykorzystując definicję iloczynu skalarnego otrzymujemy
x
z
O
y
B
r
A
r
B
l
M
r
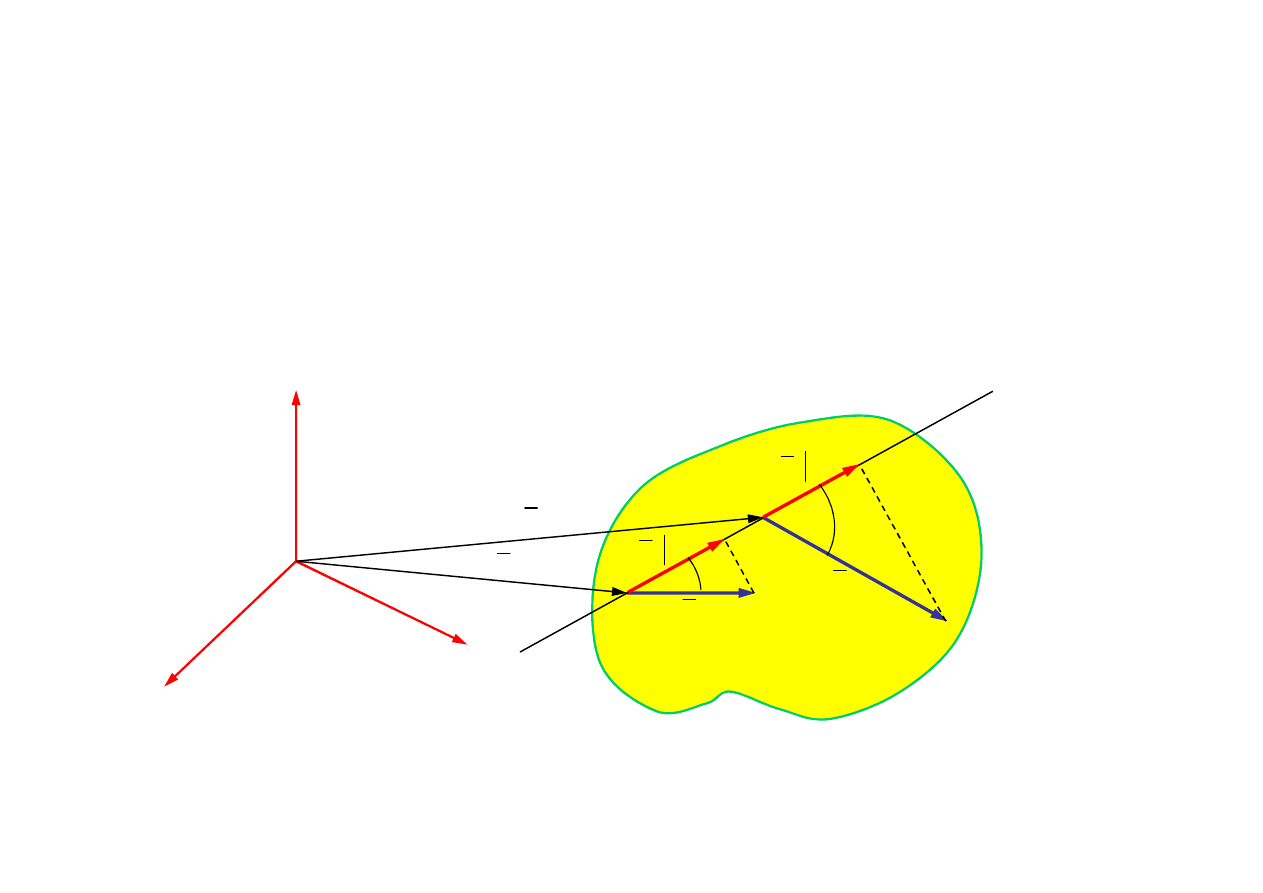
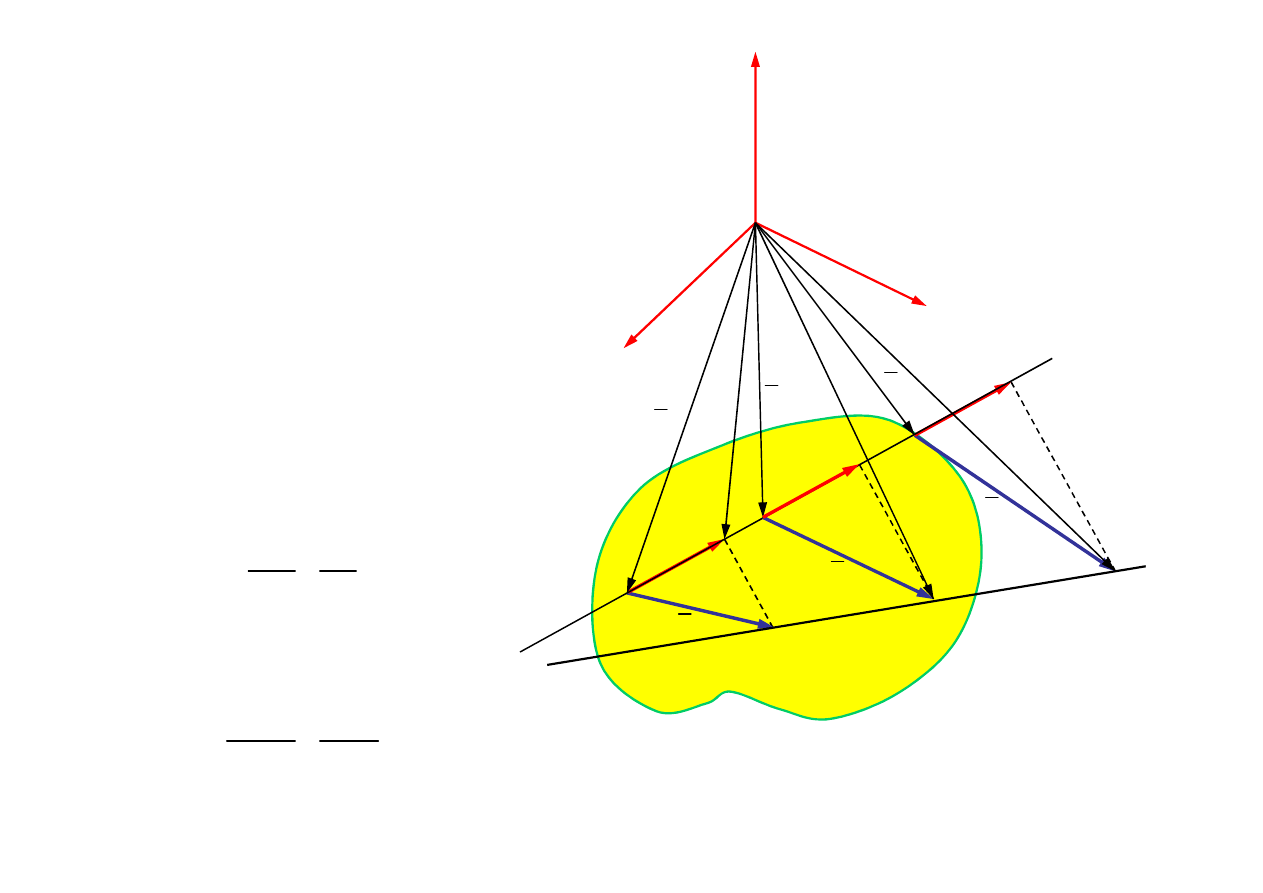
Twierdzenie 2
W ruchu dowolnym bry
ł
y sztywnej
końce wektorów prędkości
punktów leżących na prostej też
leżą na prostej
Za
ł
ożenie
22
A
B
B
υ
A
υ
M
M
υ
A'
M '
B'
Teza
1. Rozważany obiekt to cia
ł
o sztywne
2. Punkty A, M, B leżą na prostej
Punkty A’, M’, B’ leżą na prostej
0
AM
AB
×
=
0
A' M '
A' B'
×
=
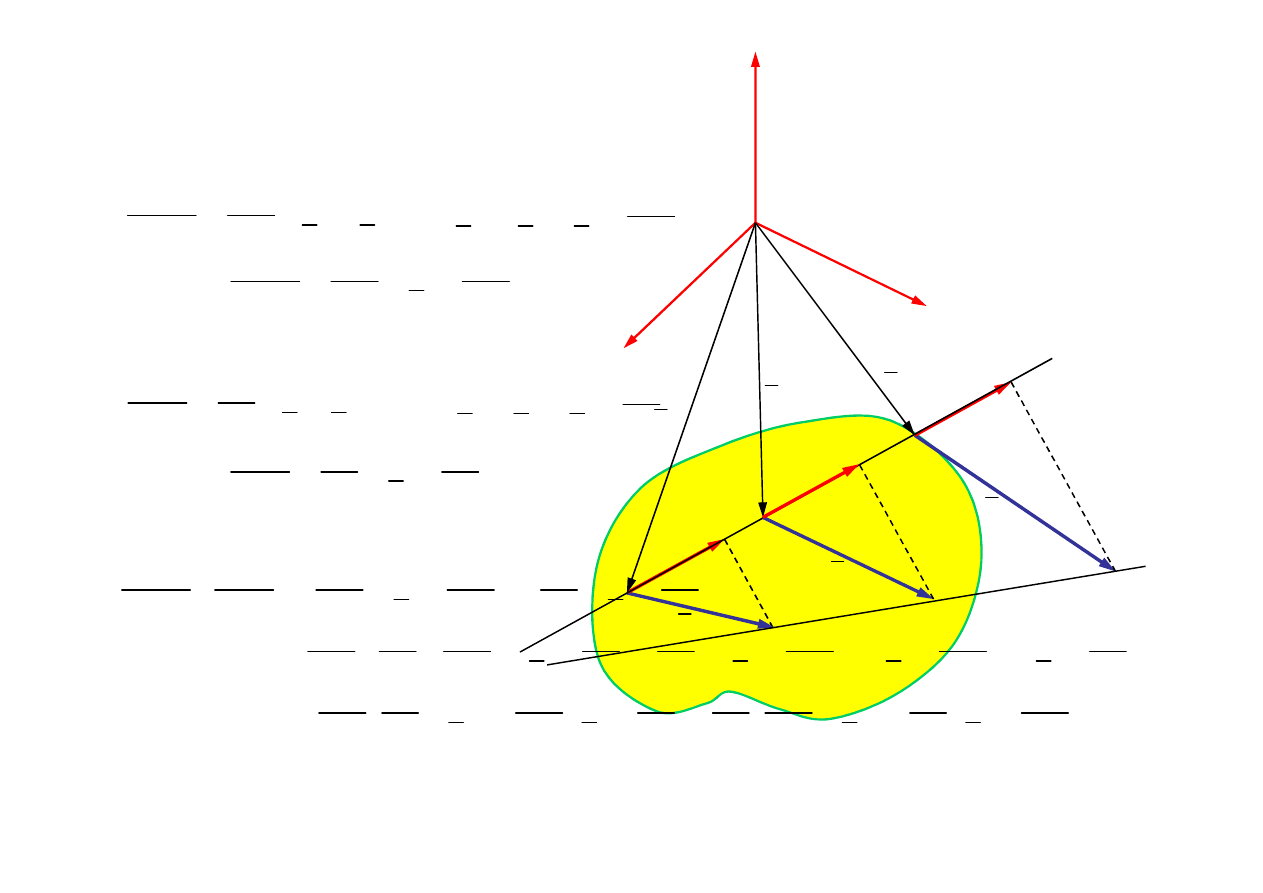
Dowód twierdzenia 2
x
z
O
y
B
r
A
r
B
l
M
r
M
A
A' M '
AM
υ
υ
=
+
−
M
A
A
υ
υ
ω
AM
=
+
×
A
A' M '
AM
ω
AM
=
+
×
b
A
A' B'
AB υ
υ
=
+ −
B
A
A
υ
υ
ω
AB
= +
×
23
A
B
B
υ
A
υ
M
M
υ
A'
M '
B'
A
A' B'
AB ω
AB
=
+
×
(
) (
)
(
)
(
) (
) (
)
(
)
(
)
(
)
(
)
A
A
A
A
A
A
A
A
A
A
A' M '
A' B'
AM
ω
AM
AB ω
AB
AM
AB
AM
ω
AB
AB
ω
AM
ω
AM
ω
AB
AM AB ω
AM ω
AB
AB AM
ω
AB ω
AM
×
=
+
×
×
+
×
=
=
×
+
×
×
−
×
×
+
×
×
×
=
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
+
⋅
⋅
=
0

Część 3
Szczególne przypadki ruchu cia
ł
a sztywnego
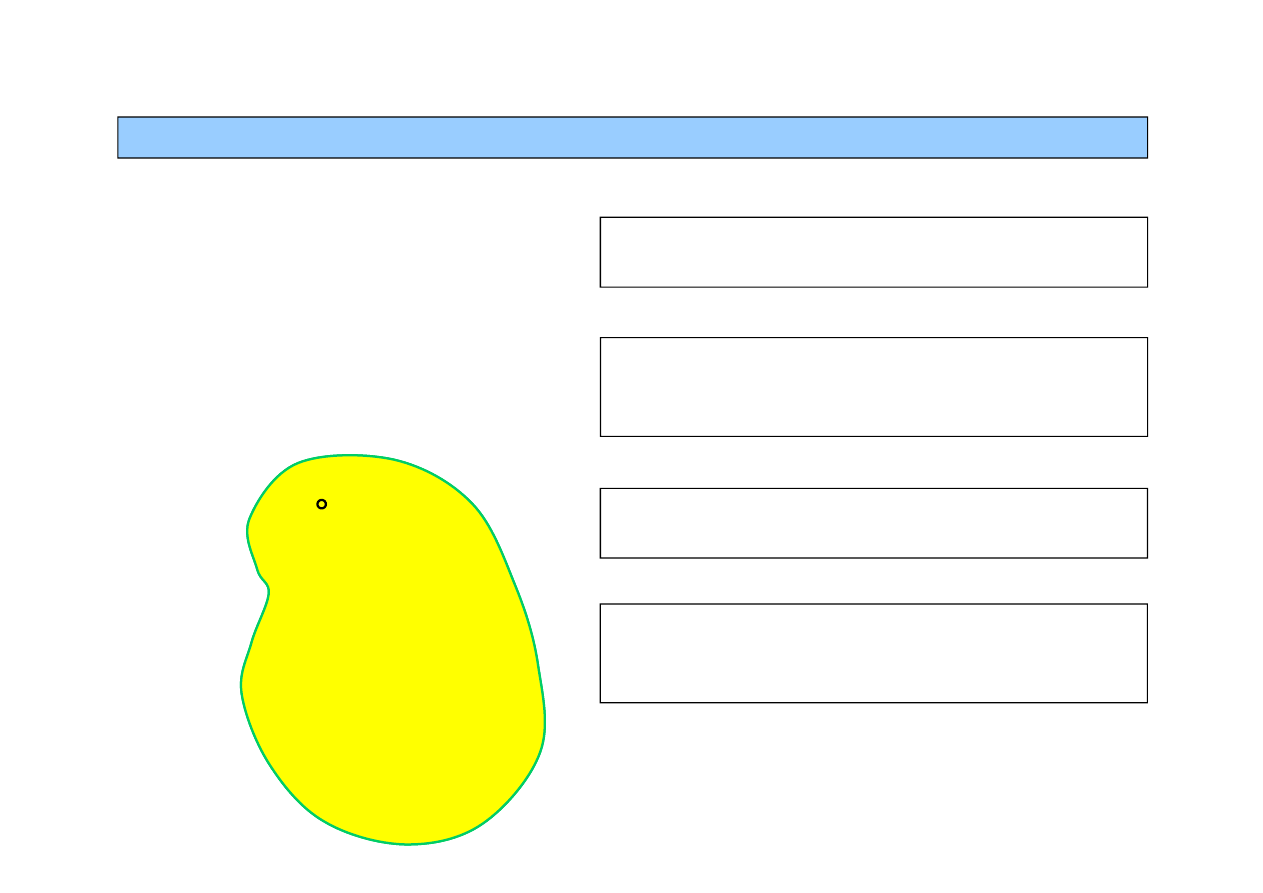
Ruch kulisty
– ruch bry
ł
y sztywnej, w którym jeden punkt bry
ł
y jest nieruchomy
Bry
ł
a unieruchomiona w jednym punkcie ma
trzy stopnie swobody – są to obroty wokó
ł
trzech osi przechodzących przez sta
ł
y punkt
3.1. Ruch kulisty bry
ł
y
Nieruchomy punkt nazywamy środkiem ruchu
25
1
A
Kąty Eulera są wspó
ł
rzędnymi uogólnionymi,
które jednoznacznie określają ten ruch
Tory punktów bry
ł
y w ruchu kulistym leżą na
sferach kulistych o środku w punkcie
unieruchomienia
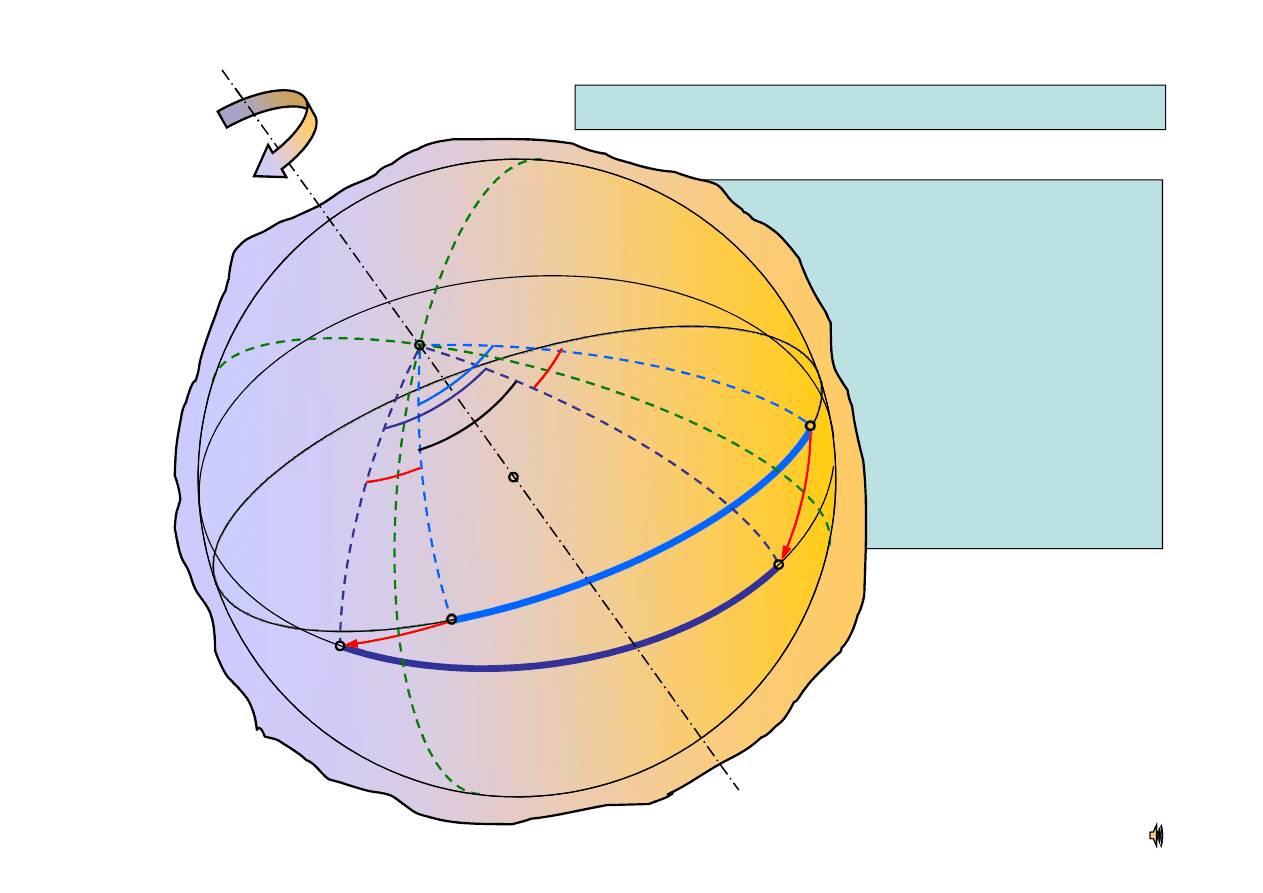
Jeżeli bry
ł
a jest w ruchu
kulistym i zajmuje
w kolejnych chwilach
dwa po
ł
ożenia to
istnieje taka oś
obrotu, względem
której można
przeprowadzić
bry
z jednego
A
P
α
α
β
γ
Twierdzenie d’Alamberta – Eulera
26
bry
ł
ę z jednego
z tych po
ł
ożeń
w drugie
O
1
A
B
1
B
D
C
γ
( )
( ) ( )
A
r t
r t
ρ t
=
+
- wektor wodzący początku uk
ł
adu ruchomego
(w ruchu kulistym równy 0)
( )
A
r t
Prędkość punktów bry
ł
y sztywnej w ruchu kulistym
( )
r t
- wektor wodzący w uk
ł
adzie nieruchomym
( )
ρ t
- wektor wodzący punktu M w uk
ł
adzie
ruchomym (wyrażony we wspó
ł
rzędnych
materialnych jest niezależny od czasu)
Promień wodzący punktów bry
ł
y sztywnej – zależność wektorowa
27
Promień wodzący punktów bry
ł
y sztywnej we wspó
ł
rzędnych przestrzennych
( ) ( ) ( )
( ) ( ) ( )
x
y
z
x t , y t ,z t
ρ t , ρ t , ρ t
=
( )
( )
( )
( )
{ }
T
x t
ξ
y t
α t
η
z t
ζ
=
( )
{ }
α t
- macierz przejścia z uk
ł
adu nieruchomego do ruchomego odpowiednia
do sposobu opisu ruchu
Promień wodzący punktów bry
ł
y sztywnej – zależność wektorowa
( )
( )
r t
ρ t
=

- prędkość punktów cia
ł
a sztywnego w ruchu dowolnym
A
υ
r
ω ρ
= + ×
&
Prędkość punktów cia
ł
a sztywnego w ruchu kulistym (zależność wektorowa)
( )
( ) ( )
υ t
ω t
ρ t
=
×
W ruchu kulistym
0
A
r
=
&
28
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
x
y
z
x
y
z
x
y
z
υ t ,υ
t ,υ t
ω t ,ω
t ,ω t
ρ
t , ρ
t , ρ t
=
×
( ) ( ) ( )
( ) ( ) ( )
( )
{ }
T
T
x
y
z
x
y
z
ξ
υ t ,υ
t ,υ t
ω t ,ω
t ,ω t
α t
η
ζ
=
×
Prędkość punktów cia
ł
a sztywnego w ruchu kulistym we wspó
ł
rzędnych
przestrzennych

Przyspieszenie punktów bry
ł
y sztywnej w ruchu kulistym
(
)
A
a
r
ω ρ
ω
ω ρ
= + × + × ×
&&
&
- przyspieszenie punktów cia
ł
a sztywnego
w ruchu dowolnym
( ) ( ) ( ) ( )
( ) ( )
(
)
a t
ε t
ρ t
ω t
ω t
ρ t
=
×
+
×
×
Przyspieszenie punktów bry
ł
y sztywnej w ruchu kulistym – zależność wektorowa
29
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
{ }
x
y
z
x
y
z
x
y
z
T
T
x
y
z
a t
a t ,a
t ,a t
ε t
ε t ,ε
t ,ε t
ω t
ω t ,ω t ,ω t
ξ
ρ t
ρ t , ρ t , ρ t
α t
η
ζ
=
=
=
=
=
Przyspieszenie punktów cia
ł
a sztywnego w ruchu kulistym we wspó
ł
rzędnych
przestrzennych
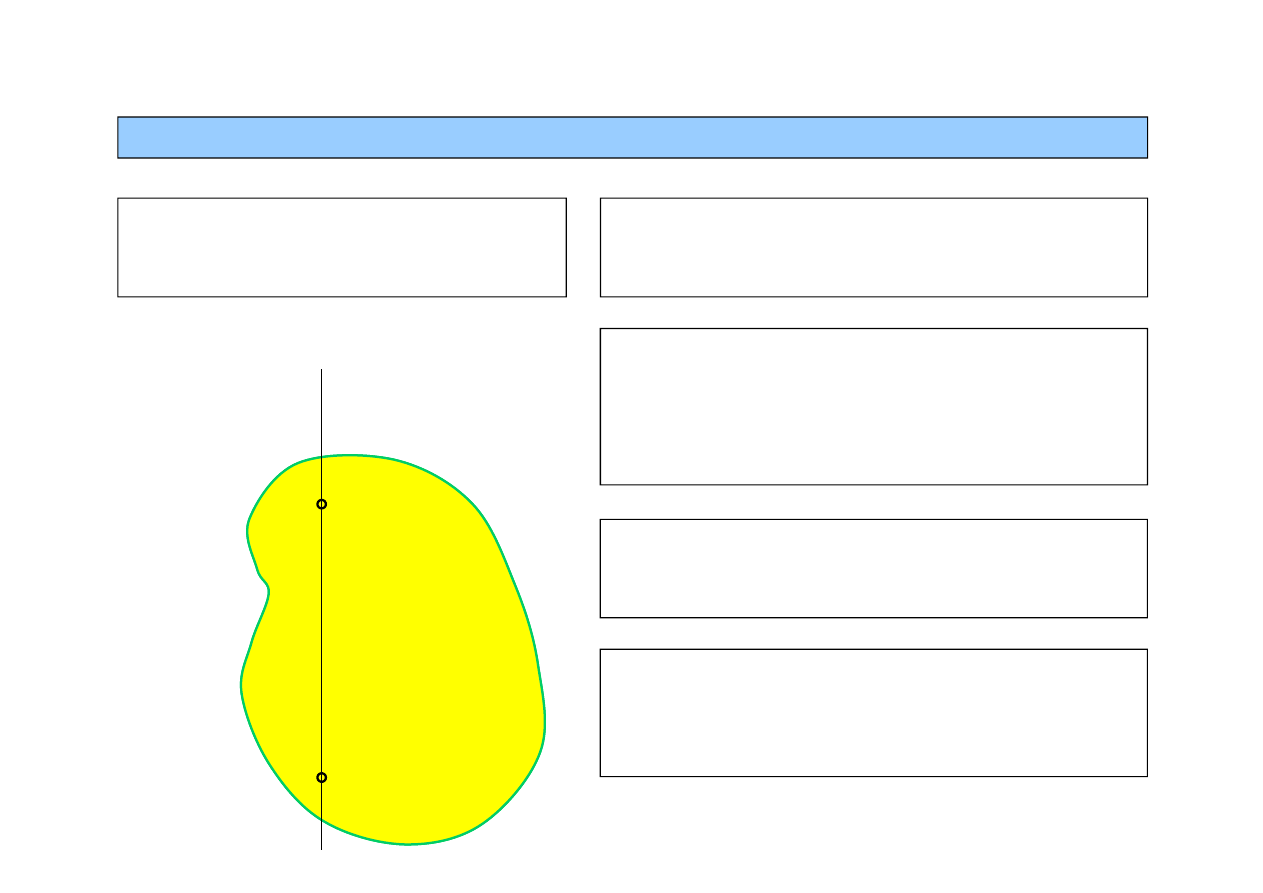
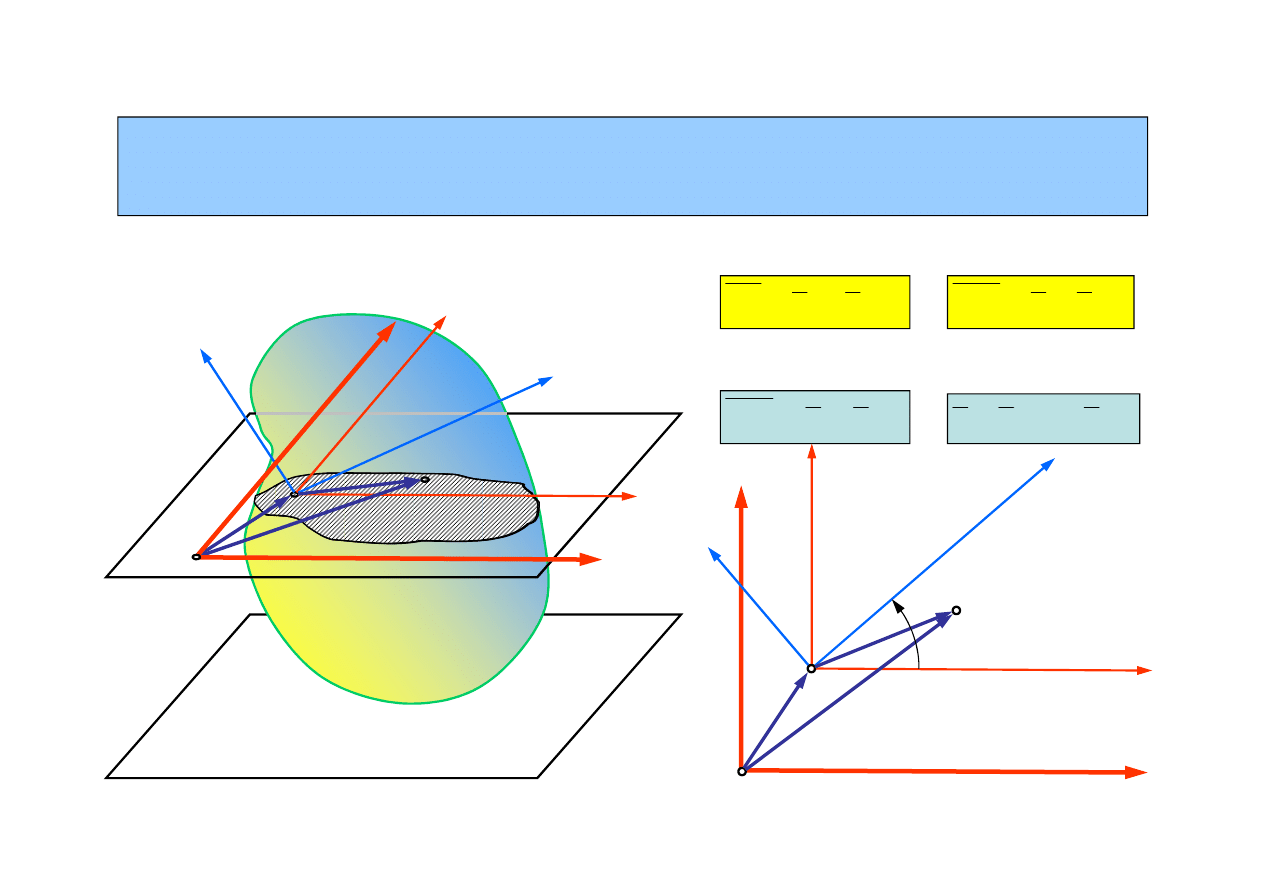
Ruch obrotowy
– ruch bry
ł
y sztywnej, w którym dwa punkty bry
ł
y są nieruchome
Bry
ł
a unieruchomiona w dwóch punktach ma
jeden stopień swobody – jest to obrót wokó
ł
osi przechodzącej przez punkty sta
ł
e
3.2. Ruch obrotowy bry
ł
y sztywnej
Prostą przechodzącą przez dwa
nieruchome punkty nazywamy osią
obrotu
Spośród trzech kątów Eulera jednoznacznie
opisujących ten ruch tylko jeden jest
niezależny. W szczególnym przypadku, gdy
oś
ζ
, z lub linia więzów pokrywają się z osią
30
oś
ζ
, z lub linia więzów pokrywają się z osią
obrotu, dwa kąty Eulera są sta
ł
e
Torami punktów bry
ł
y w ruchu obrotowym są
okręgi leżące w p
ł
aszczyźnie prostopad
ł
ej do
osi obrotu, których środki leżą na tej osi
1
A
2
A
Ruch obrotowy jest szczególnym
przypadkiem ruchu kulistego. W tym ruchu
kierunek wektora prędkości kątowej jest sta
ł
y
i pokrywa się z osią obrotu
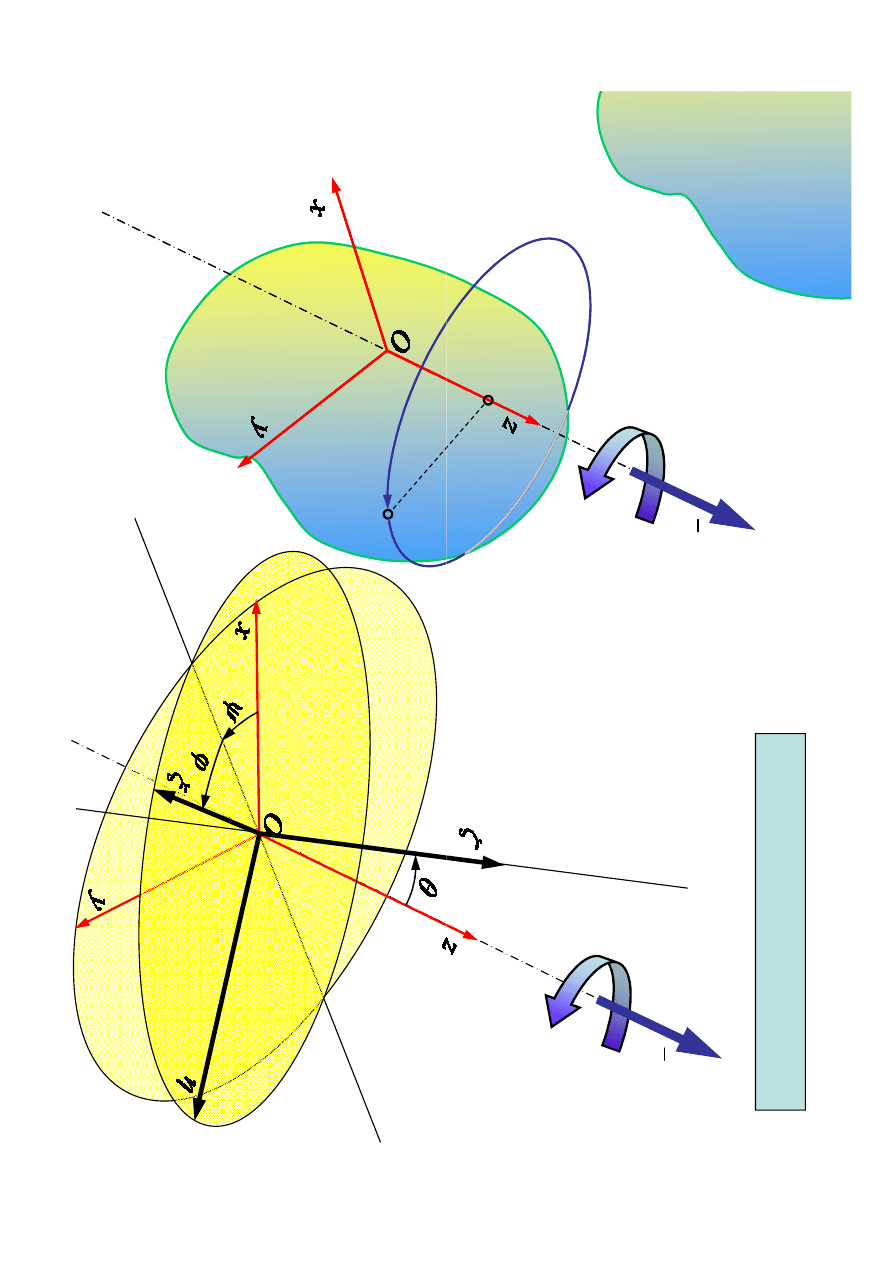
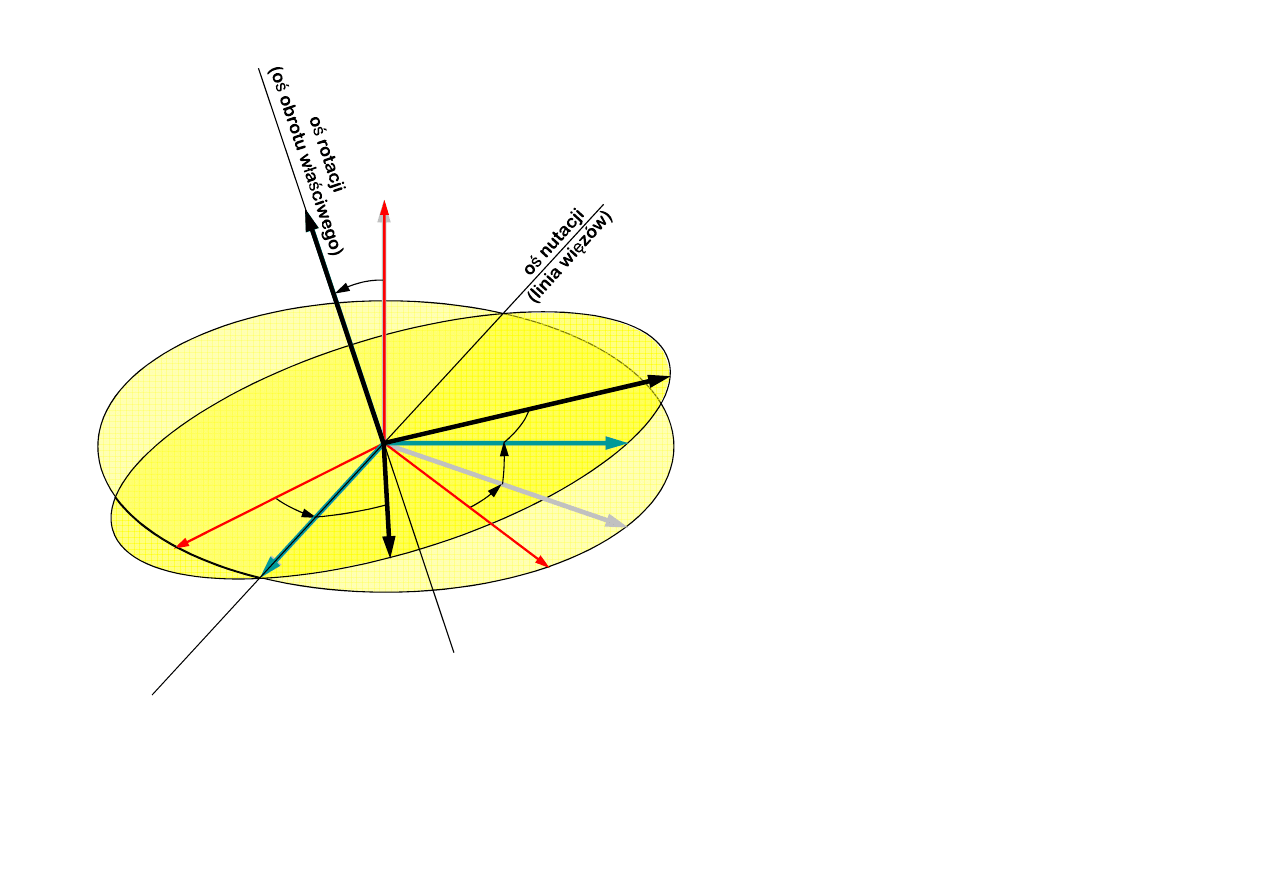
oś o
bro
tu
oś rotacji
(oś obrotu w
ł
aściwego)
l
ω
M
O
l
ω
()
ψ
ψ
t
,
θ
co
n
st
,
φ
co
n
st
=
=
=
3
1
o
ś
n
u
ta
c
ji
(li
n
ia
w
ię
z
ó
w
)
Oś
obro
tu
l
Oś
obro
tu
l
M
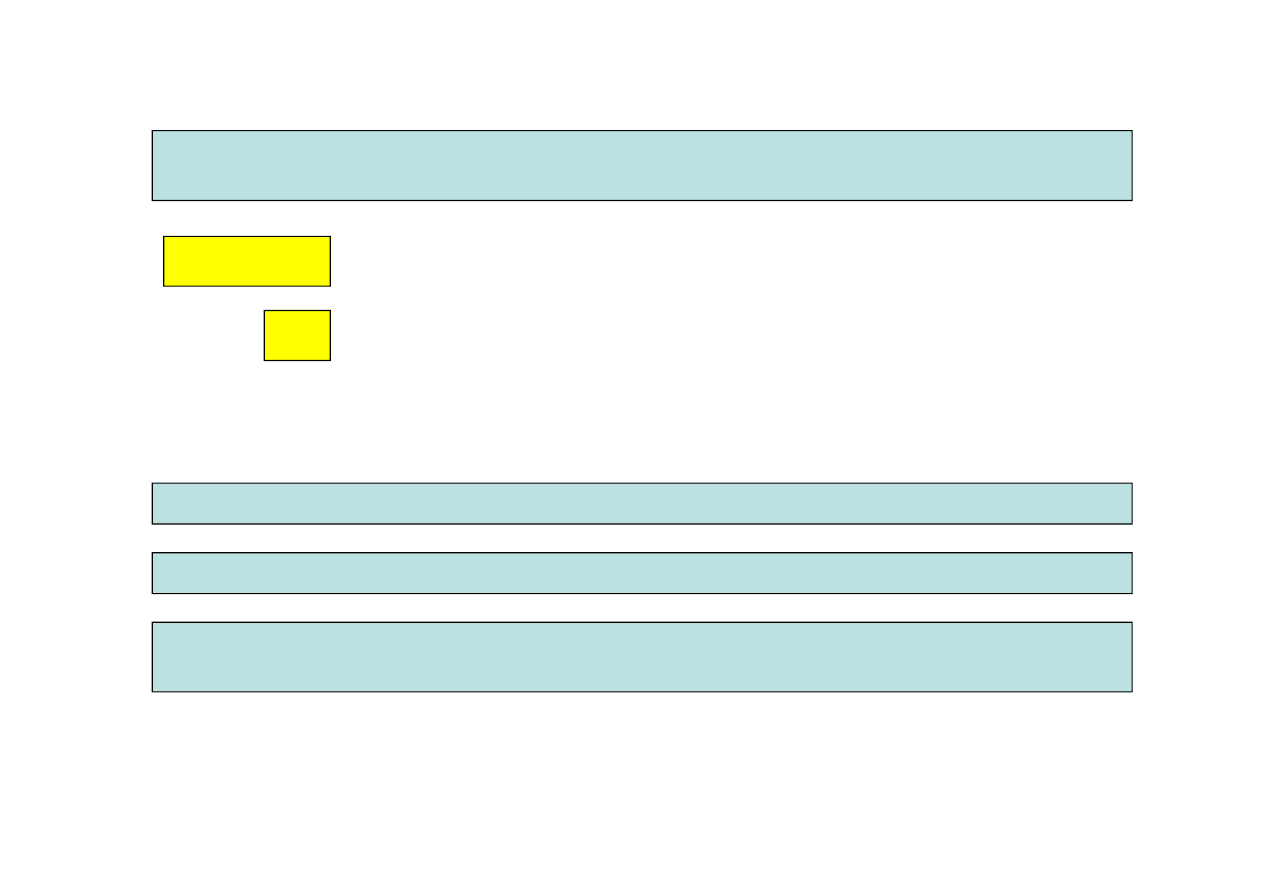
Ruch p
ł
aski
– ruch bry
ł
y sztywnej, w którym wszystkie punkty bry
ł
y poruszają się
w p
ł
aszczyznach równoleg
ł
ych do jednej p
ł
aszczyzny zwanej
p
ł
aszczyzną kierującą
3.3. Ruch p
ł
aski bry
ł
y sztywnej
Π
M
1
y
ξ
η
y
( )
A
A
OA
r
r t
= =
( )
OM
r
r t
= =
( )
AM
ρ
ρ t
= =
( ) ( )
A
r
r t
ρ t
=
+
Opis tylko w układzie bezwzgl
ę
dnym
Opis w układzie przestrzennym i materialnym
32
0
Π
Płaszczyzna kieruj
ą
ca
Π
A
M
1
x
O
x
O
x
y
M
ξ
η
1
x
1
y
A
φ
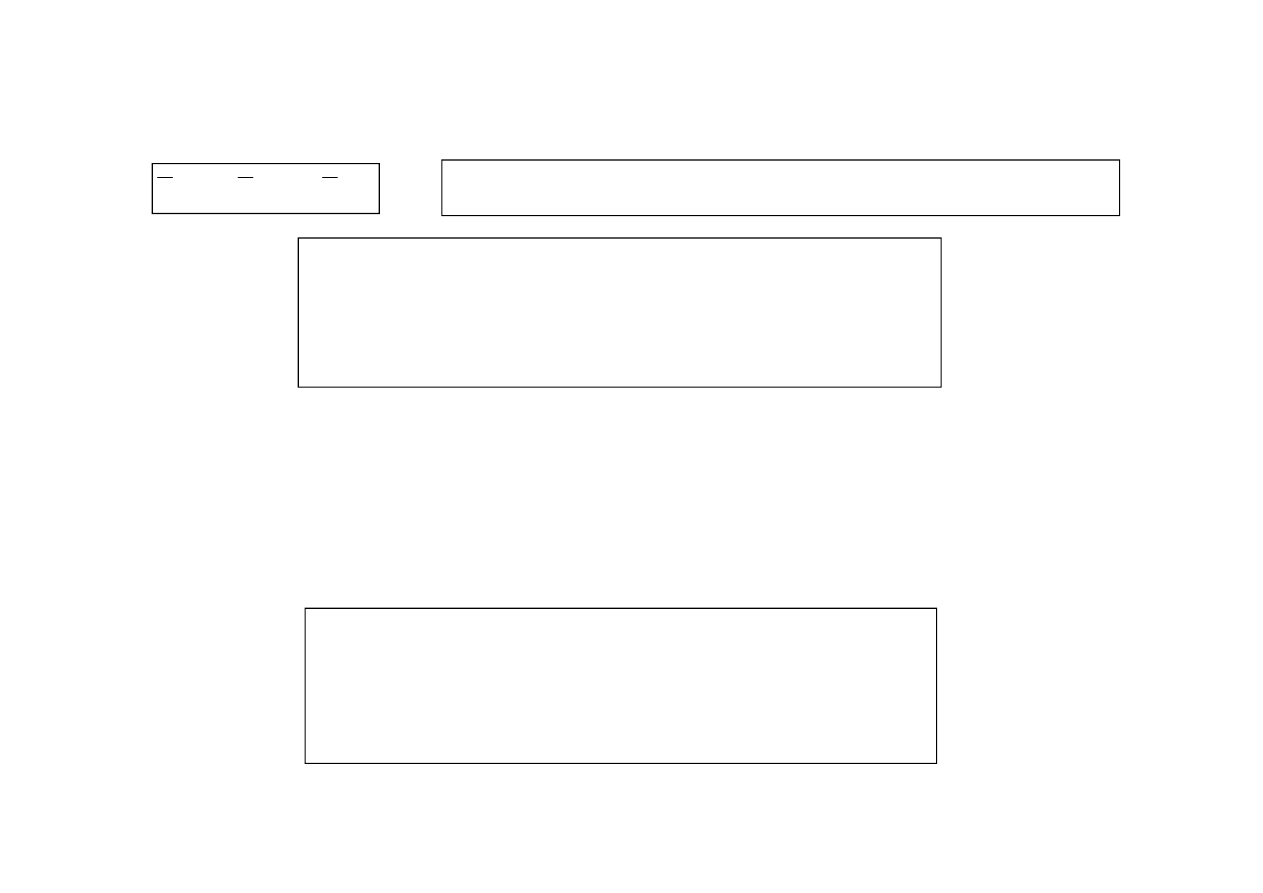
Ruch p
ł
aski bry
ł
y sztywnej jest jednoznacznie opisany za pomocą trzech
wspó
ł
rzędnych uogólnionych:
( )
( )
A
A
x
t , y
t
( )
φ t
- współrz
ę
dne ustalonego punktu A okre
ś
laj
ą
ce translacj
ę
- k
ą
t obrotu bryły wokół ustalonego punktu A
Własno
ś
ci ruchu płaskiego
33
Tory punktów le
żą
w płaszczyznach równoległych do płaszczyzny kieruj
ą
cej
Kierunek wektora pr
ę
dko
ś
ci obrotowej jest prostopadły do płaszczyzny kieruj
ą
cej
Ruch płaski jest zło
ż
eniem ruchu post
ę
powego ustalonego punktu i ruchu obrotowego
wokół tego punktu
( )
( )
( )
( )
0
cos α t
sin α t
Współrz
ę
dne dowolnego punktu M w ruchu płaskim bryły sztywnej
( )
( ) ( )
A
r t
r t
ρ t
=
+
( ) ( ) ( )
( ) ( )
( ) ( )
A
A
A
x
y
z
x t , y t ,z t
x
t , y
t ,z
ρ t , ρ t , ρ
=
+
( ) ( ) ( )
( ) ( )
( )
{ }
T
T
A
A
A
ξ
x t , y t ,z t
x
t , y
t ,z
α t
η
ζ
=
+
34
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
0
0
0
1
A
A
A
cos α t
sin α t
x t
x
t
ξ
y t
y
t
sin α t
cos α t
η
z t
z
ζ
−
=
+
⋅
( )
{ }
( )
( )
( )
( )
( )
( )
( )
( )
0
0
0
0
1
cos α t
sin α t
α t
sin α t
cos α t
= −

Prędkość punktów bry
ł
y sztywnej w ruchu p
ł
askim
- prędkość punktów cia
ł
a sztywnego w ruchu dowolnym
A
υ
r
ω ρ
= + ×
&
Prędkość punktów cia
ł
a sztywnego w ruchu p
ł
askim (zależność wektorowa)
( )
( )
( ) ( )
A
υ t
υ
t
ω t
ρ t
=
+
×
35
( ) ( ) ( )
( )
( )
( )
( ) ( )
0
0 0
x
y
z
Ax
Ay
z
x
y
z
υ t ,υ
t ,υ t
υ
t ,υ
t ,
, ,ω t
ρ
t , ρ
t , ρ
=
+
×
( ) ( ) ( )
( )
( )
( )
( )
{ }
0
0 0
T
T
x
y
z
Ax
Ay
z
ξ
υ t ,υ
t ,υ t
υ
t ,υ
t ,
, ,ω t
α t
η
ζ
=
+
×
Prędkość punktów cia
ł
a sztywnego w ruchu p
ł
askim we wspó
ł
rzędnych
przestrzennych

Przyspieszenie punktów bry
ł
y sztywnej w ruchu p
ł
askim
(
)
A
a
r
ω ρ
ω
ω ρ
= + × + × ×
&&
&
- przyspieszenie punktów cia
ł
a sztywnego
w ruchu dowolnym
( )
( ) ( ) ( ) ( )
( ) ( )
(
)
A
a t
a
t
ε t
ρ t
ω t
ω t
ρ t
=
+
×
+
×
×
Przyspieszenie punktów bry
ł
y sztywnej w ruchu p
ł
askim – zależność wektorowa
Przyspieszenie punktów cia
ł
a sztywnego w ruchu p
ł
askim we wspó
ł
rzędnych
przestrzennych
36
( )
( ) ( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( ) ( )
( )
{ }
0
0 0
0 0
x
y
z
A
Ax
Ay
z
z
T
T
x
y
z
a t
a t ,a
t ,a t
a
t
a
t ,a
t ,
ε t
, ,ε t
ω t
, ,ω t
ξ
ρ t
ρ t , ρ t , ρ
α t
η
ζ
=
=
=
=
=
=
przestrzennych
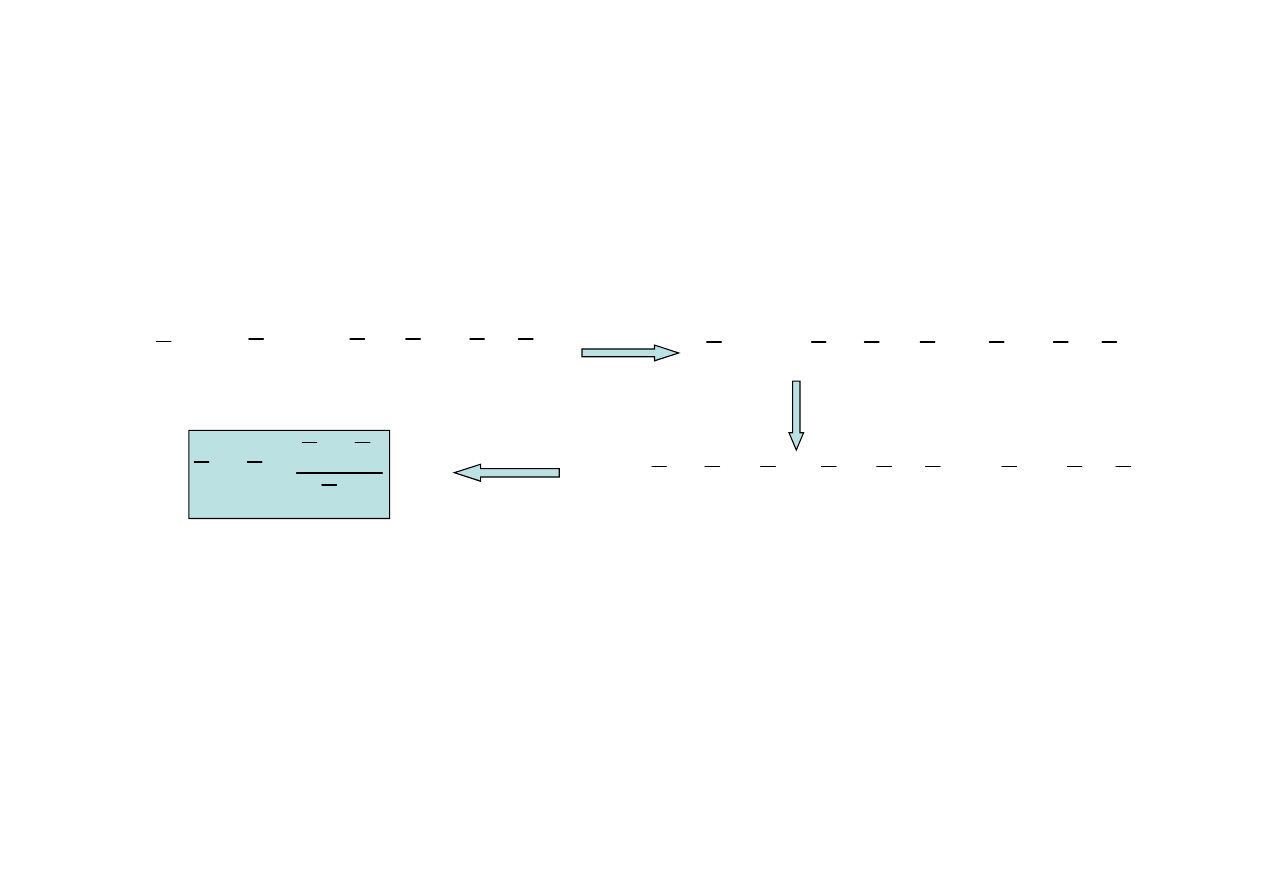
(
)
0
P
A
A
P
A
υ
υ
ω
r
r
= = +
×
−
Chwilowy
ś
rodek obrotu jest to punkt płaszczyzny, który w danej chwili w ruchu płaskim
bryły sztywnej jest nieruchomy. Chwilowy
ś
rodek obrotu nie musi by
ć
punktem bryły.
Chwilowy
ś
rodek obrotu
A
ω
/
×
(
)
0
P
A
A
A
A
P
A
υ
ω
υ
ω
ω
r
r
= =
× +
×
×
−
ω
υ
×
37
(
)
(
)
2
0
A
A
A
A
P
A
A
P
A
ω
υ
ω
ω
r
r
ω
r
r
=
× +
⋅
⋅
−
−
⋅
−
2
A
A
P
A
A
ω
υ
r
r
ω
×
= +
Powy
ż
sza zale
ż
no
ść
pozwala wyznaczy
ć
poło
ż
enie chwilowego
ś
rodka obrotu
w ogólnym przypadku
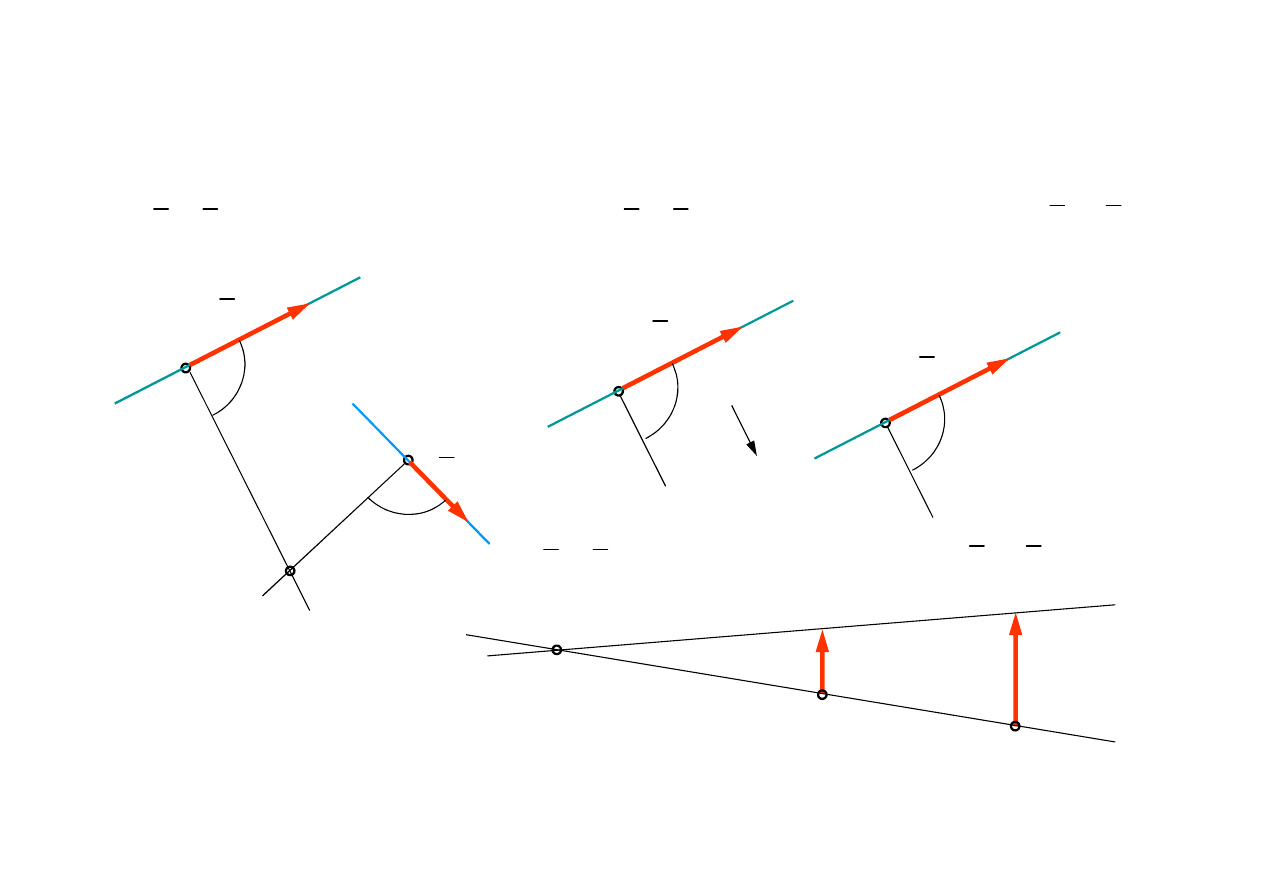
Wyznaczanie chwilowego
ś
rodka obrotu w oparciu o znane pr
ę
dko
ś
ci dwóch punktów
0
A
B
υ
υ
× =
A
υ
(kierunki równoległe) oraz
A
B
0
A
B
υ
υ
× ≠
(kierunki nie równoległe)
A
B
υ
υ
=
A
υ
A
B
υ
B
P
∞
38
B
υ
P
0
A
B
υ
υ
× =
(kierunki równoległe) oraz
A
B
υ
υ
≠
P
A
B
Uwaga: w tym przypadku pr
ę
dko
ś
ci musz
ą
by
ć
znane
Ruch ogólny
– ruch bry
ł
y sztywnej, opisany sześcioma wspó
ł
rzędnymi
uogólnionymi, z których każda jest funkcją czasu
3.4. Ogólny przypadek ruchu bry
ł
y sztywnej
( )
A
A
x
x
t
=
( )
A
A
y
y
t
=
( )
A
A
z
z
t
=
( )
φ
φ t
=
( )
ψ
ψ t
=
( )
θ
θ t
=
- współrz
ę
dne ustalonego
punktu
- k
ą
ty Eulera
39
Współrz
ę
dne dowolnego punktu M w ruchu dowolnym bryły sztywnej
( )
( ) ( )
A
r t
r t
ρ t
=
+
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
A
A
A
x
y
z
x t , y t ,z t
x
t , y
t ,z
t
ρ t , ρ t , ρ t
=
+
( ) ( ) ( )
( ) ( ) ( )
( )
{ }
T
T
A
A
A
ξ
x t , y t ,z t
x
t , y
t ,z
t
α t
η
ζ
=
+

Prędkość punktów bry
ł
y sztywnej w ruchu dowolnym
- prędkość punktów cia
ł
a sztywnego w ruchu dowolnym
A
υ
r
ω ρ
= + ×
&
Prędkość punktów cia
ł
a sztywnego w ruchu dowolnym (zależność wektorowa)
( )
( )
( ) ( )
A
υ t
υ
t
ω t
ρ t
=
+
×
40
( ) ( ) ( )
( )
( )
( )
( ) ( ) ( )
( ) ( ) ( )
x
y
z
Ax
Ay
Az
x
y
z
x
y
z
υ t ,υ
t ,υ t
υ
t ,υ
t ,υ
t
ω t ,ω
t ,ω t
ρ
t , ρ
t , ρ t
=
+
×
( ) ( ) ( )
( )
( )
( )
( ) ( ) ( )
( )
{ }
T
T
x
y
z
Ax
Ay
Az
x
y
z
ξ
υ t ,υ
t ,υ t
υ
t ,υ
t ,υ
t
ω t ,ω
t ,ω t
α t
η
ζ
=
+
×
Prędkość punktów cia
ł
a sztywnego w ruchu dowolnym we wspó
ł
rzędnych
przestrzennych

Przyspieszenie punktów bry
ł
y sztywnej w ruchu dowolnym
(
)
A
a
r
ω ρ
ω
ω ρ
= + × + × ×
&&
&
- przyspieszenie punktów cia
ł
a sztywnego
w ruchu dowolnym
( )
( ) ( ) ( ) ( )
( ) ( )
(
)
A
a t
a
t
ε t
ρ t
ω t
ω t
ρ t
=
+
×
+
×
×
Przyspieszenie punktów bry
ł
y sztywnej w ruchu dowolnym – zależność wektorowa
Przyspieszenie punktów cia
ł
a sztywnego w ruchu dowolnym we wspó
ł
rzędnych
przestrzennych
41
( )
( ) ( ) ( )
( )
( )
( )
( )
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
( ) ( ) ( )
( )
{ }
x
y
z
A
Ax
Ay
Az
x
y
z
x
y
z
T
T
x
y
z
a t
a t ,a
t ,a t
a
t
a
t ,a
t ,a
t
ε t
ε t ,ε
t ,ε t
ω t
ω t ,ω t ,ω t
ξ
ρ t
ρ t , ρ t , ρ t
α t
η
ζ
=
=
=
=
=
=
przestrzennych

Część 4
Wyznaczanie prędkości kątowej i przyspieszenia kątowego
za pomocą kątów Eulera
za pomocą kątów Eulera
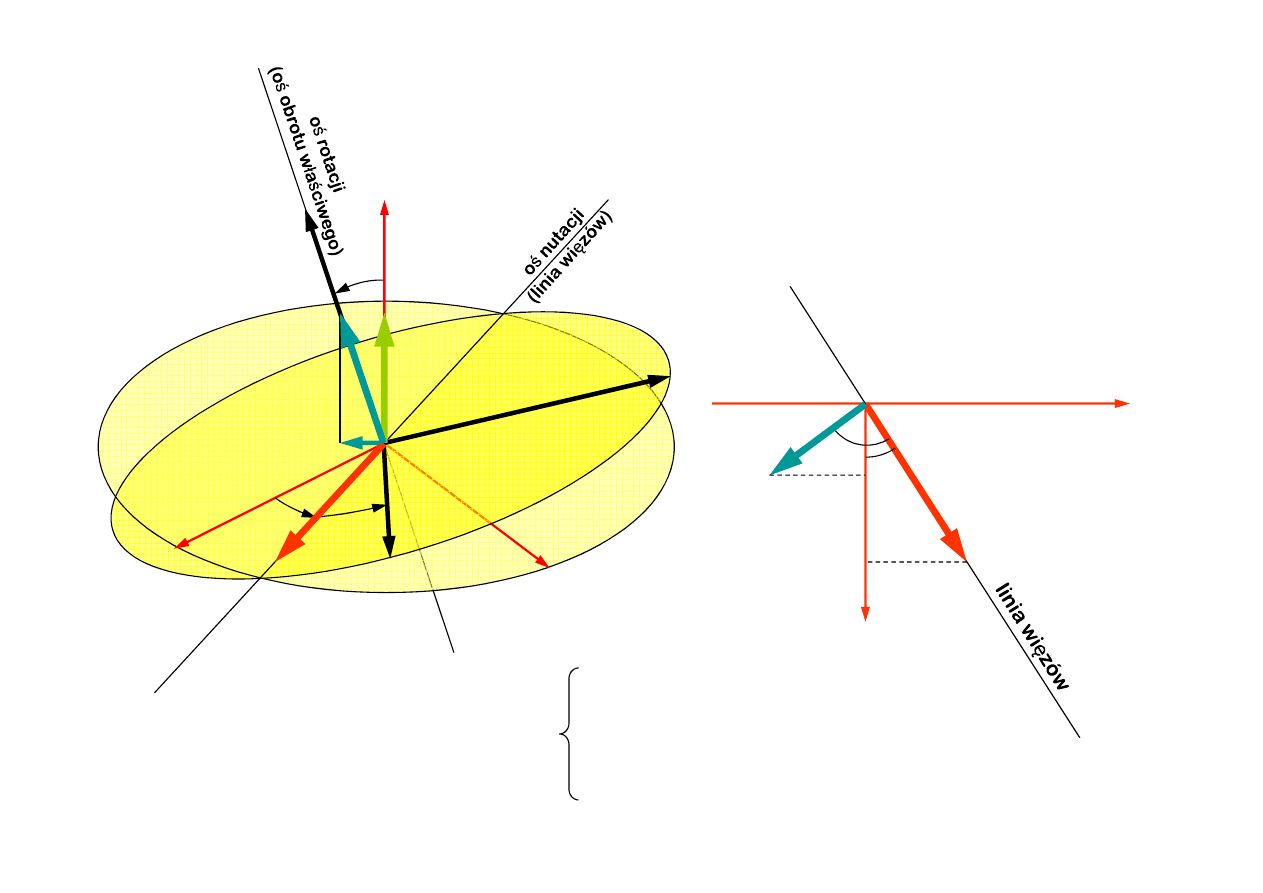
O
z
θ
ζ
η
4.1. Wyznaczenie prędkości kątowych
Widok od osi z
φ
&
ψ
&
y
43
O
x
y
ξ
φ
ψ
θ&
θ&
φ sin θ
&
ψ
x
x
y
z
ω
φ sin θ sinψ θ cos ψ
ω
φ sin θ cos ψ θ sinψ
ω
ψ
φcos θ
=
+
= −
+
= +
&
&
&
&
&
&
Wspó
ł
rzędne wektora prędkości
kątowej w uk
ł
adzie Oxyz
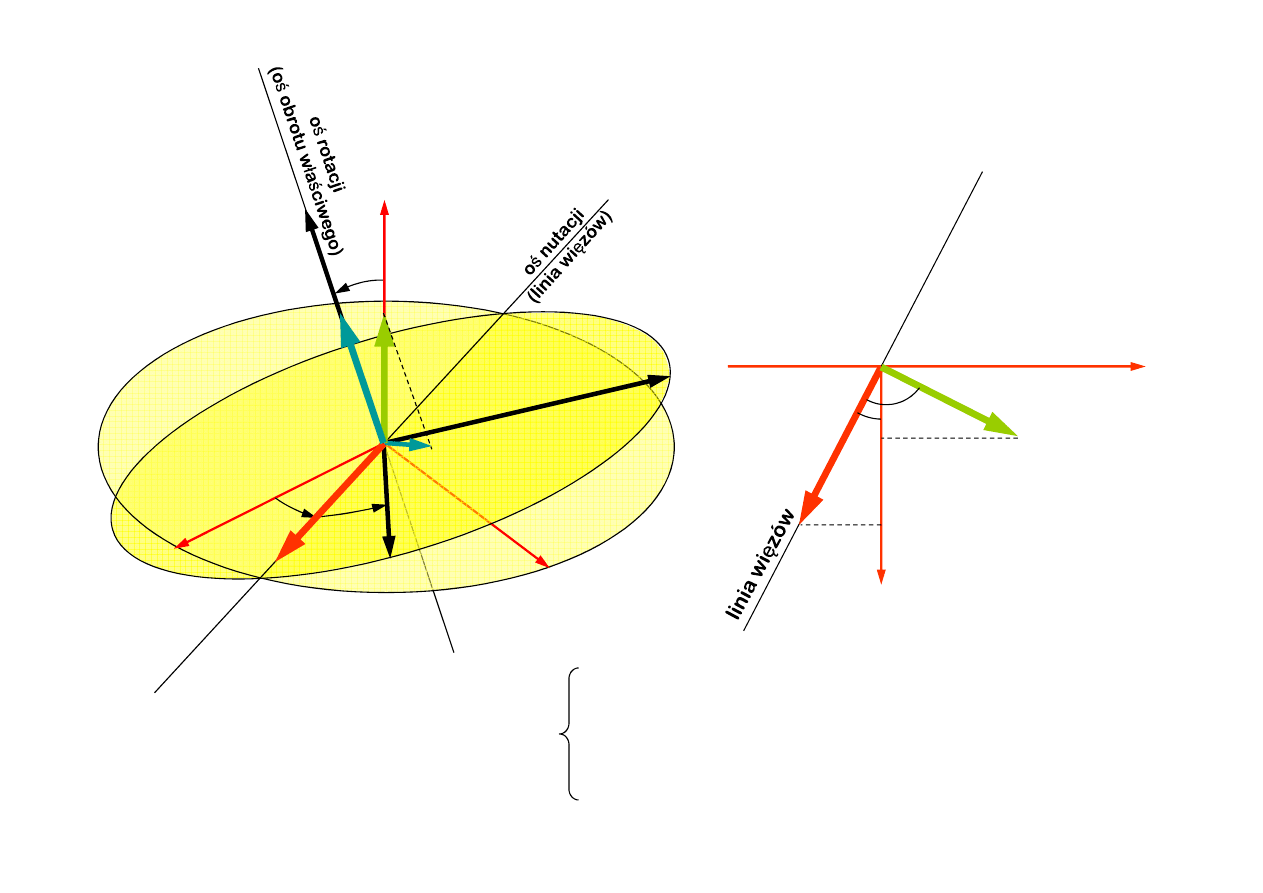
O
z
θ
ζ
η
Widok od osi
ζ
φ
&
ψ
&
θ&
ψ sin θ
&
φ
η
44
O
x
y
ξ
φ
ψ
θ&
θ φ
ξ
ξ
η
ζ
ω
ψ sin θ sin φ θ cos φ
ω
ψ sin θ cos φ θ sin φ
ω
φ ψ cos θ
=
+
=
−
= +
&
&
&
&
&
&
Wspó
ł
rzędne wektora prędkości
kątowej w uk
ł
adzie O
ξηζ

45
Wyszukiwarka
Podobne podstrony:
MT st w 06 [tryb zgodności]
MT st w 05 [tryb zgodności]
MT st w 07 [tryb zgodności]
MT st w 03 [tryb zgodno┼Ťci]
MT st w 02a [tryb zgodno┼Ťci]
MT st w 02 [tryb zgodno┼Ťci]
MT st w 10 [tryb zgodności]
MT st w 06 [tryb zgodności]
MT st w 041 [tryb zgodno┼Ťci]
MT st w 10 [tryb zgodno┼Ťci]
MT st w 11 [tryb zgodno┼Ťci]
MT st w 08 09 [tryb zgodno┼Ťci]
1 ST PiS [tryb zgodnosci]
MT st w 04 cz1 [tryb zgodności]
MT st w 04 cz2 [tryb zgodności]
więcej podobnych podstron