1

Wykład 3

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2011/12

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

TEORIA RÓWNOWAŻNOŚCI UKŁADÓW SIŁ

Część 1

SIŁY I UKŁADY SIŁ

3

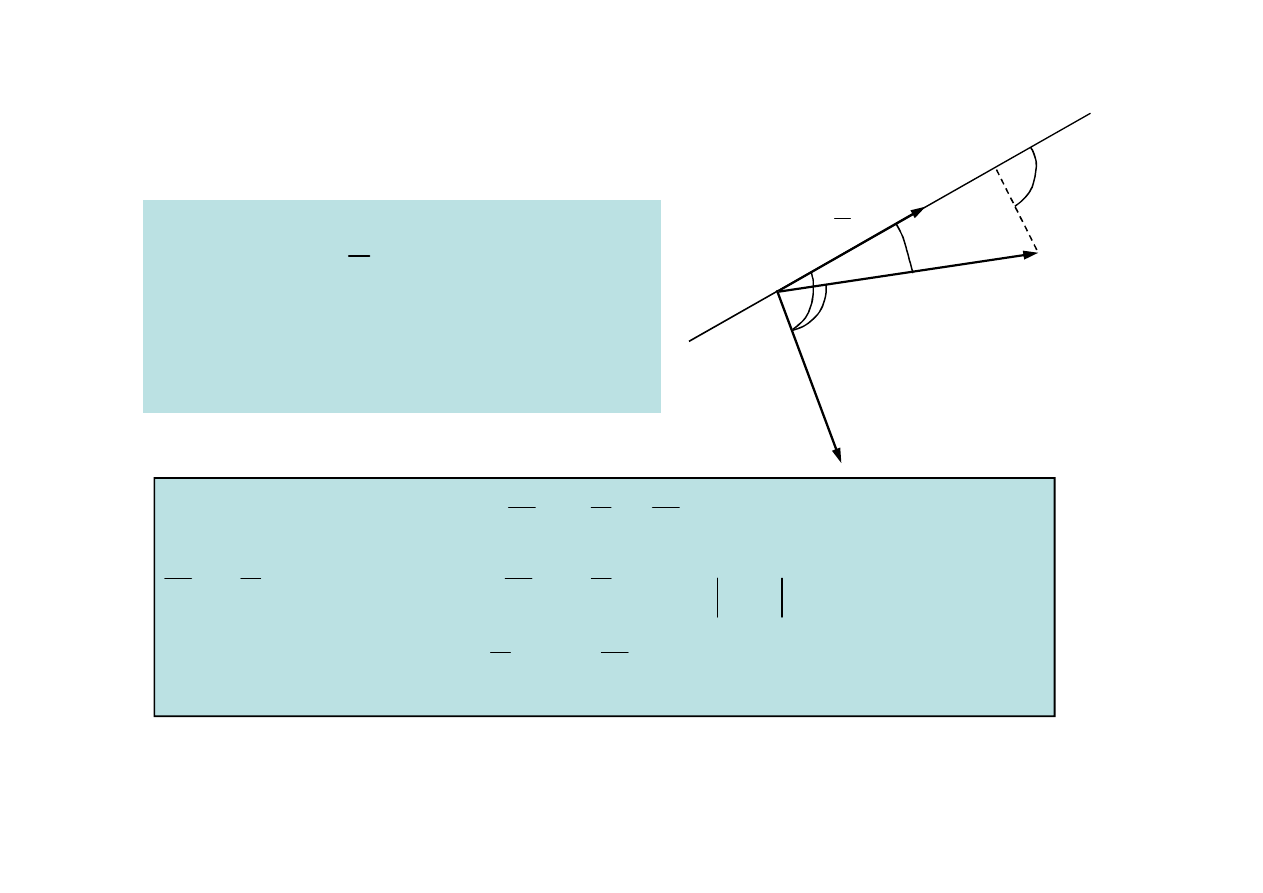
1.1. Moment siły względem punktu



































ną

prawoskręt

trójkę

stanowią

:

zwrot

:

wartość

:

kierunek

B

B

B

B

df

B

M

AB

F

AB

F

M

AB

M

F

M

AB

F

M

,

,

α

sin

|

|

|

|

|

|

:

____

____

____

____

B

M

___

____

AB

r

F

B

A

α

.

Definicja

Momentem siły względem punktu
nazywamy wektor równy iloczynowi
wektorowemu siły i wektora wyznaczone-
go przez punkt zaczepienia siły i punkt,
względem którego moment jest liczony

B

M

___

F

B

4

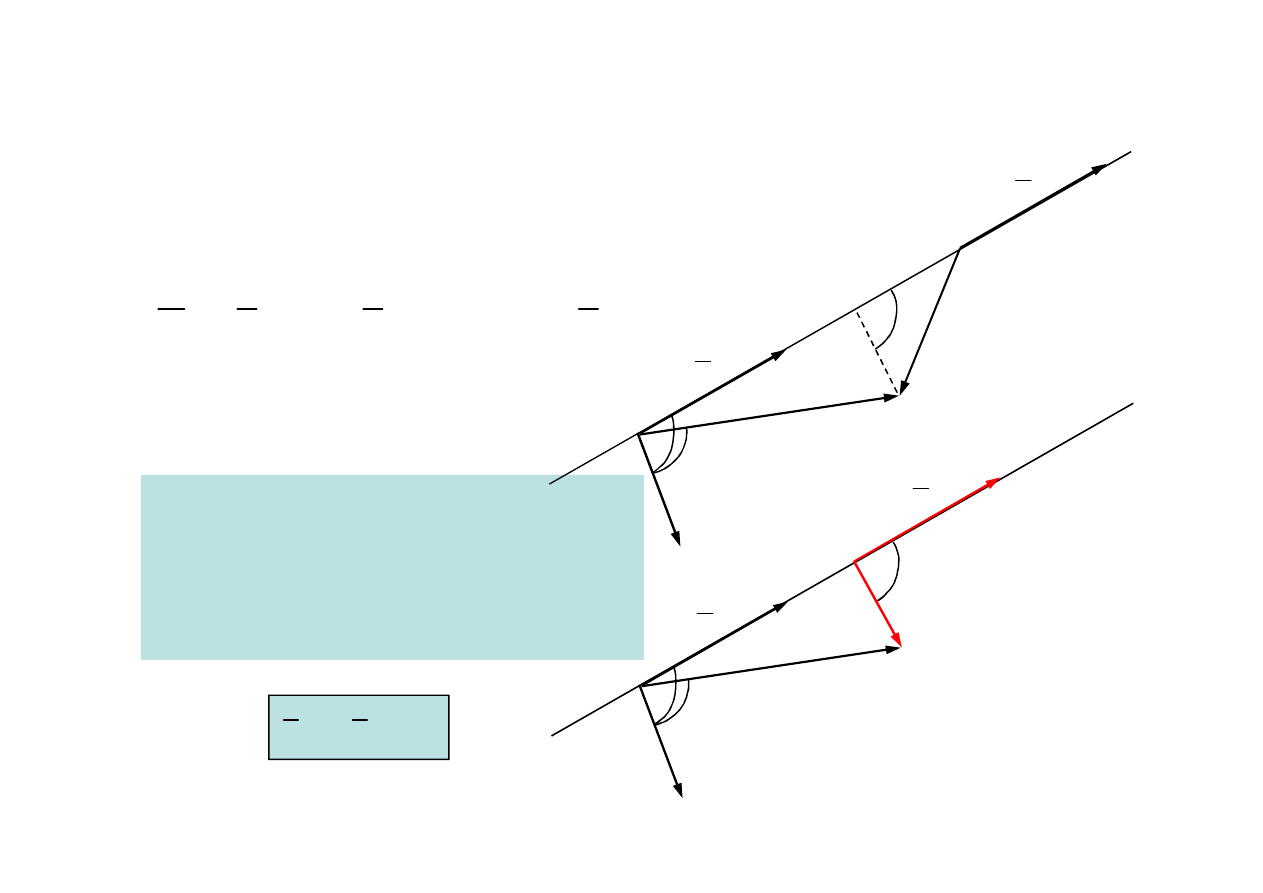
Przesunięcie siły wzdłuż jej kierunku działania

Przesunięcie siły wzdłuż jej kierunku działania nie wpływa
na zmianę wartości momentu siły względem punktu

_______

____

____

____

____

const

BR

F

BR

AB

F

AR

F

M

R

















)

(

Ramię działania siły

Jest to wektor prostopadły do prostej
działania siły, którego początek leży na
tej prostej a koniec w punkcie, względem
którego liczony jest moment siły

R

M

___

____

AR

r

F

R

A

.

B

F

____

BR

'

R

____

R

M

F

R' R





R

M

___

____

AR

F

R

A

.

F

____

' R

R

'

R

5

n

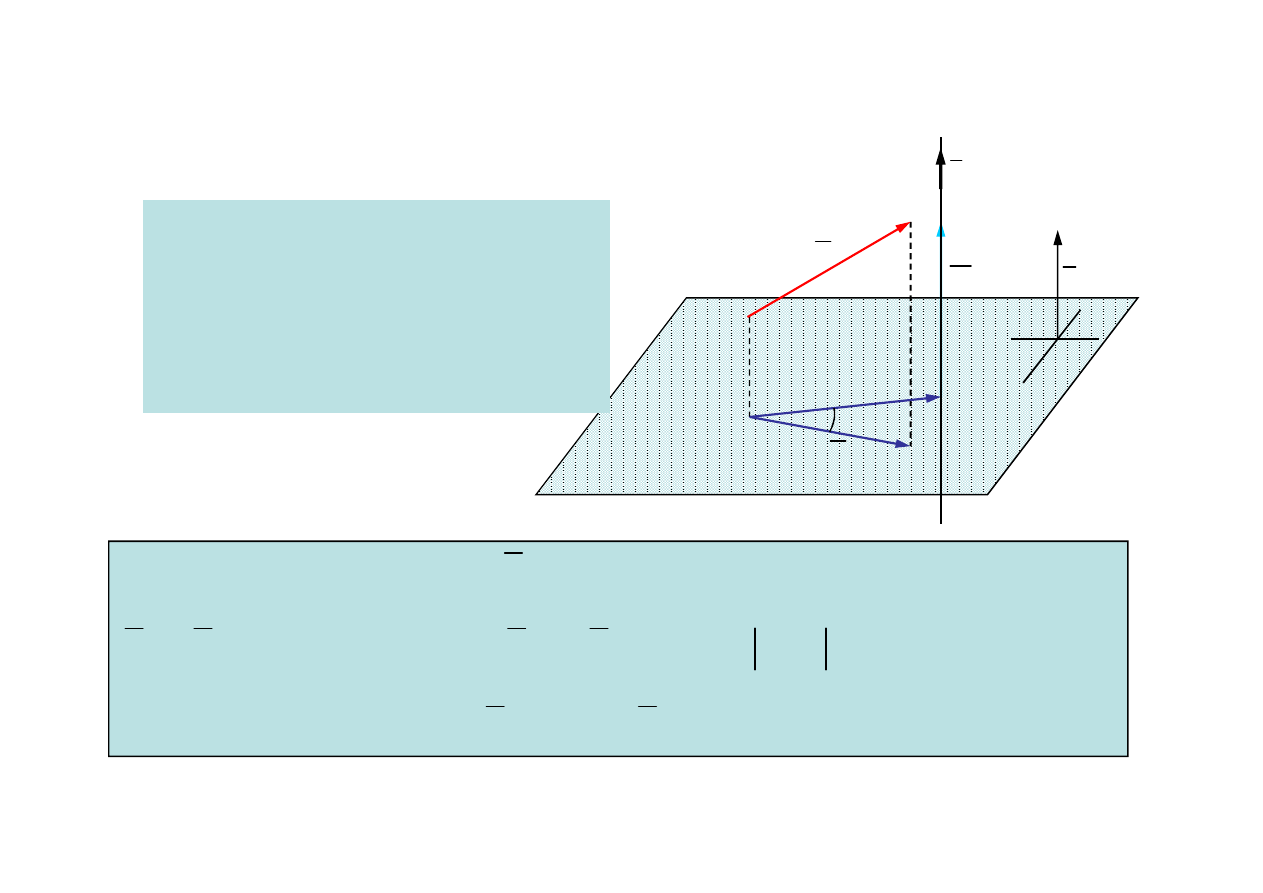
1.2. Moment siły względem prostej

____

____

π

π

____

π

||

'

:

|

| |

| |

'

| sin α

,

' ,

l

df

l

l

l

kierunek: M

l

M

F

A O

wartość: M

F

A O

zwrot:

F

A O M

stanowią trójkę prawoskrętną






















Definicja

Momentem siły względem prostej
nazywamy iloczyn wektorowy rzutu
siły na płaszczyznę prostopadłą do tej
prostej względem punktu przebicia
płaszczyzny przez tę prostą.

l

M

'

A

π

F

O



α

____

' O

A

F

l

e

A

6

l

M

n

α



____

' O

A

O

'

A

π

F

F

A

l

e

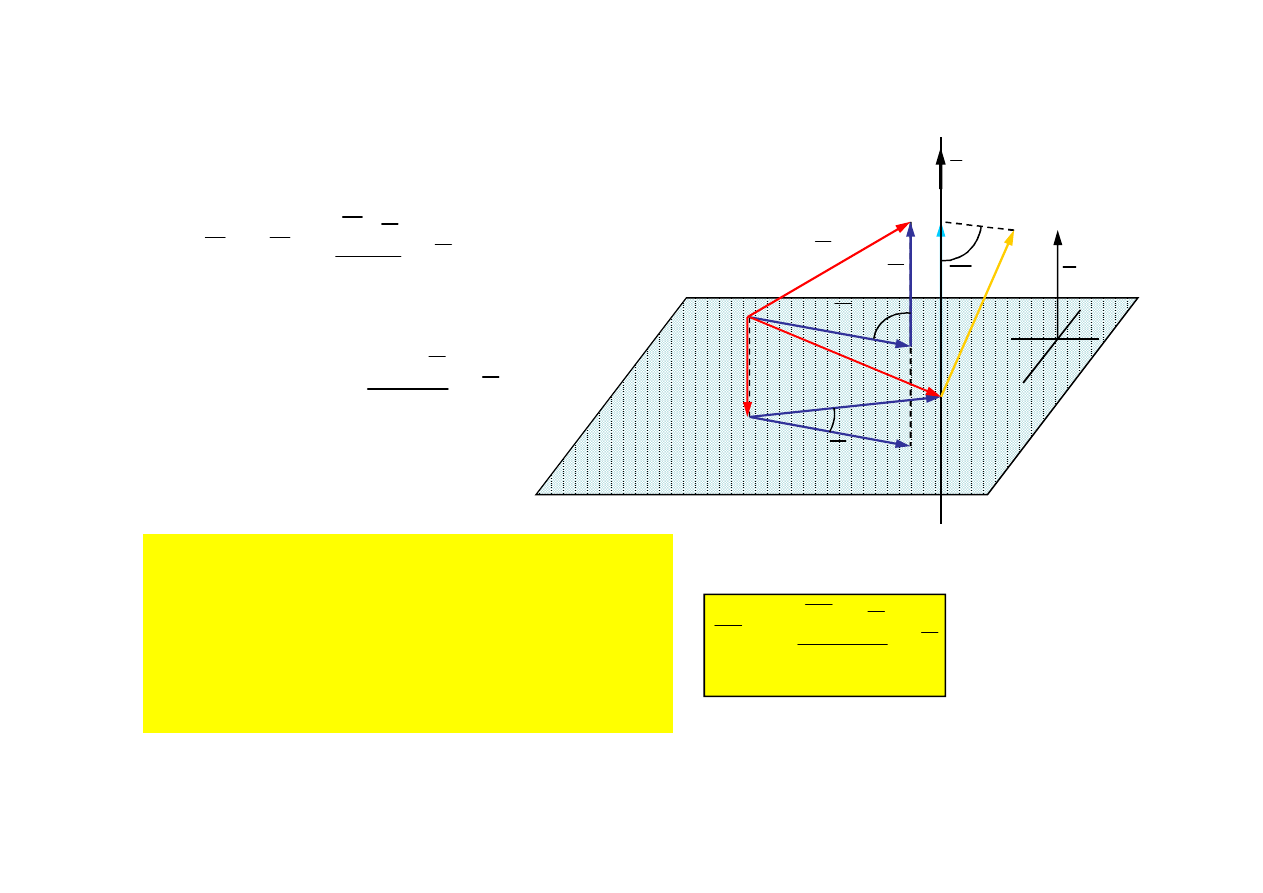
Twierdzenie

Moment siły względem prostej jest równy
rzutowi momentu siły względem dowolnego
punktu prostej na tę prostą.

Dowód pominięto

O

M

___

π

F

l

F

n

n

n

F

F

F





















2

π

n

n

n

AO

AO

O

A





























2

____

____

_____

'

n

n

n

M

M

O

l



















2

Twierdzenie o momencie siły względem prostej

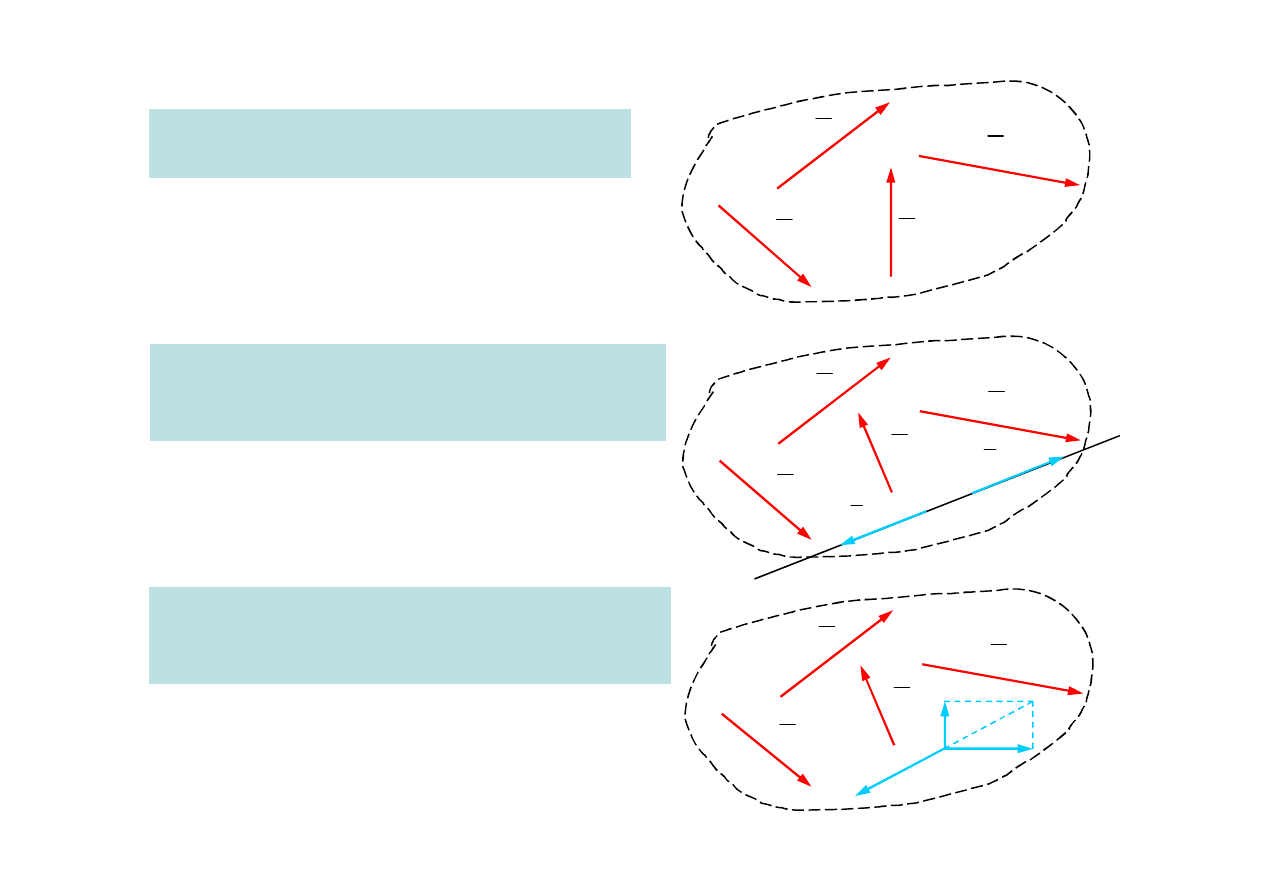
7

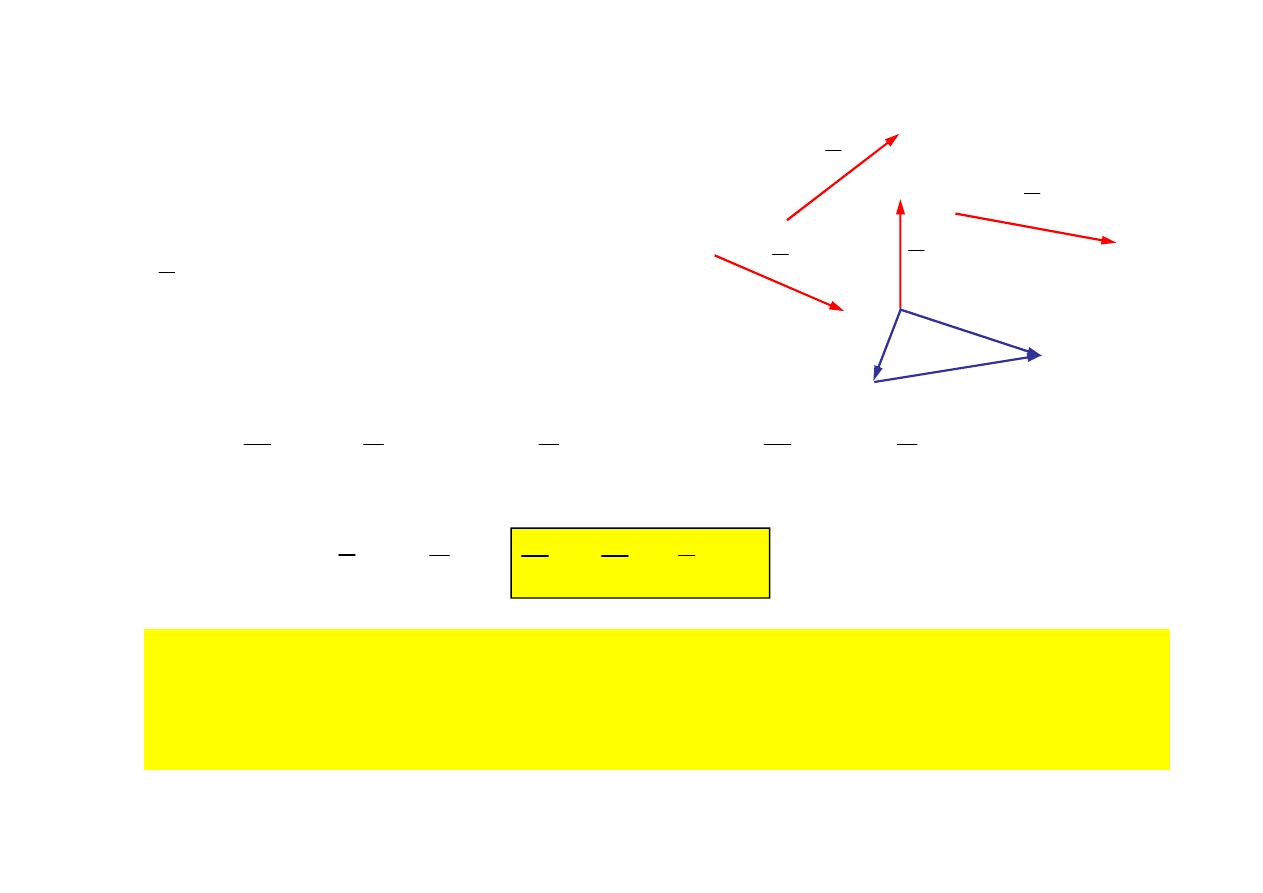
Układ sił
Zbiór sił wraz z punktami zaczepienia

n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F







Przekształcenie elementarne I-go rodzaju
Dodanie do układu lub odjęcie dwóch sił
przeciwnych działających wzdłuż prostej

Przekształcenie elementarne II-go rodzaju
Dodanie do układu lub odjęcie układu sił
zbieżnych o sumie równej 0

n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F







n

A

2

F

1

A



i

A

2

A

i

F

1

F

n

F









Przekształcenia elementarne nie zmieniają
sumy i momentu układu



F



0



F

0

8

1.3. Twierdzenie o zmianie bieguna

____

____

____

____

BR

F

M

BR

B

A

F

R

A

F

M

n

i

i

B

n

i

i

i

n

i

i

i

R











































1

1

1

)

(

i

A

n

A



2

F

1

A



i

A

2

A

B 

R

i

F

1

F

n

F

Układ

n sił

B

R

i

F

- punkt zaczepienia siły

- siła
- biegun redukcji

- nowy biegun redukcji







n

i

i

df

F

S

1

____

BR

S

M

M

B

R







Twierdzenie

Moment układu sił względem nowego bieguna jest równy sumie momentu tego układu
względem starego bieguna i iloczynu wektorowego sumy układu i wektora łączącego
stary biegun z nowym.

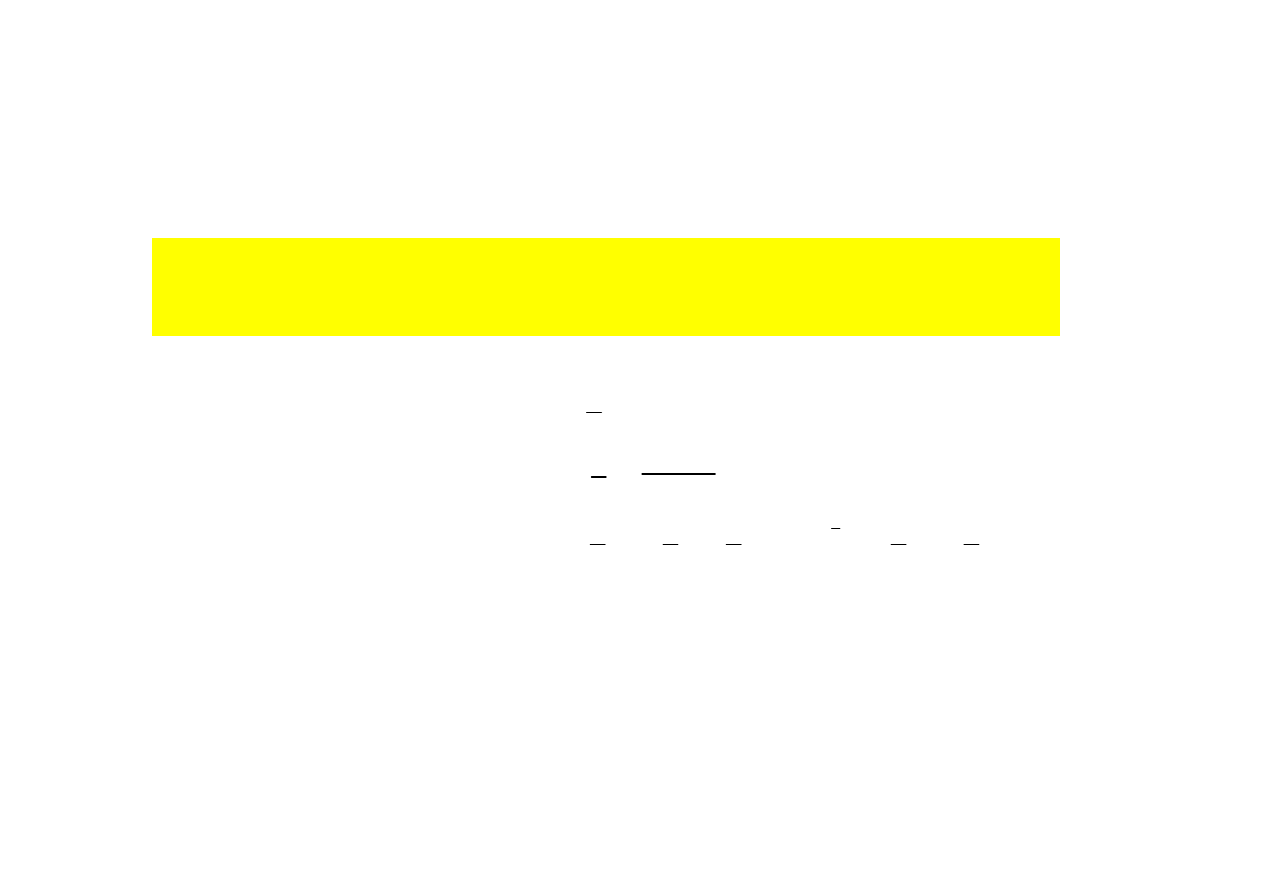
9

Wniosek 1
Jeżeli suma układu jest równa 0 to moment układu jest stały, tzn. nie zależy
od bieguna, względem którego jest liczony

Wnioski z twierdzenia o zmianie bieguna

Z: Suma układu jest równa 0

S  0

T: Moment układu jest stały

M

co n s t



D:

____

S

B

A

B

A

M

M

S

AB

M

M













0

10

Wniosek 2
Jeżeli momenty układu liczone względem trzech niewspółliniowych punktów są
równe to suma układu jest równa 0

Z: Punkty A, B, C są niewspółliniowe

0





____

____

AC

AB

oraz

C

B

A

M

M

M





T: Suma jest równa 0

0



S

D:

0

0

0















































S

AC

S

AB

S

AC

S

M

M

AB

S

M

M

A

C

A

B

____

____

____

____

Wniosek 3
Iloczyn skalarny sumy i momentu liczonego względem
dowolnego punktu jest dla danego układu sił wielkoś-
cią stałą i nosi nazwę parametru układu sił

const

S

M

K

O

df







S

M

OA

S

S

S

M

S

OA

S

M

S

M

O

O

O

A

























)

(

)

(

____

____

D:

11

1.4. Równoważność układów sił

O równoważności układu wektorów (sił) można mówić wyłącznie w odniesieniu
do rozważanego problemu. W mechanice teoretycznej rozważa się równoważność
układów sił w odniesieniu do problemu redukcji.

punkt

dowolny

)

(

)

(

)

(

)

(

O

O





















O

M

M

S

S

df

B

A

B

A

B

A

:

















n

i

n

i

A

A

A

A

F

F

F

F

...

...

...

...

2

1

2

1

A

















m

i

m

i

B

B

B

B

R

R

R

R

...

...

...

...

2

1

2

1

B

Dwa układy

i

są równoważne, jeżeli można, wykonując na jednym z nich skończoną liczbę
przekształceń I-go i II-go rodzaju, przekształcić jeden układ w drugi.

Definicja równoważności układów sił

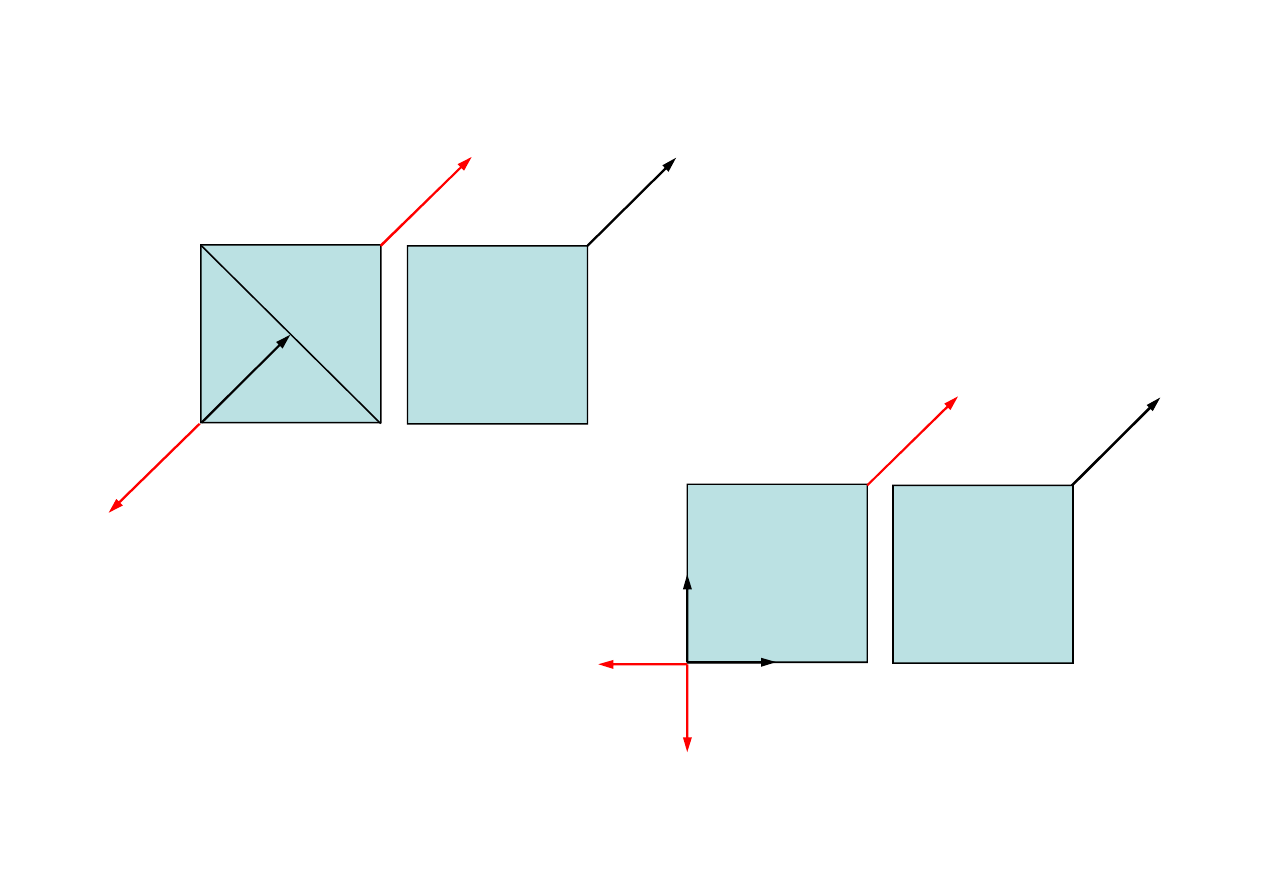
12

Równoważne układy sił

Równoważne układy sił

Przekształcenie elementarne
I

–go rodzaju

Przekształcenie elementarne
II

–go rodzaju

13

Twierdzenia o równoważności układów sił

Twierdzenie 1
Dwa układy są równoważne, gdy mają równe sumy i równe momenty liczone względem
jednego (ustalonego) punktu.

Z:

oraz

)

)

B

A

(

(

O

O

M

M



T:

D:

)

)

B

A

(

(

S

S



B

A 

)

(

)

(

OO'

)

(

)

(

)

(

OO'

)

(

)

(

)

(

O'

O'

O

O'

O

O'

B

A

B

B

B

A

A

A

M

M

S

M

M

S

M

M



























____

____

Dowód

14

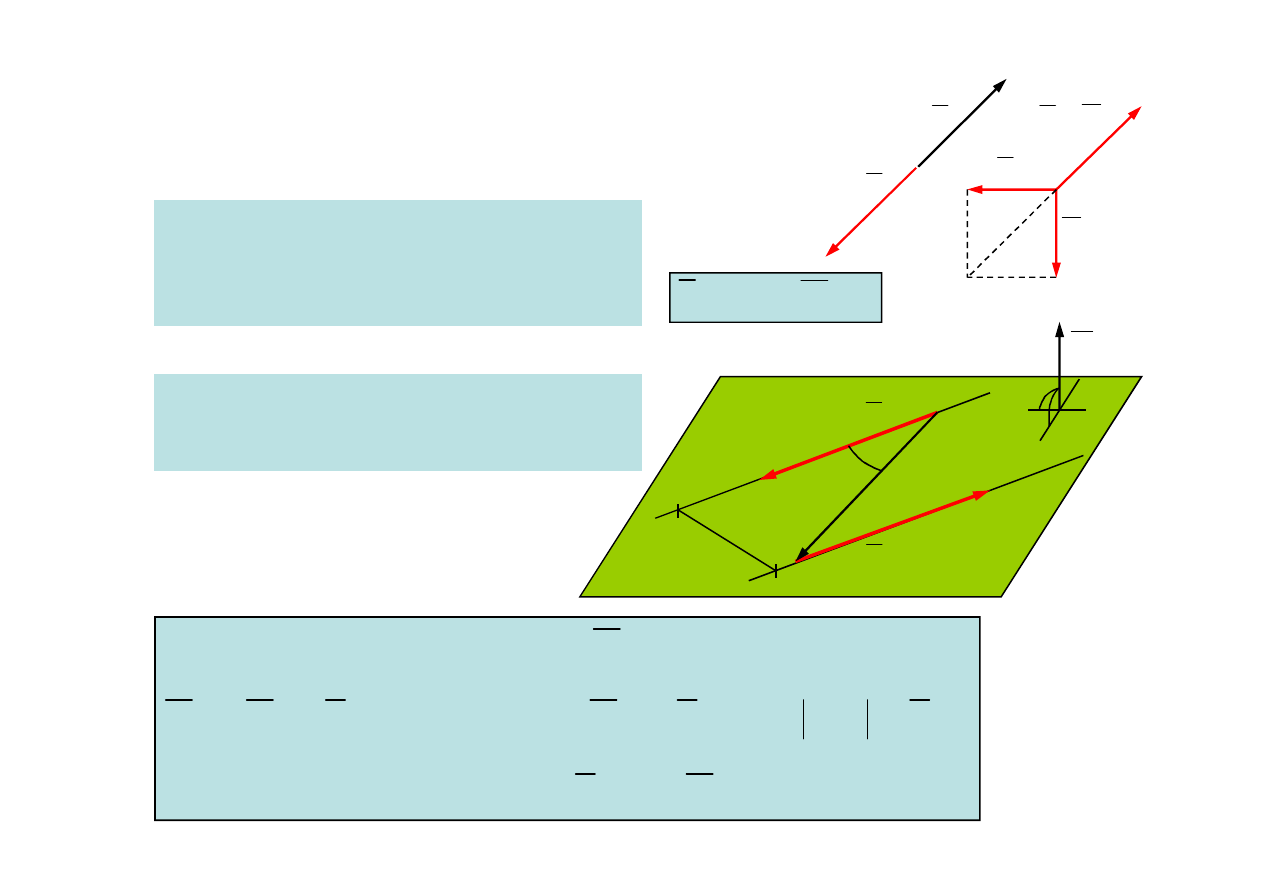
Twierdzenie 2
Dwa układy są równoważne, gdy mają (odpowiednio) równe momenty liczone
względem trzech niewspółliniowych punktów.

oraz

)

)

B

A

(

(

O

O

M

M



T:

D:

)

)

B

A

(

(

S

S



B

A 

____

____

____

____

OO"

)

(

)

(

)

(

OO"

)

(

)

(

)

(

OO'

)

(

)

(

)

(

OO'

)

(

)

(

)

(

O

O"

O

O"

O

O'

O

O'





























B

B

B

A

A

A

B

B

B

A

A

A

S

M

M

S

M

M

S

M

M

S

M

M

Dowód

Z: Punkty O, O’, O” są niewspółliniowe

)

)

B

A

(

(

O'

O'

M

M



)

)

B

A

(

(

O"

O"

M

M



czyli









0

)

(

-

)

(

OO"

do

równoległy

jest

nie

OO'

0

OO"

)

(

-

)

(

0

OO'

)

(

-

)

(

























B

A

B

A

B

A

S

S

S

S

S

S

____

____

____

____

15

1.5. Zerowy układ sił i para sił

Zerowy układ sił
Układ sił, którego suma i moment
liczony względem dowolnego punktu
jest wektorem zerowym.

Para sił
Układ dwóch niezerowych sił przeciw-
nych nie leżących na jednej prostej.

0

0







M

S

F

F



F

G

)

(

G

F 



































ne

prawoskręt

:

zwrot

:

wartość

:

kierunek

O

O

O

B

O

M

AB

F

d

F

AB

F

M

M

AB

F

M

M

,

,

|

|

α

sin

|

|

|

|

|

|

Π

:

____

____

____

F

A

B

F



O

M

0



d

Π

α

Część 2

REDUKCJA UKŁADU SIŁ

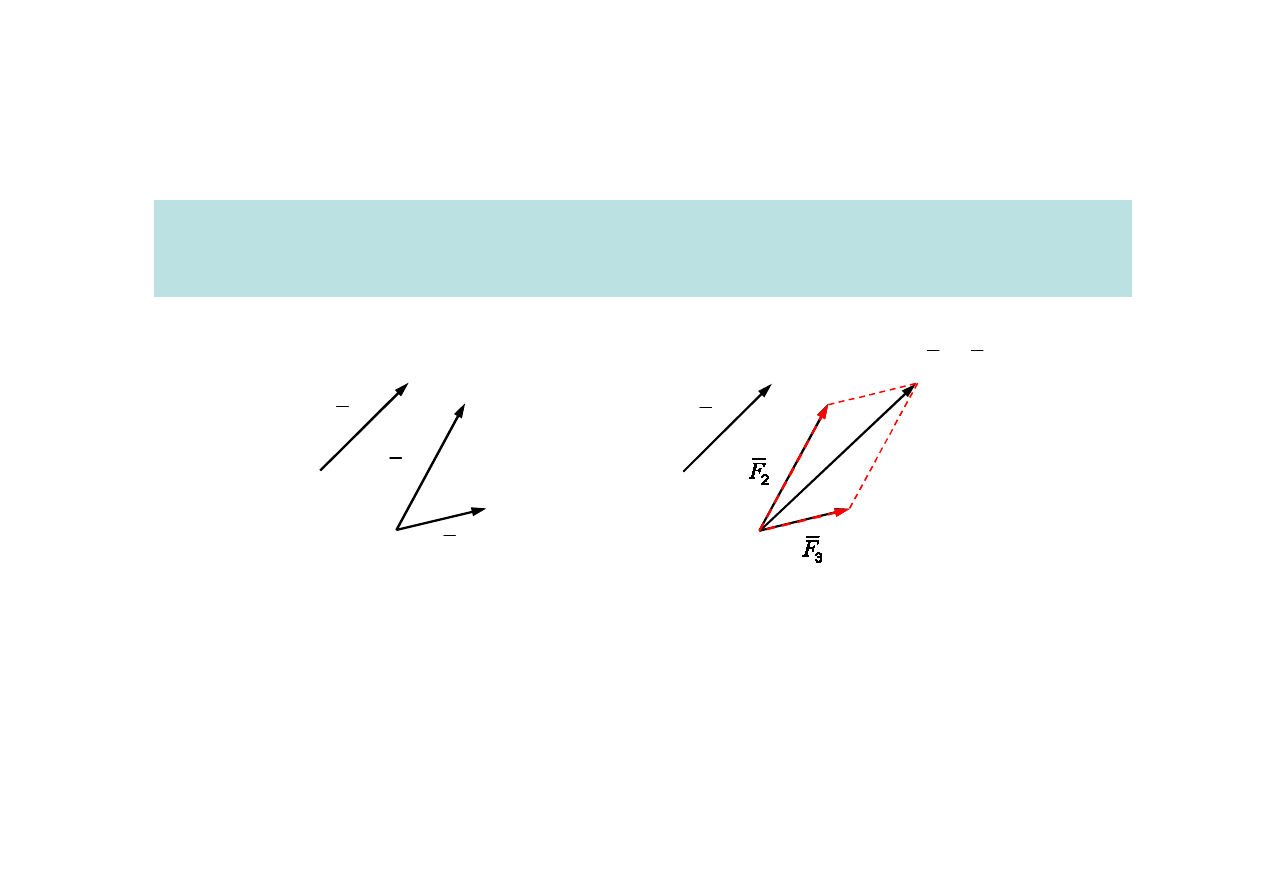
17

2.1. Redukcja układu sił w punkcie

Redukcja układ sił
Przekształcenie polegające na zastąpieniu danego układu sił równoważnym
układem prostszym, tj. złożonym z mniejszej liczby sił

F

1

F

2

F

3

F

1

F

F



2

3

F

2

F

3

Układ trzech sił

Układ równoważny,
zredukowany do dwóch sił

18

n

π

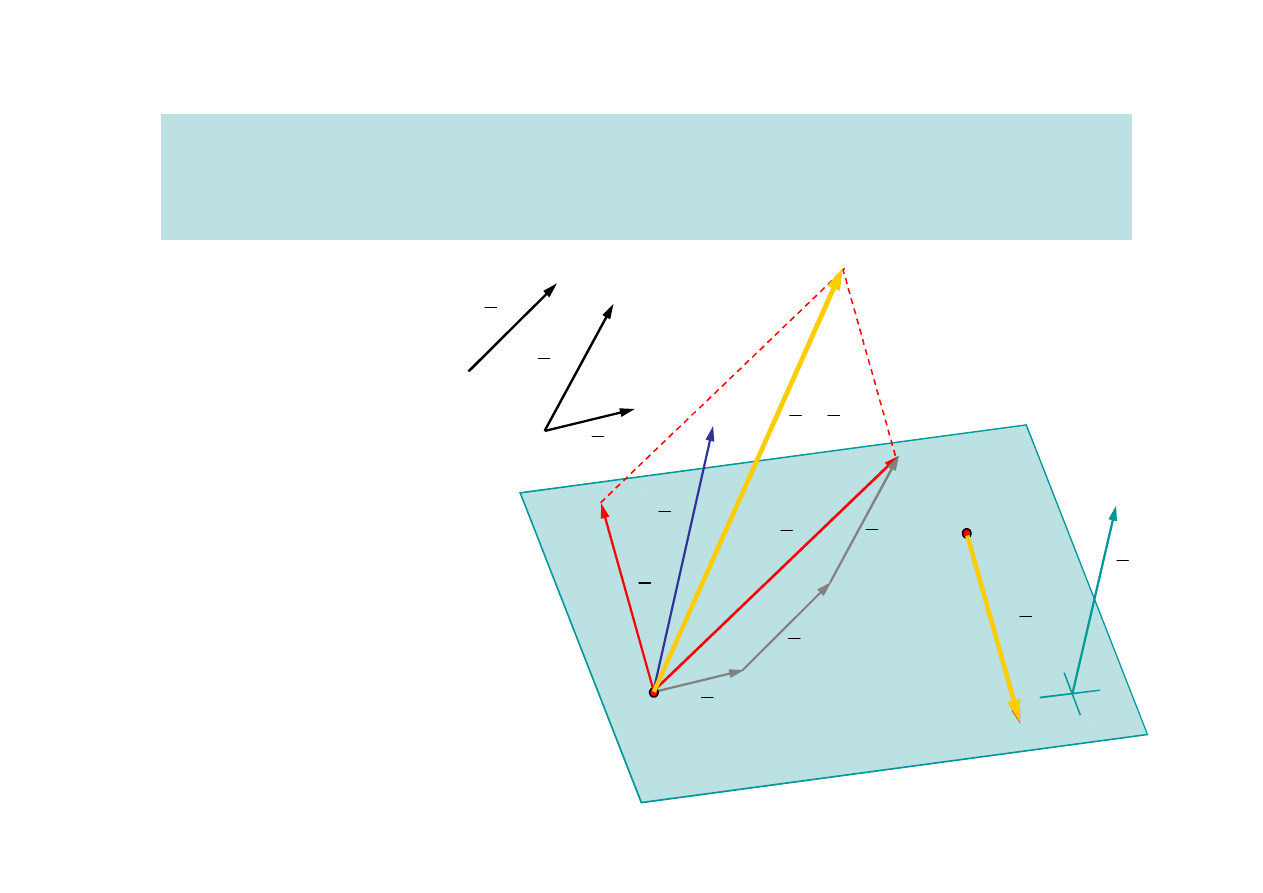
Redukcja w punkcie (w biegunie redukcji)
Zastąpienie danego układu układem równoważnym, złożonym z wektora równego
sumie układu i pary sił o momencie równym momentowi układu sił względem
bieguna redukcji

Tok postępowania:

F

1

F

2

F

3

S

F

3

F

1

F

2

O

F

F



G

O

M

S

F



1. Wybór bieguna redukcji O

2. Wyznaczenie

wektora

zaczepionego w punkcie O
równego sumie układu

3. Wyznaczenie

momentu układu

sił względem bieguna O

4. Wyznaczenie

pary sił o momencie

równym momentowi układu względem
bieguna redukcji, z których jedna jest
zaczepiona w biegunie redukcji

5. Redukcja układu do dwóch sił skośnych
poprzez dodanie sił zaczepionych w O

19

n

π

S

F

3

F

1

F

2

O

F

F



G

O

M

S

F



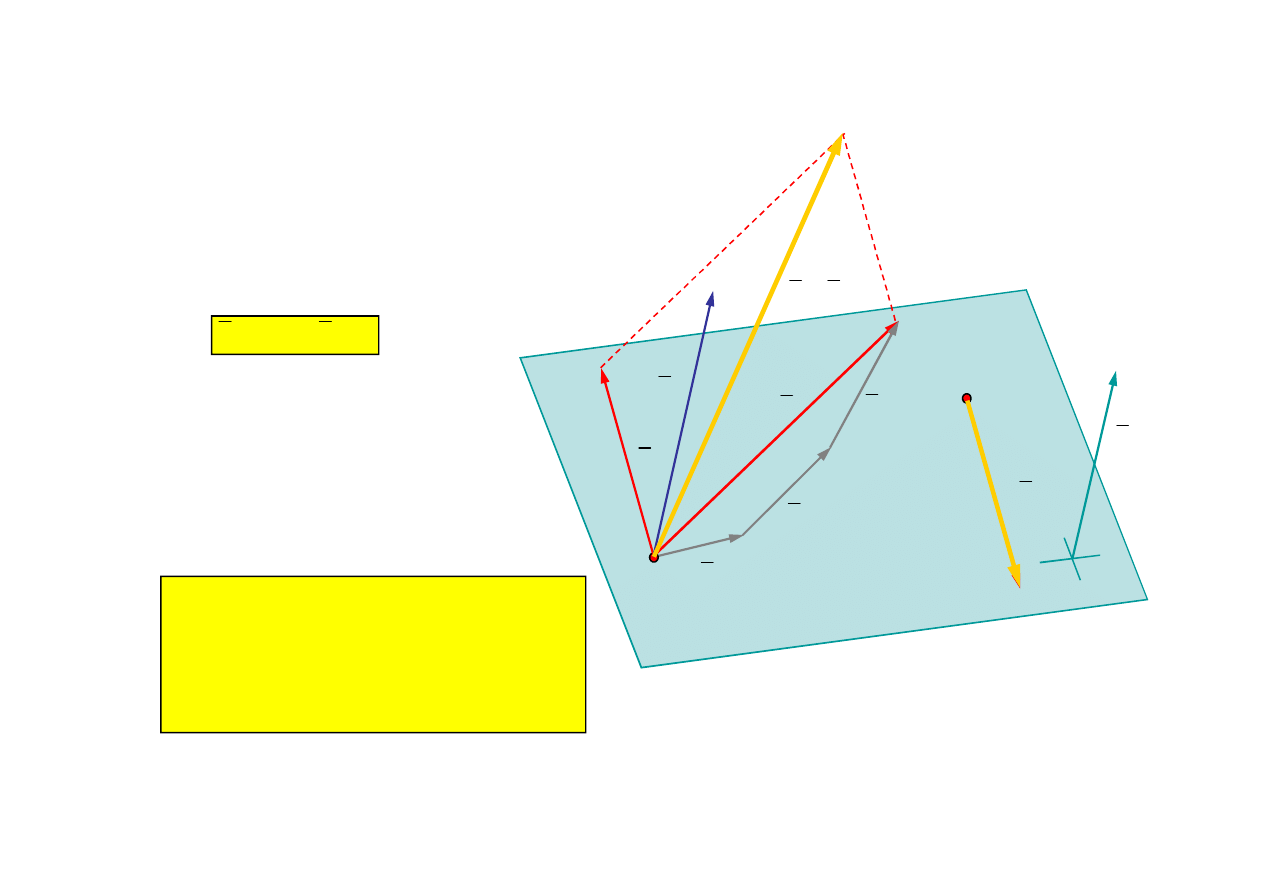
Cztery przypadki redukcji w punkcie

Przypadek 1 (ogólny):

S

M







0

0

Układ sił redukuje się do wektora
b = S zaczepionego w punkcie
redukcji oraz pary sił o momencie
M

O

równym momentowi układu sił

względem punktu redukcji

20

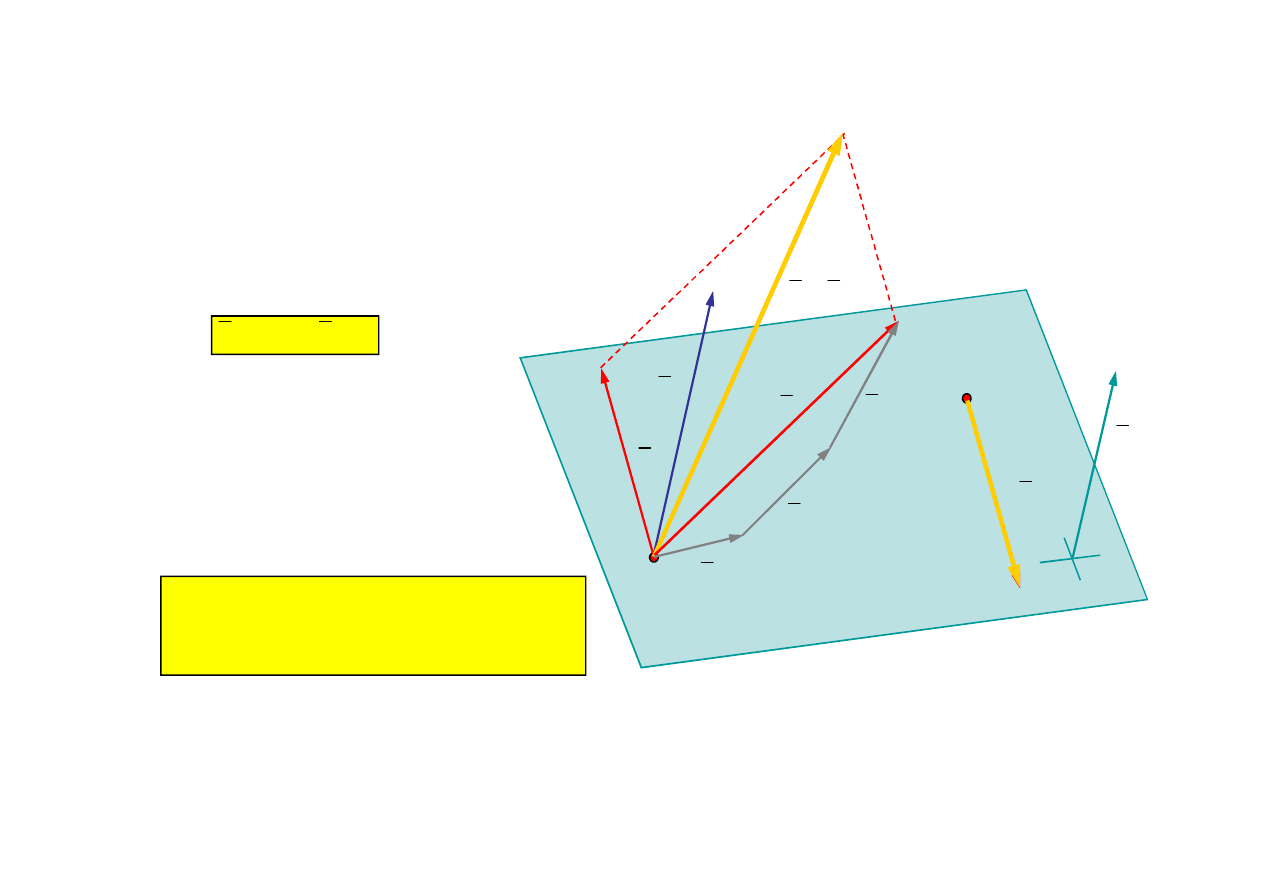
Cztery przypadki redukcji w punkcie - cd

Przypadek 2:

S

M







0

0

Układ sił redukuje się do wektora
b = S zaczepionego w punkcie
redukcji

n

π

O

F

F



G

O

M

S

F



S

F

3

F

1

F

2

21

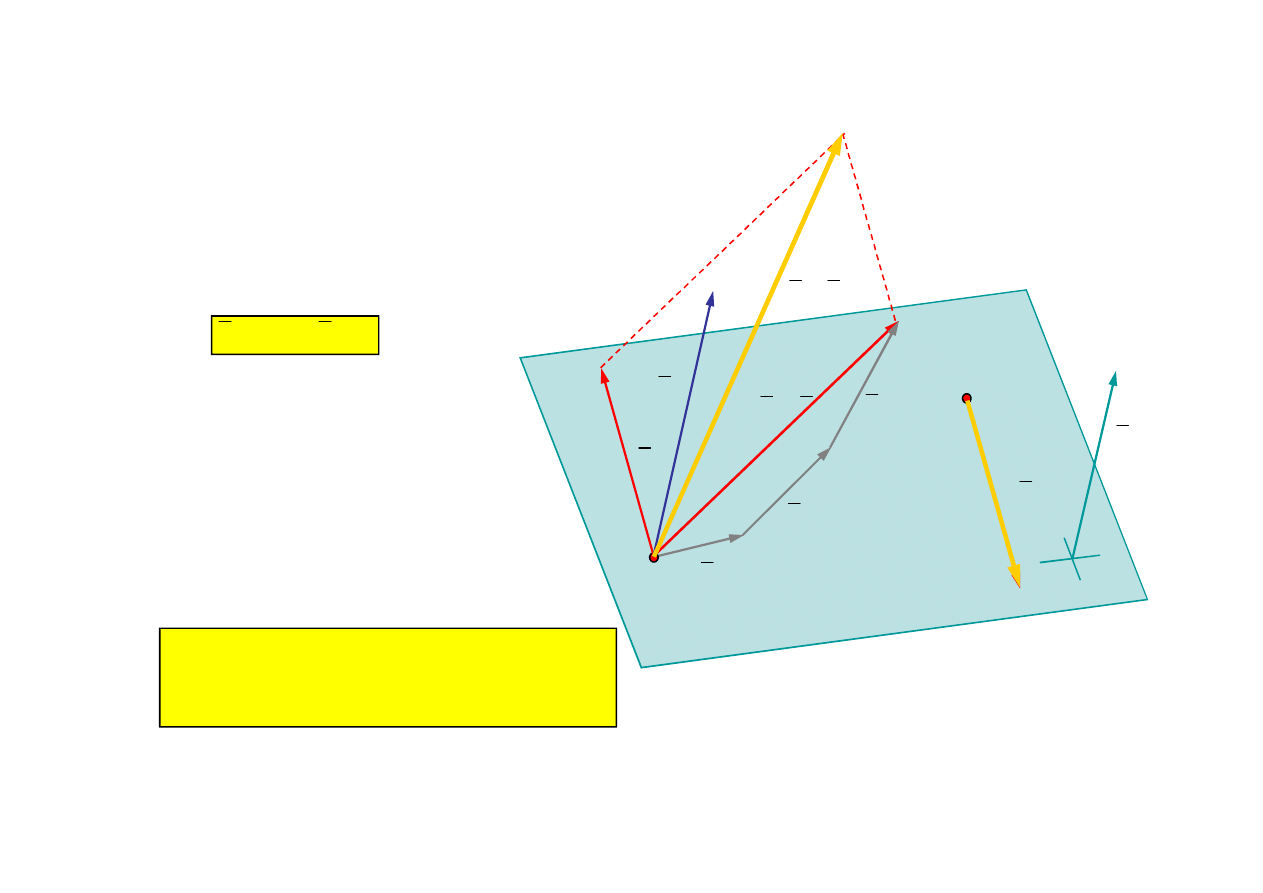
Cztery przypadki redukcji w punkcie - cd

Przypadek 3:

S

M







0

0

Układ sił redukuje się do pary sił
o momencie M

O

równym momentowi

układu sił względem punktu redukcji

n

π

b

S



F

3

F

1

F

2

O

F

F



G

O

M

S

F



22

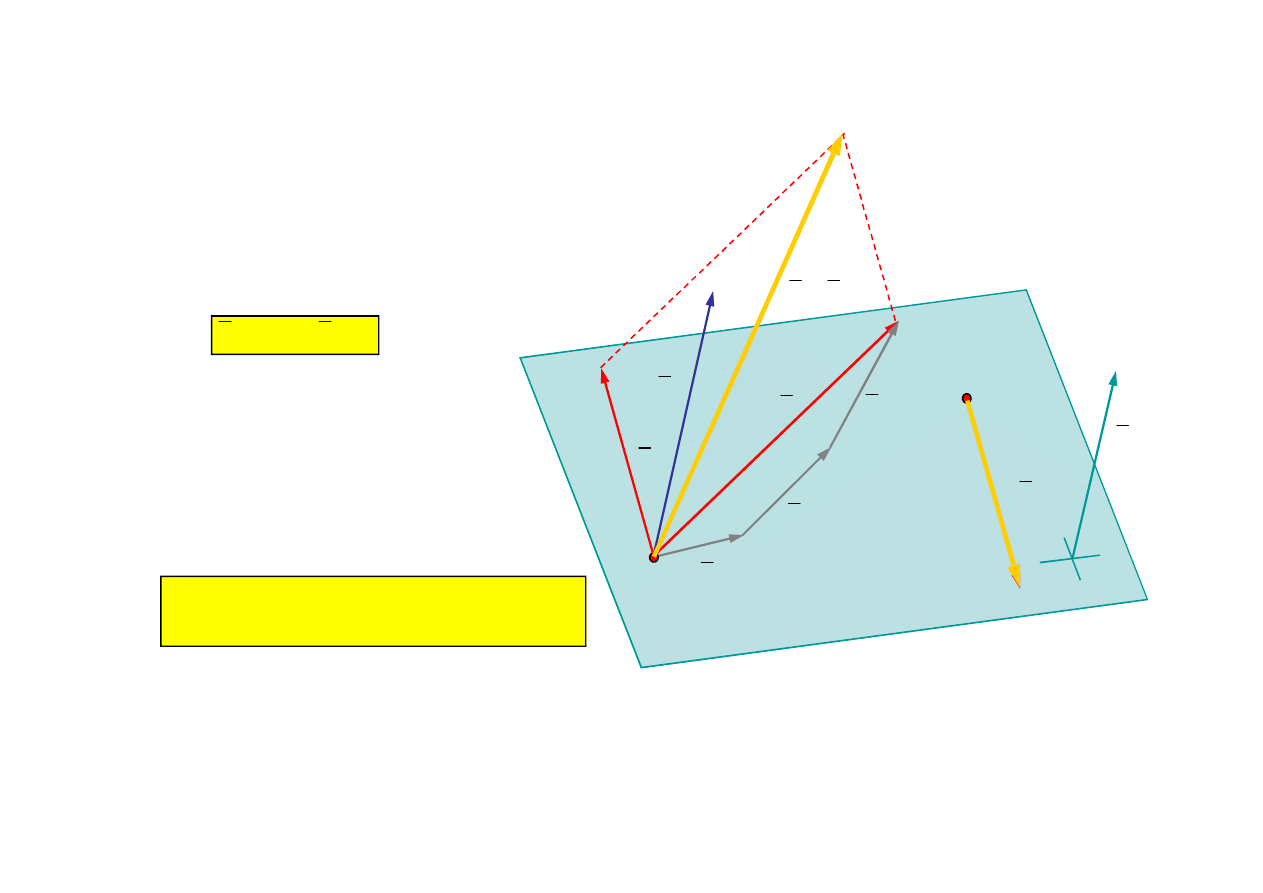
Cztery przypadki redukcji w punkcie - cd

Przypadek 4:

S

M







0

0

Układ sił redukuje się do układu
zerowego

n

π

S

F

3

F

1

F

2

O

F

F



G

O

M

S

F



23

2.2. Redukcja układu sił do najprostszej postaci

Redukcja układ sił do najprostszej postaci
Przekształcenie polegające na zastąpieniu danego układu sił układem
równoważnym złożonym z najmniejszej liczby sił

Redukcja w punkcie a redukcja do najprostszej postaci

W problemie redukcji w punkcie biegun redukcji jest znany (wybrany lub zadany)
natomiast w problemie redukcji do najprostszej postaci poszukuje się położenia
takich punktów, w których układ sił redukuje się do najprostszej postaci

24

Przypadek 1:

Jeżeli w wybranym lub zadanym biegunie redukcji układ sił redukuje się do układu
zerowego to układ zerowy jest najprostszym zredukowanym układem tego układu sił

O

S

M

O









0

0

wybrany punkt

Układ sił w każdym punkcie
redukuje się do

układu zerowego

Szczególne przypadki redukcji do najprostszej postaci

Przypadek 2:

Jeżeli w wybranym lub zadanym biegunie redukcji układ sił redukuje się do pary sił
o momencie równym momentowi układu sił względem bieguna redukcji to para sił jest
najprostszym zredukowanym układem tego układu sił

O

S

M

O









0

0

wybrany punkt

Układ sił w każdym punkcie
redukuje się do

pary sił

25

Przypadek ogólny: parametr układu jest różny od 0 – przykład:

Dany jest układ trzech sił:

























a

b

c

A

B

C





























1 2 3

1 1

1

3

2 1

0 0 1

1 1 1

1 1

1



 

 

 



S 











1 2 3

1 1

1

3

2 1

5 1 3





























O

M











 























1 2 3

1 1

1

3

2 1

5

1

5

0 0

1

1

1

1

1

1 1



 



O

K

S M













 

5 1 3

5

1

5

41



Suma układu:

Moment układu
względem punktu
(0, 0, 0):

Parametr układu:

Zadanie:

Jak zmienia się równoważny układ zredukowany w biegunie redukcji poruszającym
się wzdłuż wybranej prostej.

Równanie parametryczne
przypadkowo wybranej prostej:

x

λ , y

λ , z

λ





 

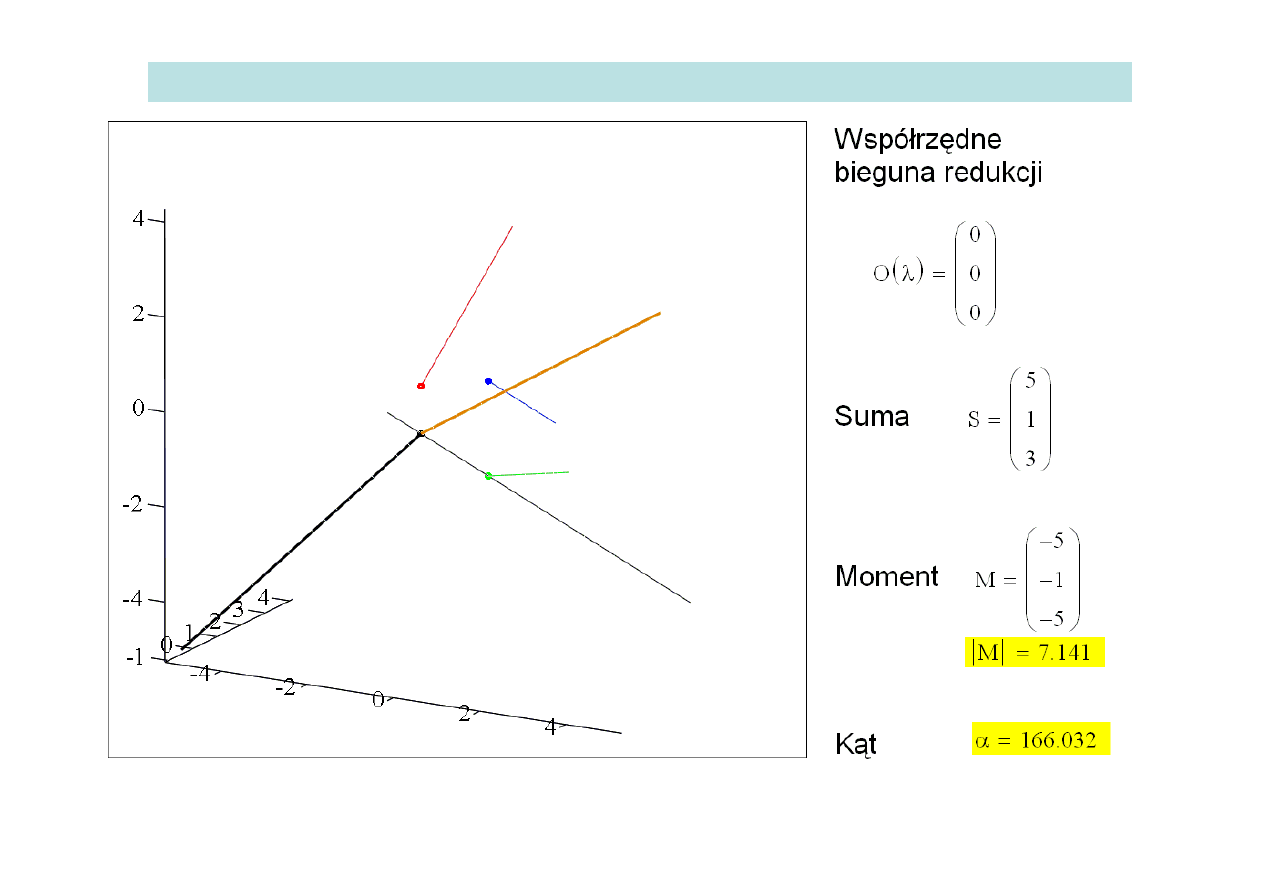
26

Rozwiązanie zadania przy l zmieniającym się w sposób ciągły od 0 do 3

27

Przypadek ogólny: parametr układu jest różny od 0 – rozważania teoretyczne





O

O

O

K

S M

S

M

cos

S ,M

const

















O

O

K

M

S cos

S ,M









O

O

M

min

S ,M

π







 



0





O

O

O

O

S

M

M

S

S ,M

K

M

S





















0:

O

K

M

S

S





2





O

O

O

O

S

M

M

S

S ,M

π

K

M

S



 











 





:

O

K

M

S

S





2

Punkty, w których układ sił o parametrze K różnym od 0 redukuje się do sumy i pary
sił o momencie równoległym do sumy leżą na prostej zwanej

osią środkową

Układ sił w punktach osi środkowej redukuje się do

skrętnika

28

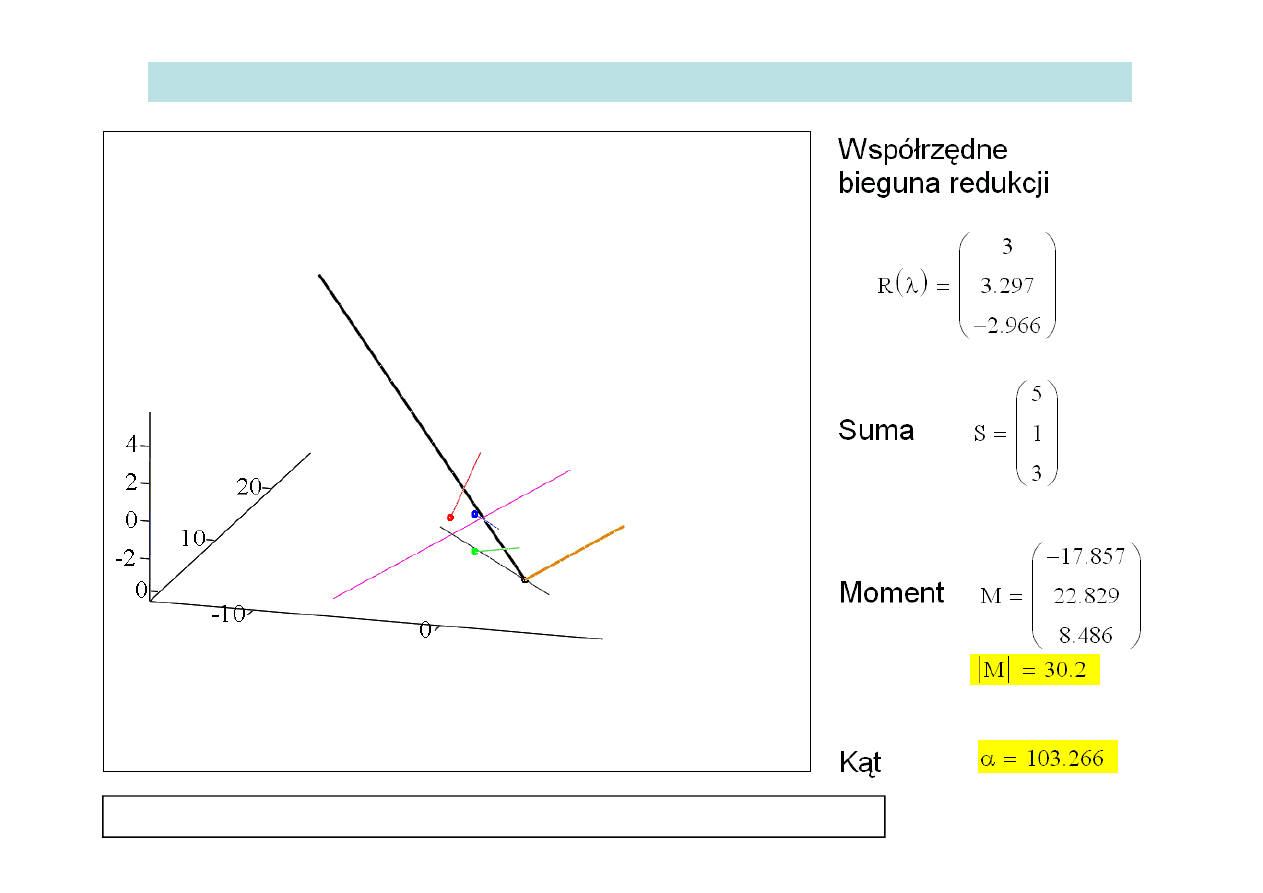
Przypadek ogólny: parametr układu jest różny od 0 – przykład:

Zadanie:

Wyznaczyć oś środkową układu sił z poprzedniego przykładu a następnie zilustrować
zmiany równoważnego układu zredukowanego gdy punkt redukcji porusza się po
prostej przecinającej się z osią środkową

W osi środkowej układ redukuje się do sumy i pary sił o momencie
równoległym do sumy i osiąga minimalną wartość (skrętnik):

R

K

M

S

S





2

Przyrównując odpowiednie współrzędne wyznacza się równanie krawędziowe lub
parametryczne osi środkowej









z

y

d

, gdzie d

x

z

d

 

























3

5 1

0

41

3

5

1

0

35









x

λ

y

λ

d

z

λ

d






























1

26

1

5

15

3

1

1

5

5

Wykorzystując twierdzenie o zmianie bieguna formułuje się wektorowe równanie
osi środkowej:





R

O

K

M

S

M

S

OR ,

R x, y, z

S











2

- punkt leżący na osi środkowej

29

Rozwiązanie zadania przy l zmieniającym się w sposób ciągły od 3 do 0

Uwaga: l  0 odpowiada punktowi leżącemu na osi środkowej

30

Przypadek 3:

Suma układu jest różna od zera a parametr jest równy 0

Trzeci szczególny przypadek redukcji do najprostszej postaci

Definicja wypadkowej:

Wypadkowa to układ sił równoważny danemu złożony z jednego wektora

Układ sił w każdym punkcie osi środkowej
redukuje się do jednego wektora

- wypadkowej

O

K

M

S

S







2

0

S

K







0

0

(moment układu jest zawsze prostopadły do sumy)

Wypadkowa działa wzdłuż ściśle określonej prostej (prosta działania wypadkowej,
oś środkowa) o tej własności, że moment układu względem punktów tej prostej jest
równy 0