Wykład 11

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

STATYKA UKŁADÓW KONSTRUKCYJNYCH

Część 1

Podpory

3

1.1. Definicja podpory

Definicja

W mechanice

podpora jest ciałem sztywnym stanowiącym więzy innych ciał.

W budownictwie

podpora jest elementem konstrukcyjnym przekazującym

obciążenia obiektu budowlanego na podłoże i ograniczającym jego ruch.

4

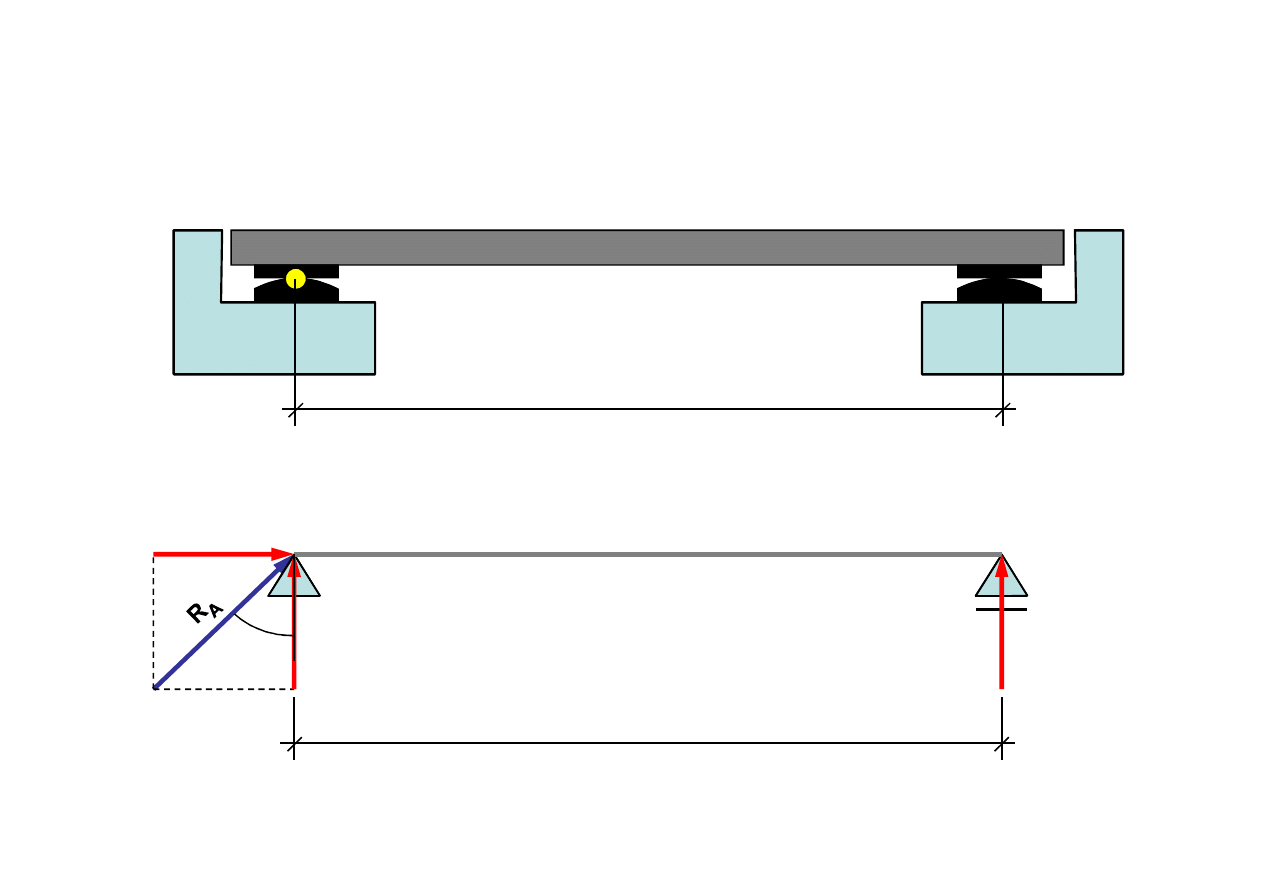
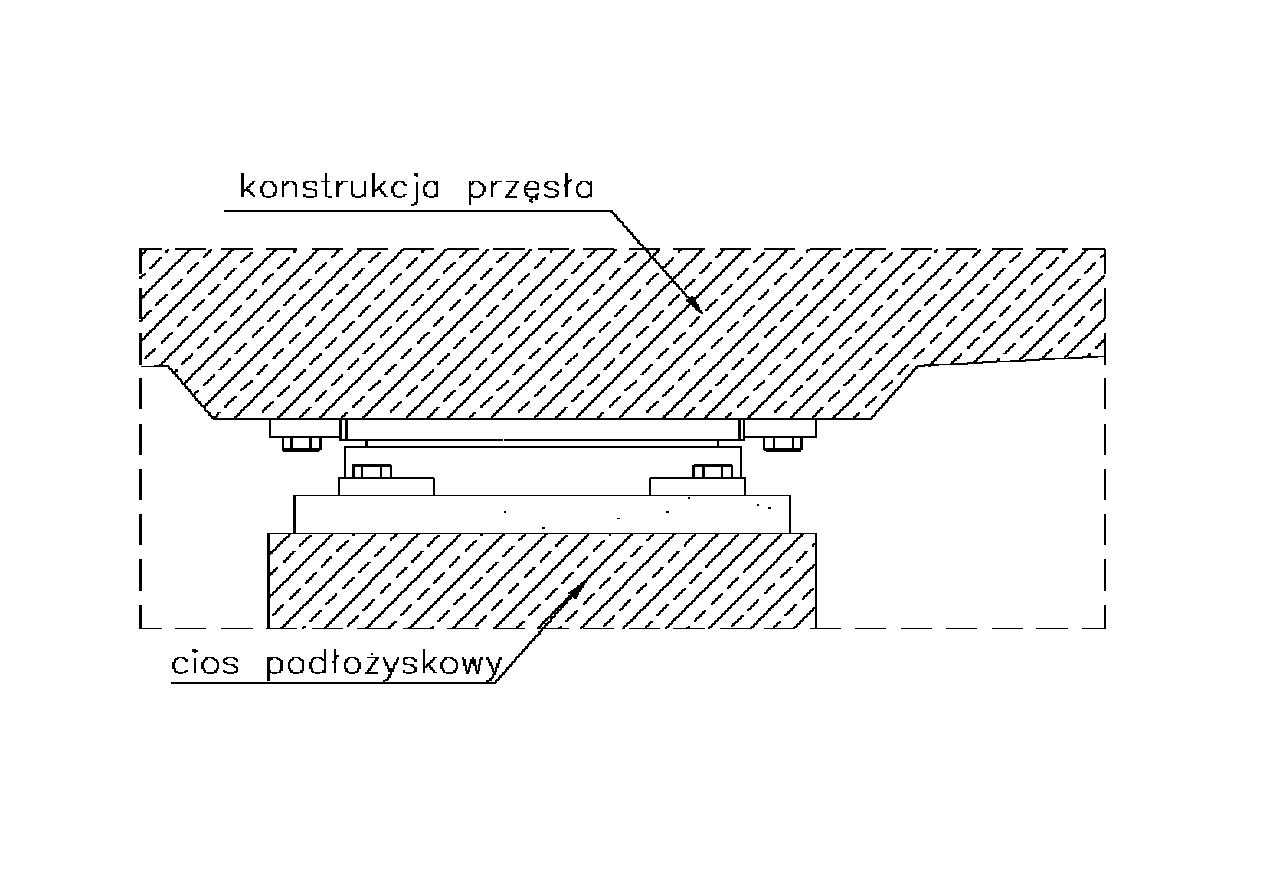
Łożysko stałe

1.2. Łożysko stałe i przesuwne

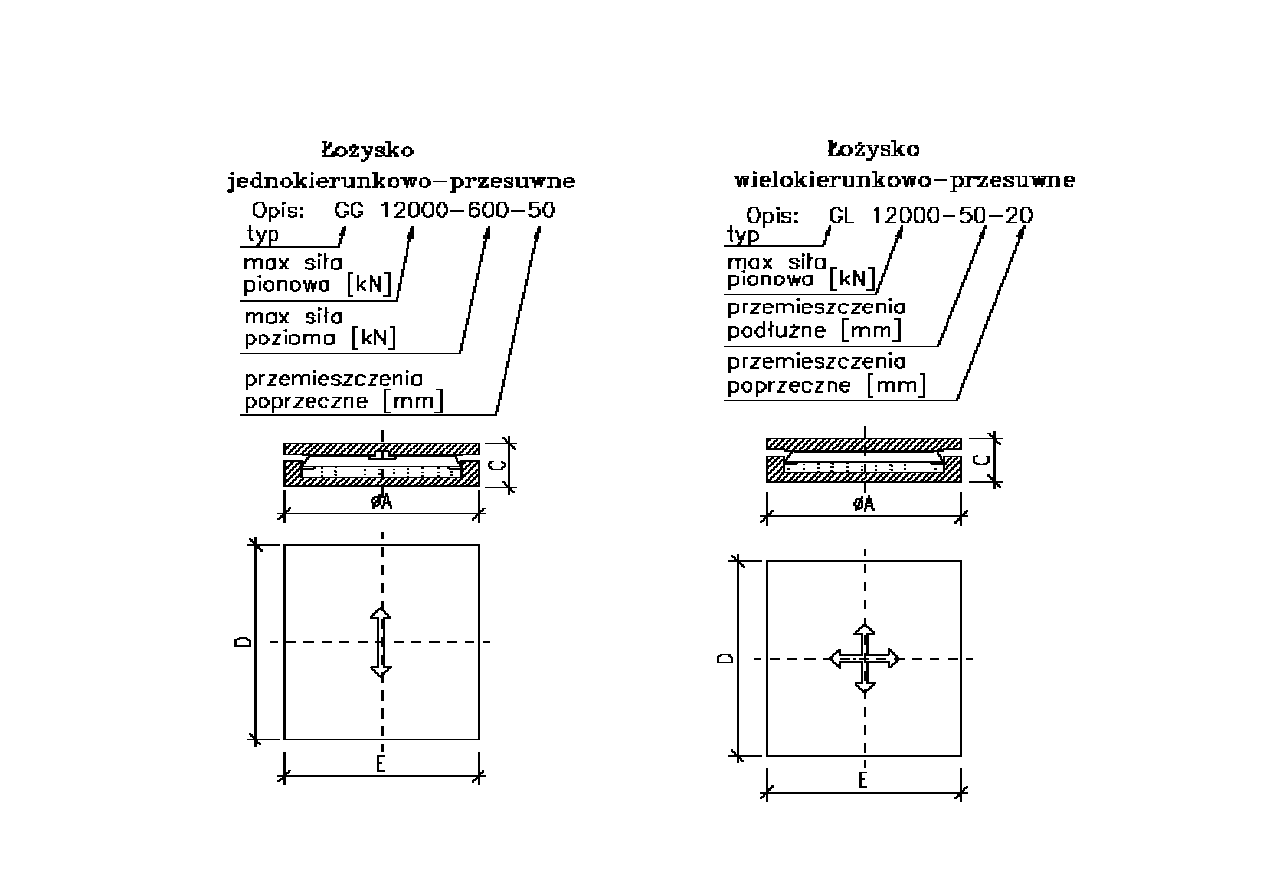
Łożysko przesuwne

A

B

H

A

V

A

R

B

L

Rozpiętość teoretyczna L

a

5

6

7

8

9

Długość teoretyczna L

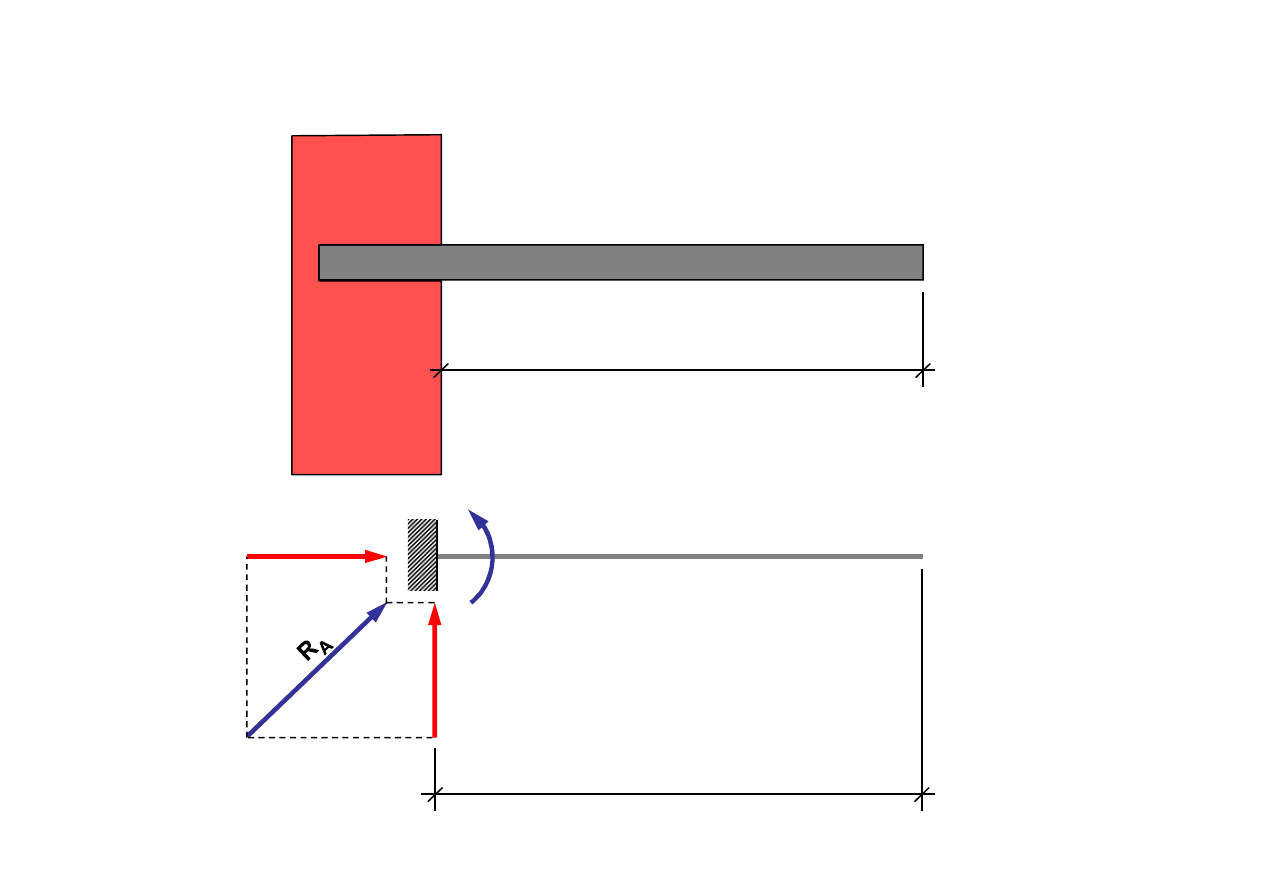
1.3. Utwierdzenie

Wspornik

A

H

A

V

A

L

M

A

10

11

12

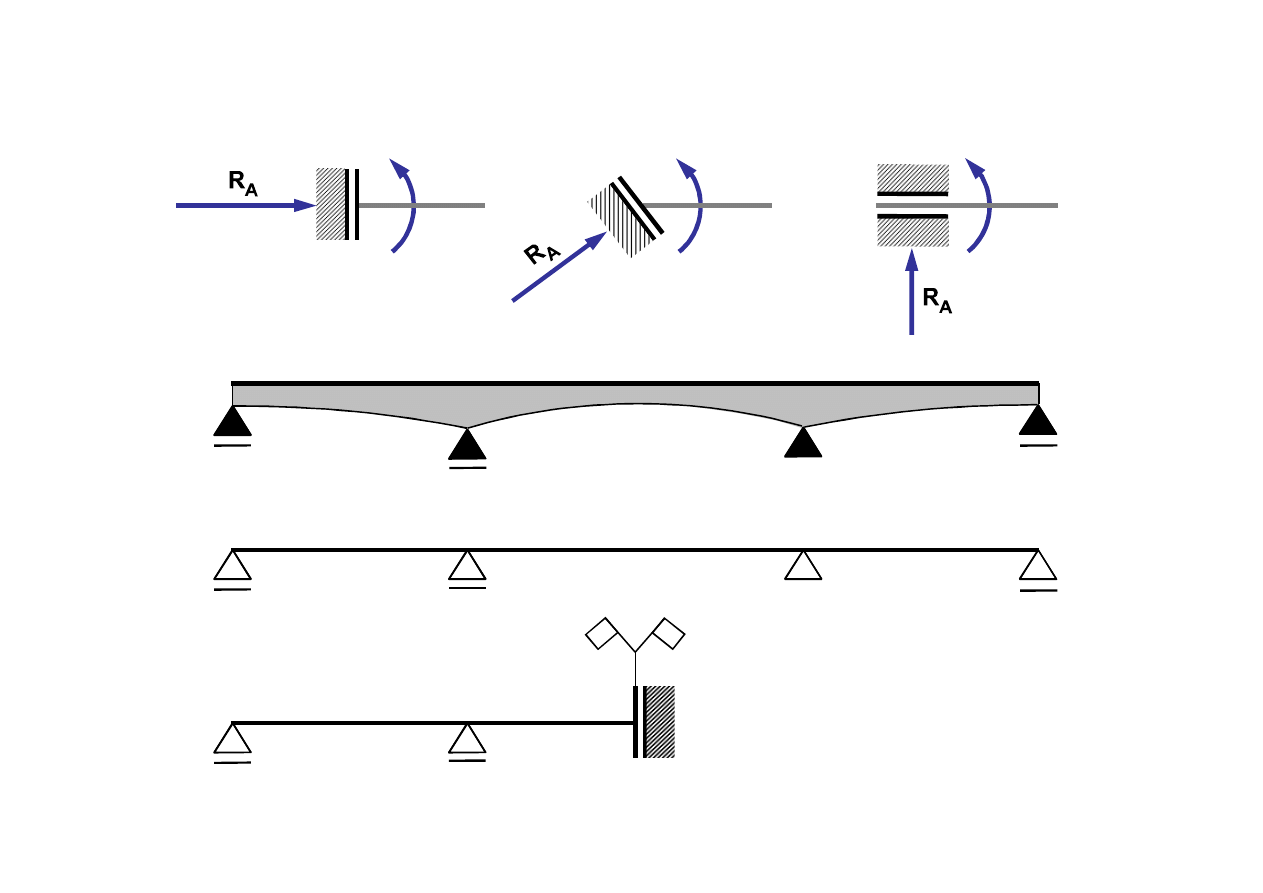
1.4. Utwierdzenie z przesuwem

Obiekt symetryczny i symetrycznie obciążony

Schemat statyczny

Schemat połówkowy

A

M

A

A

M

A

A

M

A

Część 2

Problem wyznaczalności układów konstrukcyjnych

14

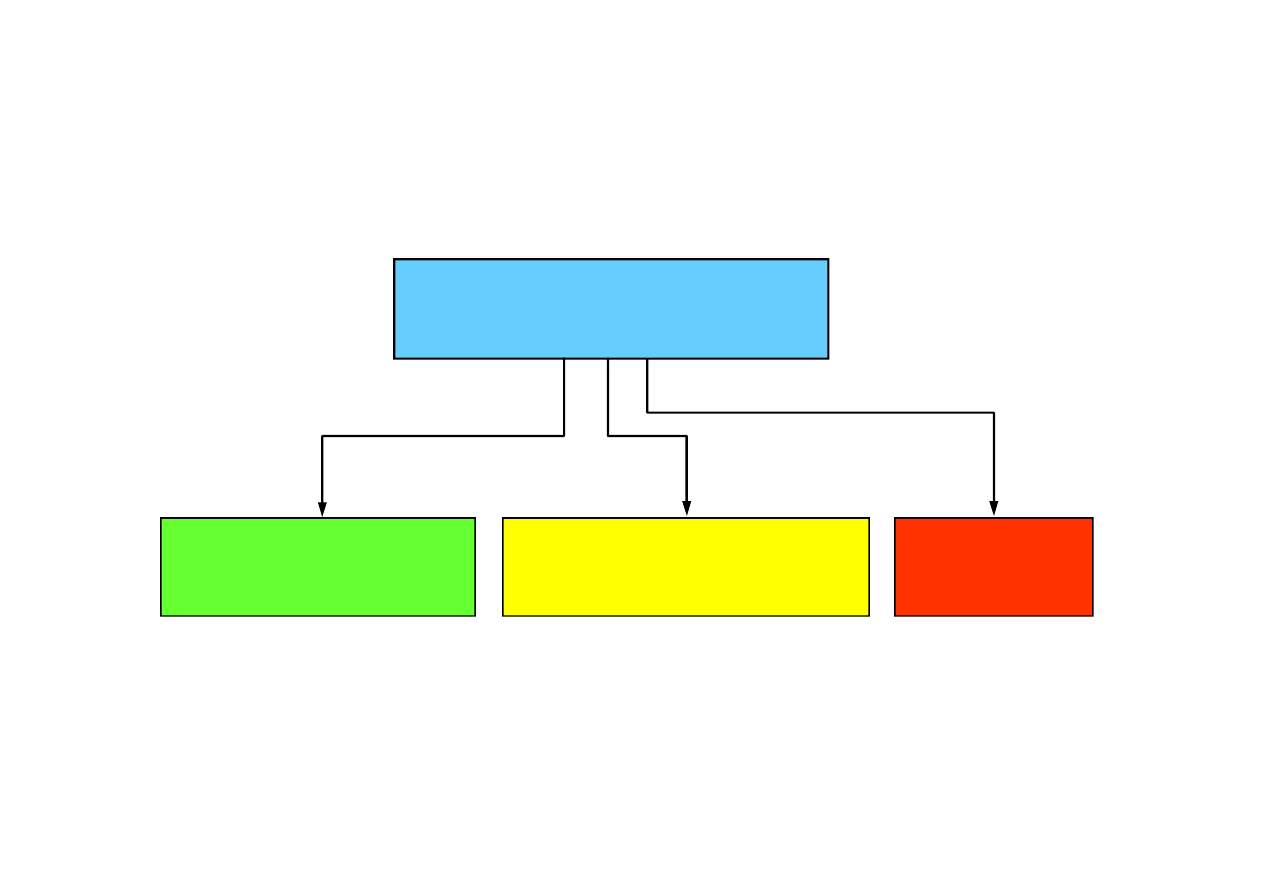
2.1. Klasyfikacja układów konstrukcyjnych ze względu

na wyznaczalność

Układy konstrukcyjne

Statycznie

wyznaczalne

Statycznie

niewyznaczalne

Chwiejne

15

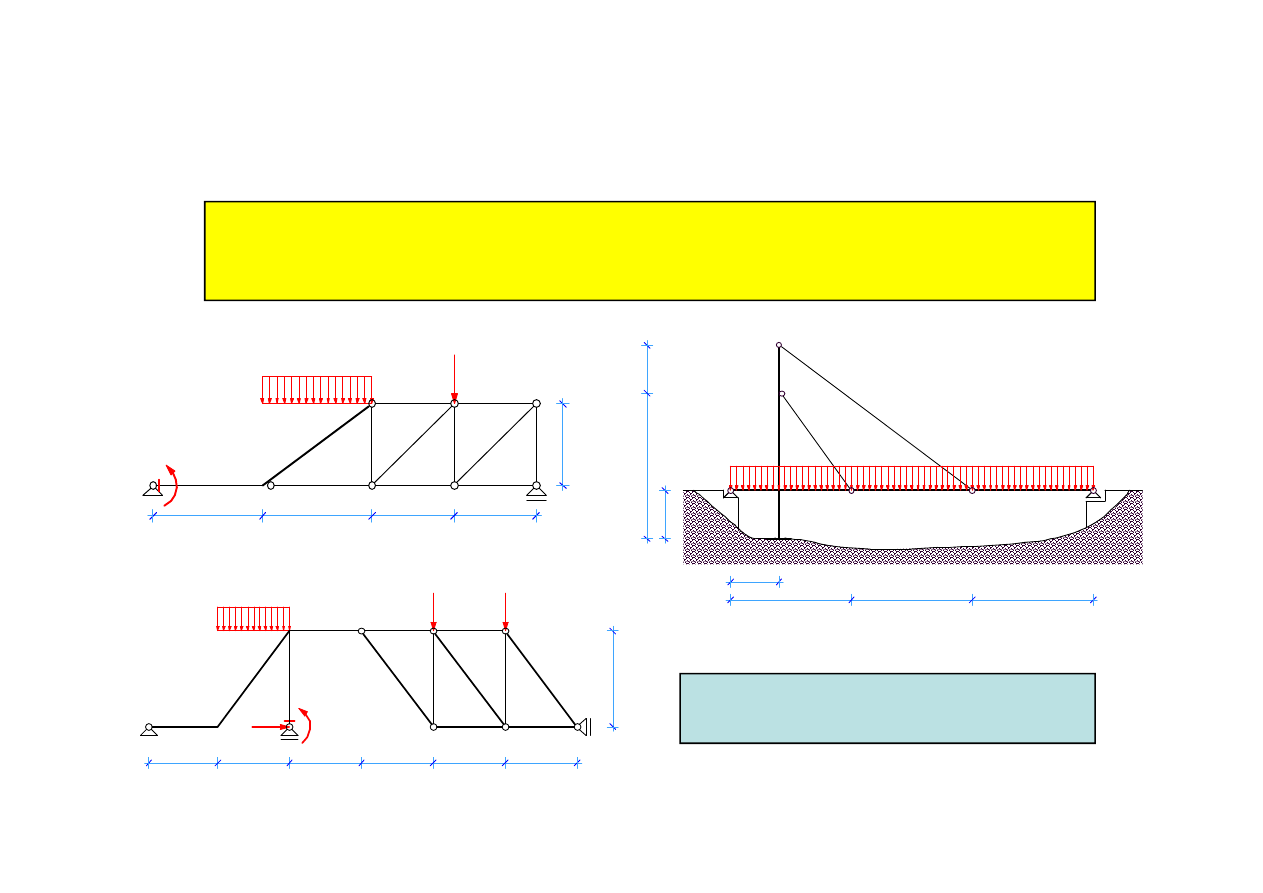
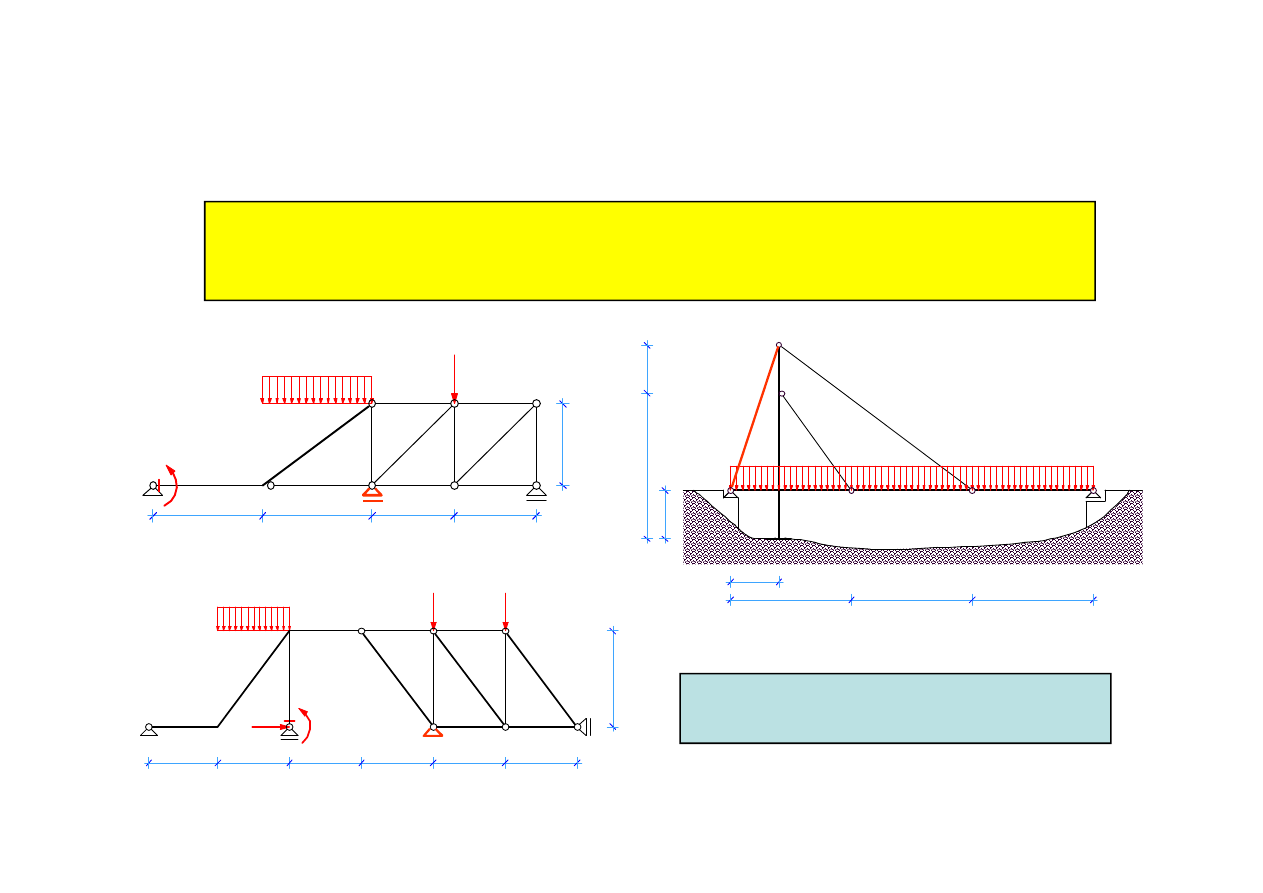
a) Układy konstrukcyjne statycznie wyznaczalne

W układach konstrukcyjnych statycznie wyznaczalnych liczba reakcji
podpór jest równa liczbie niezależnych równań równowagi a ich budowa
zapewnia geometryczną niezmienność

5

5

5

6

2

2

2

12 kN/m

3

3

3

3

3

3

4

8 kN

4 kN

A

1

2

7

8

10 kN/m

E

3 kN

9 kNm

D

C

P

B

3

4

5

6

9

4

4

3

3

3

5 kN/m

10 kN

90 kNm

1

2

6

7

8

3

4

5

9

10

11

12

A

B

C

D

Układy statycznie wyznaczalne
posiadają 0 stopni swobody

16

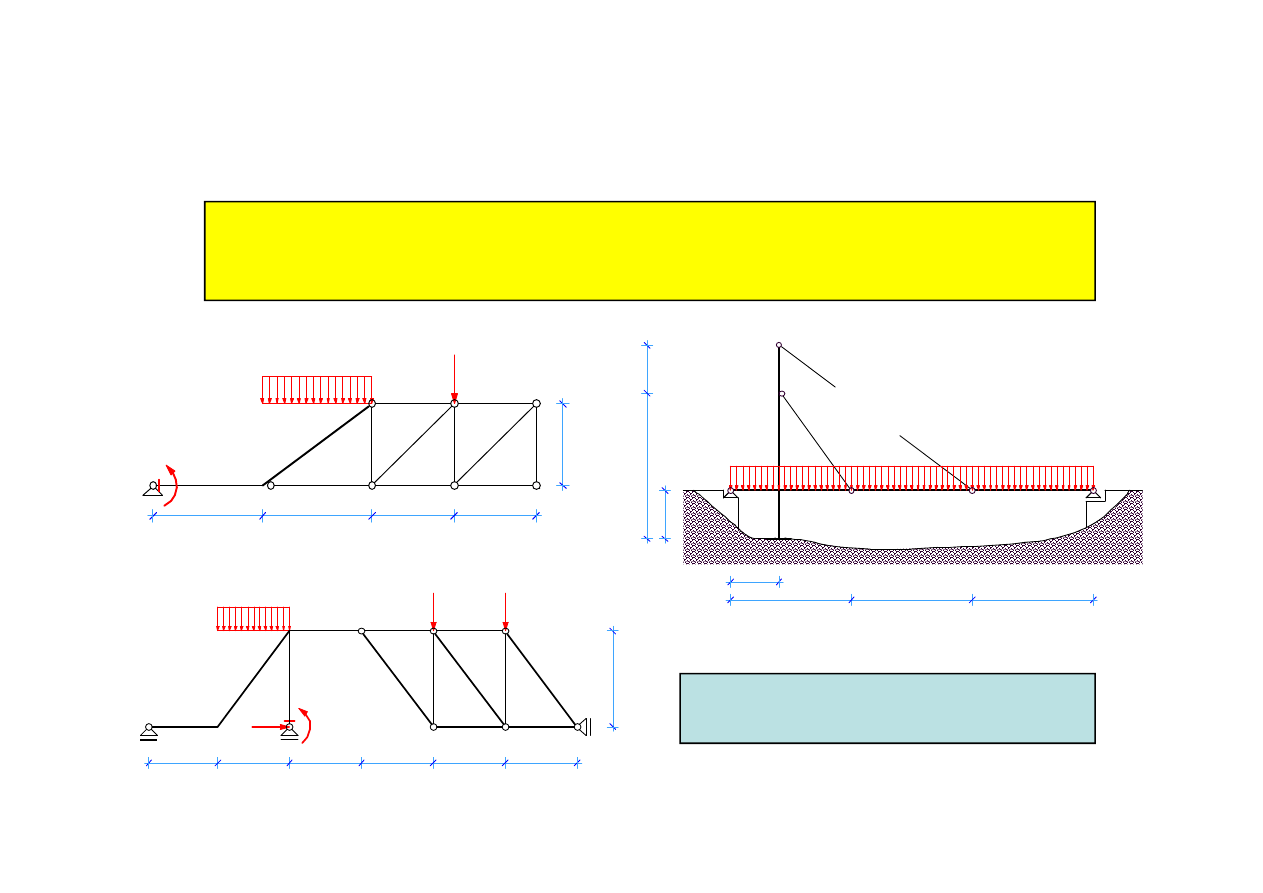
b) Układy konstrukcyjne statycznie niewyznaczalne

W układach konstrukcyjnych statycznie niewyznaczalnych liczba reakcji
podpór jest większa niż liczba niezależnych równań równowagi a ich
budowa zapewnia geometryczną niezmienność

5

5

5

6

2

2

2

12 kN/m

3

3

3

3

3

3

4

8 kN

4 kN

A

1

2

7

8

10 kN/m

E

3 kN

9 kNm

D

C

P

B

3

4

5

6

9

4

4

3

3

3

5 kN/m

10 kN

90 kNm

1

2

6

7

8

3

4

5

9

10

11

12

A

B

C

D

Układy statycznie niewyznaczalne
posiadają 0 stopni swobody

17

c) Układy konstrukcyjne chwiejne

W układach konstrukcyjnych chwiejnych liczba reakcji podpór jest mniejsza
niż liczba niezależnych równań równowagi a ich budowa nie zapewnia
geometrycznej niezmienność

5

5

5

6

2

2

2

12 kN/m

3

3

3

3

3

3

4

8 kN

4 kN

A

1

2

7

8

10 kN/m

E

3 kN

9 kNm

D

C

P

B

3

4

5

6

9

4

4

3

3

3

5 kN/m

10 kN

90 kNm

1

2

6

7

8

3

4

5

9

10

11

12

A

B

C

D

Układy chwiejne posiadają liczbę
stopni swobody większą od 0

18

2.2. Budowa układów statycznie wyznaczalnych

a) Liczba stopni swobody

A

B

C

D

B

C

B

C

x

x

y

y





Połączenie w przegubie
jest równoznaczne z wpro-
wadzeniem dwóch warunków

t

– liczba tarcz

p

– liczba przegubów

lss – liczba stopni swobody

3

2

t

p

lss

  



3ss

3ss

2ss



4ss

Gdy to lss = 3

t

p

  



3

2

3

19

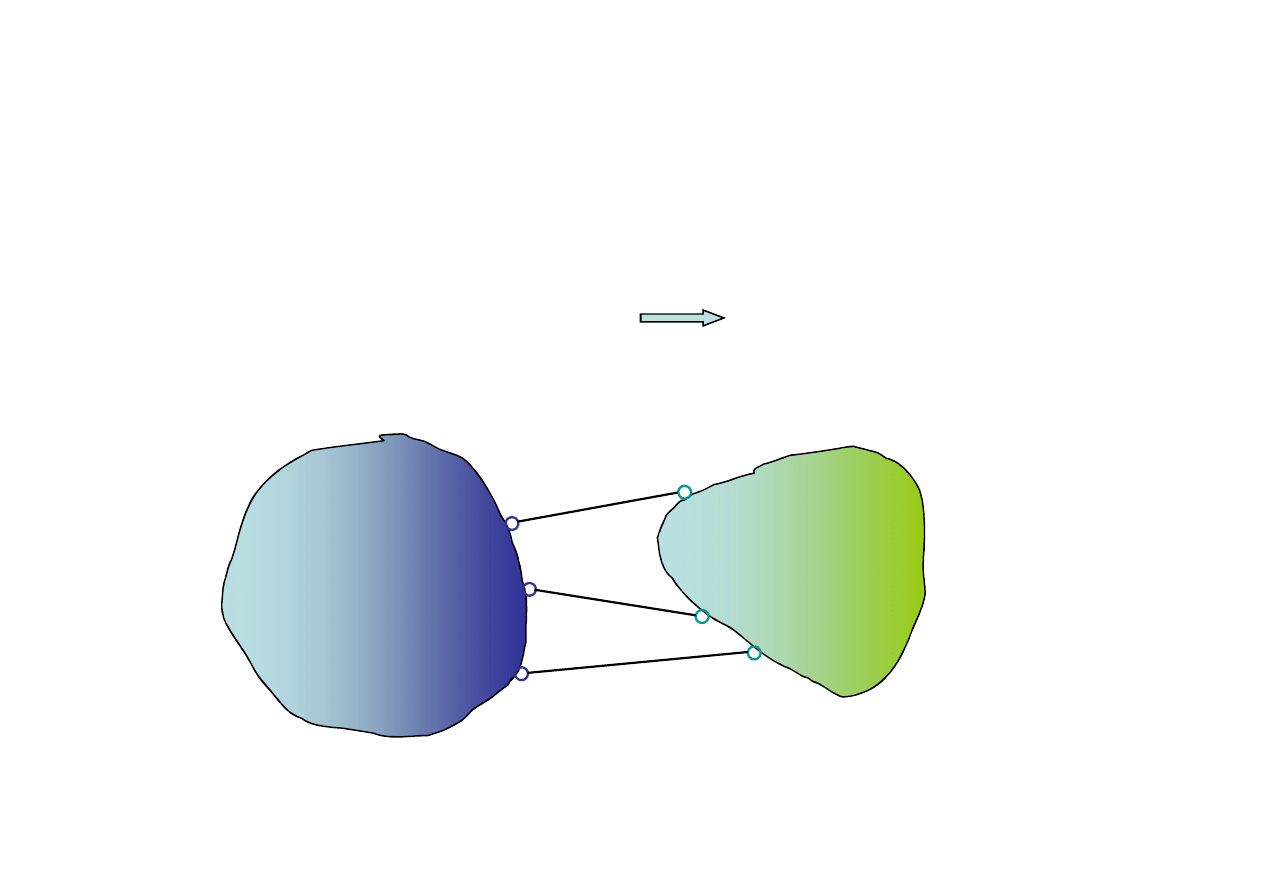
b) Sztywne połączenie dwóch tarcz

Za pomocą ilu prętów można połączyć dwie tarcze w sposób sztywny?









3 2

2 2

3

n

n





 





3

n 

20

O

Trzy pręty o osiach
przechodzących
przez jeden punkt

Trzy pręty
równoległe

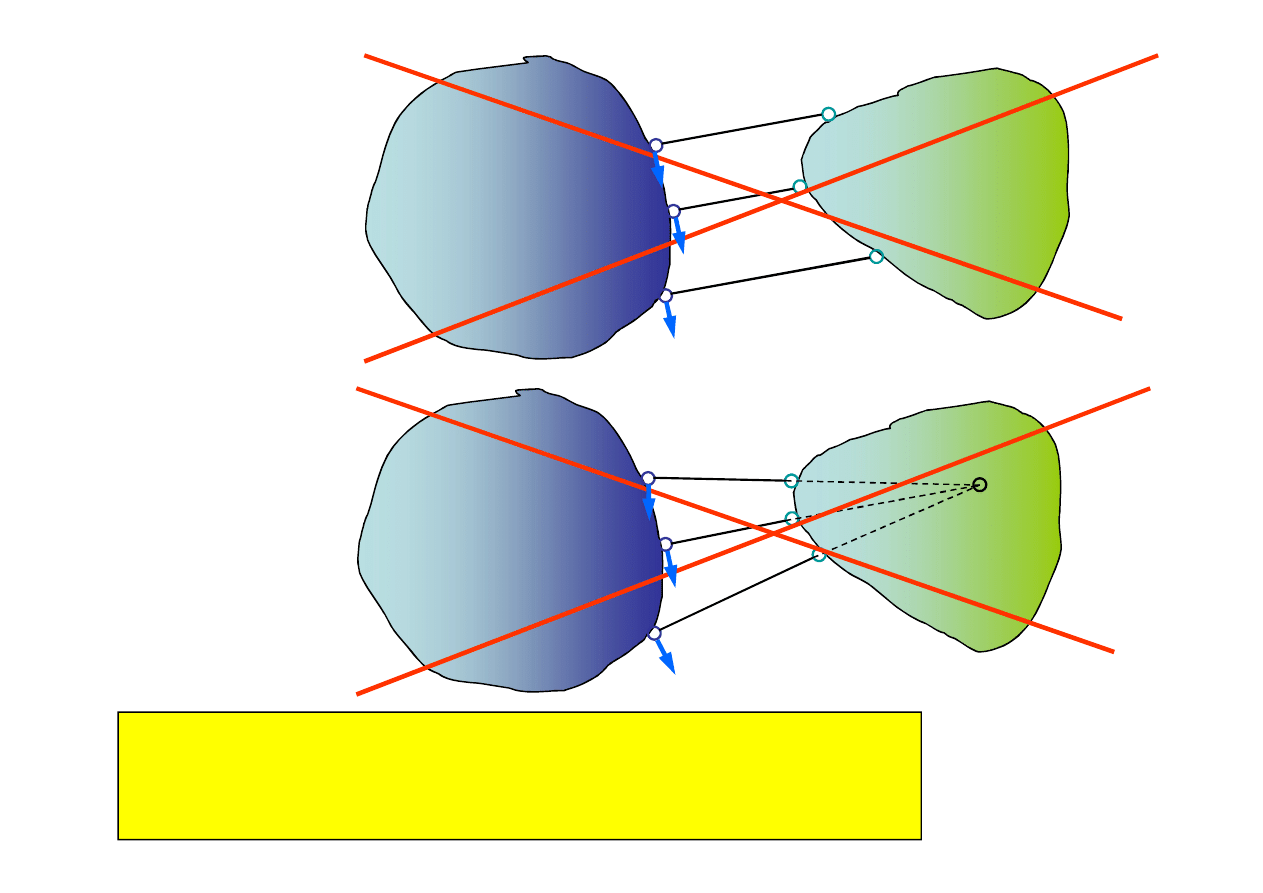
Warunkiem koniecznym i wystarczającym połączenia dwóch tarcz
za pomocą trzech prętów w sposób geometrycznie wewnętrznie
niezmienny jest, by te pręty nie były równoległe i nie przecinały się
w jednym punkcie

21

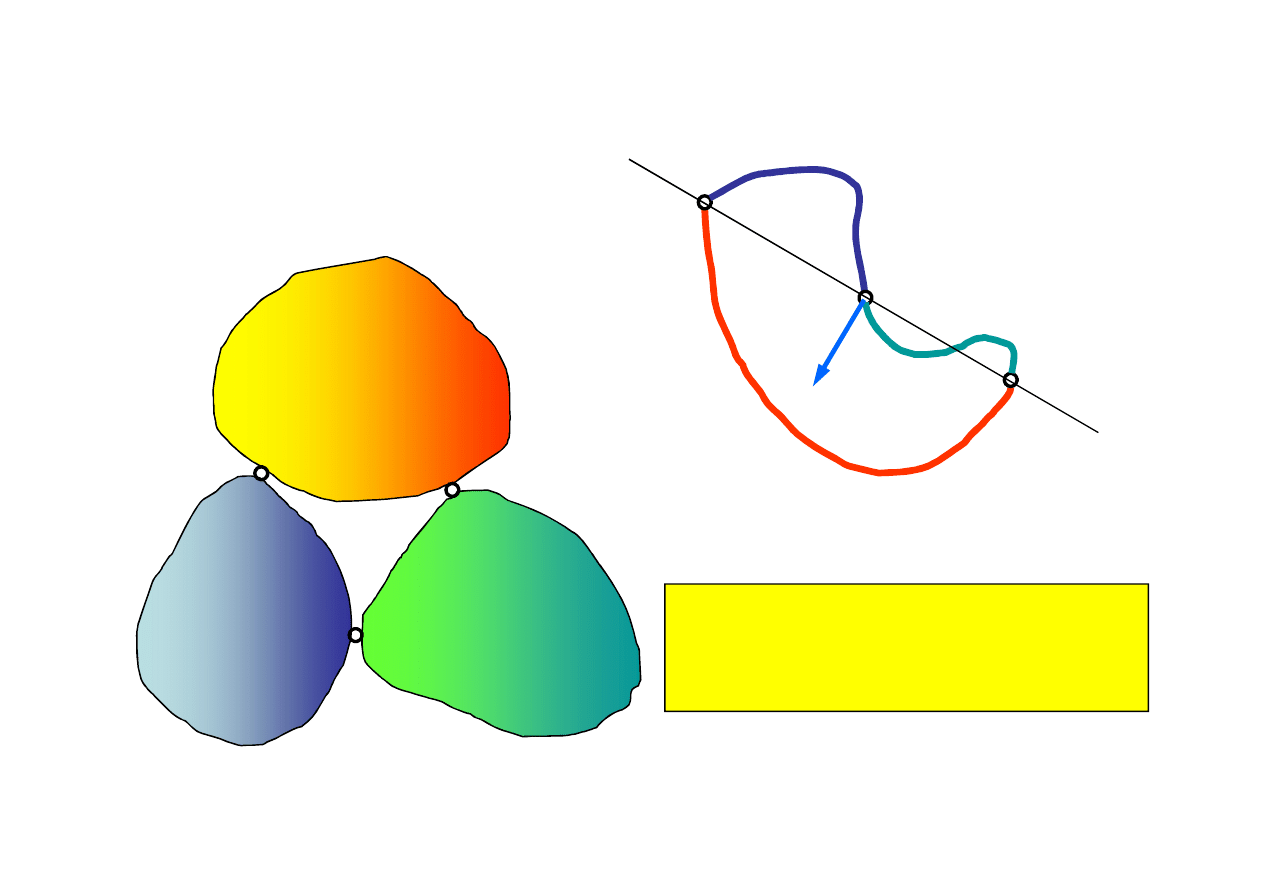
c) Sztywne połączenie trzech tarcz

Trzy tarcze można połączyć w sposób
geometrycznie wewnętrznie niezmien-
ny za pomocą trzech przegubów nie
leżących na jednej prostej

22

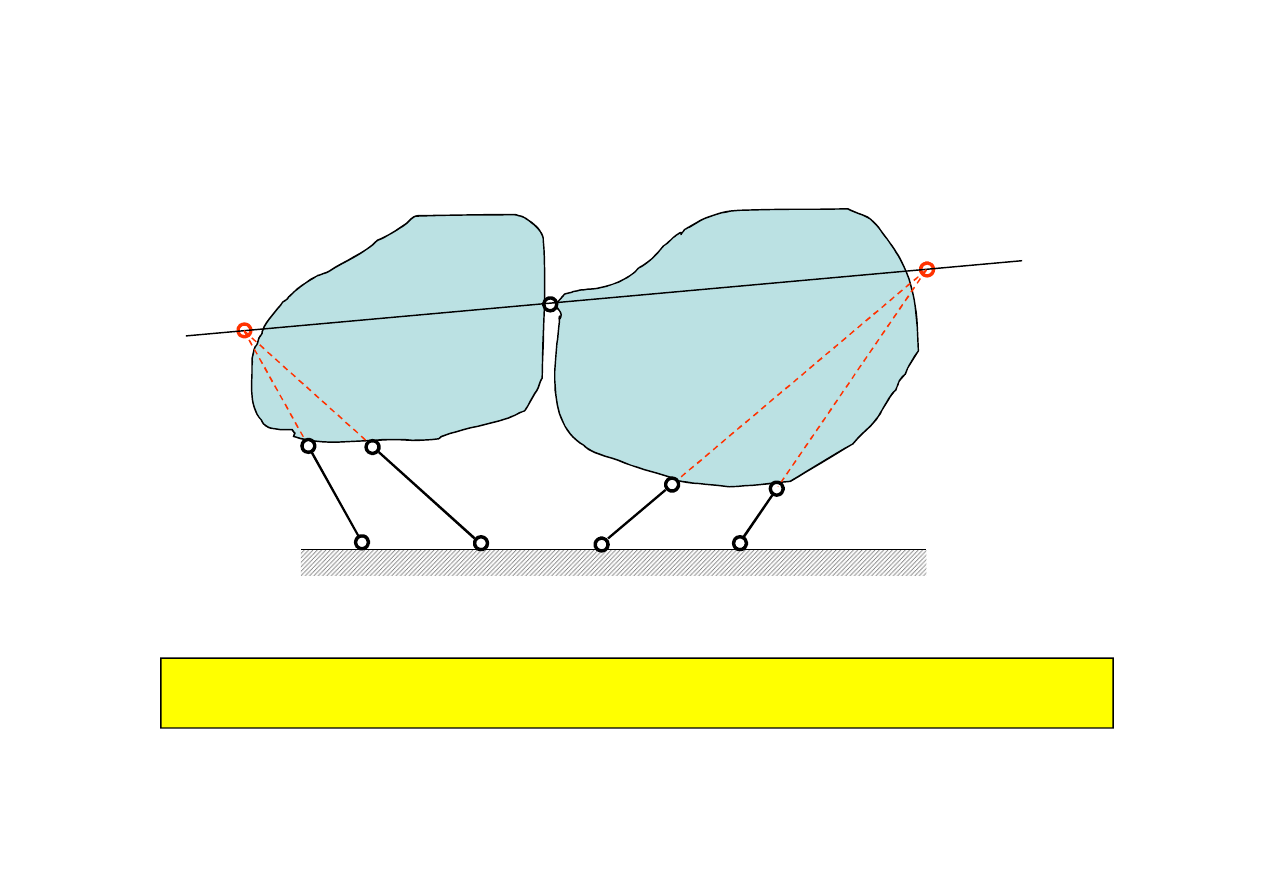
d) Sztywne połączenie dwóch tarcz z podłożem

Układ trzech tarcz jest wewnętrznie geometrycznie niezmienny gdy ich
chwilowe środki obrotu i przegub nie leżą na jednej prostej

Podłoże jako tarcza