Wykład 8,9

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

KINEMATYKA BRYŁY SZTYWNEJ

Część 1

Sposoby opisu ruchu ciała sztywnego

3

Ciało sztywne

– model fizyczny ciała o masie rozłożonej w pewnej przestrzeni,

której elementy nie mogą się względem siebie przemieszczać.
Punkt materialny jest szczególnym przypadkiem ciała sztywnego.

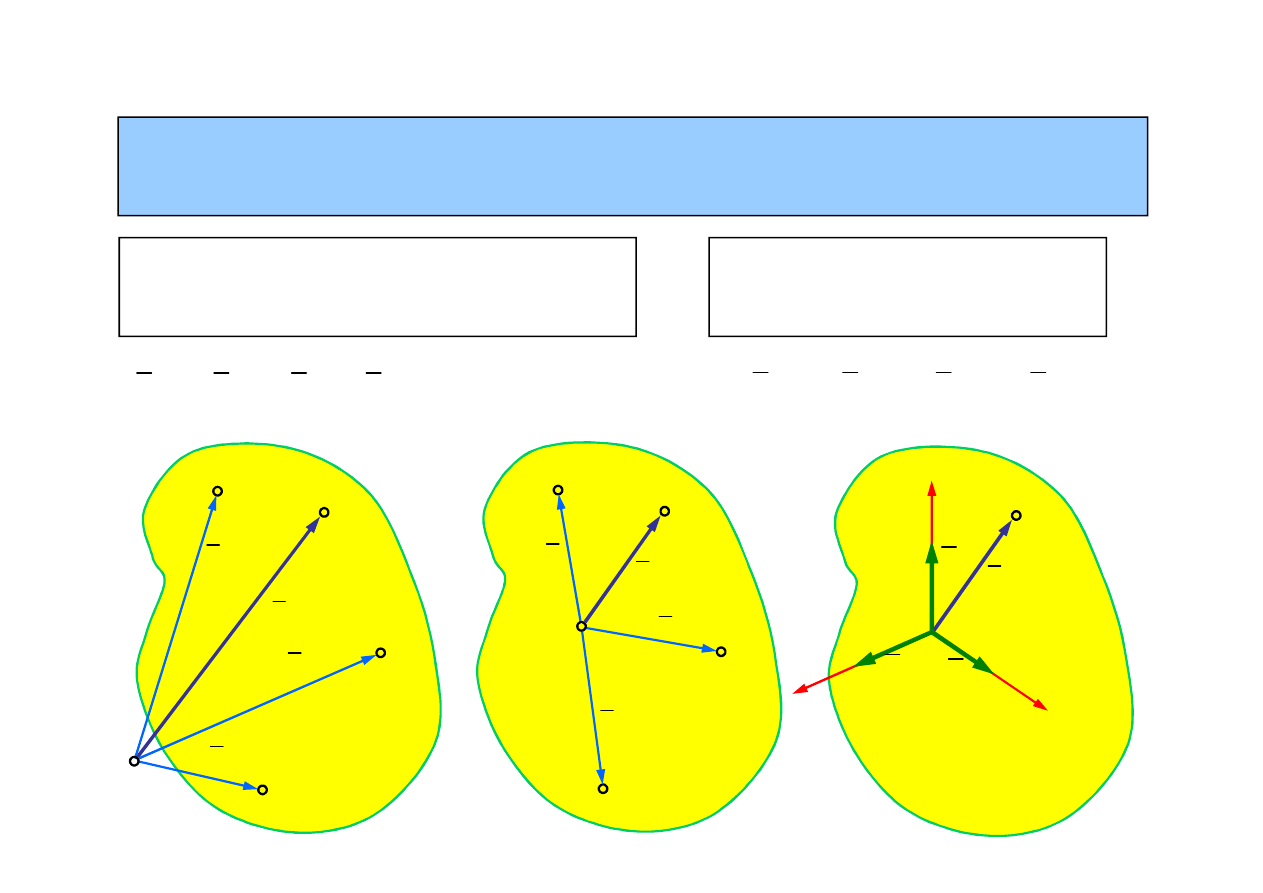
α, β, γ

Tymi wektorami mogą być
wersory układu współrzędnych
związanego z ciałem sztywnym

1

2

3

r

α r

β r

γ r

  



 

- liczby

rzeczywiste

Dowolny wektor w przestrzeni można
przedstawić w postaci kombinacji liniowej
trzech niekomplanarnych wektorów.

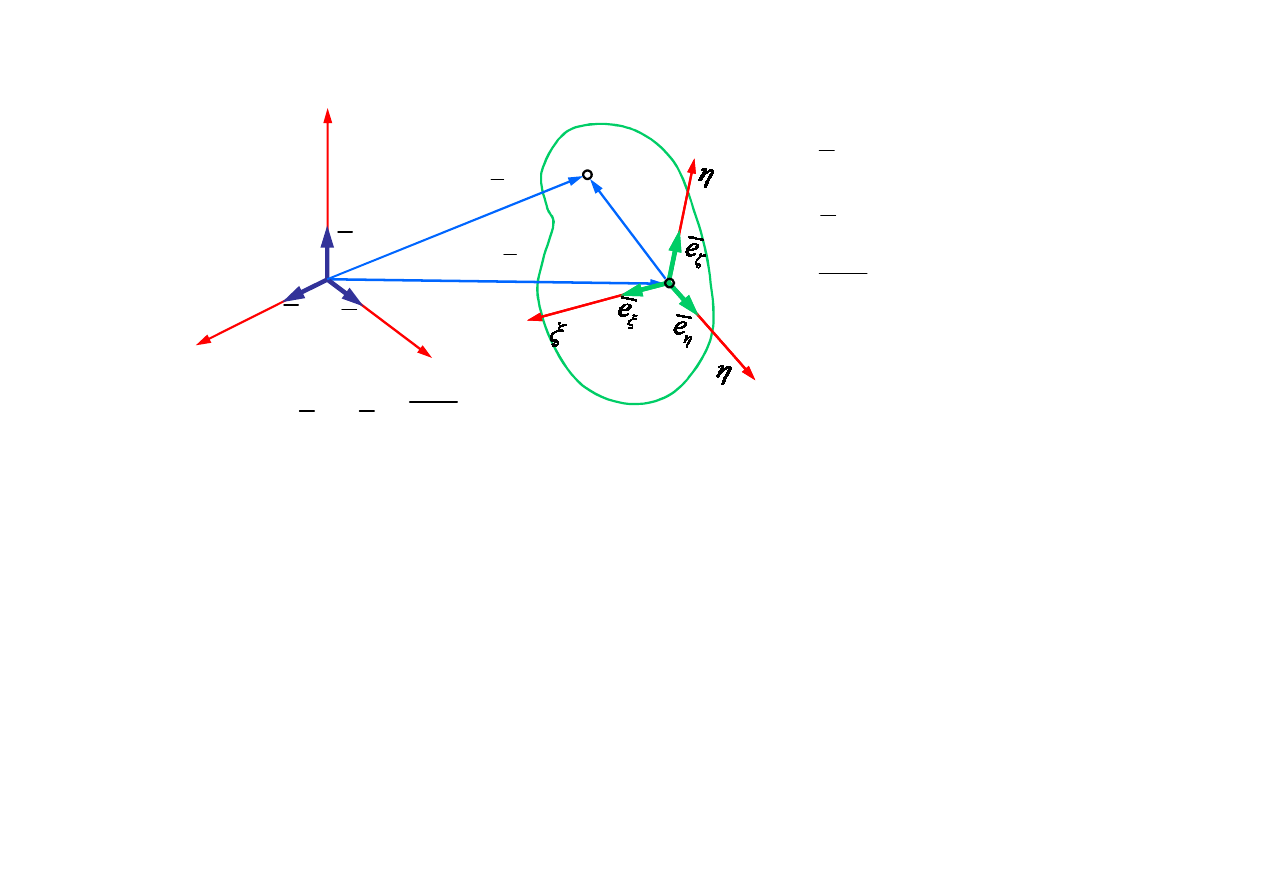
ξ

ξ

η

η

ζ

ζ

ρ

ρ e

ρ e

ρ

e













1.1. Opis cech geometrycznych ciała sztywnego

O

1

A

2

A

3

A

A

1

r

2

r

3

r

r

1

A

2

A

3

A

A

1

ρ

2

ρ

3

ρ

ρ

O

ξ

ζ

η

A

ρ

ξ

e

ζ

e

η

e

O

4

1.2. Opis położenia ciała sztywnego

1

A

2

A

3

A

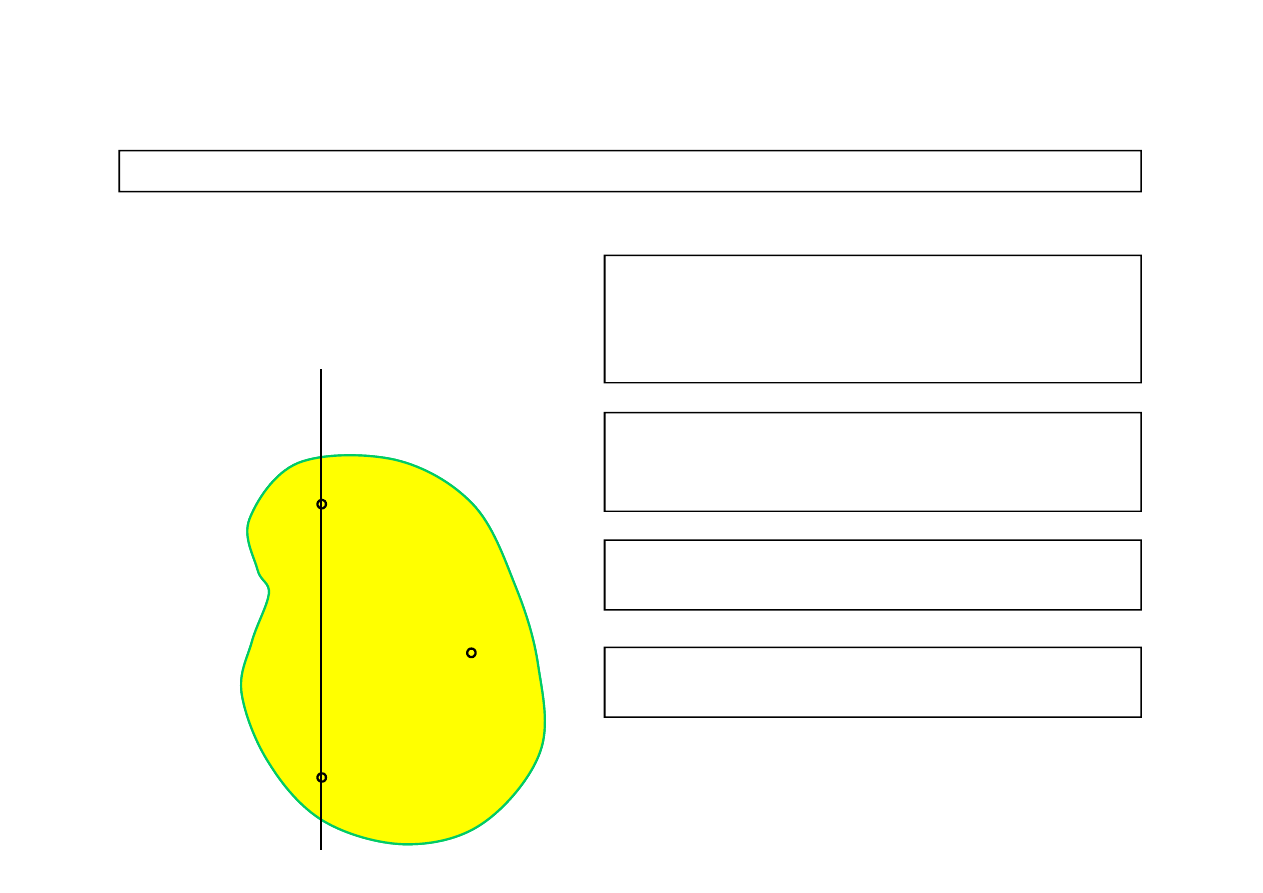
Aby unieruchomić bryłę sztywną, trzeba
unieruchomić trzy niewspółliniowe punkty

Pytanie: Ile punktów bryły należy unieruchomić, aby unieruchomić całą bryłę?

1 punkt – bryła obraca się w dowolnym

kierunku wokół dowolnej osi
przechodzącej przez ustalony
punkt

2 punkty – bryła obraca się w dowolnym

kierunku wokół osi przechodzą-
cej przez dwa ustalone punkty

3 punkty – bryła jest całkowicie

unieruchomiona

5

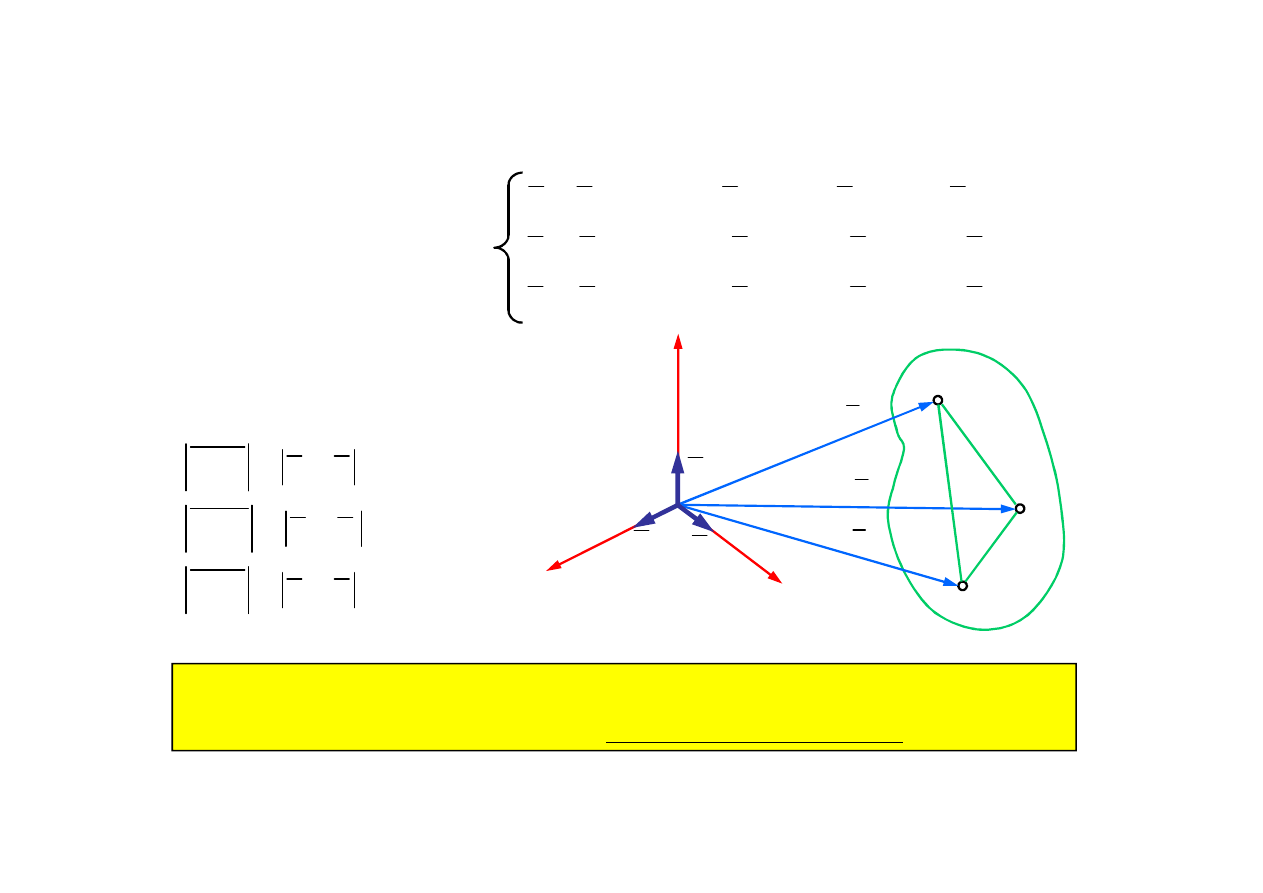
1.3. Opis ruchu ciała sztywnego przez podanie równań ruchu

trzech nie współliniowych punktów

Położenie bryły sztywnej w każdej chwili można określić za pomocą dziewięciu
skalarnych funkcji czasu które powinny spełniać trzy warunki sztywności. Sześć
niezależnych funkcji (9 – 3 = 6) nazywamy współrzędnymi uogólnionymi

 

 

 

 

2

2

2

2

2

x

y

z

r

r t

x t e

y

t e

z

t e









 

 

 

 

3

3

3

3

3

x

y

z

r

r t

x t e

y

t e

z

t e









 

 

 

 

1

1

1

1

1

x

y

z

r

r t

x t e

y t e

z t e









1

2

2

1

1

2

3

3

2

2

1

3

3

1

3

A A

r

r

d

const

A A

r

r

d

const

A A

r

r

d

const

























Równania ruchu trzech
niewspółliniowych punktów
(9 skalarnych funkcji czasu):

Warunki stałych odległości
(3 równania algebraiczne):

1

A

2

A

3

A

1

r

2

r

3

r

x

z

O

y

x

e

y

e

z

e

1

d

2

d

3

d

6

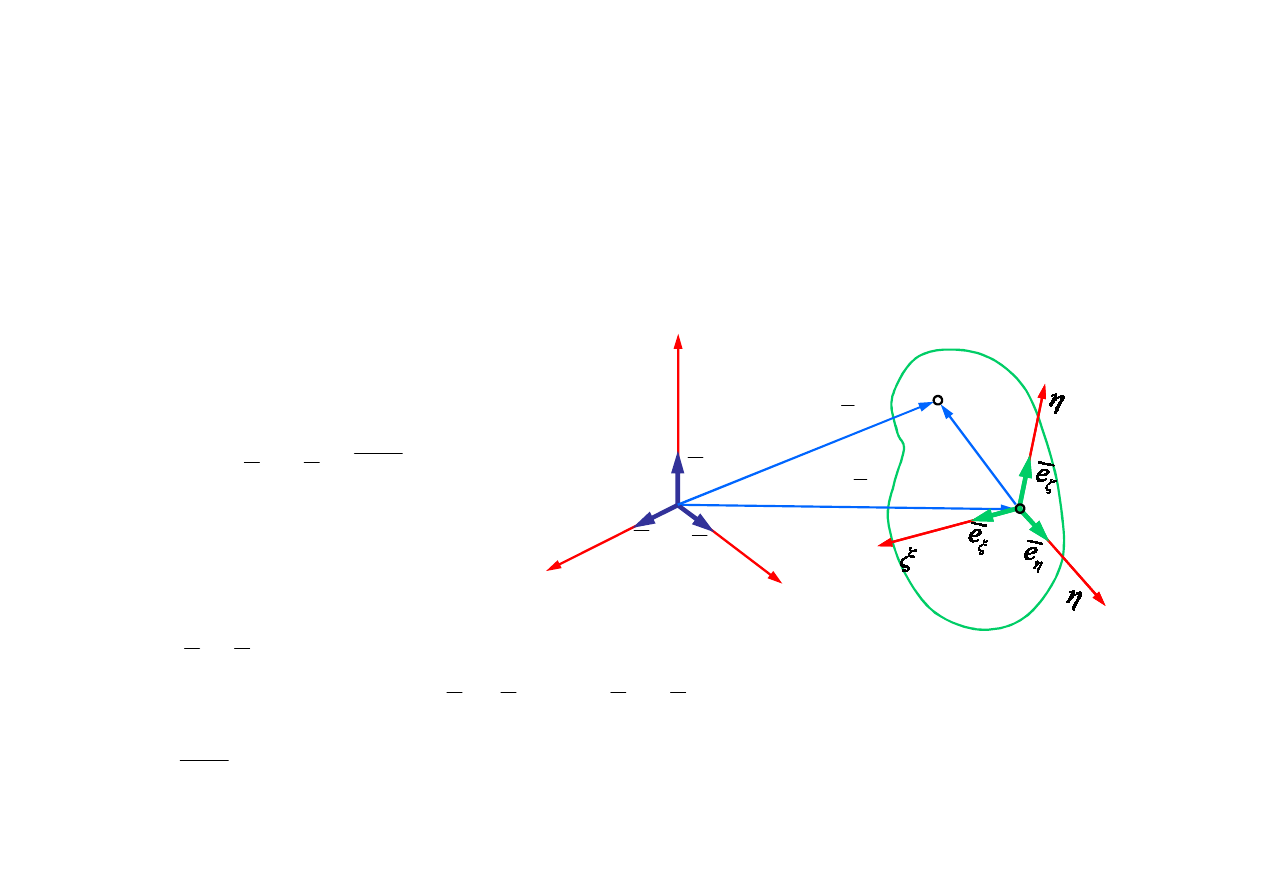
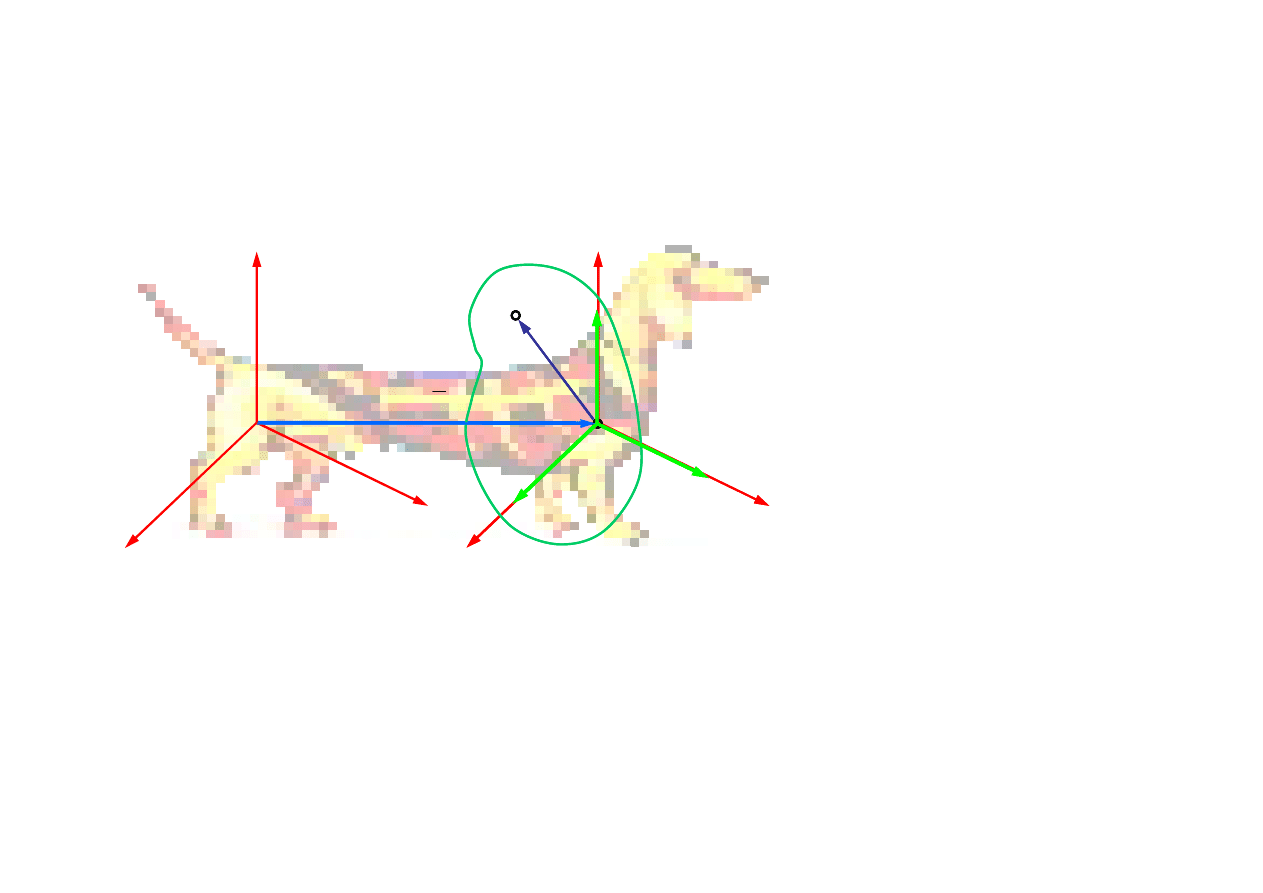
1.4. Opis ruchu ciała sztywnego we współrzędnych

przestrzennych i materialnych

M

A

r

r

AM





Układ Axhz – układ współrzędnych materialnych Lagrange’a

(niezależnych od czasu)

Związek wektorowy pomiędzy
opisem przestrzennym i materialnym

M

M

r

A

r

x

z

O

y

x

e

y

e

z

e

A

Układ Oxyz – układ współrzędnych przestrzennych Eulera

- wektor zdefiniowany we współrzędnych materialnych

niezależnych od czasu

AM

M

A

r , r

 

 

A

A

M

M

r

r t ,

r

r

t





- wektory zdefiniowane we współrzędnych przestrzennych

7

M

A

r

r

AM





w zapisie macierzowym:

Związek





































A

A

A

ξ

cos x,ξ

c os y,ξ

cos z,ξ

x

x

η

cos x,η

cos y,η

cos z,η

y

y

ζ

cos x,ζ

cos y,ζ

cos z,ζ

z

z







 









 















 









 







 













































A

A

A

x

x

cos x,ξ

cos x,η

cos x,ζ

ξ

y

y

cos y,ξ

cos y,η

cos y,ζ

η

z

z

cos z,ξ

cos z,η

cos z,ζ

ζ











 









 















 









 







 





A

A

A

ξ

x

x

η

α

y

y

ζ

z

z



 





 





 



 





 







 







A

T

A

A

x

x

ξ

y

y

α

η

z

z

ζ







 





 











 





 







 







A

A

A

A

r

x

y

z







M

r

x

y

z







AM

ξ

η

ζ



M

M

r

A

r

x

z

O

y

x

e

y

e

z

e

A

8

Własności macierzy przejścia:

Iloczyn skalarny dwóch wierszy (kolumn) jednoimiennych jest równy 1

Elementy macierzy przejścia
kosinusy kierunkowe osi układu współrzędnych przestrzennych w układzie współrzędnych
materialnych i materialnych w układzie współrzędnych przestrzennych

Kolumny macierzy przejścia
współrzędne wersorów układu
przestrzennego we współrzędnych
materialnych

Macierz przejścia zawiera 9 elementów, jednak tylko trzy są niezależne, ponieważ te
9 elementów powinno spełniać 6 niezależnych warunków





































cos x,ξ

c os y,ξ

cos z,ξ

α

cos x,η

cos y,η

cos z,η

cos x,ζ

cos y,ζ

cos z,ζ









 













Wiersze macierzy przejścia
współrzędne wersorów układu
materialnego we współrzędnych
przestrzennych

x

e



y

e



z

e



ξ

e



η

e



ξ

e



Macierz przejścia opisuje rotację ciała

Iloczyn skalarny dwóch wierszy (kolumn) różnoimiennych jest równy 0

9













2

2

2

1

ξ

ξ

e e

cos

x,ξ

c os

y,ξ

cos

z,ξ























2

2

2

1

η

η

e e

cos

x,η

c os

y,η

cos

z,η























2

2

2

1

ζ

ζ

e e

cos

x,ζ

c os

y,ζ

cos

z,ζ



































0

ξ

η

e e

cos x,ξ

cos x,η

c os y,ξ

c os y,η

cos z,ξ

cos z,η









































0

η

ζ

e e

cos x,η cos x,ζ

c os y,η c os y,ζ

cos z,η cos z,ζ









































0

ξ

ζ

e e

cos x,ξ

cos x,ζ

c os y,ξ

c os y,ζ

cos z,ξ

cos z,ζ





























2

2

2

1

x

x

e e

cos

x,ξ

c os

x,η

cos

x,η























2

2

2

1

y

y

e e

cos

y,ξ

c os

y,η

cos

y,ζ























2

2

2

1

z

z

e e

cos

z,ξ

c os

z,η

cos

z,ζ



































0

x

y

e e

cos x,ξ

cos y,ξ

c os x,η c os y,η

cos x,ζ

cos y,ζ









































0

y

z

e e

cos y,ξ

cos z,ξ

c os y,η c os z,η

cos y,ζ

cos z,ζ









































0

x

z

e e

cos x,ξ

cos z,ξ

c os x,η c os z,η

cos x,ζ

cos z,ζ

















Związki pomiędzy elementami macierzy przejścia:

10

Znajomość kątów kierunkowych pozwala na jednoznaczne wyznaczenie macierzy
przejścia a odwrotne działanie nie daje jednoznacznego wyniku

Zdefiniowanie wektora jest równoznaczne ze zdefiniowaniem trzech niezależnych

skalarnych funkcji czasu

 

 

 

 





A

A

A

A

r t

x

t

y

t

z

t



 

A

r t

 

A

A

r

r t



Jednoznaczny opis ruchu ciała sztywnego we współrzędnych przestrzennych i materialnych
sprowadza się do opisu ruchu ustalonego punktu bryły sztywnej, z którym jest związany układ
współrzędnych Lagrange’a





































cos x,ξ

c os y,ξ

cos z,ξ

α

cos x,η

cos y,η

cos z,η

cos x,ζ

cos y,ζ

cos z,ζ









 













oraz zdefiniowania dziewięciu kątów kierunkowych jako funkcji czasu występujących w
elementach macierzy przejścia z układu Lagrange’a do układu Eulera.

Spośród dziewięciu kątów kierunkowych tylko trzy są niezależne ponieważ wszystkie,
poprzez elementy macierzy przejścia, są związane sześcioma niezależnymi warunkami.
Jednak te warunki nie pozwalają na jednoznaczne wyznaczenie sześciu niewiadomych
kątów w przypadku, gdy tylko trzy są ściśle określone.

11

x'

z'

y'

x'

z'

y'

1.5. Opis ruchu ciała sztywnego za pomocą kątów Eulera

Każdy ruch bryły sztywnej można przedstawić jako złożenie ruchu postępowego
pewnego ustalonego punktu oraz ruchu obrotowego bryły wokół tego punktu

A

r

x

z

O

y

M

A

ξ

ζ

η

M

A

ξ

ζ

η

Opis ruchu

- opis ruchu postępowego punktu A w układzie przestrzennym Oxyz za pomocą

wektora r

A

- opis położenia punktu M w układzie materialnym Axhz za pomocą wektora AM

- opis ruchu obrotowego układu materialnego Axhz w układzie Ax’y’z’, przesuniętym

równolegle względem układu Oxyz , za pomocą kątów Eulera

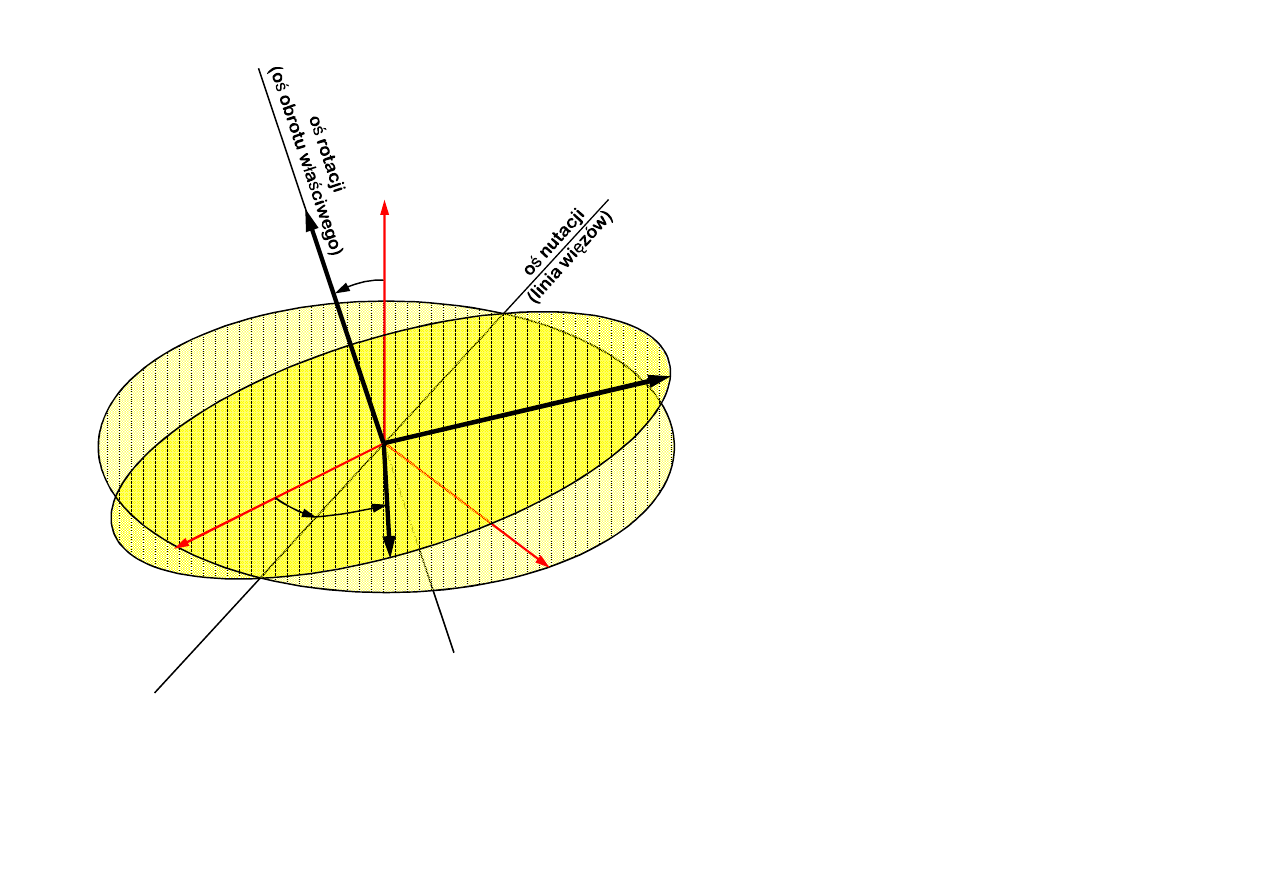
12

O

x

y

z

θ

ζ

ξ

φ

η

Kąt rotacji φ (kąt obrotu właściwego)

zawarty pomiędzy osią nutacji a osią Ox

Definicja kątów Eulera

Kąt nutacji y

zawarty pomiędzy osią Ox a osią nutacji
leżącą w płaszczyźnie Oxy

Kąt precesji q

zawarty pomiędzy osią Oz a osią Oz

ψ

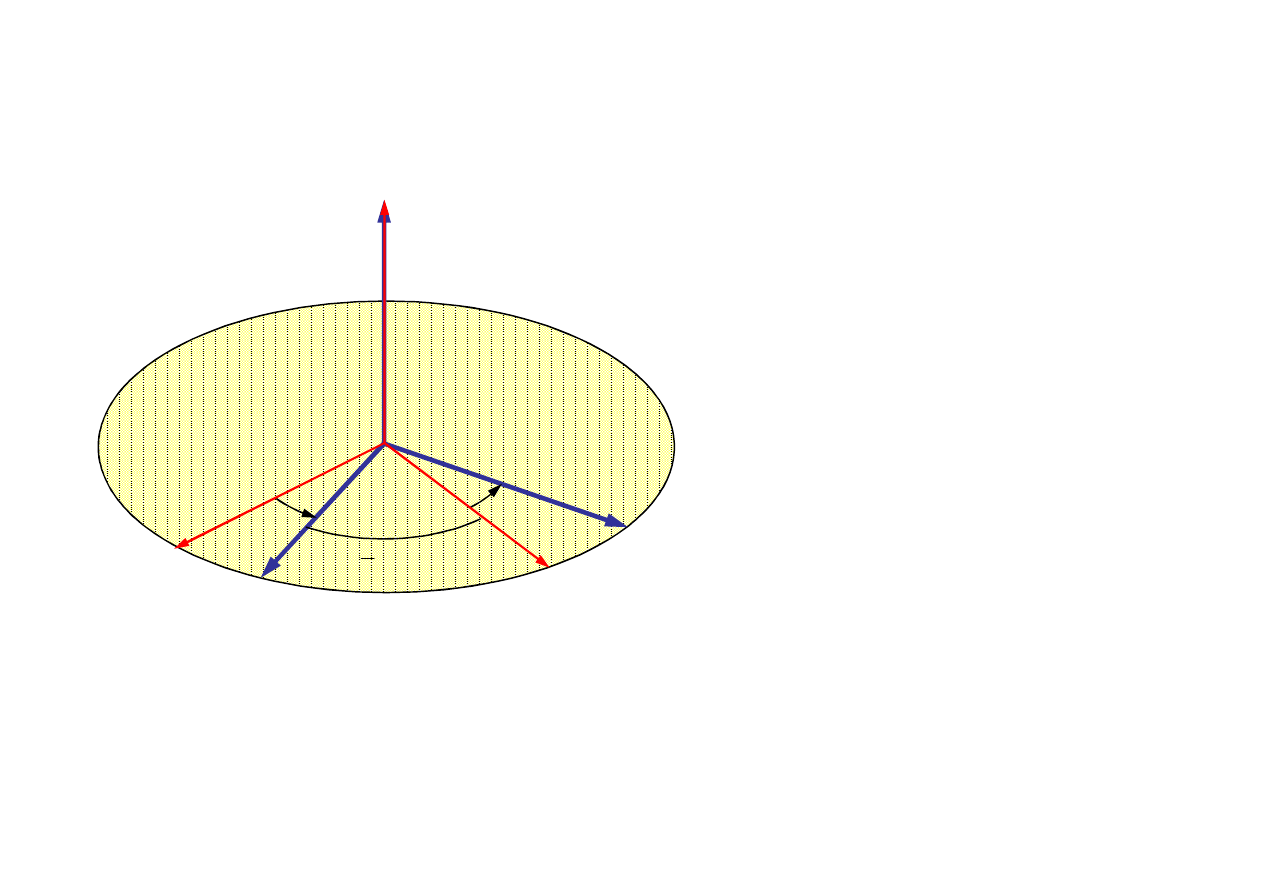
13

1

ζ

1

ξ

1

η

2

π

ψ



ψ

ψ

O

x

y

z

Obrót wokół osi Oz o kąt y (precesja, kąt precesji)

1

1

1

0

0

0

0

1

ξ

cos ψ

sinψ

x

η

sinψ

cos ψ

y

ζ

z

 



  

 



  

 



 



  

 



  

 



  

















1

1

1

1

1

0

0

0

0

1

cos x,ξ

c os y,ξ

α

cos x,η

cos y,η









 













1

0

0

0

0

1

cos ψ

sin ψ

α

sin ψ

cos ψ









 















1

1

1

ξ

x cos ψ

y sin ψ

η

x sin ψ

y cos ψ

ζ

z





 





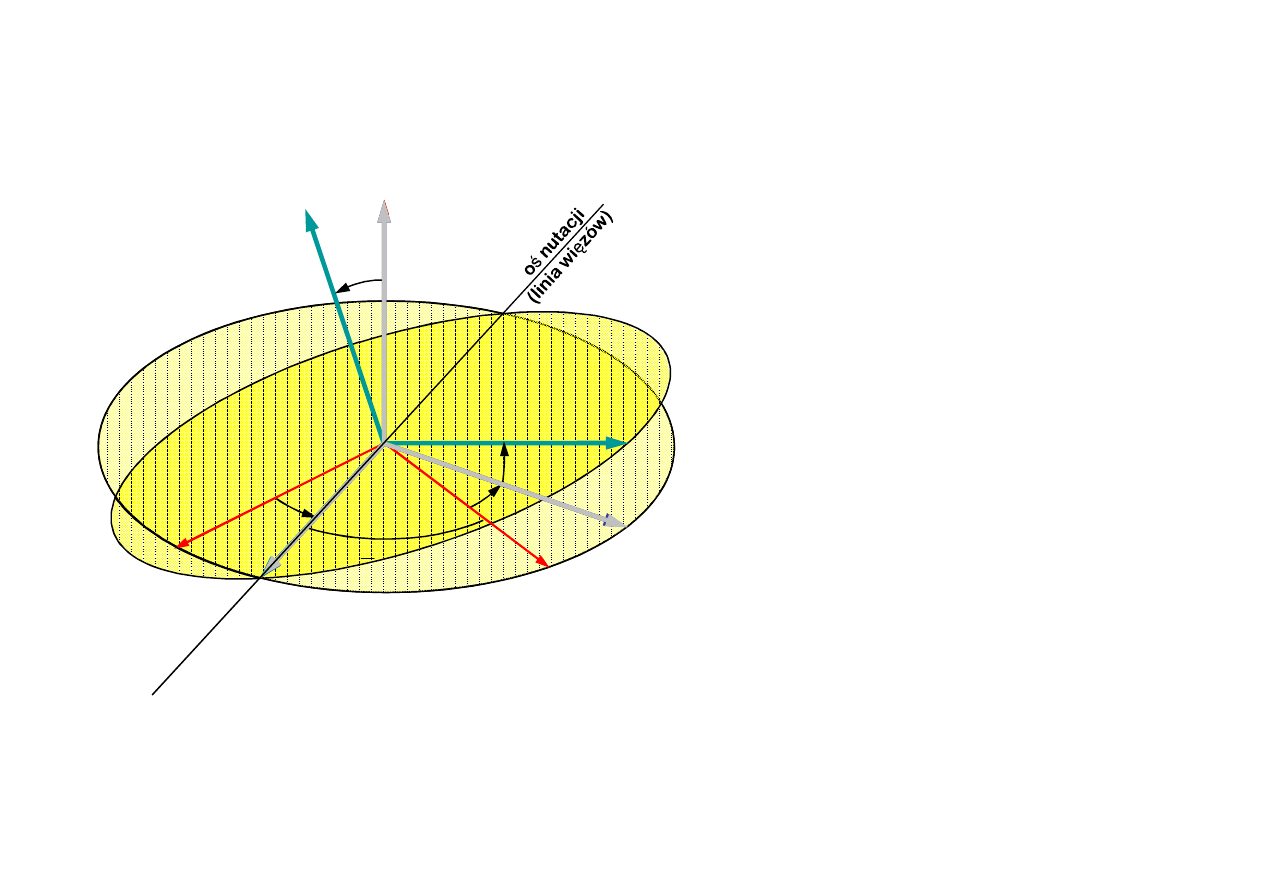
14

1

ζ

1

ξ

1

η

2

π

ψ



ψ

ψ

O

x

y

z

Obrót wokół osi Ox

1

o kąt q (nutacja, kąt nutacji)

2

1

2

1

2

1

1

0

0

0

0

ξ

ξ

η

cos θ

sin θ

η

ζ

sin θ

cos θ

ζ







  







  











  







  









  

















2

1

2

1

2

1

2

1

2

1

0

0

0

0

α

cos η ,η

c os ζ ,η

cos η ,ζ

cos ζ ,ζ









 













2

1

0

0

0

0

α

cos θ

sin θ

sin θ

cos θ



























2

1

2

1

1

2

1

1

ξ

ξ

x cos ψ

y sinψ

η

η cos θ

ζ sin θ

x cos θ sin ψ

y cos θ cos ψ

z sin θ

ζ

η sin θ

ζ cos θ

x sin θ sinψ

y sin θ cos ψ

z cos θ











 





 









2

ξ

2

η

2

ζ

θ

θ

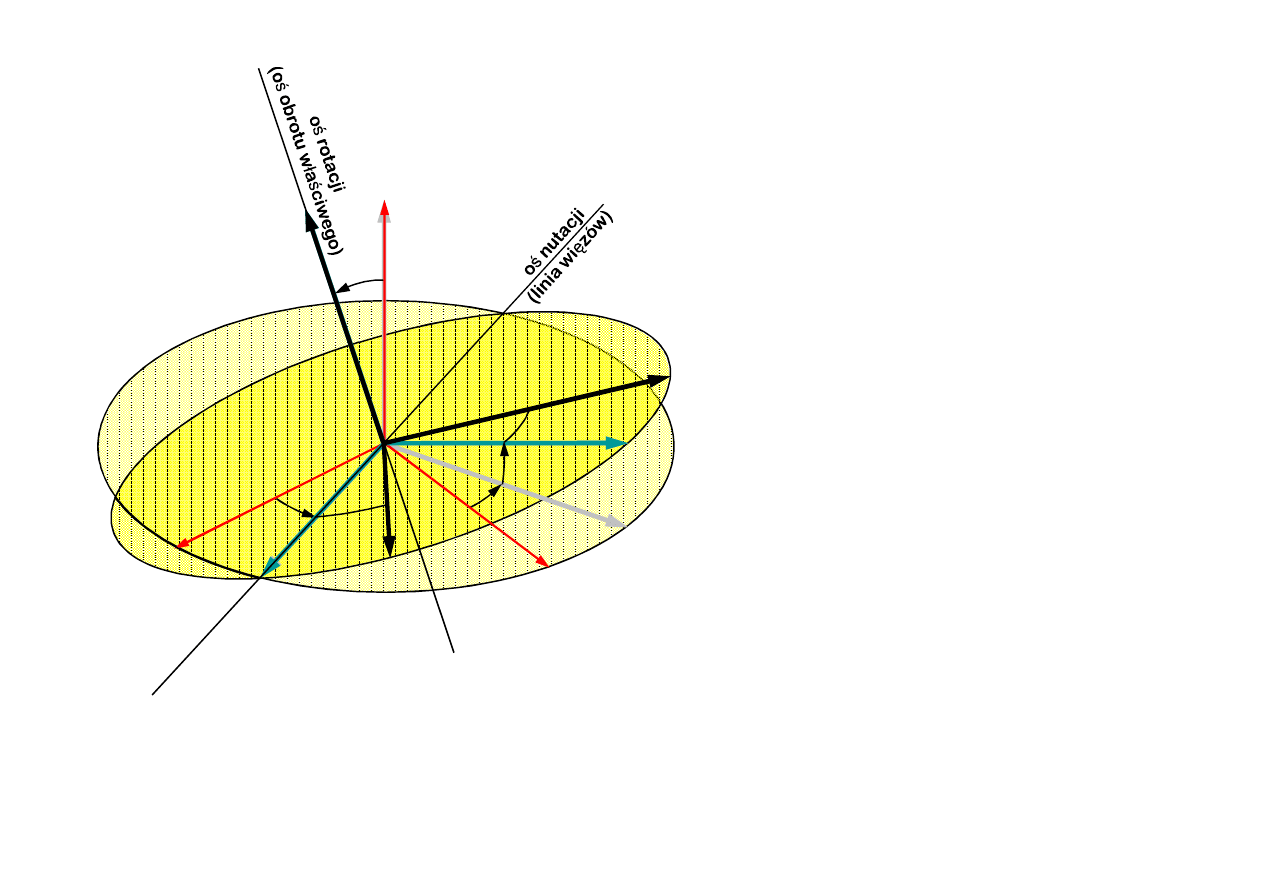
15

1

ζ

1

ξ

1

η

ψ

ψ

O

x

y

z

Obrót wokół osi Oz

2

o kąt j (rotacja, kąt rotacji)

















2

2

2

2

2

1

1

ξ

ξ cos φ η sin φ

x cos φ cos ψ

sin φ cos θ sinψ

y cos φ sin ψ

sin φ cos θ cos ψ

z sin φ sin θ

η

ξ sin φ η cos φ

x

sin φ cos ψ

cos φ cos θ sinψ

y

sin φ sin ψ

cos φ cos θ cos ψ

z cos φ sin θ

ζ

ξ

η sin θ

ζ cos θ

x sin θ sinψ

y sin θ cos ψ

z cos θ















 



















 









2

ξ

2

η

2

ζ

θ

θ

ξ

η

ζ

φ

φ

2

2

2

0

0

0

0

1

ξ

cos φ

sin φ

ξ

η

sin φ cos φ

η

ζ

ζ

 



 



 



 



 



 



 



 



 



 



 



















2

2

3

2

2

0

0

0

0

1

cos ξ ,ξ

c os η ,ξ

α

cos ξ ,η

cos η ,η









 













3

0

0

0

0

1

cos φ

sin φ

α

sin φ cos φ









 















16

ξ

cos φ cos ψ

sin φ cos θ sinψ

cos φ sinψ

sin φ cos θ cos ψ

sin φ sin θ

x

η

sin φ cos ψ

cos φ cos θ sinψ

sin φ sinψ

cos φ cos θ cos ψ

cos φ sin θ

y

ζ

sin θ sinψ

sin θ cos ψ

cos θ

z





 



  

 



  

 









 



  

 



  



 



  

cos φ cos ψ

sin φ cos θ sinψ

cos φ sinψ

sin φ cos θ cos ψ

sin φ sin θ

α

sin φ cos ψ

cos φ cos θ sinψ

sin φ sinψ

cos φ cos θ cos ψ

cos φ sin θ

sin θ sinψ

sin θ cos ψ

cos θ













 























Związek macierzowy pomiędzy współrzędnymi Eulera i Lagrange’a w opisie ruchu
obrotowego za pomocą kątów Eulera

Macierz przejścia z układu Oxyz do układu obróconego, opisanego za pomocą kątów Eulera

Część 2

Prędkości i przyspieszenia punktów ciała sztywnego

w ruchu dowolnym

18

 

 

A

r t

r t

AM





- wektor wodzący początku układu ruchomego

 

A

r t

2.1. Prędkość punktów ciała sztywnego w ruchu dowolnym

 

r t

- wektor wodzący w układzie nieruchomym

- prędkość unoszenia punktów ciała sztywnego

w ruchu dowolnym równa prędkości bezwzględnej

u

A

b

υ

r

ω AM

υ











AM

- wektor wodzący w układzie ruchomym

(niezależny od czasu)

b

υ

- prędkość bezwzględna

0

w

υ 

- prędkość względna

A

w

w

u

b

r

r

ρ

ω ρ

υ

υ

υ





















 

 

 

A

r t

r t

ρ t





- wektorowy opis ruchu punktu materialnego

w ruchu względnym

- prędkość w ruchu względnym

A

u

b

w

d

r

r

AM

ω ρ

υ

υ

dt

















0

19

w

w

a

ρ

 

- przyspieszenie względne w ruchu względnym





A

w

w

w

w

c

u

b

r

r

ρ

ω ρ

ω ρ

ω

ρ

ω ρ

a

a

a

a











 



























- przyspieszenie Coriolisa w ruchu względnym

2

c

w

a

ω ρ



 

- przyspieszenie unoszenia w ruchu względnym





u

A

a

r

ω ρ

ω

ω ρ

















2.2. Przyspieszenie punktów ciała sztywnego w ruchu dowolnym

2

2

0

w

d

a

AM

dt





2

0

c

d

a

ω

AM

dt











u

A

b

a

r

ω AM

ω

ω AM

a



















- przyspieszenie punktów ciała sztywnego

w ruchu dowolnym równe przyspieszeniu
bezwzględnemu

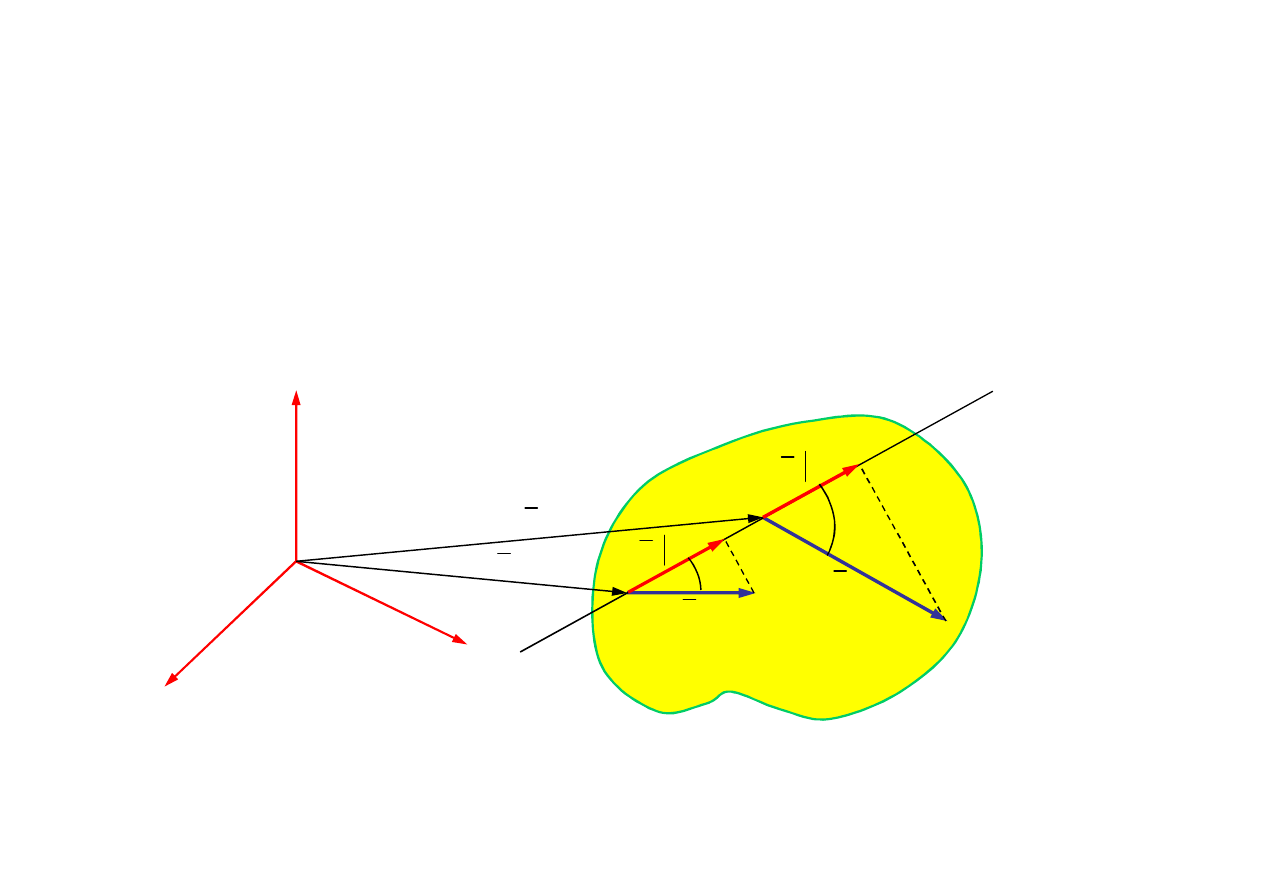
20

x

z

O

y

A

B

r

A

r

B

B

υ

A

υ

l

2.3. Twierdzenia o rozkładzie prędkości punktów ciała sztywnego

w ruchu dowolnym

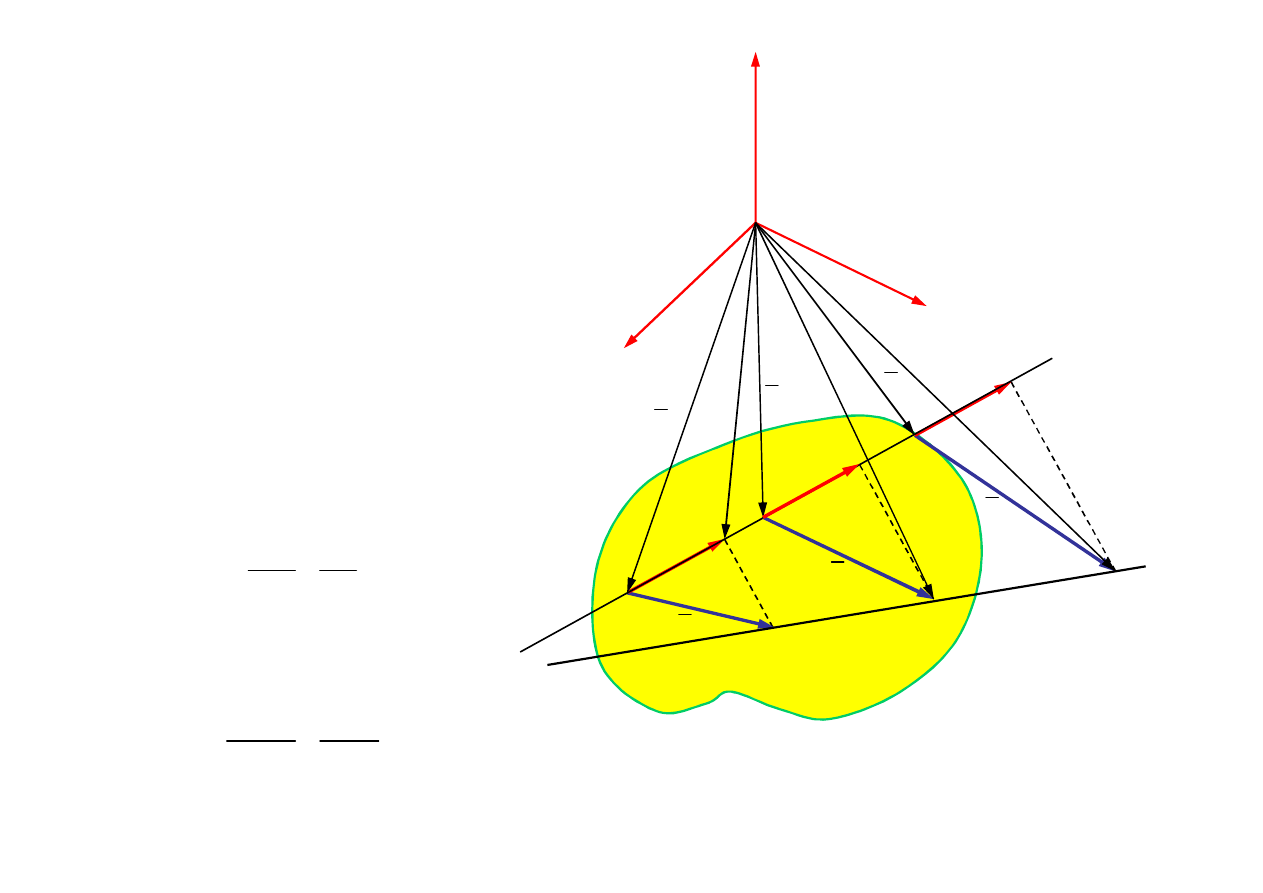
Twierdzenie 1

W ruchu dowolnym bryły sztywnej rzuty prędkości punktów leżących na
prostej na tę prostą są równe

B l

υ

A l

υ

α

β

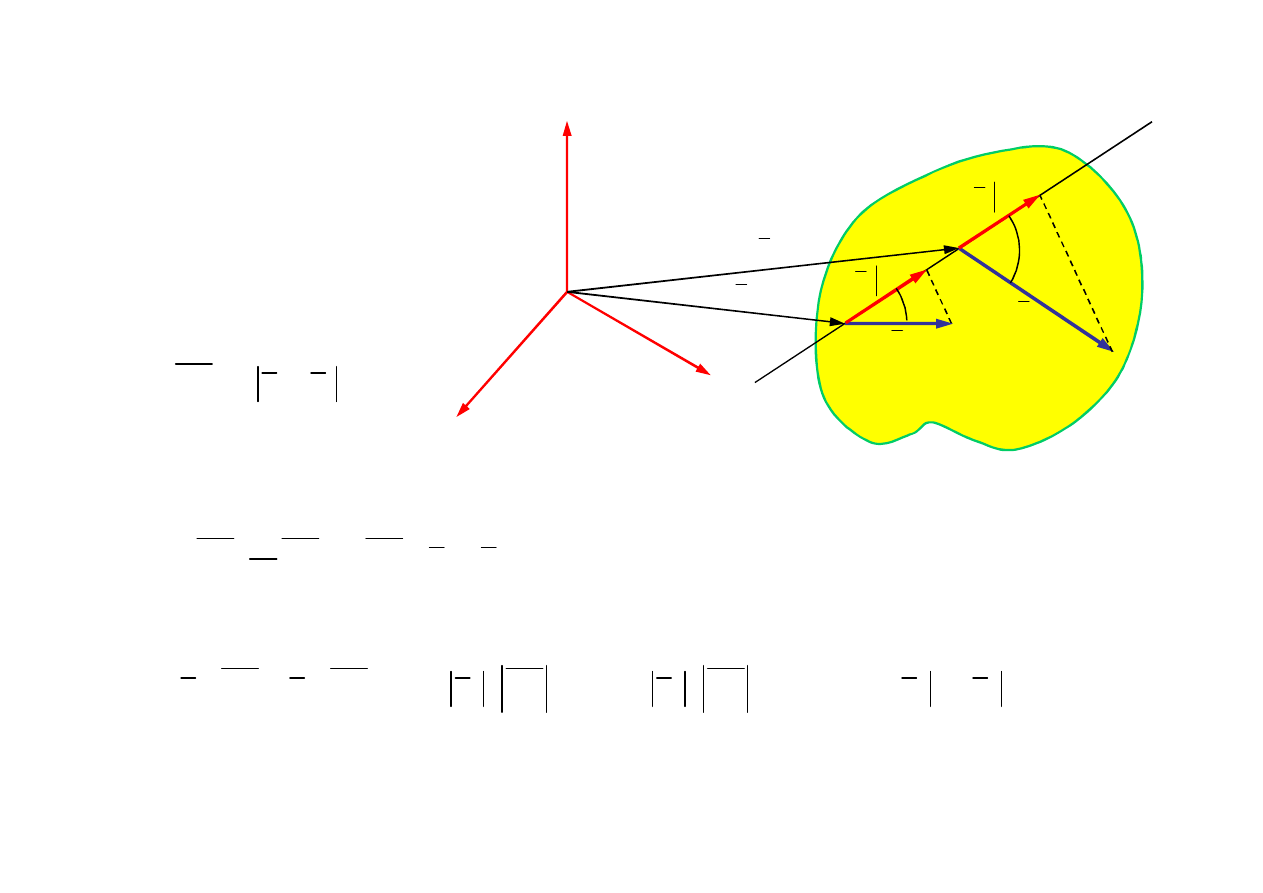
21

x

z

O

y

A

B

r

A

r

B

l

B

υ

A

υ

B l

υ

A l

υ

α

β

Dowód twierdzenia 1

2

2

B

A

AB

r

r

const











2

2

0

B

A

d

AB

AB

AB υ

υ

dt











B

A

B

A

B

A

l

l

υ

AB

υ

AB

υ

AB cos α

υ

AB cos β

υ

υ























Z założenia o sztywności
ciała

Różniczkowanie po czasie

Wykorzystując definicję iloczynu skalarnego otrzymujemy

22

x

z

O

y

A

B

r

A

r

B

B

υ

A

υ

l

M

M

υ

M

r

A'

M '

B'

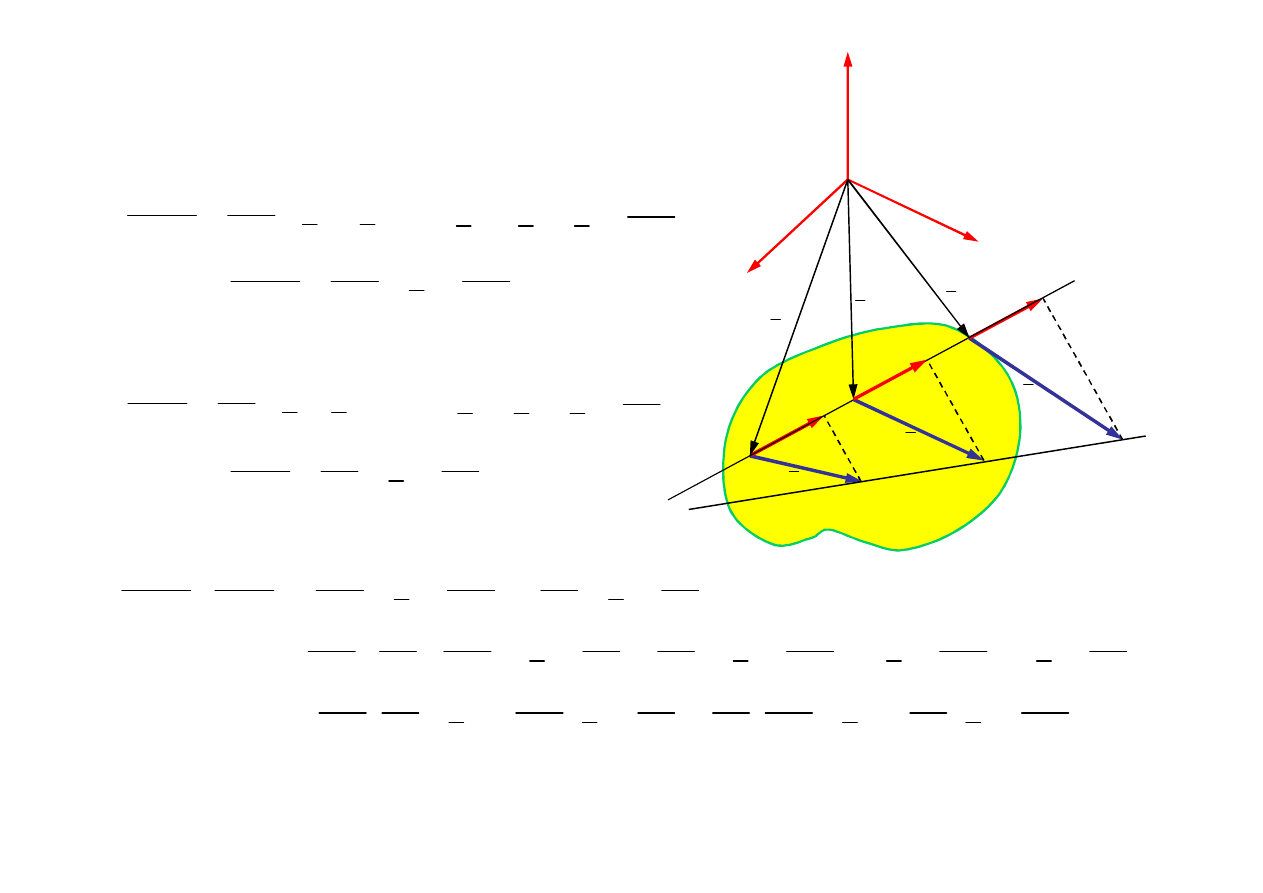
Twierdzenie 2

W ruchu dowolnym bryły sztywnej
końce wektorów prędkości
punktów leżących na prostej też
leżą na prostej

Teza

1. Rozważany obiekt to ciało sztywne

2. Punkty A, M, B leżą na prostej

Punkty A’, M’, B’ leżą na prostej

Założenie

0

AM

AB





0

A' M '

A' B'





23

Dowód twierdzenia 2

x

z

O

y

A

B

r

A

r

B

B

υ

A

υ

l

M

M

υ

M

r

A'

M '

B'

M

A

A' M '

AM

υ

υ







M

A

A

υ

υ

ω

AM







A

A' M '

AM

ω

AM







b

A

A' B'

AB υ

υ







B

A

A

υ

υ

ω

AB







A

A' B'

AB ω

AB









 









 

 



















A

A

A

A

A

A

A

A

A

A

A' M '

A' B'

AM

ω

AM

AB ω

AB

AM

AB

AM

ω

AB

AB

ω

AM

ω

AM

ω

AB

AM AB ω

AM ω

AB

AB AM

ω

AB ω

AM



































































 0

Część 3

Szczególne przypadki ruchu ciała sztywnego

25

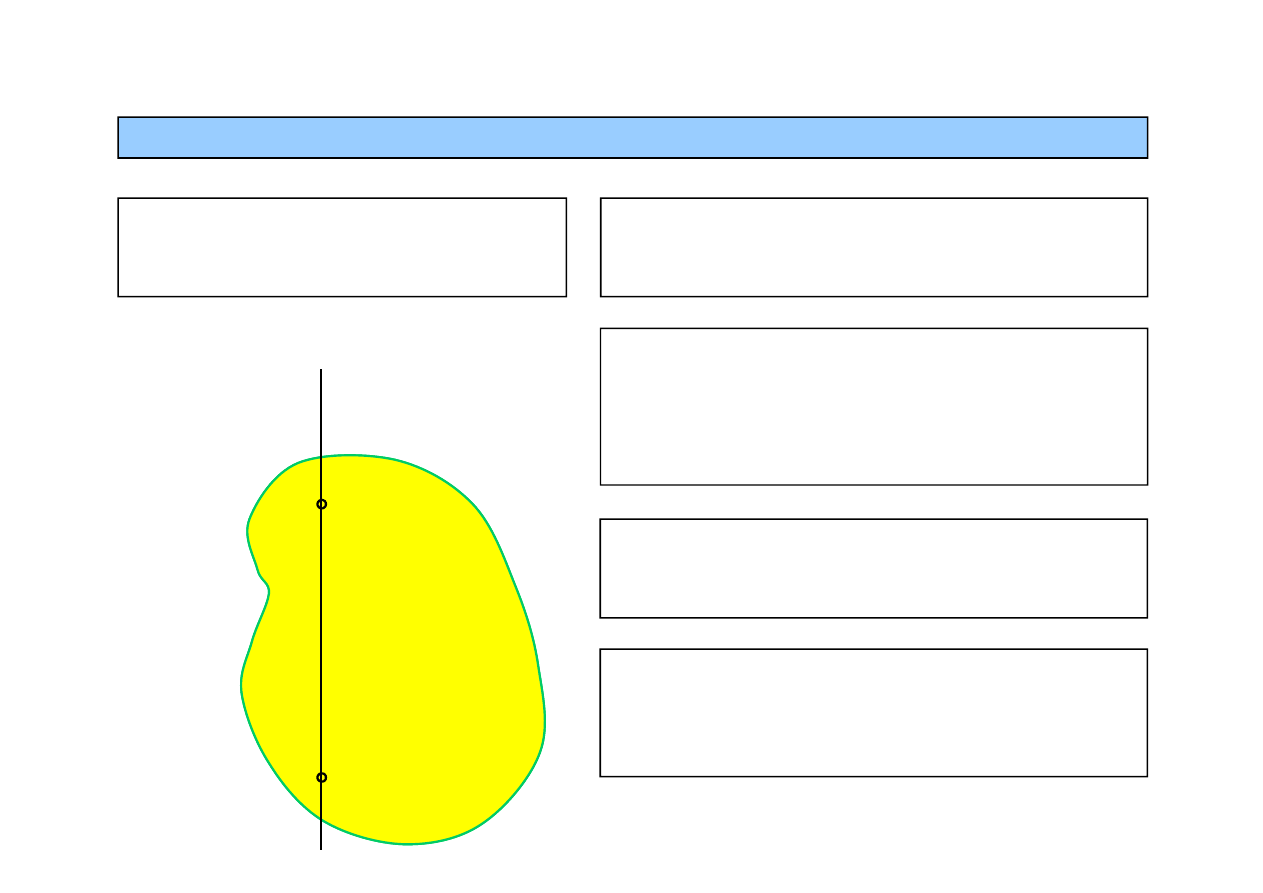
Ruch kulisty

– ruch bryły sztywnej, w którym jeden punkt bryły jest nieruchomy

Bryła unieruchomiona w jednym punkcie ma
trzy stopnie swobody – są to obroty wokół
trzech osi przechodzących przez stały punkt

3.1. Ruch kulisty bryły

Nieruchomy punkt nazywamy środkiem ruchu

1

A

Kąty Eulera są współrzędnymi uogólnionymi,
które jednoznacznie określają ten ruch

Tory punktów bryły w ruchu kulistym leżą na
sferach kulistych o środku w punkcie
unieruchomienia

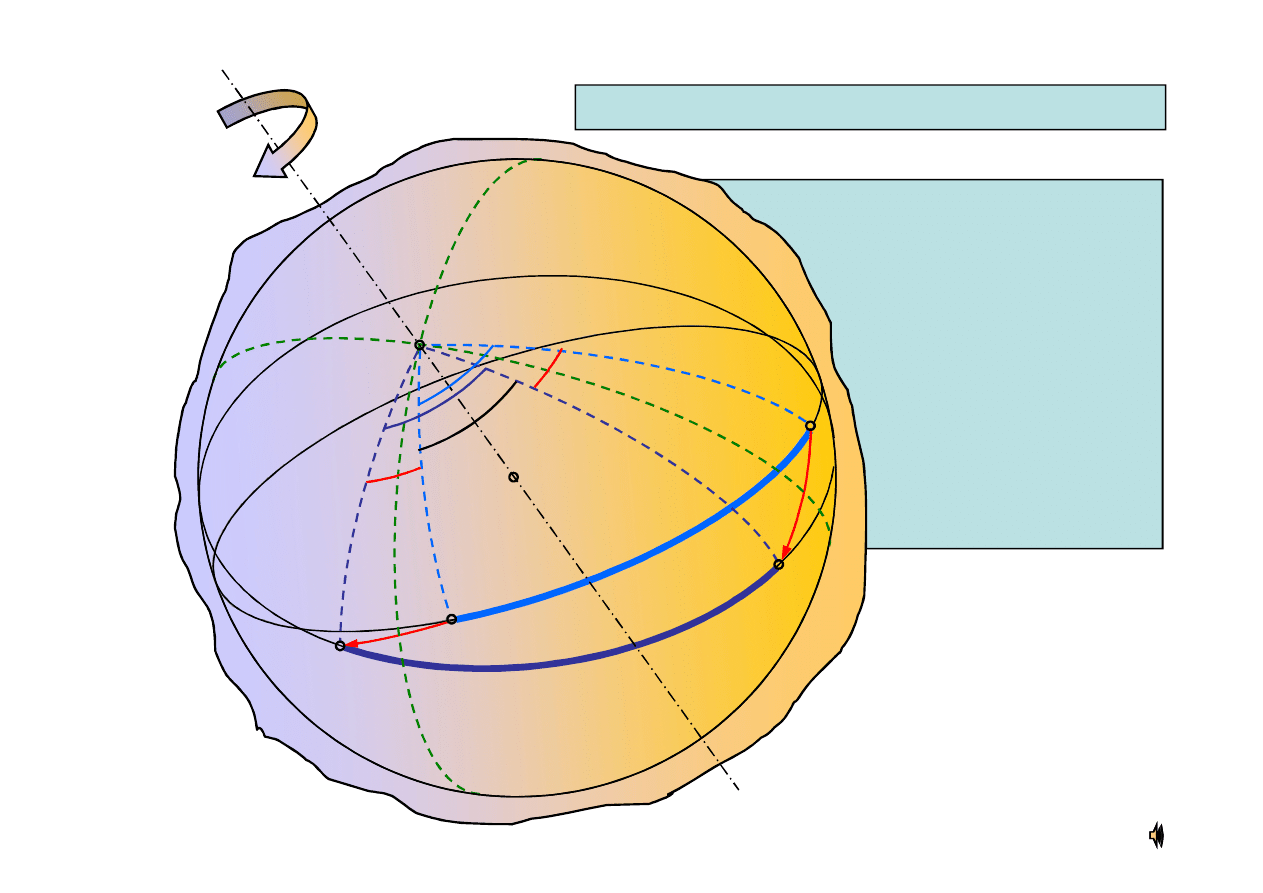
26

Jeżeli bryła jest w ruchu

kulistym i zajmuje

w kolejnych chwilach

dwa położenia to

istnieje taka oś

obrotu, względem

której można

przeprowadzić
bryłę z jednego
z tych położeń

w drugie

O

A

1

A

B

1

B

D

C

P

α

α

β

γ

γ

Twierdzenie d’Alamberta – Eulera

27

 

 

 

A

r t

r t

ρ t





- wektor wodzący początku układu ruchomego

(w ruchu kulistym równy 0)

 

A

r t

Prędkość punktów bryły sztywnej w ruchu kulistym

 

r t

- wektor wodzący w układzie nieruchomym

 

ρ t

- wektor wodzący punktu M w układzie

ruchomym (wyrażony we współrzędnych
materialnych jest niezależny od czasu)

Promień wodzący punktów bryły sztywnej we współrzędnych przestrzennych

     

 

 

 

x

y

z

x t , y t , z t

ρ t , ρ t , ρ t



















 

 

 

 





T

x t

ξ

y t

α t

η

z t

ζ





 





 







 





 

 





 





α t

- macierz przejścia z układu nieruchomego do ruchomego odpowiednia

do sposobu opisu ruchu

Promień wodzący punktów bryły sztywnej – zależność wektorowa

 

 

r t

ρ t



28

- prędkość punktów ciała sztywnego w ruchu dowolnym

A

υ

r

ω ρ









Prędkość punktów ciała sztywnego w ruchu kulistym (zależność wektorowa)

 

 

 

υ t

ω t

ρ t





W ruchu kulistym

0

A

r 



 

 

 

 

 

 

 

 

 

x

y

z

x

y

z

x

y

z

υ t ,υ

t ,υ t

ω t ,ω

t ,ω t

ρ t , ρ

t , ρ t







 













 



 

 

 

 

 

 

 





T

T

x

y

z

x

y

z

ξ

υ t ,υ

t ,υ t

ω t ,ω

t ,ω t

α t

η

ζ





 





 



















 



 





 

 





Prędkość punktów ciała sztywnego w ruchu kulistym we współrzędnych
przestrzennych

29

Przyspieszenie punktów bryły sztywnej w ruchu kulistym





A

a

r

ω ρ

ω

ω ρ





 









- przyspieszenie punktów ciała sztywnego

w ruchu dowolnym

 

 

 

 

 

 





a t

ε t

ρ t

ω t

ω t

ρ t











Przyspieszenie punktów bryły sztywnej w ruchu kulistym – zależność wektorowa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 





x

y

z

x

y

z

x

y

z

T

T

x

y

z

a t

a t ,a t ,a t

ε t

ε t ,ε

t ,ε t

ω t

ω t ,ω t ,ω t

ξ

ρ t

ρ t , ρ t , ρ t

α t

η

ζ





 







 







 







 





 

















 





 

 





Przyspieszenie punktów ciała sztywnego w ruchu kulistym we współrzędnych
przestrzennych

30

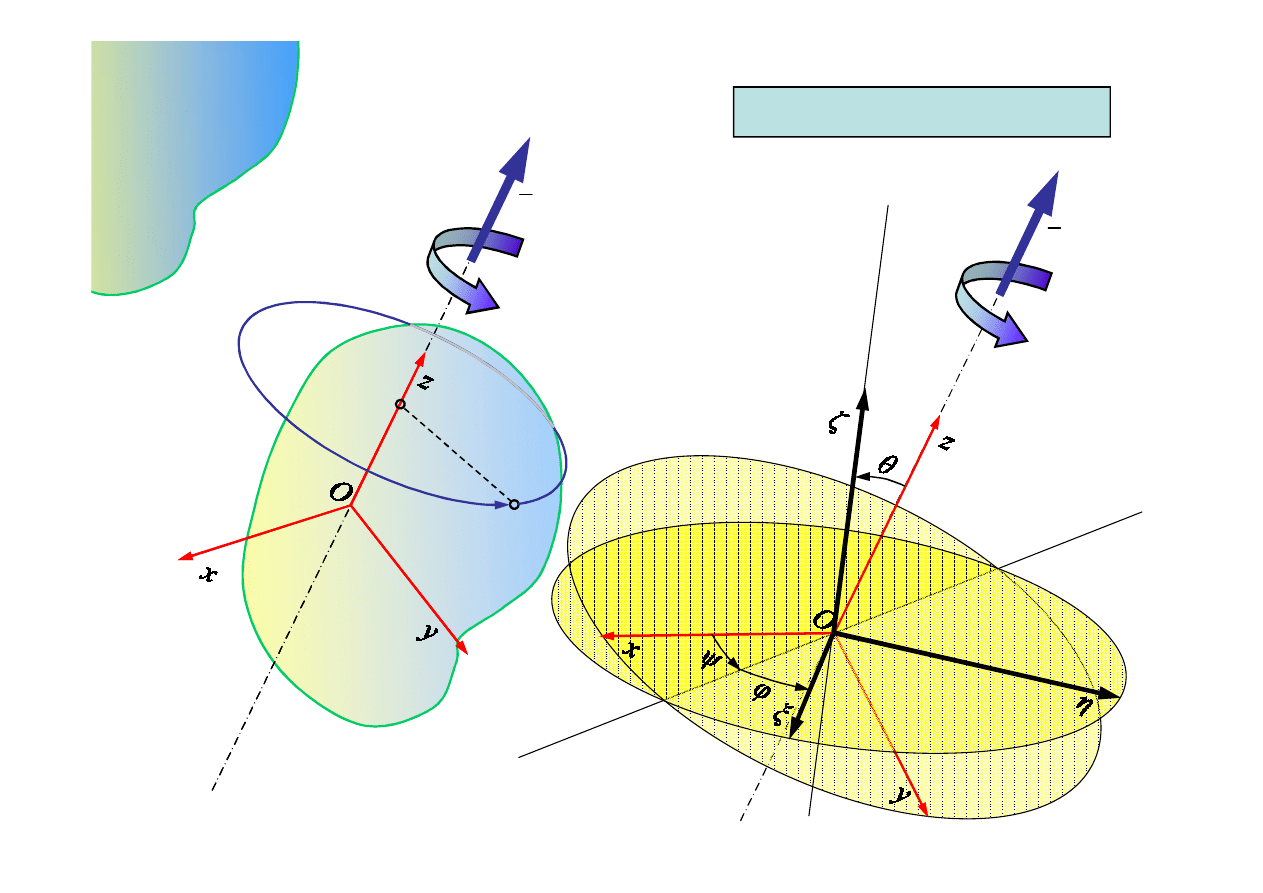
Ruch obrotowy

– ruch bryły sztywnej, w którym dwa punkty bryły są nieruchome

Bryła unieruchomiona w dwóch punktach ma
jeden stopień swobody – jest to obrót wokół
osi przechodzącej przez punkty stałe

3.2. Ruch obrotowy bryły sztywnej

Prostą przechodzącą przez dwa
nieruchome punkty nazywamy osią
obrotu

Spośród trzech kątów Eulera jednoznacznie
opisujących ten ruch tylko jeden jest
niezależny. W szczególnym przypadku, gdy
oś z, z lub linia więzów pokrywają się z osią
obrotu, dwa kąty Eulera są stałe

Torami punktów bryły w ruchu obrotowym są
okręgi leżące w płaszczyźnie prostopadłej do
osi obrotu, których środki leżą na tej osi

1

A

2

A

Ruch obrotowy jest szczególnym
przypadkiem ruchu kulistego. W tym ruchu
kierunek wektora prędkości kątowej jest stały
i pokrywa się z osią obrotu

31

oś

nut

acj

i

(lin

ia w

ięz

ów

)

o

ś

o

b

ro

tu

o

ś

ro

ta

c

ji

(o

ś

o

br

o

tu

w

ła

ś

c

iw

e

go

)

O

ś

o

b

ro

tu

l

O

ś

o

b

ro

tu

l

M

l

ω

M

O

l

ω

 

ψ

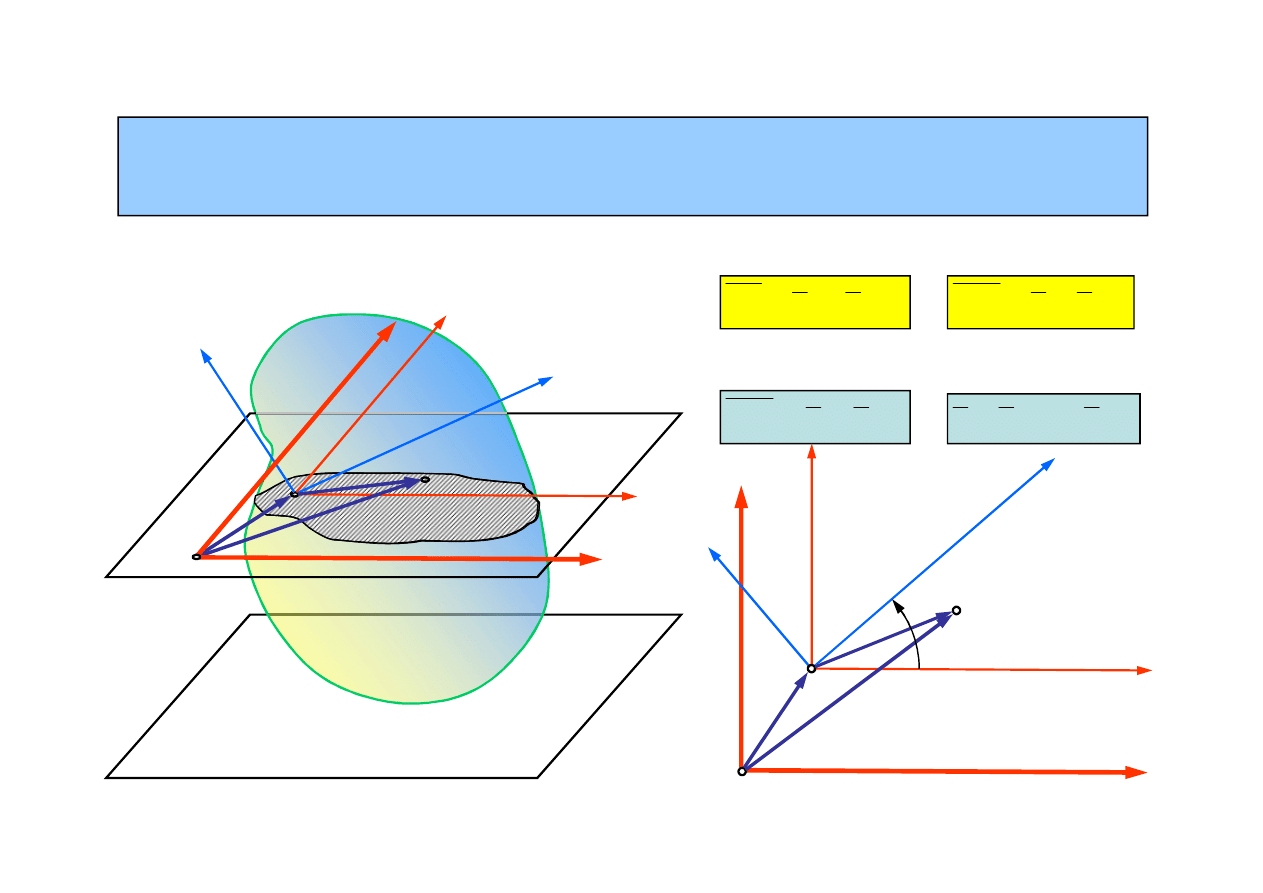
ψ t , θ

const , φ

co nst







32

0

Π

Płaszczyzna kierująca

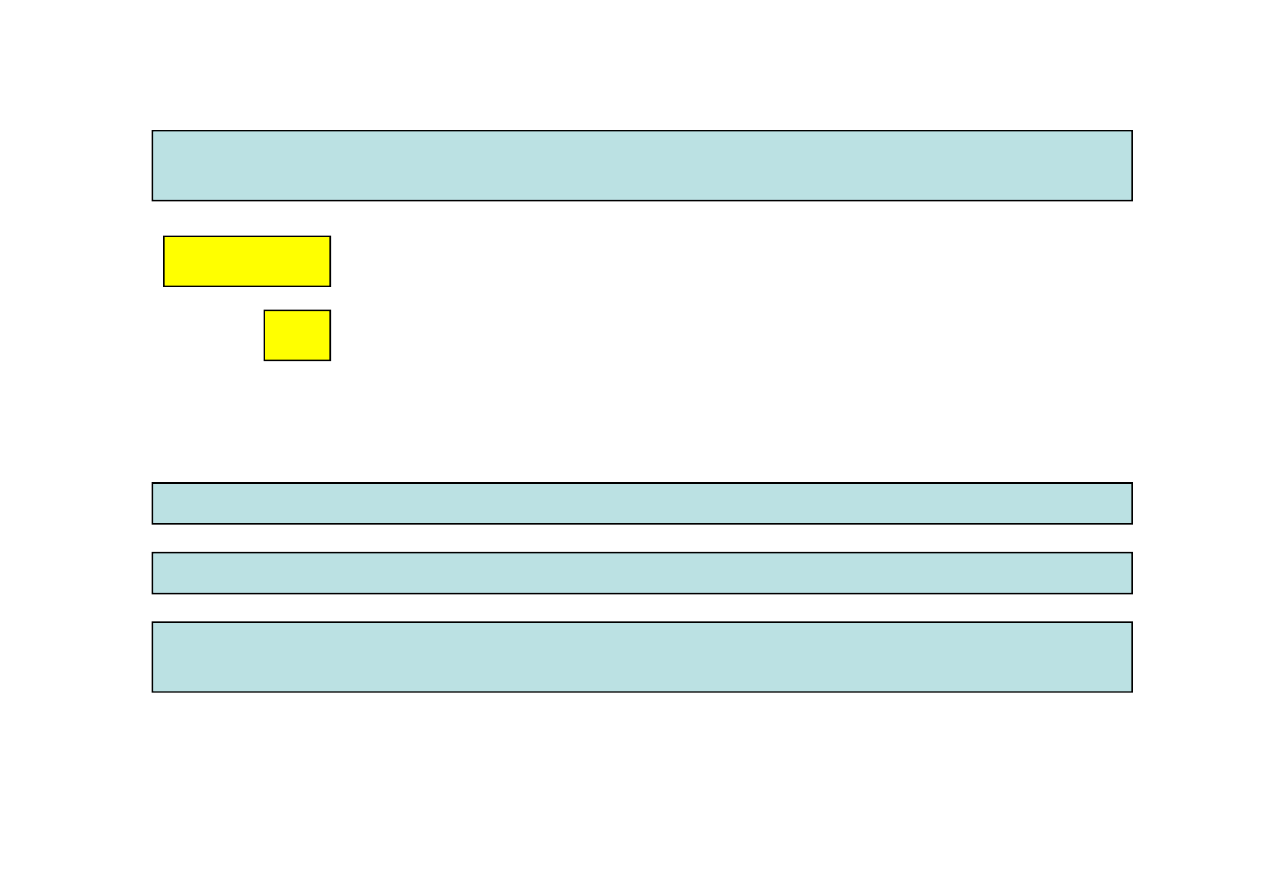
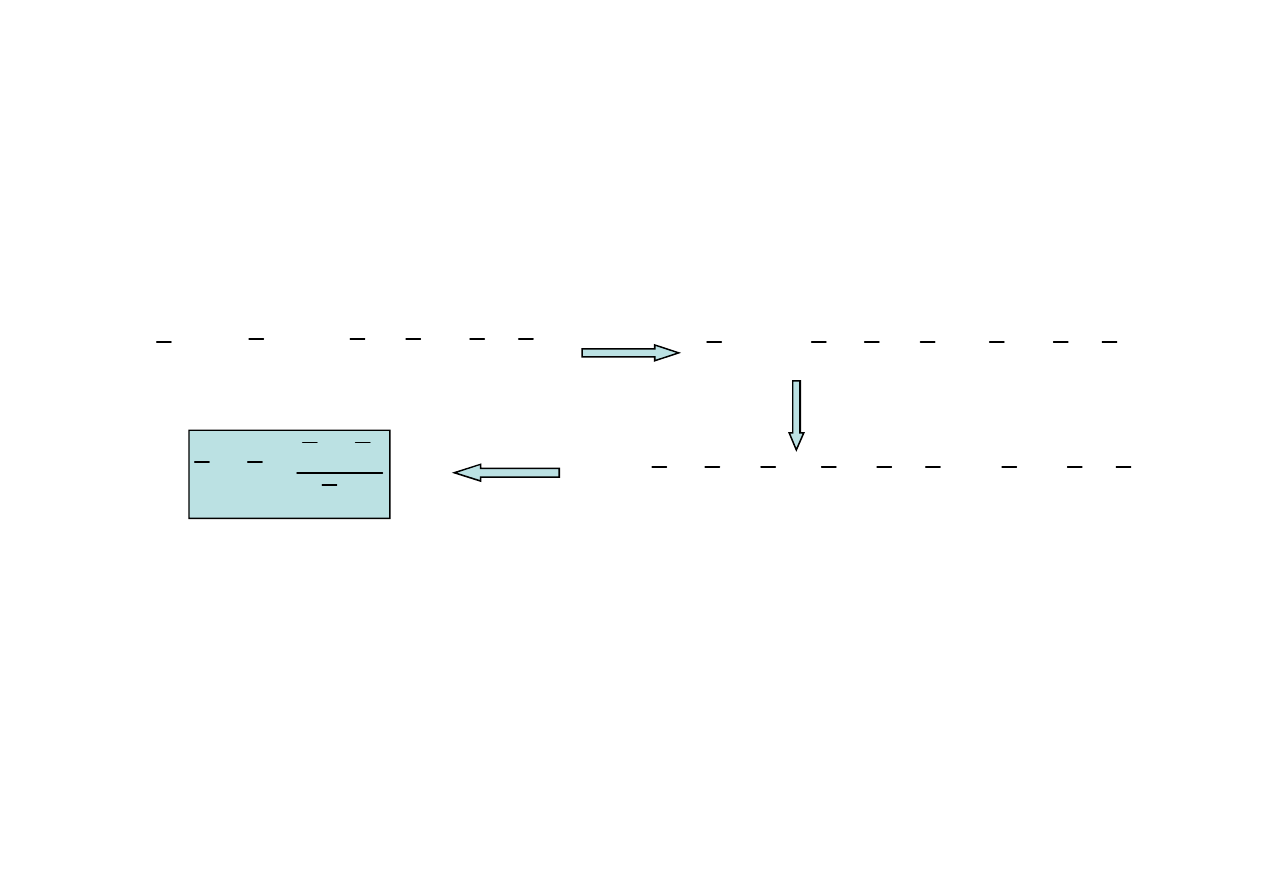
Ruch płaski

– ruch bryły sztywnej, w którym wszystkie punkty bryły poruszają się

w płaszczyznach równoległych do jednej płaszczyzny zwanej
płaszczyzną kierującą

3.3. Ruch płaski bryły sztywnej

Π

A

M

1

x

1

y

ξ

η

O

x

y

 

A

A

OA

r

r t





 

OM

r

r t





 

AM

ρ

ρ t





 

 

A

r

r t

ρ t





Opis tylko w układzie bezwzględnym

Opis w układzie przestrzennym i materialnym

O

x

y

M

ξ

η

1

x

1

y

A

φ

33

Ruch płaski bryły sztywnej jest jednoznacznie opisany za pomocą trzech
współrzędnych uogólnionych:

 

 

A

A

x

t , y

t

 

φ t

- współrzędne ustalonego punktu A określające translację

- kąt obrotu bryły wokół ustalonego punktu A

Własności ruchu płaskiego

Tory punktów leżą w płaszczyznach równoległych do płaszczyzny kierującej

Kierunek wektora prędkości obrotowej jest prostopadły do płaszczyzny kierującej

Ruch płaski jest złożeniem ruchu postępowego ustalonego punktu i ruchu obrotowego
wokół tego punktu

34

 

 

 

 

 

 





 





 





 





0

0

0

0

1

A

A

A

cos α t

sin α t

x t

x

t

ξ

y t

y

t

sin α t

cos α t

η

z t

z

ζ















 













 



















 













 

 

















 





 





 





 





 





0

0

0

0

1

cos α t

sin α t

α t

sin α t

cos α t









 

















Współrzędne dowolnego punktu M w ruchu płaskim bryły sztywnej

 

 

 

A

r t

r t

ρ t





     

 

 

 

 

A

A

A

x

y

z

x t , y t ,z t

x

t , y

t ,z

ρ t , ρ t , ρ























 



     

 

 

 





T

T

A

A

A

ξ

x t , y t ,z t

x

t , y

t ,z

α t

η

ζ





 





 



















 



 





 

 





35

Prędkość punktów bryły sztywnej w ruchu płaskim

- prędkość punktów ciała sztywnego w ruchu dowolnym

A

υ

r

ω ρ









Prędkość punktów ciała sztywnego w ruchu płaskim (zależność wektorowa)

 

 

 

 

A

υ t

υ

t

ω t

ρ t







 

 

 

 

 

 

 

 

0

0 0

x

y

z

Ax

Ay

z

x

y

z

υ t ,υ

t ,υ t

υ

t ,υ

t ,

, ,ω t

ρ

t , ρ

t , ρ







































 

 

 

 

 

 

 





0

0 0

T

T

x

y

z

Ax

Ay

z

ξ

υ t ,υ

t ,υ t

υ

t ,υ

t ,

, ,ω t

α t

η

ζ





 





 



































 





 

 





Prędkość punktów ciała sztywnego w ruchu płaskim we współrzędnych
przestrzennych

36

Przyspieszenie punktów bryły sztywnej w ruchu płaskim





A

a

r

ω ρ

ω

ω ρ





 









- przyspieszenie punktów ciała sztywnego

w ruchu dowolnym

 

 

 

 

 

 

 





A

a t

a

t

ε t

ρ t

ω t

ω t

ρ t













Przyspieszenie punktów bryły sztywnej w ruchu płaskim – zależność wektorowa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 





0

0 0

0 0

x

y

z

A

Ax

Ay

z

z

T

T

x

y

z

a t

a t ,a

t ,a t

a

t

a

t ,a

t ,

ε t

, ,ε t

ω t

, ,ω t

ξ

ρ t

ρ t , ρ t , ρ

α t

η

ζ





 







 



 







 











 





 

















 





 

 





Przyspieszenie punktów ciała sztywnego w ruchu płaskim we współrzędnych
przestrzennych

37





0

P

A

A

P

A

υ

υ

ω

r

r











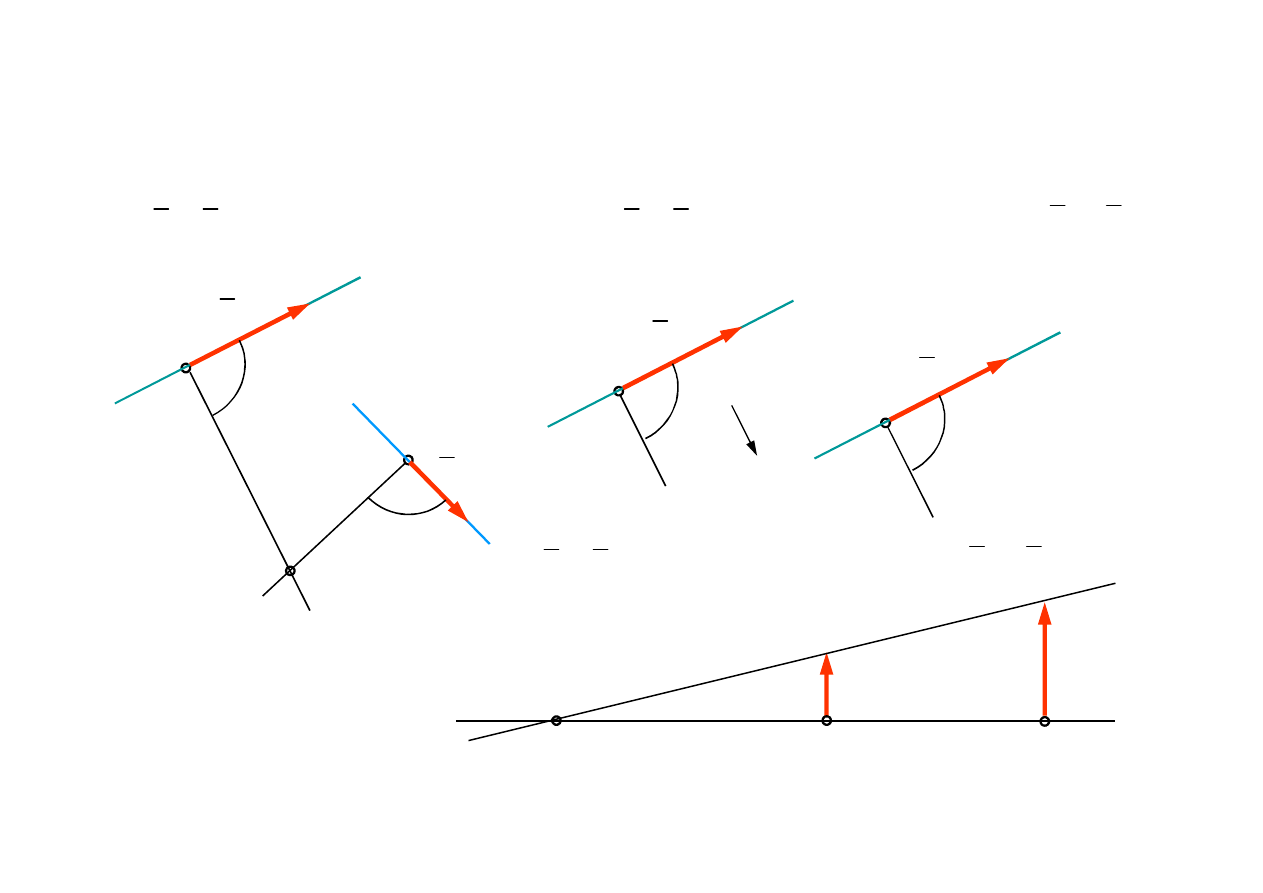
Chwilowy środek obrotu jest to punkt płaszczyzny, który w danej chwili w ruchu płaskim
bryły sztywnej jest nieruchomy. Chwilowy środek obrotu nie musi być punktem bryły.

Chwilowy środek obrotu

A

ω

/







0

P

A

A

A

A

P

A

υ

ω

υ

ω

ω

r

r































2

0

A

A

A

A

P

A

A

P

A

ω

υ

ω

ω

r

r

ω

r

r



























2

A

A

P

A

A

ω

υ

r

r

ω







Powyższa zależność pozwala wyznaczyć położenie chwilowego środka obrotu
w ogólnym przypadku

38

Wyznaczanie chwilowego środka obrotu w oparciu o znane prędkości dwóch punktów

0

A

B

υ

υ





A

υ

B

υ

(kierunki równoległe) oraz

A

B

P

0

A

B

υ

υ





(kierunki nie równoległe)

A

B

υ

υ



A

υ

A

B

υ

B

P



0

A

B

υ

υ





(kierunki równoległe) oraz

A

B

υ

υ



P

A

B

Uwaga: w tym przypadku prędkości muszą być znane

39

Ruch ogólny

– ruch bryły sztywnej, opisany sześcioma współrzędnymi

uogólnionymi, z których każda jest funkcją czasu

3.4. Ogólny przypadek ruchu bryły sztywnej

 

A

A

x

x

t



 

A

A

y

y

t



 

A

A

z

z

t



 

φ

φ t



 

ψ

ψ t



 

θ

θ t



- współrzędne ustalonego

punktu

- kąty Eulera

Współrzędne dowolnego punktu M w ruchu dowolnym bryły sztywnej

 

 

 

A

r t

r t

ρ t





     

 

 

 

 

 

 

A

A

A

x

y

z

x t , y t ,z t

x

t , y

t ,z

t

ρ t , ρ t , ρ t























 



     

 

 

 

 





T

T

A

A

A

ξ

x t , y t ,z t

x

t , y

t ,z

t

α t

η

ζ





 





 



















 



 





 

 





40

Prędkość punktów bryły sztywnej w ruchu dowolnym

- prędkość punktów ciała sztywnego w ruchu dowolnym

A

υ

r

ω ρ









Prędkość punktów ciała sztywnego w ruchu dowolnym (zależność wektorowa)

 

 

 

 

A

υ t

υ

t

ω t

ρ t







 

 

 

 

 

 

 

 

 

 

 

 

x

y

z

Ax

Ay

Az

x

y

z

x

y

z

υ t ,υ

t ,υ t

υ

t ,υ

t ,υ

t

ω t ,ω

t ,ω t

ρ

t , ρ

t , ρ t























 







 



 

 

 

 

 

 

 

 

 

 





T

T

x

y

z

Ax

Ay

Az

x

y

z

ξ

υ t ,υ

t ,υ t

υ

t ,υ

t ,υ

t

ω t ,ω

t ,ω t

α t

η

ζ





 





 





























 



 





 

 





Prędkość punktów ciała sztywnego w ruchu dowolnym we współrzędnych
przestrzennych

41

Przyspieszenie punktów bryły sztywnej w ruchu dowolnym





A

a

r

ω ρ

ω

ω ρ





 









- przyspieszenie punktów ciała sztywnego

w ruchu dowolnym

 

 

 

 

 

 

 





A

a t

a

t

ε t

ρ t

ω t

ω t

ρ t













Przyspieszenie punktów bryły sztywnej w ruchu dowolnym – zależność wektorowa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 





x

y

z

A

Ax

Ay

Az

x

y

z

x

y

z

T

T

x

y

z

a t

a t ,a t ,a t

a

t

a

t ,a

t ,a

t

ε t

ε t ,ε

t ,ε t

ω t

ω t ,ω t ,ω t

ξ

ρ t

ρ t , ρ t , ρ t

α t

η

ζ





 







 







 







 







 





 

















 





 

 





Przyspieszenie punktów ciała sztywnego w ruchu dowolnym we współrzędnych
przestrzennych

Część 4

Wyznaczanie prędkości kątowej i przyspieszenia kątowego

za pomocą kątów Eulera

43

O

x

y

z

θ

ζ

ξ

φ

η

ψ

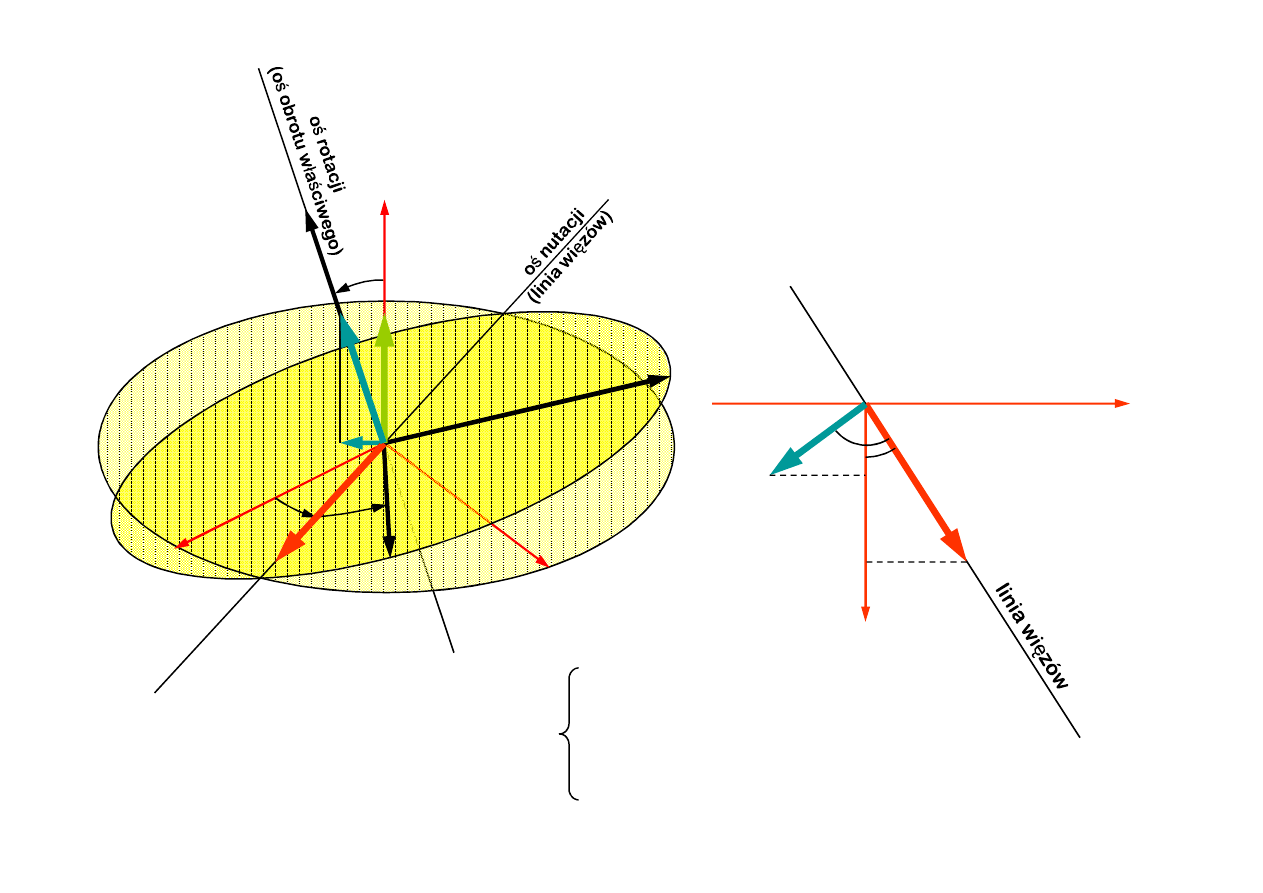
4.1. Wyznaczenie prędkości kątowych

Widok od osi z

φ

ψ

θ

θ

φ sinθ



ψ

y

x

x

y

z

ω

φ sinθ sinψ

θ cos ψ

ω

φ sinθ cosψ

θ sinψ

ω

ψ

φcos θ





 



















Współrzędne wektora prędkości
kątowej w układzie Oxyz

44

O

x

y

z

θ

ζ

ξ

φ

η

ψ

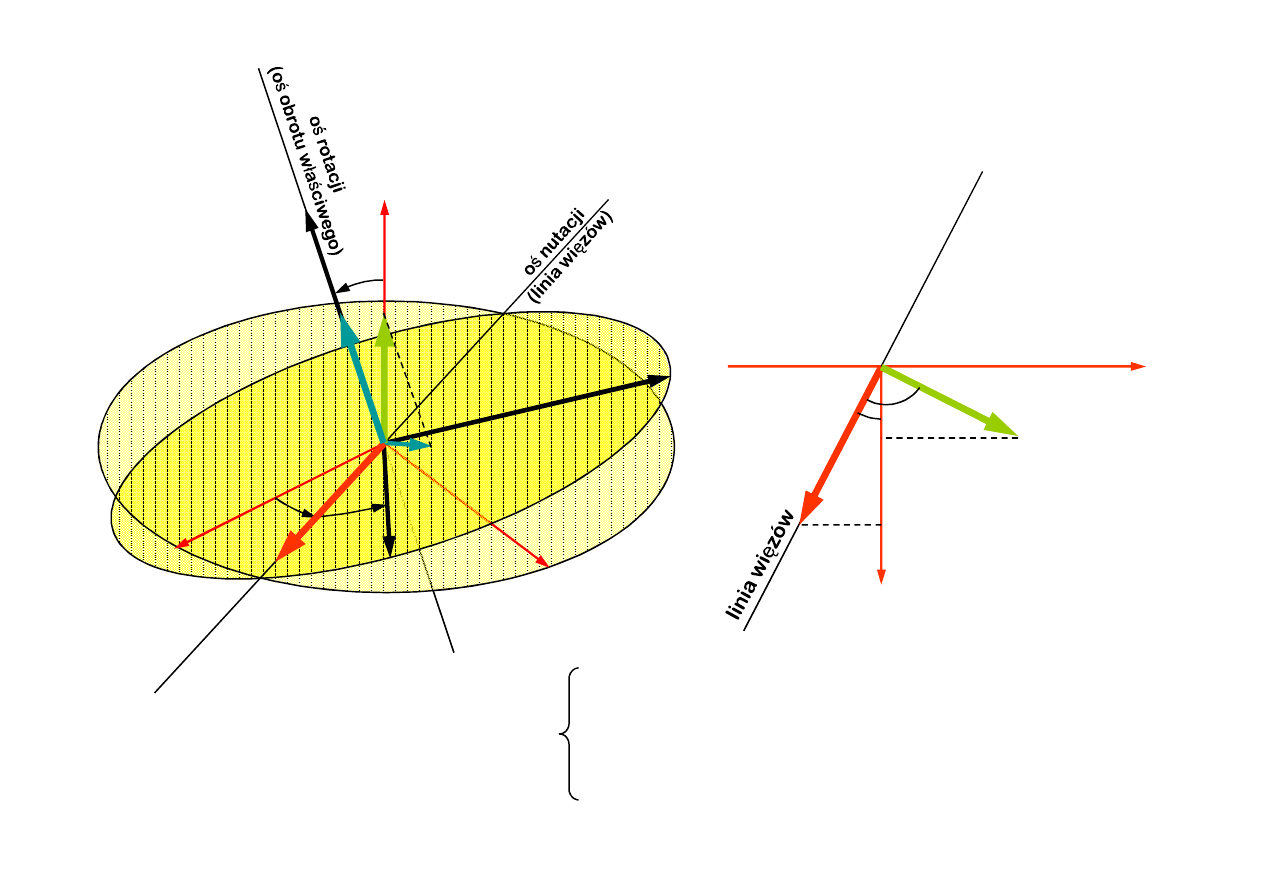
Widok od osi z

φ

ψ

θ

θ

ψ sin θ



φ

η

ξ

ξ

η

ζ

ω

ψ sinθ sin φ θ cos φ

ω

ψ sin θ cos φ θ sin φ

ω

φ ψ cos θ

























Współrzędne wektora prędkości
kątowej w układzie Oxhz

45