1

Kondensator - Zadanie 1

Treść:
Oblicz pojemności przedstawionych na rysunkach układów kondensatorów o
pojemności C każdy.

Dane:
C

Szukane:
pojemność zastępcza

Wzory:

Rozwiązanie:
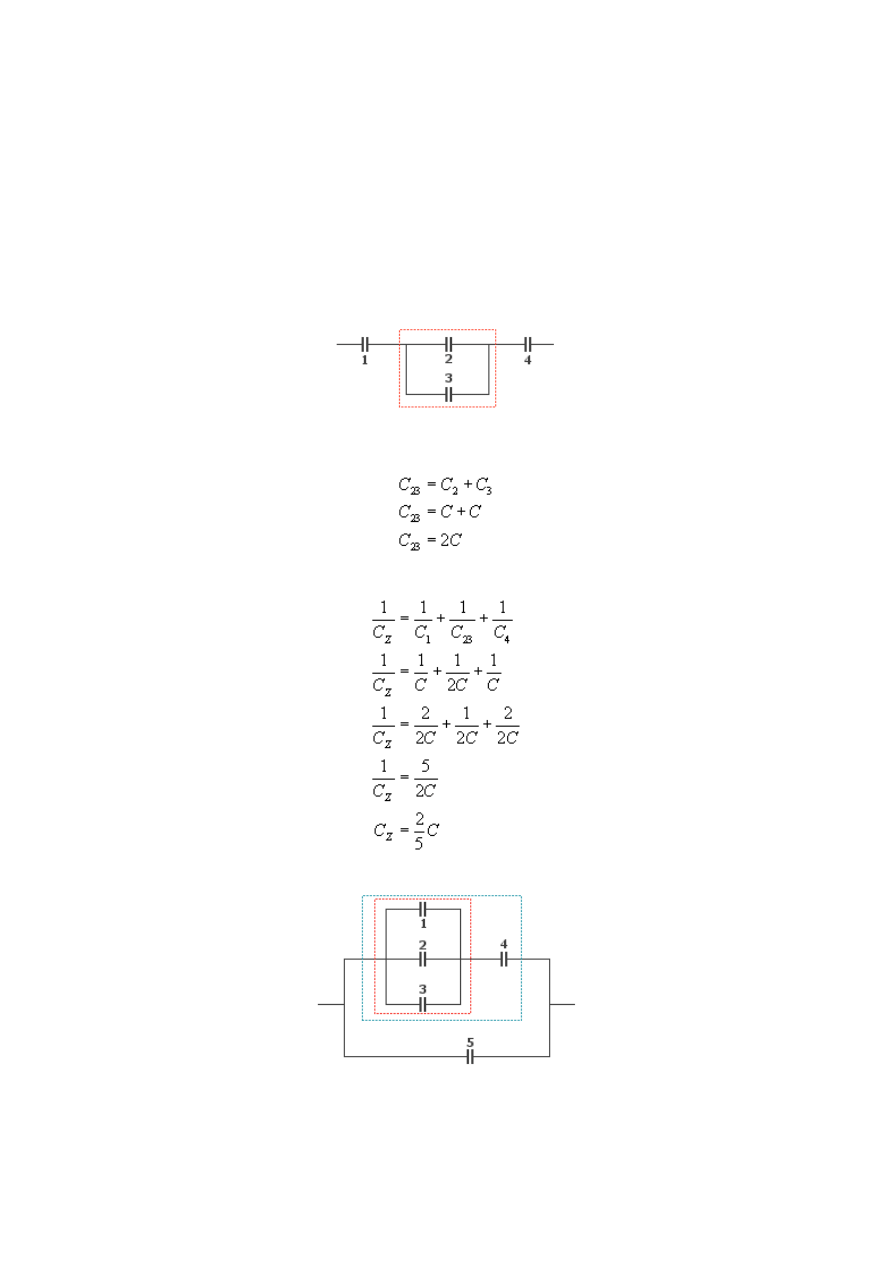
a)

Najpierw policzymy pojemność układu kondensatorów połączonych równolegle,
zaznaczonych czerwoną przerywaną linią

Teraz mamy układ kondensatorów połączonych szeregowo, zatem pojemność zastępcza:

b)

Liczymy pojemność układu równoległego otoczonego czerwoną linią

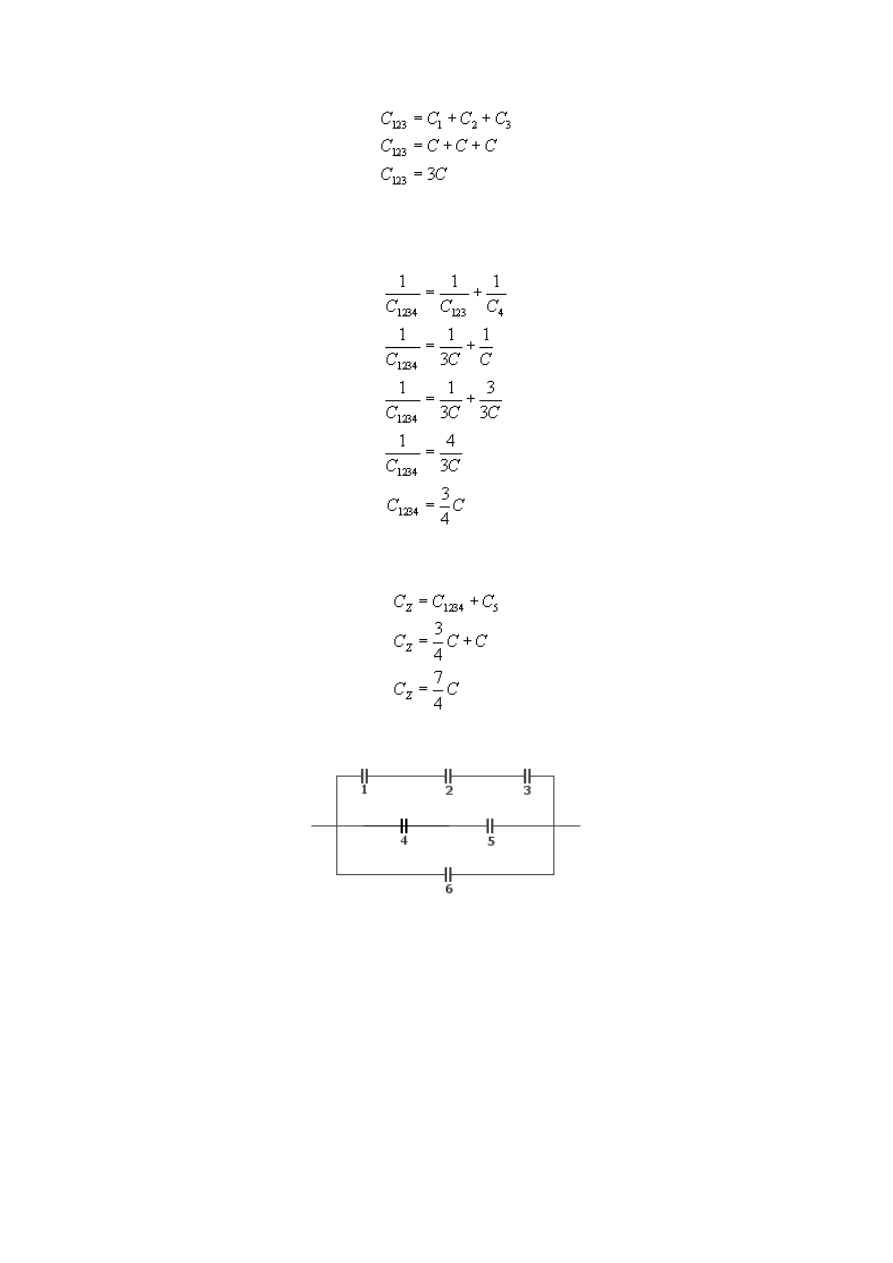
2

Teraz czas rozpatrzyć układ połączony szeregowo, otoczony niebieską linią

Czas policzyć pojemność zastępczą, czyli układu dwóch kondensatorów połączonych
równolegle

c)

Znajdujemy pojemności kondensatorów połączonych szeregowo, znajdujących się na każdej
gałęzi połączenia równoległego

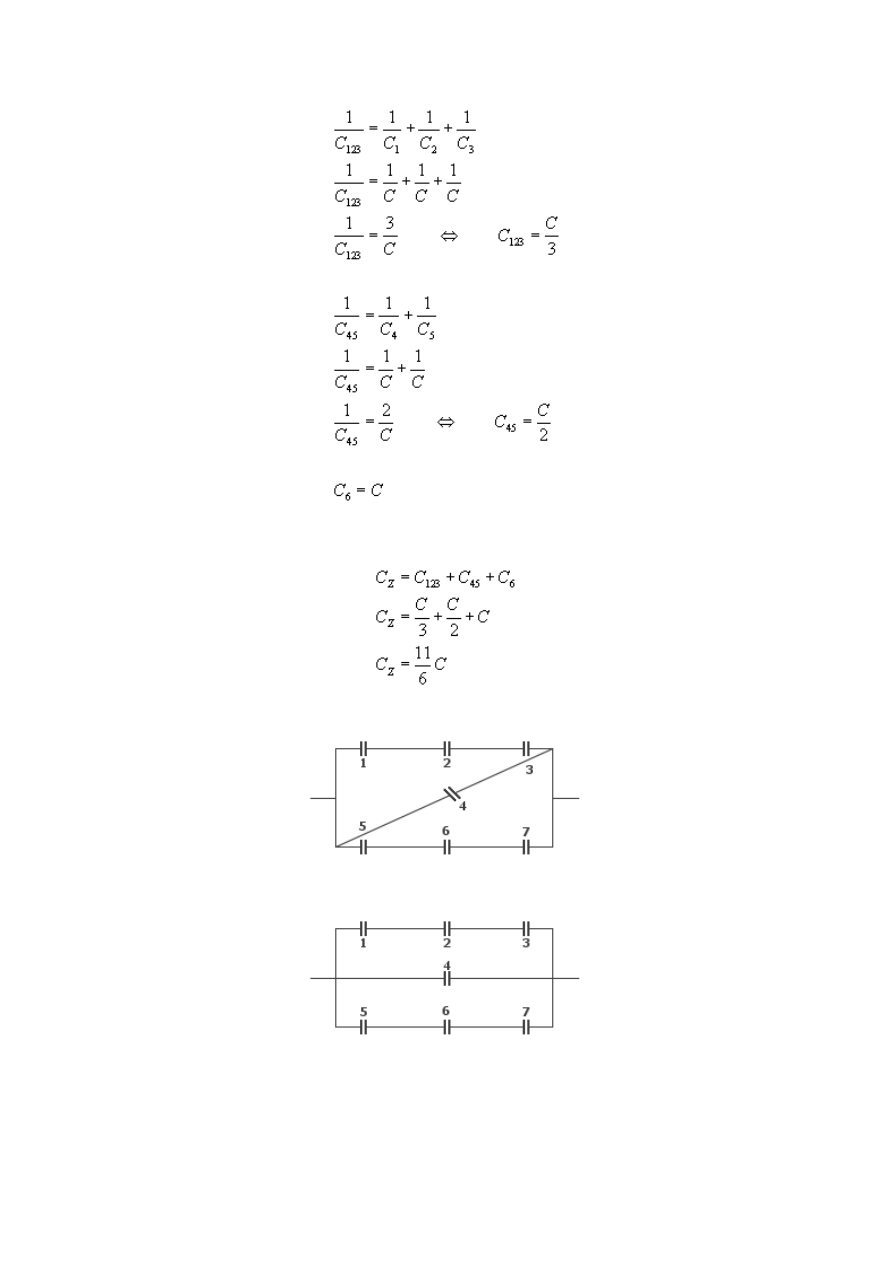
3

Teraz obliczamy pojemność zastępczą, czyli pojemność kondensatorów połączonych
równolegle:

d)

To zadanie wydaje się tylko być trudne - powyższy rysunek można zapisać także w postaci:

Podobnie jak w przykładzie d) najpierw liczymy pojemności kondensatorów połączonych
szeregowo...

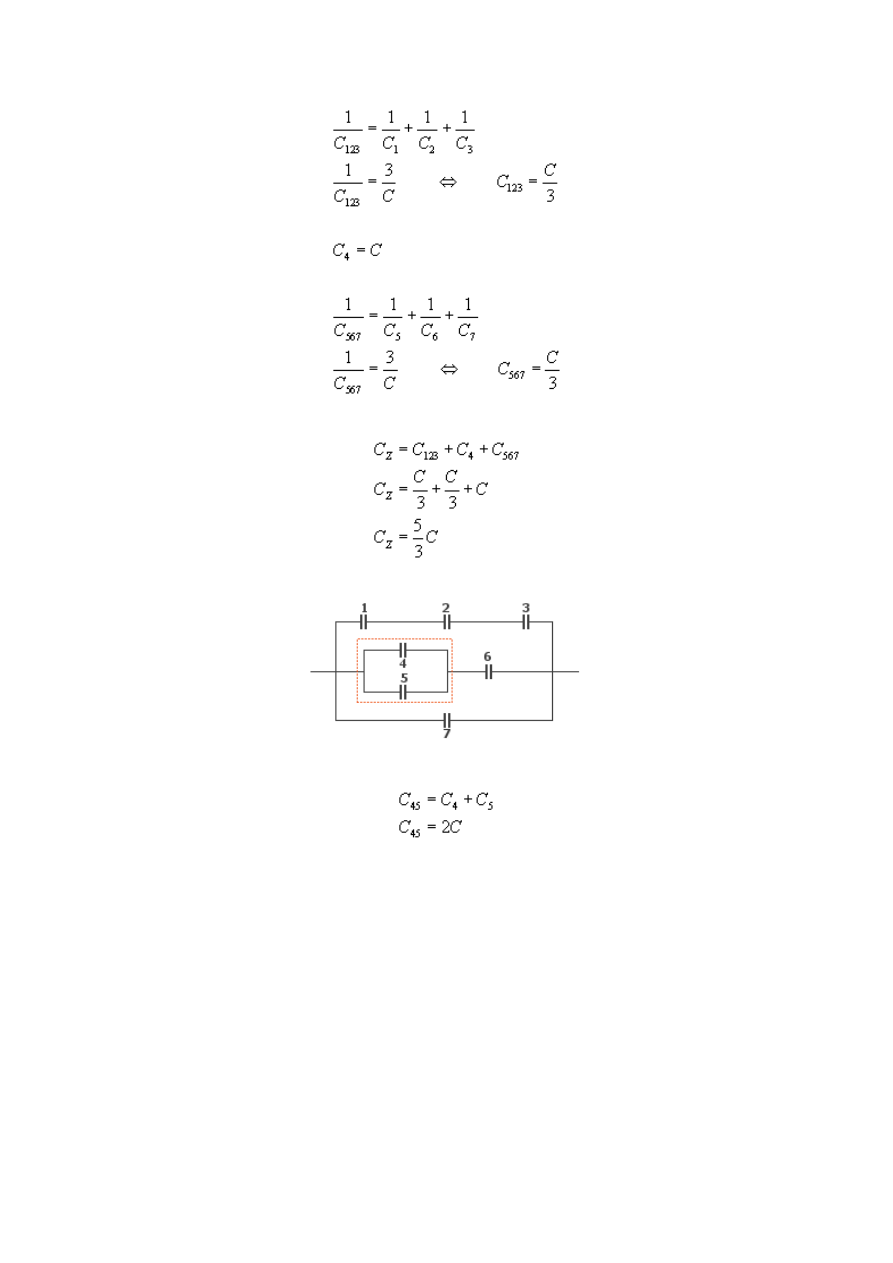
4

...a potem równolegle

e)

Szukamy pojemności układu równoległego otoczonego czerwoną przerywaną linią

Teraz mamy sytuację podobną jak w przykładach d) i e). Liczymy pojemność kondensatorów
połączonych szeregowo

5

potem połączonych równolegle:

Jamnik

Kondensator - Zadanie 2

Treść:
Okładki kondensatora płaskiego o powierzchni S=200cm

2

rozsunięto z odległości

d

1

=0.1cm na d

2

=0.4cm. Oblicz jak zmieni się energia kondensatora, jeżeli był on

cały czas podłączony do baterii o różnicy potencjałów U=300V.

Dane:
S = 200 cm

2

= 0.02 m

2

d

1

= 0.1 cm = 0.001 m

d

2

= 0.4 cm = 0.004 m

U = 300 V

Szukane:
ΔE = ?

Wzory:

Rozwiązanie:
Najpierw policzymy pojemności kondensatorów przed (C

1

) i po (C

2

) rozsunięciu okładek

kondensatora. Mamy więc

6

Teraz policzymy energie kondensatorów przed i po rozsunięciu okładek. Ponieważ
kondensator podłączony jest stale do napięcia, to w takim razie U = const. Z trzech wzorów
na energię musimy wybrać ten najlepszy, z którego najłatwiej nam się policzy. Na pewno w
tym wzorze musi być pojemność C. A ponieważ mamy stałe napięcie U, skorzystamy też
właśnie z niego. Wybieramy więc wzór

Zatem

Naszym zadaniem jest znaleźć zmianę energii

Sprawdźmy jednostkę

Zmiana energii kondensatora wynosi około 5.97 µJ.

7

Kondensator - Zadanie 3

Treść:
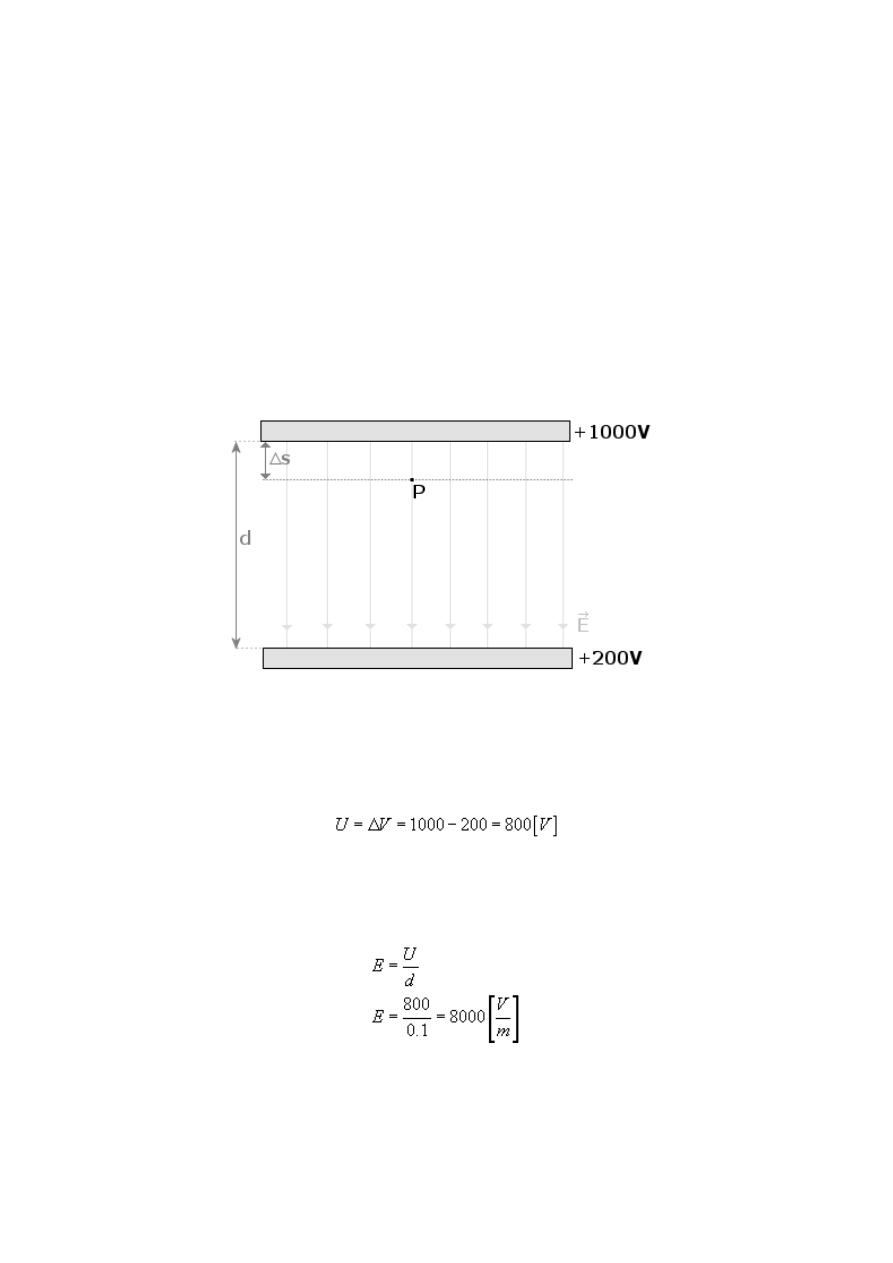
Dwie równoległe płytki ustawiono w odległości d=10cm od siebie i naładowano
do potencjałów +1000V i +200V. Jaka jest wartość i kierunek natężenia pola w
punkcie P odległym o Δs=2cm od płytki o potencjale +1000V? Jaki jest potencjał
w tym punkcie?

Dane:
d = 10 cm = 0.1 m
V

1

= 1000 V

V

2

= 200 V

Δs = 2 cm = 0.02 m

Szukane:
E = ?
V = ?

Wzory:

Rysunek:

Rozwiązanie:
Mamy dwie płyty tworzące kondensator oddalone o d naładowane do zadanych potencjałów.
Napięcie to różnica potencjałów kondensatora, a więc

Linie sił pola wewnątrz kondensatora skierowane są od potencjału wyższego do potencjału
niższego i taki będzie kierunek wektora natężenia pola w punkcie P, podobnie jak w innych
punktach. Ponieważ jest to pole jednorodne, to wartość natężenia będzie w każdym punkcie
pola taka sama, a jej wartość wynosi

Jak obliczyć potencjał w punkcie P?
Korzystamy z tego samego wzoru, z tym że zamiast d przyjmujemy Δs

8

A więc pomiędzy płytą o potencjale 1000 V a punktem P panuje napięcie 160 V Korzystamy
znów z definicji napięcia

Oznacza to, że w punkcie P jest potencjał 840 V.

Kondensator - Zadanie 4

Treść:
Przenosząc ładunek 1C w jednorodnym polu elektrycznym na odległość 5cm -
równolegle do linii pola - wykonano pracę 1J. Ile wynosi natężenie pola?

Dane:
q = 1 C
Δs = 5cm = 0.05 m
W = 1 J

Szukane:
E = ?

Wzory:

Rozwiązanie:
Pamiętajmy, że w polu jednorodnym natężenie w każdym punkcie jest identyczne i oblicza
się je jako iloraz napięcia (czyli różnicy potencjałów w dwóch punktach) i odległości (o jaką
są te punkty oddalone). Przyjmujemy zatem, że natężenie E:

Musimy znaleźć napięcie na odcinku Δs. Ponieważ daną mamy pracę, korzystamy z jednego
ze wzorów na pracę w polu elektrostatycznym, a mianowicie z

Z tego wzoru wyprowadzamy wzór na napięcie...

...i wstawiamy go do wzoru na szukane natężenie:

9

Sprawdzamy jednostkę (pamiętajmy, że jednostką natężenia pola jest wolt na metr)

Iloraz pracy przez ładunek to oczywiście napięcie.

Natężenie pola jednorodnego jest równe 20 V/m.

Kondensator - Zadanie 5

Treść:
Kulę o promieniu r naładowano ładunkiem Q. Ile wynosi pojemność kuli?

Dane:
r
Q

Szukane:
C = ?

Wzory:

Rozwiązanie:
Kulę naładowano ładunkiem Q. W skład tego ładunku wchodzą ładunki elementarne q

i

, które

zgodnie z prawami elektrostatyki rozmieszczają się równomiernie na powierzchni kuli.

Każdy taki ładunek elementarny oddalony jest od środka kuli o r i jest tam potencjał V

i

(i = 1,

2, ..., n)

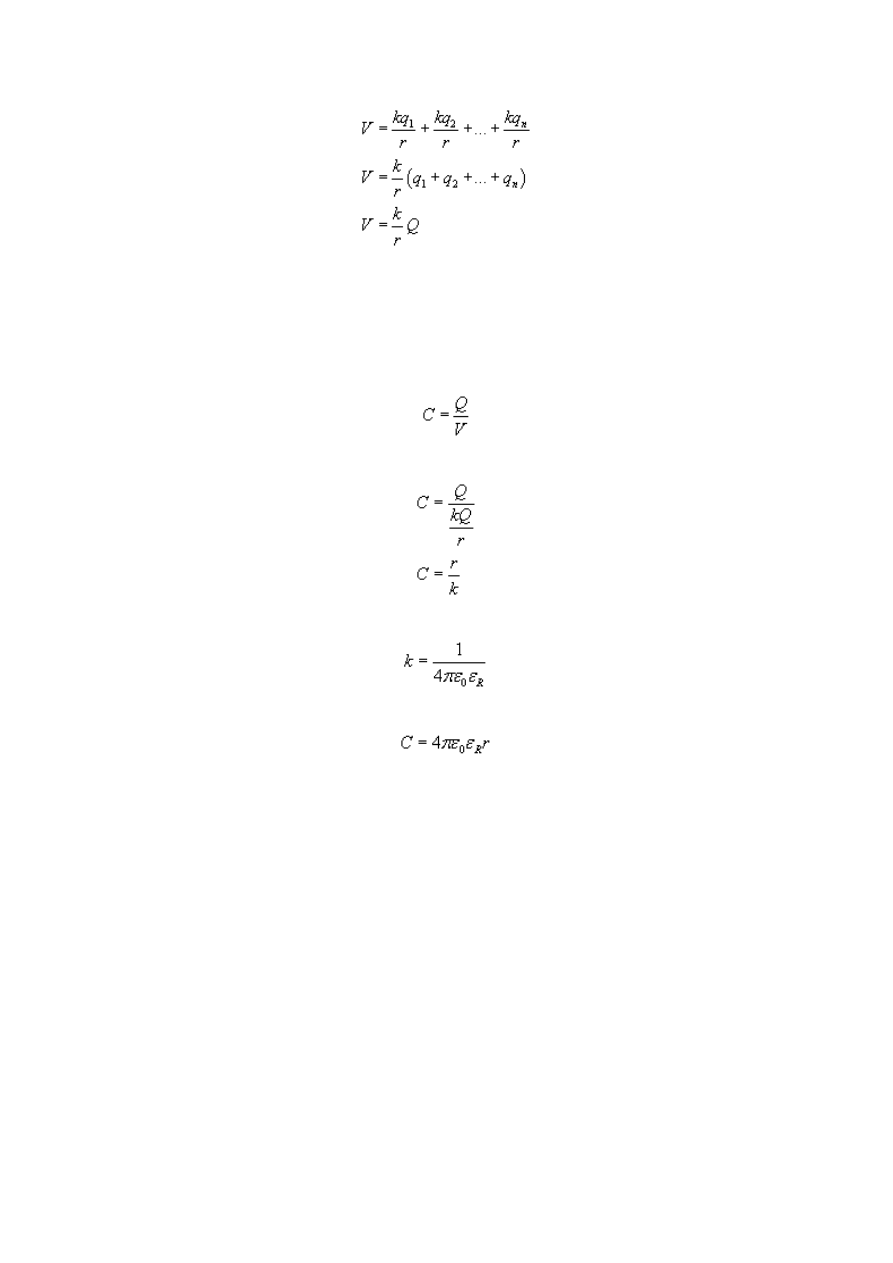
Całkowity potencjał jest sumą algebraiczną

Wobec tego

10

I tym dziwnym sposobem otrzymaliśmy wzór na potencjał kuli. Oczywiście nie musisz go
zawsze wyprowadzać, ja tylko pokazałem jak to się robi.



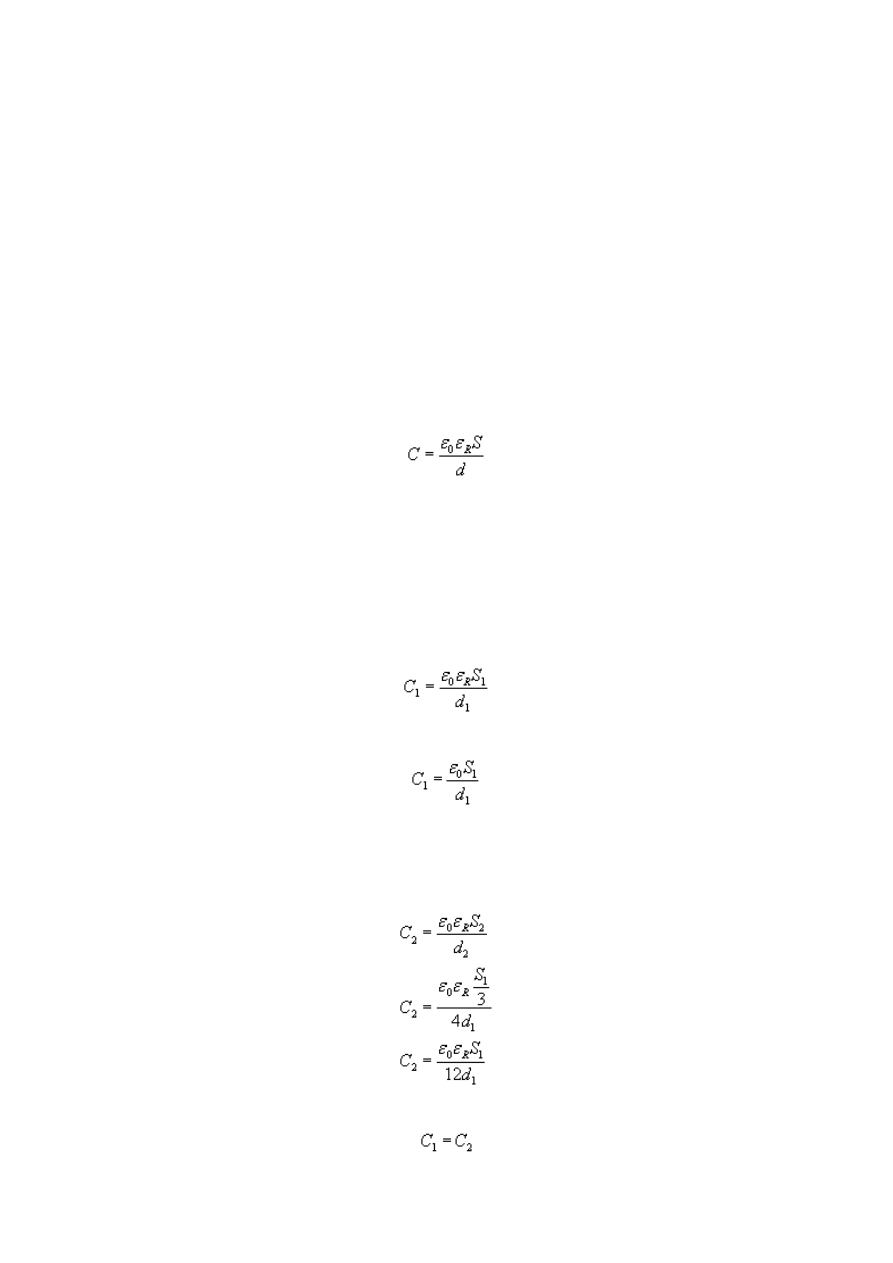
Zadanie jest proste, mamy znaleźć pojemność kuli - do wzoru

podstawiamy wzór na pojemność kuli i otrzymujemy

Stała k zależy od środowiska i wyrażamy ją wzorem

Zatem nasz wzór na pojemność kuli możemy również zapisać w postaci

gdzie:
ε

0

- przenikalność dielektryczna próżni (stała),

ε

R

- względna przenikalność dielektryczna danego środowiska (liczba niemianowana, w

próżni jej wartość wynosi 1),
r - oczywiście promień kuli.

11

Kondensator - Zadanie 6

Treść:
Odległość między okładkami kondensatora płaskiego o pojemności C zwiększono
czterokrotnie, zmniejszając równocześnie trzykrotnie powierzchnię czynną
okładek. Między okładki kondensatora wprowadzono dielektryk. Jaką powinien
on mieć względną przenikalność elektryczną, aby pojemność kondensatora nie
zmieniła się?

Dane:
C
4 d

1

= d

2

S

1

= 3 S

2

Szukane:
ε

R

= ?

Wzory:

Rozwiązanie:
Pojemność kondensatora wyrażamy wzorem

gdzie:
d - odległość między okładkami,
S - powierzchnia czynna okładek,
ε

0

- przenikalność elektryczna próżni (stała),

ε

R

- przenikalność elektryczna środowiska (liczba niemianowana, w próżni jej wartość wynosi

1).

Policzymy najpierw pojemność kondensatora przed zmianami

Dla wygody zakładamy, że ów kondensator był próżniowy, zatem

Teraz dokonujemy zmian, rozsuwamy okładki, zmniejszamy ich powierzchnię i wsuwamy
dielektryk

Z treści zadania wiemy, że kondensatory mają ciągle tę samą pojemność

12

Podstawiamy pod pojemności to, co wyliczyliśmy wcześniej

Aby pojemność kondensatora nie zmieniła się, dielektryk powinien posiadać względną
przenikalność elektryczną równą 12.

Kondensator - Zadanie 7

Treść:
Do płaskiego kondensatora wypełnionego dielektrykiem o ε

R

=5 doprowadzono

ładunek Q, wywołując na nim różnicę potencjałów U. Jak zmieni się ładunek Q'
zgromadzony na kondensatorze i napięcie U' pomiędzy jego okładkami, jeżeli
usuniemy dielektryk?

Dane:
ε

R

= 5

Q
U

Szukane:
Q' = ?
U' = ?

Wzory:

Rozwiązanie:
Liczymy najpierw pojemność kondensatora przed (C) i po (C') wyjęciu dielektryka,
korzystając oczywiście ze wzoru pierwszego.

Mamy wyrazić zmianę ładunku i napięcia po wyjęciu dielektryka z kondensatora.
Z zasady zachowania ładunku, wiemy, że ładunek nigdy "nie ginie". Oznacza to, że ładunek
kondensatora po wyjęciu dielektryka jest równy ładunkowi przed wyjęciem dielektryka
(zakładamy, że kondensator nie jest podłączony do źródła napięcia - w przeciwnym wypadku,
zamiast ładunku byłoby stałe napięcie)

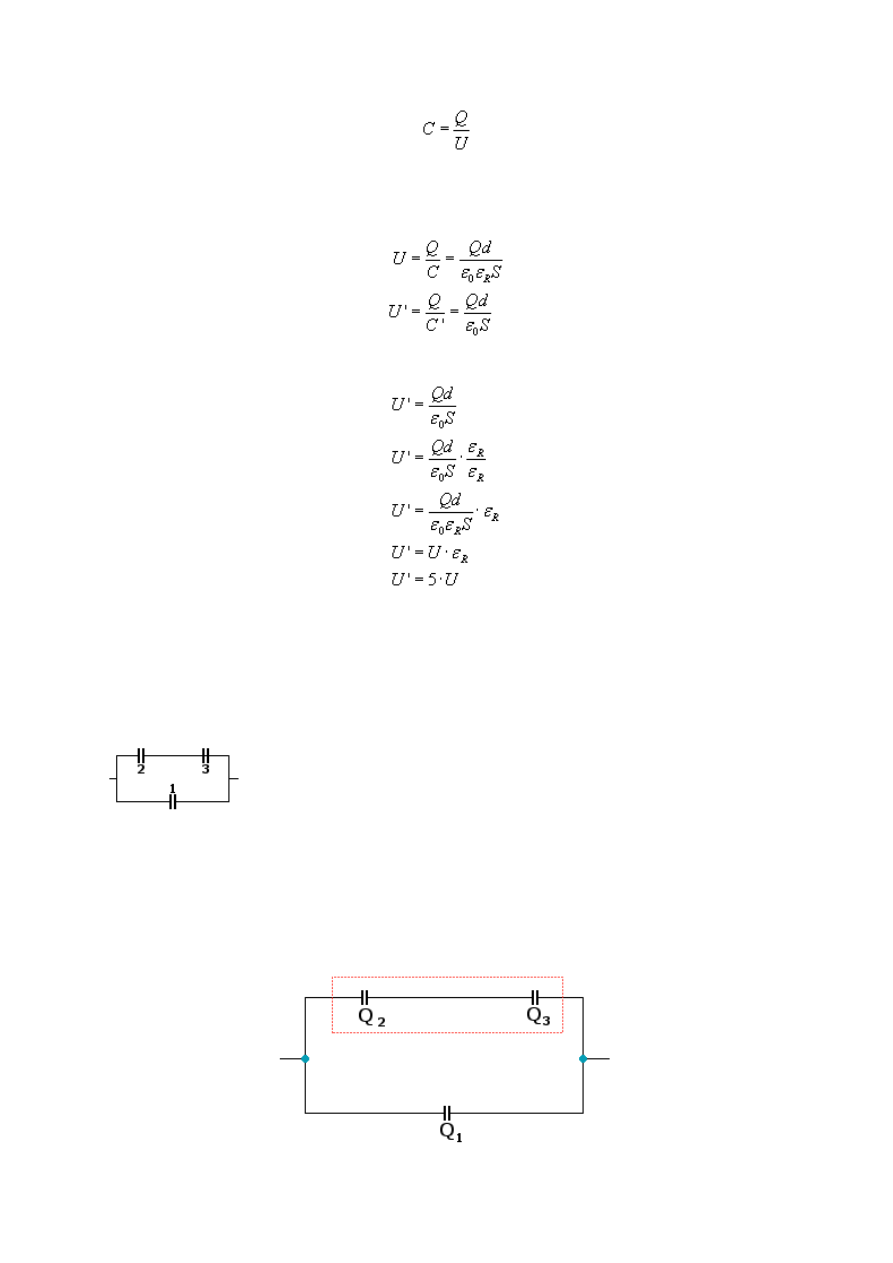
Czas zająć się napięciem, które w tym przypadku musiało się zmienić. Wyjęcie dielektryka,
zmniejsza pojemność kondensatora, a co za tym idzie - zwiększa napięcie między jego
okładkami. Skąd ten wniosek? Wystarczy spojrzeć na wzór

13

Sprawdzimy więc, o ile się zwiększy. Liczymy napięcie przed (U) i po (U') wyjęciu
dielektryka z kondensatora (przekształciłem powyższy wzór oraz uwzględniłem to, że Q =
const)

To teraz musimy jakoś porównać te napięcia. Proponuję taki sposób

Zatem po wysunięciu dielektryka z kondensatora napięcie zwiększy się pięć razy, a ładunek
nie zmieni się.

Kondensator - Zadanie 8

Treść:
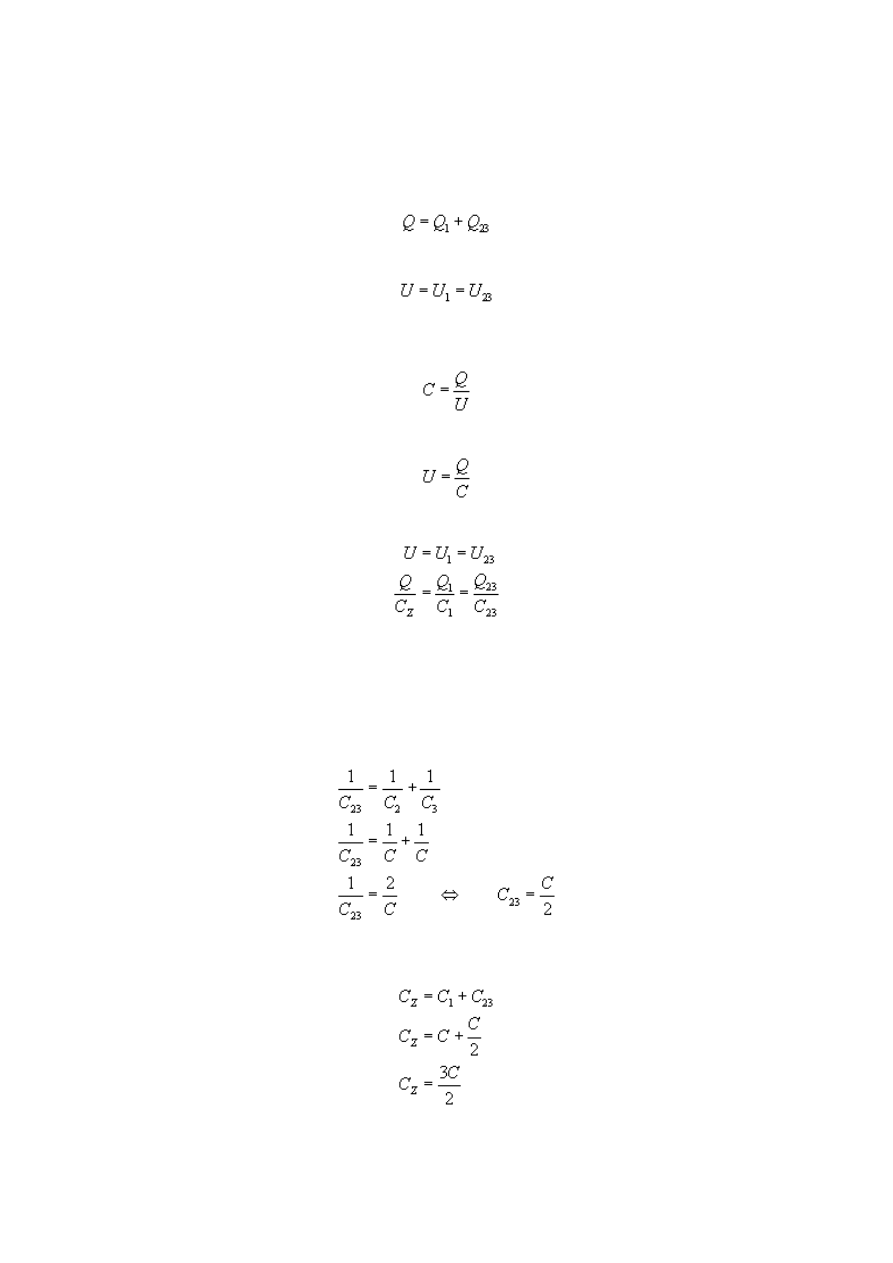
Jakie będą ładunki zgromadzone na poszczególnych
kondensatorach, jeśli do układu trzech jednakowych
kondensatorów połączonych tak, jak na rysunku, zostanie

doprowadzony ładunek Q?

Dane:
Q

Szukane:
Q

1

= ?

Q

2

= ?

Q

3

= ?

Wzory:

Rysunek:

14

Rozwiązanie:
Ponieważ mamy połączenie równoległe, to w węźle zaznaczonym na niebiesko
(którymkolwiek - zależy to od kierunku prądu) całkowity ładunek ulega podzieleniu wg
zasady

natomiast napięcie pozostaje stałe:

Trzeba więc wyliczyć, w jakich proporcjach dzieli się ładunek całkowity, w tym celu
skorzystamy ze wzoru

który przekształcimy do postaci

Mamy więc:

Potrzebujemy znaleźć pojemności układów kondensatorów, z których każdy pojedynczy ma
wartość C.
C

1

to po prostu C. C

23

to pojemność układu szeregowego kondensatorów, zaznaczonego

czerwoną linią na rysunku; jego pojemność

C

Z

to pojemność zastępcza wszystkich trzech kondensatorów wyliczana w sposób

następujący:

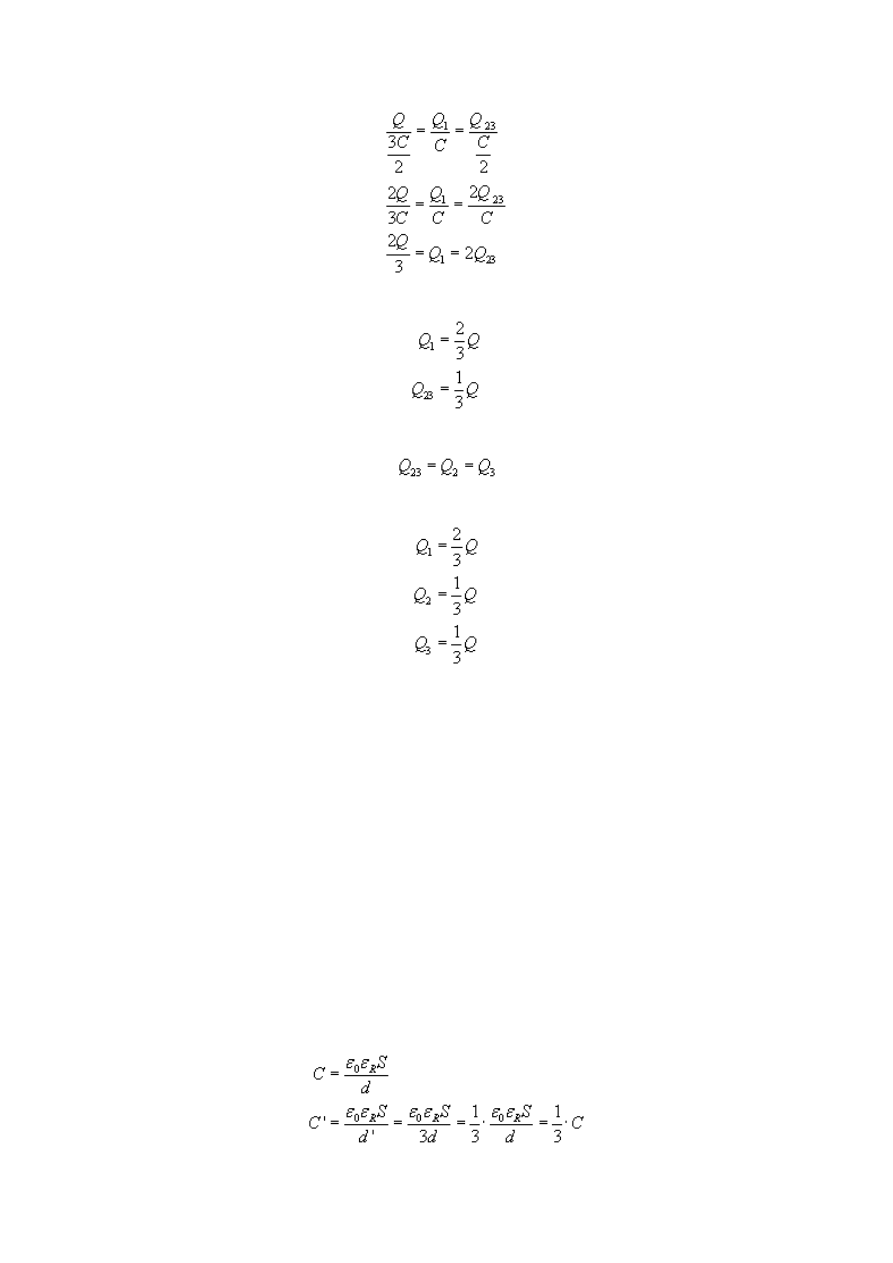
Kontynuujemy więc nasze równanie:

15

Z tej równości możemy wyliczyć, że

Gdy kondensatory połączone są szeregowo, oznacza to, że ładunek się nie zmienia, czyli

Tak więc ładunki zgromadzone na poszczególnych kondensatorach wynoszą:

Kondensator - Zadanie 9

Treść:
Kondensator płaski o pojemności C naładowano ładunkiem Q i odłączono od
źródła prądu. Jaką należy wykonać pracę, aby zwiększyć trzykrotnie odległość
między okładkami tego kondensatora?

Dane:
Q
C
d' = 3 d

Szukane:
W = ?

Wzory:

Rozwiązanie:
Aby znaleźć wartość wykonanej pracy, należy obliczyć różnicę energii kondensatora przed
(E) i po (E') rozsunięciu okładek. Potrzebne nam będą również pojemności kondensatorów w
obu przypadkach; aby je znaleźć, korzystamy z pierwszego wzoru:

16

Aby wyliczyć energię kondensatora, będziemy korzystać ze wzoru, w którym oczywiście
występuje pojemność oraz ładunek, ponieważ ten przed i po rozsunięciu okładek ma wartość
stałą (Q = const).
Teraz wyliczamy energię przed rozsunięciem okładek...

...oraz po ich rozsunięciu:

Szukana praca to różnica tych energii (większa minus mniejsza), zatem:

Aby rozsunąć trzykrotnie okładki kondensatora należy wykonać pracę Q

2

/ C.

Kondensator - Zadanie 10

Treść:
Płaski kondensator próżniowy o pojemności C=5

.

10

-3

µF naładowano do napięcia

U=100V i odłączono. Oblicz zmianę energii kondensatora wskutek zbliżenia jego
okładek na k=5 razy mniejszą odległość.

Dane:
C = 5

.

10

-3

µF

U = 100 V
k = 5

Szukane:
ΔE = ?

Wzory:

Rozwiązanie:
Ponieważ kondensator najpierw naładowano do napięcia U, a potem to napięcie odłączono,
oznacza to, że ładunek Q w kondensatorze będzie stały przed i po zmianach (Q = const).
Policzmy pojemność kondensatora przed rozsunięciem okładek (C) oraz po rozsunięciu
okładek (C')

17

Policzymy teraz energię kondensatora przed rozsunięciem okładek (E) i po rozsunięciu
okładek (E'). Mamy do wykorzystania trzy wzory na energię. Który najbardziej będzie nam
odpowiadać? Na pewno ten, który posiada wartość Q, ponieważ jest ona stała. A ponieważ
przesunięcie okładek wpływa na zmianę pojemności (patrz wzory powyżej), to właśnie
skorzystamy z pojemności:

Policzymy teraz zmianę energii ΔE

Nie mamy danej energii przed rozsunięciem okładek E, ale mamy napięcie przed
rozsunięciem okładek i pojemność kondensatora przed rozsunięciem okładek, korzystamy
więc z innego wzoru na energię

Zatem

Zmiana energii kondensatora wskutek zbliżenia okładek wynosi 0.02 milidżuli.

18

Kondensator - Zadanie 11

Treść:
Dwa płaskie kondensatory, jeden próżniowy, a drugi wypełniony dielektrykiem o
przenikalności ε=2 połączono szeregowo, naładowano do napięcia U=80V i
odłączono od baterii. Wyznacz pojemność zastępczą układu kondensatorów, jeżeli
kondensatory te mają jednakowe powierzchnie okładek S=2

.

10

-6

m

2

i odległości

między okładkami d=3mm. Jakie będzie napięcie na zaciskach zewnętrznych tego
połączenia kondensatorów, jeżeli okładki kondensatora próżniowego rozsunie się
na n=2 razy większą odległość?

Dane:
ε = 2
U = 80 V
S = 2

.

10

-6

m

2

d = 3 mm = 0.003 m
n = 2
ε

0

= 8.85

.

10

-12

F/m (stała)

Szukane:
C = ?
U' = ?

Wzory:

Rysunek:

Rozwiązanie:
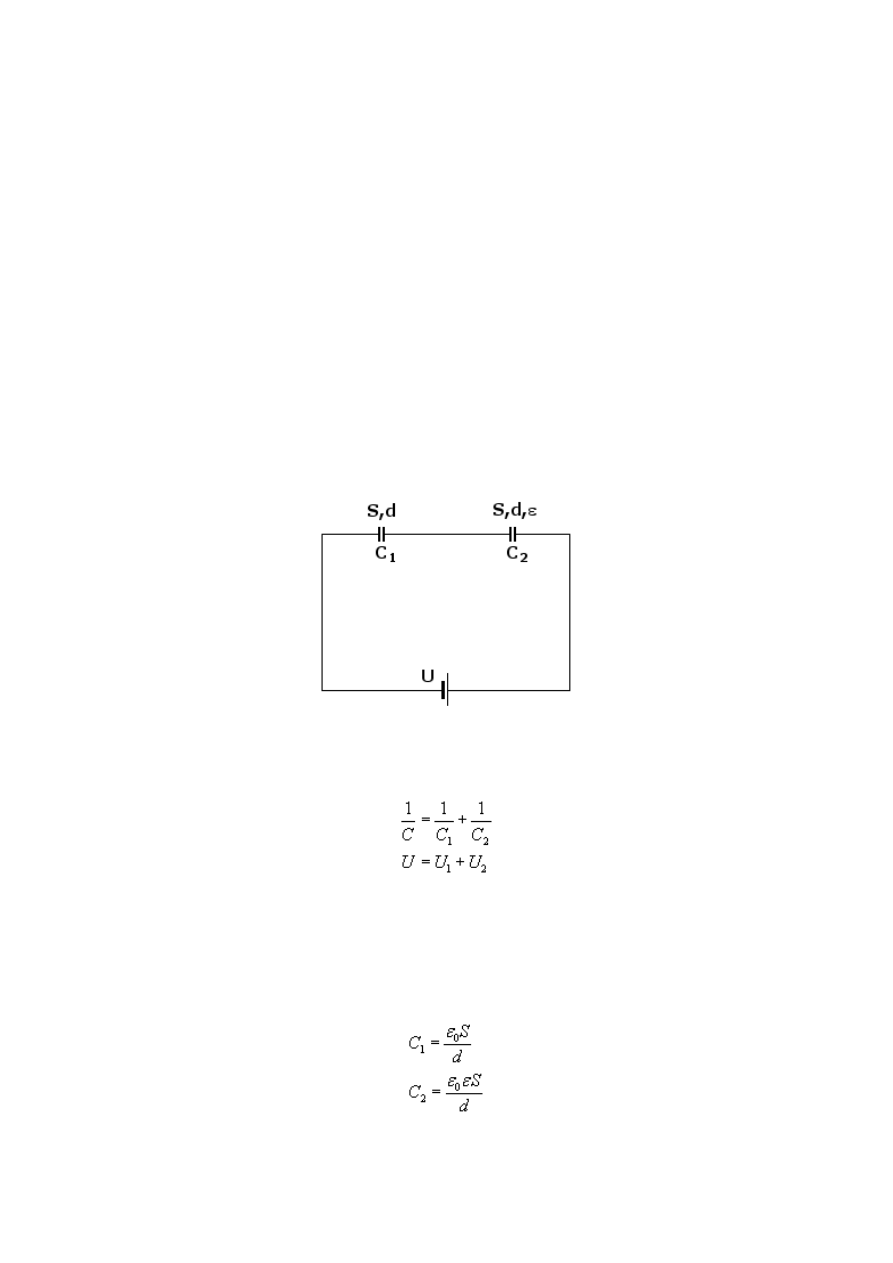
Powyższy rysunek przedstawia sytuację przed odłączeniem napięcia od kondensatorów.
Kondensatory te są połączone szeregowo, co oznacza, że:

Pojemność C jest pojemnością zastępczą, czyli taką, jaką należy przyłożyć zamiast dwóch
danych kondensatorów, by otrzymać identyczny efekt.

Zajmiemy się pierwszą częścią zadania, czyli znajdziemy pojemność zastępczą układu.
Zgodnie ze wzorem musimy znaleźć pojemności poszczególnych kondensatorów. Zgodnie z
treścią zadania:

19

Szukana pojemność zastępcza C wynosi

Zamieniamy licznik z mianownikiem i liczymy dalej:

Zatem pojemność zastępcza wynosi około 3.93 femtofaradów (fF).

Szukamy teraz napięcia na zaciskach zewnętrznych naszego połączenia kondensatorów, jeżeli
w kondensatorze próżniowym zwiększymy odległość okładek dwa razy. Wtedy pojemność
kondensatorów wynosi

Zatem pojemność zastępcza C':

Znów zamieniamy licznik z mianownikiem...

20

Przekształcając wzór na pojemność elektryczną, a dokładnie wyprowadzając z niego napięcie
U otrzymujemy (stan po rozsunięciu okładek)

Nie mamy wartości ładunku Q. Ponieważ wartość ładunku jest stała (odłączono napięcie), to
ładunek możemy obliczyć jako iloczyn pojemności zastępczej i napięcia przed rozsunięciem
okładek kondensatora. Napięcie mamy dane, pojemność wyliczyliśmy w pierwszej części
zadania, czyli

Szukane napięcie wynosi około 133 V.

Kondensator - Zadanie 12

Treść:
Dwa kondensatory o jednakowych pojemnościach C - próżniowy i wypełniony
dielektrykiem o stałej ε

R

- połączono równolegle, naładowano do napięcia U i

odłączono od baterii. Oblicz wartość napięcia na obu kondensatorach po
przełożeniu dielektryka do kondensatora próżniowego. Ile wynosi wtedy energia
każdego z kondensatorów?

Dane:
C
ε

R

U

Szukane:
U

1

' = ?

U

2

' = ?

E

1

' = ?

E

2

' = ?

Wzory:

Rysunek:

21

Rozwiązanie:
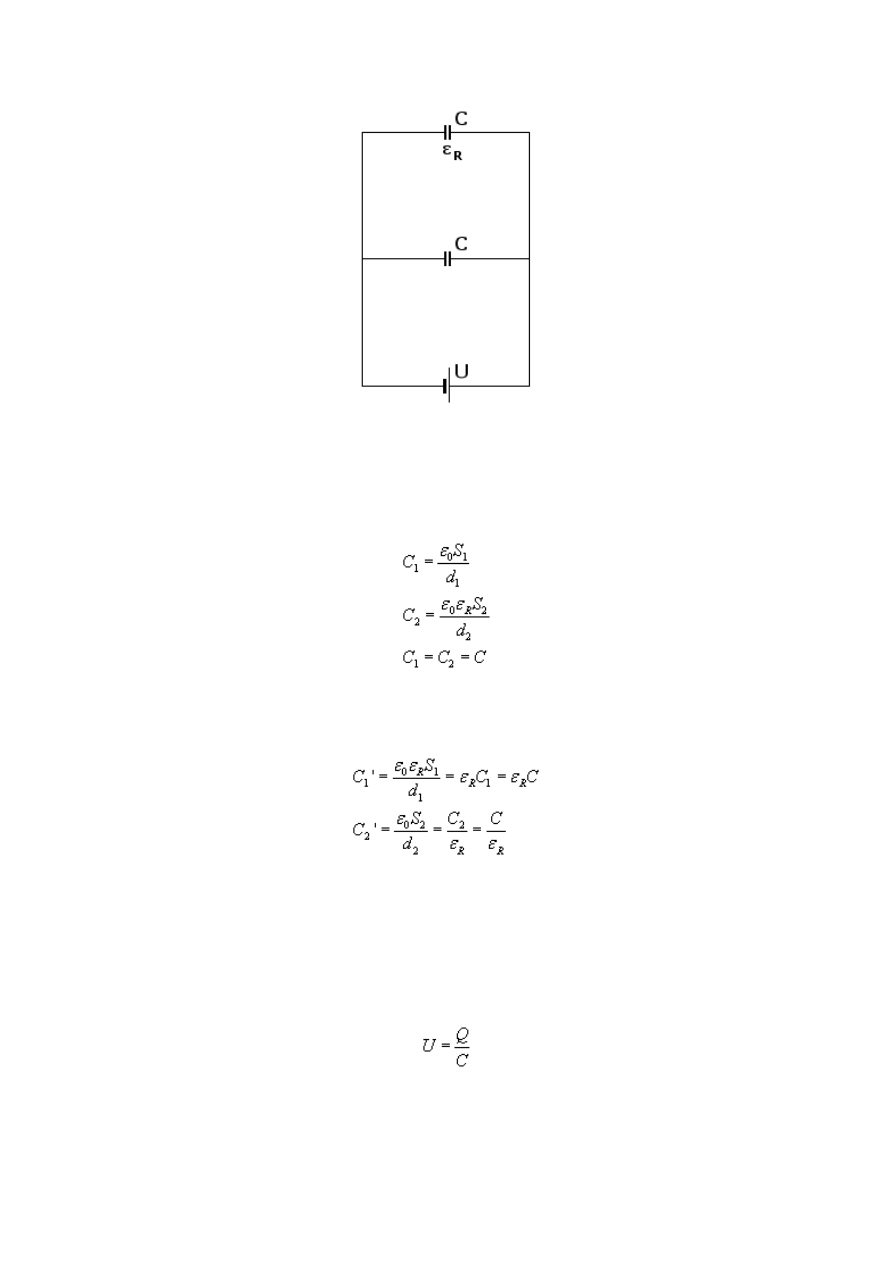
Rysunek przedstawia sytuację przed odłączeniem napięcia. Kondensatory połączone są
równolegle, zatem każdy kondensator naładował się do napięcia U. Odłączamy napięcie.
Najpierw policzymy pojemności kondensatorów przed przełożeniem dielektryka, zakładamy,
że najpierw dielektryk był w kondensatorze o indeksie 2:

Kondensatory mają wtedy jednakowe pojemności, a ponieważ w jednym z nich jest
dielektryk, zatem parametry S i d są różne.
Przekładamy dielektryk (teraz znajduje się on w kondensatorze o indeksie 1)

Oczywiście pojemności C

1

' i C

2

' nie są sobie teraz równe.

Policzymy teraz wartość napięcia na obu kondensatorach po przełożeniu dielektryka.
Pamiętamy, że przed przełożeniem dielektryka oba kondensatory miały napięcie U.
Korzystamy ze wzoru na pojemność elektryczną, który przekształcamy do postaci:

Oczywiście zarówno przed i po przełożeniu ładunek Q w kondensatorze jest stały, ponieważ
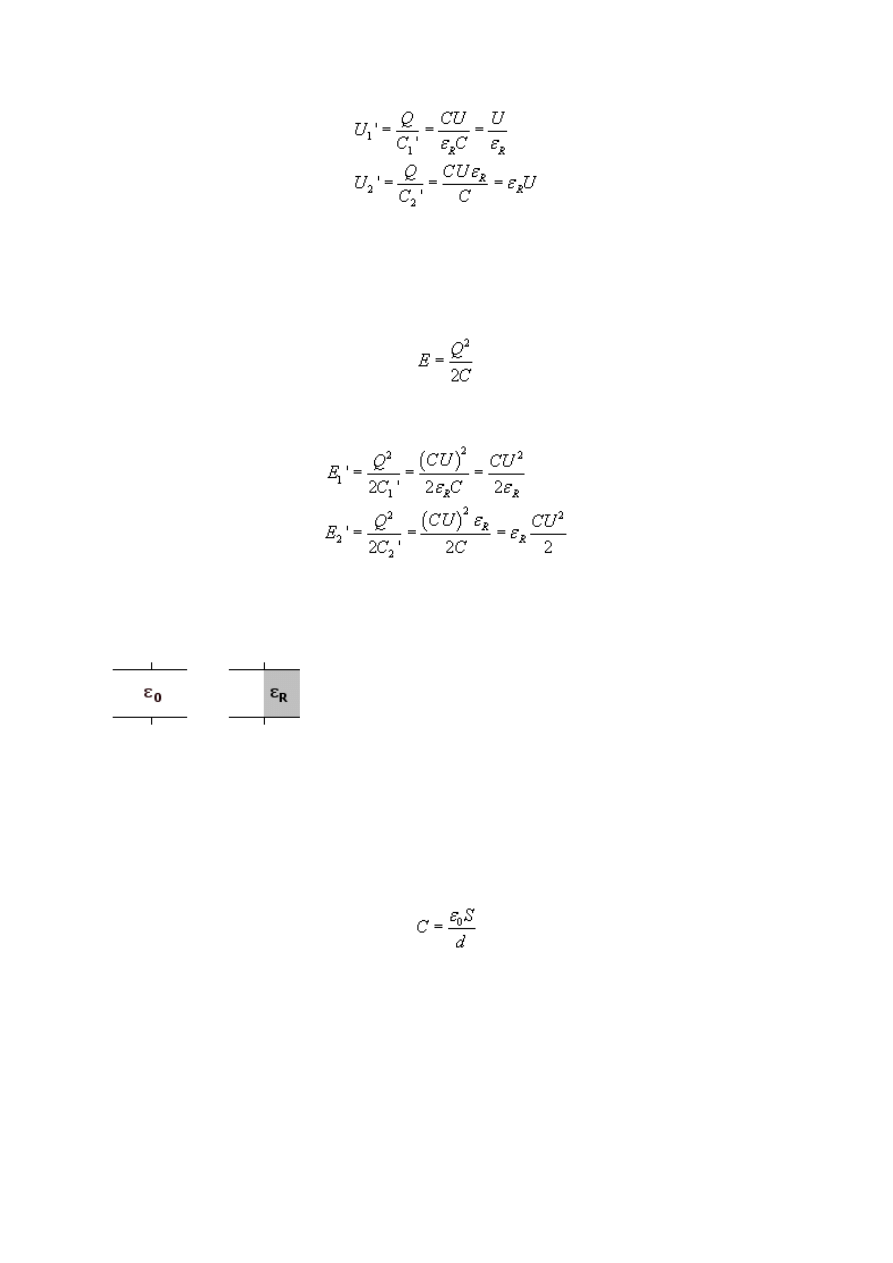
odłączyliśmy napięcie (Q = const) i wynosi on Q = CU. Liczymy napięcia dla
poszczególnych kondensatorów, po przełożeniu dielektryka:

22

Teraz szukamy energii każdego z kondensatorów po przełożeniu dielektryka. Korzystamy z
jednego ze wzorów na energię, a mianowicie tego, w którym jest ładunek (u nas stała) i
oczywiście pojemność

Teraz liczymy energie po przełożeniu dielektryka

Kondensator - Zadanie 13

Treść:
Pomiędzy okładki kondensatora próżniowego
wsunięto dielektryk o stałej dielektrycznej ε

R

w ten

sposób, że wypełnił on połowę wnętrza tego

kondensatora. Oblicz stosunek pojemności kondensatora z wsuniętym
dielektrykiem do pojemności kondensatora próżniowego.

Dane:
ε

R

Szukane:
C' / C = ?

Wzory:

Rozwiązanie:
Policzmy na samym początku pojemność kondensatora przed włożeniem dielektryka

Ponieważ jest to kondensator próżniowy, to przenikalność dielektryczna ε

R

wynosi 1 i została

pominięta.
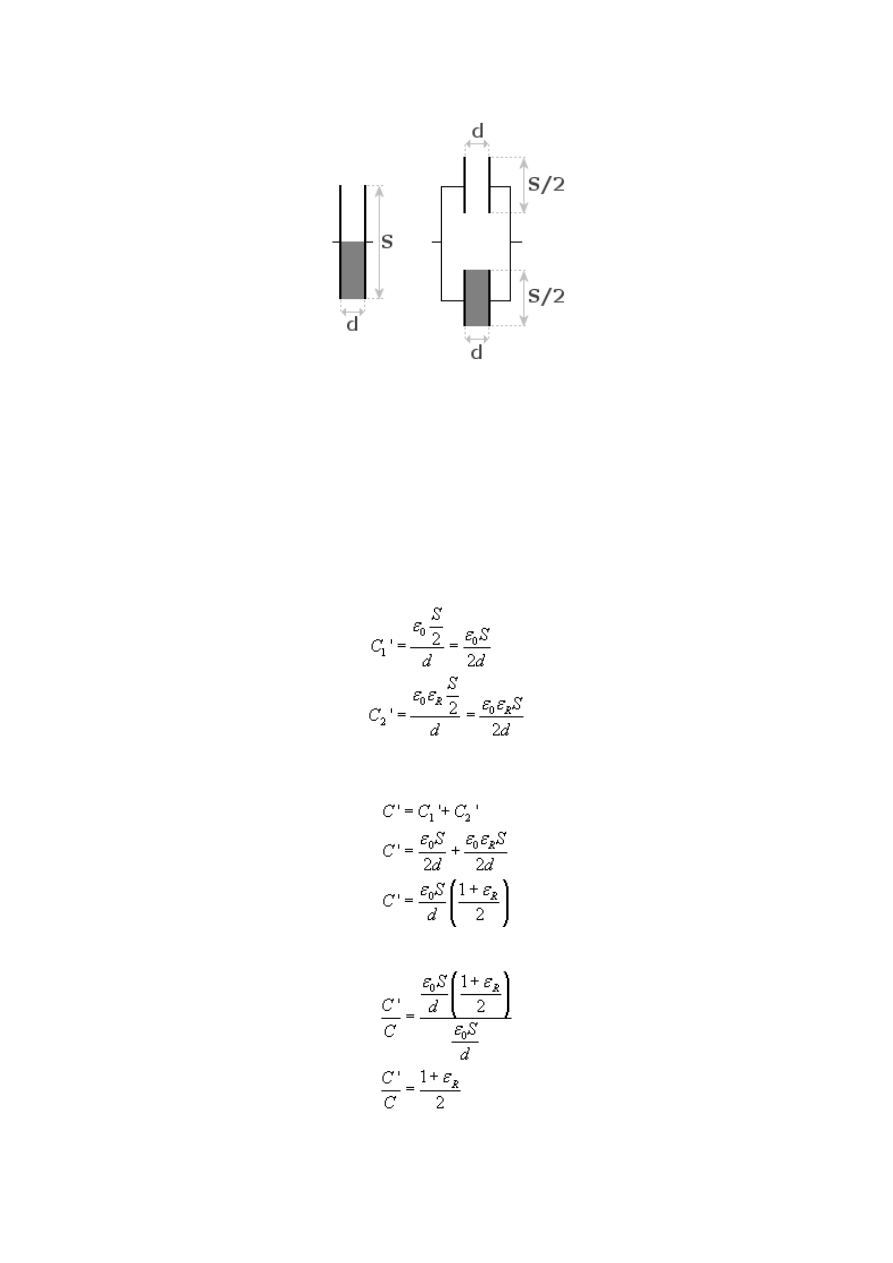
Czas zająć się kondensatorem po włożeniu dielektryka. Jak policzyć jego pojemność? Trzeba
wpaść na pewien pomysł, spójrzmy na rysunek.

23

Kondensator z częściowym wypełnieniem dielektrykiem został podzielony na dwa
kondensatory - jeden próżniowy, drugi z dielektrykiem (to tak, jakbyśmy je "przecięli" na
dwie połowy). Dwa nowe kondensatory te połączone są równolegle, gdyż przecinamy na pół
powierzchnie okładek. Teraz wynoszą one S / 2 a odległość między okładkami nadal wynosi
d.


Oznaczmy przez C

1

' pojemność kondensatora próżniowego, a przez C

2

' pojemność

kondensatora z dielektrykiem (oba kondensatory są oczywiście efektem powyższego
podzielenia). Mamy więc

Szukaną pojemnością C' będzie oczywiście pojemność zastępcza równoległego układu
kondensatorów C

1

' i C

2

'

Nasz szukany stosunek wynosi

24

Kondensator - Zadanie 14

Treść:
Kondensator próżniowy o pojemności C=1µF wypełniono
dielektrykiem o ε

R

=4 i grubości d

2

=d/3, umieszczonym równolegle

do okładek. Ile wynosi pojemność kondensatora po włożeniu

dielektryka?

Dane:
d

2

= d / 3

C = 1 µF
ε

R

= 4

Szukane:
C' = ?

Wzory:

Rysunek:

Rozwiązanie:
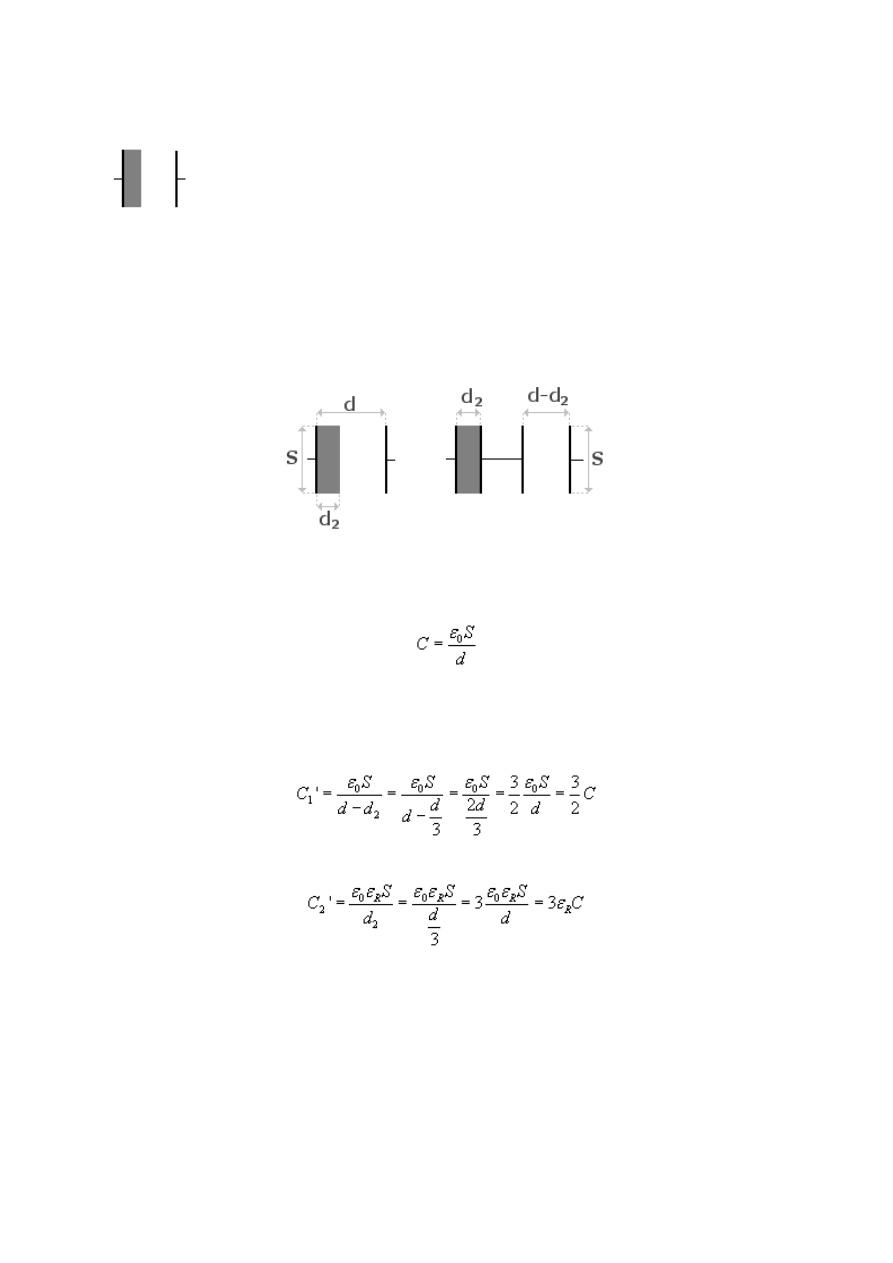
Najpierw wyprowadzamy wzór na pojemność kondensatora próżniowego przed włożeniem
dielektryka

Zadanie jest podobne do poprzedniego, z tym że teraz inaczej wsuwamy dielektryk. Teraz nie
przecinamy powierzchnię okładek, tylko ich odległość, powstanie zatem układ szeregowy
kondensatorów.
Oznaczmy przez C

1

' pojemność kondensatora próżniowego

Natomiast przez C

2

' oznaczymy pojemność kondensatora z dielektrykiem o szczelinie d

2

Szukaną pojemnością C' będzie pojemność szeregowego układu kondensatorów

25

Pojemność kondensatora po włożeniu dielektryka wynosi 4 / 3 mikrofaradów.

Kondensator - Zadanie 15

Treść:
Kondensator o pojemności C naładowano do napięcia U i połączono równolegle z
drugim, nienaładowanym kondensatorem o pojemności nC. Ile wynosi napięcie na
okładkach pierwszego kondensatora po połączeniu? Ile wynosi energia układu
połączonych kondensatorów, jeżeli energia kondensatora przed połączeniem
wynosi W?

Dane:
C
nC
U
W

Szukane:
U

1

= ?

W' = ?

Wzory:

Rysunek:

Rozwiązanie:
Na rysunku po lewo mamy naładowany kondensator o pojemności C, a po prawo ten sam

26

kondensator połączony równolegle z kondensatorem o pojemności nC (liczba n oznacza tu
jakąkolwiek dodatnią wielokrotność wartości C).
W połączeniu równoległym parametry obu kondensatorów oznaczyłem na czarno, natomiast
parametry całego układu kondensatorów zaznaczyłem na czerwono.
Zauważmy że w kondensatorze po lewo i w układzie kondensatorów po prawo całkowity
ładunek Q nie ulega zmianie i zgodnie z tym (ze wzoru na pojemność kondensatora
wyprowadziłem ładunek Q)

Napięcie U' układu równoległego kondensatorów, będzie również napięciem każdego z
kondensatora, ponieważ w połączeniach równoległych

Musimy znaleźć jeszcze pojemność C', która jest tu pojemnością zastępczą połączenia
szeregowego i zgodnie z regułami tego typu połączeń

Możemy więc wyliczyć szukane napięcie

Czas na drugą część zadania dotyczącą energii kondensatorów.
Korzystamy z jednego ze wzorów na energię, a mianowicie z tego, w którym jest pojemność
oraz stały ładunek.
Sytuację na rysunku po lewo możemy opisać wzorem (przez W oznaczamy energię)

Gdy dołączymy szeregowo kondensator o pojemności nC energia układu przyjmie postać

I w ten sposób rozwiązaliśmy całe zadanie. :)

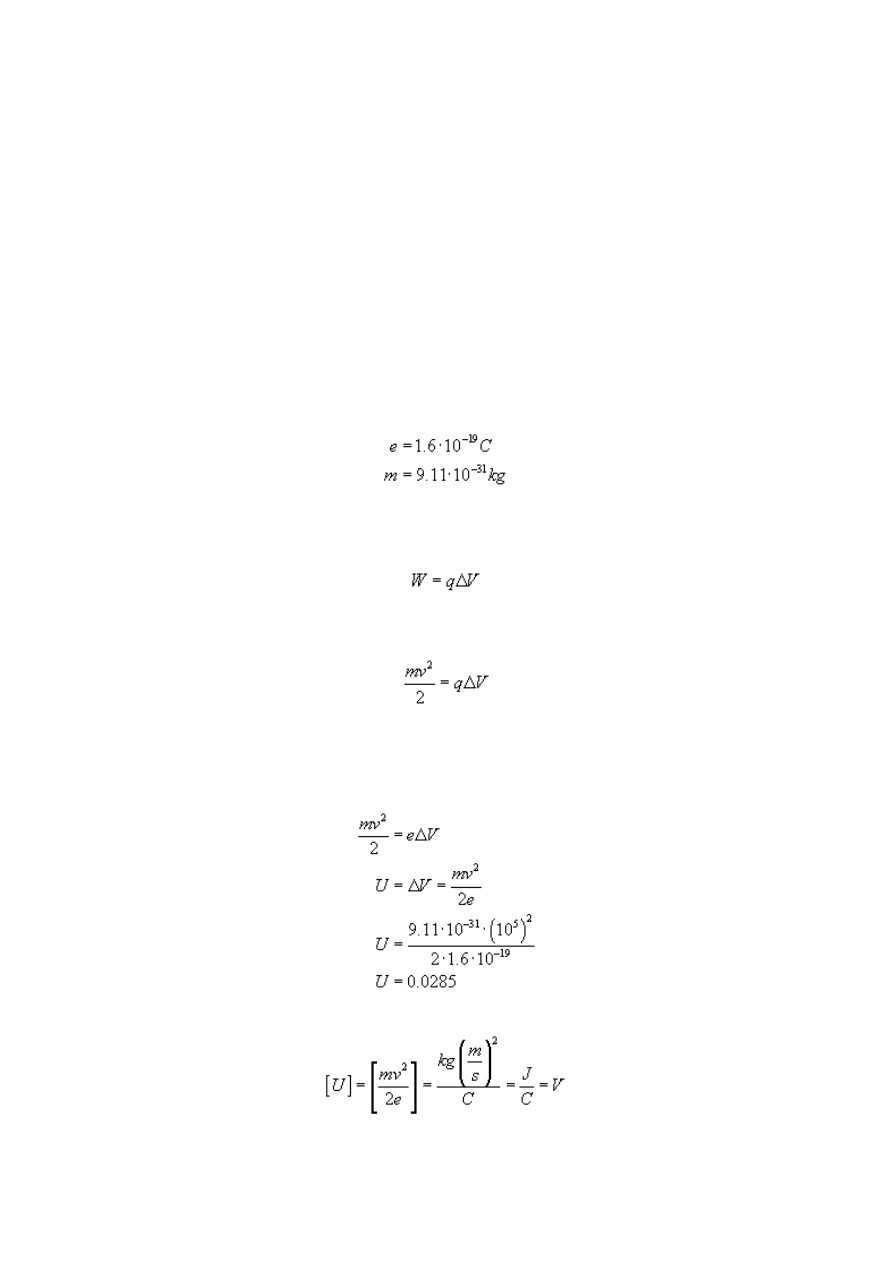
27

Kondensator - Zadanie 16

Treść:
Elektron poruszając się prostopadle do okładek kondensatora płaskiego, po
przebyciu odległości d=5mm, uzyskał szybkość v=10

5

m/s. Jaka jest różnica

potencjałów między okładkami kondensatora i natężenie pola elektrostatycznego
wewnątrz kondensatora?

Dane:
v = 10

5

m/s

d = 5 mm = 0.005 m

Szukane:
ΔV = U = ?
E = ?

Wzory:

Rozwiązanie:
Mamy do czynienia z elektronem, w takim razie więc możemy jeszcze uzyskać dwie
wartości, które będą potrzebne nam w zadaniu - są nimi ładunek elektronu e oraz masa
elektronu m. Wartości te znajdziesz w każdych tablicach fizycznych:

Szukamy różnicy potencjałów ΔV pomiędzy okładkami kondensatora, czyli inaczej mówiąc
napięcia U.
Jeden ze wzorów na pracę w polu elektrostatycznym mówi, że

Wykonana praca jest równa energii kinetycznej, jaką uzyskał elektron po przebyciu
odległości d

Ładunkiem q jest wartość ładunku elektronu e, a z otrzymanego wzoru wyliczamy szukane
napięcie

Sprawdzamy jednostkę

Teraz liczymy natężenie pola elektrostatycznego E (w polu jednorodnym wewnątrz

28

kondensatora natężenie pola jest w każdym punkcie takie samo) - nie jest to trudne,
korzystamy ze wzoru

Tak więc:

Różnica potencjałów (napięcie) między okładkami kondensatora wynosi około 0.0285 V, a
natężenie pola elektrostatycznego wewnątrz kondensatora ma wartość 5.7 V/m.


Kondensator - Zadanie 17

Treść:
Pomiędzy okładki kondensatora próżniowego, równolegle do jego okładek,
zostaje wstrzelony proton o szybkości v

0

=10000m/s. Oblicz przyrost energii

kinetycznej protonu po przejściu przez kondensator, jeżeli odległość między
okładkami wynosi d=5mm, napięcie między nimi U=1200V, a długość okładek
l=0.05m.

Dane:
v

0

= 10000 m/s

d = 5 mm = 0.005 m
U = 1200 V
l = 0.05 m

Szukane:
ΔE

K

= ?

Wzory:

Rysunek:

Rozwiązanie:
Cząstką, którą wstrzeliwujemy do kondensatora, jest proton, którego masę m oraz ładunek q
podajemy z tablic fizycznych

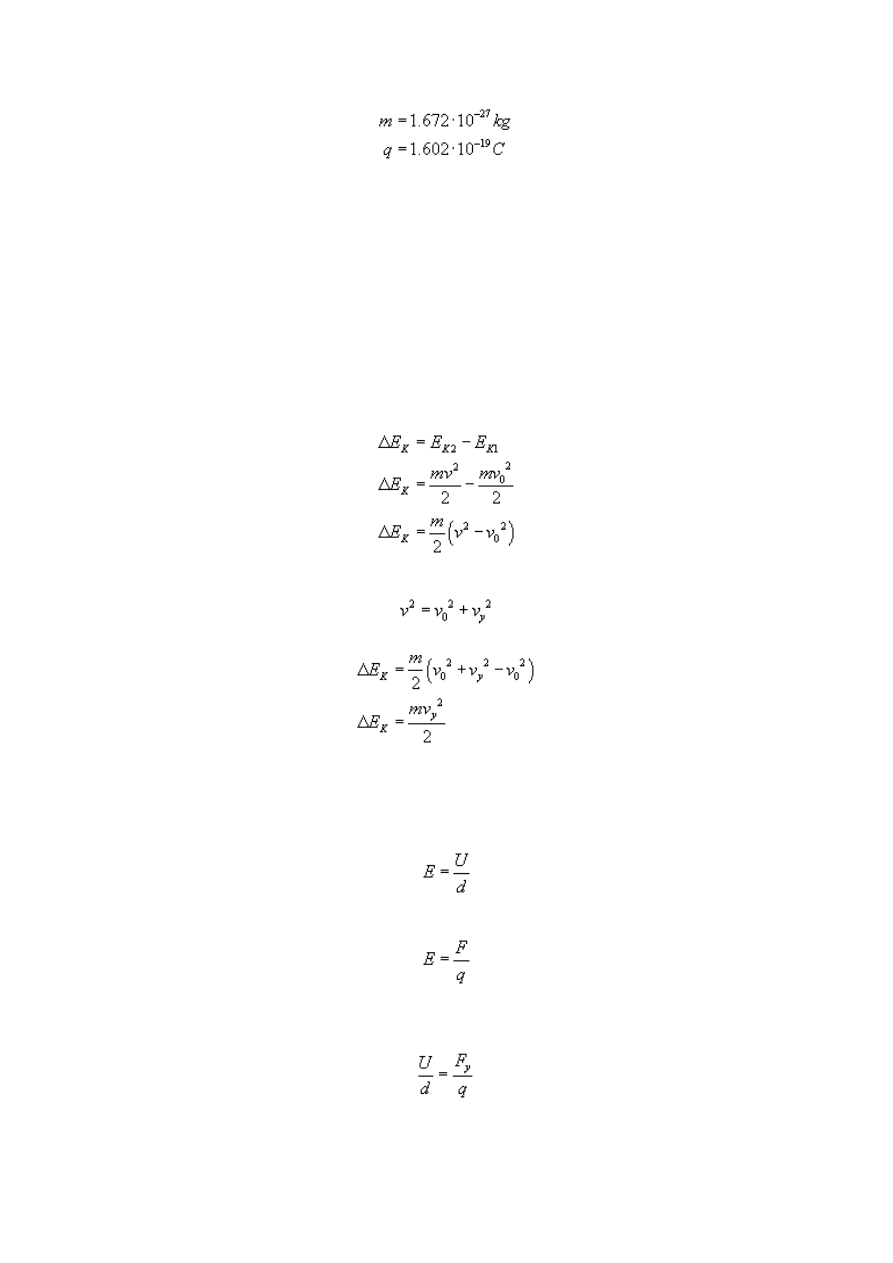
29

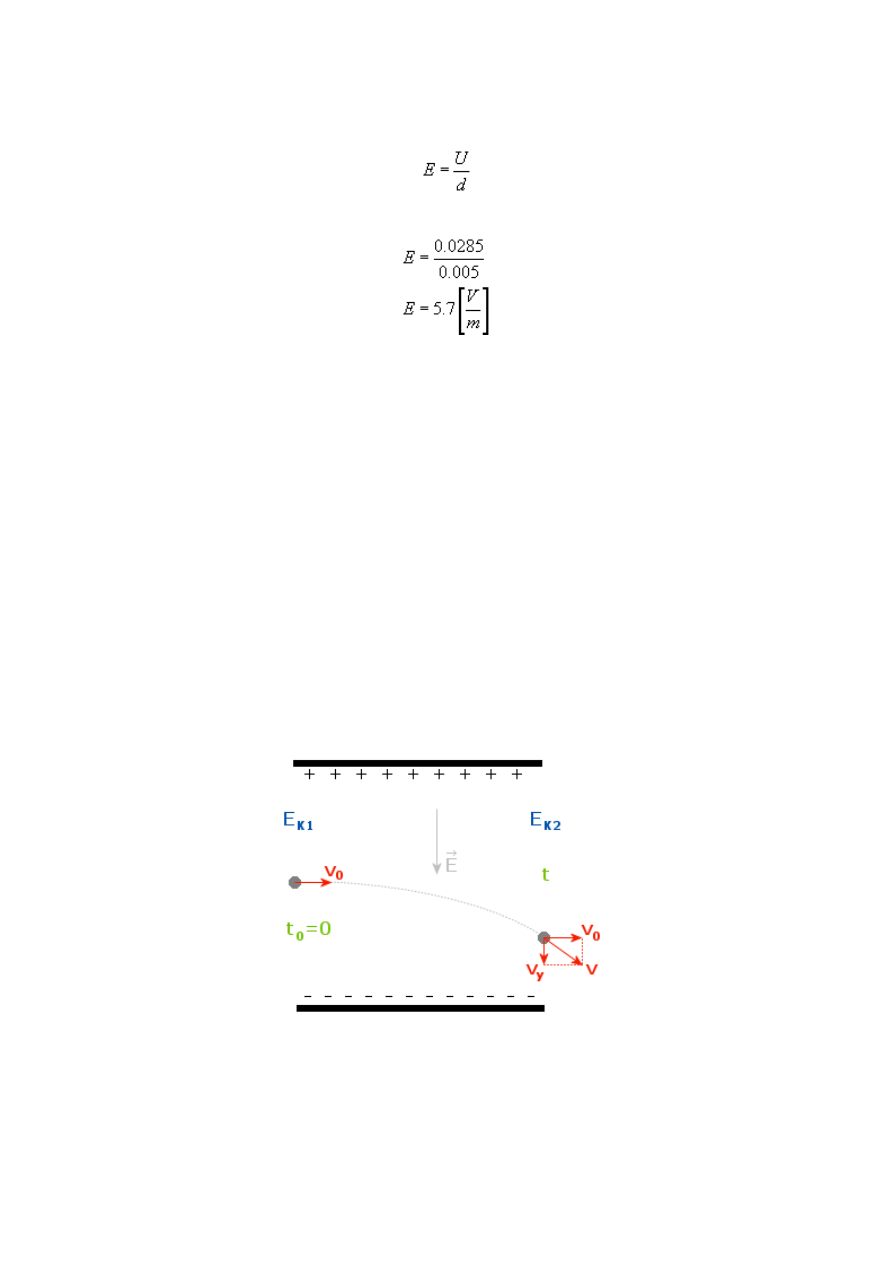
Sytuacja z zadania przedstawiona jest na powyższym rysunku.
Otóż proton wchodzi do kondensatora z prędkością v

0

. Ponieważ proton ma ładunek dodatni,

to wewnątrz kondensatora jest on przyciągany przez okładkę ujemną i tor ruchu zakrzywia się
(sytuacja podobna do rzutu poziomego).
Gdy proton wyjdzie z kondensatora porusza się on z prędkością v, którą możemy rozłożyć na
składowe:
- w kierunku poziomym proton porusza się ruchem jednostajnym prostoliniowym z
prędkością v

0

,

- w kierunku pionowym proton porusza się ruchem jednostajnie przyspieszonym z prędkością
v

y

.

W zadaniu mamy policzyć zmianę energii kinetycznej

Musimy zatem znaleźć prędkość v, która jest wypadkową prędkości v

0

i v

y

(patrz rysunek)

Wzór na zmianę energii przybierze postać:

Jak się okazuje, naszym głównym zadaniem jest znalezienie prędkości v

y

.

Prędkość ta pojawia się wskutek działania pola elektrostatycznego jednorodnego wewnątrz
kondensatora, które wyrazić możemy na dwa sposoby. Pole elektrostatyczne jednorodne to
stosunek napięcia U panującego pomiędzy okładkami do odległości d tych okładek

Jednocześnie pole elektrostatyczne to stosunek siły działającej wzdłuż linii sił pola na ładunek

do wartości tego ładunku

Porównujemy nasze wzory; siłą F będzie siła powodująca przyciąganie protonu do okładki
ujemnej

Ponieważ w kierunku pionowym mamy do czynienia z ruchem jednostajnie przyspieszonym,
to siłę tę możemy wyrazić poprzez drugą zasadę dynamiki:

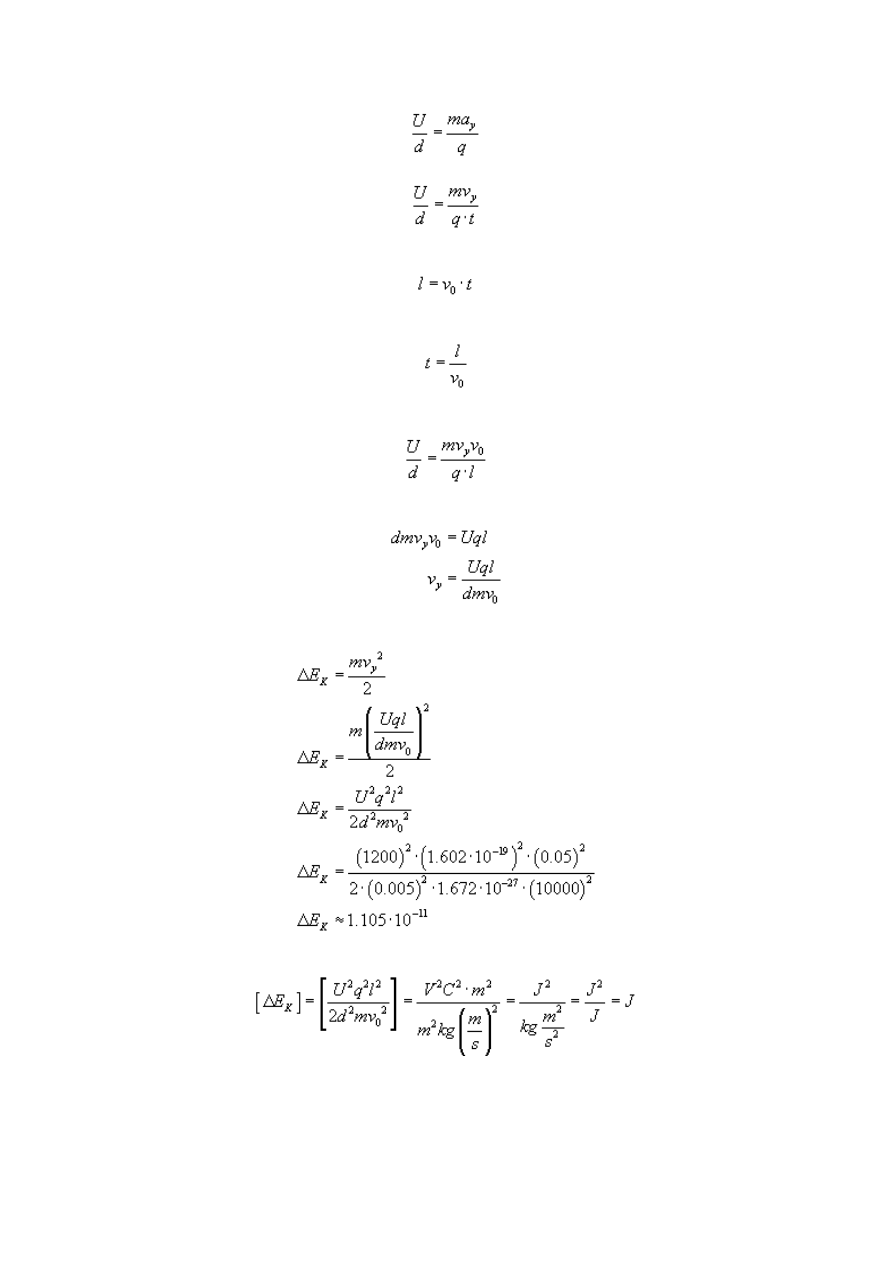
30

Przyspieszenie to stosunek prędkości do czasu

No tak, ale nie mamy jeszcze czasu t. Aby znaleźć ten czas, skorzystamy z ruchu poziomego
(ruch jednostajny prostoliniowy). Po tym samym czasie t wartość drogi w tym ruchu wynosi

stąd czas t:

Czyli nasze równanie przybiera postać:

Wszystko już mamy dane, możemy w takim razie wyprowadzić wzór na v

y

...

...i znaleźć wartość szukanej zmiany energii kinetycznej:

Przy tak wyrafinowanym wzorze warto sprawdzić poprawność jednostki

Przyrost energii kinetycznej wynosi około 1.105

.

10

-11

J.