sta

PODSTAWY MECHANIKI

PRACA DOMOWA

OBLICZENIA BELKI O PRZEKROJU KOŁOWYM

Wykonał:

Stanisław Musiolik

Politechnika Śląska wydział Elektryczny

Studia niestacjonarne

kierunek: Elektrotechnika

rok akademicki 2007/2008

sta

1. Dane do obliczeń.

l1 [mm]

l2 [mm]

l3 [mm]

L [mm]

P [N]

P

1

[N]

P

2

[N]

q [N/mm]

Re [MPa]

600

700

800

3000

2000

20000

6000

10

300

- belka o przekroju kołowym

ponieważ Pa = Nm

-2

, stąd obliczenia wykonano dla jednostek:

l1 [m]

l2 [m]

l3 [m]

L [m]

P [N]

P

1

[N]

P

2

[N]

q [N/m]

Re

[Pa = Nm

-2

]

0,6

0,7

0,8

3

2000

20000

6000

10000

300*10

6

obliczona długość l4 = L-(l1+l2+l3) = 0,9 m

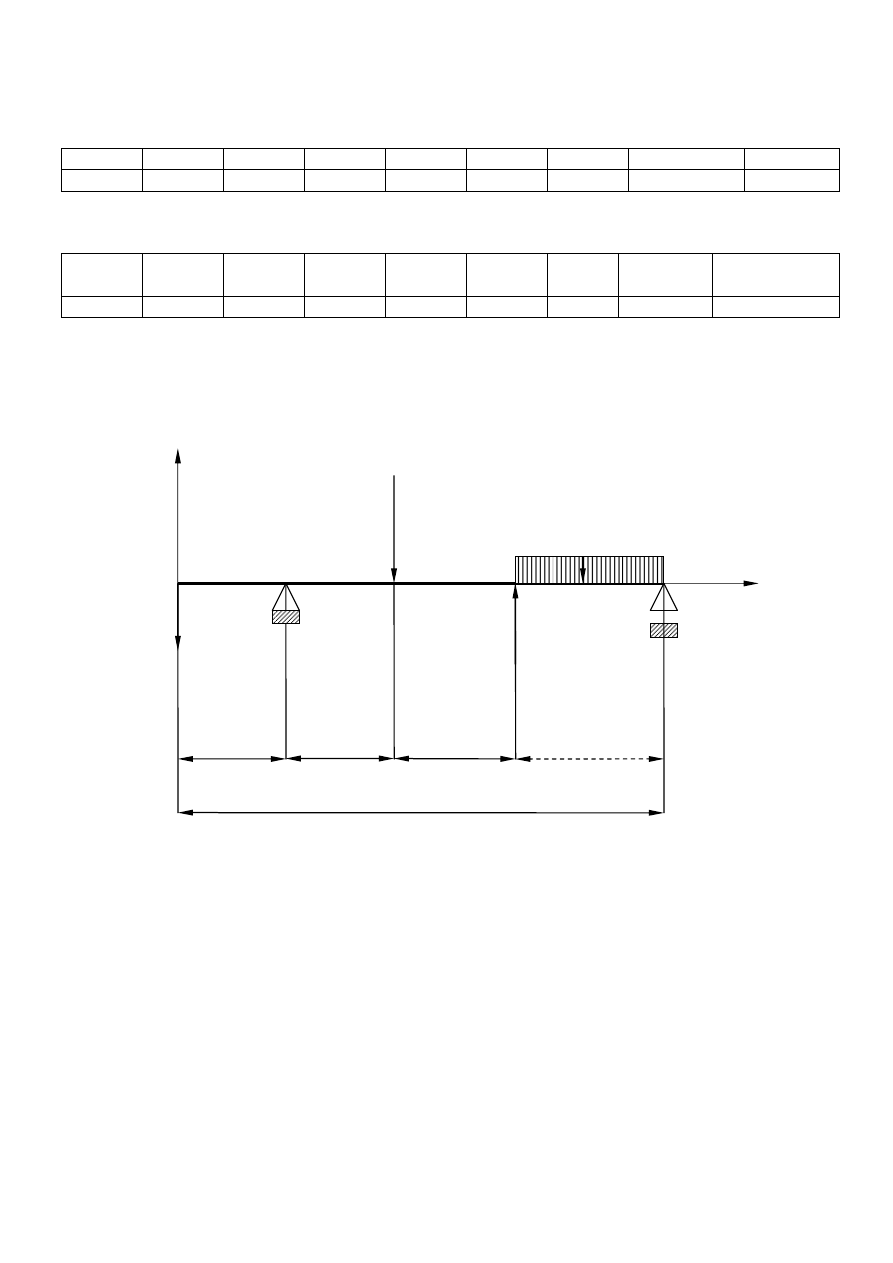
Szkic

2. Obliczenia reakcji podpór
Z warunków równowagi:
ΣPix = 0; (równanie 1) P - Ra + P1 - P2 + q*l4 - Rb = 0
ΣMia = 0; (równanie 2) P*l1 – P1*l2 + P2*(l2+l3) – q*l4*(l2+l3+l4/2) + Rb*(L-l1) = 0

z równania 2 wyznaczymy Rb
Rb = [-P*l1 + P1*l2 - P2*(l2+l3) + q*l4*(l2+l3+l4/2)] / (L-l1)
po podstawieniu danych Rb = 8895,83 [Nm]

y

x

A

B

l1

l2

l3

L

P

P1

P2

q

0

l4

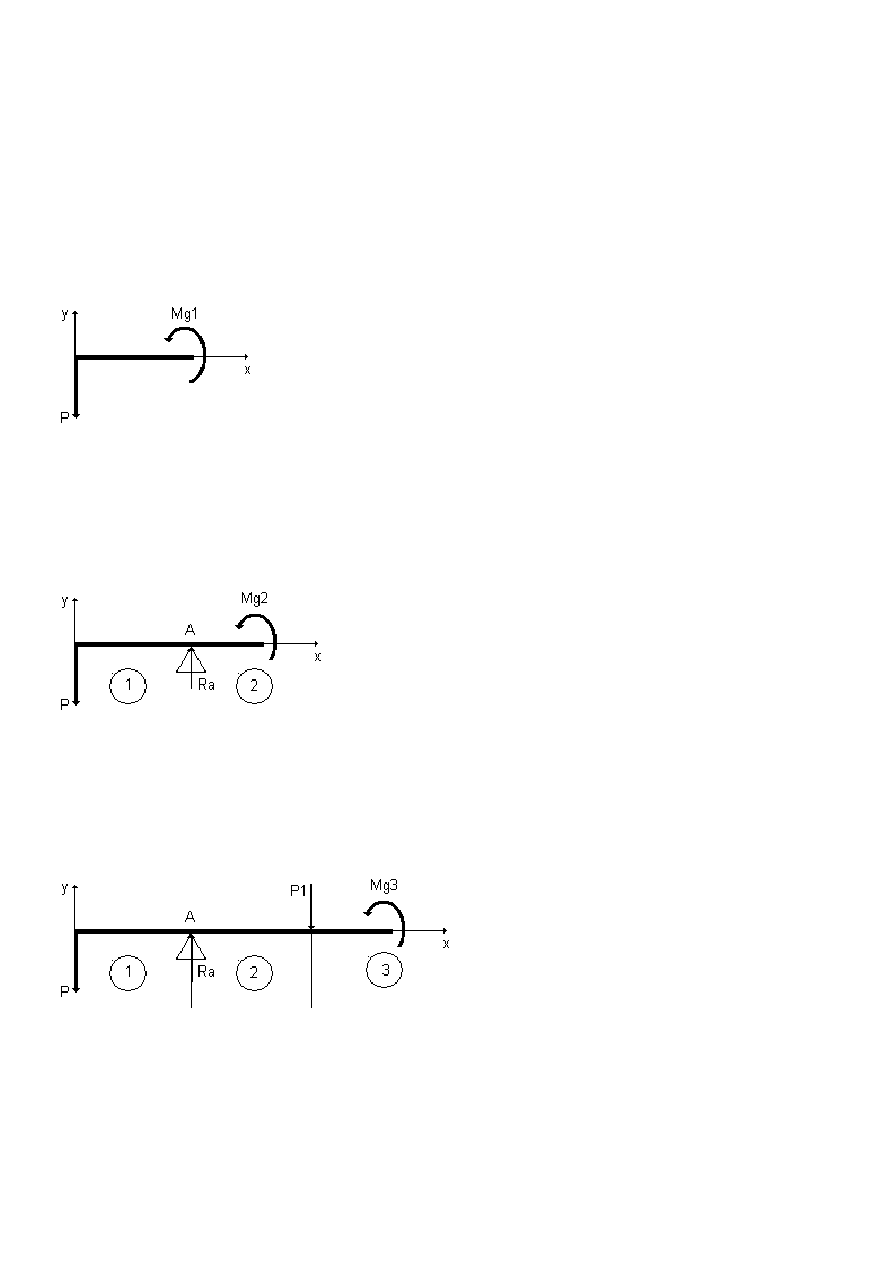
sta

z równania 1 wyznaczymy Ra
Ra = P + P1 - P2 + q*l4 - Rb
po podstawieniu danych Ra = 16104,17 [Nm]


3. Rozkład momentów gnących na długości belki.
W celu wyznaczenia momentów gnących belkę dzielimy na cztery przedziały:

przedział 1 dla 0 ≤

≤

≤

≤ x ≤

≤

≤

≤ l1

P*x + Mg1 = 0
po przekształceniu otrzymamy
Mg1 = -Px


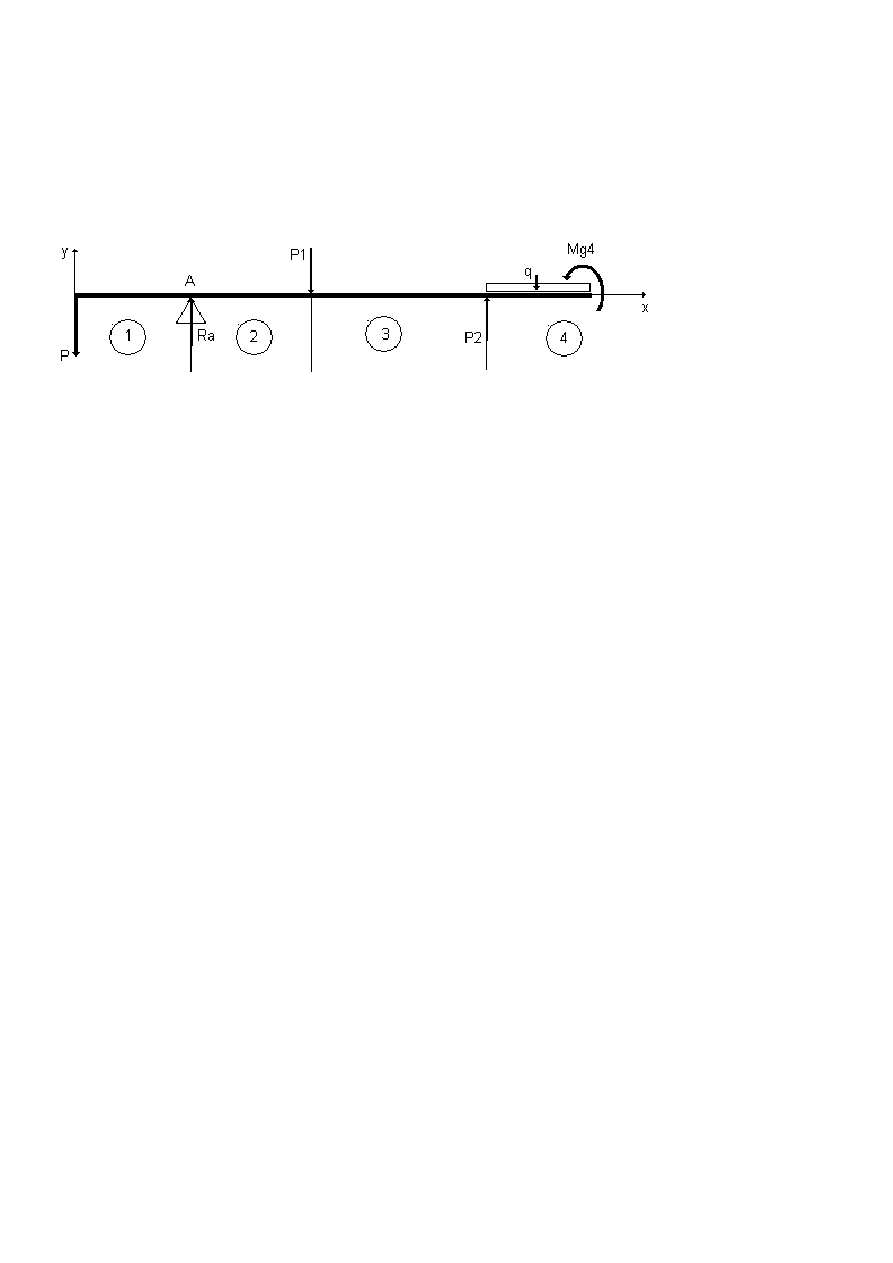
przedział 2 dla l1 ≤

≤

≤

≤ x ≤

≤

≤

≤ l1+l2

P*x – Ra*(x-l1) + Mg2 = 0
po przekształceniu otrzymamy
Mg2 = - P*x + Ra*(x-l1)


przedział 3 dla l1+l2 ≤

≤

≤

≤ x ≤

≤

≤

≤ l1+l2+l3

P*x – Ra*(x-l1) + P1*[x-(l1+l2)] + Mg3 = 0
po przekształceniu otrzymamy
Mg3 = - P*x + Ra*(x-l1) - P1*[x-(l1+l2)]

sta

przedział 4 dla l1+l2+l3 ≤

≤

≤

≤ x ≤

≤

≤

≤ L-( l1+l2+l3)

P*x – Ra*(x-l1) + P1*[x-(l1+l2)] – P2[x-(l1+l2+l3)] + q/2[x-(l1+l2+l3)]

2

+ Mg4 = 0

po przekształceniu otrzymamy
Mg4 = - P*x + Ra*(x-l1) - P1*[x-(l1+l2)] + P2[x-(l1+l2+l3)] - q/2[x-(l1+l2+l3)]

2

4. Wyznaczenie naprężenia zginającego dopuszczalnego kg dla obciążeń stałych.

kg = 0,53 * Re
gdzie:
kg – naprężenie dopuszczalne dla materiału z którego wykonana jest belka,
Re - granica plastyczności materiału. W zadaniu Re = 300MPa,
0,53 - współczynnik bezpieczeństwa (wg. tabeli określającej średnie wartości współczynników
bezpieczeństwa)

stąd

kg = 0,53 * 300 = 159 [MPa = MNm

-2

]

5. Wyznaczenie średnicy belki.

Przekształcając zależność

σg = M(x)/Wg ≤ kg

gdzie:
σg – naprężenie zginające w belce wywołane momentem gnącym (σg = kg),
M(x) – moment gnący,
Wg – wskaźnik wytrzymałości przekroju na zginanie, dla przekroju kołowego Mg = Πd

3

/32, gdzie d średnica

przekroju,
kg – naprężenie dopuszczalne.

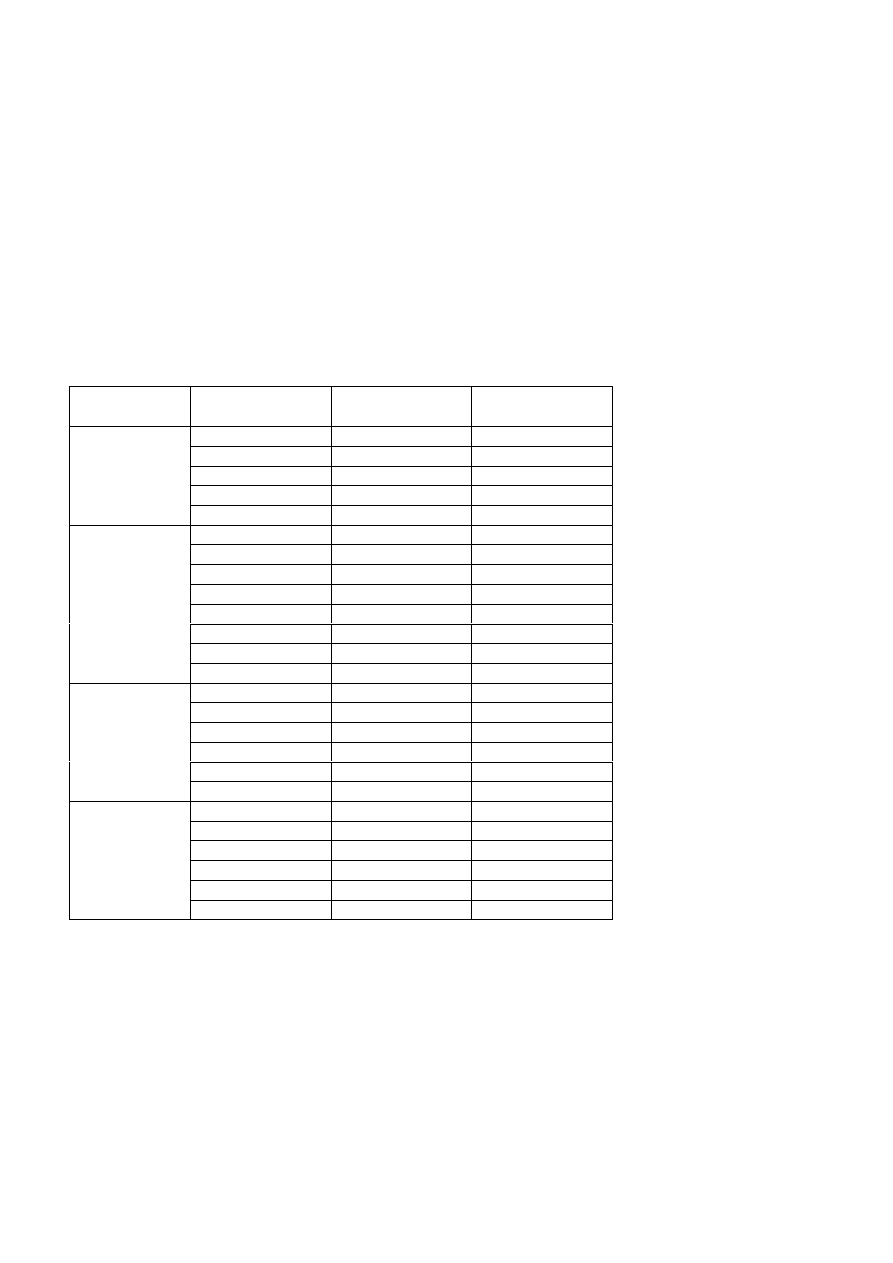
sta

stąd:
M(x)/ Πd

3

/32 = kg

d =

3

√32 * M(x)/ kg * Π

po podstawieniu danych dla wybranych długości z:
przedziału 1, długości 0,2[m], M(x) = Mg1(0,2) = 400 [Nm], kg = 159 * 10

6

[Pa=Nm

-2

]

d =

3

√32 * 400/ 159 * 10

3

* 3,14 = 0,02947 m = 29,47 mm

przedziału 2, długości 0,7[m], M(x) = Mg1(0,7) = 210,42 [Nm], kg = 159 * 10

6

[Pa=Nm

-2

]

d =

3

√32 * 210,42/ 159 * 10

3

* 3,14 = 0,02381 m = 23,81 mm

6. Zestawienie wyników w tabeli.

Przedział

x [m]

Mg [Nm]

d [mm]

0

0

0

0,2

-400

29,47

0,4

-800

37,16

0,5

-1000

40,02

1

0,6

-1200

42,53

0,6

-1200

42,53

0,65

-494,79

31,65

0,685

0

0

0,7

210,42

23,81

0,8

1620,83

47,01

1

4441,67

65,79

1,2

7262,50

77,5

2

1,3

8672,92

82,22

1,3

8672,92

82,22

1,4

8083,33

80,32

1,6

6904,17

76,2

1,8

5725,00

71,58

2

4545,83

66,3

3

2,1

3956,25

63,3

2,1

3956,25

63,3

2,2

3916,67

63,08

2,4

3537,50

60,98

2,6

2758,33

56,13

2,8

1579,17

46,6

4

3

0,00

0

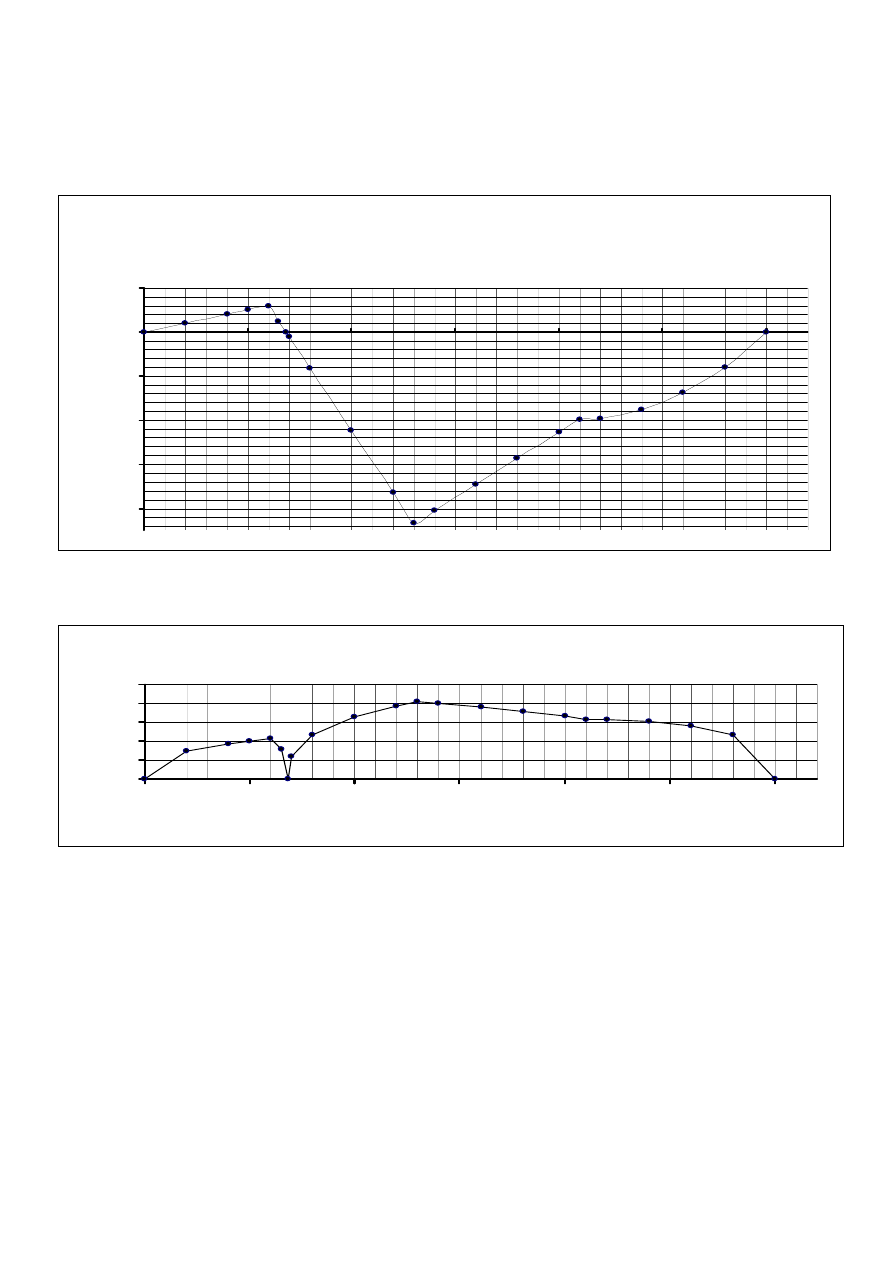
sta

6.1 wykres momentów gnących występujących na długości belki

Mg = f(L)

-2000

0

2000

4000

6000

8000

0

0,5

1

1,5

2

2,5

3

L [m]

M

g

[

N

/m

]

6.2 wykres średnicy belki na długości

d = f(L)

0

20

40

60

80

100

0

0,5

1

1,5

2

2,5

3

L [m]

d

[m

m

]