Zadanie 1 .

Firma „Semator” posiada trzy zakłady - Z1, Z2, Z3. Zakłady te mogą

wytwarzać tę samą farbę W-1. Pomiędzy łącznym kosztem produkcji wytworzonej w

zakładach Z1, Z2, Z3, a roczną wielkością produkcji tych zakładów zachodzi zależność

K(x

1

,x

2

,x

3

) = x

1

2

+ 2x

2

+ x

3

2

gdzie x

1

, x

2

, x

3

oznaczają odpowiednio wielkości rocznej produkcji farby W-1 w zakładach

Z1, Z2, Z3 w tys. litrów. Firma planuje roczną wielkość produkcji farby W-1 w ilości 9000

litrów.

Jakie ilości farby W-1 powinny produkować zakłady Z1, Z2, Z3 aby łączny koszt produkcji

był minimalny?

Zadanie 2.

Przedsiębiorca postanowił unowocześnić linie produkcyjne: francuską,

szwedzką oraz polską. W zależności od wysokości nakładów inwestycyjnych na

unowocześnienie linii produkcyjnej danego typu, można osiągnąć różny wzrost zdolności

produkcyjnych (w tonach). Dane dotyczące wzrostu zdolności w zależności od nakładów

zestawiono w tabeli

Nakłady w jp

0

1

2

3

Linia francuska

Linia szwedzka

Linia polska

0

0

0

6

5

4

12

9

10

14

10

14

Przedsiębiorca może otrzymać kredyt w wysokości co najwyżej 3 jp. W jaki sposób

rozdzielić otrzymany kredyt, aby zakład osiągnął maksymalny wzrost zdolności produk-

cyjnych, jeśli założono, że na linię szwedzką należy przeznaczyć co najmniej 1 jp.?

Zadanie 3.

Firma zamierza prowadzić reklamę swojego nowego wyrobu w telewizji,

radiu i prasie. Na reklamę można przeznaczyć co najwyżej 3 jp. Jaką kwotę należy

przeznaczyć na reklamę i w jaki sposób rozdzielić pomiędzy wymienione kanały reklamowe,

aby przyrost sprzedaży był maksymalny, jeśli założono, że na telewizję należy przeznaczyć

co najmniej 1 jp.? Skuteczność reklamy, mierzona przyrostem sprzedaży w zależności od

kanału reklamy, podaje tabela:

Nakład w jp

0

1

2

3

Telewizja

Prasa

Radio

0

0

0

120

100

150

150

200

150

200

200

300

Zadanie 4.

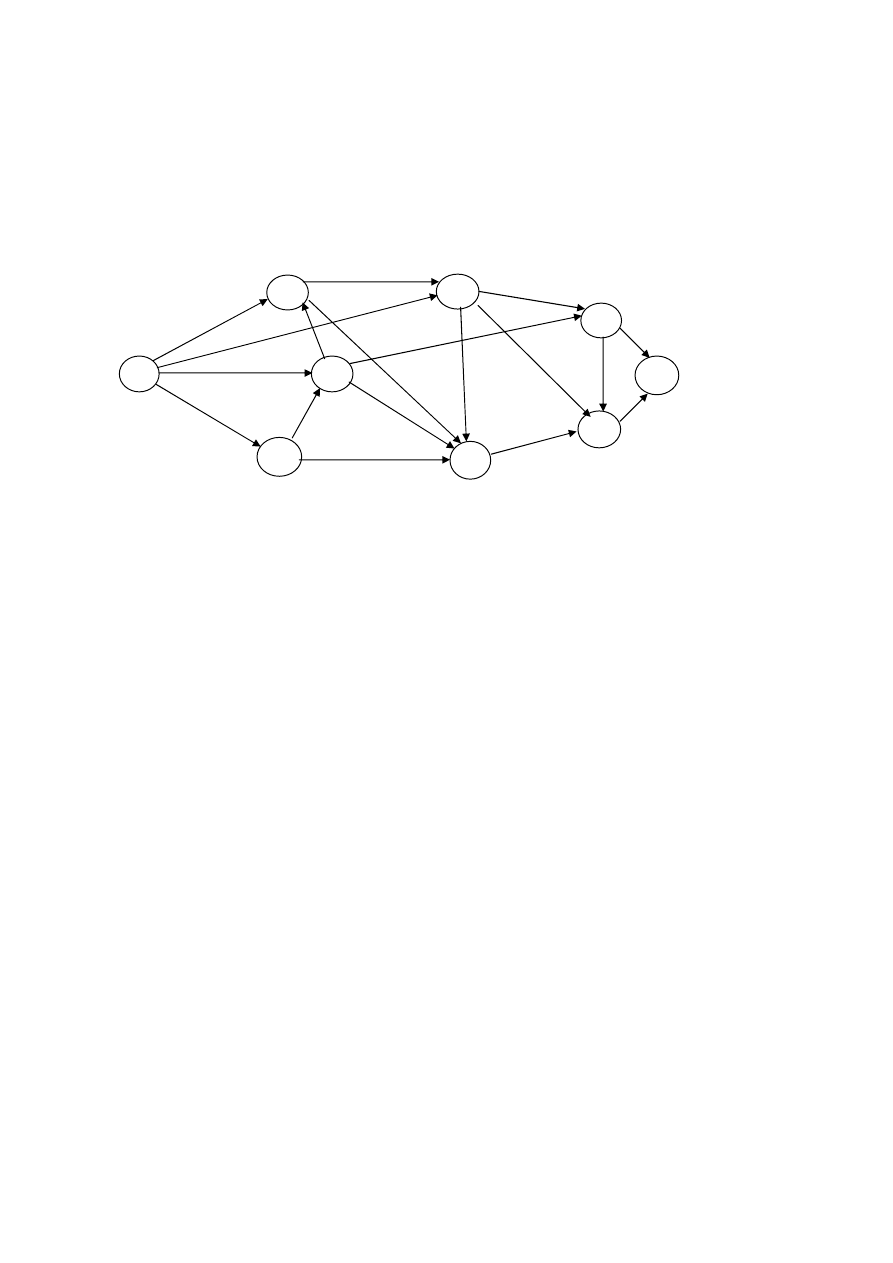
Firma transportowa TRANSYS chce ustalić nową tras przejazdu swoich

ciężarówek ze Słupska do Katowic. Na podstawie atlasu samochodowego ustalono kilka

możliwych tras, oznaczając wybrane miasta przez które będą przejeżdżać ciężarówki cyframi

od 1 do 9. Problem polega na znalezieniu najkrótszej drogi łączącej 1 z 9, pamiętając, że w

mieście o numerze 5, ciężarówki zostawiają część towaru. Połączenia pomiędzy miastami

zaznaczono na grafie, długości połączeń opisano na łukach.

90

2 5

170

100

7

200 80 300 15

1

40

4

80

120

30

9

90 60

200

130

8 25

3

130

6 50

Zadanie 5.

Firma DOSTAWCA CUD chce opracować program produkcji

wprowadzanego na rynek nowego wyrobu dla kolejnych trzech miesięcy. Po

przeprowadzeniu akcji reklamowej oszacowano, że w ciągu następnych dwóch miesięcy

popyt będzie stały i równy 4 jednostki, a w trzecim miesiącu zmaleje o jedną jednostkę. Czas

przygotowania partii wyrobów jest na tyle mały, że produkcja wytworzona w miesiącu t=1,2

lub 3 może być od razu przeznaczona do sprzedaży (bez magazynowania). Koszty

magazynowania wyrobów są jednakowe w ciągu trzech miesięcy i wynoszą 2 jp za jednostkę.

Koszty produkcji K zależą od wielkości serii i wynoszą K(0) = 0, K(1) = 13, K(2) = 19,

K(3) = 23, K(4) = 27, K(5) = 29.

Uwaga: Pod koniec trzeciego miesiąca w magazynie mają pozostać 2 jednostki. Maksymalna

liczba wyrobów, które może pomieścić magazyn jest równa 7.

Podać plan produkcji na kolejne trzy miesiące, dla którego koszty będą najmniejsze.

Zadanie 6.

Trzy wyroby A, B i C produkowane są z tego samego surowca którego

zapas 100 t powinien zostać całkowicie zużyty. Na 20 sztuk wyrobu A zużywa się 0,25 t

surowca, na 1000 sztuk wyrobu B - 10 t , a na 1000 sztuk wyrobu C – 1,5 t Ustalić wielkość

produkcji tych wyrobów tak, aby zminimalizować funkcję kosztu jednostkowego określoną

wzorem

f(x,y,z) = 2x

2

+ 10y

2

– 14y + 5 + z

gdzie

x - liczba wyrobów A,

y - liczba wyrobów B,

z - liczba wyrobów C.

Zadanie 7.

Planowane są prace modernizacyjne w trzech kopalniach. Rezultatem tych

prac ma być łącznie wzrost o 20.000 t dziennego wydobycia. Koszty prac modernizacyjnych

w zależności od planowanego wzrostu wydobycia w poszczególnych kopalniach

(odpowiednio x, y, z) wyraża funkcja

f(x,y) = x

2

+ 2y

2

– 2y + 14 +10z

Zaplanować wielkość przyrostu wydobycia dla poszczególnych kopalń tak, aby koszty prac

modernizacyjnych były jak najniższe.

Zadanie 8.

Rozdzielić dzienną produkcję energii 100 MWh między dwie elektrownie

tak, aby dzienne koszty zużycia paliwa opisane funkcją

f(x,y,z) = 2(–x+1)

2

+ (y–3)

2

gdzie x - zużycie paliwa w elektrowni I, y - zużycie paliwa w elektrowni II, były najniższe.

Wiadomo ponadto, że z 1 tony paliwa elektrownia I uzyskuje 5 MWh energii, a elektrownia

II - 3 MWh.

Zadanie 9.

Z elektrociepłowni energia przesyłana jest do trzech zużywających ją

zakładów produkcyjnych. Funkcja kosztów przesyłania energii do tych zakładów w zależności

od wielkości przesyłu

(x do zakładu I, y do zakładu II, z do zakładu III) dana jest wzorem

f(x,y,z) = 5x

2

- 8x – 7y + 7y

2

+ 10z

Rozdzielić dzienną produkcję energii 20 MWh pomiędzy zakłady tak, aby zminimalizować

koszty przesyłu energii.

Zadanie 10.

Przedsiębiorstwo korzysta z trzech bocznic - własnej, bocznicy huty i

PKP. Koszty związane z przestojem wagonów wyraża następująca funkcja:

f(x,y,z) = 0,25x

2

+ 0,5y

2

+4x + 0,6z

gdzie: x - czas trwania wyładunku na bocznicy własnej (w dniach),

y - czas trwania wyładunku na bocznicy PKP,

z - czas trwania wyładunku na bocznicy huty.

Pociągi towarowe wożące surowiec do przedsiębiorstwa mają w swym składzie 200

wagonów. Dzienna zdolność przeładunkowa bocznicy własnej wynosi 20 wagonów, bocznicy

huty - 10 wagonów i bocznicy PKP - 30 wagonów. Jak rozdzielić wagony między bocznice,

aby koszt związany z przestojem był jak najmniejszy?.

Zadanie 11.

Przedsiębiorstwo produkuje dla własnych potrzeb wypełniacz w

wydziałach produkcji pomocniczej. Wypełniacz ten wytwarzany jest w brykietach odpo-

wiednio jedno- , dwu- i trzykilogramowych. Oszacowana funkcja kosztów wytwarzania

wypełniacza ma postać

f(x,y,z) = 0,25x

2

+ 1,5x + y

2

+ y + 2z

gdzie: x – liczba jednokilogramowych brykietów wypełniacza ,

y – liczba dwukilogramowych brykietów wypełniacza ,

z – liczba trzykilogramowych brykietów wypełniacza .

Przedsiębiorstwo zużywa w procesie produkcji 2000 kg wypełniaczy. Ile powinny wynosić

rozmiary produkcji wypełniaczy, aby koszty produkcji były jak najmniejsze?

Zadanie 12.

Trzy olejarnie o zdolnościach przerobowych 15, 20 i 10 ton ziarna

dziennie , mają przerobić 2000 ton ziarna na olej. Straty oleju w ziarnie zależą od procesów

technologicznych. Funkcja łączonych strat oleju w ziarnie (w kg) dla olejarni dana jest

wzorem

f(x,y,z) = 20x + 3y

2

– 4y + 30z

gdzie: x, y, z - to czasy trwania kampanii odpowiednio w pierwszej, drugiej i trzeciej olejarni.

Jak długo powinny trwać kampanie w olejarniach, aby straty oleju w ziarnie były minimalne?

Zadanie 13.

Dany jest obiekt, będący zespołem urządzeń U1, U2, U3 połączonych

równolegle (awaria układu jest równoważna awarii wszystkich urządzeń). Poniżej

przedstawiono macierz P=(p

ij

), gdzie p

ij

jest prawdopodobieństwem tego, że jeśli na remont i-

tego urządzenia przeznaczono j jednostek pieniężnych, to nie ulegnie ono awarii.

0 jp

1 jp

2 jp

3 jp

4jp

U1

U2

U3

0,2

0,1

0,2

0,2

0,3

0,3

0,4

0,5

0,4

0,6

0,6

0,6

0,7

0,8

0,8

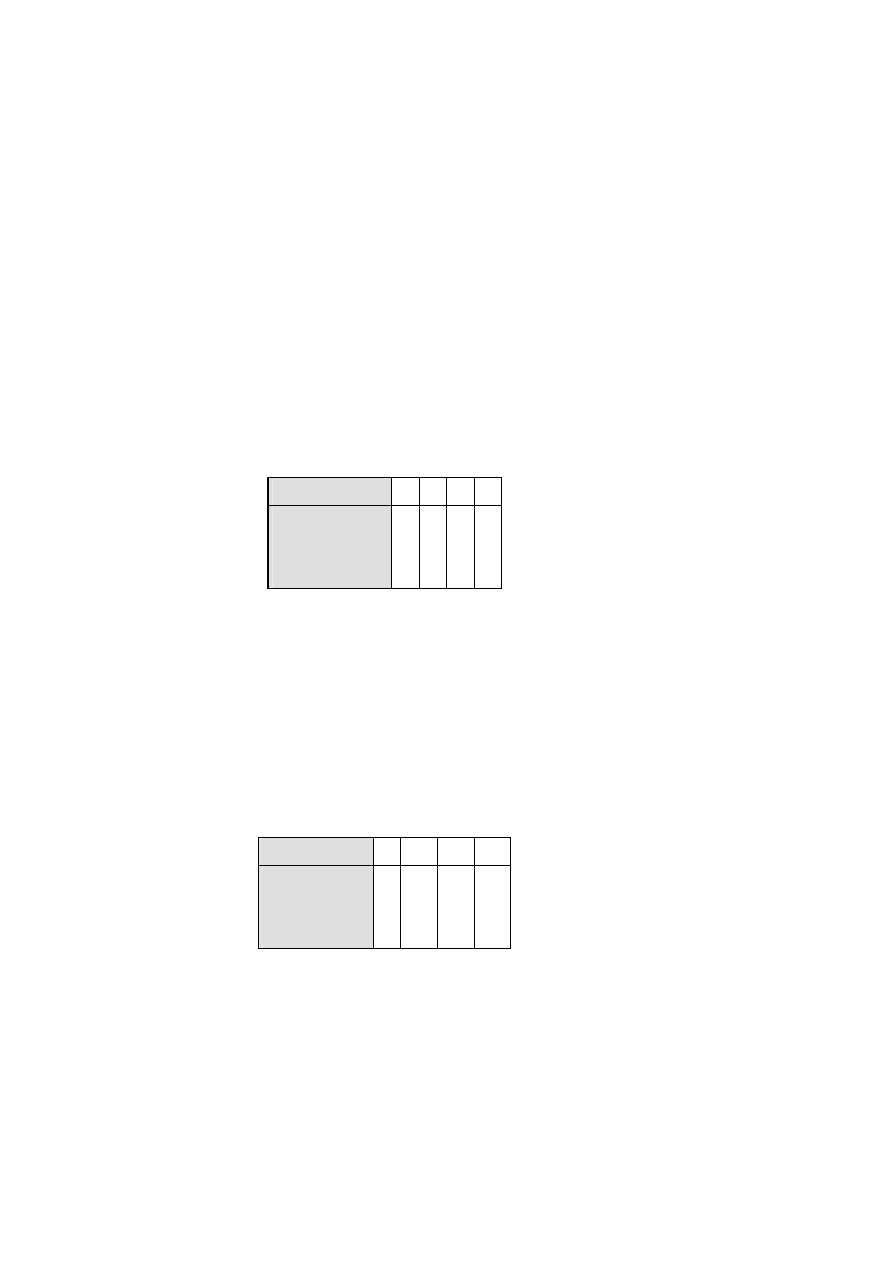
Przedsiębiorstwo przeznaczyło 4 jp na remont całego obiektu. Określić optymalny przydział

środków maksymalizujący prawdopodobieństwo braku awarii całego obiektu po dokonaniu

remontu poszczególnych urządzeń.

Uwaga: Urządzenia ulegają awariom niezależnie.

Zadanie 14.

W zakładzie KONPOL należy zaplanować produkcję na najbliższe trzy

lata. Jeśli przez i oznaczymy numer roku (i=1,2,3), to s

i

jest wielkością posiadanego przez

zakład funduszu na początku tego roku. Środki te mogą zostać rozdzielone do realizacji

dwóch różnych rodzajów produkcji. Ich podział na y

i

i s

i

– y

i

wiąże się z:

(1) uzyskaniem zysku w wielkościach y

i

2

i 5(s

i

– y

i

), dla i = 1,2,3

(2) redukcją funduszy, które mogą być rozdzielone do wielkości s

i+1

= 0,5y

i

+ 0,9(s

i

– y

i

) wraz

z końcem roku dla i = 1,2. Fundusze te odliczane są z zysku. Przyjmując s

1

=5 wyznaczyć

zmienne y

1

, y

2

, y

3

maksymalizujące sumaryczny zysk zakładu w ciągu całego trzyletniego

okresu.

Zadanie 15.

Agencja planuje w pewnym kraju telewizyjną kampanię nowego

produktu. Cel ten realizowany jest za pomocą trzech stacji telewizyjnych. Szacuje się, że jeśli

j jest numerem stacji, to przeznaczenie na reklamę funduszu y

j

jp przyniesie dochód R

j

(y

j

)

jednostek pieniężnych. Agencja zakłada, że łączna liczba nadanych reklam ma być nie

większa niż 50. Dodatkowo wiadomo, że przeznaczenie w stacji j-tej y

j

jp gwarantuje

nadanie przez tę stację dokładnie K

j

(y

j

) reklam. Ile łącznie należy przeznaczyć jednostek

pieniężnych na reklamę, aby spełnić założenia agencji i zmaksymalizować wynikające z

kampanii korzyści jeśli:

K

j

(y

j

) = y

j

, j=1,2,3

R

1

(y

1

) = 2y

1

+14,

R

2

(y

2

) = y

2

2

–y

2

+1,

R

3

(y

3

) = 5y

3

, y

1

, y

2

, y

3

- liczby całkowite.

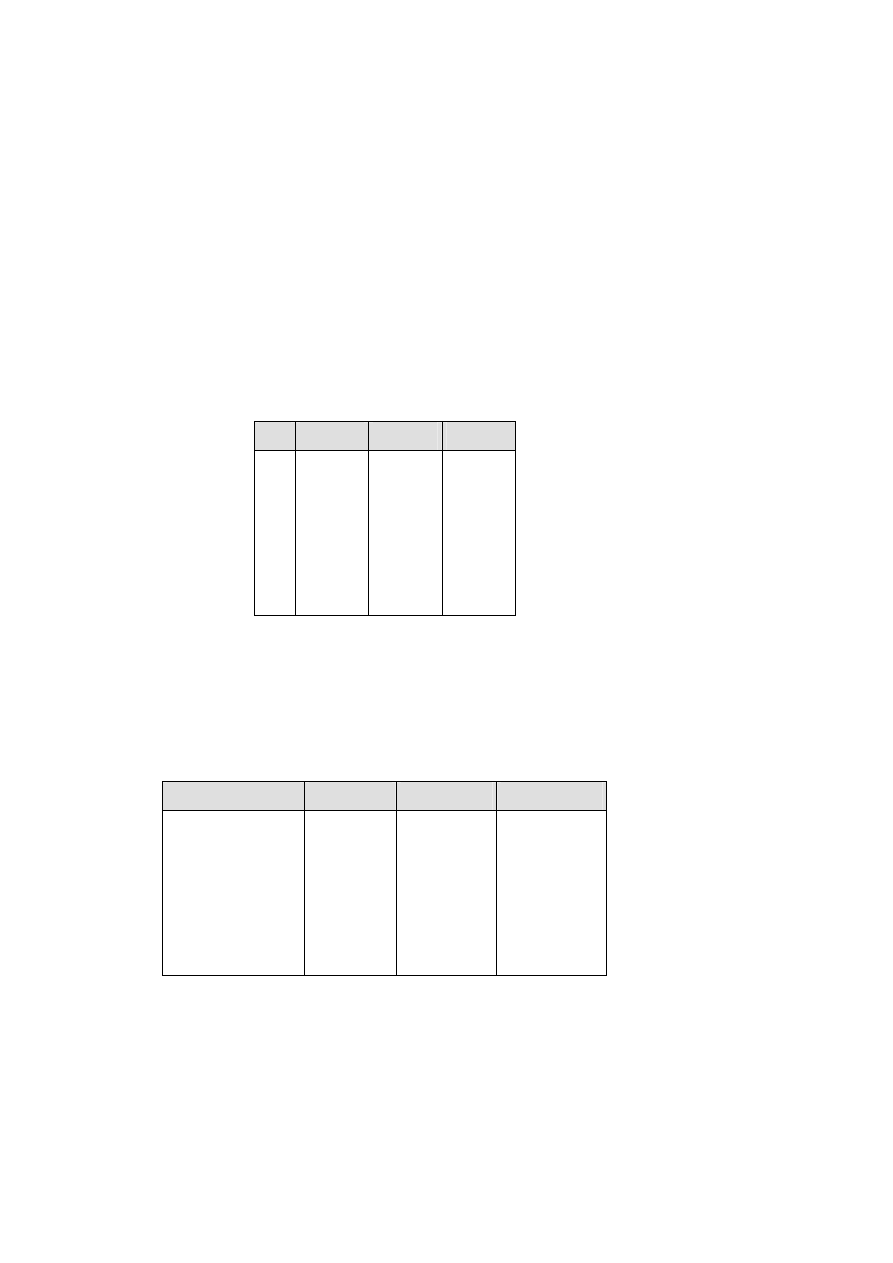
Zadanie 16.

Agencja planuje w pewnym kraju telewizyjną kampanię nowego

produktu. Cel ten realizowany jest za pomocą trzech stacji telewizyjnych. Szacuje się, że jeśli

j jest numerem stacji, to przeznaczenie na reklamę funduszu y

j

jp przyniesie dochód R

j

(y

j

)

jednostek pieniężnych. Agencja zakłada, że łączna liczba nadanych reklam ma być nie

większa niż 50. Dodatkowo wiadomo, że przeznaczenie w stacji j-tej y

j

jp gwarantuje nadanie

przez tę stację dokładnie K

j

(y

j

) reklam. Ile łącznie należy przeznaczyć jednostek pieniężnych

na reklamę, aby spełnić założenia agencji i zmaksymalizować wynikające z kampanii

korzyści, jeśli

K

j

(y

j

) = y

j

, j=1,2,3

Wiadomo, że w stacji numer 3 należy nadać co najmniej 10 reklam.

jp

R

1

(y

1

)

R

2

(y

2

)

R

3

(y

3

)

0

10

20

30

40

50

0

10

10

20

25

35

0

15

15

18

20

35

0

5

10

15

30

35

Zadanie 17.

Trzy zakłady B1,B2,B3 firmy POLBUD wytwarzają ten sam produkt.

Badania rynku wykazały, że można będzie sprzedać co najmniej 15.000 sztuk tego produktu

w ciągu roku. Roczną wielkość produkcji w każdym z zakładów, a także koszty ponoszone w

związku z produkcją podano w tabelce

Wielkość produkcji Koszty w B1 Koszty w B2

Koszty w B3

0

5000

10000

15000

20000

25000

0

5

7

15

16

17

0

7

9

12

13

14

0

4

10

15

16

16

Zaplanować roczną produkcję w taki sposób, aby zminimalizować jej łączny koszt wiedząc,

że w zakładzie B2 należy produkować nie mniej niż 5000 sztuk.

Zadanie 18.

Trzy zakłady B1,B2,B3 (własność firmy „KOLMAD”) wytwarzają ten

sam produkt. Jeśli przez x

i

oznaczymy wielkość rocznej produkcji w zakładzie B

i

, to funkcja

określająca łączną roczną wielkość kosztów produkcji w tych zakładach ma następującą

postać

f(x

1

,x

2

,x

3

) = x

1

2

– x

1

+ 1 + 3x

2

+ x

3

2

Badania rynku wykazują, że zapotrzebowanie na produkt wytwarzany przez wspomniane

zakłady będzie równy co najmniej 5 jednostek. Zaplanować rozkład rocznej produkcji w

zakładach firmy „KOLMAD” minimalizując łączne, roczne koszty.

Zadanie 19.

Przedsiębiorca Zenon Kula, może otrzymać kredyt inwestycyjny w

wysokości co najwyżej 6 jp oraz halę produkcyjną w Murckach, postanowił zainstalować

nowoczesne linie do wyrobu makaronu M-1, M-2, M-3. W zależności od wysokości

nakładów inwestycyjnych przeznaczonych na zainstalowanie linii produkcyjnej danego typu,

można osiągnąć różne dobowe zdolności produkcyjne zestawione w tablicy

Nakłady [w jp]

0

1

2

3

4

5

6

M-1

0

6

12

12

12

13

18

M-2

0

5

8

11

13

15

17

M-3

0

4

15

15

15

15

16

Pan Zenon Kula musi więc w tym przypadku podjąć decyzję dotyczącą wielkości

zaciągniętego kredytu oraz podziału kredytu pomiędzy poszczególne programy inwestycyjne

tak, aby zakład osiągnął maksymalną, dobową zdolność produkcyjną.

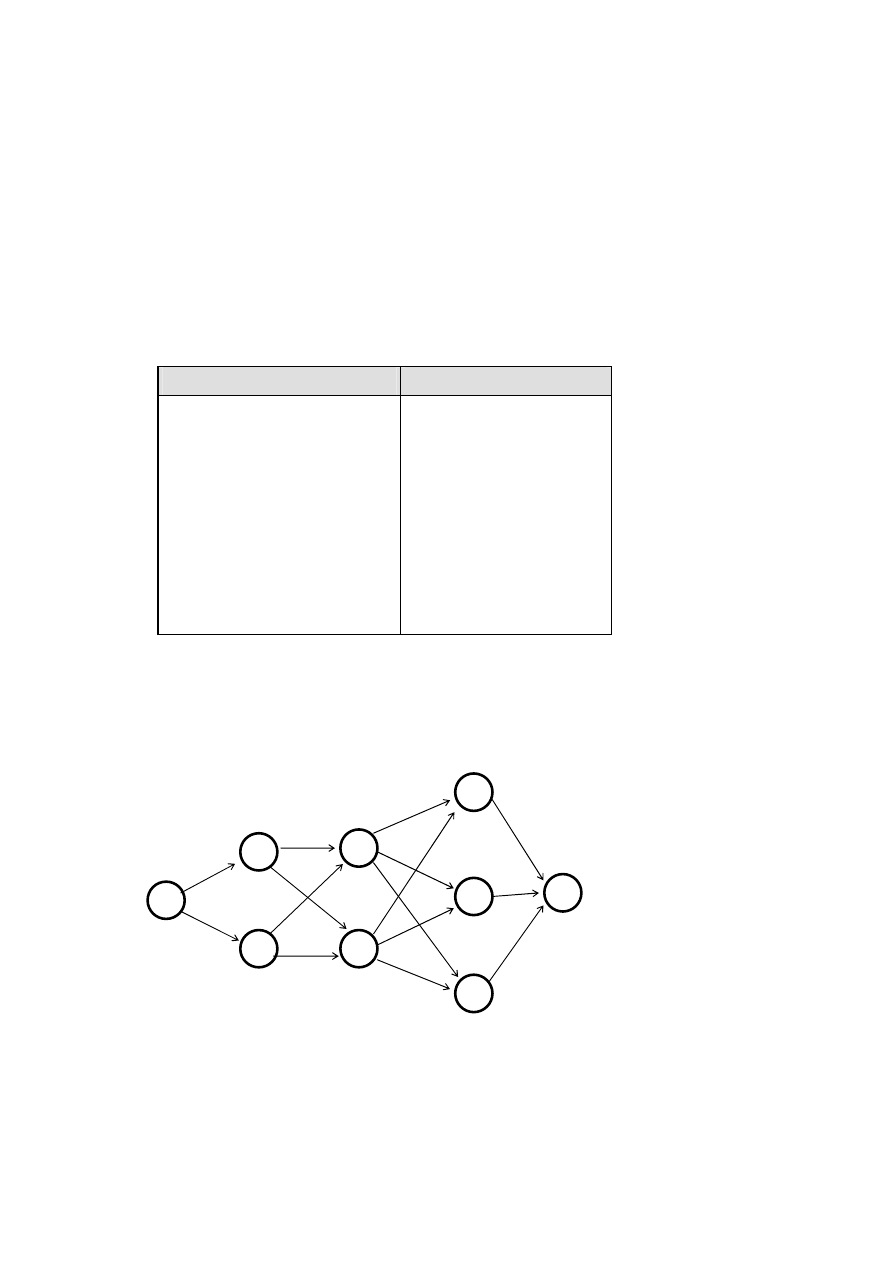
Zadanie 20.

Firma transportowa Autokam, ustalając nowe trasy przejazdu swych

ciężarówek z Polski do Hiszpanii, podzieliła całą trasę na pięć etapów. W każdym z etapów

wyznaczono po kilka miast, przez które przejeżdżać będą ciężarówki. Problem polega na

znalezieniu najkrótszej drogi przejazdu pomiędzy Polską (1) a Austrią (9). Odległości

drogowe pomiędzy miastami zaznaczono na rysunku

4

200

200

150

7

250

150

2

120

80

100

9

5

1

180

130

130

80

8

3

150

120

110

190

6

Zadanie 21.

Grupa ratunkowa, której siedzibą jest miejscowość 1 ma pod swoją

opieką kilkanaście wiosek położonych w obszarze górzystym. Jedynymi drogami w tym

rejonie jest sieć dróg lokalnych o nawierzchni szutrowej. Podczas akcji ratunkowych liczy się

często każda minuta, dlatego też podczas poprzednich akcji zmierzono czasy przejazdu

między wioskami. Zebrane dane przedstawione zostały w tablicy. Posługując się informacjami

o czasach przejazdu wyznacz najszybsze trasy z 1 do wiosek będących pod opieką grupy.

Odcinek Czas przejazdu

Odcinek Czas przejazdu

z 1 do 2 17
z 1 do 3 21
z 1 do 4 13
z 2 do 3 25
z 2 do 5 16
z 2 do 7 10
z 3 do 6 20
z 3 do 8 10
z 4 do 1 15
z 4 do 3 12
z 4 do 6 19
z 4 do 9 10
z 5 do 7 9

z 5 do 8 18
z 6 do 8 17
z 6 do 9 21
z 7 do 8 14
z 7 do 11 15
z 8 do 9 8
z 8 do 11 10
z 8 do 12 11
z 9 do 10 20
z 9 do 12 13
z 10 do 12 9
z 11 do 12 9

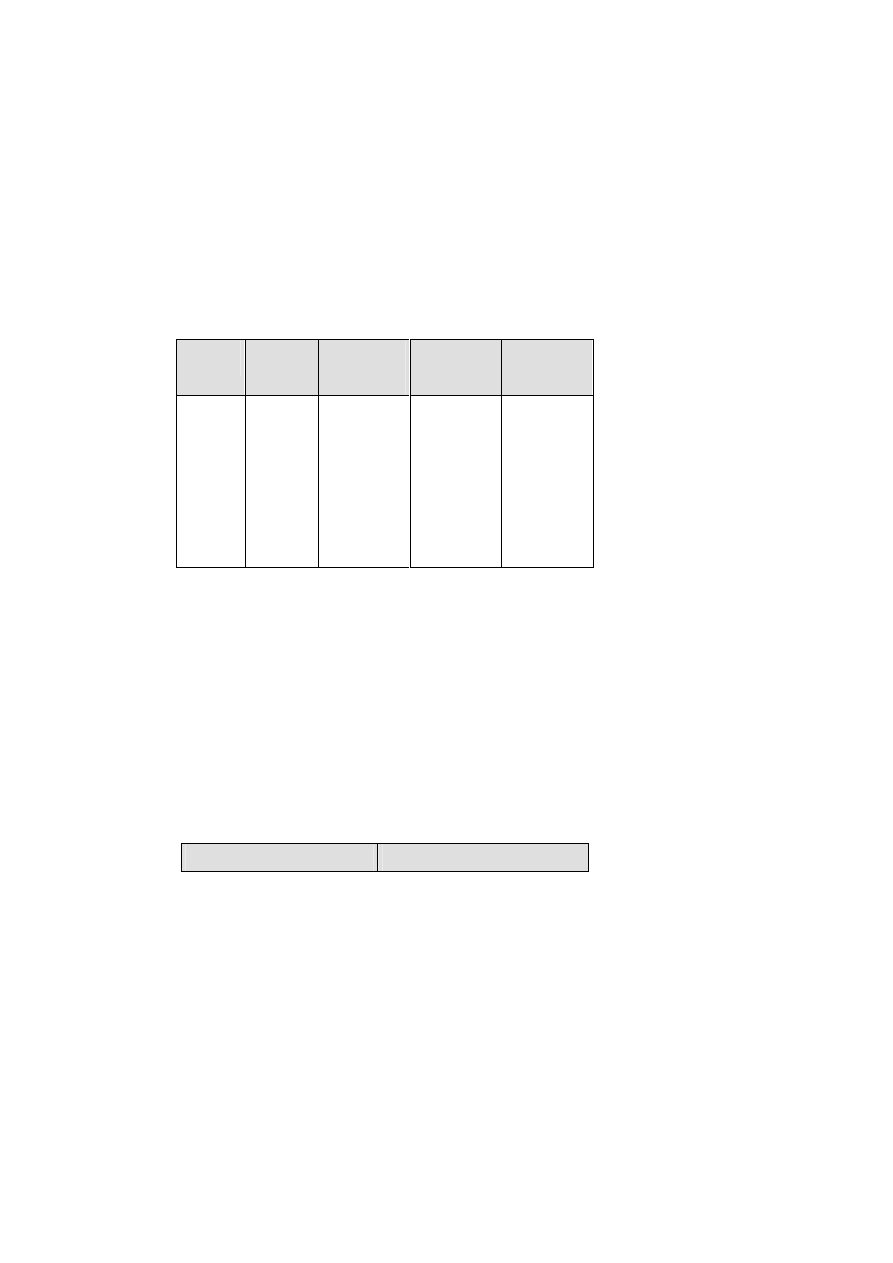
Zadanie 22.

Prywatna firma przewozowa ma zaplanować przebieg linii autobusowej z

Krakowa (1) do Paryża (9) tak, aby zapewnić jej największą frekwencję. Badania rynku

wykazały, że frekwencja na danej linii zależy w bezpośredni sposób od atrakcyjności trasy

przejazdu. Na rysunku przedstawiono możliwe warianty przebiegu trasy wraz ze spodziewaną

liczbą pasażerów na każdym z etapów.

9

6

12

13

11

11

14

9

1

12

14

7

13

4

5

2

3

4

10

10

8

6

7

8

Zadanie 23

. Producent prętów stalowych otrzymuje zamówienia na pręty o ośmiu

średnicach, ponumerowanych od 1 do 6. Odbiorcy wyrażają zgodę na ewentualne zastąpienie

prętów o zamawianej średnicy prętami o średnicy większej. Znane są koszty stałe związane z

przestrajaniem urządzeń i rozpoczęciem produkcji prętów o poszczególnych średnicach,

niezależne od skali produkcji, oraz koszty jednostkowe poszczególnych rodzajów

asortymentów, które rosną wraz ze zwiększaniem się średnicy prętów. Wartości liczbowe

podano w tablicy. Określić, jakie ilości prętów poszczególnych rodzajów powinien wytwarzać

producent, by zminimalizować swe koszty i jednocześnie zrealizować zamówienia klientów.

Numer

Średnicy

Średnica

(mm)

Wielkość

zamówienia

(tys. szt.)

Koszty stałe

(tys. zł)

Koszty

jednostkowe

(tys. zł)

1

2

3

4

5

6

26

30

34

38

42

46

40

45

35

20

28

36

22,5

23,6

24,8

26,0

27,1

28,3

0,5

0,6

0,7

0,9

1,0

1,2

Zadanie 24.

Pewna firma kupuje i sprzedaje te same artykuły i w związku z tym

potrzebuje dużo miejsca do ich składowania. Firma ta posiada w jednym magazynie

pomieszczenie na 500 sztuk danego wyrobu. Piętnastego dnia miesiąca może po podanych

niżej cenach zamówić dostawy, które są realizowane pierwszego dnia następnego miesiąca. W

każdym miesiącu firma może sprzedać tyle sztuk wyrobów, ile wynosi cały zapas

magazynowy, również po podanych niżej cenach. W przypadku gdy rozpoczyna ona rok z

zapasem magazynowym w wysokości 200 sztuk, powstaje pytanie, ile powinna miesięcznie

kupować i sprzedawać, by maksymalizować swój roczny zysk (zysk = kwota uzyskana ze

sprzedaży minus kwota wydana na zakup). Ceny zakupu i sprzedaży przedstawiono w tablicy.

Cena zakupu

Cena sprzedaży

15 stycznia 150

15 lutego 155

15 marca 165

15 kwietnia 160

15 maja 160

styczeń 165

luty 165

marzec 185

kwiecień 175

maj 170

Zadanie 25.

Stwierdzono, że pomiędzy wartością produkcji a trzema jej

substytucyjnymi czynnikami A, B, C zachodzi zależność

P(x

1

,x

2

,x

3

) =

1

2000

x

1

x

2

x

3

gdzie x

1

, x

2

, x

3

oznaczają odpowiednio wielkości zużywanych czynników A, B, C. Koszt

zużycia jednostki czynnika A, B i C wynosi odpowiednio

k

1

= 1 , k

2

= 2 , k

3

= 1

Określić optymalne zużycie odpowiednich czynników produkcji, przyjmując za kryterium

optymalności wartość produkcji przy założeniu, że koszt zużycia wymienionych czynników

wynosi 4000 jednostek pieniężnych.

Zadanie 26.

Należy dostarczać 7 jednostek nowego produktu na rynek. W tym celu

należy uruchomić produkcję tego produktu w odpowiedniej liczbie spośród trzech

wytypowanych zakładów (istniejących lub specjalnie do tego celu wybudowanych).

Dla i = 1, 2, 3 oznaczamy:

a

i

- maksymalna ilość produktu, jaka może być wytworzona w i-tym zakładzie,

d

i

- koszt stały uruchomienia produkcji w i-tym zakładzie,

c

i

- bieżący koszt wytworzenia jednostki produktu w i-tym zakładzie.

Odpowiednie dane są podane w tablicy.

i

a

i

d

i

c

i

1

3

130

50

2

5

250

20

3

4

180

40

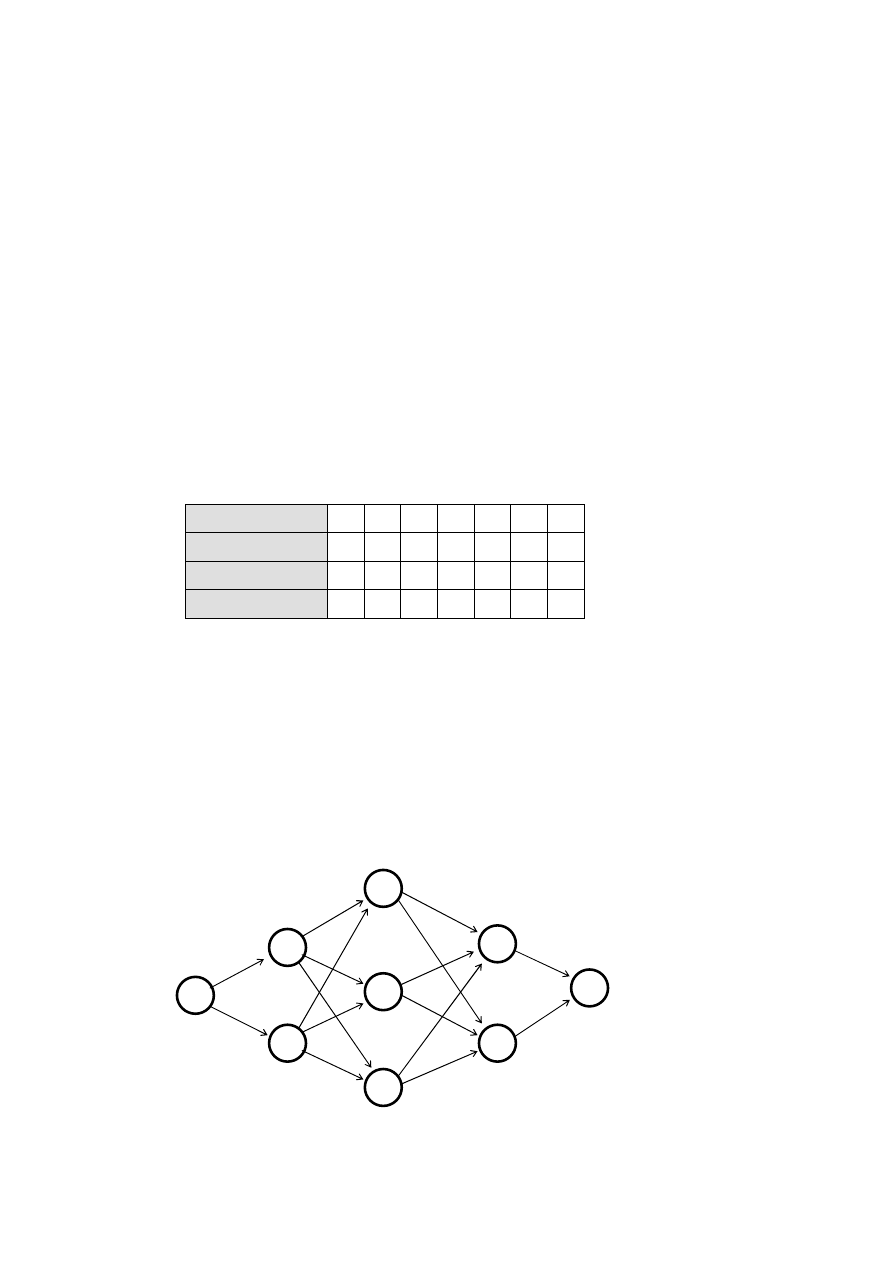
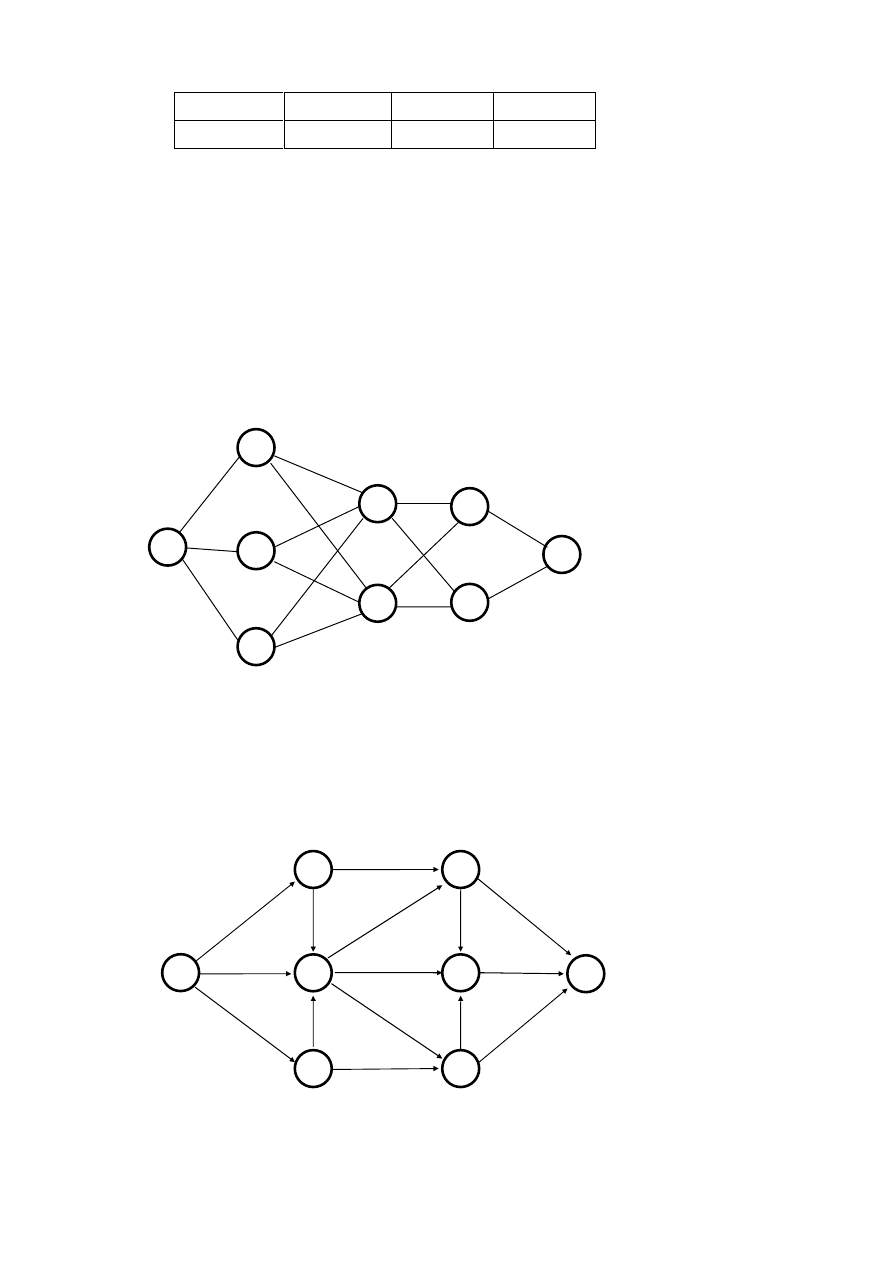
Zadanie 27.

Stosując zasady programowania dynamicznego, należy w

przedsięwzięciu przedstawionym na rysunku znaleźć najdłuższą drogą między punktami 1 i 9.

Zadanie 28.

Stosując zasadę programowania dynamicznego znaleźć najtańszą trasę z

1 do 8,

30

60

60

40

100

50

40

Etap 1

Etap 3

Etap 5

1

9

50

40

100

50

5

6

7

Etap 4

8

80

120

70

120

2

Etap 2

3

4

30

70

50

60

20

40

40

50

1

40

30

2

3

4

30

8

40

40

40

20

5

6

7

Zadanie 29

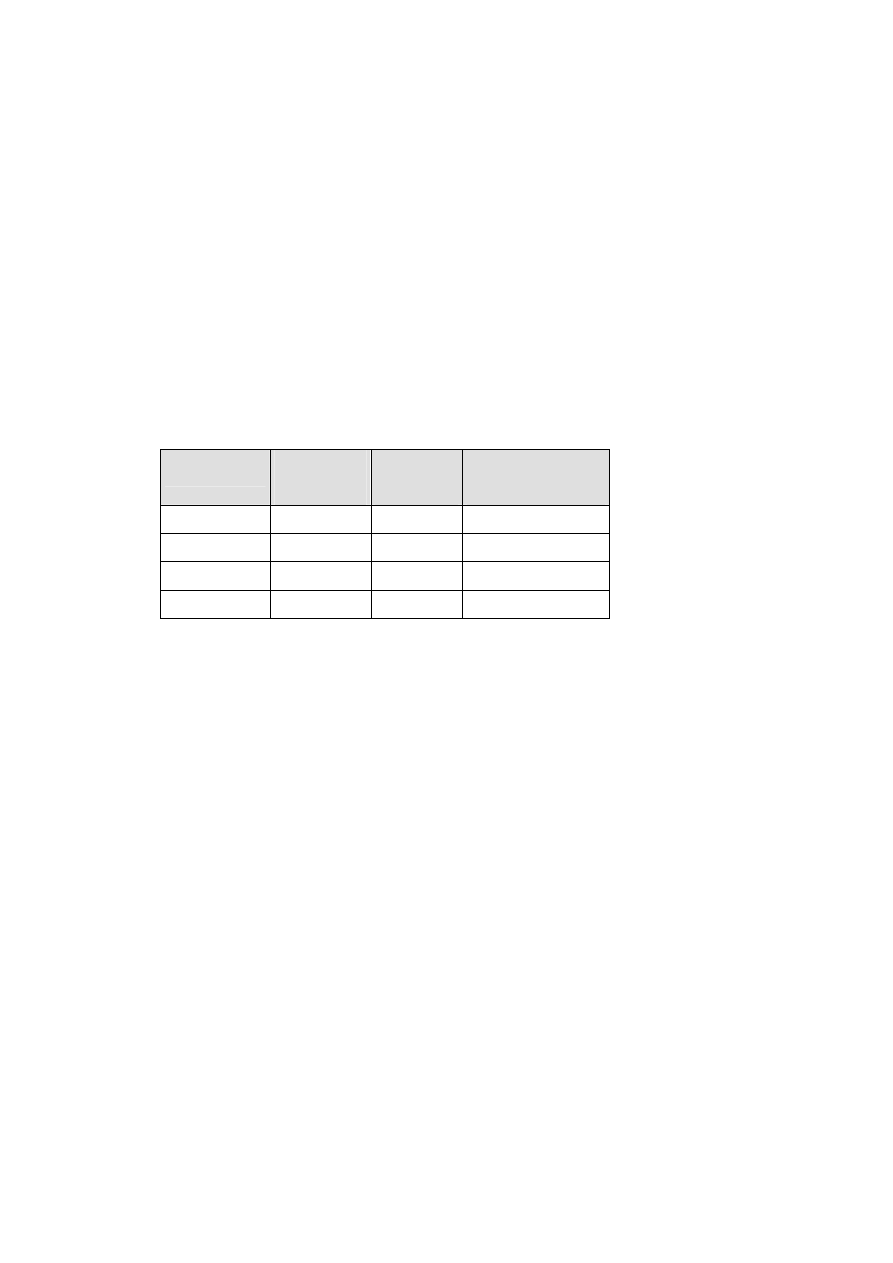
. Inwestor ma możliwość zainwestowania 20 000 zł. W tablicy podano

listę dostępnych możliwości inwestycyjnych oraz dostępne informacje o tych inwestycjach.

Określić optymalny sposób alokacji posiadanych środków przez inwestora.

Możliwość

inwestycyjna

Koszt

jednostkowy

(w zł)

Dostępność

(w tysiącach

sztuk)

Oczekiwany zysk na

jednostce

(w zł)

Akcja 1

2

5

0,4

Akcja 2

3

3

0,5

Akcja 3

2

2

0,45

Akcja 4

4

5

0,35

Zadanie 30.

Dysponujemy pewnym zasobem początkowym w ilości 1 jednostki.

Zasób ten można kierować w całości lub części na jeden z dwóch celów. Skierowanie x

jednostek zasobu na I cel w ciągu jednego okresu przynosi zysk

f

1

(x) = 5 + 3x – x

2

powodując jego 20-procentowe zużycie. Skierowanie y jednostek zasobu na II cel w ciągu

jednego okresu przynosi zysk

f

2

(y) = 5 + 2y – y

2

i nie powoduje zużycia tego zasobu. Jakie wielkości zasobu należy kierować w trzech

kolejnych okresach na oba cele, aby łączny zysk uzyskany w tych okresach był maksymalny?

Zadanie 31.

Zakład produkcyjny winien pokryć zapotrzebowanie na pewien produkt

w ciągu 6 pierwszych miesięcy pewnego roku. Zapotrzebowanie na produkt w każdym

miesiącu wynosi 3 jednostki.

W każdym miesiącu zakład może uruchomić produkcję produktu. Uruchomienie produkcji

pociąga za sobą koszt 13 tysięcy złotych. Zakład może wyprodukować w każdym miesiącu co

najwyżej 5 jednostek produktu, przy czym wytwarzanie ułamków jednostki produktu jest

niedopuszczalne. Wytworzenie pierwszej jednostki produktu kosztuje 3 tys.zł, drugiej - 2

tys.zł, zaś trzeciej i czwartej po 1 tys. zł. Produkowanie piątej jednostki wymaga

uruchomienia dodatkowych urządzeń, a stąd koszt jej uruchomienia wynosi 4 tys. zł.

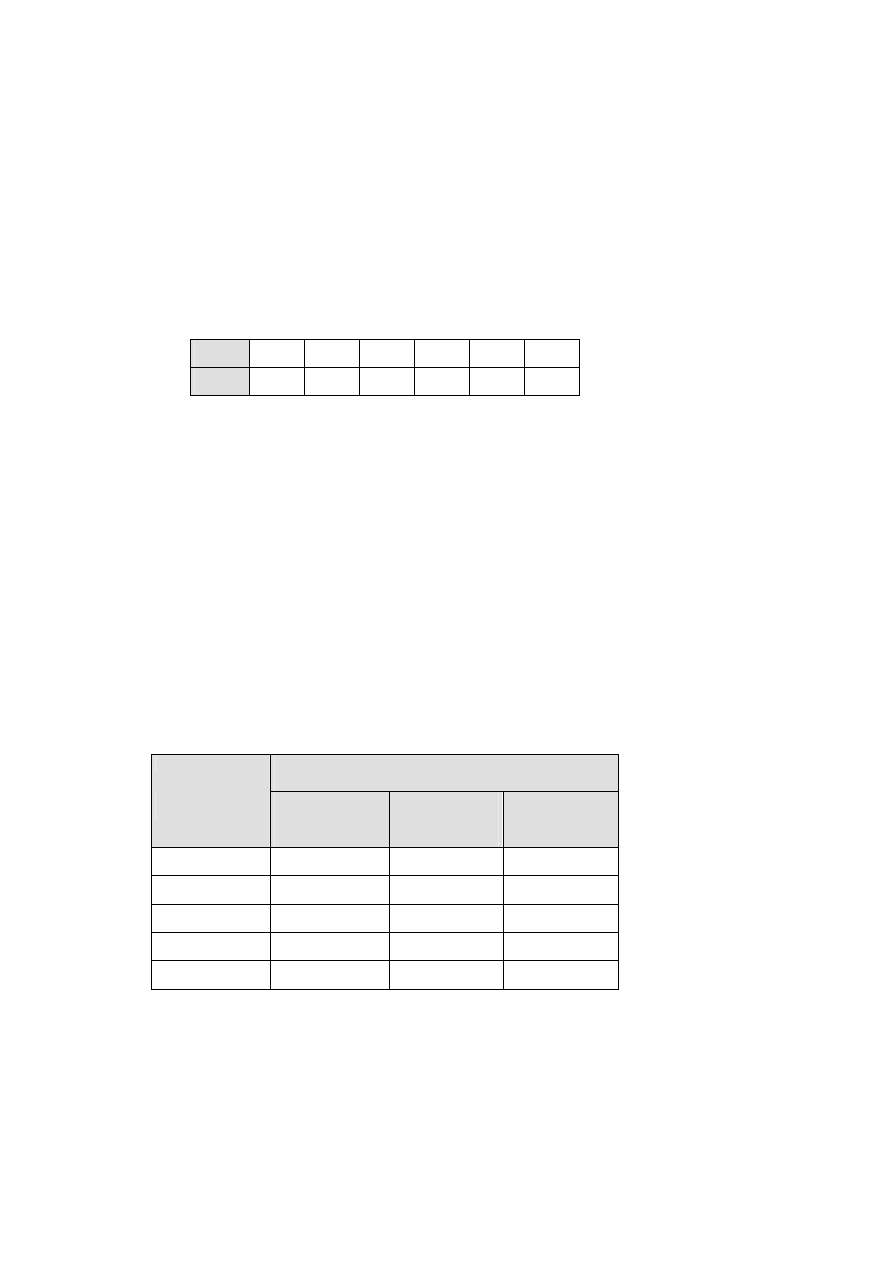
Reasumując, funkcja f(x) kosztów produkcji x jednostek w danym miesiącu przyjmuje

wartości podane w tablicy.

x

0

1

2

3

4

5

f(x)

0

16

18

19

20

24

Zapotrzebowanie w każdym miesiącu może być pokrywane produktem wytworzonym w

danym miesiącu lub w miesiącach poprzednich. W tym drugim przypadku zakład ponosi

dodatkowy koszt magazynowania wynoszący 2 tys. zł. za jednostkę magazynową w ciągu

miesiąca. Pojemność magazynu pozwala na magazynowanie co najwyżej 4 jednostek.

Jakie ilości produktu należy wytwarzać, aby łączne koszty produkcji i magazynowania były

jak najmniejsze, jeśli zapas na początku stycznia i w końcu czerwca ma wynosić 0 jednostek?

Zadanie 32.

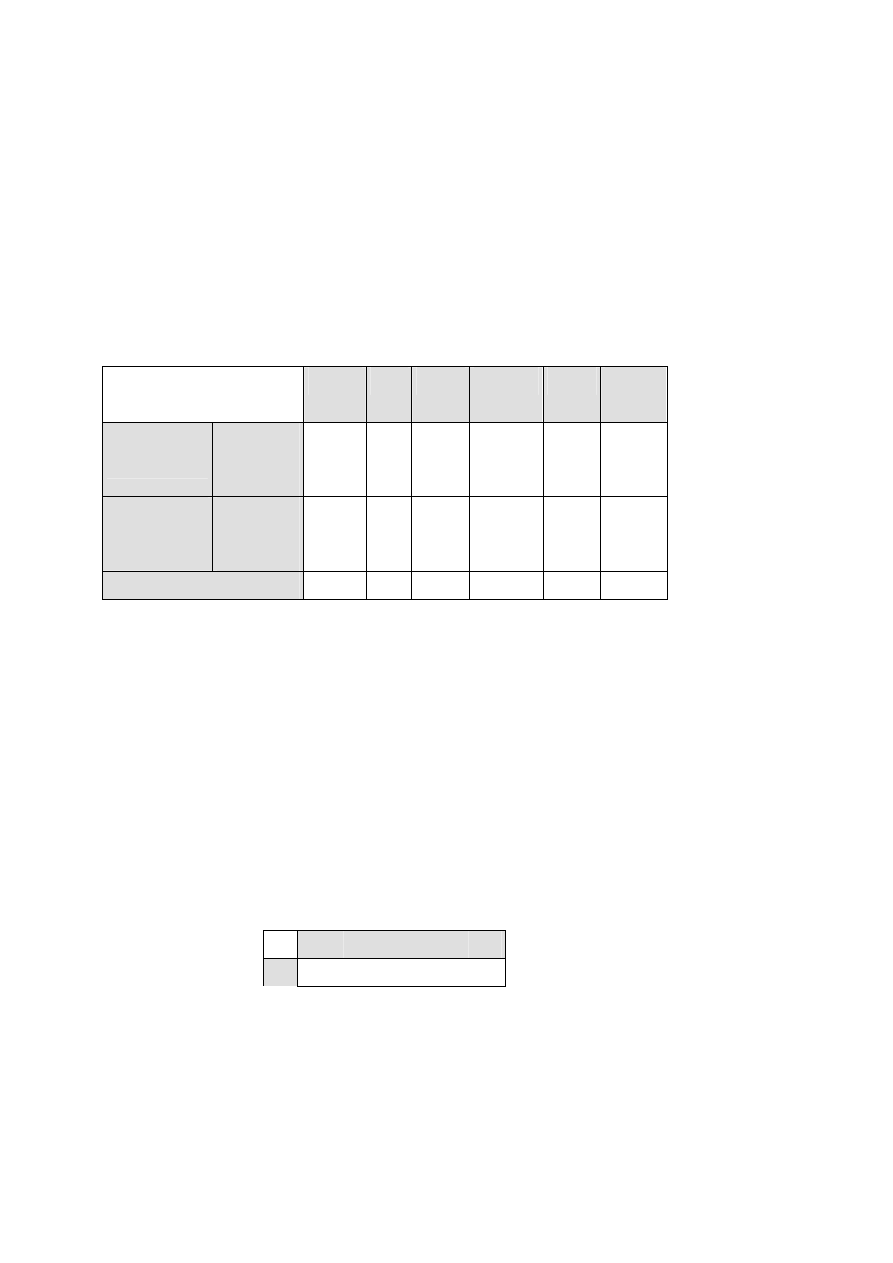
Spółka handlowa może otworzyć pięć sklepów w trzech różnych

miastach {K, L, M.}. Miesięczny dochód przedsiębiorstwa zależy od tego, ile sklepów zostało

otwartych w każdym z miast. Zależność tę przestawia poniższa tabela.

Ilość sklepów

Miesięczny dochód przedsiębiorstwa w

poszczególnych miastach

n

K

v

1

(x

1

)

L

v

2

(x

2

)

M.

v

3

(x

3

)

1

10

8

13

2

18

18

20

3

20

22

22

4

25

26

24

5

30

31

30

Metodą programowania dynamicznego należy wyznaczyć takie rozwiązanie, które maksyma-

lizuje dochód całej firmy w ciągu miesiąca.

Zadanie 33.

Przypuśćmy, że pewna firma może produkować ograniczoną liczbę

jednostek przy normalnym zatrudnieniu i w ustawowym czasie pracy oraz dodatkową liczbę

jednostek przy zatrudnieniu pracowników w godzinach nadliczbowych. Odpowiednie dane

znajdują się w tablicy.

Styczeń Luty Marzec Kwiecień

Maj

Czerwie

c

Czas pracy
Według umowy
o pracę

Koszty
Jednostkowe
Zdolności
Produkcyjne

2

3

4

1

2

4

5

3

2

1

6

3

Godziny
Nadliczbowe

Koszty
Jednostkowe
Zdolności
Produkcyjne

5

6

6

3

6

3

6

2

3

0

7

1

Wielkość popytu D

t

1

2

7

6

0

2

Zmienność kosztów z okresu na okres wynika ze szczególnych warunków na rynku pracy jak

również ze zmiennych cen surowców i materiałów. Załóżmy, że każda jednostka zapasów

pozostałych na koniec danego okresu ma koszt składowania h

t

= 1 dla wszystkich okresów.

Zaplanować taką strategię produkcji i składowanie zapasów w poszczególnych miesiącach,

aby zminimalizować koszty.

Zadanie 34.

Dany jest obiekt, będący zespołem urządzeń U

1

, U

2

, U

3

połączonych

szeregowo (awaria jednego z nich jest awarią całego układu). Poniżej przedstawiono macierz

P. = [p

ij

], gdzie p

ij

jest prawdopodobieństwem tego, że jeśli ne remont i-tego urządzenia

przeznaczono j jednostek pieniężnych, to nie ulegnie ono awarii.

0 jp 1 jp 2 jp 3 jp 4 jp

U

1

0.1

0.2

0.4

0.6

0.7

U

2

0.1

0.3

0.5

0.5

0.8

U

3

0.3

0.3

0.4

0.6

0.6

Przedsiębiorstwo przeznaczyło 4 jp na remont całego obiektu. Określić optymalny przydział

środków, maksymalizujący prawdopodobieństwo braku awarii całego obiektu po dokonaniu

remontu poszczególnych urządzeń.

Uwaga: Urządzenia ulegają awariom niezależnie.

Zadanie 35.

Towarzystwo dobroczynne „Wspólny Fundusz” zamierza wysłać 10

ochotników do ściągania datków z przedsiębiorstw, które mają swoją siedzibę w trzech

wielkich biurowcach w centrum miasta. Prezes towarzystwa szacuje, że jeżeli skieruje y

j

ochotników do budynku j, to datki ogółem z tego wyniosą R

j

(y

j

) setek dolarów, gdzie R

j

(0) =

0 oraz

R

1

(1) = 5,

R

2

(1) = 3,

R

3

(1) = 20,

R

1

(2) = 10,

R

2

(2) = 6,

R

3

(2) = 35,

R

1

(3) = 15,

R

2

(3) = 12,

R

3

(3) = 45,

R

1

(4) = 25,

R

2

(4) = 18,

R

3

(4) = 55,

R

1

(5) = 35,

R

2

(5) = 30,

R

3

(5) = 60,

R

1

(6) = 50,

R

3

(6) = 65,

R

1

(7) = 55.

(Prezes wie, że dodatkowych datków nie osiągnie posyłając do budynku 1 więcej niż 7 ochot-

ników, do budynku 2 więcej niż 5, a do budynku 3 więcej niż 6). Ilu ochotników należy

wysłać do każdego z budynków? Sformułuj odpowiedni model programowania dynamicznego

i wyznacz rozwiązanie optymalne.

Zadanie 36.

Dyrektor przedsiębiorstwa „Polifarb Co.” Musi zaplanować wielkość

produkcji farb, mierzoną liczbą puszek, na każdy z następnych 9 miesięcy (N = 9). Polityka

przedsiębiorstwa polega na podejmowaniu nowej produkcji w momencie, gdy wyczerpują się

zapasy; gdy poziom zapasów spada do zera, dyrektor podejmuje decyzję o wielkości partii

(mierzoną liczbą miesięcy, na które wystarcza podaż), którą należy wyprodukować.

Załóżmy, że miesięczny popyt na wytwarzany produkt jest wystarczająco stabilny i dla

celów planowania produkcji może być traktowany jako stały w przyjętym horyzoncie planu.

Do dalszych rozważań przyjmijmy, że miesięczny popyt jest równy 1000 puszek.

Przypuśćmy, że produkcja zakładu i posiadane magazyny ograniczają dopuszczalne wielkości

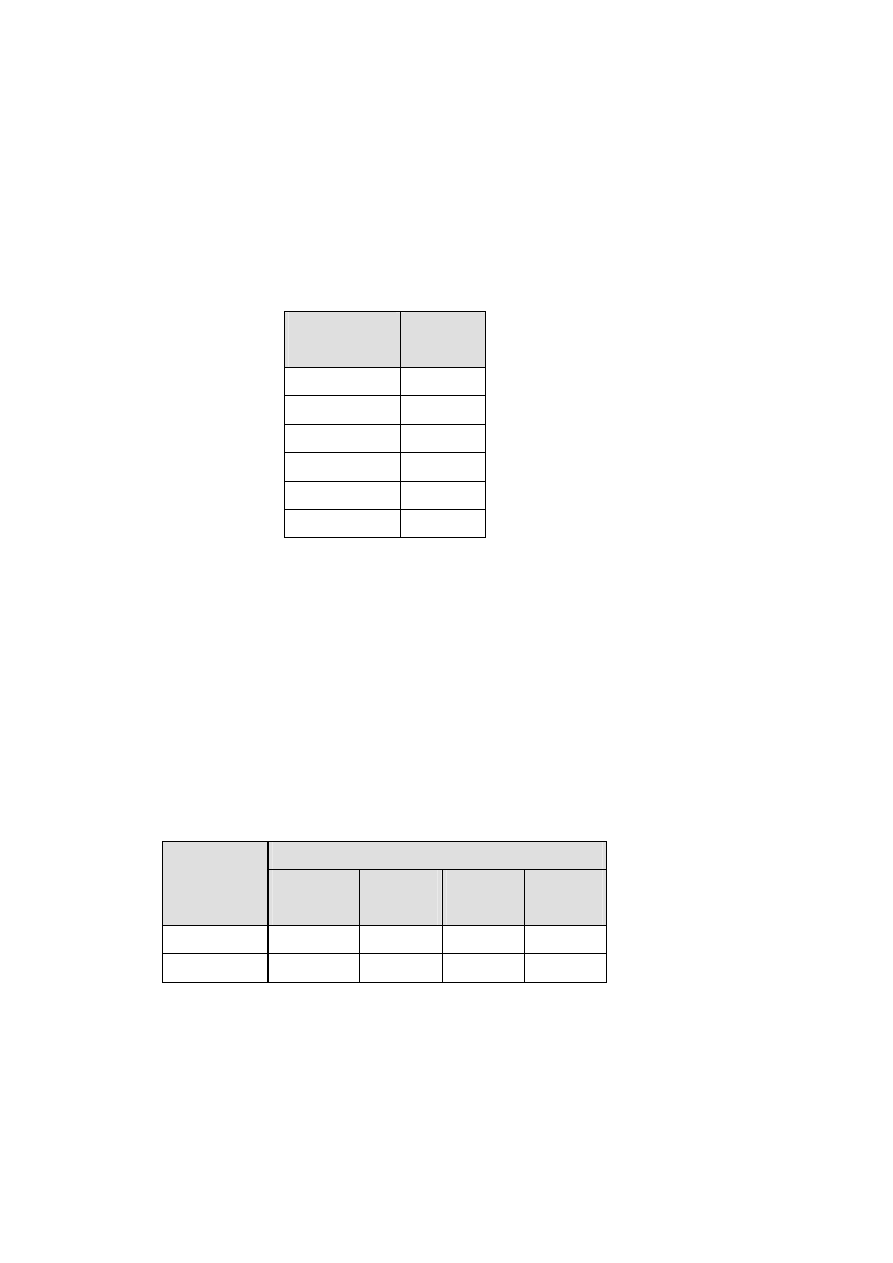
partii do wielkości wystarczającej na pokrycie popytu w skali od 1 do 6 miesięcy. Zyski R

j

,

odpowiadające decyzji o produkcji partii, której wielkość pokryje popyt w ciągu j miesięcy,

zawiera tablica. Produkcja partii odpowiadającej trzymiesięcznemu popytowi, tzn. liczącej

3000 puszek, przynosi zysk równy 17 tys. dolarów.

Wielkość partii

j

Zysk

R

j

1

4

2

11

3

17

4

24

5

28

6

36

Problem firmy „Polifarb Co.” (Wielkość partii jest wyrażona w jednostkach odpowiadających

popytowi jednomiesięcznemu i równemu 1000 jednostek towaru; zysk wyrażony jest w 1000

dolarów).

Jak powinien wyglądać plan produkcji farb w ciągu kolejnych miesięcy, przynoszący

maksymalny zysk.

Zadanie 37.

Właściciel firmy handlowej „Nabiał, Sery Co.”, Mr Little, powinien

podzielić tygodniowy zapas jajek równy N między s sklepów. Z doświadczenia wie, że jeżeli

przeznaczy y

j

jajek do sklepu j, to otrzyma zysk równy R

j

(y

j

). Właściciel firmy przypuszcza,

że w celu maksymalizacji zysku nie powinien przeznaczać wszystkich jajek do sprzedaży w

jednym sklepie i stawia sobie za zadanie wyznaczenie optymalnego rozdziału posiadanych w

magazynie jajek między wszystkie sklepy.

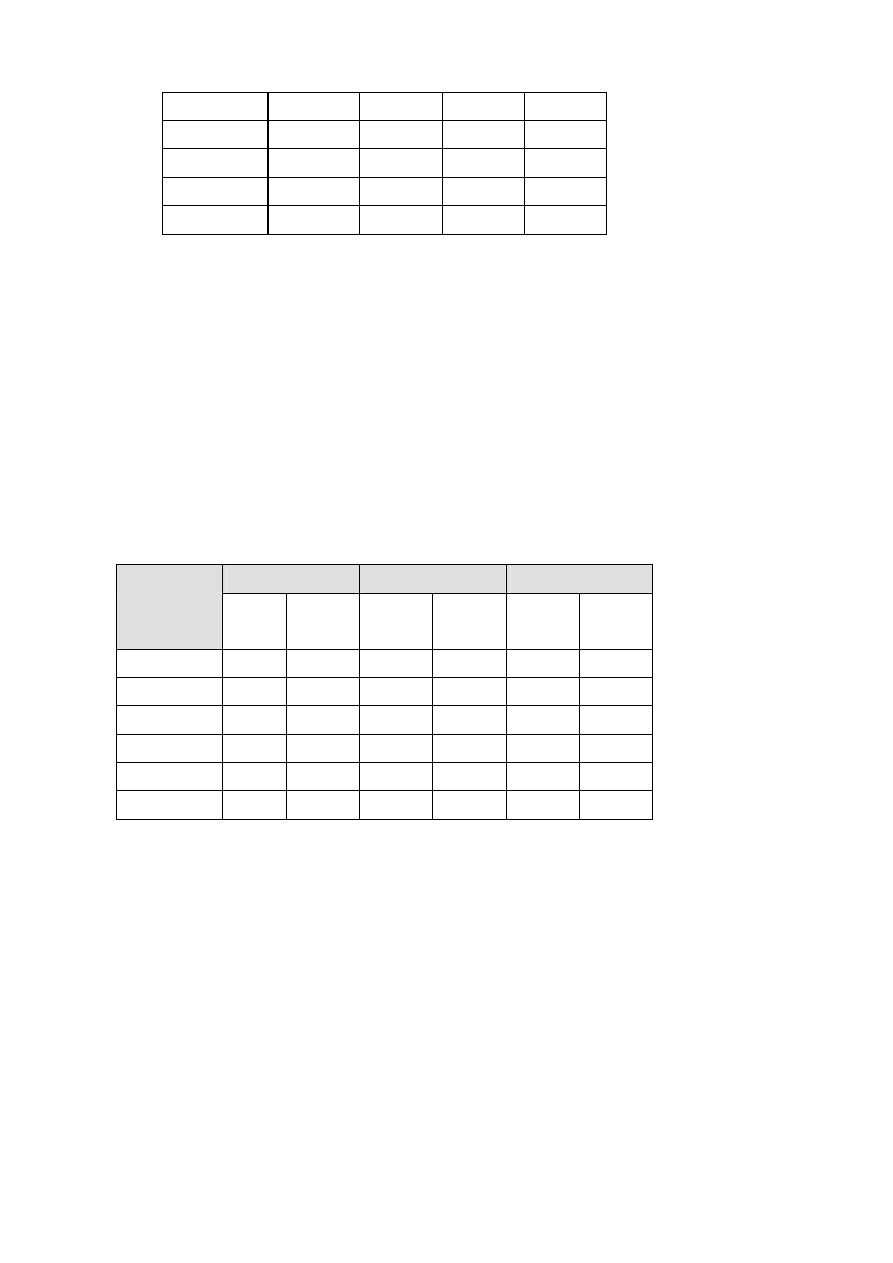
Liczba skrzyń

Zysk netto

z jajkami

y

sklep 1

R

1

(y)

sklep 2

R

2

(y)

sklep 3

R

3

(y)

sklep 4

R

4

(y)

0

0

0

0

0

1

6

3

2

5

2

10

10

6

9

3

14

15

14

13

4

16

19

20

17

5

18

21

22

21

6

20

22

24

25

Załóżmy, że właściciel firmy dysponuje N = 6 skrzyniami z jajkami, które chce podzielić mię-

dzy s = 4 sklepy (będziemy zakładać, że nie może dzielić zawartości skrzyni na różne sklepy).

Zyski netto, jakie może otrzymać kierując odpowiednią liczbą skrzyń do każdego ze sklepów

zawiera tablica. Zyski te są różne w różnych sklepach i zależą od wielkości popytu w każdym

ze sklepów oraz od kosztów transportu i magazynowania.

Określić optymalny rozdział skrzyń z jajkami do sklepów.

Zadanie 38.

Firma budowlana „Domek” inwestuje rocznie kilkanaście milionów

dolarów w nieruchomości oraz w budowę centrów handlowych i dzielnic mieszkaniowych.

Firma ma podjąć decyzję o zainwestowaniu nie więcej niż 10 mln dolarów w jedno lub więcej

z trzech przedsięwzięć. Dane charakteryzujące te przedsięwzięcia zawiera tablica.

Poziom

Przedsięwzięcie 2

Przedsięwzięcie 3

Przedsięwzięcie 4

Inwestowania

Y

koszty

I

2

(y)

wartość

R

2

(y)

koszty

I

3

(y)

wartość

R

3

(y)

Koszty

I

4

(y)

wartość

R

4

(y)

0

0

0

0

0

0

0

1

3

8

4

9

6

17

2

5

13

5

13

7

18

3

7

18

8

18

8

21

4

8

19

9

19

9

22

5

9

21

10

23

10

24

Zauważmy, że każde z trzech przedsięwzięć może być realizowane na jednym z pięciu

różnych poziomów inwestowania. Na przykład firma może zdecydować się na

zainwestowanie 3, 5, 7, 8 lub 9 mln dolarów w przedsięwzięcie 2. Jeżeli wybór padnie na

poziom 1, co oznacza zainwestowanie 3 mln dolarów w przedsięwzięcie 2, to obecną wartość

przyszłych dochodów szacuje się na R

2

(1) = 0,8 mln dol. Natomiast, jeżeli wybrany zostanie

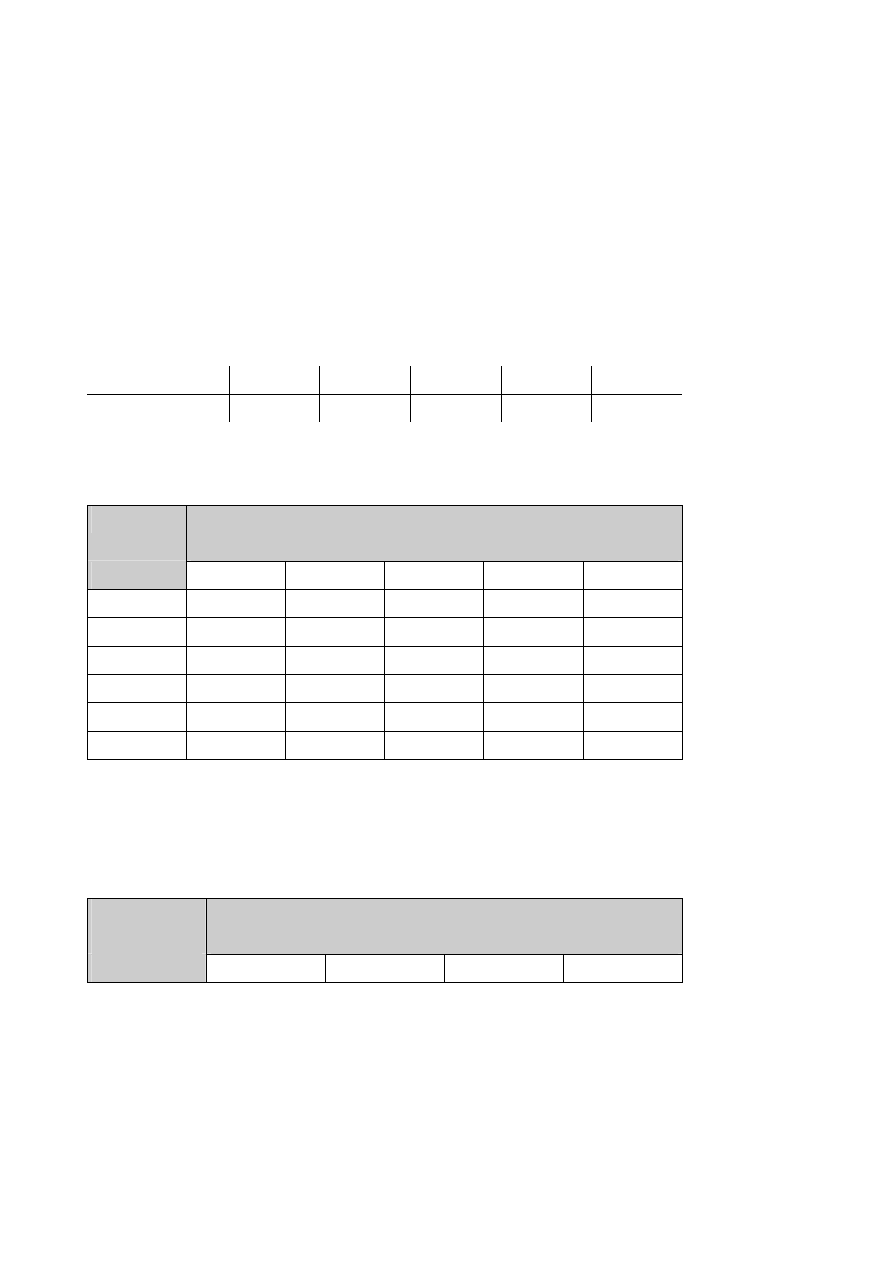
poziom inwestowania 5, co oznacza zainwestowanie 9 mln dol., to wartość przyszłych

dochodów wzrośnie do

R

2

(5) = 2,1 mln dol. Podobną interpretację można odnieść do dwu pozostałych przedsięwzięć.

Określić optymalny plan inwestycji dla firmy „Domek”.

Zadanie 39.

W budynku zainstalowany jest hydrofor o pojemności zbiornika 10 m

3

.

Dobę podzielono na 5 okresów, w których następuje rozliczenie zużycia wody.

Zapotrzebowanie na wodę w poszczególnych okresach jest następujące:

T

1

2

3

4

5

Zużycie wody w m

3

2

3

8

4

6

W każdym z wyróżnionych okresów można uzupełnić zbiornik co najwyżej o 5 m

3

. Koszty

uzupełniania zależą od ilości uzupełnionej wody i od okresu. Są one przedstawione w tablicy.

Ilość wody

Koszt w okresie

1

2

3

4

5

0

0

0

0

0

0

1

3

1

2

2

1

2

4

2

4

3

3

3

6

5

7

6

6

4

7

7

9

9

8

5

10

10

12

11

12

Zakłada się, że na początku pierwszego i końcu piątego okresu zbiornik musi zawierać 2 m

3

wody. Jak należy uzupełniać wodę w zbiorniku, aby koszt uzupełnienia był minimalny przy

pełnym zaspokojeniu potrzeb?

Zadanie 40

. Działka ogrodnicza została podzielona na 4 części. Plony są uzależnione

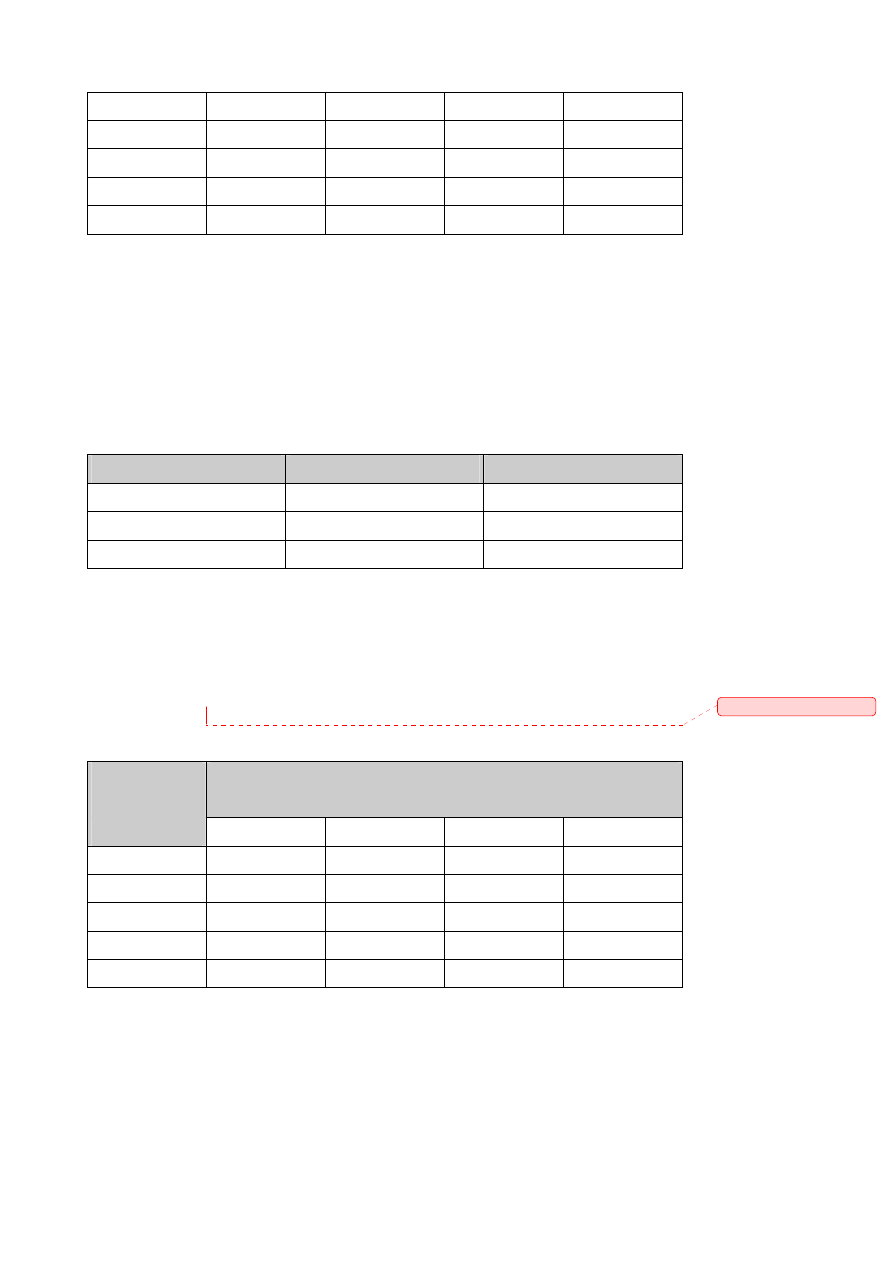
od dawki nawozu, jaki wysiejemy na każdej z części. W tablicy podano te zależności.

Dawka nawozu

w kg/część

Wartość plonów w zł

1

2

3

4

30

200

300

280

220

40

250

320

340

250

50

350

340

380

320

60

400

400

420

400

70

410

450

450

430

Na każdą część należy przeznaczyć co najmniej 30 kg nawozu. Jak zużytkować 200 kg

nawozu, aby wartość plonów była największa?

Zadanie 41.

Na wyprawę wysokogórską żywność pakowana jest w znormalizowane

pojemniki. Istnieją 3 typy zestawów żywnościowych. Wagę i kaloryczność kazdego zestawu

podaje tabela:

Typ zestawu

Waga w kg

Kaloryczność w kcal

A

1,5

8

B

2

11

C

2,5

15

Na wyprawę należy zabrać przynajmniej po 2 pojemniki z zestawem A i C. Ile każdego z

zestawów powinien zabrać każdy z uczestników wyprawy, jeżeli waga żywności nie może

przekroczyć 15 kg, a wartość kaloryczna ma być maksymalna?

Zadanie 41

. W przedsiębiorstwach P

1

, P

2

, P

3

, P

4

opracowano perspektywiczne plany

rozwoju, rozpatrując między innymi przyrost wartości produkcji w zależności od nakładów

inwestycyjnych. Przewidywane zależności przedstawia tabela:

Nakłady w mln

zł

Roczny przyrost wartości produkcji w mln zł

P

1

P

2

P

3

P

4

0

0

0

0

0

10

15

20

18

12

20

25

30

28

30

30

40

40

45

50

40

60

70

65

60

Komentarz [MJB1]:

50

70

80

75

70

Opracować wariant przydziału funduszów, gdy do podziału jest 100 mln zł. łącznie

maksymalizując łączny przyrost wartości produkcji zakładów.

Zadanie 42.

Dana jest liczba R>0. Znaleźć takie liczby x, y, z ≥ 0 , że

x + y + z =R

a ich iloczyn był maksymalny.

Zadanie 43.

Utworzyć czteroletni plan zatrudnienia pracowników w Zakładzie

PONAMONA jeśli jedynym kryterium jest minimalizacja kosztów. Wiadomo, że minimalne

zapotrzebowania b

i

na pracowników w kolejnych latach i = 1, 2, 3, 4 wynosi 6, 4, 8, 6 osób.

Jeśli oznaczymy przez y

i

zatrudnienie w i-tym roku to koszty związane z zatrudnieniem y

i

– b

i

pracowników ponad minimalne zakładane zapotrzebowanie wynoszą 3(y

i

– b

i

) (i = 1, 2, 3, 4).

Koszty związane z zatrudnianiem i zwalnianiem pracowników można określić za pomocą

funkcji

4+ 2(y

i

–y

i-1

) dla y

i

> y

i-1

K(y

i

– y

i-1

)=

3 dla y

i

< y

i-1.