DOPASOWANIE PUNKTÓW POMIAROWYCH FUNKCJĄ

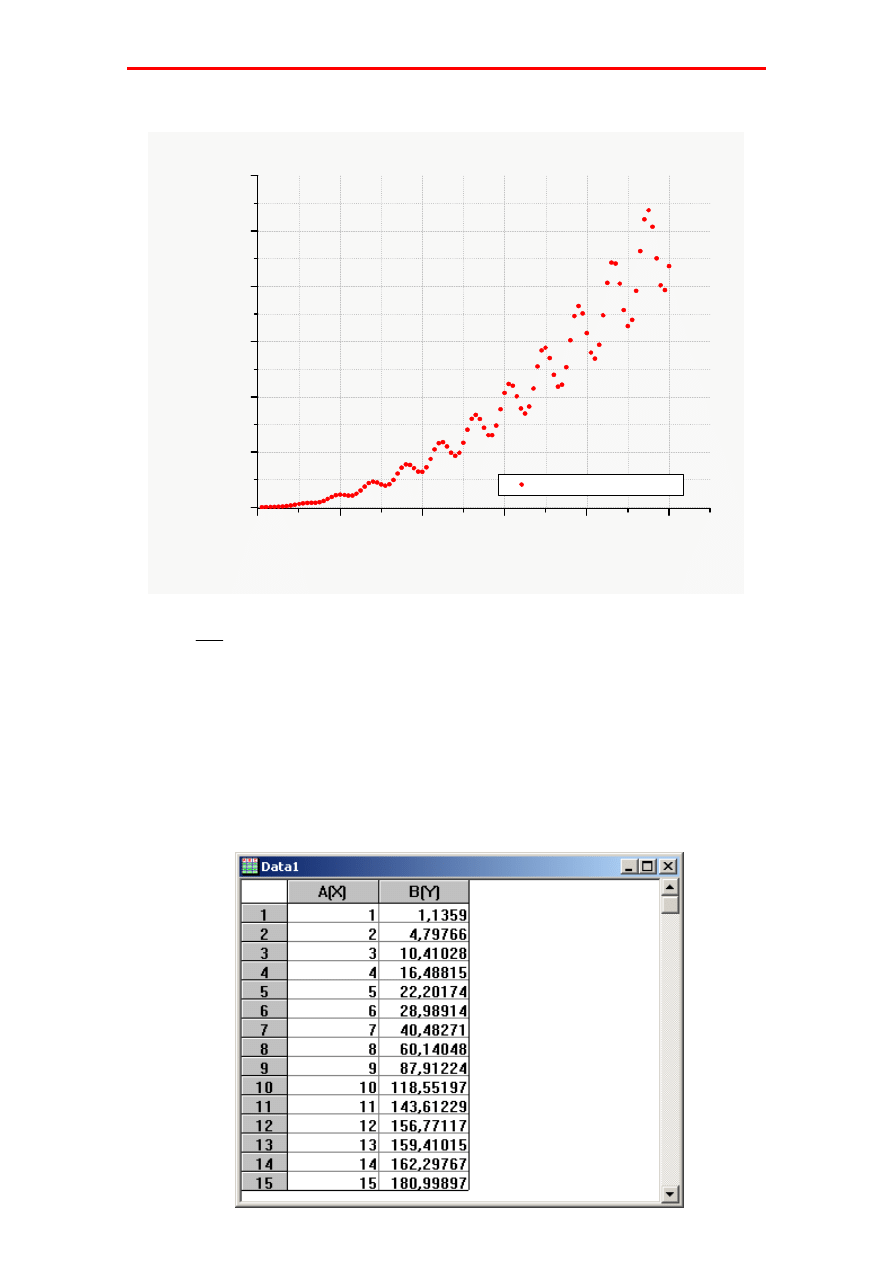
Wynik pomiarów pewnego zjawiska fizycznego przedstawia wykres:

0

20

40

60

80

100

0

2000

4000

6000

8000

10000

12000

Punkty pomiarowe

y

x

Z rozważań teoretycznych wiadomo, że punkty pomiarowe powinny układać się według wzoru:

2

2

180

sin

x

x

B

x

A

y

⋅













⋅

+

⋅

=

π

gdzie A i B są pewnymi współczynnikami. Znajomość wartości współczynników

jest niezbędna do analizy badanego zjawiska fizycznego.


Jak znaleźć wartości A i B korzystając z programu Origin Pro 7.5?

1.

Tabela z wynikami pomiarów zamieszczona jest na ostatniej stronie. Uruchom program Origin 7.5 Pro.
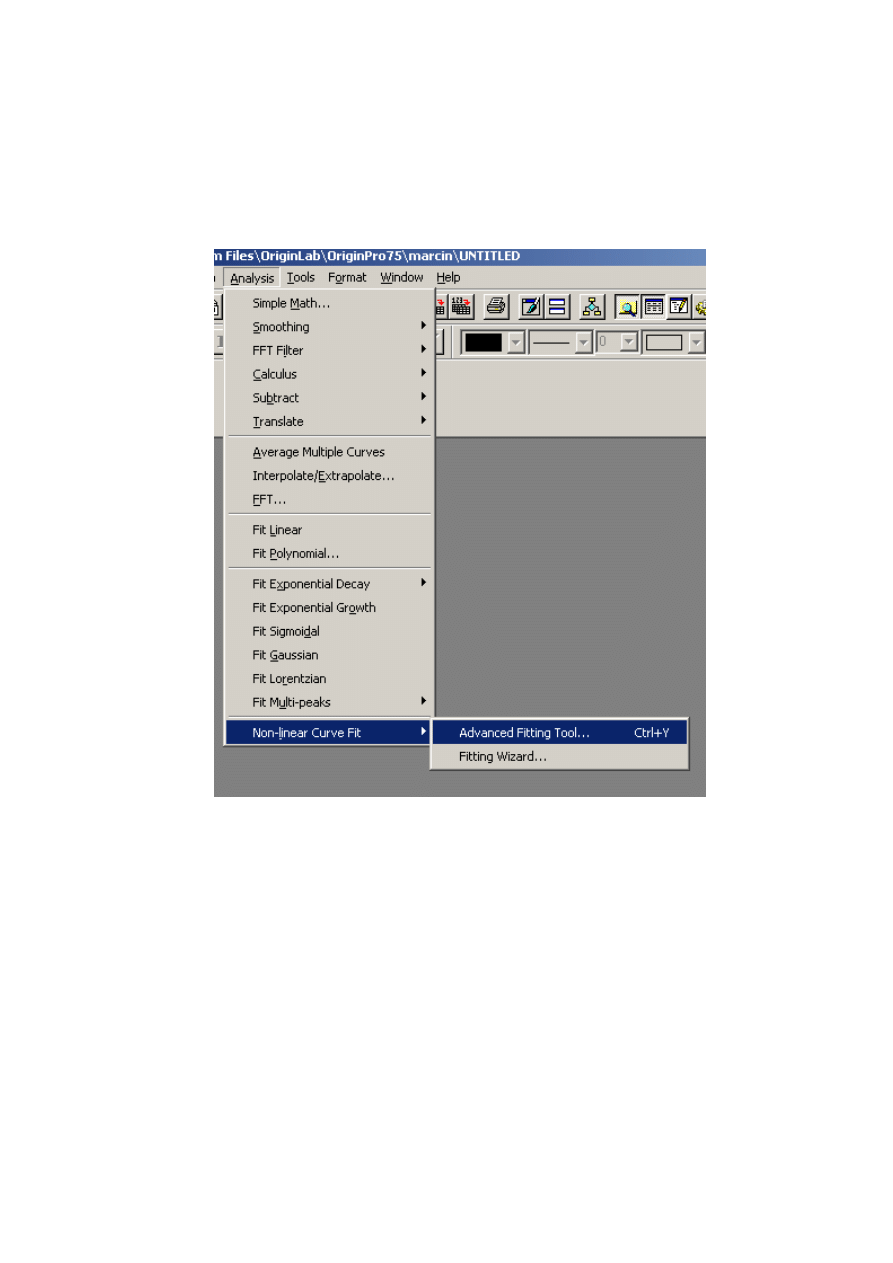
Zaznacz i skopiuj kolumny x i y z tabeli z wynikami pomiarów do arkusza danych (DATA1). Po
skopiowaniu arkusz DATA1 powinien wyglądać tak :

2.

Klikając na jeden z nagłówków kolumn A(X) i B(X) zaznacz obie kolumny i naciśnij prawy przycisk
myszy co rozwinie menu podręczne. Aby utworzyć wykres punktowy wybierz z menu PLOT i
SCATTER.

3.

Sformatuj wykres tak aby wyglądał podobnie do wykresu na pierwszym rysunku.

4.

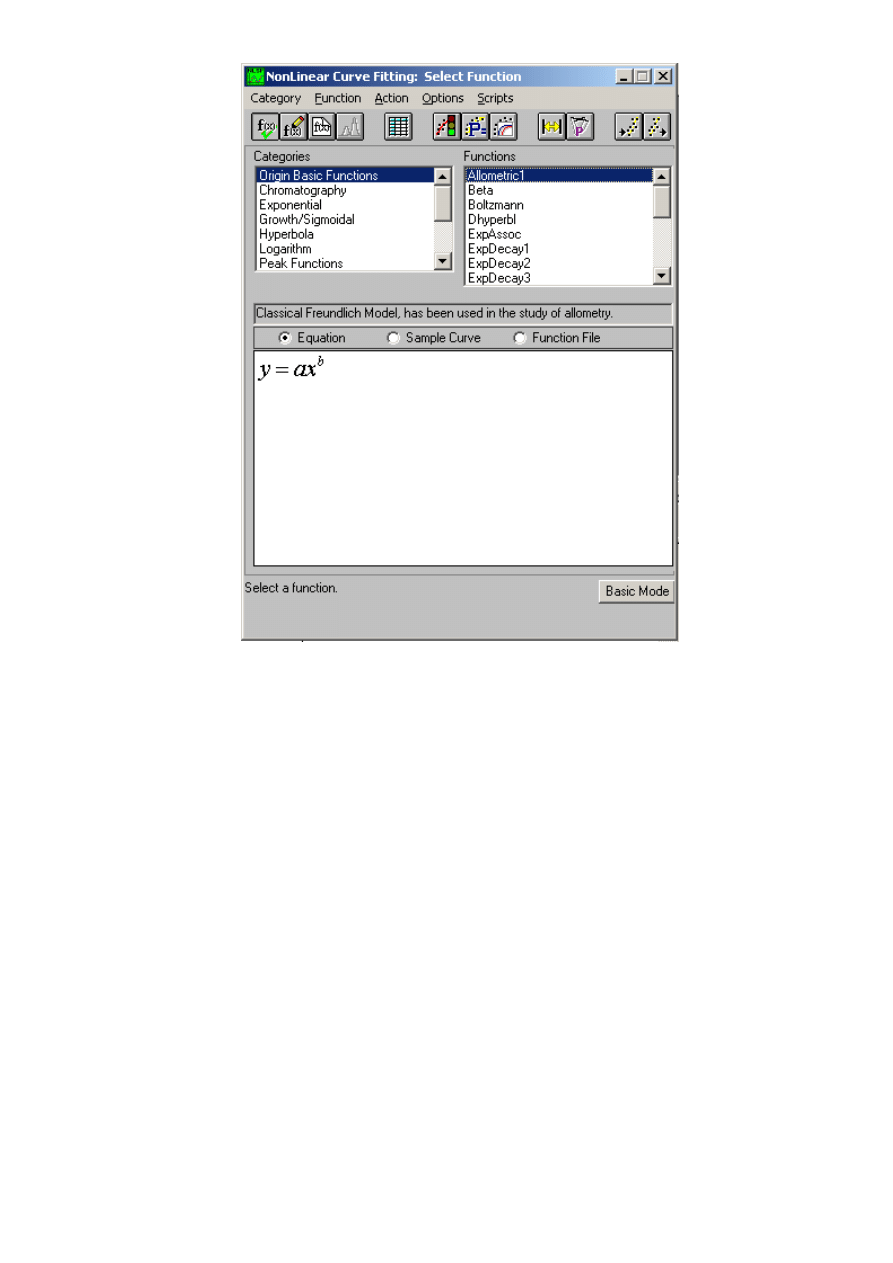
Z głównego menu programu wybierz ANALYSIS | Non-linear Curve Fit | Advanced Fitting Tool

5.

Otworzy się okno w którym będziemy mogli wybrać wzór (funkcję) jaką będziemy dopasowywali
(fittowali) dane doświadczalne. Gdyby w programie nie było funkcji, która jest potrzebna do fitowania,
można ją stworzyć klikając na Function | New. Zauważ, że dostępne funkcje podzielone są na kilka
kategorii (pole o nazwie Categories). Lista funkcji w danej kategorii jest wyświetlona w polu o nazwie
Functions. Po wybraniu funkcji jej wzór zostanie pokazany w dolnej części okienka.

6.

Dodajmy nową własną kategorię funkcji. W tym celu kliknij na Category | New i jako nazwe wpisz
„Moje funkcje”.

7.

Upewnij się, że w polu Categories wybrana jest kategoria „Moje funkcje” i dodaj nową funkcję
klikając na Function | New.

8.

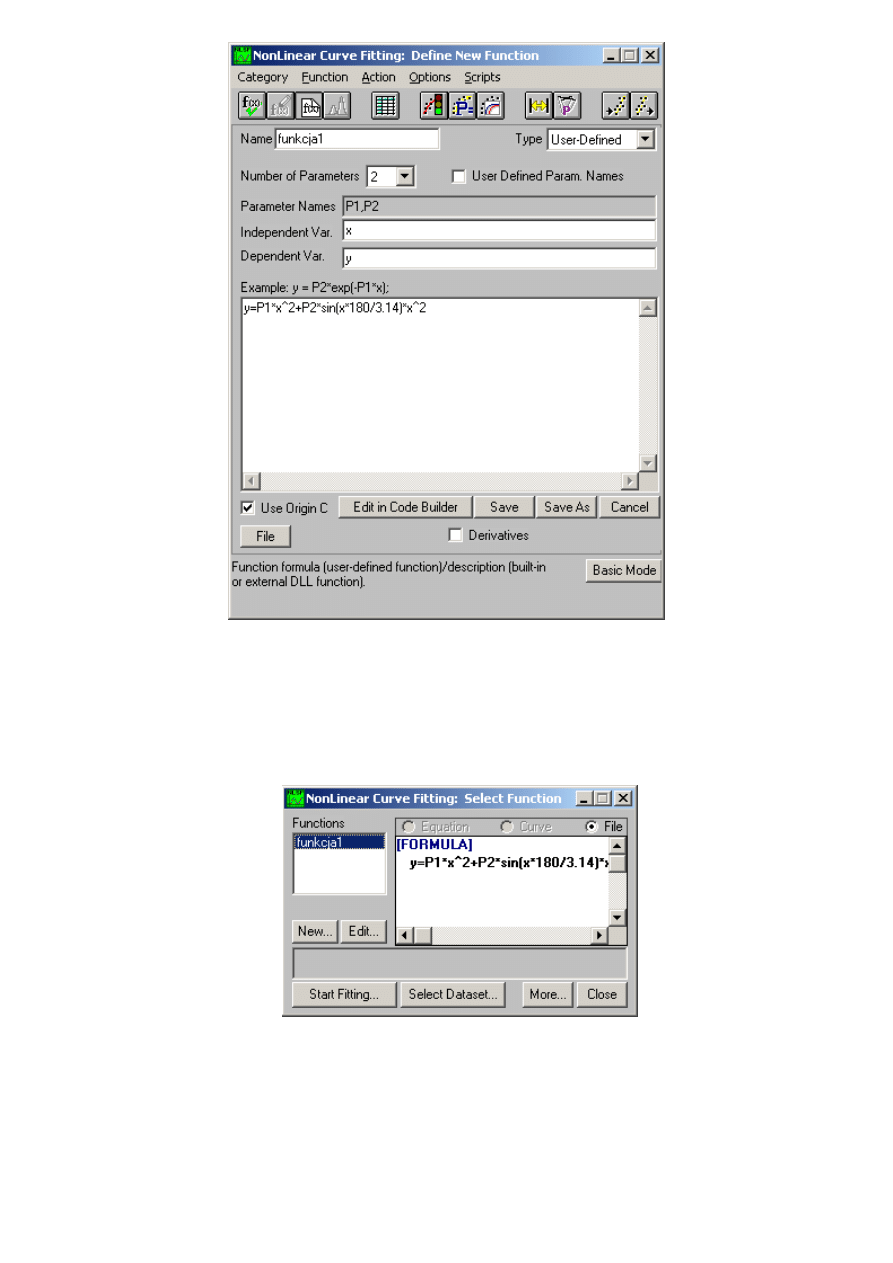
Otworzy się okienko do edycji wzoru funkcji. Pole Number of Parameters określa liczbę szukanych
parametrów. W naszym przypadku są to dwa. W polu Parameters Names wyświetlone są literki
(nazwy) pod jakimi te parametry są widziane przez program Origin. Domyślnie są to: P1 i P2. Pole
Independent Var. określa pod jaką literką widziany jest argument funkcji – najczęściej jest to „x”, pole
Dependent Var. wartość funkcji – najczęściej jest to „y”. Wzór funkcji wpisujemy w duże białe pole
poniżej. Przykład poprawnego wzoru funkcji jest pokazany nad nim.

UWAGA : Program Origin żadnym komunikatem nie informuje, że wzór funkcji jest błędnie wpisany.
W takim przypadku dopasowanie wykresu do wzoru nie będzie możliwe, dlatego jeśli Origin nie rysuje
krzywej dopasowania na wykresie to w pierwszej kolejności należy sprawdzić, czy wzór funkcji jest
poprawnie zapisany.

9.

Uzupełnij okno do edycji wzoru funkcji zgodnie z tym co jest pokazane na rysunku.

10.

Aby zapisać funkcję kliknij SAVE

11.

Aby przejść do „fittowania” wykresu kliknij BASIC MODE i ACCEPT. Otworzy się nowe okienko w
którym wybieramy Start Fitting.

12.

Przed rozpoczęciem fittowania należy podać wartości szukanych parametrów. Najlepiej podać wartości,
które spodziewamy się uzyskać, albo wartości rozsądne dla danego parametru (np. parametr określający
pole powierzchni nie może być ujemny). Gdy nie wiemy jakie wartości podać należy wpisać losową
liczbę. Następnie klikamy w przycisk 100 Iter. i obserwujemy co dzieje się z wykresem. Gdy
kilkukrotne kliknięcie w przycisk 100 Iter. nie zmienia wyglądu wykresu zamykamy okienko klikając
na DONE. O jakości dopasowania świadczy pokrywanie się krzywej dopasowania z punktami
pomiarowymi.

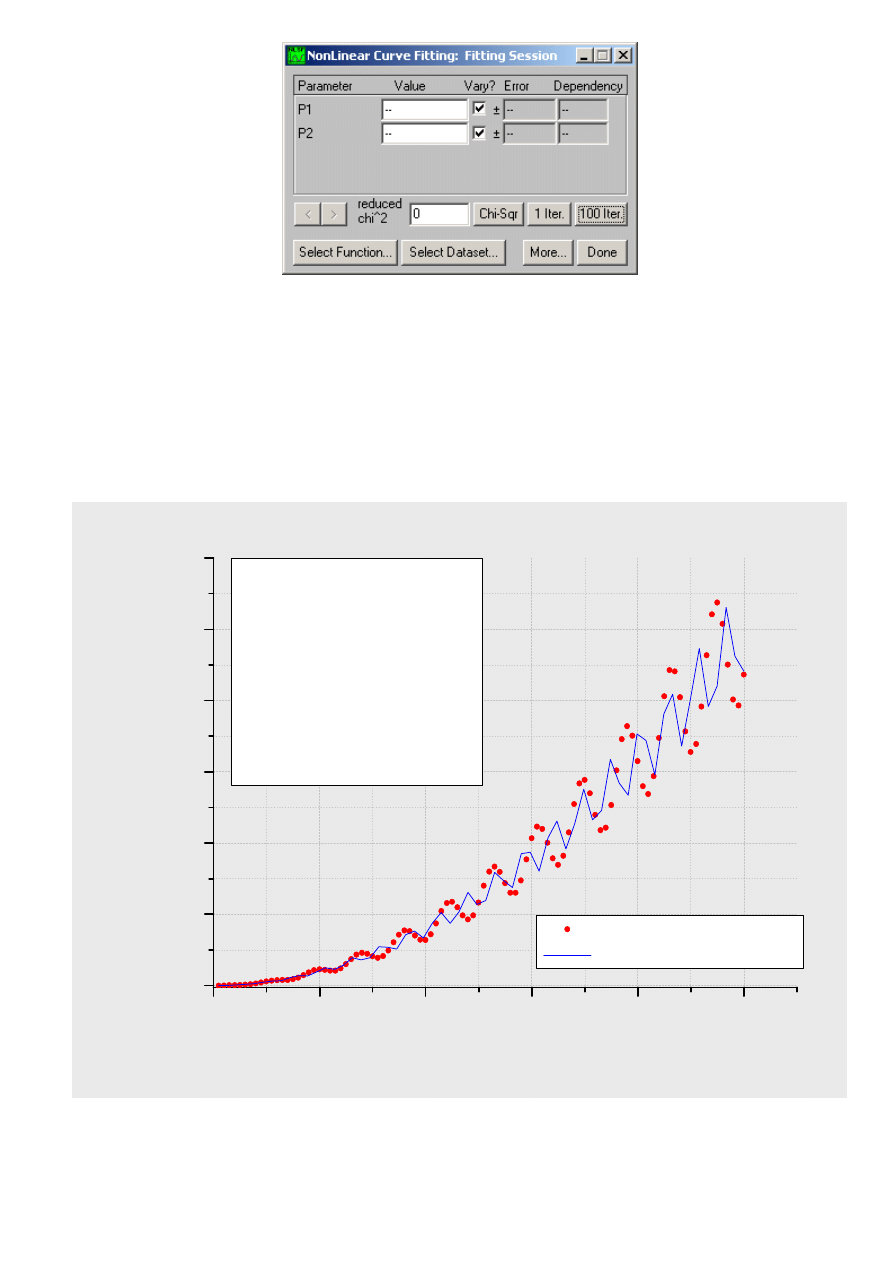
Jako wartości początkowe P1 i P2 podaj 1.

Uwaga!

Jakość dopasowania może zależeć od wartości początkowych parametrów P1 i P2, oraz od

kolejności ich „fitowania” – jest możliwość „fitowania” najpierw jednego parametru, a dopiero potem
drugiego. Jeśli wartości początkowe zostaną źle dobrane dopasowanie będzie niemożliwe o czym
poinformuje stosowny komunikat.

Aby zablokować „fitowanie” danego parametru należy „odfajkować” kwadracik w kolumnie VARY.

13.

Dopasowany wykres powinien wyglądać mniej więcej tak jak na rysunku poniżej:

0

20

40

60

80

100

0

2000

4000

6000

8000

10000

12000

Data: Data11_D
Model: funkcja1
Weighting:
y

No weighting

Chi^2/DoF

= 208005.40673

R^2

= 0.97763

P1

0.99508

±0.01011

P2

-0.14184

±0.01408

Punkty pomiarowe
Krzywa dopasowania

y

x

Tabela z wynikami pomiarów:

x

y

1

1,1359045

2

4,7976558

3

10,410276

4

16,488153

5

22,201739

6

28,98914

7

40,482708

8

60,140485

9

87,912242

10

118,55197

11

143,61229

12

156,77117

13

159,41015

14

162,29767

15

180,99897

16

226,5609

17

296,75235

18

374,01156

19

433,07878

20

455,44498

21

442,64188

22

419,55564

23

423,67897

24

484,42534

25

603,63514

26

749,56612

27

870,32729

28

921,6968

29

894,69305

30

826,24108

31

784,0831

32

831,31149

33

988,80072

34

1217,4584

35

1433,2738

36

1550,413

37

1530,573

38

1410,5994

39

1289,8651

40

1280,2476

41

1443,5212

42

1750,8672

43

2090,0141

44

2320,6952

45

2351,4606

46

2196,0825

47

1975,5461

48

1859,5218

49

1975,1006

50

2331,5962

51

2805,2929

52

3197,7771

53

3341,0277

54

3193,8952

55

2875,0617

56

2609,0601

57

2608,9971

58

2956,9293

59

3548,6307

60

4138,2561

61

4465,0402

62

4397,0872

63

4013,3104

64

3573,7518

65

3387,398

66

3644,2708

67

4302,727

68

5097,9781

69

5674,6376

70

5777,4588

71

5398,1822

72

4794,6484

73

4364,1326

74

4432,4704

75

5070,6177

76

6041,4121

77

6913,101

78

7286,165

79

7014,58

80

6299,3942

81

5596,4222

82

5379,203

83

5880,1453

84

6951,0104

85

8125,318

86

8858,3597

87

8821,7403

88

8093,4892

89

7134,5301

90

6554,3718

91

6784,6216

92

7834,9152

93

9268,6385

94

10421,593

95

10754,743

96

10153,999

97

9010,817

98

8030,144

99

7859,0694

100

8731,4833