Politechnika Świętokrzyska

Wydział Elektrotechniki, Automatyki i Informatyki

Katedra Zastosowań Informatyki

Metody obliczeniowe – laboratorium

Instrukcja laboratoryjna nr 5: Różniczkowanie numeryczne

Opracował: dr inż. Andrzej Kułakowski
Data: 6.11.2012 r.

1.

Wzór Taylora

Wzór na pochodną (dowolną) f(x) wyrażona za pomocą różnic wstecznych:

k=1

(1)

k=2

(2)

k=3

(3)

Tablica różnic wstecznych

x

f(x)

f(x)

f(x)

x

0

-4h

f(x

0

-4h)

f(x

0

-3h)

f(x

0

-2h)

f(x

0

- h)

f(x

0

)

f(x

0

-2h)

f(x

0

- h)

f(x

0

)

f(x

0

- h)

f(x

0

)

f(x

0

)

x

0

-3h

f(x

0

-3h)

x

0

-2h

f(x

0

-2h)

x

0

- h

f(x

0

- h)

x

0

f(x

0

)

Przykład

Dla funkcji f(x) = ln(x) oblicz wartość dokładną i w przybliżeniu dla 1-nej pochodnej w punkcie

x

0

=1;

x zmienia się od x = 0,6 do x = 1 z krokiem h=0,1

Tablica różnic wstecznych

X

f(x)

f(x)

f(x)

0,6

-0,51083

0,15415
0,13353
0,11778
0,10536

-0,02062

-0,01575

-0,01242

0,00487

0,00333

-0,00154

0,7

-0,35667

0,8

-0,22314

0,9

-0,10536

1

0

Wg (1)

Wartość dokładna:

ln(x)

(1)

|

x= x0

= 1

Błąd bezwzględny: r = |1 - 0,9988| = 0,0012

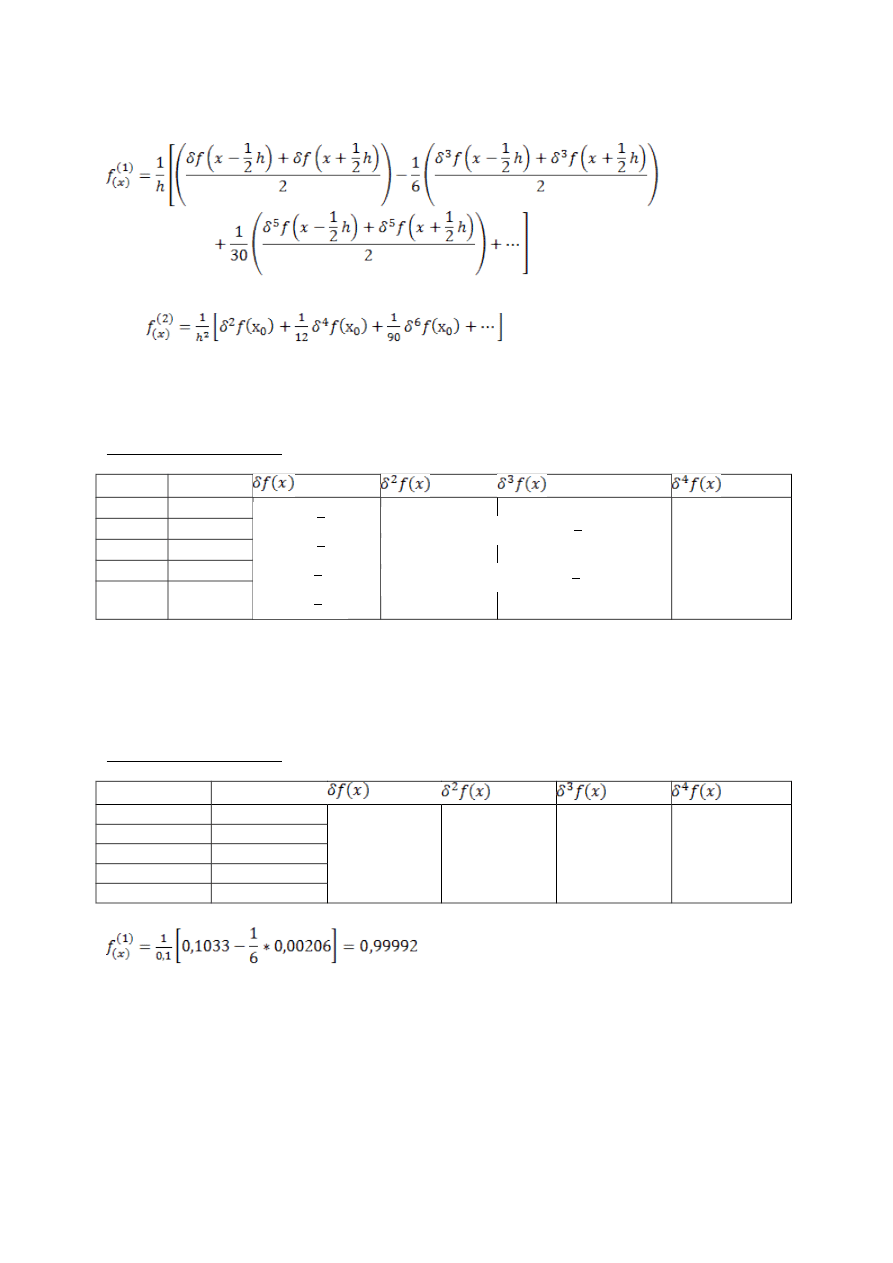
2.

Wzór Stirlinga

oraz

Tablica różnic centralnych

x

f(x)

x

0

-2h

f(x

0

-2h)

δf ( x

0

−

3
2

h)

δf ( x

0

−

1
2

h)

δf ( x

0

+

1
2

h )

δf ( x

0

+

3
2

h )

δ

2

f ( x

0

−

h )

δ

2

f ( x

0

)

δ

2

f ( x

0

+

h)

δ

3

f ( x

0

−

1
2

h )

δ

3

f ( x

0

+

1
2

h)

δ

4

f ( x

0

)

x

0

- h

f(x

0

- h)

x

0

f(x

0

)

x

0

+ h

f(x

0

+ h)

x

0

+2h

f(x

0

+ 2h)

Przykład:

Dla funkcji f(x) = ln(x) oblicz wartość dokładną i w przybliżeniu dla 1-nej pochodnej w punkcie

x

0

=1;

x zmienia się od x = 0,8 do x = 1,2 z krokiem h = 0,1

Tablica różnic centralnych

X

f(x)

0,8

-0,22314

0,11778
0,10536
0,095310
0,08701

-0,01242

-0,01005

-0,00830

0,00237

0,00175

0,00062

0,9

-0,10536

1

0

1,1

0,09531

1,2

0,18232

Wartość dokładna:

ln(x)

(1)

|

x= x0

= 1

r= |1-0,99992|=0,00008 tzn. ta metoda jest dokładniejsza

Zadania do wykonania w sprawozdaniu:

- wprowadzenie o różniczkowaniu

- listing programu do wybranej metody

- screeny z działanie programu dla wylosowanych punktów

- obliczenie i analiza błędów

Literatura:

instrukcja powstała na podstawie:

- slajdów dostępnych na serwerze

Katedry Wytrzymałości Materiałów i Metod Komputerowych Mechaniki

Wydziału Mechanicznego Technologicznego

Politechniki Śląskiej

- książek Wydawnictwa Politechniki Śląskiej