Zadanie 1.

Znale minimaln warto wyra enia f(x,y,z)=2x-3y-5z+2 przy zadanych ograniczeniach:

x+y-z-2>=0, -x>=3+z+y, 2x+y=4+z, x>=0.

Podstawi po zmienna "x_opt" punkt w którym znajduje si warto najmniejsza, pod zmienn

"w_opt" warto funkcji f(x,y,z) w tym punkcie

Do rozwi zania zadania wykorzystujemy funkcj SciLaba linpro(), funkcja f(x,y,z) jest bowiem

wyra eniem liniowym. linpro() znajdzie warto najmniejsz wyra enia f

1

(x,y,z)=2x-3y-5z.

Funkcj celu zapisujemy w postaci macierzowej jako:

−

−

=

=

5

3

2

,

*

)

,

,

(

p

z

y

x

p

z

y

x

f

T

Ograniczenia zapisujemy jako:

3

2

4

2

−

≤

+

+

−

≤

+

−

−

=

−

+

z

y

x

z

y

x

z

y

x

Polecenia zapisujemy jako:

// parametr m okre la liczb ogranicze równo ciowych

p=[2;-3;-5], C=[2,1,-1;-1,-1,1;1,1,1], b=[4;-2;-3], m=1

// okre lenie zakresu w którym poszukujemy warto ci zmiennych x,y,z

ci=[0;-100000;-100000], cs=[100000;100000;100000]

[x_opt,lagr,f]=linpro(p,C,b,ci,cs,m)

w_opt= f+2

// uzyskane rozwi zanie: x_opt=[0;0.5;-3.5], w_opt=18

Zadanie 2.

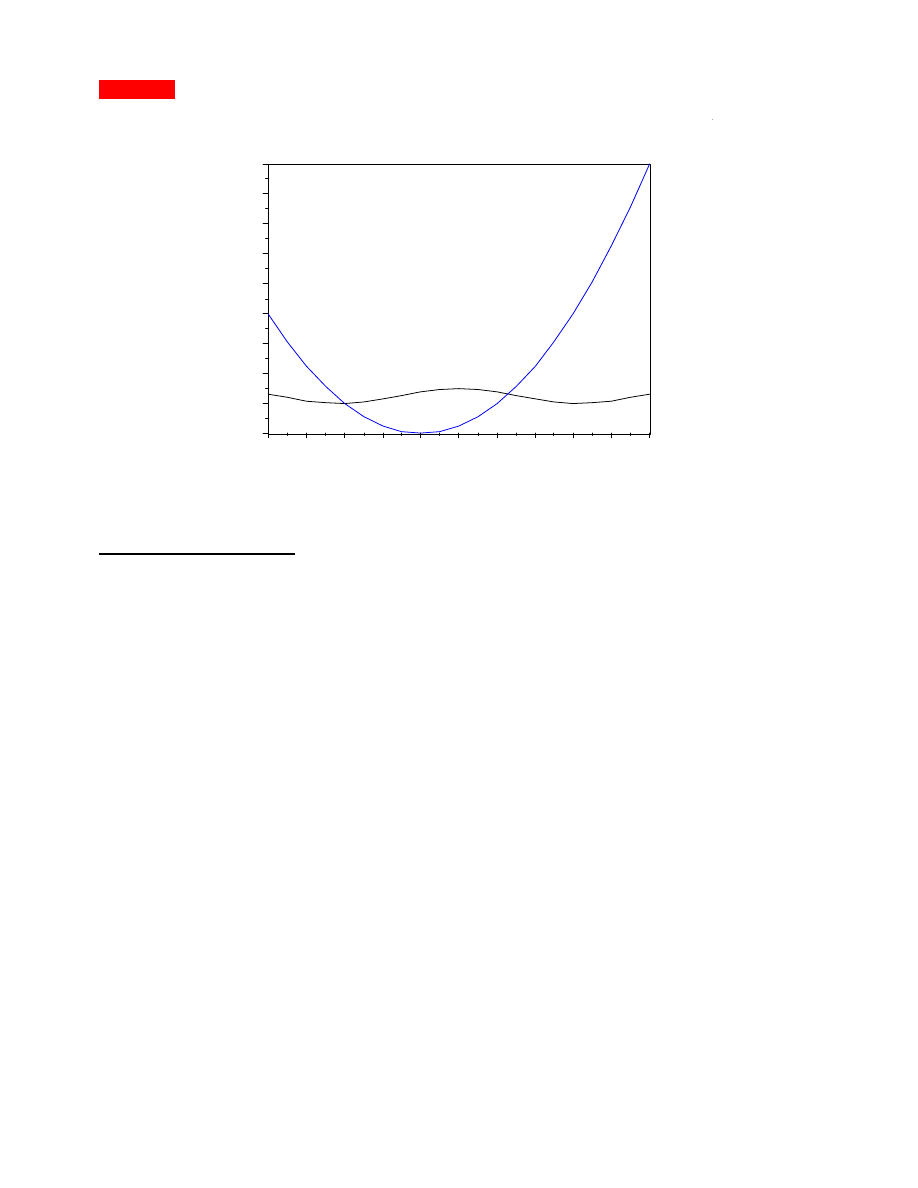
Obliczy pole figury ograniczonej krzywymi: y = cos(x)+8; y = x^2+2*x+4

-5

-4

-3

-2

-1

0

1

2

3

4

5

3

7

11

15

19

23

27

31

35

39

Jeden ze sposobów rozwi zania polegałby na znalezieniu punktów przeci cia si wykresów obu

funkcji, obliczenia dwóch całek pojedynczych, oraz ich ró nicy.

Polecenia zapisujemy jako:

// znalezienie punktów przeci cia – wykorzystanie funkcji SciLaba

// fsolve() – tworzymy układ równa :

//

y - cos(x)- 8 = 0

// y - x^2-2*x-4 = 0

function [y]=fst(z)

// w definiowanej funkcji przyjmujemy z=[x;y]

a=[0,0;-1,0]; b=[0,1;-2,1]; c=[-8;-4]; d=[-1,0;0,0]

y=a*z^2+b*z+c+d*cos(z)

endfunction

// u ycie funkcji fsolve() – pocz tkowym rozwi zaniem punkt (0,0)

xy1=fsolve([0;0],fst);

// znalezione rozwi zanie: xy1=[ 1.2959523; 8.2713968]

xy2=fsolve([-3;0],fst);

// znalezione rozwi zanie: xy2=[ - 3.0024159; 7.0096695]

// obliczenie całek pojedynczych

c1= integrate('cos(x)+8','x',xy1(1),xy2(1))

c2= integrate('x^2+2*x+4','x',xy1(1),xy2(1))

pole = c1-c2

// znalezione rozwi zanie: pole = 15.882402

Zadanie 3.

Zapisz funkcj o nazwie "styczne(x0,f,g)" która oblicza przybli one rozwi zanie równania f(x)=0

wykorzystuj c algorytm metody stycznych (patrz prezentacja Laboratorium nr 2) wykonuj c 10

iteracji. Punktem startowym jest argument "x0", funkcj argument "f" , argument "g" oznacza

funkcj b d c pochodn funkcji "f"

Algorytm metody stycznych:

( )

( )

i

i

i

i

x

f

x

f

x

x

'

1

−

=

+

Polecenia zapisujemy jako:

function x=styczne(x0,f,g)

for i=1:10

x=x0-f(x0)/g(x0)

x0=x

end

endfunction

Zadanie 3a.

Zapisz funkcj o nazwie "sieczne(x0,x1,f)" która oblicza przybli one rozwi zanie równania f(x)=0

wykorzystuj c algorytm metody siecznych (patrz prezentacja Laboratorium nr 2) wykonuj c 10

iteracji. Punktami startowymi s argumenty "x0,x1", funkcj argument "f"

Algorytm metody siecznych:

(

)

( ) ( ) ( )

i

i

i

i

i

i

i

x

f

x

f

x

f

x

x

x

x

1

1

1

−

−

+

−

−

−

=

Polecenia zapisujemy jako:

function x=sieczne(x0,x1,f)

for i=1:10

x=x1-(x1-x0)*f(x1)/(f(x1)-f(x0))

x0=x1

x1=x

end

endfunction

Zadanie 4.

Oblicz przybli on warto całki z funkcji f(x) = sin(2x)+x-3 na [0,10] przy u yciu kwadratury

zło onej - wzoru trapezów, dziel c przedział całkowania na 5 cz ci (np. wykorzystuj c funkcj

inttrap()).

Polecenia zapisujemy jako:

// u ycie funkcji linspace():

// wygenerowanie wektora 6 punktów dziel cych [0,10] na 5 cz

ci

x=linspace(0,10,6)

y=sin(2*x)+x-3

c=inttrap(x,y)

// otrzymany wynik c=19.729104

Zadanie 4a.

Oblicz przyblizon warto całki z funkcji f(x) = sin(2x)+x-3 na [0,10] przybli aj c j funkcj

sklejan w oparciu o punkty w złowe {0,2,4,6,8,10} (wykorzystuj c funkcj intsplin()).

Polecenia zapisujemy jako:

x=[0,2,4,6,8,10]

y=sin(2*x)+x-3

c=intsplin(x,y)

// otrzymany wynik c= 18.784725