Politechnika Świętokrzyska

Wydział Elektrotechniki, Automatyki i Informatyki

Katedra Zastosowań Informatyki

Metody obliczeniowe – laboratorium

Instrukcja laboratoryjna nr 2: Interpolacja

Opracował: dr inż. Andrzej Kułakowski
Data: 1.06.2012 r.

1. Wprowadzenie

Interpolacja:

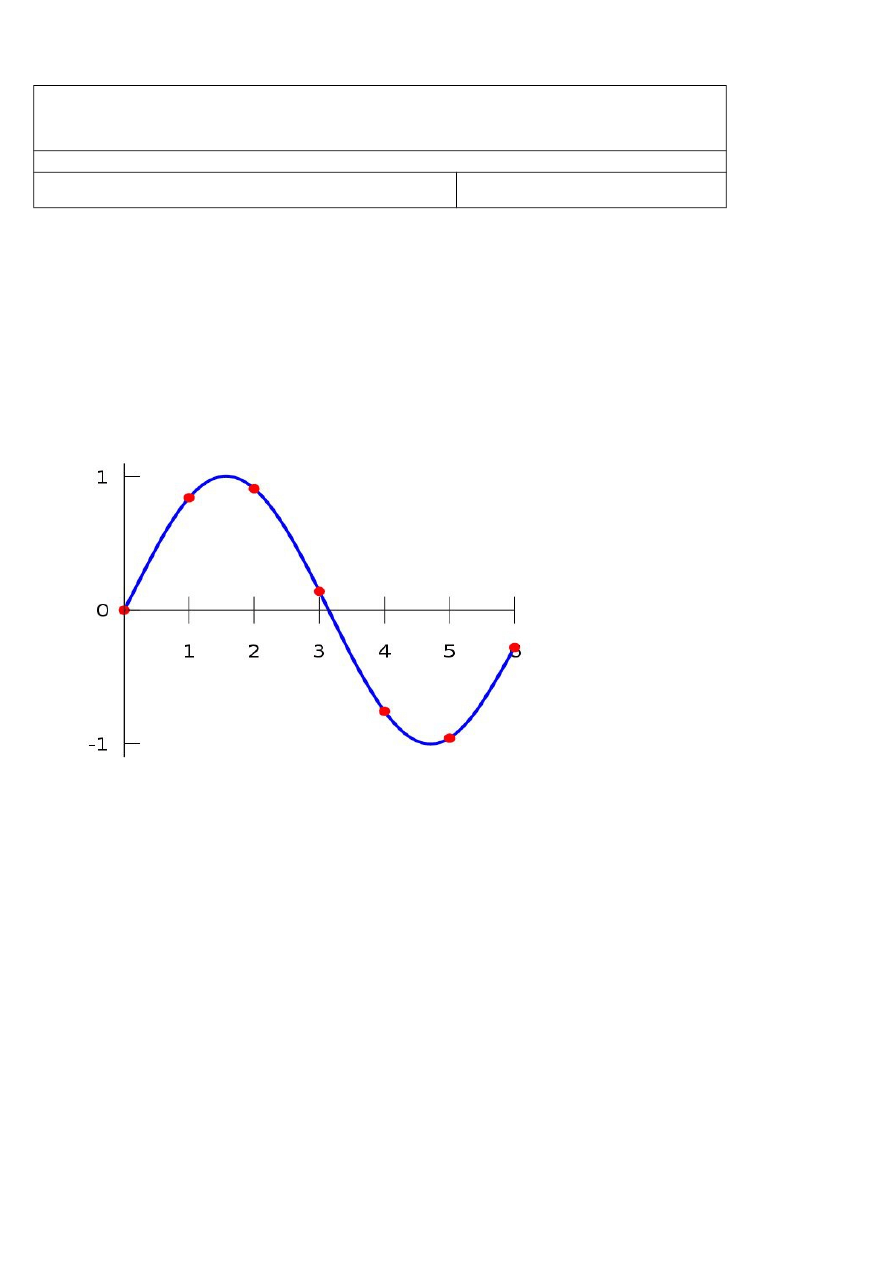
Interpolacją funkcji nazywa się wyznaczenie przybliżonych wartości funkcji f(x) dla dowolnego argumentu x

w przedziale [a, b], przy znanych jej wartościach f(x

0

), f(x

1

), …, f(x

n

)

w ustalonych kolejnych punktach x

0

, x

1

, …, x

n

zwanych węzłami interpolacji.

Rys. 1. Węzły interpolacji i wyznaczona krzywa interpolacyjna.

2. Interpolacja wielomianem Lagrange'a

Wzór wielomianu interpolacyjnego Lagrange'a:

W

n



x =

∑

j =0

n

y

j

⋅



x−x

0

⋅

x −x

1



x− x

j−1

⋅

x−x

j 1



x−x

n





x

j

−

x

0

⋅

x

j

−

x

1



x

j

−

x

j −1

⋅

x

j

−

x

j 1



x

j

−

x

n



(1)

odstępy pomiędzy punktami x

i

mogą być dowolne.

Przykład 1:

Znaleźć wielomian interpolacyjny metodą Lagrange'a:

Punkty do obliczeń:
i

0

1

2

3

x

1

2

3

4

y

3

1

-1

2

Wzór interpolacyjny Lagrange'a dla 4 punktów:

W

3



x = y

0

⋅



x− x

1

⋅

x−x

2

⋅

x−x

3





x

0

−

x

1

⋅

x

0

−

x

2

⋅

x

0

−

x

3





y

1

⋅



x− x

0

⋅

x− x

2

⋅

x− x

3





x

1

−

x

0

⋅

x

1

−

x

2

⋅

x

1

−

x

3





y

2

⋅



x−x

0

⋅

x−x

1

⋅

x− x

3





x

2

−

x

0

⋅

x

2

−

x

1

⋅

x

2

−

x

3





y

3

⋅



x− x

0

⋅

x− x

1

⋅

x−x

2





x

3

−

x

0

⋅

x

3

−

x

1

⋅

x

3

−

x

2



(2)

Po podstawieniu punktów z tabeli:

W

3



x =3⋅



x−2⋅ x−3⋅ x−4 



1−2⋅1−3⋅1−4



1⋅



x−1⋅ x −3⋅ x−4



2−1⋅2−3⋅2−4



−1⋅



x−1⋅ x−2⋅ x−4



3−1⋅3−2⋅3−4



2⋅



x−1⋅ x−2⋅ x−3



4−1⋅4−2⋅4−3

(3)

ciąg dalszy po wykonaniu obliczeń:

=−

1
2

⋅

x

3

−

9⋅x

2



26⋅x−24

1
2

⋅

x

3

−

8⋅x

2



19⋅x −12

1

2

⋅

x

3

−

7⋅x

2



14⋅x −8

1
3

⋅

x

3

−

6⋅x

2



11⋅x−6

=

5
6

⋅

x

3

−

5⋅x

2



43

6

⋅

x0

Jest to wynik którego szukaliśmy.

3. Interpolacja wielomianem Newton'a

Wzór wielomianu interpolacyjnego Newton'a:

W

n



x = y

0





y

0

h

⋅

x−x

0





2

y

0

2!⋅h

2

⋅

x−x

0

⋅

x−x

1







n

y

0

n!⋅h

n

⋅

x−x

0

⋅

x−x

1

⋅⋅

x −x

n−1



(4)

Metoda Newtona zakłada, że odstępy pomiędzy punktami x

i

są jednakowe i równe h.

We wzorze mamy wykorzystane operatory różnic zwykłych, które obliczamy wg schematu:

Obliczenia operatorów w tablicy różnic zwykłych:

i

x

i

f  x

i

=

y

i



f  x

i





2

f  x

i





3

f x

i



0

x

0

f  x

0





f x

0





2

f  x

0





3

f  x

0



1

x

0

+h

f  x

0



h



f x

0



h



2

f x

0



h

2

x

0

+2h

f  x

0



2h



f x

0



2h

3

x

0

+3h

f  x

0



3h

Przykład 2:

Znaleźć wielomian interpolacyjny metodą Newtona:

Punkty do obliczeń:
i

0

1

2

3

x

1

1.5

2

2.5

y

2

2.5

3.5

4.0

Obliczenia operatorów w tablicy różnic zwykłych:

i

x

i

f  x

i

=

y

i



f x

i

 

2

f  x

i





3

f  x

i



0

1.0

2.0

0.5

0.5

-1.0

1

1.5

2.5

1.0

-0.5

2

2.0

3.5

0.5

3

2.5

4.0

Po podstawieniu punktów i operatorów oraz wyliczeniu:

W

3



x =2.0

0.5

1
2

⋅

x−1

0.5

2!⋅

1
2

2

⋅

x−1⋅ x −1.5

−

1.0

3!⋅

1

2

3

⋅

x −1⋅ x−1.5⋅ x−2

=−

4
3

⋅

x

3



7⋅x

2

−

10

1
6

⋅

x6

1
2

Jest to wynik którego szukaliśmy.

4. Zadania do wykonania

a) dla podanego przez prowadzącego zajęcia przykładu, obliczyć wielomian interpolacyjny wybraną metodą.

b) dla podanego przez prowadzącego zajęcia zadania domowego:

- napisać program komputerowy obliczający wielomian interpolacyjny wybraną metodą.