
Wstęp do programowania
wykład 12
Agata Półrola
Wydział Matematyki i Informatyki UŁ
sem. zimowy 2012/2013
Agata Półrola Wydział Matematyki i Informatyki UŁ
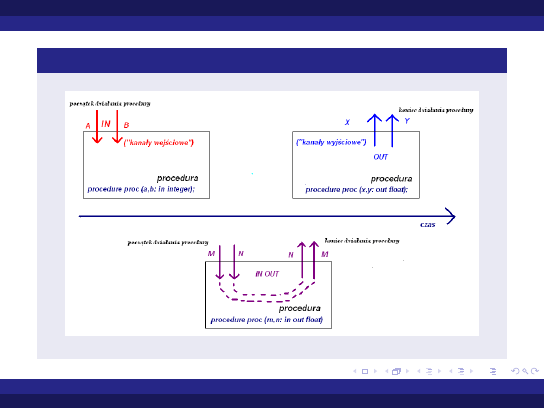
Tryby parametrów
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
tryby parametrów
tryby parametrów dotyczą procedur i funkcji, przy czym
jedynym dopuszczalnym trybem parametrow funkcji jest tryb
in
tryb parametrów określa się przy ich specyfikacji, wpisując
nazwę trybu pomiędzy dwukropkiem a nazwą typu
przykład:
procedure P1 (a:
in integer; x,y:
in out float; z:
out float) is
...
jeżeli tryb parametrów nie jest podany, to domyślnie przyjmuje
się że jest to in
przykład:
function F1 (a:
in integer; b:
in float) return integer is ...
function F1 (a:
integer; b:
float) return integer is ...
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
tryby parametrów - cd
tryb in
(
parametry wejściowe
):
parametr formalny jest stałą inicjalizowaną wartością
odpowiadającego mu parametru aktualnego
dla parametrów w tym trybie niedozwolone są instrukcje mogące zmienić
ich wartość; dozwolone jest tylko czytanie tej wartości
tryb in out
(
parametry wejściowo-wyjściowe
):
parametr formalny jest zmienną inicjalizowaną wartością
odpowiadającego mu parametru aktualnego; dozwolone jest
odczytywanie i aktualizowanie wartości parametru aktualnego
tryb out
(
parametry wyjściowe
):
parametr formalny jest niezainicjalizowaną zmienną;
dozwolone jest aktualizowanie wartości odpowiadającego
parametru aktualnego
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Procedura z wieloma parametrami o różnych trybach)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 3
i s
p r o c e d u r e
P r o s t o k a t ( b1 , b2 :
i n
i n t e g e r ;
p o l e , obwod :
o u t
i n t e g e r )
i s
b e g i n
p o l e := b1 ∗ b2 ; obwod :=2∗ b1+2∗b2 ;
end P r o s t o k a t ;
a , b , p , o :
i n t e g e r ;
b e g i n
p u t l i n e ( ” p o d a j
b o k i
p r o s t o k a t a : ” ) ;
g e t ( a ) ;
g e t ( b ) ;
p r o s t o k a t ( a , b , p , o ) ;
p u t ( ” p o l e
p r o s t o k a t a
w y n o s i ” ) ;
p u t ( p ) ;
n e w l i n e ;
p u t ( ” obwod p r o s t o k a t a
w y n o s i ” ) ;
p u t ( o ) ;
end w 1 3 p r o c 3 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Procedury z wieloma parametrami - przykł.2)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 4
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
p r o c e d u r e WypiszTab ( t :
i n Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p
p u t ( t ( i ) ,
3 ) ;
p u t ( ” , ” ) ;
end l o o p ;
n e w l i n e ;
end WypiszTab ;
p r o c e d u r e P o b i e r z T a b ( t :
o u t Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p
p u t ( ” p o d a j
e l e m e n t ” & i n t e g e r ’ i m a g e ( i ) & ” : ” ) ;
g e t ( t ( i ) ) ;
end l o o p ;
end P o b i e r z T a b ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Procedury z wieloma parametrami - przykł.2 cd)
p r o c e d u r e Z e r u j U j e m n e ( t :
i n
o u t Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )<0 t h e n t ( i ) : = 0 ; end
i f ;
end l o o p ;
end Z e r u j U j e m n e ;
x : Tab ( 1 . . 1 0 ) ;
b e g i n
p u t l i n e ( ” p o d a j d a n e do
t a b l i c y : ” ) ;
P o b i e r z T a b ( x ) ;
p u t l i n e ( ” t a b l i c a : ” ) ;
w y p i s z T a b ( x ) ;
p u t l i n e ( ” t a b l i c a
po z a m i a n i e u j e m n y c h na z e r a : ” ) ;
Z e r u j U j e m n e ( x ) ;
w y p i s z T a b ( x ) ;
end w 1 3 p r o c 4 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Uwagi - cd
przekazywanie parametrów
Przekazywanie wartości parametru aktualnego do procedury lub
funkcji może wyglądać różnie w zależności od ich typu:
parametry typów skalarnych (tj. dyskretnych i rzeczywistych) i
tzw. typów dostępu (czyli tzw. wskaźniki) są przekazywane
przez wartość
procedura operuje na kopii parametru aktualnego
jeśli parametr jest tablicą lub rekordem, to mechanizm
kopiowania może, ale nie musi być użyty; alternatywnie dana
implementacja Ady może użyć mechanizmu przekazania przez
referencję
przekazanie przez referencję oznacza, że procedura operuje na “oryginale”
obiektu będącego parametrem aktualnym, wykorzystując przy odwołaniach jego
adres w pamięci
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Przekazywanie parametrów out - test)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 5
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
p r o c e d u r e
L i c z ( a :
i n
i n t e g e r ; b :
o u t
i n t e g e r )
i s
b e g i n
p u t ( ” p o c z a t k o w a w a r t o s c
p a r a m e t r u o u t
p r o c e d u r y
L i c z : ” ) ; p u t ( b ) ; b :=2∗ a ;
end L i c z ;
p r o c e d u r e WypiszTab ( t :
i n Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p p u t ( t ( i ) , 3 ) ;
p u t ( ” , ” ) ;
end l o o p ;
n e w l i n e ;
end WypiszTab ;
p r o c e d u r e P o b i e r z T a b ( t :
o u t Tab )
i s
b e g i n
p u t l i n e ( ” p o c z a t k o w a w a r t o s c
p a r a m e t r u o u t
p r o c e d u r y
P o b i e r z t a b : ” ) ;
WypiszTab ( t ) ;
f o r
i
i n t ’ r a n g e l o o p
p u t ( ” p o d a j
e l e m e n t ” & i n t e g e r ’ i m a g e ( i ) & ” : ” ) ;
g e t ( t ( i ) ) ;
end l o o p ;
end P o b i e r z T a b ;
x : Tab ( 1 . . 5 ) : = ( o t h e r s =>0);
y :
i n t e g e r : = 0 ; z :
i n t e g e r ;
b e g i n
p u t ( ” p o d a j
w a r t o s c
p i e r w s z e g o
p a r a m e t r u : ” ) ;
g e t ( z ) ;
L i c z ( z , y ) ;
n e w l i n e ;
p u t ( ” w a r t o s c
w y l i c z o n a
p r z e z
p r o c e d u r e : ” ) ;
p u t ( y ) ;
n e w l i n e ( 3 ) ;
−−−−−−−−−−−−−−−−−−−−−−−−−
P o b i e r z T a b ( x ) ;
p u t l i n e ( ” t a b l i c a
po p o b r a n i u : ” ) ;
end w 1 3 p r o c 5 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
przekazywanie parametrów - cd
parametry pewnych typów (jeszcze nie omawianych) są
zawsze przekazywane przez referencję. Te typy to:
zadania (tasks)
typy chronione (protected)
typy rekordowe ze znacznikami (tagged records)
typy limited
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
ograniczenia dla parametrów
Ograniczenia dla parametrów obsługiwane są w następujący
sposób:
w przypadku typów skalarnych:
in, in out - w momencie wywołania procedury ograniczenia
na parametr formalny muszą być spełnione przez parametr
aktualny
in out, out - w momencie wyjścia z procedury parametry
formalne muszą spełniać ograniczenia na zmienną będącą
parametrem aktualnym
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Ograniczenia - parametry skalarne)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 6
i s
s u b t y p e do10
i s
i n t e g e r
r a n g e
1 . . 1 0 ;
p r o c e d u r e
L i c z ( a :
i n
i n t e g e r ; b :
o u t
i n t e g e r )
i s
b e g i n
b :=2∗ a ;
end L i c z ;
l 1 ,
l 2 :
do10 ;
b e g i n
p u t ( ” p o d a j
l i c z b e : ” ) ;
g e t ( l 1 ) ;
L i c z ( l 1 , l 2 ) ;
p u t ( ” l i c z b a
p o d w o j o n a : ” ) ;
p u t ( l 2 ) ;
−− t e s t : p o d a n i e
l i c z b y 2 ( d z i a l a ) ,
p o d a n i e
l i c z b y 8 ( b l a d )
end w 1 3 p r o c 6 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
ograniczenia dla parametrów - cd
w przypadku typów tablicowych:
jeśli parametr formalny należy do zawężonego typu
tablicowego, to parametr aktualny musi być tego samego
rozmiaru
oczywiście wymagana jest rownież zgodność typów
jeśli parametr formalny należy do niezawężonego typu
tablicowego, to dziedziczy on ograniczenia po parametrze
aktualnym
podobnie było w przypadku funkcji
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Ograniczenia - parametry tablicowe)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 7
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
p r o c e d u r e WypiszTab ( t :
i n Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p
p u t ( t ( i ) ,
3 ) ;
p u t ( ” , ” ) ;
end l o o p ;
n e w l i n e ;
end WypiszTab ;
p r o c e d u r e P o b i e r z T a b ( t :
o u t Tab )
i s
b e g i n
f o r
i
i n t ’ r a n g e l o o p
p u t ( ” p o d a j
e l e m e n t ” & i n t e g e r ’ i m a g e ( i ) & ” : ” ) ;
g e t ( t ( i ) ) ;
end l o o p ;
end P o b i e r z T a b ;
x : Tab ( 1 . . 1 0 ) ;
y : Tab ( 1 . . 3 ) ;
b e g i n
p u t l i n e ( ” p o d a j d a n e do
t a b l i c y
1 : ” ) ;
P o b i e r z T a b ( x ) ;
p u t l i n e ( ” t a b l i c a
1 : ” ) ;
w y p i s z T a b ( x ) ;
p u t l i n e ( ” p o d a j d a n e do
t a b l i c y
2 : ” ) ;
P o b i e r z T a b ( y ) ;
p u t l i n e ( ” t a b l i c a
2 : ” ) ;
w y p i s z T a b ( y ) ;
end w 1 3 p r o c 7 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
zmienne
procedura może mieć swoje własne zmienne (
zmienne
lokalne
), deklarowane w jej części deklaracyjnej
zmienna lokalna jest widziana tylko wewnątrz procedury
z tego powodu zmienne lokalne różnych procedur mogą mieć
takie same nazwy
zmienne lokalne procedury to nie to samo co jej
parametry i nie można dowolnie zastępować jednego
drugim!!!
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
zmienne
procedura nie powinna raczej korzystać ze zmiennych
globalnych
→ wszystkie dane dla procedury powinny być przekazane przez parametry,
efektem działania powinno być raczej - poza zupełnie wyjątkowymi przypadkami
- tylko modyfikacja wartości wejściowo-wyjściowych i nadanie wartości
parametrom wyjściowym (a nie np. modyfikacja zmiennych globalnych).
jeśli zmienna lokalna procedury ma taką nazwę jak zmienna
globalna, to zmienna lokalna przesłania globalną
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
typy anonimowe i (nie)zawężone
parametry procedury mogą być różnych typów, ale nie może
to być typ anonimowy
parametr wejściowy lub wejściowo-wyjściowy procedury może
być typu niezawężonego. W takim przypadku ograniczenia
(wartości atrybutów ’range, ’length itd) odpowiadają
ograniczeniom dla parametru aktualnego. Użycie zawężenia w
liście parametrów jest niedozwolone
zamiast zawężenia można w liście parametrów uzyć nazwy podtypu typu
niezawężonego
parametr wyjściowy procedury może być typu niezawężonego,
jednak w praktyce zawsze jest to wartość “zawężona”.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
zakończenie działania procedury
w odróznieniu od funkcji procedura nie musi zawierać
instrukcji return
użycie tej instrukcji jest jednak dozwolone; jej użycie
umożliwia zakończenie działania procedury w dowolnym
miejscu
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Procedura z nietypowym return)
w i t h ada . t e x t i o , ada . f l o a t t e x t i o , ada . n u m e r i c s . e l e m e n t a r y f u n c t i o n s ;
u s e ada . t e x t i o , ada . f l o a t t e x t i o , ada . n u m e r i c s . e l e m e n t a r y f u n c t i o n s ;
p r o c e d u r e w 1 3 p r o c 8
i s
p r o c e d u r e rown kw ( a , b , c :
i n
f l o a t ; x1 , x2 :
o u t
f l o a t ; ok :
o u t b o o l e a n )
i s
d :
f l o a t ;
b e g i n
d := b∗b − 4 . 0 ∗ a∗c ;
i f
d <0.0 o r a =0.0 t h e n
ok :=
f a l s e ;
r e t u r n ;
end
i f ;
x1 := (−b−s q r t ( d ) ) / ( 2 . 0 ∗ a ) ;
x2 := (−b+s q r t ( d ) ) / ( 2 . 0 ∗ a ) ;
ok := t r u e ;
end rown kw ;
l 1 , l 2 , l 3 , w1 , w2 :
f l o a t ; ok :
b o o l e a n ;
b e g i n
p u t ( ” p o d a j 3 l i c z b y
( w s p o l c z y n n i k i
r o w n a n i a k w a d r a t o w e g o ) > ” ) ;
g e t ( l 1 ) ;
g e t ( l 2 ) ;
g e t ( l 3 ) ;
rown kw ( l 1 , l 2 , l 3 , w1 , w2 , ok ) ;
i f
ok t h e n
p u t ( ” p i e r w i a s t k i
r o w n a n i a : ” ) ;
p u t ( w1 ,
e x p =>0); p u t ( w2 ,
e x p =>0);
e l s e
p u t ( ” b r a k
p i e r w i a s t k o w
( l u b
r o w n a n i e
n i e
j e s t
k w a d r a t o w e ) ” ) ;
end
i f ;
end w 1 3 p r o c 8 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Procedury rekurencyjne
Przypomnienie:
rekurencja polega na tym, że procedura lub funkcja wywołuje
samą siebie (chociaż być może dla innych danych niż te dla
których sama została wywołana)
aby nie powodowalo to nieskończonego ciągu wywołań,
procedura/funkcja musi dla pewnych danych zachować się
“nierekurencyjnie”, tj. wykonać pewne czynności wśród
których nie ma kolejnego wywołania jej samej.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zadania
1
Napisać program rozwiązujący problem wież Hanoi (z trzema
wieżami) dla podanej przez użytkownika liczby krążków N.
wieże Hanoi: Mamy trzy słupki (wieże); na pierwszy z nich nałożone są
krążki o różnych średnicach, w kolejności od największej do najmniejszej.
Problem polega na odbudowaniu, z zachowaniem kształtu, wieży z
pierwszego słupka na trzecim słupku, przy czym podczas przekładania
wolno się posługiwać dodatkowym słupkiem, ale nie wolno kłaść krążka o
większej średnicy na mniejszy ani przekładać kilku krążków jednocześnie.
anegdota: http: // www. math. edu. pl/ wieza-hanoi
opis: http: // www. algorytm. org/ inne/ problem-wiez-hanoi. html ,
http: // www. jakubas. pl/ pr-komp/ hanoi/ opis-hanoi. htm
Ogólna zasada rozwiązania:
Jeśli N=1 to przenosimy jeden krążek ze słupka “początkowego” na
“docelowy”. Jeśli N>1, to przenosimy najpierw N-1 krążków na słupek
pomocniczy, następnie N-ty krążek na słupek docelowy, i na koniec N-1
krążków ze słupka pomocniczego na docelowy.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Wieże Hanoi - rozwiązanie rekurencyjne)
w i t h ada . t e x t i o ,
ada . I n t e g e r T e x t I O ;
u s e ada . t e x t i o ,
ada . I n t e g e r T e x t I O ;
p r o c e d u r e
p r o g h a n o i
i s
t y p e w i e z e
i s
( w i e z a A ,
w i e z a B ,
w i e z a C ) ;
p a c k a g e
w i e z e i o
i s new ada . T e x t I O . E n u m e r a t i o n I O ( w i e z e ) ;
u s e
w i e z e i o ;
p r o c e d u r e
p r z e n i e s ( i l e :
i n
i n t e g e r ;
w i e z a z ,
w i e z a d o ,
w i e z a p o m :
w i e z e ;
i r :
i n
o u t
i n t e g e r )
i s
b e g i n
i f
i l e =1 t h e n
p u t ( w i e z a z ) ;
p u t ( ”−>” ) ;
p u t ( w i e z a d o ) ;
n e w l i n e ;
i r := i r +1;
e l s e
p r z e n i e s ( i l e −1, w i e z a z ,
w i e z a p o m ,
w i e z a d o , i r ) ;
p r z e n i e s ( 1 , w i e z a z , w i e z a d o , w i e z a p o m , i r ) ;
p r z e n i e s ( i l e −1, w i e z a p o m , w i e z a d o , w i e z a z , i r ) ;
end
i f ;
end p r z e n i e s ;
n :
i n t e g e r ;
i l e r u c h o w :
i n t e g e r ;
b e g i n
i l e r u c h o w : = 0 ;
p u t ( ” i l e
j e s t
k r a z k o w ? ” ) ;
g e t ( n ) ;
p r z e n i e s ( n , w i e z a A , w i e z a C , w i e z a B , i l e r u c h o w ) ;
p u t ( ” p r z e n i e s i e n i e
n a s t a p i l o w ” ) ;
p u t ( i l e r u c h o w ,
end p r o g h a n o i ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - cd
Wiele podprogramów
procedur i funkcji może być w programie wiele, jedna może
wywoływać drugą
może być nawet kilka procedur lub funkcji o tych samych
nazwach
jeśli mają np. różne typy parametrów - będą rozróżniane, jeśli
nie mogą być rozróżnione - będą przesłaniane
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - jeszcze o parametrach
Wywołując funkcję lub procedurę możemy używać notacji
pozycyjnej lub nazywanej
WypiszTab(x);
WypiszTab(t=>x);
notacje można łączyć, podobnie jak w agregatach tablic
(najpierw notacja pozycyjna, dalej - nazywana). jednak w
odróznieniu od agregatów użycie słowa others nie jest
dozwolone.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - parametry domyślne
Możliwe jest nadawanie parametrom podprogramów wartości
domyslnych
wartości domyślne nadawane są przy specyfikacji parametrów
wartość domyślną można nadać tylko parametrom w trybie in
nie jest dozwolone nadawanie wartości domyślnej parametrom
operatorów, ale jest dozwolone w przypadku parametrów
funkcji
wartość domyślna parametru może być zadana dowolnym
wyrażeniem, więc przy róznych wywołaniach może być różna
wartość domyślna jest używana tylko wtedy, gdy wywołanie
podprogramu nie zawiera innej wartości tego parametru
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - parametry domyślne
Możliwe jest nadawanie parametrom podprogramów wartości
domyslnych
wartości domyślne nadawane są przy specyfikacji parametrów
wartość domyślną można nadać tylko parametrom w trybie in
nie jest dozwolone nadawanie wartości domyślnej parametrom
operatorów, ale jest dozwolone w przypadku parametrów
funkcji
wartość domyślna parametru może być zadana dowolnym
wyrażeniem, więc przy róznych wywołaniach może być różna
wartość domyślna jest używana tylko wtedy, gdy wywołanie
podprogramu nie zawiera innej wartości tego parametru
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Parametry domyślne)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 2 p r o c 9
i s
p r o c e d u r e
j a k a s
( a :
i n
i n t e g e r
: = 1 0 ; b :
i n
i n t e g e r : = 2 ;
x :
o u t
i n t e g e r )
i s
b e g i n
x := a ∗ b ;
end j a k a s ;
a :
i n t e g e r ;
b e g i n
j a k a s ( x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( a=>2,x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( 2 , 3 , a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
end w 1 2 p r o c 9 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - przeciążanie
Przeciążanie dotyczy nie tylko operatorów, ale wszelkich
podprogramów
pojawienie się kolejnego podprogramu o takiej samej nazwie,
kolejności i typie bazowym parametrów i takim samym typie
wyniku (jeśli podprogram jest funkcją) powoduje przesłonięcie
poprzedniego podprogramu
nazwy parametrów, ich tryb, ograniczenia lub brak ograniczeń i wartości
domyślnych parametrów nie mają znaczenia
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Przeciążanie)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 1 0
i s
p r o c e d u r e
j a k a s
( a :
i n
i n t e g e r
: = 1 0 ; b :
i n
i n t e g e r : = 2 ; x :
o u t
i n t e g e r )
i s
b e g i n
x := a∗b ;
end j a k a s ;
a :
i n t e g e r ;
b e g i n
j a k a s ( x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( a=>2,x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( 2 , 3 , a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
d e c l a r e
p r o c e d u r e
j a k a s
( x1 :
i n
i n t e g e r
: = 0 ; b :
i n
i n t e g e r : = 0 ; x :
o u t
i n t e g e r )
i s
b e g i n
x := x1+b ;
end j a k a s ;
b e g i n
j a k a s ( x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( x1=>2,x=>a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
j a k a s ( 2 , 3 , a ) ;
p u t ( ” w y n i k :
” ) ;
p u t ( a , 0 ) ;
n e w l i n e ;
end ;
end w 1 3 p r o c 1 0 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Document Outline
Wyszukiwarka
Podobne podstrony:
1213z wdprog ww04
1213z wdprog ww02
1213z wdprog ww07
1213z wdprog ww11
1213z wdprog ww09
1213z wdprog ww08
1213z wdprog ww10
1213z wdprog ww13
1213z wdprog ww06
1213z wdprog ww14
1213z wdprog ww05
1213z wdprog ww03
1213z wdprog ww01
1213z wdprog ww02
więcej podobnych podstron