
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Wstęp do programowania
wykład 5
Agata Półrola
Wydział Matematyki i Informatyki UŁ
sem. zimowy 2012/2013
Agata Półrola Wydział Matematyki i Informatyki UŁ

Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Instrukcje pętli
Pętle i ich rodzaje
Pętle
umożliwiają iteracyjne wykonywanie pewnych kroków
pewien fragment programu możemy wykonać wielokrotnie raz za razem (być może dla
zmienionych danych)
Zazwyczaj w językach programowania można wyróżnić dwa rodzaje
pętli:
pętle wykonujące się określoną liczbę razy
pętle wykonujące się do momentu spełnienia pewnego
warunku
przy czym tak naprawdę pętle pierwszego rodzaju są wygodniejszym zapisem pewnych
pętli drugiego rodzaju
Agata Półrola Wydział Matematyki i Informatyki UŁ

Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Instrukcje pętli
Pętle i ich rodzaje
Pętle
umożliwiają iteracyjne wykonywanie pewnych kroków
pewien fragment programu możemy wykonać wielokrotnie raz za razem (być może dla
zmienionych danych)
Zazwyczaj w językach programowania można wyróżnić dwa rodzaje
pętli:
pętle wykonujące się określoną liczbę razy
pętle wykonujące się do momentu spełnienia pewnego
warunku
przy czym tak naprawdę pętle pierwszego rodzaju są wygodniejszym zapisem pewnych
pętli drugiego rodzaju
Agata Półrola Wydział Matematyki i Informatyki UŁ

Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Instrukcje pętli
Pętle i ich rodzaje
Pętle
umożliwiają iteracyjne wykonywanie pewnych kroków
pewien fragment programu możemy wykonać wielokrotnie raz za razem (być może dla
zmienionych danych)
Zazwyczaj w językach programowania można wyróżnić dwa rodzaje
pętli:
pętle wykonujące się określoną liczbę razy
pętle wykonujące się do momentu spełnienia pewnego
warunku
przy czym tak naprawdę pętle pierwszego rodzaju są wygodniejszym zapisem pewnych
pętli drugiego rodzaju
Agata Półrola Wydział Matematyki i Informatyki UŁ
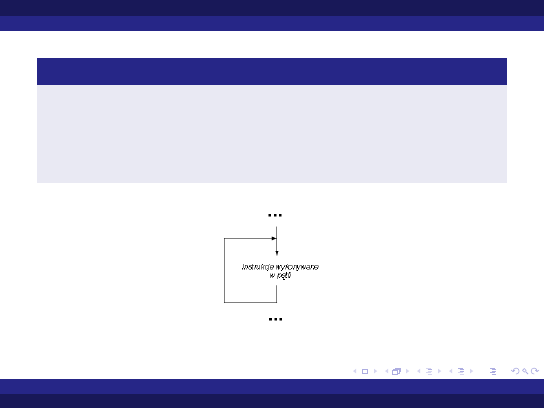
Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Najprostsza pętla (nieskończona)
loop
instrukcje
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Pętla nieskończona)
with ada . t e x t i o ;
use ada . t e x t i o ;
p r o c e d u r e w 0 5 D e s z c z z e s n i e g i e m
i s
b e g i n
l o o p
p u t ( ” \
∗ ” ) ;
end l o o p ;
end w 0 5 D e s z c z z e s n i e g i e m ;
działanie programu z taką pętlą można przerwać tylko “siłowo”, np. kombinacją
klawiszy Ctrl-C
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Pętle których wykonanie zależy od warunku
Można wyrożnić dwa rodzaje pętli “sterowanych” warunkiem:
pętle wykonujące się do momentu zajścia pewnego warunku
pętle wykonujące się dopóki zachodzi pewien warunek
Agata Półrola Wydział Matematyki i Informatyki UŁ
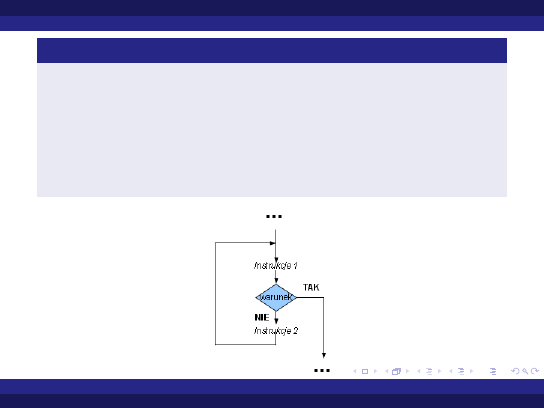
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Pętla wykonująca się do momentu zajścia warunku
loop
instrukcje_1
exit when warunek;
instrukcje_2
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Pętla z wyjściem)
with ada . t e x t i o ;
use ada . t e x t i o ;
p r o c e d u r e w 0 5 D e s z c z 5 0 0 0 i s
x :
i n t e g e r : = 0 ;
b e g i n
l o o p
p u t ( ” \
∗ ” ) ;
x := x +1;
e x i t when x =5000;
end l o o p ;
end w 0 5 D e s z c z 5 0 0 0 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Uwagi
poprzednio pokazana pętla wykonywała się
do momentu
zajścia warunku
jeśli warunek zaszedł - następowało wyjście z pętli,
instrukcje 2 nie wykonywały się po raz kolejny
z tego wynika, że instrukcje 1 zawsze wykonają się
przynajmniej raz, instrukcje 2 mogą nie być wykonane ani
razu
szczególne przypadki:
gdyby instrukcji 1 nie było (tj. exit when... byłoby na poczatku
pętli) - warunek byłby sprawdzany przed pierwszym wykonaniem pętli (a
więc mogłaby nie być wykonana ani razu)
gdyby instrukcji 2 nie było - warunek byłby sprawdzany na koniec pętli
(a więc całość pętli wykonywałaby się przynajmniej raz)
Agata Półrola Wydział Matematyki i Informatyki UŁ
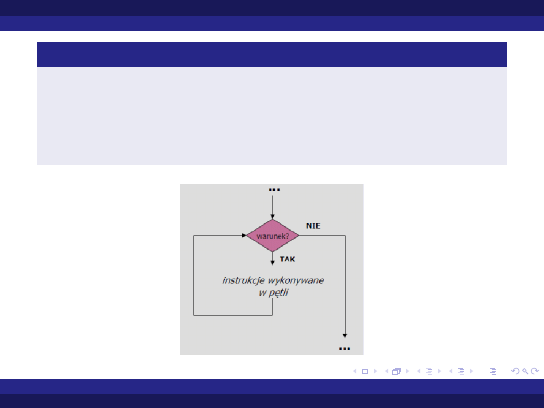
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Pętla wykonująca się dopóki zachodzi warunek
while warunek loop
instrukcje
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Pętla while)
with ada . t e x t i o ;
use ada . t e x t i o ;
p r o c e d u r e w 0 5 D e s z c z 5 0 0 0 w h i l e
i s
x :
i n t e g e r : = 0 ;
b e g i n
w h i l e x <50000 l o o p
p u t ( ” \
∗ ” ) ;
x := x +1;
end l o o p ;
end w 0 5 D e s z c z 5 0 0 0 w h i l e ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Uwagi (do wszystkich petli sterowanych warunkiem)
warunek sterujący pętlą może zawierać zmienne dowolnego
typu
zmienne występujące w warunku nie deklarują się
automatycznie, musimy to zrobić sami
jeśli chcemy aby pętla kiedyś się zakończyła, instrukcje
wewnątrz pętli muszą umożliwiać zmianę wartości
logicznej warunku sterującego pętlą
instrukcji wewnątrz pętli może być dowolnie dużo, moga być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Uwagi (do wszystkich petli sterowanych warunkiem)
warunek sterujący pętlą może zawierać zmienne dowolnego
typu
zmienne występujące w warunku nie deklarują się
automatycznie, musimy to zrobić sami
jeśli chcemy aby pętla kiedyś się zakończyła, instrukcje
wewnątrz pętli muszą umożliwiać zmianę wartości
logicznej warunku sterującego pętlą
instrukcji wewnątrz pętli może być dowolnie dużo, moga być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Uwagi (do wszystkich petli sterowanych warunkiem)
warunek sterujący pętlą może zawierać zmienne dowolnego
typu
zmienne występujące w warunku nie deklarują się
automatycznie, musimy to zrobić sami
jeśli chcemy aby pętla kiedyś się zakończyła, instrukcje
wewnątrz pętli muszą umożliwiać zmianę wartości
logicznej warunku sterującego pętlą
instrukcji wewnątrz pętli może być dowolnie dużo, moga być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Uwagi (do wszystkich petli sterowanych warunkiem)
warunek sterujący pętlą może zawierać zmienne dowolnego
typu
zmienne występujące w warunku nie deklarują się
automatycznie, musimy to zrobić sami
jeśli chcemy aby pętla kiedyś się zakończyła, instrukcje
wewnątrz pętli muszą umożliwiać zmianę wartości
logicznej warunku sterującego pętlą
instrukcji wewnątrz pętli może być dowolnie dużo, moga być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Obu rodzajów pętli “sterowanych warunkiem” można zazwyczaj
używać zamiennie, chociaż w niektórych sytuacjach któryś rodzaj
może być wygodniejszy
Przykłady (Rózne petle, takie samo działanie)
i: integer;
|
i: integer;
...
|
...
i:=10;
|
i:=10;
while i<=100 loop
|
loop
put(i);
|
put(i);
i:=i+10;
|
i:=i+10;
end loop;
|
exit when i>100;
|
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Wypisywanie “pełnych dziesiątek” z zakresu 1-100 - v.1)
with ada . t e x t i o , ada . i n t e g e r t e x t i o ;
use ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 0 5 w h i l e l o o p
i s
i :
i n t e g e r ;
b e g i n
p u t l i n e ( ” w y p i s a n i e
’ p e l n y c h
d z i e s i a t e k ’ do 100 ” ) ;
i : = 1 0 ;
w h i l e i <=100 l o o p
p u t ( i ) ;
i := i +10;
end l o o p ;
end w 0 5 w h i l e l o o p ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Wypisywanie “pełnych dziesiątek” z zakresu 1-100 - v.2)
with ada . t e x t i o , ada . i n t e g e r t e x t i o ;
use ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 0 5 e x i t l o o p
i s
i :
i n t e g e r ;
b e g i n
p u t l i n e ( ” w y p i s a n i e
’ p e l n y c h
d z i e s i a t e k ’ do 100 ” ) ;
i : = 1 0 ;
l o o p
p u t ( i ) ;
i := i +10;
e x i t when i >100;
end l o o p ;
end w 0 5 e x i t l o o p ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Zadanie 1
Napisać program sumujący liczby całkowite podawane przez
użytkownika. Wprowadzenie liczby 0 oznacza zakończenie
podawania.
Agata Półrola Wydział Matematyki i Informatyki UŁ
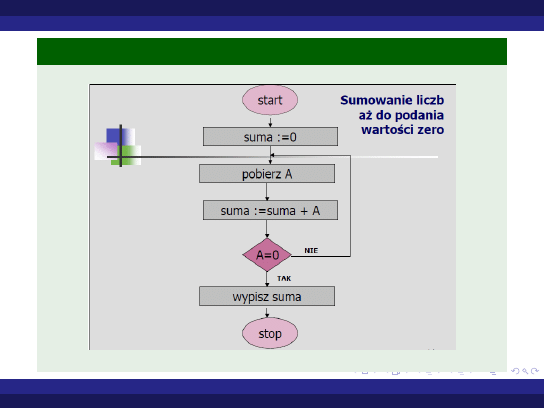
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Sumowanie liczb do podania 0 - algorytm)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Sumowanie liczb do podania 0 - wersja 1)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w05 sumado0
i s
suma , a :
i n t e g e r ;
b e g i n
p u t l i n e ( ” p r o g r a m s u m u j e podawane
l i c z b y ” ) ;
p u t l i n e ( ” p o d a n i e 0 k o n c z y s u m o w a n i e ” ) ;
suma : = 0 ;
l o o p
p u t ( ” p o d a j
l i c z b e : ” ) ;
g e t ( a ) ;
e x i t when a =0;
suma := suma+a ;
end l o o p ;
p u t ( ” suma p o d a n y c h
l i c z b
w y n o s i ” ) ;
p u t ( suma , 0 ) ;
end w05 sumado0 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Sumowanie liczb do podania 0 - wersja 2 (gorsza ;-) ))
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 0 5 s u m a d o 0 v 2
i s
suma , a :
i n t e g e r ;
b e g i n
p u t l i n e ( ” p r o g r a m s u m u j e podawane
l i c z b y ” ) ;
p u t l i n e ( ” p o d a n i e 0 k o n c z y s u m o w a n i e ” ) ;
suma : = 0 ;
a : = 1 ;
−− k o n i e c z n i e
t r z e b a
n a d a c w a r t o s c !
w h i l e a/=0 l o o p
p u t ( ” p o d a j
l i c z b e : ” ) ;
g e t ( a ) ;
suma := suma+a ;
end l o o p ;
p u t ( ” suma p o d a n y c h
l i c z b
w y n o s i ” ) ;
p u t ( suma , 0 ) ;
end w 0 5 s u m a d o 0 v 2 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Zadanie 2
Kotka rodzi jednorazowo do 6 kociąt i może mieć kocięta 2 razy w
ciągu roku. Po pół roku młode mogą mieć kocięta. Mamy jedną
kotkę. Napisać program obliczający, w którym pokoleniu kocia
rodzinka może - w wariancie “pesymistycznym” - osiagnąć
liczebność podaną przez użytkownika.
... a po rozwiązaniu tego zadania i popatrzeniu na wyniki -
zachęcam do zajrzenia tutaj
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla
Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for) Pętle - dodatki
Przykład (Rozwiązanie zadania 2)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e
p r 2 0 k o t y
i s
r o z m i a r r o d z i n k i ,
p o k o l e n i e ,
l i c z b a m l o d y c h , g :
i n t e g e r ;
b e g i n
p u t l i n e ( ” Program
l i c z y
po
i l u
p o k o l e n i a c h
k o c i a
r o d z i n a ” ) ;
p u t l i n e ( ” moze o s i a g n a c p o d a n a
l i c z e b n o s c . ” ) ;
p u t l i n e ( ” P o d a j t e
l i c z e b n o s c : ” ) ;
g e t ( g ) ;
r o z m i a r r o d z i n k i := 1 ;
p o k o l e n i e := 1 ;
w h i l e
r o z m i a r r o d z i n k i < g l o o p
p o k o l e n i e := p o k o l e n i e + 1 ;
l i c z b a m l o d y c h := 6 ∗ r o z m i a r r o d z i n k i ;
r o z m i a r r o d z i n k i := r o z m i a r r o d z i n k i + l i c z b a m l o d y c h ;
end l o o p ;
p u t ( ” R o d z i n k a
o s i a g n i e
p o d a n y r o z m i a r w
” ) ;
p u t ( p o k o l e n i e , 0 ) ;
p u t l i n e ( ” p o k o l e n i u ” ) ;
p u t ( ” ( d o k l a d n i e mozemy m i e c w t e d y ” ) ;
p u t ( r o z m i a r r o d z i n k i , 0 ) ;
p u t l i n e ( ” kotow ) ” ) ;
end p r 2 0 k o t y ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
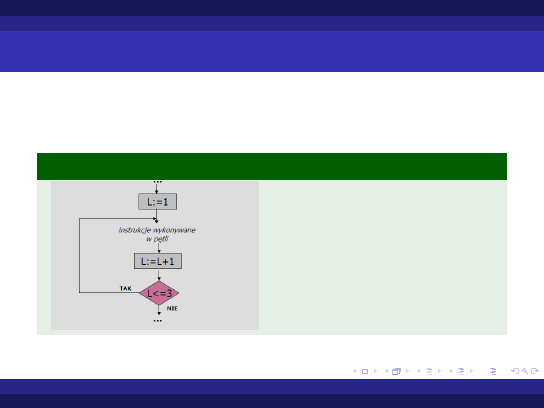
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Pętle wykonujące się podaną liczbę razy
Jeśli chcemy wykonać pewien fragment programu określoną liczbę
razy, możemy użyć jednej z pętli poznanych wcześniej
Przykład (Trzykrotne wykonanie pewnych instrukcji)
L: integer;
|
L: integer;
...
|
L:=1;
| L:=1;
while l<=3 loop | loop
instrukcje
|
instrukcje
L:=L+1;
|
L:=L+1;
end loop;
|
exit when L>3;
| end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
.... ale istnieją specjalne pętle które mogą być użyte w takich
przypadkach
Idea
Musimy z góry znać liczbę powtórzeń (
przebiegów
) pętli
liczba ta nie musi być znana w momencie pisania programu, może też być podana
przez użytkownika w trakcie jego wykonywania
W pętli funkcjonuje pewna zmienna, zwana
licznikiem pętli
,
“pamiętająca” ile razy pętla została wykonania
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
.... ale istnieją specjalne pętle które mogą być użyte w takich
przypadkach
Idea
Musimy z góry znać liczbę powtórzeń (
przebiegów
) pętli
liczba ta nie musi być znana w momencie pisania programu, może też być podana
przez użytkownika w trakcie jego wykonywania
W pętli funkcjonuje pewna zmienna, zwana
licznikiem pętli
,
“pamiętająca” ile razy pętla została wykonania
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Postać
for licznik_pętli in początek..koniec loop
instrukcje
end loop;
--------------------------------
for licznik_pętli in reverse początek..koniec loop
instrukcje
end loop;
Przykłady
for i in 1..10 loop
|
for i in reverse 1..10 loop
put(i);
|
put(i);
end loop;
|
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Postać
for licznik_pętli in początek..koniec loop
instrukcje
end loop;
--------------------------------
for licznik_pętli in reverse początek..koniec loop
instrukcje
end loop;
Przykłady
for i in 1..10 loop
|
for i in reverse 1..10 loop
put(i);
|
put(i);
end loop;
|
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi
zmiennej będącej licznikiem pętli nie deklarujemy (zostanie
zadeklarowana automatycznie)
poza pętlą tej zmiennej już nie ma - nie można się do niej
odwołać
początek i koniec muszą być tego samego typu
dyskretnego. Mogą być dowolnymi literałami (wartościami
“konkretnymi”, zmiennymi, wyrażeniami do obliczenia)
pętla wykona się tylko wowczas, gdy początek będzie nie
większy niż koniec
uwaga - także przy pętlach idących “do tyłu” początek jest wartością mniejszą!
instrukcji wewnątrz pętli może być dowolnie dużo, mogą być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi
zmiennej będącej licznikiem pętli nie deklarujemy (zostanie
zadeklarowana automatycznie)
poza pętlą tej zmiennej już nie ma - nie można się do niej
odwołać
początek i koniec muszą być tego samego typu
dyskretnego. Mogą być dowolnymi literałami (wartościami
“konkretnymi”, zmiennymi, wyrażeniami do obliczenia)
pętla wykona się tylko wowczas, gdy początek będzie nie
większy niż koniec
uwaga - także przy pętlach idących “do tyłu” początek jest wartością mniejszą!
instrukcji wewnątrz pętli może być dowolnie dużo, mogą być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi
zmiennej będącej licznikiem pętli nie deklarujemy (zostanie
zadeklarowana automatycznie)
poza pętlą tej zmiennej już nie ma - nie można się do niej
odwołać
początek i koniec muszą być tego samego typu
dyskretnego. Mogą być dowolnymi literałami (wartościami
“konkretnymi”, zmiennymi, wyrażeniami do obliczenia)
pętla wykona się tylko wowczas, gdy początek będzie nie
większy niż koniec
uwaga - także przy pętlach idących “do tyłu” początek jest wartością mniejszą!
instrukcji wewnątrz pętli może być dowolnie dużo, mogą być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi
zmiennej będącej licznikiem pętli nie deklarujemy (zostanie
zadeklarowana automatycznie)
poza pętlą tej zmiennej już nie ma - nie można się do niej
odwołać
początek i koniec muszą być tego samego typu
dyskretnego. Mogą być dowolnymi literałami (wartościami
“konkretnymi”, zmiennymi, wyrażeniami do obliczenia)
pętla wykona się tylko wowczas, gdy początek będzie nie
większy niż koniec
uwaga - także przy pętlach idących “do tyłu” początek jest wartością mniejszą!
instrukcji wewnątrz pętli może być dowolnie dużo, mogą być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi
zmiennej będącej licznikiem pętli nie deklarujemy (zostanie
zadeklarowana automatycznie)
poza pętlą tej zmiennej już nie ma - nie można się do niej
odwołać
początek i koniec muszą być tego samego typu
dyskretnego. Mogą być dowolnymi literałami (wartościami
“konkretnymi”, zmiennymi, wyrażeniami do obliczenia)
pętla wykona się tylko wowczas, gdy początek będzie nie
większy niż koniec
uwaga - także przy pętlach idących “do tyłu” początek jest wartością mniejszą!
instrukcji wewnątrz pętli może być dowolnie dużo, mogą być
nimi także kolejne instrukcje pętli
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi cd.
licznik pętli może być wykorzystany także inaczej: jeśli
chcemy na przykład, aby pewne czynności były wykonane
najpierw dla wartości 1, potem dla 2, itd, aż do 10 - to
zmienną “przebiegającą” te wartości może być licznik pętli
petla nie musi zaczynać działania z wartością licznika 1 -
dozwolone jest nadanie licznikowi dowolnej wartości
początkowej
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwagi cd.
licznik pętli może być wykorzystany także inaczej: jeśli
chcemy na przykład, aby pewne czynności były wykonane
najpierw dla wartości 1, potem dla 2, itd, aż do 10 - to
zmienną “przebiegającą” te wartości może być licznik pętli
petla nie musi zaczynać działania z wartością licznika 1 -
dozwolone jest nadanie licznikowi dowolnej wartości
początkowej
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Przykład (Wypisanie liczb całkowitych od 1 do 100)
with ada . t e x t i o , ada . i n t e g e r t e x t i o ;
use ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 0 5 f o r l o o p
i s
b e g i n
p u t l i n e ( ” W y p i s a n i e w a r t o s c i od 1 do 100 ” ) ;
f o r
i
i n 1 . . 1 0 0 l o o p
p u t ( i ) ;
end l o o p ;
end w 0 5 f o r l o o p ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Przykład (Zsumowanie dziesięciu wprowadzonych liczb)
with ada . t e x t i o , ada . i n t e g e r t e x t i o ;
use ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e w05 suma10 i s
a , suma :
i n t e g e r ;
b e g i n
p u t l i n e ( ” Program l i c z y sume 10 p o d a n y c h l i c z b ” ) ;
suma := 0 ;
f o r
i
i n 1 . . 1 0 l o o p
p u t ( ” l i c z b a ” ) ; p u t ( i , 0 ) ;
p u t ( ” : ” ) ;
g e t ( a ) ;
suma := suma + a ;
end l o o p ;
p u t ( ” suma p o d a n y c h l i c z b
w y n o s i ” ) ; p u t ( suma , 0 ) ;
end w05 suma10 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku
Pętle wykonujące się podaną liczbę razy (pętle for)
Uwaga “ogólna”
W niektórych językach programowania pętle tego rodzaju
pozwalają na zwiększanie licznika inaczej niż poprzez przyjmowanie
kolejnych wartości w danym typie; może być też dozwolone kilka
liczników.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for)
Pętle dodatki
Pętle nieskończone
W językach programowania możemy zazwyczaj napisać również
pętlę nieskończoną
loop
instrukcje
end loop;
-----------------------------
while true loop
instrukcje
end loop;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for)
Opuszczenie pętli
Z pętli możemy “wyskoczyć”:
bezwarunkowo - instrukcją
exit;
gdy zachodzi pewien warunek - instrukcją
exit when warunek;
W takim przypadku instrukcje między exit a end loop nie
wykonają się.
Powyższe instrukcje powodują opuszczenie pętli “najbliższej” danej
instrukcji (i tylko jednej, jeśli pętle są zagnieżdżone). Jeśli chcemy
opuścić kilka pętli - musimy użyć
pętli nazywanych
.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for)
Opuszczenie pętli
Z pętli możemy “wyskoczyć”:
bezwarunkowo - instrukcją
exit;
gdy zachodzi pewien warunek - instrukcją
exit when warunek;
W takim przypadku instrukcje między exit a end loop nie
wykonają się.
Powyższe instrukcje powodują opuszczenie pętli “najbliższej” danej
instrukcji (i tylko jednej, jeśli pętle są zagnieżdżone). Jeśli chcemy
opuścić kilka pętli - musimy użyć
pętli nazywanych
.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for)
Pętle nazywane
Postać:
nazwa_petli:
loop
instrukcje
exit nazwa_petli;
end loop nazwa_petli;
Nazywanie pętli nie ogranicza się tylko do pętli tej postaci.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Instrukcje pętli - wstęp Najprostsza pętla Pętle których wykonanie zależy od warunku Pętle wykonujące się podaną liczbę razy (pętle for)
Przykład
w i t h ada . t e x t i o ;
u s e ada . t e x t i o ;
p r o c e d u r e w 0 5 n a m e d l o o p
i s
b e g i n
aa :
l o o p
p u t l i n e ( ” w e j s c i e do
p e t l i
aa ” ) ;
bb :
f o r
i
i n
1 . . 2
l o o p
p u t l i n e ( ” w e j s c i e do
p e t l i
bb ” ) ;
p u t l i n e ( ”−−−nnnnnnnnnnnnnnnnn−−−” ) ;
e x i t
aa ;
end l o o p bb ;
p u t ( ” k o n i e c
p e t l i
z e w n e t r z n e j ” ) ;
end l o o p aa ;
p u t ( ” k o n i e c ” ) ;
end w 0 5 n a m e d l o o p ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Document Outline
- Instrukcje petli - wstep
- Najprostsza petla
- Petle których wykonanie zalezy od warunku
- Petle wykonujace sie podana liczbe razy (petle for)
- Petle - dodatki
Wyszukiwarka
Podobne podstrony:
1011z wdprog ww05
1213z wdprog ww04
1213z wdprog ww02
1213z wdprog ww07
1213z wdprog ww11
1213z wdprog ww09
1213z wdprog ww08
1213z wdprog ww12
1213z wdprog ww10
1213z wdprog ww13
1213z wdprog ww06
1213z wdprog ww14
1213z wdprog ww03
1213z wdprog ww01
1011z wdprog ww05
1213z wdprog ww02
więcej podobnych podstron