
Wstęp do programowania
wykład 11
Agata Półrola
Wydział Matematyki i Informatyki UŁ
sem. zimowy 2012/2013
Agata Półrola Wydział Matematyki i Informatyki UŁ
Uwagi - cd
funkcje a wyjątki
wartość zwracana przez funkcję powinna być poprawnym
wynikiem danej operacji, nadającym się do dalszego
przetwarzania przez program
→ przykład: funkcja o dwóch parametrach rzeczywistych a,b zwracająca wynik
dzielenia a/b nie powinna zwracać np. 0 jako “informacji” że dzielenia nie dało
się wykonać - zero może być też poprawnym wynikiem dzielenia, więc
“informacja” o niewykonalności jest fałszywa; z drugiej strony wykonanie
dalszych obliczeń na takim “wyniku” da niepoprawny wynik ostateczny
jeśli podanie takiego wyniku jest niemożliwe (wynik nie
istnieje), to funkcja powinna zgłaszać wyjątek
→ taki wyjątek może być potem obsłużony w kodzie zawierającym
wywołanie funkcji, np. w programie głównym
funkcja może zawierać obsługę wyjątków
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Funkcja z mylącym wynikiem)
Funkcja zwraca największą wartość z tablicy typu Tab, gdzie
type Tab is array (integer range <>) of natural;
f u n c t i o n MaxTab ( t : Tab )
r e t u r n
n a t u r a l
i s
max : i n t e g e r : = 0 ;
b e g i n
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )>max t h e n max:= t ( i ) ;
end
i f ;
end l o o p ;
r e t u r n max ;
end maxTab ;
Dla pustej tablicy wejściowej zwracana jest “myląca” wartość 0.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (cd - konsekwencje wykorzystania funkcji z poprz. slajdu)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 f u z l y w y n i k
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
n a t u r a l ;
f u n c t i o n MaxTab ( t : Tab )
r e t u r n
n a t u r a l
i s
max : i n t e g e r : = 0 ;
b e g i n
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )>max t h e n max:= t ( i ) ;
end
i f ;
end l o o p ;
r e t u r n max ;
end maxTab ;
i l e :
i n t e g e r ;
b e g i n
p u t l i n e ( ” p o d a j
i l o s c
k i e r o w c o w
b i o r a c y c h
u d z i a l w a n k i e c i e : ” ) ;
g e t ( i l e ) ;
d e c l a r e
x : Tab ( 1 . . i l e ) ;
m:
i n t e g e r ;
b e g i n
p u t ( ” P o d a j
t e r a z
i l e
k a z d a z n i c h
u z y s k a l a punktow k a r n y c h : ” ) ;
f o r
i
i n x ’ r a n g e l o o p
g e t ( x ( i ) ) ;
end l o o p ;
n e w l i n e ;
m:=maxTab (X ) ;
i f m=0 t h e n p u t ( ” g r a t u l a c j e − w y s o k i p o z i o m k i e r o w c o w ! ” ) ;
e l s i f m>50 t h e n p u t ( ” Chyba k o g o s
t r z e b a
p r z e s z k o l i c . . . ” ) ;
e l s e
p u t ( ” S r e d n i o
d o b r z e ” ) ;
end
i f ;
end ;
end w 1 0 f u z l y w y n i k ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
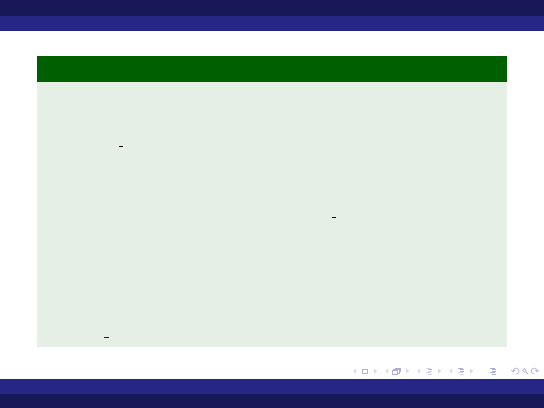
Przykład (Funkcja z wyjątkiem)
Funkcja zwraca największą wartość z tablicy typu Tab, gdzie
type Tab is array (integer range <>) of natural;
t a b l i c a p u s t a :
e x c e p t i o n ;
f u n c t i o n MaxTab ( t : Tab )
r e t u r n
n a t u r a l
i s
max : i n t e g e r : = 0 ;
b e g i n
i f
t ’ l e n g t h =0 t h e n
r a i s e
t a b l i c a p u s t a ; end
i f ;
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )>max t h e n max:= t ( i ) ;
end
i f ;
end l o o p ;
r e t u r n max ;
end maxTab ;
Dla pustej tablicy wejściowej zgłaszany jest wyjątek
tablica pusta
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (cd - wykorzystanie funkcji z poprz. slajdu)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 0 f u w y j
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
n a t u r a l ;
t a b l i c a p u s t a :
e x c e p t i o n ;
f u n c t i o n MaxTab ( t : Tab )
r e t u r n
n a t u r a l
i s
max : i n t e g e r : = 0 ;
b e g i n
i f
t ’ l e n g t h =0 t h e n
r a i s e
t a b l i c a p u s t a ; end
i f ;
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )>max t h e n max:= t ( i ) ;
end
i f ; end l o o p ;
r e t u r n max ;
end maxTab ;
i l e :
i n t e g e r ;
b e g i n
p u t l i n e ( ” p o d a j
i l o s c
k i e r o w c o w
b i o r a c y c h
u d z i a l w a n k i e c i e : ” ) ;
g e t ( i l e ) ;
d e c l a r e
x : Tab ( 1 . . i l e ) ; m:
i n t e g e r ;
b e g i n
p u t ( ” P o d a j
t e r a z
i l e
k a z d a z n i c h
u z y s k a l a punktow k a r n y c h : ” ) ;
f o r
i
i n x ’ r a n g e l o o p
g e t ( x ( i ) ) ;
end l o o p ;
n e w l i n e ;
m:=maxTab (X ) ;
i f m=0 t h e n p u t ( ” g r a t u l a c j e
− w y s o k i poziom k i e r o w c o w ! ” ) ;
e l s i f m>50 t h e n p u t ( ” Chyba k o g o s
t r z e b a
p r z e s z k o l i c . . . ” ) ;
e l s e
p u t ( ” S r e d n i o
d o b r z e ” ) ;
end
i f ;
e x c e p t i o n
when t a b l i c a p u s t a => p u t ( ” Z e r o a n k i e t o w a n y c h o s o b − b r a k o c e n y ” ) ;
end ;
end w 1 0 f u w y j ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
funkcji może być w programie wiele, jedna funkcja może
wywoływać drugą
funkcja może również wywoływać samą siebie - nazywamy ją
wtedy
funkcją rekurencyjną
Agata Półrola Wydział Matematyki i Informatyki UŁ
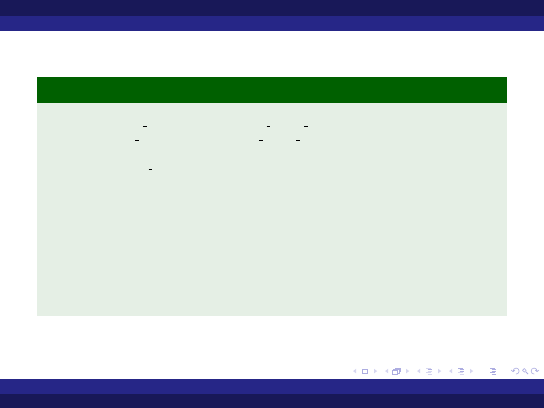
Przykład (Program z funkcją wywołującą inną funkcję)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 f u n i e z r o z 2 f
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
f u n c t i o n
I l e U j e m n y c h ( t : Tab )
r e t u r n
n a t u r a l
i s
i l e
:
n a t u r a l : = 0 ;
b e g i n
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )<0 t h e n
i l e := i l e +1; end
i f ; end l o o p ;
r e t u r n
i l e ;
end I l e U j e m n y c h ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Program z funkcją wywołującą inną funkcję - cd)
f u n c t i o n
T a b l i c a U j e m n y c h ( t : Tab )
r e t u r n Tab i s
t a b w y n i k o w a : Tab ( 1 . . I l e U j e m n y c h ( t ) ) ;
k : i n t e g e r ;
b e g i n
k : = 1 ;
f o r
i
i n t ’ r a n g e l o o p
i f
t ( i )<0 t h e n
t a b w y n i k o w a ( k ) : = t ( i ) ; k := k +1; end
i f ;
end l o o p ;
r e t u r n
t a b w y n i k o w a ;
end T a b l i c a U j e m n y c h ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Program z funkcją wywołującą inną funkcję - cd)
x : Tab ( 1 . . 1 0 ) ;
b e g i n
p u t l i n e ( ” p o d a j
e l e m e n t y
t a b l i c y
: ” ) ;
f o r
i
i n x ’ r a n g e l o o p
g e t ( x ( i ) ) ;
end l o o p ;
p u t l i n e ( ” T a b l i c a : ” ) ;
f o r
i
i n x ’ r a n g e l o o p
p u t ( x ( i ) , 2 ) ; end l o o p ;
n e w l i n e ;
d e c l a r e
y : Tab:= T a b l i c a U j e m n y c h ( x ) ;
b e g i n
p u t l i n e ( ” T a b l i c a
w a r t o s c i
u j e m n y c h : ” ) ;
f o r
i
i n y ’ r a n g e l o o p
p u t ( y ( i ) , 2 ) ; end l o o p ;
end ;
end w 1 0 f u n i e z r o z 2 f ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
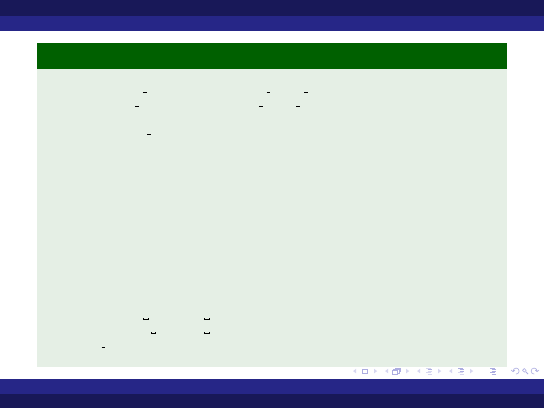
Przykład (Funkcja rekurencyjna)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 f u r e k
i s
f u n c t i o n
s i l n i a ( n :
n a t u r a l )
r e t u r n
n a t u r a l
i s
b e g i n
i f
n=0 t h e n
r e t u r n
1 ;
e l s e
r e t u r n n ∗ s i l n i a ( n − 1 ) ;
end
i f ;
end
s i l n i a ;
i :
i n t e g e r ;
b e g i n
p u t ( ” p o d a j
l i c z b e : ” ) ; g e t ( i ) ;
p u t ( ” S i l n i a
w y n o s i ” ) ;
p u t ( s i l n i a ( i ) ) ;
end w 1 0 f u r e k ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

O rekurencji
rekurencja polega na tym, że funkcja (ew. procedura)
wywołuje sama siebie, chociaż być może dla innych danych
aby nie powodowalo to nieskończonego ciągu wywołań,
funkcja/procedura musi dla pewnych danych zachować się
“nierekurencyjnie”, tzn. wykonać czynność inną niż wywołanie
siebie (np. zwrócić wynik będący konkretną liczbą)
Agata Półrola Wydział Matematyki i Informatyki UŁ

O rekurencji
rekurencja polega na tym, że funkcja (ew. procedura)
wywołuje sama siebie, chociaż być może dla innych danych
aby nie powodowalo to nieskończonego ciągu wywołań,
funkcja/procedura musi dla pewnych danych zachować się
“nierekurencyjnie”, tzn. wykonać czynność inną niż wywołanie
siebie (np. zwrócić wynik będący konkretną liczbą)
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
nazwa funkcji (zazwyczaj) jest identyfikatorem
czyli może być ciągiem znaków złożonym z liter, cyfr i znakow podkreślenia i
zaczynającym się od litery
wyjątkiem od tej reguły są
operatory
Agata Półrola Wydział Matematyki i Informatyki UŁ

Operatory
Operatory to specjalne funkcje.
Nazwy tych funkcji mogą być pewnymi ciągami znaków nie
będącymi identyfikatorami - pod warunkiem, że dany ciąg jest
ujęty w apostrofy
dopuszczalne nazwy operatorów to abs, and, mod, not,
or, rem, xor, =, /=, <, <=, >, >=, +, -, *, /,
**, &
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Nowy operator)
w i t h ada . t e x t i o , ada . f l o a t t e x t i o , ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o , ada . f l o a t t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 o p e r a t o r 1
i s
−− z d e f i n i o w a n i e
o p e r a t o r a
k t o r e g o
n i e
b y l o
f u n c t i o n ”+” ( a : i n t e g e r ; b : f l o a t )
r e t u r n
f l o a t
i s
b e g i n
r e t u r n
f l o a t ( a)+b ;
end ”+” ;
l 1 : i n t e g e r ;
l 2 ,
l 3 : f l o a t ;
b e g i n
p u t ( ” l 1 > ” ) ;
g e t ( l 1 ) ;
p u t ( ” l 2 > ” ) ;
g e t ( l 2 ) ;
l 3 := l 1+l 2 ;
−− l 3 :=”+”( l 1 , l 2 ) ;
−− i n n y
z a p i s
p u t ( ” l 1 + l 2 = ” ) ;
p u t ( l 3 , e x p =>0);
−−
l 3 := l 2+l 1 ;
−− n i e k o m p i l o w a l n e
−−
p u t ( ” l 1 + l 2 = ” ) ;
p u t ( l 3 , e x p =>0);
end w 1 0 o p e r a t o r 1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Przedefiniowanie istniejącego operatora)
w i t h ada . t e x t i o , ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 o p e r a t o r 2
i s
−− p r z e d e f i n i o w a n i e
i s t n i e j a c e g o
o p e r a t o r a
f u n c t i o n ”+” ( a : i n t e g e r ; b : i n t e g e r )
r e t u r n
i n t e g e r
i s
b e g i n
r e t u r n
2 ∗ ( s t a n d a r d .”+ ” ( a , b ) ) ;
−− uwaga − n i e mozna n a p i s a c po p r o s t u ”+”
−− ( c z y l i
r e t u r n
2 ∗ ( a+b ) ;
end ”+” ;
l 1 ,
l 2 ,
l 3 : i n t e g e r ;
b e g i n
p u t ( ” l 1 > ” ) ;
g e t ( l 1 ) ;
p u t ( ” l 2 > ” ) ;
g e t ( l 2 ) ;
l 3 := l 1+l 2 ;
p u t ( ” l 1 + l 2 = ” ) ;
p u t ( l 3 , 0 ) ;
end w 1 0 o p e r a t o r 2 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Przedefiniowanie istniejącego operatora - 2)
w i t h ada . t e x t i o , ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o , ada . i n t e g e r t e x t i o ;
p r o c e d u r e
w 1 0 o p e r a t o r 3
i s
t y p e Tab i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
f u n c t i o n
s u m a e l e m e n t o w ( t : Tab )
r e t u r n
i n t e g e r
i s
s :
i n t e g e r : = 0 ;
b e g i n
f o r
i
i n t ’ r a n g e l o o p
s := s+t ( i ) ;
end l o o p ;
r e t u r n
s ;
end s u m a e l e m e n t o w ;
f u n c t i o n ”<” ( t 1 , t 2 : Tab )
r e t u r n
b o o l e a n
i s
b e g i n
r e t u r n
s u m a e l e m e n t o w ( t 1 )<s u m a e l e m e n t o w ( t 2 ) ;
end ”<” ;
a , b : t a b ( 1 . . 3 ) ;
b e g i n
p u t ( ” p o d a j
p i e r w s z a
t a b l i c e : ” ) ;
f o r
j
i n a ’ r a n g e l o o p
g e t ( a ( j ) ) ;
end l o o p ;
p u t ( ” p o d a j d r u g a
t a b l i c e : ” ) ;
f o r
j
i n b ’ r a n g e l o o p
g e t ( b ( j ) ) ;
end l o o p ;
i f
a<b t h e n p u t ( ” p i e r w s z a
t a b l i c a
m n i e j s z a ” ) ;
e l s e
p u t ( ” d r u g a
t a b l i c a
m n i e j s z a ” ) ;
end
i f ;
end w 1 0 o p e r a t o r 3 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Zadania (funkcje, typ napisowy)
1
Napisać i przetestować funkcję zamieniającą w napisie
wszystkie duże litery na spacje
2
napisać i przetestować funkcję tworzącą łańcuch powstały z
łaćucha wejściowego przez usunięcie wszystkich dużych liter
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Rozwiązanie zadań - cz.1)
w i t h ada . t e x t i o ;
u s e ada . t e x t i o ;
p r o c e d u r e p r o g 1
i s
f u n c t i o n
z a m i e n ( x : s t r i n g )
r e t u r n
s t r i n g
i s
y : s t r i n g := x ;
b e g i n
f o r
i
i n y ’ r a n g e l o o p
i f
y ( i )
i n
’A ’ . . ’ Z ’
t h e n y ( i ) : = ’
’ ; end
i f ; end l o o p ;
r e t u r n y ;
end z a m i e n ;
f u n c t i o n
u s u n ( x : s t r i n g )
r e t u r n
s t r i n g
i s
i l e D u z y c h : i n t e g e r : = 0 ;
b e g i n
f o r
i
i n x ’ r a n g e l o o p
i f
x ( i )
i n
’A ’ . . ’ Z ’
t h e n i l e D u z y c h := i l e D u z y c h +1; end
i f ; end l o o p ;
d e c l a r e
y : s t r i n g ( 1 . . x ’ l e n g t h −i l e D u z y c h ) ;
g :
i n t e g e r ;
b e g i n
g : = 1 ;
f o r
i
i n x ’ r a n g e l o o p
i f
x ( i ) n o t
i n
’A ’ . . ’ Z ’
t h e n y ( g ) : = x ( i ) ;
g := g +1; end
i f ;
end l o o p ;
r e t u r n y ;
end ;
end u s u n ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Rozwiązanie zadań - cd)
nap , nap1 :
s t r i n g ( 1 . . 3 0 ) ;
n : i n t e g e r ;
b e g i n
nap : = ( o t h e r s=> ’
’ ) ;
p u t ( ” p o d a j
n a p i s ” ) ;
g e t l i n e ( nap , n ) ;
p u t ( ” n a p i s
: ” ) ;
p u t l i n e ( nap ) ;
nap1 := z a m i e n ( nap ) ;
p u t ( ” d u z e na s p a c j e
: ” ) ; p u t l i n e ( nap1 ) ;
p u t ( ” b e z d u z y c h
: ” ) ;
p u t ( u s u n ( nap ) ) ;
end p r o g 1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Rozwiązanie zadań - cd)
nap , nap1 :
s t r i n g ( 1 . . 3 0 ) ;
n : i n t e g e r ;
b e g i n
nap : = ( o t h e r s=> ’
’ ) ;
p u t ( ” p o d a j
n a p i s ” ) ;
g e t l i n e ( nap , n ) ;
p u t ( ” n a p i s
: ” ) ;
p u t l i n e ( nap ) ;
nap1 := z a m i e n ( nap ) ;
p u t ( ” d u z e na s p a c j e
: ” ) ; p u t l i n e ( nap1 ) ;
p u t ( ” b e z d u z y c h
: ” ) ;
p u t ( u s u n ( nap ) ) ;
end p r o g 1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podprogramy - cd
Podprogramy w Adzie (przypomnienie)
Podprogramy
to sparametryzowane, wydzielone fragmenty
programów
podprogramy w Adzie to
funkcje
i
procedury
funkcje wywoływane są jako elementy wyrażeń i zwracają
wartość stanowiącą element wyrażenia
przykład:
x:=
sqrt(10.0)
+ 2.12;
procedury wywoływane są jako samodzielne instrukcje
przykład:
put(12.4);
Agata Półrola Wydział Matematyki i Informatyki UŁ

Po co podprogramy (przypomnienie)
bardziej czytelny kod
jednokrotne pisanie powtarzających się fragmentów programu
podprogram umieszczony w pakiecie może być użyty w wielu
programach
Agata Półrola Wydział Matematyki i Informatyki UŁ

Procedury
Struktura procedury
Ciało procedury
ma postać:
procedure nazwa_procedury (lista_parametrów) is
-- część deklaracyjna
begin
-- część wykonywalna
end nazwa_procedury;
Przykład
p r o c e d u r e WypiszDane ( im , nazw :
i n
s t r i n g )
i s
b e g i n
p u t ( ” I m i e : ” ) ;
s e t c o l ( 1 5 ) ;
p u t l i n e ( im ) ;
p u t ( ” N a z w i s k o : ” ) ;
s e t c o l ( 1 5 ) ;
p u t l i n e ( nazw ) ;
end WypiszDane ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Uwagi
ciała procedur umieszczamy w części deklaracyjnej programu (lub w
osobnym pakiecie)
procedury wywoływane są jako osobne instrukcje
przykład:
WypiszDane("Jan","Nowak");
parametry procedury wymienione w nawiasie na początku jej
ciała nazywamy
parametrami (argumentami) formalnymi
wartości dla parametrów formalnych podane w wywołaniu
procedury nazywamy
parametrami aktualnymi (argumentami
wywołania)
procedura może być także bezparametrowa
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Procedura 1)
w i t h ada . t e x t i o ;
u s e ada . t e x t i o ;
p r o c e d u r e w 1 3 p r o c 1
i s
p r o c e d u r e Wizytowka
i s
b e g i n
n e w l i n e ( 2 ) ;
s e t c o l ( 6 0 ) ;
p u t l i n e ( ” A u t o r : XXX” ) ;
end Wizytowka ;
p r o c e d u r e
S z l a c z e k ( z :
i n
c h a r a c t e r ; n :
i n
i n t e g e r )
i s
b e g i n
f o r
i
i n
1 . . n l o o p
p u t ( z ) ;
end l o o p ;
n e w l i n e ;
end S z l a c z e k ;
b e g i n
S z l a c z e k ( ’ ∗ ’ ,
8 0 ) ;
S z l a c z e k ( ’ 8 ’ ,
2 0 ) ;
Wizytowka ;
end w 1 3 p r o c 1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Procedura 2)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 1 3 p r o c 2
i s
p r o c e d u r e WypiszDane ( im , nazw :
i n
s t r i n g )
i s
d l , i l e :
i n t e g e r ;
b e g i n
i f
nazw ’ l e n g t h >im ’ l e n g t h
t h e n
d l := nazw ’ l e n g t h ;
e l s e
d l := im ’ l e n g t h ; end
i f ;
i l e :=17+ d l ;
f o r
i
i n
1 . . i l e /2+1 l o o p p u t ( ” ∗∗ ” ) ;
end l o o p ;
n e w l i n e ;
Put ( ” ∗ ” ) ;
p u t ( ” I m i e : ” ) ;
s e t c o l ( 1 5 ) ;
p u t ( im ) ;
s e t c o l ( c o u n t ( i l e /2+1)∗2 −1); p u t ( ” ∗ ” ) ;
n e w l i n e ;
p u t ( ” ∗ ” ) ;
p u t ( ” N a z w i s k o : ” ) ;
s e t c o l ( 1 5 ) ;
p u t ( nazw ) ;
s e t c o l ( c o u n t ( i l e /2+1)∗2 −1); p u t ( ” ∗ ” ) ;
n e w l i n e ;
f o r
i
i n
1 . . i l e /2+1 l o o p p u t ( ” ∗∗ ” ) ;
end l o o p ;
end WypiszDane ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Procedura 2 - cd)
n :
i n t e g e r ;
d l i m ,
d l n a z w :
i n t e g e r ;
b e g i n
p u t ( ” p o d a j maksymalna d l u g o s c
i m i e n i a
i
n a z w i s k a ” &
” ( d w i e
l i c z b y ) : ” ) ;
g e t ( d l i m ) ;
g e t ( d l n a z w ) ;
s k i p l i n e ;
d e c l a r e
i m i e :
s t r i n g ( 1 . . d l i m ) : = ( o t h e r s=> ’
’ ) ;
n a z w i s k o :
s t r i n g ( 1 . . d l n a z w ) : = ( o t h e r s=> ’
’ ) ;
b e g i n
p u t ( ” P o d a j
i m i e : ” ) ;
g e t l i n e ( i m i e , n ) ;
i f
n=i m i e ’ l e n g t h
t h e n
s k i p l i n e ; end
i f ;
p u t ( ” P o d a j n a z w i s k o : ” ) ;
g e t l i n e ( n a z w i s k o , n ) ;
i f
n=n a z w i s k o ’ l e n g t h
t h e n
s k i p l i n e ; end
i f ;
n e w l i n e ( 5 ) ;
WypiszDane ( i m i e ,
n a z w i s k o ) ;
end ;
end w 1 3 p r o c 2 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
główne różnice między funkcjami i procedurami
nazwa procedury musi być identyfikatorem
nie ma od tego żadnych wyjątków (w przypadku funkcji wyjątkiem były nazwy
operatorów)
procedura nie zwraca wartości
funkcja zwracała dokładnie jedną wartość.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
parametry procedur
procedura może mieć wiele parametrów, które mogą być
różnych typów
parametry mogą mieć różne
tryby
(ang. modes):
in
,
out
albo
in out
elementy listy parametrów jednego typu i tybu oddzielamy przecinkami,
deklaracje parametrów różnych typów lub o różnym trybie - średnikami
przykład:
procedure Proc1 (a:
in integer; x,y:
in out float; z:
out float)
is ...
Agata Półrola Wydział Matematyki i Informatyki UŁ
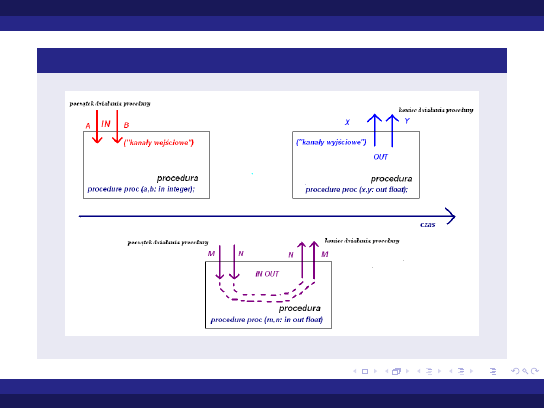
Tryby parametrów
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
tryby parametrów
tryby parametrów dotyczą procedur i funkcji, przy czym
jedynym dopuszczalnym trybem parametrow funkcji jest tryb
in
tryb parametrów określa się przy ich specyfikacji, wpisując
nazwę trybu pomiędzy dwukropkiem a nazwą typu
przykład:
procedure P1 (a:
in integer; x,y:
in out float; z:
out float) is
...
jeżeli tryb parametrów nie jest podany, to domyślnie przyjmuje
się że jest to in
przykład:
function F1 (a:
in integer; b:
in float) return integer is ...
function F1 (a:
integer; b:
float) return integer is ...
Agata Półrola Wydział Matematyki i Informatyki UŁ

Uwagi - cd
tryby parametrów - cd
tryb in
(
parametry wejściowe
):
parametr formalny jest stałą inicjalizowaną wartością
odpowiadającego mu parametru aktualnego
dla parametrów w tym trybie niedozwolone są instrukcje mogące zmienić
ich wartość; dozwolone jest tylko czytanie tej wartości
tryb in out
(
parametry wejściowo-wyjściowe
):
parametr formalny jest zmienną inicjalizowaną wartością
odpowiadającego mu parametru aktualnego; dozwolone jest
odczytywanie i aktualizowanie wartości parametru aktualnego
tryb out
(
parametry wyjściowe
):
parametr formalny jest niezainicjalizowaną zmienną;
dozwolone jest aktualizowanie wartości odpowiadającego
parametru aktualnego
Agata Półrola Wydział Matematyki i Informatyki UŁ
Document Outline
Wyszukiwarka
Podobne podstrony:
1213z wdprog ww04
1213z wdprog ww02
1213z wdprog ww07
1213z wdprog ww09
1213z wdprog ww08
1213z wdprog ww12
1213z wdprog ww10
1213z wdprog ww13
1213z wdprog ww06
1213z wdprog ww14
1213z wdprog ww05
1213z wdprog ww03
1213z wdprog ww01
1213z wdprog ww02
więcej podobnych podstron