Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Wstęp do programowania

wykład 8

Agata Półrola

Wydział Matematyki i Informatyki UŁ

sem. zimowy 2011/2012

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Wektory boolowskie

Szczególnym przypadkiem tablic jednowymiarowych są

wektory

boolowskie

(jednowymiarowe tablice złożone z elementów typu

logicznego)
Poza standardowymi operacjami na tablicach jednowymiarowych
można na nich wykonywać

operacje logiczne

, używając operatorów

not, and, or i xor

w przypadku operatorów dwuargumentowych
wektory-argumenty muszą być tej samej długości

wynikiem jest agregat tablicy powstały poprzez wykonanie
danej operacji logicznej na poszczególnych elementach
wektora/wektorów

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Wektory boolowskie)

w i t h ada . t e x t i o , ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o , ada . i n t e g e r t e x t i o ;

p r o c e d u r e

w 0 8 w e k t o r l o g

i s

p a c k a g e

b i o

i s new ada . t e x t i o . e n u m e r a t i o n i o ( b o o l e a n ) ;

u s e

b i o ;

t y p e

w e k t o r l o g i c z n y

i s

a r r a y ( 1 . . 4 )

o f

b o o l e a n ;

p , q , w and , w o r , w x o r , w n o t : w e k t o r l o g i c z n y ;
k : p o s i t i v e c o u n t ;

b e g i n

p : = ( o t h e r s=>t r u e ) ;

p u t l i n e ( ” P o d a j w e k t o r q − m o z l i w e

w a r t o s c i

j e g o

s k l a d o w y c h t o TRUE i FALSE” ) ;

f o r

i

i n q ’ r a n g e l o o p

p u t ( ” q ( ” ) ; p u t ( i , 0 ) ; p u t ( ”)= ” ) ;

g e t ( q ( i ) ) ;

end l o o p ;

w and := p and q ;

w o r := p o r q ;

w x o r := p x o r q ;

w n o t := n o t q ;

p u t l i n e ( ”A o t o

w y n i k i

d z i a l a n na w e k t o r a c h : ” ) ;

p u t ( ” w e k t o r ” ” p ” ” : ” ) ;

k : = 1 3 ;

f o r

i

i n p ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( p ( i ) ) ;

end l o o p ;

n e w l i n e ;

p u t ( ” w e k t o r ” ” q ” ” : ” ) ; k : = 1 3 ;

f o r

i

i n q ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( q ( i ) ) ; end l o o p ;

n e w l i n e ;

p u t ( ” w e k t o r ” ” n o t q ” ” : ” ) ; k : = 1 3 ;

f o r

i

i n q ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( w n o t ( i ) ) ; end l o o p ;

n e w l i n e ;

p u t ( ” w e k t o r ” ” p and q ” ” : ” ) ; k : = 1 3 ;

f o r

i

i n w and ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( w and ( i ) ) ; end l o o p ;

n e w l i n e ;

p u t ( ” w e k t o r ” ” p o r q ” ” : ” ) ; k : = 1 3 ;

f o r

i

i n w o r ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( w o r ( i ) ) ; end l o o p ;

n e w l i n e ;

p u t ( ” w e k t o r ” ” p x o r q ” ” : ” ) ; k : = 1 3 ;

f o r

i

i n

w x o r ’ r a n g e l o o p k := k +7;

s e t c o l ( k ) ;

p u t ( w x o r ( i ) ) ; end l o o p ;

end w 0 8 w e k t o r l o g ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Jednowymiarowe tablice dynamiczne

Rozmiar standardowo zadeklarowanej tablicy określamy w czasie
pisania programu - czyli jest on znany w momencie kompilacji

Tablice dynamiczne

to takie tablice, których rozmiar jest znany

dopiero w czasie uruchomienia programu (i przy każdym
uruchomieniu ten rozmiar może być inny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Jednowymiarowe tablice dynamiczne

Rozmiar standardowo zadeklarowanej tablicy określamy w czasie
pisania programu - czyli jest on znany w momencie kompilacji

Tablice dynamiczne

to takie tablice, których rozmiar jest znany

dopiero w czasie uruchomienia programu (i przy każdym
uruchomieniu ten rozmiar może być inny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tworzenie tablic dynamicznych

Można zdefiniować zarówno anonimową tablicę dynamiczną,
jak i odpowiedni nowy typ tablicowy

W obu przypadkach używamy do tego celu bloku z częścią
declare

uwagi:

zadeklarowana tablica i ew. zdefiniowany typ są widoczne
tylko wewnątrz danego bloku
rozmiar tablicy musi być podany przed jej zadeklarowaniem

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tworzenie tablic dynamicznych

Można zdefiniować zarówno anonimową tablicę dynamiczną,
jak i odpowiedni nowy typ tablicowy

W obu przypadkach używamy do tego celu bloku z częścią
declare

uwagi:

zadeklarowana tablica i ew. zdefiniowany typ są widoczne
tylko wewnątrz danego bloku
rozmiar tablicy musi być podany przed jej zadeklarowaniem

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Tworzenie tablicy dynamicznej)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 0 8 t a b d y n

i s

i l o s c :

p o s i t i v e ;

b e g i n

p u t ( ” i l e

l i c z b

b e d z i e s z

c h c i a l

z a p a m i e t a c ? ” ) ;

g e t ( i l o s c ) ;

d e c l a r e

t y p e t a b

i s

a r r a y

( i n t e g e r

r a n g e

1 . . i l o s c ) o f

i n t e g e r ;

t :

t a b ;

b e g i n

p u t l i n e ( ” p o d a j

t e r a z

t e

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( ” l i c z b a ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

g e t ( t ( i ) ) ;

end l o o p ;

n e w l i n e ( 2 ) ;
p u t l i n e ( ” Twoje

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( t ( i ) ) ;

end l o o p ;

end ;

end w 0 8 t a b d y n ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tablice jednowymiarowe - zadania

Zadanie 1

Napisać program pobierający od użytkownika tablicę liczb
całkowitych o podanej przez niego długości, a następnie wypisujący
informację czy tablica zawiera dwa sąsiadujące z sobą elementy
dodatnie.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd,

czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”

odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

długość tablicy ma być podana przez użytkownika - czyli
będzie konieczny

blok declare

algorytm sprawdzania czy w tablicy są obok siebie dwie liczby
dodatnie:

sprawdzamy pary sąsiednich elementów - pierwszy i drugi, drugi i trzeci
itd, czyli

i-ty i i+1-szy

- czyli aby nie wyjść poza tablicę musimy użyć

pętli przebiegającej indeksy

tablica’first..tablica’last-1

jeśli obie liczby w sprawdzanej parze są dodatnie, to znaczy że tablica
zawiera to czego szukamy - możemy przerwać szukanie i udzielić
odpowiedzi “tak, w tablicy sąsiadują z sobą dwie liczby dodatnie”
odpowiedzi “w tablicy nie ma obok siebie dwóch liczb dodatnich”
możemy udzielić dopiero po sprawdzeniu całej tablicy, jeśli nie
znaleźliśmy w niej odpowiedniej pary

czyli jest to “algorytm z poglądem”. Pogląd na to czy były liczby na

początku musi być “nie było pary” (false) [bo taki pogląd ma nam

pozostać jeśli nic się nie wydarzy, tzn. przeglądając tablicę nie zobaczymy

pary liczb dodatnich], znalezienie odpowiedniej pary zmienia go na “była

para” (true).

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Rozwiązanie zad.1)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 0 8 z a d 1 a

i s

i l o s c :

p o s i t i v e ;

c z y j e s t :

b o o l e a n ;

b e g i n

p u t ( ” i l e

l i c z b

b e d z i e s z

c h c i a l

z a p a m i e t a c ? ” ) ;

g e t ( i l o s c ) ;

d e c l a r e

t y p e t a b

i s

a r r a y

( i n t e g e r

r a n g e

1 . . i l o s c ) o f

i n t e g e r ;

t :

t a b ;

b e g i n

p u t l i n e ( ” p o d a j

t e r a z

t e

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( ” l i c z b a ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

g e t ( t ( i ) ) ;

end l o o p ;

c z y j e s t := f a l s e ;
p u t l i n e ( ” p r z e g l a d a n e

p a r y

s a s i e d n i c h

e l e m e n t o w : ” ) ;

f o r

i

i n t ’ f i r s t . . t ’ l a s t −1 l o o p

p u t ( t ( i ) ) ;

p u t ( t ( i + 1 ) ) ;

n e w l i n e ;

i f

t ( i )>0 and t ( i +1)>0 t h e n

c z y j e s t := t r u e ;
e x i t ;

end

i f ;

end l o o p ;

i f

c z y j e s t =t r u e

t h e n p u t ( ” b y l a

o d p o w i e d n i a

p a r a ” ) ;

e l s e

p u t ( ” n i e

b y l o dwoch d o d o a t n i c h obok

s i e b i e ” ) ;

end

i f ;

end ;

end w 0 8 z a d 1 a ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Zadanie 2

Napisać program pobierający od użytkownika tablicę liczb
całkowitych o podanej przez niego długości, a następnie wypisujący
wszystkie pary uporządkowane jakie można utworzyć z elementów
tej tablicy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze

tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary uporządkowane (czyli para
(A,B) i (B,A) to dwie różne pary - kolejność elementów jest
istotna)

np. dla tablicy z liczbami 1,2,3 będą to pary:
(1,1), (1,2), (1,3)

(2,1), (2,2), (2,3)

(3,1), (3,2), (3,3)

a tablicy z liczbami 1,2,2 będą to pary:
(1,1), (1,2), (1,2)

(2,1), (2,2), (2,2)

(2,1), (2,2), (2,2)

- również pary “element sam z sobą” są dopuszczalne (nie jest powiedziane że

mają to być pary elementów tablicy stojących na różnych pozycjach)

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą w
parze
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy

... podobnie jak w zad.1 z wykładu 6 (pary szef - podwładny)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Rozwiązanie zad.2)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 0 8 z a d 2

i s

i l o s c :

p o s i t i v e ;

b e g i n

p u t ( ” i l e

l i c z b

b e d z i e s z

c h c i a l

z a p a m i e t a c ? ” ) ;

g e t ( i l o s c ) ;

d e c l a r e

t y p e t a b

i s

a r r a y

( i n t e g e r

r a n g e

1 . . i l o s c ) o f

i n t e g e r ;

t :

t a b ;

b e g i n

p u t l i n e ( ” p o d a j

t e r a z

t e

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( ” l i c z b a ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

g e t ( t ( i ) ) ;

end l o o p ;

p u t l i n e ( ” p a r y ” ) ;
f o r

i n d e k s p i e r w s z e g o

i n t ’ r a n g e l o o p

f o r

i n d e k s d r u g i e g o

i n t ’ r a n g e l o o p

p u t ( t ( i n d e k s p i e r w s z e g o ) ) ;

p u t ( t ( i n d e k s d r u g i e g o ) ) ; n e w l i n e ;

end l o o p ;

end l o o p ;

end ;

end w 0 8 z a d 2 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Zadanie 3

Napisać program pobierający od użytkownika tablicę liczb
całkowitych o podanej przez niego długości, a następnie wypisujący
wszystkie dwójki (pary nieuporządkowane) różnych wartości
występujących w tej tablicy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary

tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

Mamy wypisać wszystkie pary nieporządkowane (czyli (A,B)
i (B,A) to to samo - kolejność elementów nie jest istotna)

mają to być pary różnych wartości (a więc pary złożone z
dwóch takich samych liczb nie są dozwolone)

np. dla tablicy z liczbami 1,2,3 będą to pary: 1 i 2,

1 i 3,

2 i 3 a dla

tablicy z liczbami 1,2,2 będzie to pary: 1 i 2,

1 i 2

w takim razie aby utworzyć wszystkie takie pary:

wybieramy element tablicy który ma być pierwszą liczbą pary
tworzymy wszystkie możliwe pary postaci: (wybrana wcześniej
pierwsza liczba w parze, druga liczba w parze) - gdzie drugą
liczbą w parze może być każdy element tablicy nie występujący
dotąd w roli pierwszego elementu pary

... podobnie jak w zad.1 z wykładu 6 (pary “równorzędne”)

z powyższych par wypisujemy tylko te, które są złożone z
różnych liczb.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Rozwiązanie zad.3)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 0 8 z a d 3

i s

i l o s c :

p o s i t i v e ;

b e g i n

p u t ( ” i l e

l i c z b

b e d z i e s z

c h c i a l

z a p a m i e t a c ? ” ) ;

g e t ( i l o s c ) ;

d e c l a r e

t y p e t a b

i s

a r r a y

( i n t e g e r

r a n g e

1 . . i l o s c ) o f

i n t e g e r ;

t :

t a b ;

b e g i n

p u t l i n e ( ” p o d a j

t e r a z

t e

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( ” l i c z b a ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

g e t ( t ( i ) ) ;

end l o o p ;

p u t l i n e ( ” p a r y ” ) ;
f o r

i n d e k s p i e r w s z e g o

i n t ’ r a n g e l o o p

f o r

i n d e k s d r u g i e g o

i n

i n d e k s p i e r w s z e g o + 1 . . t ’ l a s t

l o o p

i f

t ( i n d e k s p i e r w s z e g o )/= t ( i n d e k s d r u g i e g o ) t h e n
p u t ( t ( i n d e k s p i e r w s z e g o ) ) ;

p u t ( t ( i n d e k s d r u g i e g o ) ) ; n e w l i n e ;

end

i f ;

end l o o p ;

end l o o p ;

end ;

end w 0 8 z a d 3 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Zadanie 4

Napisać program pobierający od użytkownika tablicę liczb
całkowitych o podanym przez niego zakresie indeksu, a następnie
wypisujący wszystkie wartości występujące w tablicy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy

sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)

jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy

... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Elementy schematu postępowania

inaczej niż dotąd - pobieramy początkowy i końcowy indeks
tablicy zamiast jej długości

mamy wypisać wszystkie wartości występujące w tablicy -
czyli jeśli liczba występuje w tablicy w kilku miejscach, to jest
wypisywana raz

wyszukiwanie takich liczb:

bierzemy element tablicy
sprawdzamy, czy ta liczba znajduje się we wcześniejszej części
tablicy

jeśli była - nie wypisujemy (bo już była wypisana)
jeśli jej nie było - wypisujemy ją

i tak po kolei dla wszystkich elementów tablicy
... przy czym sprawdzanie czy liczba była we wcześniejszej
części tablicy to kolejny przykład algorytmu “z poglądem”

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Rozwiązanie zad.4)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 0 8 z a d 4

i s

i n d 1 ,

i n d 2 :

i n t e g e r ;

c z y b y l a :

b o o l e a n ;

b e g i n

p u t ( ” p o d a j

j a k i

i n d e k s ma m i e c

p i e r w s z y

e l e m e n t ” ) ;

g e t ( i n d 1 ) ;

p u t ( ” p o d a j

j a k i

i n d e k s ma m i e c

o s t a t n i

e l e m e n t ” ) ;

g e t ( i n d 2 ) ;

d e c l a r e

t y p e t a b

i s

a r r a y

( i n t e g e r

r a n g e i n d 1 . . i n d 2 ) o f

i n t e g e r ;

t :

t a b ;

b e g i n

p u t l i n e ( ” p o d a j

t e r a z

t e

l i c z b y : ” ) ;

f o r

i

i n t ’ r a n g e l o o p

p u t ( ” l i c z b a

na p o z y c j i ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

g e t ( t ( i ) ) ;

end l o o p ;

n e w l i n e ;

p u t l i n e ( ” Twoja

t a b l i c a : ” ) ;

f o r

i

i n t ’ r a n g e l o o p p u t ( t ( i ) , 0 ) ;

p u t ( ” ” ) ;

end l o o p ;

n e w l i n e ;

p u t l i n e ( ” W a r t o s c i

w y s t e p u j a c e w t a b l i c y : ” ) ;

f o r

p o z l i c z b y

i n t ’ r a n g e l o o p

−− s p r c z y b y l a

w c z e s n i e j

c z y b y l a := f a l s e ;
f o r

i

i n t ’ f i r s t . . p o z l i c z b y −1 l o o p

i f

t ( i )= t ( p o z l i c z b y ) t h e n
c z y b y l a := t r u e ;

e x i t ;

end

i f ;

end l o o p ;

i f

c z y b y l a= f a l s e

t h e n p u t ( t ( p o z l i c z b y ) , 0 ) ;

p u t ( ” ” ) ;

end

i f ;

end l o o p ;

end ;

end w 0 8 z a d 4 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tablice wielowymiarowe

Tablice wielowymiarowe, podobnie jak jednowymiarowe,
przechowują elementy tego samego typu
przykłady:

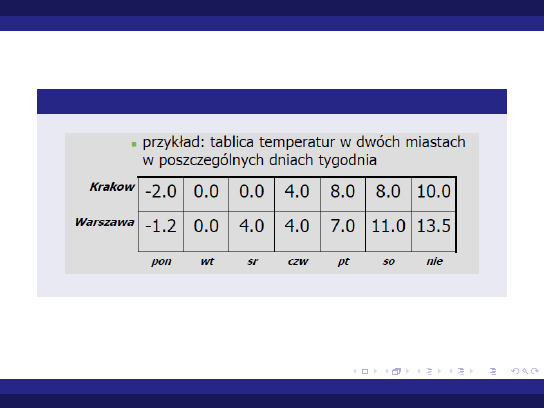
tablica temperatur w dwóch miastach w poszczególnych
dniach tygodnia

szachownica

plansza do gry w okręty

...

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład tablicy dwuwymiarowej

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Deklaracja tablic wielowymiarowych

Zmienne tablicowe możemy deklarować jako będące

anonimowego typu tablicowego

:

zmienna : array (określenie_indeksu_1, określenie_indeksu_2,

... określenie_indeksu_n) of typ_składowych ;

Przykłady

sudoku : array (1..9, 1..9) of integer;
-----------------------------------------------
dwa_na_trzy_na_cztery: array (integer range 1..2, integer range 1..3,

integer range 10..13) of float;

----------------------------------------------
type miasta is (Krakow, Warszawa, Lodz, Poznan);
type miesiace is (sty,lut, mar, kwie);
opady: array (miasta, miesiace range sty..mar) of integer;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Deklaracja tablic wielowymiarowych - cd

kolejna możliwość to zdefiniowanie

typu tablicowego

posiadającego własną

nazwę, a potem zadeklarowanie zmiennej tego typu:

type nazwa_typu is array (określenie_indeksu_1, określenie_indeksu_2,

... określenie_indeksu_n) of typ_składowych ;

zmienna_tablicowa: nazwa_typu;

Przykłady

type TypDlaSudoku is array (1..9, 1..9) of integer;
sudoku: TypDlaSudoku;
---------------------------------------------------
type Tablice_2_3_4 is array (integer range 1..2, integer range 1..3,

integer range 10..13) of float;

dwa_na_trzy_na_cztery: Tablice_2_3_4;
--------------------------------------------------
type miasta is (Krakow, Warszawa, Lodz, Poznan);
type miesiace is (sty,lut, mar, kwie);
type TablicaOpadow is array (miasta, miesiace range sty..mar)

of integer;

opady: TablicaOpadow;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Indeksy tablic wielowymiarowych - uwagi

każde określenie indeksu może być postaci takiej jak w
przypadku tablic jednowymiarowych

każdy indeks musi być typu dyskretnego

każdy z indeksów tablicy wielowymiarowej może być innego
typu (por. tablicę opady z przykładów)

jeśli typ któregoś indeksu nie jest podany jawnie, to przyjmuje
się że jest on odpowiedniego typu uniwersalnego

krańce zakresu indeksu mogą być zadane dowolnym
wyrażeniem

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Odwołania do elementów tablic

Do elementów tablic odwołujemy się przez nazwę zmiennej
tablicowej i wartości indeksów umieszczone w okrągłych nawiasach
i rozdzielone przecinkami (przy czym wartości te mogą być dane
dowolnymi wyrażeniami).

Przykłady

sudoku(1,2):=7;

dwa_na_trzy_na_cztery(1,3,4):= 0.12;

opady(Warszawa,sty):=12;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Wypełnianie tablic wartościami

nie wypełniona “jawnie” danymi tablica wielowymiarowa
zawiera wartości przypadkowe

tablica może zostać wypełniona danymi przez kolejne
przypisywanie wartości wszystkim jej składowym

często wykorzystuje się wówczas pętle zagnieżdżone (po jednej pętli dla każdego

indeksu, czyli “wymiaru”)

inną metodą jest przypisanie wartości wszystkim składowym
równocześnie, jedną instrukcją, co wymaga użycia agregatu
tablicy

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Agregaty tablic wielowymiarowych

Mamy tablice:

type miasta is (Krakow, Lodz);
t: array (miesiace range lipiec..wrzesien, miasta) of float;
m: array(integer range 1..2, integer range 1..2) of integer

notacja pozyzyjna:

t:=((20.1,23.0), (20.2, 19.4), (19.0, 19.0));

m := ((0,1), (4,2));

notacja nazywana i mieszana

t:=(lipiec => (Krakow =>20.1, Lodz => 23.0),

sierpien => (Krakow => 20.2, Lodz => 19.4),
wrzesien => (others=>19.0));

m := (1=>(1=>0, 2=> 1), 2=>(1=> 4,2=> 2));

t:=(lipiec=>(20.1,23.0), sierpien => (20.2, 19.4),

wrzesien => (others=>19.0));

m := (1=>(0,1), 2=>(4,2));

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tablice wielowymiarowe - operacje i atrybuty

z tablic wielowymiarowych nie można “wykrawać”
wielowymiarowych podtablic

tablice wielowymiarowe tego samego typu można porównać za
pomocą = i /=

można używać atrybutów takich jak dla tablic
jednowymiarowych, ale trzeba dodać do którego indeksu
(wymiaru) dany atrybut się odnosi (przykłady: t’first(1) -
zwróci lipiec, t’last(2) - zwróci Lodz). Bez określenia jak
powyżej atrybut (np. t’first) odnosi się do pierwszego
wymiaru.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Użycie tablicy dwuwymiarowej)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ;

p r o c e d u r e w09 tab2wym

i s

s u b t y p e

f l t n i e u j

i s

f l o a t

r a n g e

0 . 0 . . f l o a t ’ l a s t ;

t y p e

d n i

i s

( pon , wt , s r , czw , pt , so , n i e ) ;

p a c k a g e d n i o

i s new ada . t e x t i o . E n u m e r a t i o n I O ( d n i ) ;

u s e d n i o ;

t y p e

w y d a t k i w r o k u

i s

a r r a y ( i n t e g e r

r a n g e

1 . . 5 3 , d n i ) o f

f l t n i e u j ;

mojewyd2011 :

w y d a t k i w r o k u ;

n r t y g :

i n t e g e r ;

c z y :

c h a r a c t e r ;

b e g i n

mojewyd2011 : = ( o t h e r s=>(o t h e r s = >0.0));
l o o p

p u t ( ” c z y

w y p e l n i a s z

j a k i s

t y d z i e n ? t−t a k ,

i n n e − k o n i e c ” ) ;

g e t ( c z y ) ;

e x i t when c z y /= ’ t ’ and c z y /= ’T ’ ;

p u t ( ” p o d a j numer t y g o d n i a do w y p e l n i e n i a ” ) ;

g e t ( n r t y g ) ;

f o r

i

i n mojewyd2011 ’ r a n g e ( 2 )

l o o p

p u t ( i ) ;

p u t ( ”> ” ) ;

g e t ( mojewyd2011 ( n r t y g , i ) ) ;

end l o o p ;

end l o o p ;

p u t l i n e ( ” w y d a t k i w r o k u 2 0 1 1 : ” ) ;
f o r

i

i n mojewyd2011 ’ r a n g e ( 1 )

l o o p

f o r

j

i n mojewyd2011 ’ r a n g e ( 2 )

l o o p

p u t ( mojewyd2011 ( i , j ) , a f t =>2, e x p =>0, f o r e =>4);

end l o o p ;

n e w l i n e ;

end l o o p ;

end w09 tab2wym ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Tablice dynamiczne wielowymiarowe

Dynamiczne tablice wielowymiarowe tworzymy tak samo jak
jednowymiarowe (korzystając z bloku deklaracyjnego)
Dynamicznie ustalana może być dowolna liczba wymiarów.

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wektory boolowskie

Jednowymiarowe tablice dynamiczne

Tablice jednowymiarowe - zadania

Tablice wielowymiarowe

Przykład (Użycie dynamicznej tablicy dwuwymiarowej)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ;

p r o c e d u r e w09 tab2wymd

i s

s u b t y p e

f l t d o d

i s

f l o a t

r a n g e

0 . 0 . . f l o a t ’ l a s t ;

t y p e

d n i

i s

( pon , wt , s r , czw , pt , so , n i e ) ;

p a c k a g e d n i o

i s new ada . t e x t i o . E n u m e r a t i o n I O ( d n i ) ;

u s e d n i o ;

n r t y g ,

i t :

i n t e g e r ;

c z y :

c h a r a c t e r ;

b e g i n

p u t ( ” i l e

t y g o d n i

c h c e s z m i e c w t a b l i c y ? ” ) ;

g e t ( i t ) ;

d e c l a r e

t y p e

w y d a t k i w r o k u

i s

a r r a y ( i n t e g e r

r a n g e

1 . . i t , d n i ) o f

f l t d o d ;

mojewyd2011 :

w y d a t k i w r o k u ;

b e g i n

mojewyd2011 : = ( o t h e r s=>(o t h e r s = >0.0));
l o o p

p u t ( ” c z y

w y p e l n i a s z

j a k i s

t y d z i e n ? t−t a k ,

i n n e − k o n i e c ” ) ;

g e t ( c z y ) ;

e x i t when c z y /= ’ t ’ and c z y /= ’T ’ ;

p u t ( ” p o d a j numer t y g o d n i a do w y p e l n i e n i a ” ) ;

g e t ( n r t y g ) ;

f o r

i

i n mojewyd2011 ’ r a n g e ( 2 )

l o o p

p u t ( i ) ;

p u t ( ”> ” ) ;

g e t ( mojewyd2011 ( n r t y g , i ) ) ;

end l o o p ;

end l o o p ;

p u t l i n e ( ” w y d a t k i w r o k u 2 0 1 1 : ” ) ;
f o r

i

i n mojewyd2011 ’ r a n g e ( 1 )

l o o p

f o r

j

i n mojewyd2011 ’ r a n g e ( 2 )

l o o p

p u t ( mojewyd2011 ( i , j ) , a f t =>2, e x p =>0, f o r e =>4); end l o o p ;

n e w l i n e ;

end l o o p ;

end ;

end w09 tab2wymd ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania