Wstęp do programowania

wykład 14

Agata Półrola

Wydział Matematyki i Informatyki UŁ

sem. zimowy 2012/2013

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wybrane pakiety dostępne w języku

Pakiet Ada.Calendar

Pakiet umożliwia wykonywanie różnych operacji związanych z
czasem

Poza w/w pakietem zdefiniowany jest predefiniowany typ
Duration (typ stałoprzecinkowy, służący do reprezentowania
odległości dwóch punktów w czasie z dokładnością do
ułamków sekund)

wartości tego typu używane są np. w instrukcji delay
powodującej zatrzymanie programu na podaną liczbę sekund
(przykład użycia: delay 2.0; )

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wybrane pakiety dostępne w języku

Pakiet Ada.Calendar

Pakiet umożliwia wykonywanie różnych operacji związanych z
czasem

Poza w/w pakietem zdefiniowany jest predefiniowany typ
Duration (typ stałoprzecinkowy, służący do reprezentowania
odległości dwóch punktów w czasie z dokładnością do
ułamków sekund)

wartości tego typu używane są np. w instrukcji delay
powodującej zatrzymanie programu na podaną liczbę sekund
(przykład użycia: delay 2.0; )

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

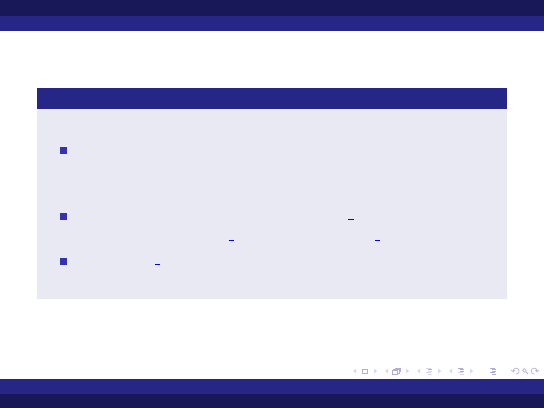
Pakiet Ada.Calendar - cd

W pakiecie Ada.Calendar dostępne są m.in.:

typ prywatny

Time

służący do reprezentowania punktów w

czasie (z przedziału 1.01.1901 - 31.12.2399, z dokładnością do
ułamków sekund)

podtypy typu integer o nazwach

Year Number

(zakres od

1901 do 2399),

Month Number

(1-12) i

Day Number

(1-31)

podtyp

Day Duration

typu Duration (zakres 0.0..86400.0;

liczba sekund w ciągu doby)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

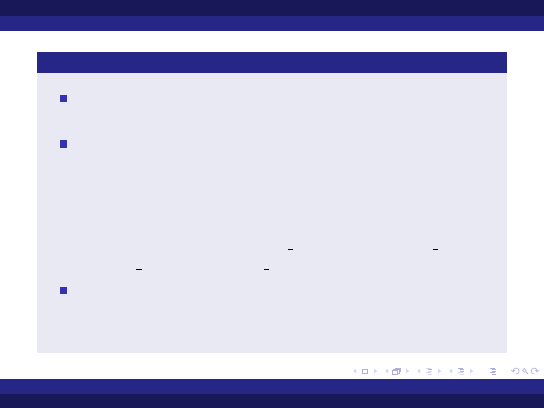
Pakiet Ada.Calendar - cd

bezparametrowa funkcja

Clock

zwracająca wartość typu Time

(bieżącą datę i czas)

procedura

Split

dzielącą wartość typu Time podaną jako

parametr na rok, miesiąc, dzień i godzinę w postaci liczby
sekund jakie upłynęły od godziny 0:0 danego dnia (wywołanie:
Split(t,r,m,d,s), gdzie t jest parametrem wejściowym -
wartością typu Time, a pozostałe parametry (wyjściowe) są
odpowiednio typów: r - Year Number, m - Month Number,
d - Day Number, s - Day Duration

fumkcje

Year

,

Month

,

Day

,

Seconds

, zwracające odpowiednie

części wartości typu Time podanej jako parametr (typy wyniku
j.w.)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

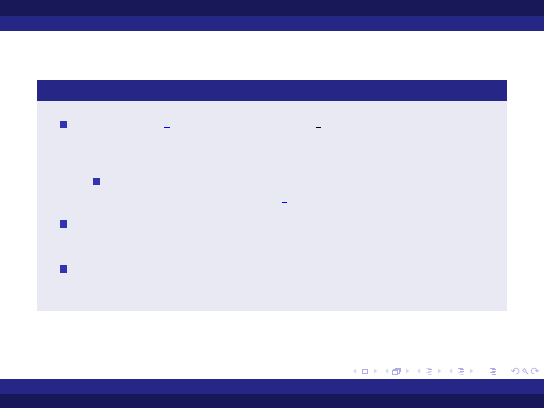
Pakiet Ada.Calendar - cd

funkcję

Time Of

(wywołanie: Time Of(r,m,d,s)) zwracającą

wartośc typu Time otrzymaną z roku r, miesiąca m, dnia d i
liczby sekund od początku dnia s

jeśli któraś z wartości przekracza dopuszczalny zakres,
zwracany jest wyjątek

Time Error

operatory + i - (dodawanie i odejmowanie) dla wartości typu
Time i Duration

operacje porównywania <, <=, >, >= wartości typu Time
(wcześniejsza data jest uważana za mniejszą)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (użycie pakietu Ada.Calendar)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . c a l e n d a r ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . c a l e n d a r ;

p r o c e d u r e

w 1 5 c a l e n d a r

i s

b i e z a c y c z a s :

t i m e ;

r , m, d :

i n t e g e r ;

s :

d u r a t i o n ;

b e g i n

b i e z a c y c z a s := c l o c k ;

s p l i t ( b i e z a c y c z a s , r , m, d , s ) ;

p u t ( ” r o k : ” ) ;

p u t ( r , 0 ) ;

p u t ( ” m i e s i a c : ” ) ;

p u t (m, 0 ) ;

p u t ( ” d z i e n : ” ) ;

p u t ( d , 0 ) ;

p u t ( ” s e k u n d po p o l n o c y : ” ) ;

p u t ( i n t e g e r ( s ) , 0 ) ;

n e w l i n e ( 2 ) ;

p u t ( ” t e r a z

czekamy . . . ” ) ;

d e l a y

5 . 0 ;

r := y e a r ( c l o c k ) ; m:= month ( c l o c k ) ;

d := d a y ( c l o c k ) ;

s := s e c o n d s ( c l o c k ) ;

n e w l i n e ;

p u t ( ” r o k : ” ) ;

p u t ( r , 0 ) ;

p u t ( ” m i e s i a c : ” ) ;

p u t (m, 0 ) ;

p u t ( ” d z i e n : ” ) ;

p u t ( d , 0 ) ;

p u t ( ” s e k u n d po p o l n o c y : ” ) ;

p u t ( i n t e g e r ( s ) , 0 ) ;

end w 1 5 c a l e n d a r ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

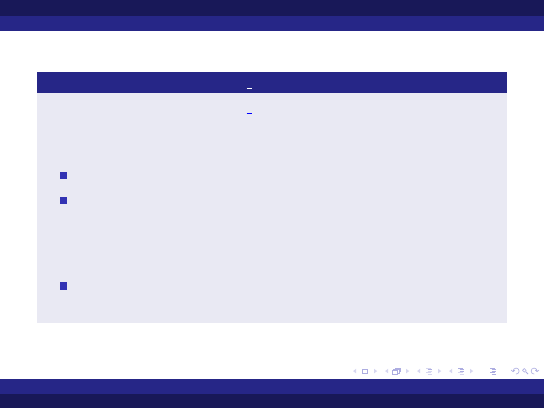
Pakiet Ada.Numerics.Float Random

Pakiet

Ada.Numerics.Float Random

umożliwia wygenerowanie

zbioru losowych wartości z przedziału [0,1].
Pakit udostępnia m.in.:

typ

Generator

procedury

Reset

- jedną z parametrem typu Generator,

drugą z dwoma parametrami - pierwszym typu Generator,
drugim typu Integer (inicjalizator generatora), umożliwiające
nadanie generatorowi nowej wartości

funkcję

Random

z parametrem typu Generator zwracającą

kolejną wartość w sekwencji generatora

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (losowanie wartości rzeczywistych)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . f l o a t r a n d o m ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o , ada . f l o a t t e x t i o ,

ada . n u m e r i c s . f l o a t r a n d o m ;

p r o c e d u r e

w 1 5 f l o r a n d

i s

g :

g e n e r a t o r ;

l i c z b a :

f l o a t ;

i l e :

i n t e g e r ;

b e g i n

p u t ( ” i l e

l i c z b

c h c e s z w y g e n e r o w a c ? ” ) ;

g e t ( i l e ) ;

f o r

i

i n

1 . . i l e

l o o p

l i c z b a := random ( g ) ;

p u t ( l i c z b a ,

e x p =>0); n e w l i n e ;

end l o o p ;

n e w l i n e ( 2 ) ;

p u t l i n e ( ” n a s t e p n e

l o s o w a n i e ” ) ;

r e s e t ( g ) ;

−− n i e z b e d n e aby m i e c i n n e w y n i k i

f o r

i

i n

1 . . i l e

l o o p

l i c z b a := random ( g ) ;

p u t ( l i c z b a ,

e x p =>0); n e w l i n e ;

end l o o p ;

end w 1 5 f l o r a n d ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Pakiet Ada.Numerics.Discrete Random

Pakiet

Ada.Numerics.Discrete Random

jest pakietem o

działaniu podobnym jak Ada.Numerics.Float random, ale
dla wartości typów dyskretnych (umożliwia wygenerowanie
losowych wartości z pewnego zbioru)

jest to pakiet rodzajowy - wymaga konkretyzacji dla typu z
którego będziemy losować wartości

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (losowanie wartości dyskretnych)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,
ada . n u m e r i c s . d i s c r e t e r a n d o m ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e

w 1 5 d i s r a n d

i s

s u b t y p e o c e n y

i s

i n t e g e r

r a n g e

1 . . 6 ;

p a c k a g e

l o s o c e n y

i s new ada . n u m e r i c s . d i s c r e t e r a n d o m ( o c e n y ) ;

u s e

l o s o c e n y ;

t y p e

d n i

i s

( pon , wt ,

s r , czw ,

pt ,

so ,

n i e ) ;

p a c k a g e

l o s d n i

i s new ada . n u m e r i c s . d i s c r e t e r a n d o m ( d n i ) ;

p a c k a g e

d n i i o

i s new ada . t e x t i o . e n u m e r a t i o n i o ( d n i ) ;

u s e

l o s d n i , d n i i o ;

g :

l o s o c e n y . g e n e r a t o r ; gd :

l o s d n i . g e n e r a t o r ;

l i c z b a , i l e :

i n t e g e r ;

d : d n i ;

b e g i n

p u t ( ” i l e

l i c z b

i

d n i

c h c e s z w y g e n e r o w a c ? ” ) ;

g e t ( i l e ) ;

r e s e t ( g ) ;

r e s e t ( gd ) ;

f o r

i

i n

1 . . i l e

l o o p

l i c z b a := random ( g ) ;

p u t ( l i c z b a ,

0 ) ;

n e w l i n e ;

d := random ( gd ) ;

p u t ( d ) ;

n e w l i n e ;

end l o o p ;

end w 1 5 d i s r a n d ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Inne pakiety

W sieci dostępnych jest wiele pakietów oferujących różnorodne
funkcje. Przykłady:

console io - pakiet umożliwiający obsługę znaków
narodowych

AdaGraph - pakiet umożliwiający tworzenie grafiki

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (losowanie wartości dyskretnych)

w i t h ada . t e x t i o , c o n s o l e i o ;

−− p a k i e t do d o g r a n i a

u s e

c o n s o l e i o ;

p r o c e d u r e

z n a k i t e s t

i s

x :

s t r i n g ( 1 . . 2 0 ) : = ( o t h e r s=> ’

’ ) ;

n :

i n t e g e r ;

b e g i n

p u t ( ” p o d a j

n a p i s : ” ) ;

g e t l i n e ( x , n ) ;

ada . t e x t i o . n e w l i n e ;
p u t ( ” w p r o w a d z i ł e s : ” ) ;

p u t ( x ) ;

end z n a k i t e s t ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Typy rekordowe

Tablice to złożone struktury danych, których składowe są tego
samego typu

Rekordy

to złożone struktury danych, których składowe (tzw.

pola

) mogą być różnych typów

istnieją pewne ograniczenia co do dopuszczalnych typów pol - np anonimowy typ

tablicowy nie jest dozwolony

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Definicja typu rekordowego

type nazwa_typu is record

pole1: typ_pola1;
pole2: typ_pola2;
...

end record;

nazwy pól tego samego typu można oddzielić przecinkami

Przykłady

type punkt_plaszczyzny is record

x,y: float;

end record;

type osoba is record

imie, nazwisko: string(1..20);
wiek: natural;
pesel: string(1..11);

end record;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Deklaracje zmiennych, odwołania do pól

deklaracja zmiennej typu rekordowego ma postać
nazwa zmiennej :

nazwa typu;

Przykład

A: punkt plaszczyzny;
sasiad:

osoba;

do poszczególnych pól rekordu odwołujemy się pisząc
nazwa zmiennej.nazwa pola

Przykład

A.x:=0.0; A.y:=0.0;
put(sasiad.imie);

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (rekordy - program 1)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . E l e m e n t a r y F u n c t i o n s ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . E l e m e n t a r y F u n c t i o n s ;

p r o c e d u r e

w 1 5 p l a s z c z

i s

t y p e p u n k t

i s

r e c o r d

x , y :

i n t e g e r ;

end r e c o r d ;

p r o c e d u r e

P o b i e r z ( p :

o u t p u n k t )

i s

b e g i n

p u t ( ” p i e r w s z a

w s p o l r z e d n a > ” ) ;

g e t ( p . x ) ;

p u t ( ” d r u g a

w s p o l r z e d n a > ” ) ;

g e t ( p . y ) ;

end P o b i e r z ;

p r o c e d u r e W y p i s z ( p :

i n

p u n k t )

i s

b e g i n

p u t ( ” ( ” ) ;

p u t ( p . x , 0 ) ;

p u t ( ” , ” ) ;

p u t ( p . y , 0 ) ;

p u t ( ” ) ” ) ;

end W y p i s z ;

f u n c t i o n

O d l e g l o s c ( p1 , p2 : p u n k t )

r e t u r n

f l o a t

i s

b e g i n

r e t u r n

s q r t ( f l o a t ( ( p2 . x−p1 . x )∗∗2+( p2 . y−p1 . y ) ∗ ∗ 2 ) ) ;

end O d l e g l o s c ;

A , B :

p u n k t ;

b e g i n

p u t l i n e ( ” p u n k t A ” ) ;

p o b i e r z ( a ) ;

p u t l i n e ( ” p u n k t B ” ) ;

p o b i e r z ( b ) ;

p u t ( ” o d l e g l o s c

punktow : ” ) ;

w y p i s z ( a ) ;

p u t ( ” i ” ) ;

w y p i s z ( b ) ;

p u t ( ” t o ” ) ;

p u t ( o d l e g l o s c ( a , b ) , e x p =>0);

end w 1 5 p l a s z c z ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przypisywanie wartości zmiennym rekordowym

Wartości przypisujemy zmiennym rekordowym w następujący
sposób:

przez przypisywanie wartości poszczególnym polom

Przykład

A.x:=0.0; get(A.y);

przez przypisywanie wartości całym rekordom, używając
agregatów rekordów

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Agregaty rekordów

Zmienne w przykładach: A: punkt; s:

student;

notacja pozycyjna

A:= (0.0, 1.0);
s:=("Grzegorz

", "Brzeczyszczykiewicz",

21,"90121212345");

notacja nazywana

A:= (x=>0.0, y=>1.0);
A:= (others=>0.0);
s:= (imie=>"Grzegorz

",

nazwisko=>"Brzeczyszczykiewicz",
wiek=>21,pesel=>"90121212345");

s:= ("Grzegorz

",

"Brzeczyszczykiewicz",
wiek=>21,pesel=>"90121212345");

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Agregaty rekordu - cd

w agregatach można używać słowa others i znaku |
(oczywiście przy polach rekordu tego samego typu)

A:=(others => 0.0);
A:=(x|y => 0.0);

Słowo others występuje na końcu agregatu rekordu

nie jest dopuszczalne używanie zakresów
(czyli nie jest dozwolone pole i..pole j => ...)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Wartości początkowe w definicji typu

Możliwe jest nadanie pewnym polom wartości początkowej już w
momencie definiowania typu rekordowego:

type punkt_ekranu is record

x: natural range 0..80 :=0;
y: natural range 0..120 :=0;

end record;
----------------------------------
type osoba is record

imie, nazwisko string(1..2) := (others=>’ ’);
wiek: natural:=0;

end record;
----------------------------------
type pracownik is record

imie, nzawisko:=(others=>’ ’);

staz_pracy:integer;

end record;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Stałe typu rekordowego

Możliwe jest deklarowanie stałych rekordowych:

type punkt_ekranu is record

x: natural range 0..80 :=0;
y: natural range 0..120 :=0;

end record;

gorny_rog_ekranu: constant punkt_ekranu :=(0,0);

Nie jest możliwe zadeklarowanie pewnych pól jako stałych

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Podstawowe operacje

Podstawowymi predefiniowanymi operacjami dla typow
rekordowych są:

podstawienie (:=)

porównywanie (=, /=).

Porównywane są poszczególne pola rekordów

Inne operacje należy zaimplementować samemu jako odpowiednie
funkcje - operatory (np. <, >)

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (rekordy - uzupełnienie programu 1)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . E l e m e n t a r y F u n c t i o n s ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ,

ada . f l o a t t e x t i o ,

ada . n u m e r i c s . E l e m e n t a r y F u n c t i o n s ;

p r o c e d u r e

w 1 5 p l a s z c z 2

i s

t y p e p u n k t

i s

r e c o r d

x , y :

i n t e g e r ;

end r e c o r d ;

p r o c e d u r e

P o b i e r z ( p :

o u t p u n k t )

i s

b e g i n

p u t ( ” p i e r w s z a

w s p o l r z e d n a > ” ) ;

g e t ( p . x ) ;

p u t ( ” d r u g a

w s p o l r z e d n a > ” ) ;

g e t ( p . y ) ;

end P o b i e r z ;

p r o c e d u r e W y p i s z ( p :

i n

p u n k t )

i s

b e g i n

p u t ( ” ( ” ) ;

p u t ( p . x , 0 ) ;

p u t ( ” , ” ) ;

p u t ( p . y , 0 ) ;

p u t ( ” ) ” ) ;

end W y p i s z ;

f u n c t i o n

O d l e g l o s c ( p1 , p2 : p u n k t )

r e t u r n

f l o a t

i s

b e g i n

r e t u r n

s q r t ( f l o a t ( ( p2 . x−p1 . x )∗∗2+( p2 . y−p1 . y ) ∗ ∗ 2 ) ) ;

end O d l e g l o s c ;

s r o d e k :

c o n s t a n t p u n k t : = ( x=>0,y =>0);

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (rekordy - uzupełnienie programu 1 cd.)

f u n c t i o n ”<” ( p1 , p2 : p u n k t )

r e t u r n

b o o l e a n

i s

b e g i n

i f

o d l e g l o s c ( p1 , s r o d e k )< o d l e g l o s c ( p2 , s r o d e k ) t h e n

r e t u r n

t r u e ;

e l s e

r e t u r n

f a l s e ;

end

i f ;

end ”<” ;

f u n c t i o n ”>” ( p1 , p2 : p u n k t )

r e t u r n

b o o l e a n

i s

b e g i n

r e t u r n

o d l e g l o s c ( p1 , s r o d e k )> o d l e g l o s c ( p2 , s r o d e k ) ;

end ”>” ;

A , B :

p u n k t ;

b e g i n

p u t l i n e ( ” p u n k t A ” ) ;

p o b i e r z ( a ) ;

p u t l i n e ( ” p u n k t B ” ) ;

p o b i e r z ( b ) ;

p u t ( ” o d l e g l o s c

punktow : ” ) ;

w y p i s z ( a ) ;

p u t ( ” i ” ) ;

w y p i s z ( b ) ;

p u t ( ” t o ” ) ;

p u t ( o d l e g l o s c ( a , b ) , e x p =>0);

n e w l i n e ;

i f

a>b t h e n p u t ( ” p i e r w s z y

j e s t

d a l e j

od s r o d k a ” ) ;

e l s i f

a<b t h e n p u t ( ” d r u g i

j e s t

d a l e j

od s r o d k a ” ) ;

e l s e

i f

a=b t h e n p u t ( ” t o t e n sam p u n k t ” ) ;

e l s e

p u t ( ” p u n k t y s a w r o w n e j

o d l e g l o s c i

od s r o d k a ” ) ;

end

i f ; end

i f ;

end w 1 5 p l a s z c z 2 ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Struktury danych “wielokrotnie złożone”

elementem (polem) rekordu może być inny rekord

polem rekordu może być tablica

można tworzyć tablice przechowujące rekordy

itd

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Przykład - rekord z polem będącym rekordem)

w i t h ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

u s e ada . t e x t i o ,

ada . i n t e g e r t e x t i o ;

p r o c e d u r e w 1 5 d a t a u r

i s

t y p e d a t a

i s

r e c o r d

d :

i n t e g e r

r a n g e

1 . . 3 1 ;

m:

i n t e g e r

r a n g e

1 . . 1 2 ;

r :

i n t e g e r

r a n g e

1 8 0 0 . . 2 0 1 2 ;

end r e c o r d ;

t y p e o s o b a

i s

r e c o r d

im , nazw :

s t r i n g ( 1 . . 2 0 ) ;

d a t a U r :

d a t a ;

end r e c o r d ;

o :

o s o b a ;

n :

i n t e g e r ;

b e g i n

o . im : = ( o t h e r s=> ’

’ ) ; o . nazw : = ( o t h e r s=> ’

’ ) ;

p u t ( ” p o d a j

i m i e : ” ) ;

g e t l i n e ( o . im , n ) ;

i f

n=o . im ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j

n a z w i s k o : ” ) ;

g e t l i n e ( o . nazw , n ) ;

i f

n=o . nazw ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j

d a t e

u r o d z e n i a − d z i e n ” ) ;

g e t ( o . d a t a U r . d ) ;

p u t ( ” m i e s i a c ” ) ;

g e t ( o . d a t a U r .m) ;

p u t ( ” d z i e n ” ) ;

g e t ( o . d a t a U r . r ) ;

p u t l i n e ( ” Podana o s o b a : ” ) ;
p u t l i n e ( ” i m i e : ” & o . im ) ;

p u t l i n e ( ” n a z w i s k o : ” & o . nazw ) ;

p u t ( ” d a t a

u r o d z e n i a : ” ) ;

p u t ( o . d a t a U r . d , 0 ) ; p u t ( ”−” ) ; p u t ( o . d a t a U r . m, 0 ) ;
p u t ( ”−” ) ; p u t ( o . d a t a U r . r , 0 ) ;

end w 1 5 d a t a u r ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Przykład - rekord z polem będącym tablicą)

w i t h ada . t e x t i o ,

ada . I n t e g e r T e x t I O ;

u s e ada . t e x t i o ,

ada . I n t e g e r T e x t I O ;

p r o c e d u r e w 1 5 s t u d

i s

s u b t y p e o c e n a

i s

i n t e g e r

r a n g e

1 . . 6 ;

t y p e t a b o c

i s

a r r a y

( i n t e g e r

r a n g e

1 . . 1 0 )

o f o c e n a ;

t y p e o s o b a

i s

r e c o r d

im , nazw :

s t r i n g ( 1 . . 2 0 ) ;

o c e n y :

t a b o c ;

end r e c o r d ;

o :

o s o b a ;

n :

i n t e g e r ;

b e g i n

o . im : = ( o t h e r s=> ’

’ ) ; o . nazw : = ( o t h e r s=> ’

’ ) ;

p u t ( ” p o d a j

i m i e : ” ) ;

g e t l i n e ( o . im , n ) ;

i f

n=o . im ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j

n a z w i s k o : ” ) ;

g e t l i n e ( o . nazw , n ) ;

i f

n=o . nazw ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j o c e n y o s o b y : ” ) ;

f o r

i

i n o . o c e n y ’ r a n g e l o o p

p u t ( ” p r z e d m i o t ” ) ; p u t ( i , 0 ) ; p u t ( ” : ” ) ;

g e t ( o . o c e n y ( i ) ) ;

end l o o p ;

end w 1 5 s t u d ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania

Przykład (Przykład - tablica rekordów mających pole “tablicowe”)

w i t h ada . t e x t i o ,

ada . I n t e g e r T e x t I O ;

u s e ada . t e x t i o ,

ada . I n t e g e r T e x t I O ;

p r o c e d u r e

w 1 5 t a b s t u d

i s

s u b t y p e o c e n a

i s

i n t e g e r

r a n g e

1 . . 6 ;

t y p e t a b o c

i s

a r r a y

( i n t e g e r

r a n g e

1 . . 1 0 )

o f o c e n a ;

t y p e o s o b a

i s

r e c o r d

im , nazw :

s t r i n g ( 1 . . 2 0 ) ;

o c e n y :

t a b o c ;

end r e c o r d ;

t y p e

k l a s a

i s

a r r a y ( i n t e g e r

r a n g e

1 . . 3 )

o f o s o b a ;

k :

k l a s a ; n :

i n t e g e r ;

b e g i n

f o r

i

i n k ’ r a n g e l o o p

p u t ( ” o s o b a ” ) ;

p u t ( i , 0 ) ;

p u t ( ” : ” ) ;

n e w l i n e ;

k ( i ) . im : = ( o t h e r s=> ’

’ ) ; k ( i ) . nazw : = ( o t h e r s=> ’

’ ) ;

p u t ( ” p o d a j

i m i e : ” ) ;

g e t l i n e ( k ( i ) . im , n ) ;

i f

n=k ( i ) . im ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j

n a z w i s k o : ” ) ;

g e t l i n e ( k ( i ) . nazw , n ) ;

i f

n=k ( i ) . nazw ’ l e n g t h

t h e n

s k i p l i n e ; end

i f ;

p u t ( ” p o d a j o c e n y o s o b y : ” ) ;

f o r

j

i n k ( i ) . o c e n y ’ r a n g e l o o p

p u t ( ” p r z e d m i o t ” ) ; p u t ( j , 0 ) ; p u t ( ” : ” ) ;

g e t ( k ( i ) . o c e n y ( j ) ) ;

s k i p l i n e ;

end l o o p ;

end l o o p ;

end w 1 5 t a b s t u d ;

Agata Półrola Wydział Matematyki i Informatyki UŁ

Wstęp do programowania