Probabilistyka i Statystyka
mgr inż. Krzysztof Świder
e-mail: kswid@wp.pl
Kombinatoryka
Wariacja bez powtórzeń
Wariacją (rozmieszczeniem) bez powtórzeń z n elementów po k elementów nazywamy
uporządkowany zbiór składający się z k różnych elementów, wybranych z pośród n różnych
elementów.
Liczbę wariacji bez powtórzeń z n elementów po k oznaczamy symbolem
k
n
V i obliczamy ze
wzoru:
(
)
!
!
k
n
n
V
n k
=
−
Zadanie 1 Ile można wykonać różnych trójkolorowych chorągiewek z sześciu barw?
Rozwiązanie:
1. Tworzymy zbiory trójelementowe ze zbioru 6 – elementowego
2. Kolejność układu barw w chorągwi odgrywa rolę
3. Chorągiewki mają być trójkolorowe, a więc w tworzonych zbiorach elementy nie
mogą się powtarzać.
Z 1, 2, 3 wnioskujemy, że tyle jest różnych trójkolorowych chorągiewek, ile jest różnych
wariancji bez powtórzeń z 6 elementów po 3, tj.
(
)
3
6
6!
120
6 3 !
V
=
=
−
Zadanie 2 Obliczyć, ile jest liczb czterocyfrowych, w których nie powtarza się żadna cyfra i
zero nie występuje na pierwszym miejscu.
Rozwiązanie:
1. tworzymy zbiory czteroelementowe ze zbioru 10 – elementowego
2. cyfry w liczbach nie mogą się powtarzać
3. pierwsza liczba musi być różna od zera
4
3
10
9
4536
V
V
−
=
lub alternatywnie
4
4
10
10
1
4536
10
V
V
−
=
Zadanie 3 Ile można utworzyć liczb parzystych czterocyfrowych o nie powtarzających się
cyfrach i przy założeniu, że zero nie występuje na pierwszym miejscu
Rozwiązanie:
1. liczba jest parzysta, jeśli kończy się cyfrą 0, 2, 4, 6, 8.
2. Pozostałe dziewięć cyfr rozmieszczamy na trzech pierwszych pozycjach
3. należy wyeliminować przypadki z zerem na początku
3
2
10
8
5
4
2296
V
V
−
=
Wariacje z powtórzeniami
1
Wariacją (rozmieszczeniem) z powtórzeniami z n elementów po k nazywamy uporządkowany
zbiór składający się z k elementów różnych lub nie różniących się między sobą, wybranych
spośród n różnych elementów.
k
k
n
V
n
=
Zadanie 4 Ile można utworzyć liczb pięciocyfrowych z cyfr 4, 5, 6?
Rozwiązanie:
1. Tworzymy zbiory 5-elemntowe ze zbioru trójelementowego
2. W tworzonych zbiorach kolejność odgrywa rolę (liczby są uporządkowanymi
zbiorami cyfr)
3. Cyfry w danej liczbie mogą się powtarzać
5
5
3
3
243
V
=
=
Zadanie 5 Sześć osób ma do dyspozycji 5 różnokolorowych kieliszków i 2 różne gatunki
win. Iloma sposobami mogą się napić?
Rozwiązanie:
1. Kieliszki są różnokolorowe i jednej osobie dajemy nie więcej niż jeden kieliszek
2. Przy każdym ustawieniu 5 kieliszków można do nich nalać dwa gatunki win
•
ten sam gatunek wina z konieczności powtórzy się w różnych kieliszkach
•
jest istotne, jakie wino do jakiego kieliszka jest nalewane, tzn. nie można brać
pod uwagę tylko liczby kieliszków napełnionych danym gatunkiem wina
5
5
6
2
720 32
V V
⋅
=
⋅
Permutacje bez powtórzeń
Zbiór składający się z n elementów uporządkowanych i różnych nazywamy permutacją
(przemianą) bez powtórzeń z n elementów. Liczbę utworzonych w ten sposób zbiorów
oznaczamy symbolem P
n
i wyrażamy wzorem
!
n
P
n
=
Zadanie 6 W urnie są 3 kule o numerach 1, 2, 3. Wyciągamy kolejno trzy kule i notujemy ich
numery według kolejności wyciągnięcia. Ile można tym sposobem otrzymać różnych liczb?
3! 6
n
P
=
=
Zadanie 7 Ile jest permutacji liczb 1, 2, ….,n, w których
1. liczby 1, 2 nie sąsiadują ze sobą;
2. liczby 1, 2, 3 nie tworzą kolejnych wyrazów (niezależnie od porządku)?
Rozwiązanie
1. Liczba wszystkich możliwych permutacji z n elementów
!
n
P
n
=
Liczba permutacji z n – 2, gdy dwa pierwsze są ustalone:
(
)
2
2 !
n
P
n
−
=
−
Gdy na drugim miejscu wystąpi jedynka, a na trzecim dwójka, wtedy
(
)
2
2 !
n
P
n
−
=
−
Wszystkich permutacji z n elementów, gdy 1 i 2 sąsiadują ze sobą w kolejności 1 ,2 jest
2
(
)
(
) (
) (
)
2
1
1
2 !
1 !
n
n
P
n
n
n
−
−
=
−
−
=
−
Analogicznie, wszystkich permutacji z n elementów, gdy 1 i 2 sąsiadują ze sobą w kolejności
2, 1, jest
(
)
(
) (
) (
)
2
1
1
2 !
1 !
n
n
P
n
n
n
−
−
=
−
−
=
−
Zatem wszystkich permutacji z n elementów , w których liczby 1, 2 sąsiadują ze sobą, jest
(
)
2
1 !
n
−
Stąd rozwiązanie
(
)
! 2
1 !
n
n
−
−
2. Liczba permutacji, w których elementy 1, 2, 3 są ustawione w kolejności 1, 2, 3:
(
) (
) (
)
2
3 !
2 !
n
n
n
−
−
=
−
Liczba permutacji z trzech liczb jest równa 3!, a zatem
(
)
! 3!
2 !
n
n
−
−
Kombinacje bez powtórzeń
Kombinacją bez powtórzeń z n elementów po k nazywamy zbiór składający się z k różnych
elementów wybranych spośród n różnych elementów, przy czym obojętne jest, w jakim
porządku elementy tego zbioru są rozmieszczone
(
)
!
!
!
k
n
n
n
C
k
k n k
ć
=
=
−
č ř
Zadanie 8 Ile nastąpi powitań, gdy jednocześnie spotka się 6 znajomych?
Rozwiązanie:
1. n = 6 jest liczbą wszystkich osób, k = 2 jest liczbą osób, które jednocześnie podają
sobie ręce
2. zakładamy, że porządek przy witaniu się dwóch osób nie odgrywa roli
2
6
6
15
2
C
ć
=
=
č ř
Zadanie 9 Dana jest grupa elementów ABCD oraz grupa elementów x, y, z. Tworzymy
kombinacje po pięć elementów w ten sposób, że trzy elementy wybieramy z pierwszej grupy i
dwa z drugiej grupy. Obliczyć, ile takich kombinacji można utworzyć?
Rozwiązanie:
1. Z czterech elementów A, B, C, D można utworzyć
3
4
4
C
=
kombinacje po trzy
elementy
2. Z trzech elementów x, y, z można utworzyć
2
3
3
C
=
kombinacje po 2 elementy
3. ponieważ każda kombinacja pierwszej grupy łączona jest z każdą kombinacją drugiej
grupy, więc ogólna liczba kombinacji równa się iloczynowi liczby kombinacji
pierwszej grupy przez liczbę drugiej:
3
2
4
3
12
C C
⋅
=
Zadanie 10 Iloma sposobami można położyć 12 książek na trzech półkach tak, by ba
pierwszej półce znajdowało się cześć książek, na drugiej cztery ksiązki, a na trzeciej reszta?
6
4
2
12
6
2
13860
C C C
⋅
⋅
=
Prawdopodobieństwo
3
Prawdopodobieństwem nazywamy stosunek mocy zbioru zdarzeń sprzyjających do mocy
przestrzeni zdarzeń elementarnych, czyli:
Ω
=
A
A
P )
(
Zadanie 11 Dziecko ma ustawić na półce 10 książek w identycznych oprawach. Wśród nich
są 3 kryminały, a resztę stanowią bajki. Jakie jest prawdopodobieństwo, że przy losowym
ustawieniu książek, kryminały będą stały jako pierwsze.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na tym, że dziecko ustawi 10 książek na
półce (ciąg złożony z 10-ciu elementów – bezsprzecznie jest to permutacja).
Ω
=
!
10
10
=
P
A – zbiór zdarzeń sprzyjających, polegających na tym, że kryminały zostaną ustawione jako
„pierwsze” (cały zbiór został podzielony na dwa: 3 i 7-mio elementowy).
!
7
!
3
7
3
⋅
=
⋅
=
P
P
A
120
1
10
9
8
3
2
1
!
10
!
7
!
3
)
(
=
⋅
⋅
⋅
⋅
=
⋅
=
A
P
Zadanie 12 Osiem osób, wśród których są koledzy Jacek(J) i Marek(M) ustawia się w kolejce
do kasy w sposób losowy. Oblicz prawdopodobieństwo zdarzenia, że koledzy staną obok
siebie.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na losowym ustawieniu się 8-miu osób
w kolejce (ciąg 8-mio elementowy).
!
8
8
=
=
Ω
P
A – zbiór zdarzeń sprzyjających, polegających na tym, że koledzy J i M staną obok siebie.
Uwaga: Zadanie jest zbliżone do poprzedniego, lecz należy wziąć poprawkę na możliwość
zmiany pozycji kolegów. Spróbujmy to zilustrować:
J,M,-,-,-,-,-,-,
-,J,M,-,-,-,-,-,
itd. aż do końca. Możliwości jest 7, a więc:
!
7
!
2
7
!
6
!
2
7
6
2
⋅
=
⋅
⋅
=
⋅
⋅
=
P
P
A
4
1
!
8
!
7
!
2
)
(
=
⋅
=
A
P
Zadanie 13 Ze zbioru liczb
{
}
7
;
6
;
5
;
4
;
3
;
2
;
1
losujemy kolejno dwa razy po jednej liczbie bez
zwracania. Oblicz prawdopodobieństwo tego, że pierwsza wylosowana liczba będzie
parzysta, a druga nieparzysta.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu (kolejno) dwóch liczb.
4
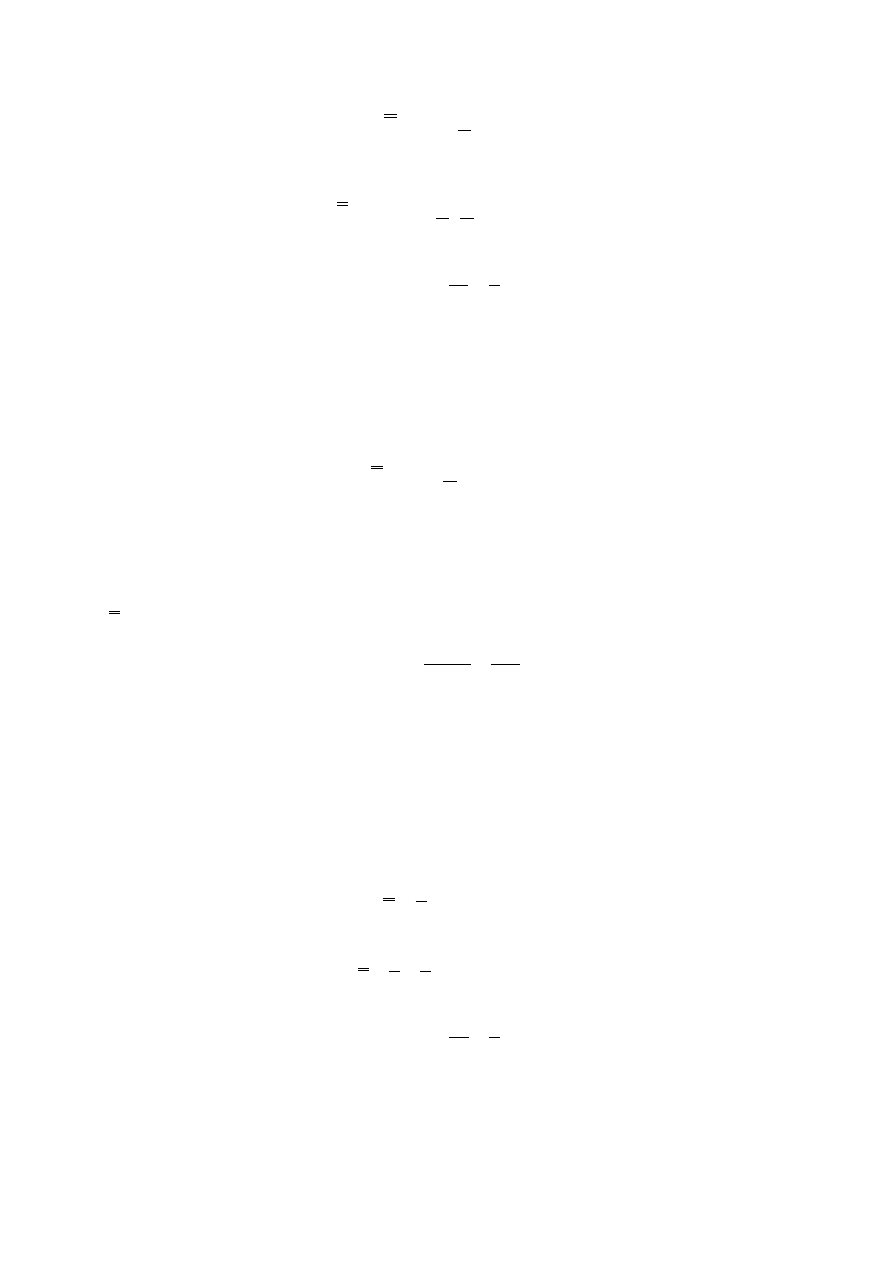
42
!
5
!
7
2
7
=
=
=
Ω
V
A – zbiór zdarzeń sprzyjających, polegających na tym, że pierwsza wylosowana liczba będzie
parzysta, a druga nieparzysta.
12
4
3
!
3
!
4
!
2
!
3
1
4
1
3
=
⋅
=
⋅
=
⋅
=
V
V
A
7
2
42
12
)
(
=
=
A
P
Zadanie 14 Ze zbioru
{
}
9
;.....;
2
;
1
losujemy kolejno trzy razy po jednej liczbie i tworzymy w
ten sposób liczbę trzycyfrową zaczynając od cyfry setek. Oblicz prawdopodobieństwo
utworzenia liczby większej od 473.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na tym, że w wyniku trzech kolejnych
losowań utworzymy liczbę trzycyfrową.
9
8
7
!
6
!
9
3
9
⋅
⋅
=
=
=
Ω
V
A – zbiór zdarzeń sprzyjających, polegających na wylosowaniu liczby większej od 473.
Uwaga: Jak widać zadanie jest zbliżone do poprzedniego, jednakże rozumowanie musi być
bardziej drobiazgowe, przy pomocy „pewniaków”:pierwsza cyfra większa od 4, a dwie
następne dowolne lub pierwsza 4, druga większa od 7, a trzecia dowolna lub pierwsza 4,
druga 7, a trzecia większa od 3 (pamiętając, że dwie takie cyfry zostały wylosowane).
298
4
1
1
7
2
1
8
7
5
1
4
1
1
1
1
1
7
1
2
1
1
2
8
1
5
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
⋅
⋅
+
⋅
⋅
+
⋅
=
V
V
V
V
V
V
V
V
A
252
149
9
8
7
298
)
(
=
⋅
⋅
=
A
P
.
Zadanie 15 Rzucamy dwa razy symetryczną kostką do gry i zapisujemy cyfry tworząc liczby
dwucyfrowe. Oblicz prawdopodobieństwo utworzenia liczby parzystej.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych polegających na utworzeniu liczby dwucyfrowej,
powstałej z zanotowania cyfr wyrzuconych kostką.
Uwaga: Wielokrotny rzut kostką, bądź jednorazowo wieloma kostkami, to zawsze wariacja z
powtórzeniami wielokrotna, ze zbioru 6 – elementowego.
36
6
2
2
6
=
=
=
Ω
V
A – zbiór zdarzeń sprzyjających, polegających na utworzeniu dwucyfrowej liczby parzystej.
18
3
6
1
1
1
3
1
6
=
⋅
=
⋅
=
V
V
A
2
1
36
18
)
(
=
=
A
P
Zadanie 16 Z pojemnika, w którym znajdują się dwie kule białe i cztery czarne, losujemy
trzy razy jedną kulę, zwracając ją po każdym losowaniu do pojemnika. Oblicz
prawdopodobieństwo, że kulę białą wylosujemy co najmniej raz.
5
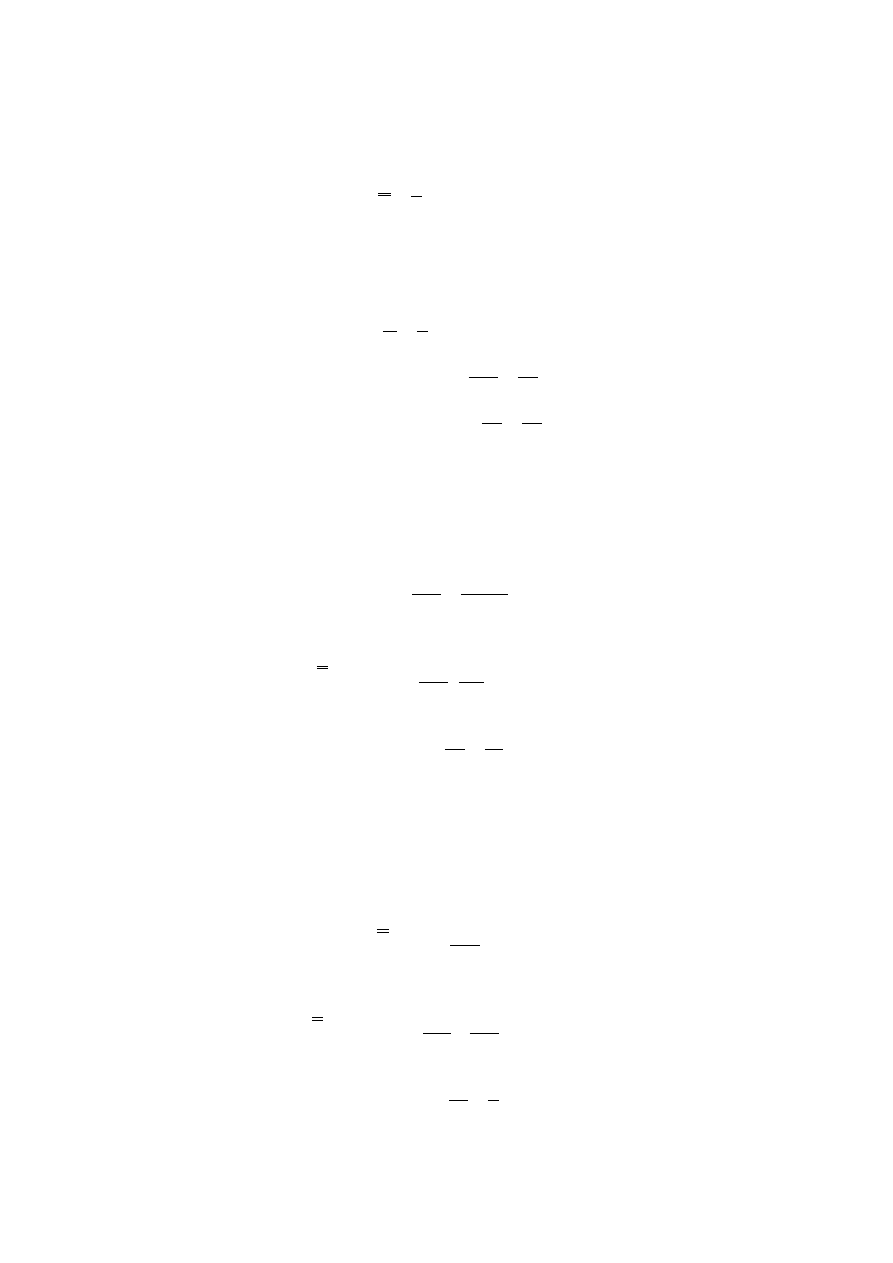
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na trzykrotnym losowaniu jednej kuli z
pojemnika, zwracając ją po każdym losowaniu do pojemnika.
216
6
3
3
6
=
=
=
Ω
V
A – zbiór zdarzeń sprzyjających, polegających na tym, że kulę białą wylosujemy co najmniej
raz.
Uwaga: Oczywistym jest, że w tym wypadku prościej jest obliczyć moc zbioru zdarzeń
niesprzyjających i wykorzystać własność:
)
'
(
1
)
(
A
P
A
P
−
=
'
A - zbiór zdarzeń niesprzyjających, polegających na tym, że wylosujemy tylko kule czarne.
64
4
'
3
3
4
=
=
=
V
A
27
8
216
64
)
'
(
=
=
A
P
27
19
27
8
1
)
(
=
−
=
A
P
Zadanie 17 Z pojemnika, w którym znajduje się pięć kul białych oraz cztery czarne, losujemy
jednocześnie trzy kule. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu trzech kul
(jednocześnie z pośród dziewięciu).
Ω=
84
3
2
1
9
8
7
!
6
!
3
!
9
3
9
=
⋅
⋅
⋅
⋅
=
⋅
=
C
A – zbiór zdarzeń sprzyjających, polegających na tym, że zostaną wylosowane dwie kule
białe (pamiętajmy, że wszystkich kul musi być trzy, a więc jedna musi być czarna).
40
4
10
!
3
!
1
!
4
!
3
!
2
!
5
1
4
2
5
=
⋅
=
⋅
⋅
⋅
=
⋅
=
C
C
A
21
10
84
40
)
(
=
=
A
P
Zadanie 18 Ze zbioru
{
}
7
;...;
2
;
1
losujemy jednocześnie dwie liczby. Oblicz
prawdopodobieństwo wylosowania dwóch liczb, których suma jest parzysta.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu dwóch liczb ze zbioru
7-mio elementowego.
21
!
5
!
2
!
7
2
7
=
⋅
=
=
Ω
C
A – zbiór zdarzeń sprzyjających, polegających na wylosowaniu dwóch liczb, których suma
jest parzysta (dwie liczby parzyste lub dwie nieparzyste).
9
6
3
!
2
!
2
!
4
!
1
!
2
!
3
2
4
2
3
=
+
=
⋅
+
⋅
=
+
=
C
C
A
7
3
21
9
)
(
=
=
A
P
Podstawowe właściwości prawdopodobieństwa
6
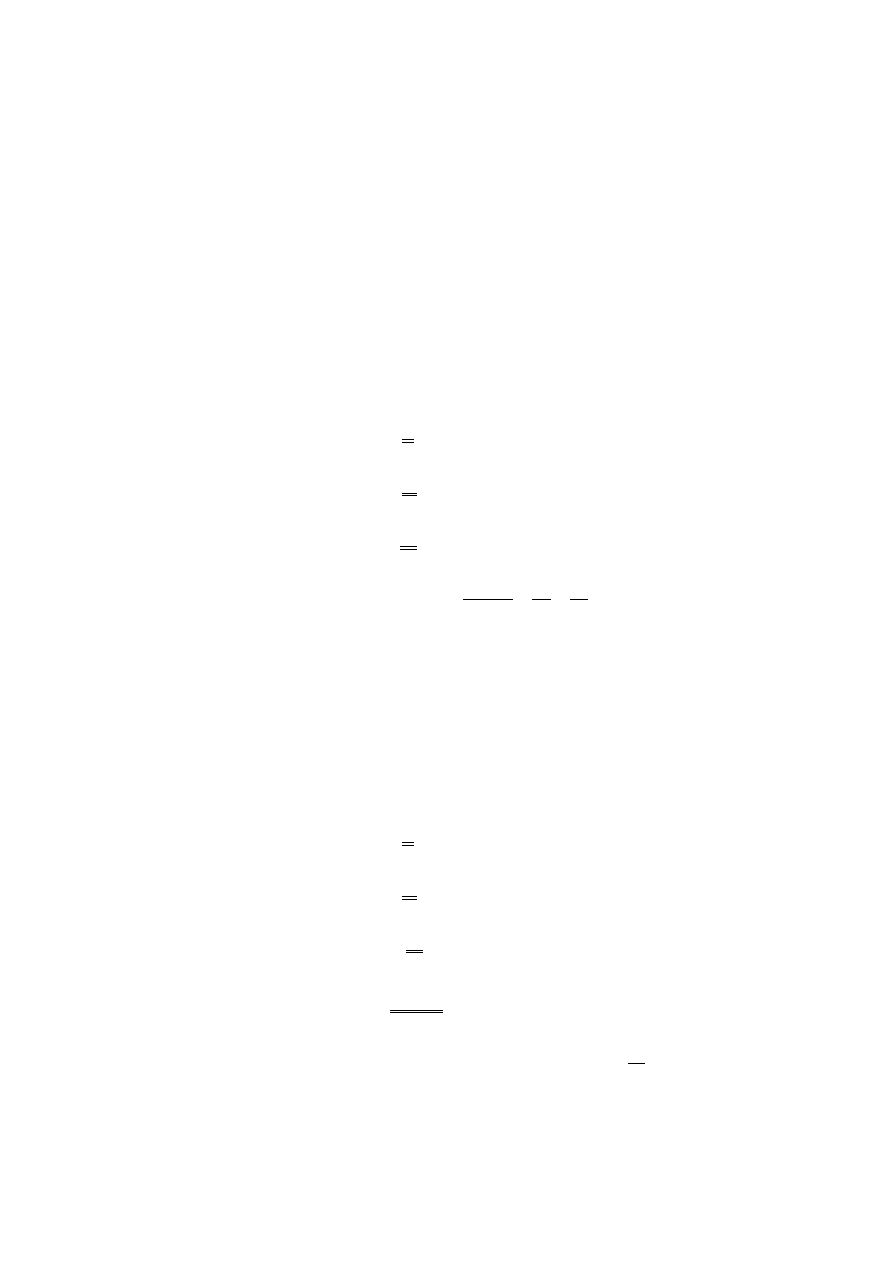
Właściwość 1
Prawdopodobieństwo P(A) zdarzenia pewnego równa się 1
Właściwość 2
Prawdopodobieństwo P(A) zdarzenia niemożliwego równa się 0.
Właściwość 3
Prawdopodobieństwo P(A) każdego zdarzenia spełnia nierówność
( )
0
1
P A
Ł
Ł
Właściwość 4
Prawdopodobieństwo zdarzenia A polegającego na zajściu jednego z dwu wykluczających się
zdarzeń A
1
lub A
2
równa się sumie prawdopodobieństw
( )
(
)
( )
( )
1
2
1
2
P A
P A
A
P A
P A
=
=
+
Č
Zadanie 19 Obliczyć prawdopodobieństwo, że losując z talii 52 kart jedną kartę, otrzymamy
pika lub kiera.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu jednej karty z 52.
1
52
Ω
52
C
=
=
A
1
– zbiór zdarzeń sprzyjających, polegających na wylosowaniu pika
1
1
12
12
A
C
=
=
A
2
– zbiór zdarzeń sprzyjających, polegających na wylosowaniu kier
1
2
12
12
A
C
=
=
( )
(
)
1
2
12 12
24
6
52
52 13
P A
P A
A
+
=
=
=
=
Č
Właściwość 5
Prawdopodobieństwo zdarzenia A polegającego na zajściu przynajmniej jednego ze zdarzeń
A
1
, A
2
równa się sumie prawdopodobieństw tych zdarzeń zmniejszonej o
prawdopodobieństwo łącznego ich zajścia
( )
(
)
( )
( )
(
)
1
2
1
2
1
2
P A
P A
A
P A
P A
P A
A
=
=
+
−
∩
Č
Zadanie 20 Obliczyć prawdopodobieństwo tego, że losując z talii 52 kart jedną kartę,
otrzymamy pika lub asa.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu jednej karty z 52.
1
52
Ω
52
C
=
=
A
1
– zbiór zdarzeń sprzyjających, polegających na wylosowaniu pika
1
1
12
12
A
C
=
=
A
2
– zbiór zdarzeń sprzyjających, polegających na wylosowaniu asa
1
2
4
4
A
C
=
=
1
2
A
A
∩
- zbiór zdarzeń sprzyjających polegający na wylosowaniu asa pik
1
1
2
1
1
A
A
C
∩
=
=
( )
(
)
( )
( )
(
)
1
2
1
2
1
2
4
13
P A
P A
A
P A
P A
P A
A
=
=
+
−
∩
=
Č
Właściwość 6
7
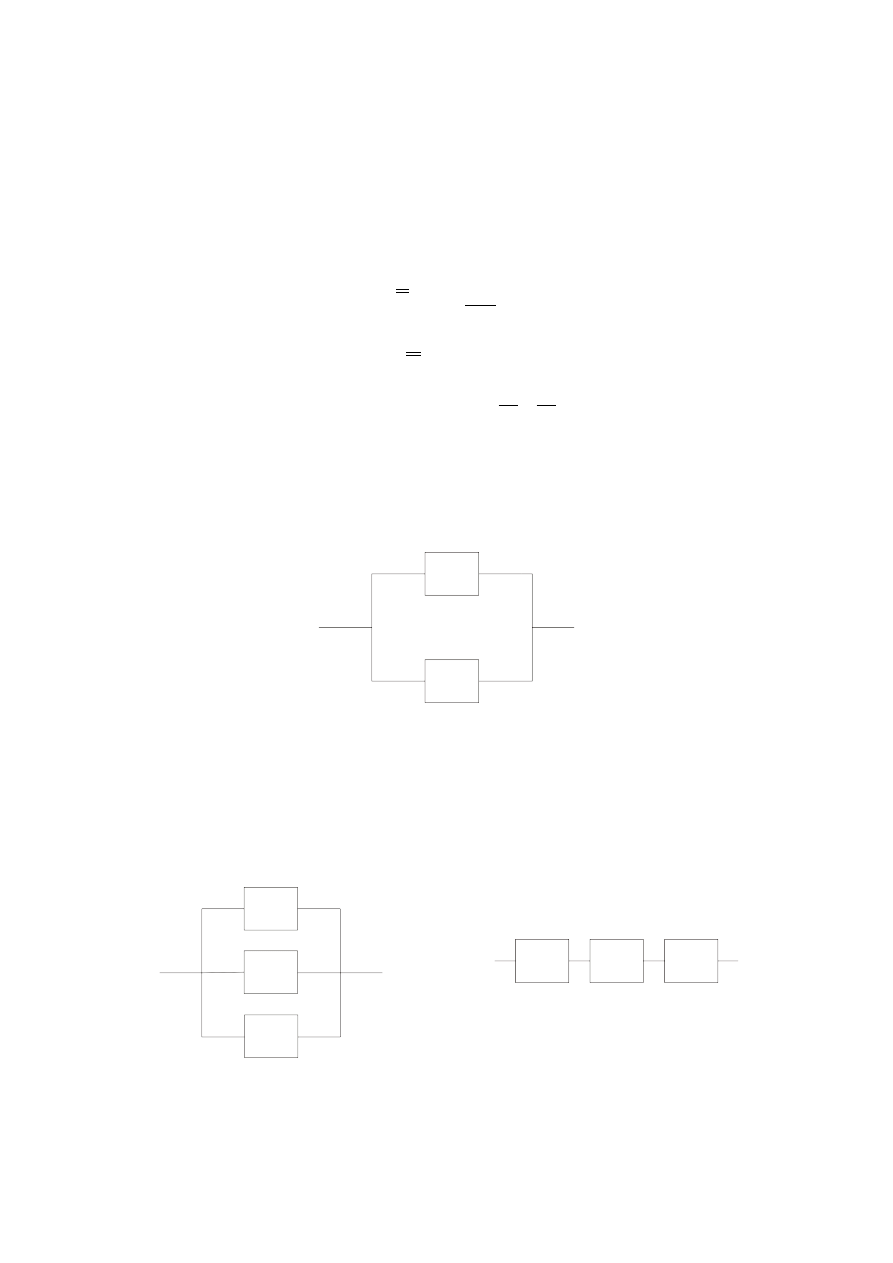
Prawdopodobieństwo zajścia zdarzenia przeciwnego zdarzeniu A równa się jedności
zmniejszonej o prawdopodobieństwo zdarzenia A
( )
( )
1
P A
P A
˘
= −
Zadanie 21 Z pojemnika w którym znajduje się 5 kul białych oraz 4 czarne losujemy
jednocześnie 3 kule. Oblicz prawdopodobieństwo otrzymania co najmniej 1 kuli białej.
Rozwiązanie:
Ω – przestrzeń zdarzeń elementarnych, polegających na wylosowaniu jednocześnie 3 kul z 9
3
9
9!
Ω
6!3!
C
=
=
A’ – zbiór zdarzeń niesprzyjających, polegających na wylosowaniu 3 kul czarnych
3
4
4
A
C
˘
=
=
( )
( )
4
20
1
1
84
21
P A
P A˘
= −
= −
=
Zadanie 22 Na rysunku przedstawiono schemat fragmentu sieci komputerowej. Niech A
i
,
i = 1, 2, oznacza zdarzenie, że hub a
i
będzie sprawny co najmniej przez czas t. Obliczyć
prawdopodobieństwo poprawnego działania sieci co najmniej przez czas t jeżeli
P(A
1
) = P(A
2
) = p oraz P(A
1
A
2
) = p
2
Rys.1
P(A) – prawdopodobieństwo bezawaryjnego działania sieci w czasie t
( )
( )
(
)
( )
(
)
(
) (
)
2
1
2
1 1
1
1 1
1
2
P A
P A
P A
p
p
p p
= − −
−
= − −
−
=
−
Zadanie 23 Obliczyć niezawodność sieci komputerowych złożonych z trzech hubów
połączonych a) równolegle, b) szeregowo, przy założeniu, że huby działają niezależnie i
niezawodność każdego z nich jest p
a)
b)
Rys.2
a)
( )
(
)
3
3
2
1 1
3
3
P A
p
p
p
p
= − −
=
−
+
b)
( )
3
P A
p
=
Zadanie 24 W każdej chwili odcinka czasu T jednakowo możliwe jest nadejście do
odbiornika każdego z dwóch sygnałów, które w tym odcinku czasu zostaną przesłane.
8
a
1
a
2
Odbiornik nie może przyjąć drugiego sygnału, jeśli nadejdzie on w czasie krótszym niż τ od
chwili nadejścia wcześniejszego sygnału. Obliczyć prawdopodobieństwo przyjęcia przez
odbiornik obu sygnałów.
Rozwiązanie: niech x i y oznaczają chwile nadejścia sygnałów do odbiornika, wtedy
warunkiem poprawnego odbioru obu sygnałów przez odbiornik jest następujący |x - y| > τ
Rys.3
( )
(
)
(
)
2
2
2
2
1
1
2
2
1
T
T
P A
T
T
τ
τ
τ
−
+
−
ć
=
=
−
č
ř
Zadanie 25 Dwa źródła napięcia sinusoidalnego o jednakowej częstotliwości są włączone
niezależnie od siebie. Obliczyć prawdopodobieństwo, że różnica faz między generowanymi
sinusoidami nie będzie większa niż 30 stopni.
( )
(
)
30
30
1
360
6
P A
− −
=
=
Prawdopodobieństwo warunkowe
Prawdopodobieństwem warunkowym P(A|B) zdarzenia A przy założeniu, że zaszło zdarzenie
B nazywamy iloraz prawdopodobieństwa łącznego zajścia zdarzeń A i B i
prawdopodobieństwa zdarzenia B
( )
(
)
( )
P A B
P A B
P B
∩
=
Zadanie 21
W urnie znajdują się 3 kule białe i 4 kule czarne. Jakie jest prawdopodobieństwo zajścia
zdarzenia AB polegającego na otrzymaniu dwóch kul białych, przy założeniu, że losujemy z
urny dwa razy i po pierwszym losowaniu kula nie zostaje zwrócona do urny?
Ω – przestrzeń zdarzeń elementarnych polegających na wylosowaniu jednej kuli z urny
Ω 7
=
A – zbiór zdarzeń sprzyjających polegających na wylosowaniu kuli białej
3
A
=
9
T
T
τ
τ
x
y
( )
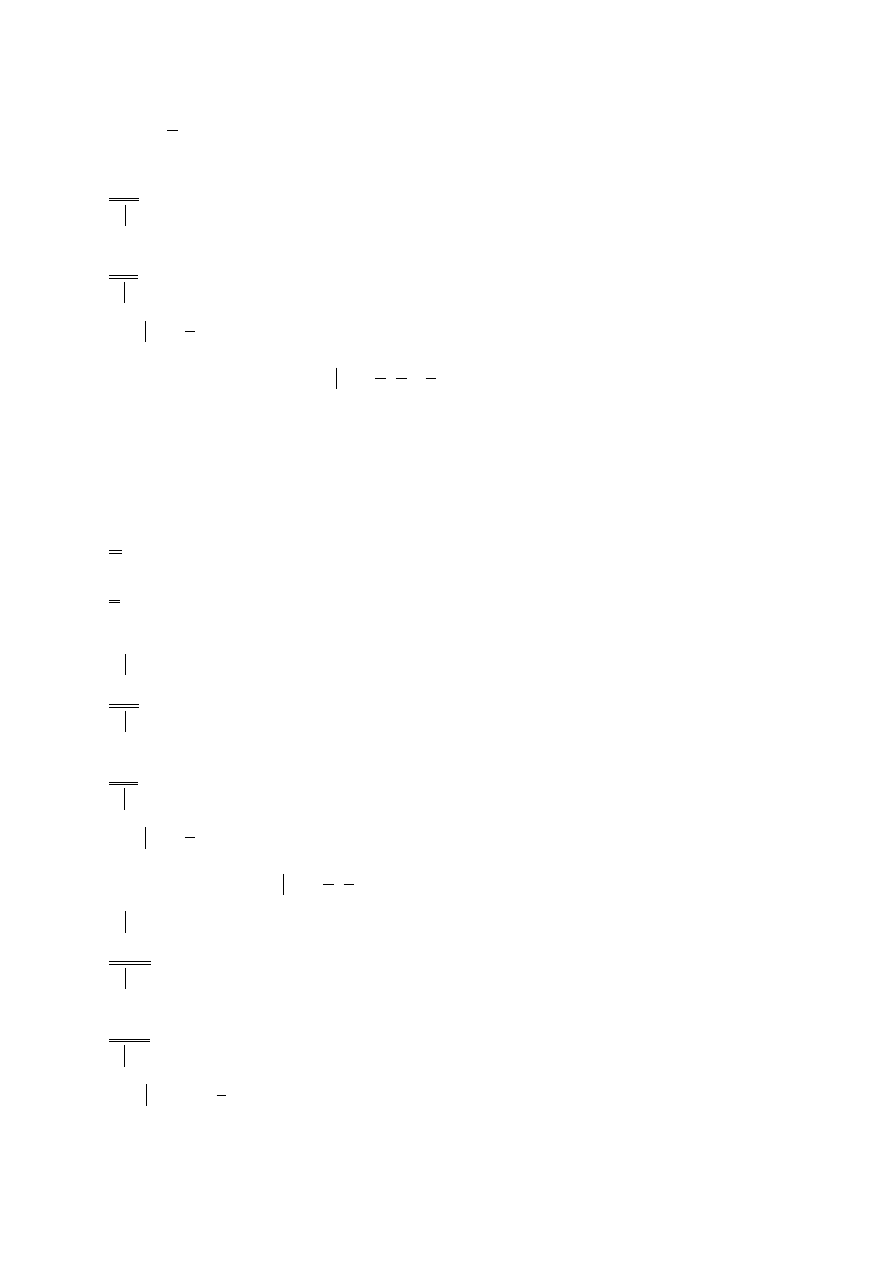
3
7
P A
=
Ω|A – przestrzeń zdarzeń elementarnych polegających na wylosowaniu kuli z urny, pod
warunkiem, że wcześniej wyciągnięto jedną kulę
Ω
6
A
=
B|A – zbiór zdarzeń sprzyjających polegających na wylosowaniu kuli białej pod warunkiem,
że wcześniej wylosowano kulę białą
2
B A
=
( )
2
6
P B A
=
( )
(
)
( )
( )
3 2
1
7 6
7
P C
P A B
P A P B A
=
∩
=
= ⋅ =
Zadanie 22
Słowo tatarak złożono z kartek, na których umieszczone zostały poszczególne litery alfabetu.
Kartki z literami tworzącymi to słowo dokładnie zmieszano, aby następnie kolejno wyciągnąć
cztery z nich i ułożyć w szereg. Jakie jest prawdopodobieństwo, że otrzymano w ten sposób
słowo tata?
Rozwiązanie
Ω
- przestrzeń zdarzeń elementarnych polegających na wylosowaniu 1 kartki
Ω 7
=
A – zbiór zdarzeń sprzyjających polegających na wyciągnięciu litery „t”
1
2
2
A C
=
=
P(A) = 2/7
Ω A - przestrzeń zdarzeń elementarnych polegających na wylosowaniu 1 litery pod
warunkiem, że wcześniej wylosowano jedną literę
Ω
6
A
=
B|A – zbiór zdarzeń sprzyjających polegających na wylosowaniu litery „a” pod warunkiem,
że wcześniej wylosowano literę „t”
3
B A
=
( )
3
6
P B A
=
(
)
( )
( )
2 1
7 2
P A B
P A P B A
∩
=
⋅
= ⋅
Ω AB - przestrzeń zdarzeń elementarnych polegających na wylosowaniu litery pod
warunkiem, że wcześniej wylosowano 2 literki
Ω
5
AB
=
C|AB – zbiór zdarzeń sprzyjających polegających na wylosowaniu literki „t” pod warunkiem,
że wcześniej wylosowano literki t i a
1
C AB
=
(
)
1
5
P C A B
∩
=
10
(
)
(
)
(
)
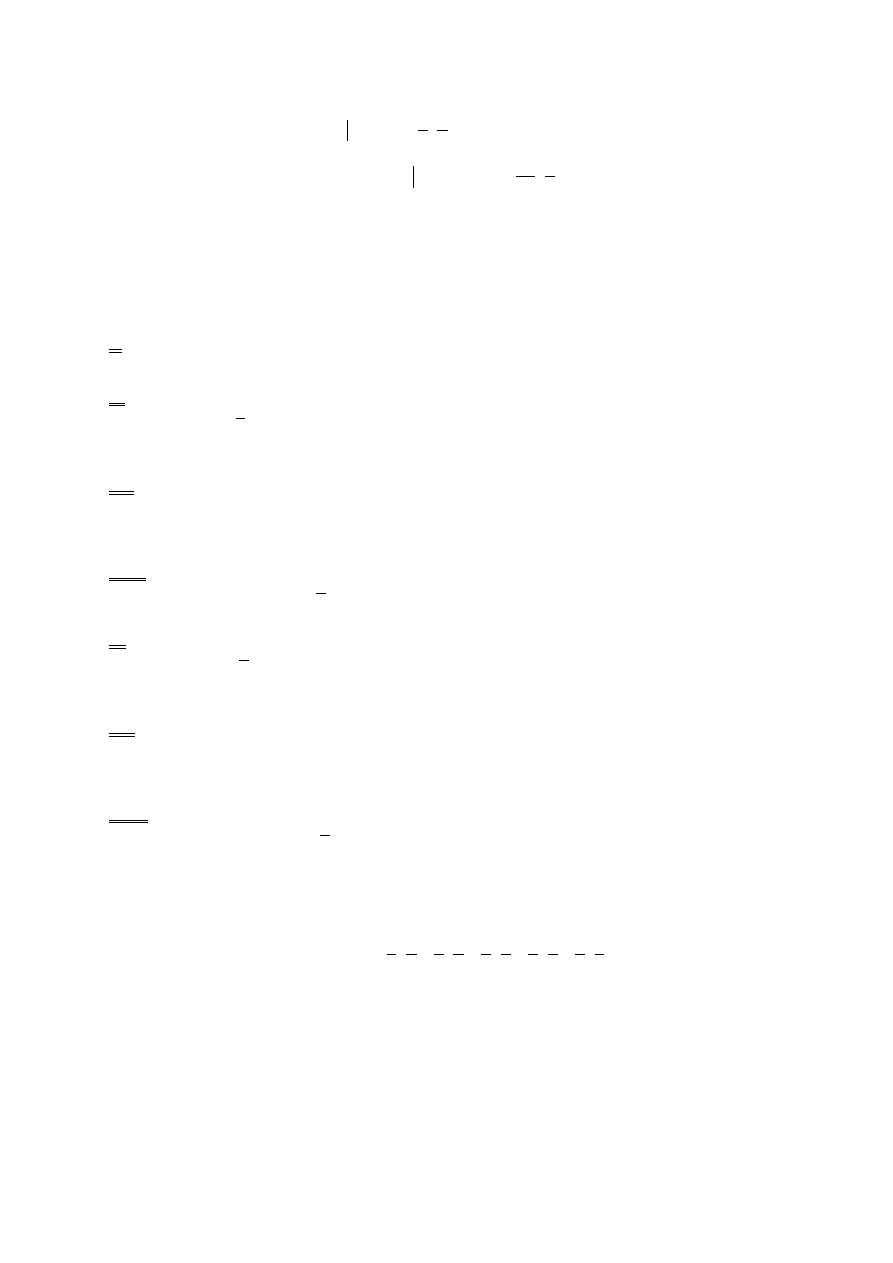
1 1
5 7
P A B C
P A B P C A B
∩ ∩
=
∩
⋅
∩
= ⋅
(
)
(
)
(
)
1 1
35 2
P A B C
D
P A B C P D A B C
∩ ∩
∩
=
∩ ∩
⋅
∩ ∩
=
⋅
Zadanie 23
Mamy 5 urn, z których 2 zawierają po jednej białej i 5 czarnych kul, jedna urna – 2 białe i 5
czarnych kul, pozostałe zaś dwie urny – po 3 białe i po 5 czarnych kul. Wybiera się losowo
jedną urnę i z niej również losowo wyciąga się jedną kulę. Jakie jest prawdopodobieństwo
wyciągnięcia białej kuli?
Ω
- przestrzeń zdarzeń elementarnych polegających na wylosowaniu urny
Ω 5
=
A
1
– zbiór zdarzeń sprzyjających polegających na wylosowaniu pierwszej urny
1
1
1
1
( )
5
A
P A
=
=
Ű
1
Ω
A
– przestrzeń zdarzeń elementarnych polegających na wylosowaniu jednej kuli z pierwszej
urny
1
1
6
Ω
6
A
C
=
=
1
|
B A - zbiór zdarzeń sprzyjających polegających na wylosowaniu kuli białej pod warunkiem,
że wcześniej wylosowano pierwszą urnę
1
1
1
1
1
|
1
( | )
6
B A
C
P B A
=
=
=
Ű
A
2
– zbiór zdarzeń sprzyjających polegających na wylosowaniu drugiej urny
2
2
1
1
( )
5
A
P A
=
=
Ű
2
Ω
A
– przestrzeń zdarzeń elementarnych polegających na wylosowaniu jednej kuli z drugiej
urny
2
1
6
Ω
6
A
C
=
=
1
|
B A - zbiór zdarzeń sprzyjających polegających na wylosowaniu kuli białej pod warunkiem,
że wcześniej wylosowano drugą urnę
1
2
1
2
1
|
1
( |
)
6
B A
C
P B A
=
=
=
Ű
…….
ostatecznie otrzymujemy
( )
( ) (
)
( ) (
)
( ) (
)
( ) (
)
( ) (
)
( ) (
)
1
1
2
2
3
3
4
4
5
5
6
6
|
|
|
|
1 1 1 1 1 2 1 3 1 3
|
|
5 6 5 6 5 7 5 8 5 8
P B
P A P B A
P A P B A
P A P B A
P A P B A
P A P B A
P A P B A
=
+
+
+
+
+
+
= ⋅ + ⋅ + ⋅ + ⋅ + ⋅
Twierdzenie Bayesa
11