fizyka statystyczna

fizyka statystyczna

stan makroskopowy

p

y

układ - skończony obszar przestrzenny

(

ól

ś i i l

)

t

d

ik f

l

i

V T

(w szczególności izolowany)

termodynamika fenomenologiczna

p, V, T

teoria kinetyczno-molekularna

<v

2

>

termodynamika statystyczna

n(v)

stan makroskopowy

wyrównywanie temperatur:

czas rzędu l/v

s

, gdzie v

s

= 330 m/s (prędkość dźwięku)

s

1

10

9

ę

s

g

s

( ę

ę

)

weźmy: l = 1 m , t = 3 · 10

–3

s

to jest „długi” czas, zachodzi

zderzeń

s

stan mikroskopowy

p

y

3

19

cm

1

10

7

.

2

⋅

≈

N

i

= 1, 2, 3, ... N – numeruje cząstki

(

)

zi

yi

xi

i

i

i

v

v

v

z

y

x

,

,

,

,

,

(

)

zi

yi

xi

zi

yi

xi

p

p

p

q

q

q

,

,

,

,

,

pełna informacja o układzie:

lub

y

y

y

przestrzeń fazowa jest 6N wymiarowa

można przyjąć że są to wielkości losowe

...można przyjąć, że są to wielkości losowe

objętość zajmowana przez cząstkę: 10

–30

m

3

w przestrzeni fazowej objętość komórki
(co najwyżej z jedną cząstką):

3

=

z

y

x

dp

dp

dp

dz

dy

dx

ħ

postulat równego prawdopodobieństwa :

t

i

ó

i

tki

ik

t

ó

d

d b

z

y

x

p

p

p

y

w stanie równowagi wszystkie mikrostany są równoprawdopodobne

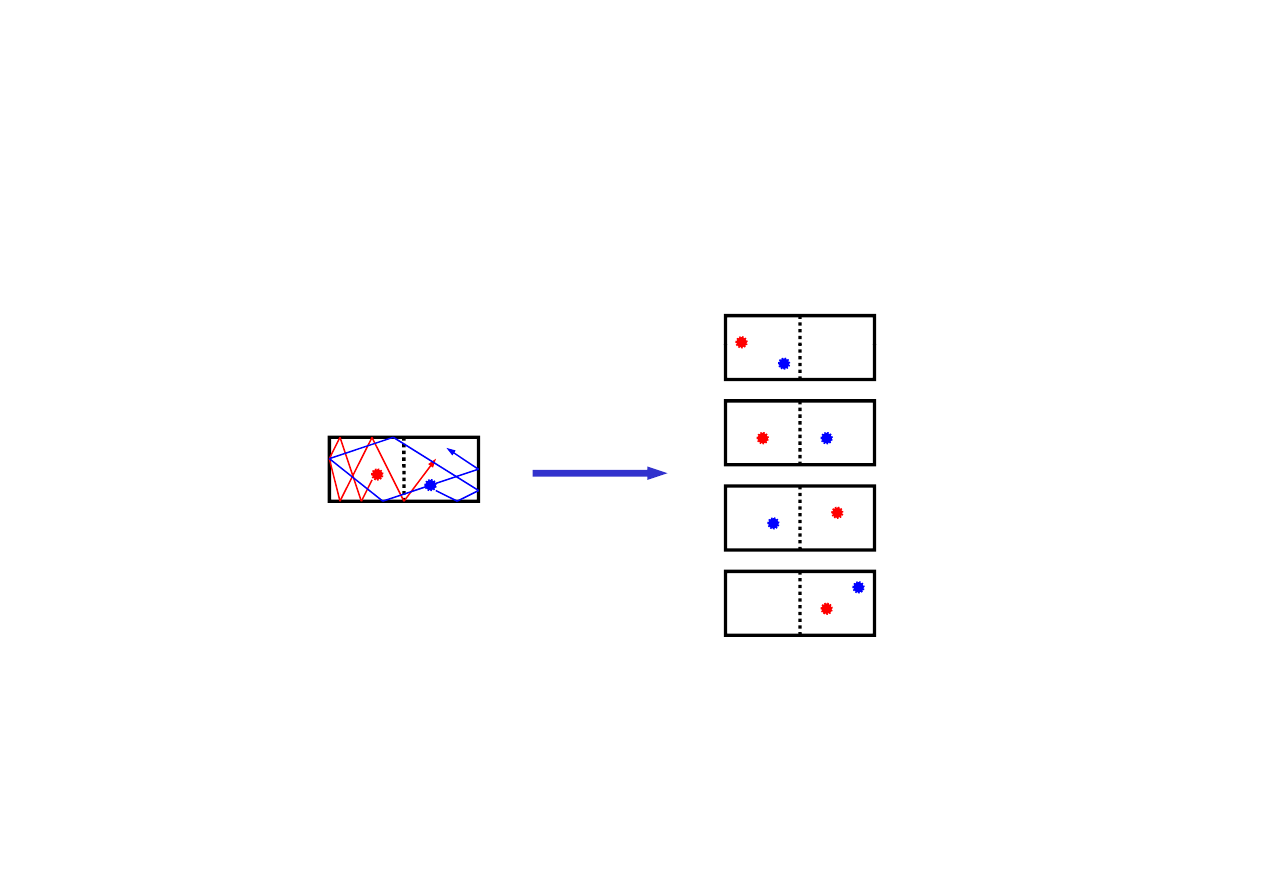
zespół statystyczny

p

y y

y

bió

i lki j li b

kł dó id

h

zbiór wielkiej liczby układów identycznych

hipoteza ergodyczna:

uśrednianie po czasie jest

równoważne uśrednianiu po zespole statystycznym

równoważne uśrednianiu po zespole statystycznym

stan równowagi

g

ź

kł d i l

k śl

h

h

k

weźmy układ izolowany o określonych parametrach makro:
∈ (E, E + dE)

Q(E)

ół t

ó

ik

Q(E)

– zespół stanów mikro

Ω(E) – liczba tych stanów

Jeżeli prawdopodobieństwa znalezienia układu izolowanego w
dowolnym mikrostanie spośród Q(E) są jednakowe to układ

dowolnym mikrostanie spośród Q(E) są jednakowe to układ
znajduje się w równowadze (statystycznej).

Jeżeli nie, to z upływem czasu układ będzie dążył do stanu, w

p y

ę

ą y

którym wszystkie dozwolone stany będą równoprawdopodobne.
Czyli układ dąży do stanu równowagi.

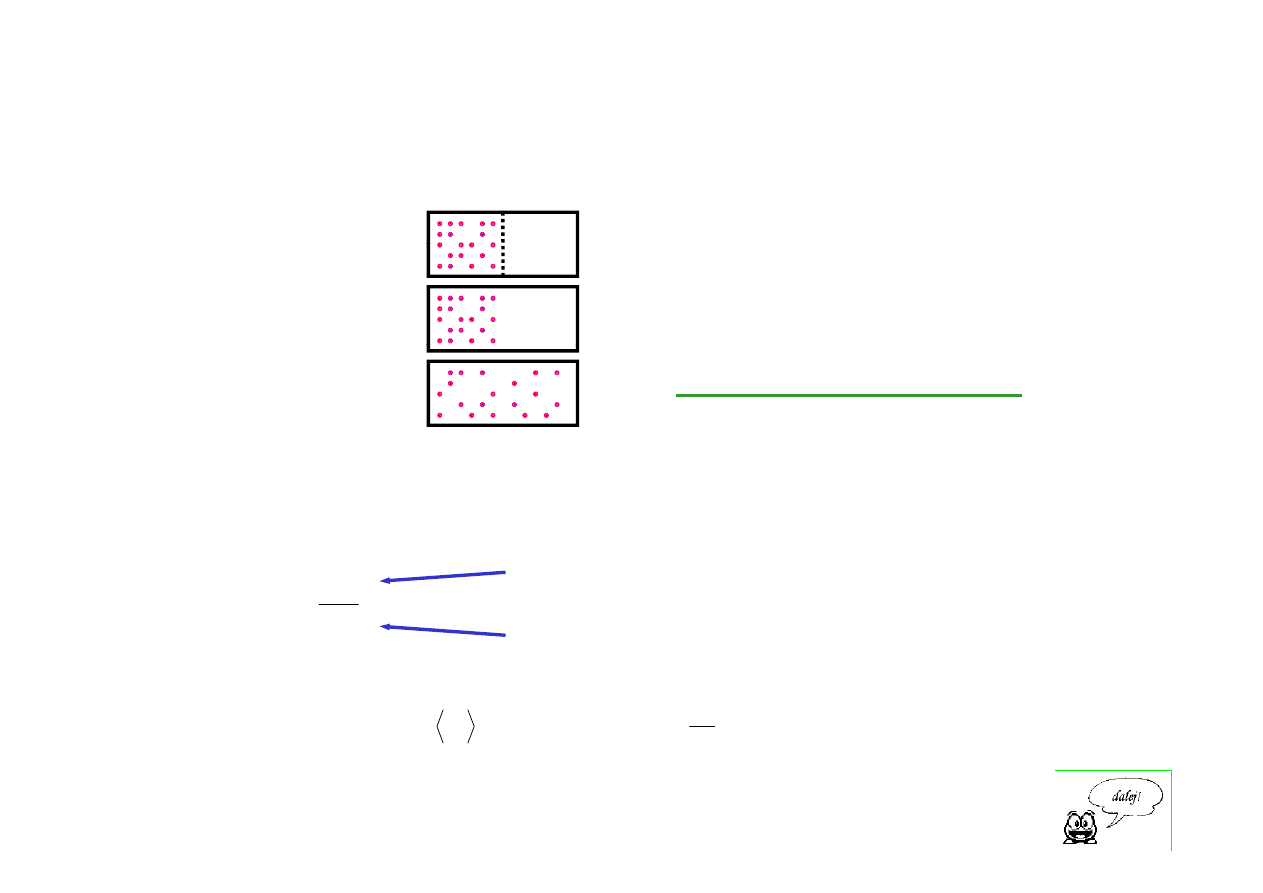
zespół mikrokanoniczny

p

y

j ż li

ki d

l

przykład:

jeżeli wszystkie dozwolone
stany z E = const są
jednakowo prawdopodobne to:

zespół mikrokanoniczny

wielkość y przyjmuje wartość y

j

w j – tym mikrostanie

( )

Ω

Ω

=

j

j

y

P

liczba wszystkich dozwolonych stanów

liczba stanów mających y = y

j

( )

∑

∑

Ω

Ω

=

=

N

j

j

j

N

j

j

j

y

y

y

P

y

1

1

1

liczba wszystkich dozwolonych stanów

=

=

Ω

j

j

1

1

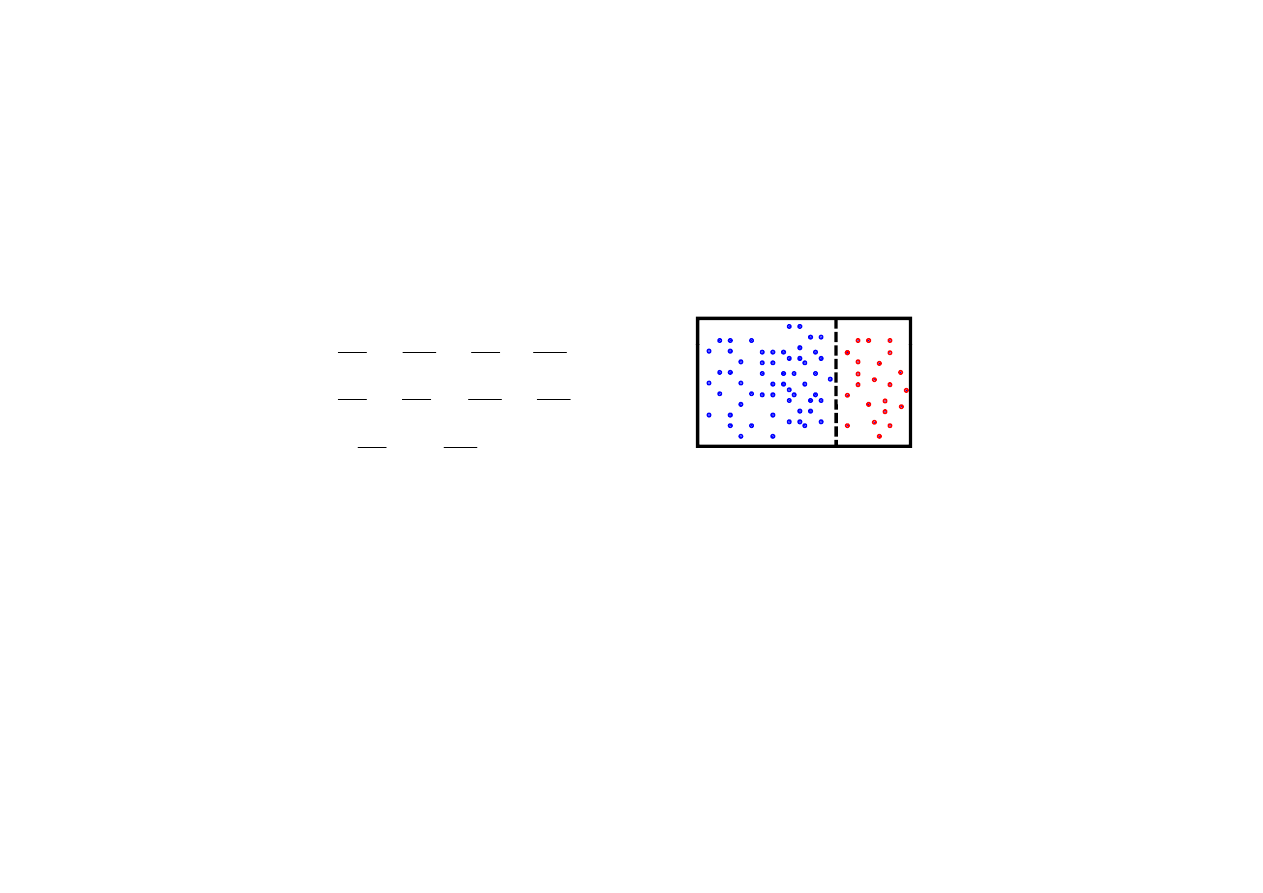
oddziaływanie termiczne

y

E

E

E

=

′′

+

′

=

const

E

E

E

E

E

E

E

E

′′

−

′′

=

′

−

′

′′

+

′

=

′′

+

′

0

0

0

0

Q

E

E

=

′′

Δ

=

′

Δ

K

przy oddziaływaniu termicznym nie zmieniają się wartości
poziomów energii tylko prawdopodobieństwa obsadzeń

ogólne oddziaływanie

g

y

∑

=

i

i

i

E

P

E

w procesie infinitezymalnym:

(

)

∑

∑

∑

+

=

+

=

i

i

i

i

i

i

i

i

i

dE

P

dP

E

dP

E

dE

P

E

d

∑

∑

i

i

W

Q

dU

δ

δ

−

=

czyli:

W

Q

dU

δ

δ

czyli:

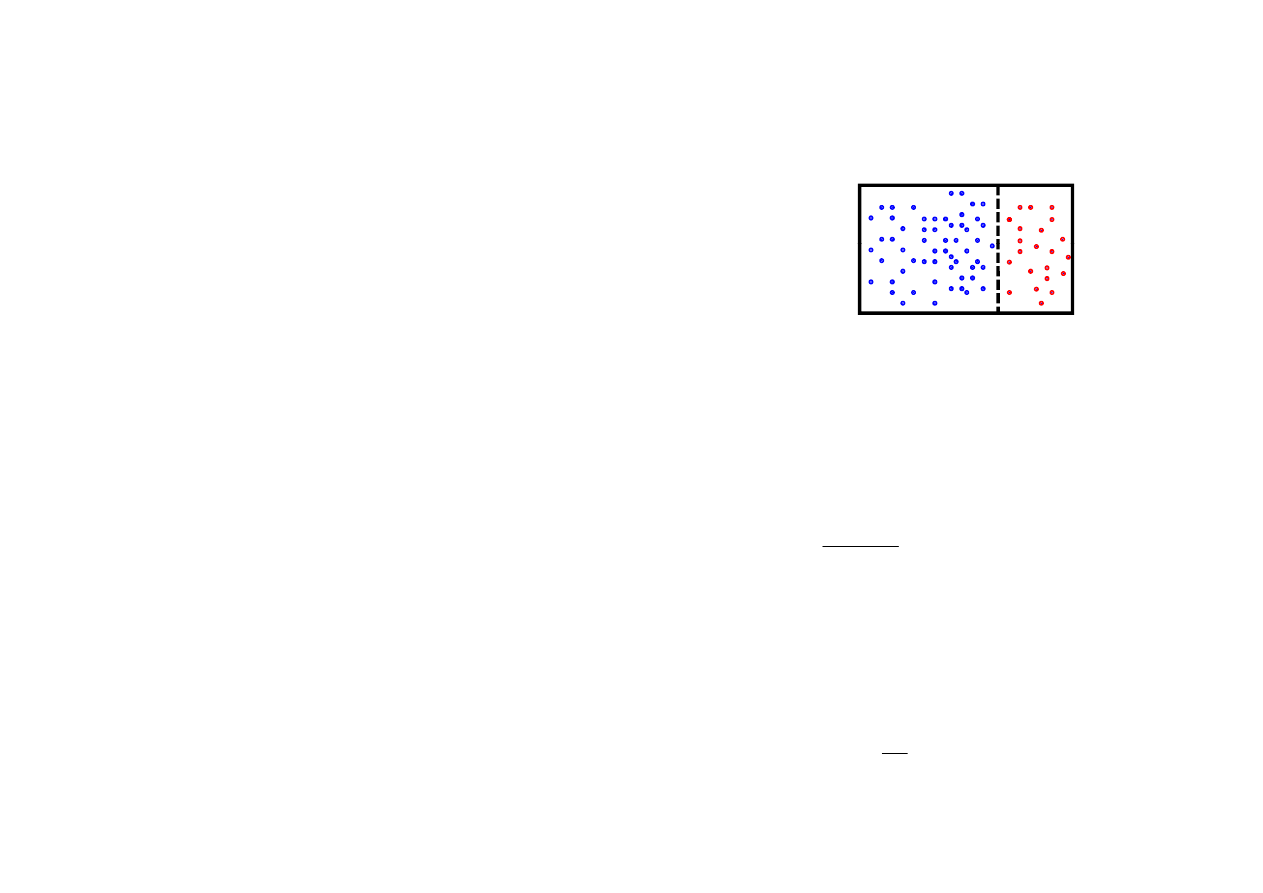
entropia statystyczna

p

y y

E´

+

E´´

=

E

kł d

ż

kł d

ó

d

zakładamy, że układy są w równowadze
termodynamicznej

liczba stanów w przedziale (E´, E´

+

dE´)

jest:

Ω´(E´)

liczba stanów w przedziale (E´´, E´´

+

dE´´)

jest:

Ω´´(E´´)

Jakie jest prawdopodobieństwo, że energia układu z lewej
jest w przedziale (E´, E´

+

dE´)

?

( )

( )

′

Ω

=

′

E

E

P

( )

Ω

=

E

P

Ω(E´) – liczba stanów pełnego układu z warunkiem

li b

ki h

ó

ł

kł d

Ω – liczba wszystkich stanów pełnego układu

( )

( ) (

)

E

E

E

E

P

′

Ω ′′

′

Ω′

=

′

1

Ω(E´) = Ω´(E´) Ω´´(E´´) = Ω´(E´) Ω´´(E E´)

( )

( ) (

)

E

E

E

E

P

−

Ω

Ω

Ω

=

Ω(E ) = Ω (E ) Ω (E ) = Ω (E ) Ω (E – E )

cd.

( )

( ) (

)

E

E

E

E

P

′

−

Ω ′′

′

Ω′

Ω

=

′

1

( )

( ) (

)

Ω

Ω

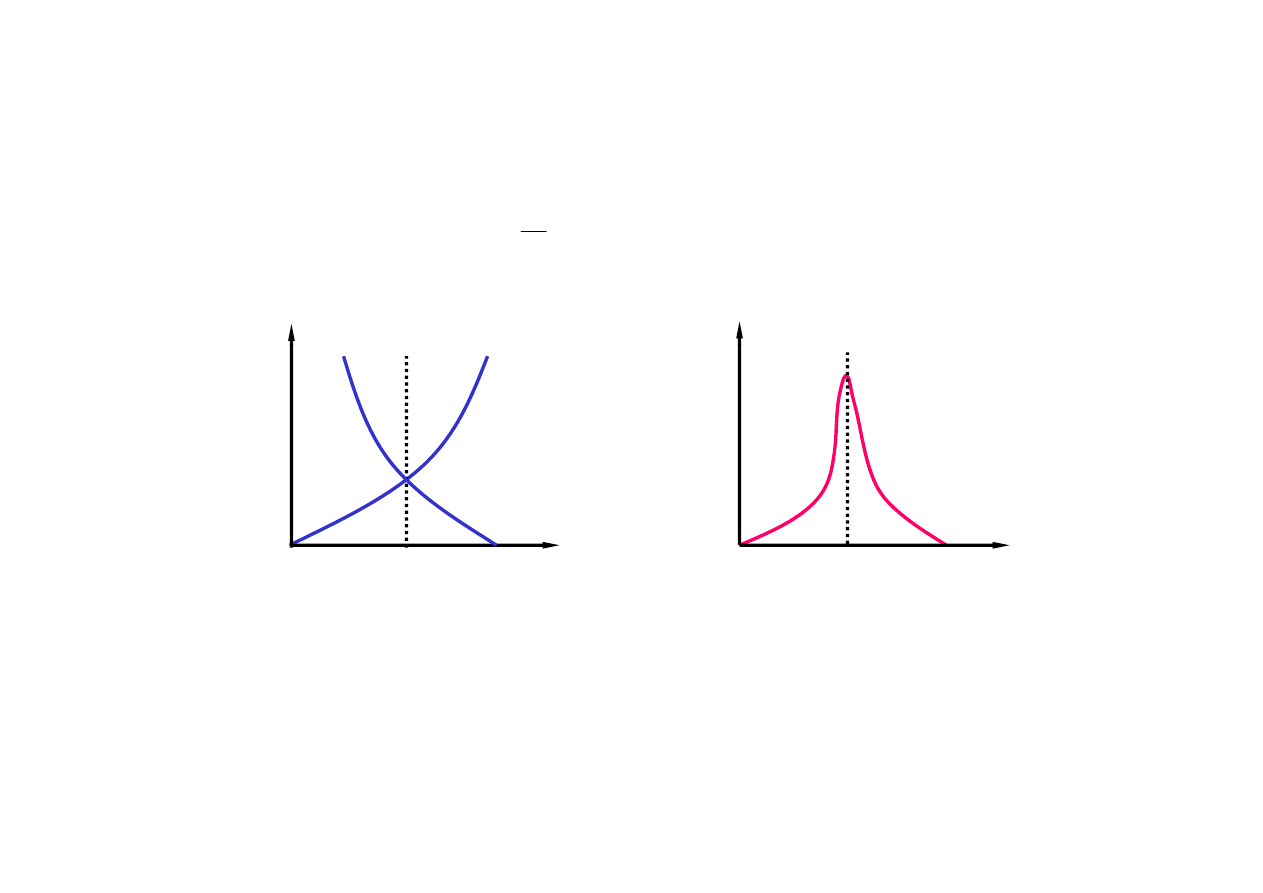
P(E´)

Ω

P(E´)

E´

E´

liczba stanów jest szybko rosnącą funkcją energii

liczba stanów jest szybko rosnącą funkcją energii

→ ostre maksimum

cd.

dwa podukłady osiągają równowagę właśnie przy energii

d

i d j

j t

k i

dP

odpowiadającej temu maksimum

0

=

′

E

d

dP

maksimum?

0

1

=

⎟

⎠

⎞

⎜

⎝

⎛

′

′′

∂

Ω ′′

∂

Ω′

−

′

′

∂

Ω′

∂

Ω ′′

Ω

=

E

d

E

E

d

E

dP

stąd:

E

E

′′

∂

Ω ′′

∂

Ω ′′

=

′

∂

Ω′

∂

Ω′

1

1

( )

( )

const

ln

ln

=

′′

∂

′′

Ω ′′

∂

=

′

∂

′

Ω′

∂

K

E

E

E

E

∂

∂

E

E

temperatura statystyczna

p

y y

( )

E

Ω

∂ ln

wniosek:

( )

E

E

∂

Ω

∂ ln

istnieje funkcja statystyczna

która osiąga jednakową wartość dla układów w równowadze

( )

E

1

ln

Ω

∂

która osiąga jednakową wartość dla układów w równowadze

k

t ł B lt

( )

kT

E

=

∂

def

k

- stała Boltzmanna

Ω

= ln

k

S

def

oznaczmy:

entropia statystyczna

l

t i

i

li b d

l

h t

ó

– logarytmiczna miara liczby dozwolonych stanów

– miara nieuporządkowania

1

−

⎟

⎞

⎜

⎛

∂

=

S

T

⎟

⎠

⎜

⎝

∂

=

E

T

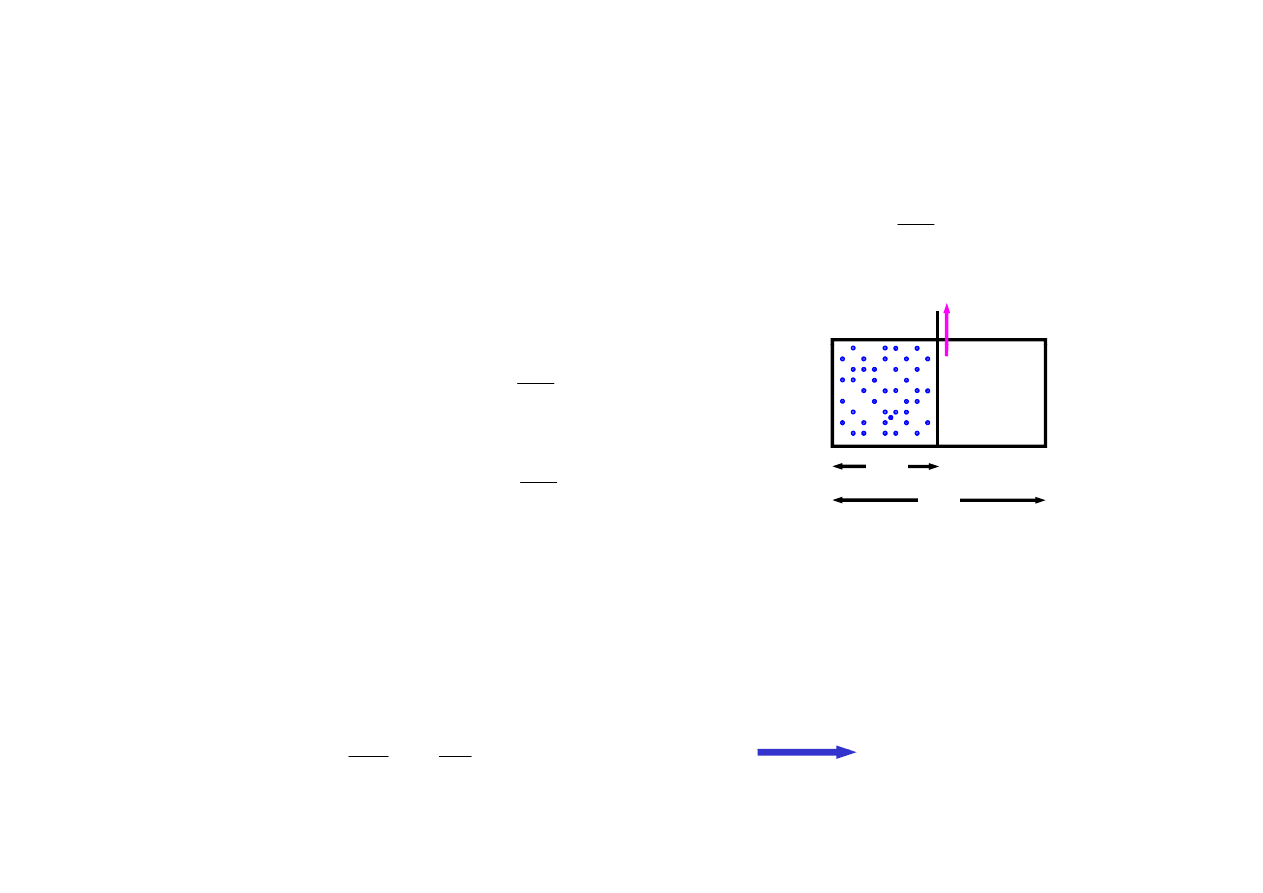
przykład

dz

dy

dx

d

=

τ

p y

y

( )

τ

d

V

1

1

1

≈

Ω

ilość dozwolonych stanów jednej cząstki:

τ

d

N

ilość dozwolonych stanów N cząstek:

( )

( )

( )

N

N

d

V ⎟

⎠

⎞

⎜

⎝

⎛

≈

Ω

Ω

Ω

=

Ω

τ

1

1

2

1

1

1

1

L

N

⎞

⎛

( )

( )

( )

N

N

d

V ⎟

⎠

⎞

⎜

⎝

⎛

≈

Ω

Ω

Ω

=

Ω

τ

2

2

2

2

1

2

2

L

V

1

V

2

w równowadze mikrostany są równoprawdopodobne

d

d bi ń t

ż

t

i

bj t ś i V

N

V

P

⎟⎟

⎞

⎜⎜

⎛

Ω

1

1

24

10

N

1

<<

P

prawdopodobieństwo, że gaz pozostanie w objętości V

1

:

V

P

⎟⎟

⎠

⎜⎜

⎝

=

Ω

=

2

1

2

1

24

10

≈

N

1

<<

P

przyrost entropii

p y

p

2

ln

ln

ln

Ω

=

Ω

−

Ω

=

−

=

Δ

k

k

k

S

S

S

1

1

2

1

2

ln

ln

ln

Ω

=

Ω

Ω

=

=

Δ

k

k

k

S

S

S

N

R

k

=

– stała Boltzmanna

A

N

2

2

ln

ln

V

R

k

S

ν

=

Ω

=

Δ

termodynamika fenomenologiczna

1

1

ln

ln

V

R

k

S

ν

Ω

Δ

E

Q

Δ

=

δ

E

Q

<<

δ

termodynamika fenomenologiczna…

ogólnie:

Q

δ

(

)

( )

L

+

∂

Ω

∂

+

Ω

=

+

Ω

Q

E

E

Q

E

δ

δ

ln

ln

ln

ogólnie:

∂E

(

)

( )

kT

Q

E

Q

E

δ

δ

=

Ω

−

+

Ω

ln

ln

T

Q

dS

δ

=

kT

T

rozkład kanoniczny

y

E

E

E

′′

+

′

=

E

E

′′

<<

′

dwa układy:

przy

jakie jest prawdopodobieństwo, że mały układ ma energię E´

i

?

y

y

(

)

i

i

E

E

P

′

−

Ω ′′

~

(

)

( )

( )

kT

E

E

E

E

E

E

E

i

i

i

′

−

Ω ′′

=

′

′′

∂

Ω ′′

∂

−

Ω ′′

≈

′

−

Ω ′′

ln

ln

ln

ln

kT

E

i

i

∂

(

)

( )

kT

E

E

E

E

i

i

−

Ω ′′

=

′

−

Ω ′′

exp

kT

kT

E

C

P

i

i

−

= exp

E

rozkład kanoniczny

1

exp

=

−

=

∑

∑

i

i

i

i

kT

E

C

P

1

exp

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=

∑

i

E

C

suma statystyczna

exp

⎟

⎠

⎜

⎝

∑

i

kT

C

suma statystyczna

cd.

E

średnia w zespole kanonicznym:

∑

∑

−

=

=

i

i

i

i

i

i

kT

E

y

C

y

P

y

exp

E

ogólna postać rozkładu kanonicznego;

( )

( )

kT

E

E

C

E

P

i

−

Ω

=

exp

w gazie

g

i d

k

ł

t

i

ó

i

tk

ż

w gazie doskonałym w stanie równowagi cząstkę gazu można
traktować jako mały układ i zastosować rozkład kanoniczny

(

)

z

y

x

i

i

p

p

p

z

y

x

E

E

,

,

,

,

,

=

(

)

kT

p

r

E

C

P

i

r

r,

exp −

=

z

y

x

dp

dp

dp

dz

dy

dx

kT

E

C

dP

−

= exp

1

=

∫

dP

cd.

i

tki

i d

k

ł

(

)

(

)

2

2

2

2

z

y

x

v

v

v

m

mv

v

v

v

z

y

x

E

+

+

=

=

energia cząstki w gazie doskonałym:

(

)

2

2

,

,

,

,

,

z

y

x

v

v

v

z

y

x

E

=

=

(

)

dv

dv

dv

d

mv

C

v

v

v

z

y

x

dP

τ

exp

2

−

=

(

)

z

y

x

z

y

x

dv

dv

dv

d

kT

C

v

v

v

z

y

x

dP

τ

2

exp

,

,

,

,

,

=

jest to prawdopodobieństwo, że

(

)

r

d

r

r

r

r

r +

∈ ,

(

)

współrzędne:

(

)

v

d

v

v

r

r

r

+

∈ ,

a prędkości:

cząstki poruszają się niezależnie więc zespół statystyczny

cząstki poruszają się niezależnie więc zespół statystyczny

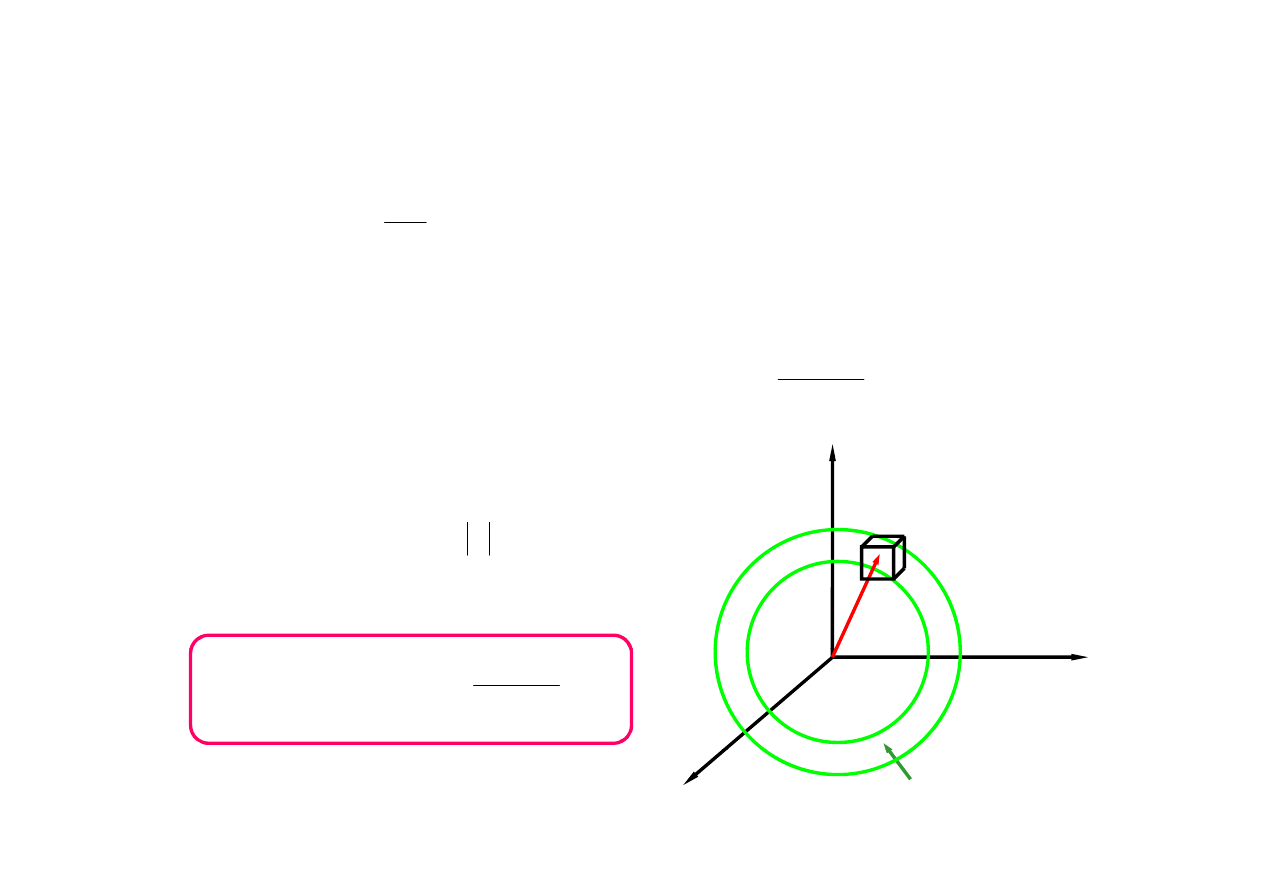
rozkład Maxwella prędkości

p ę

N

dN

dP

=

dN –

liczba cząstek w d

τ

N

(

)

v

d

v

v

r

r

r

+

,

2

z prędkościami w

( )

z

y

x

z

y

x

dv

dv

dv

kT

mv

C

dv

dv

dv

v

n

2

exp

2

−

=

r

kł d M

ll

dk ś i

rozkład Maxwella prędkości

pytanie:

( )

( )

?

=

=

v

n

v

n

r

v

z

pytanie:

( )

( )

v

r

( )

dv

kT

mv

v

C

dv

v

n

2

exp

2

2

−

=

v

v

y

objętość: 4

πv

2

dv

v

x

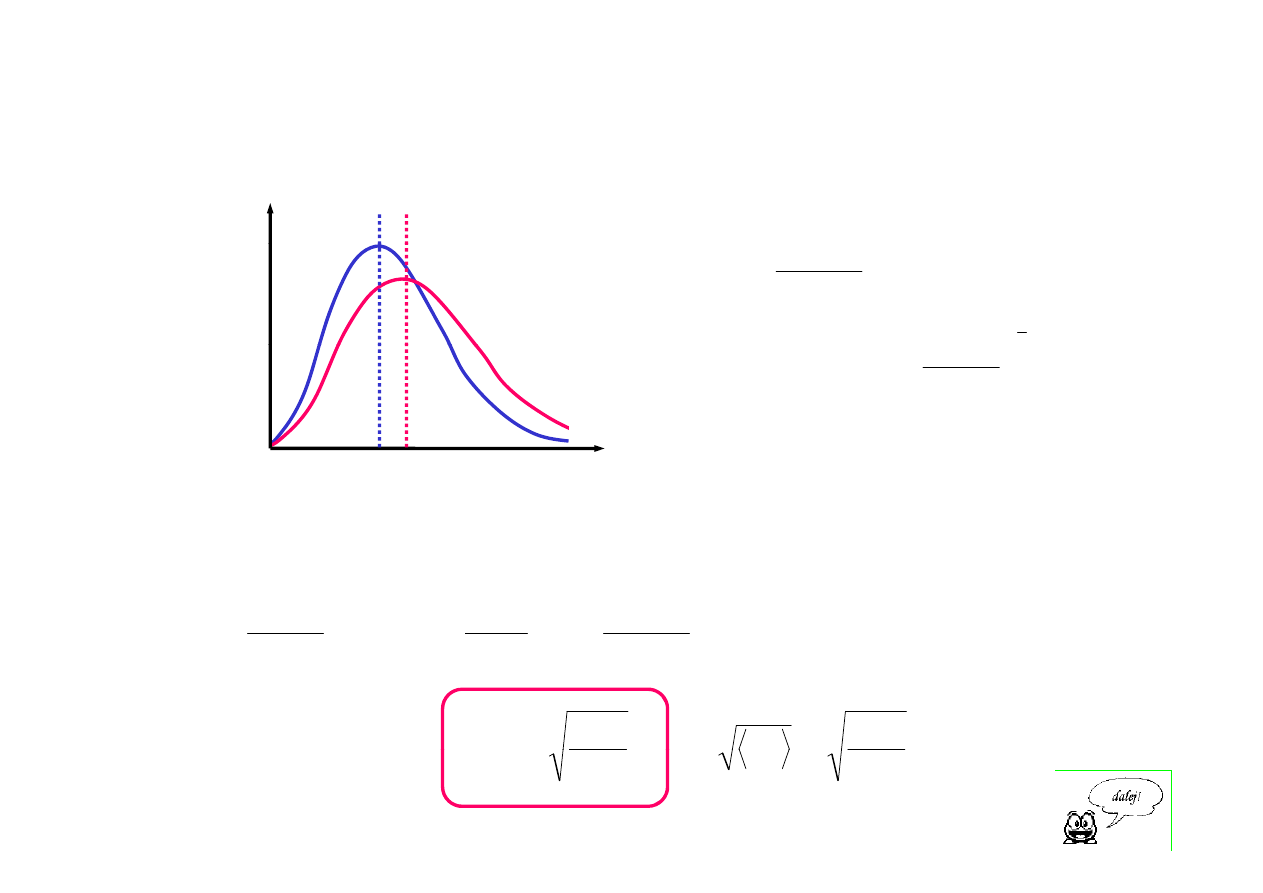
rozkład

2

n(v)

( )

kT

mv

v

C

v

n

2

exp

2

2

−

=

n(v)

2

3

⎞

⎛ m

2

2

4

⎟

⎠

⎞

⎜

⎝

⎛

=

kT

m

C

π

π

prędkość najbardziej prawdopodobna:

v

0

prędkość najbardziej prawdopodobna:

( )

0

2

exp

2

2

3

=

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=

kT

mv

kT

mv

v

C

dv

v

dn

2

⎠

⎝

kT

kT

dv

kT

v

2

=

kT

v

3

2

=

m

v

p

=

m

v

=

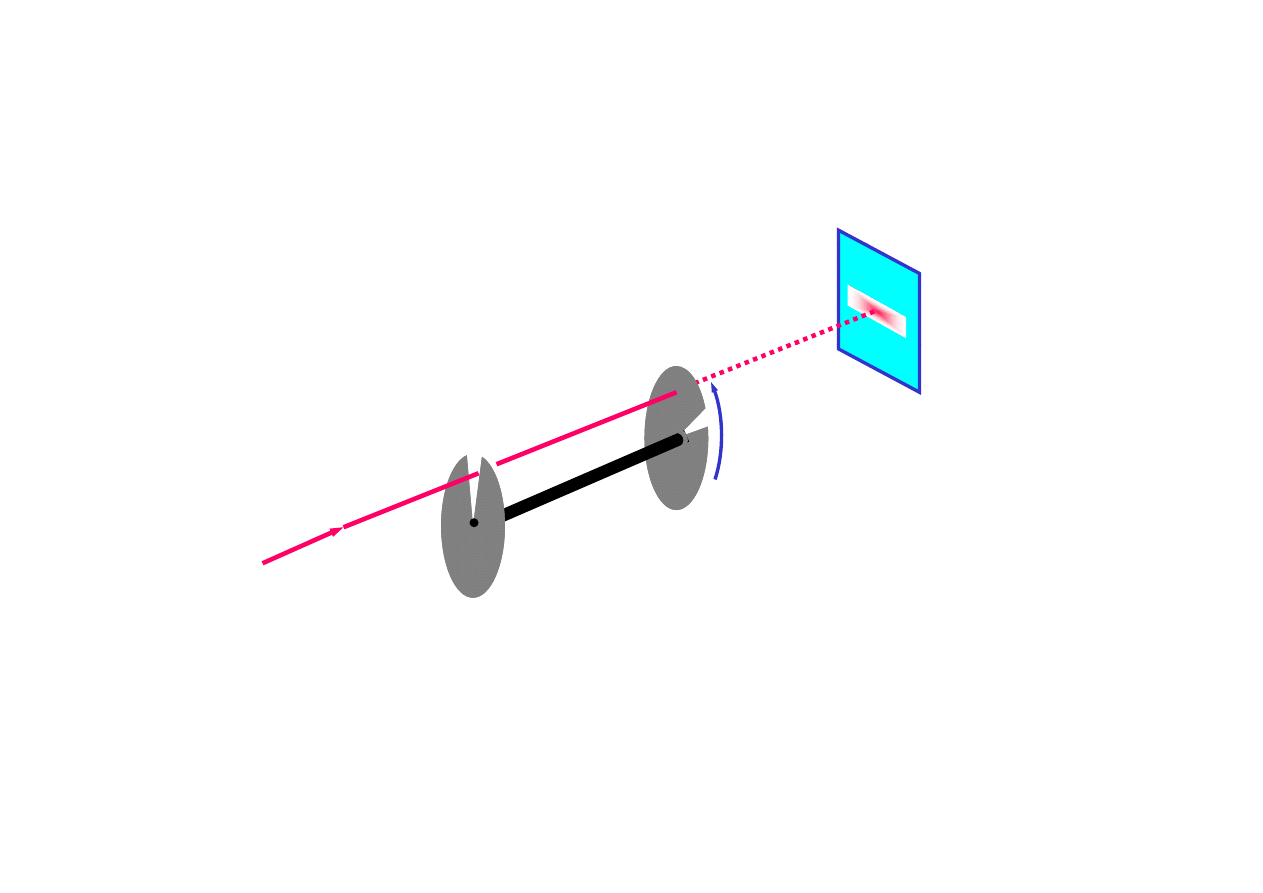
weryfikacja

y

j

Hg

ver-01