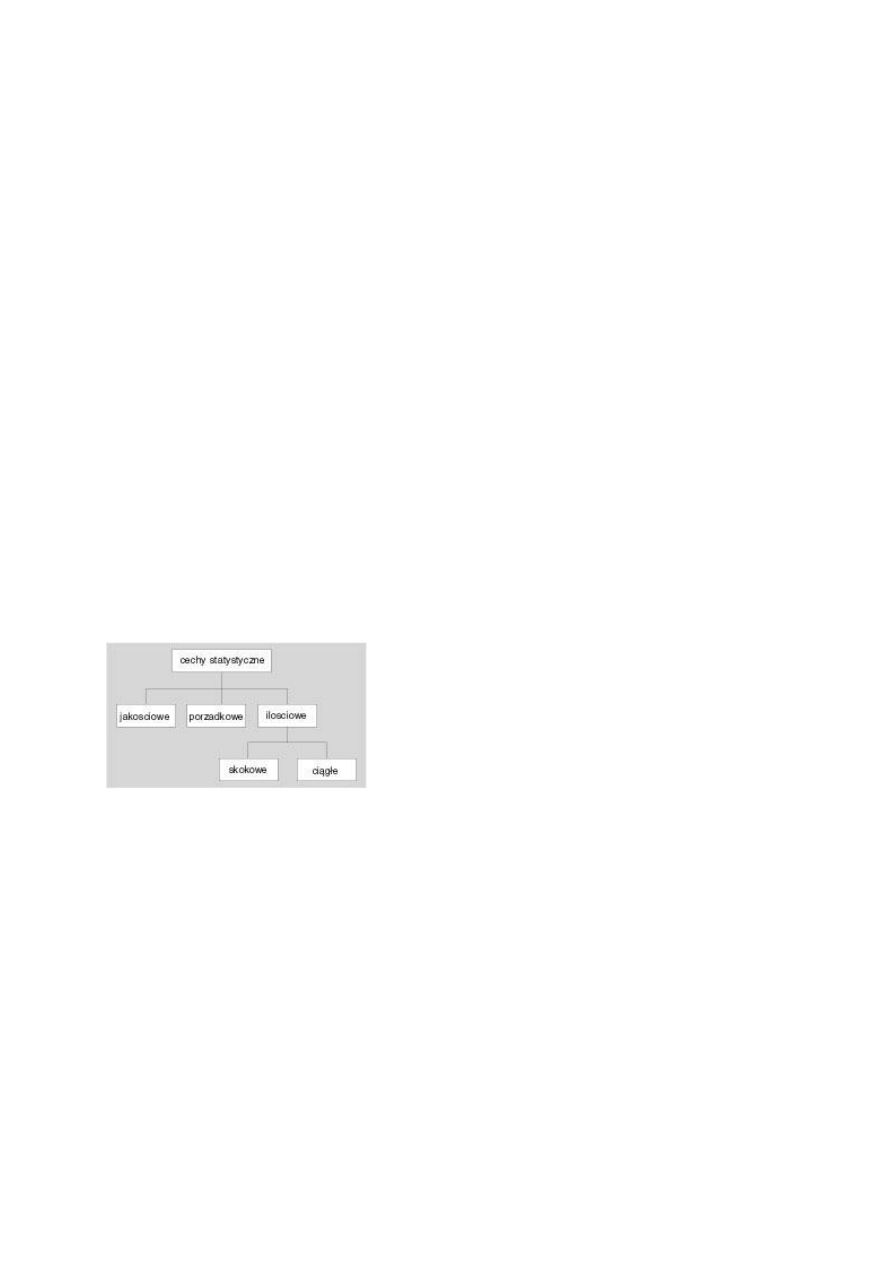
Rodzaje cech statystycznych
Statystyki opisowe - miary położenia

Podstawy statystyki dla prowadzących badania naukowe
Odcinek 2: Rodzaje cech statystycznych. Statystyki opisowe - miary położenia

mgr Andrzej Stanisz z Zakładu Biostatystyki i Informatyki Medycznej Collegium Medicum
UJ w Krakowie
Data utworzenia: 03.02.2000
Ostatnia modyfikacja: 30.04.2007
Opublikowano w Medycyna Praktyczna 1998/09

Po ustaleniu celu badania, określając zbiorowość statystyczną musimy również ściśle ustalić
co jest jednostką statystyczną. O każdej jednostce zbieramy bowiem informacje. Na
przykład niech celem badania będzie poznanie reakcji organizmu osób cierpiących na pewną
chorobę po podaniu nowo wyprodukowanego leku. Jednostką statystyczną będzie wówczas
każdy z 200 pacjentów leczonych na daną chorobę w określonym szpitalu. Właściwe
zdefiniowanie jednostek badanych jest bardzo ważne, ponieważ od tego zależy poprawność i
dokładność obrazu rzeczywistości. Cechy wyróżniające jednostki wchodzące w skład badanej
zbiorowości nazywamy cechami statystycznymi. Zbiorowość statystyczna może mieć dużo
rozmaitych cech. W zależności od celu badania wybieramy tylko niektóre z nich,
najważniejsze w odniesieniu do interesującego nas problemu.
Rozróżniamy trzy zasadnicze typy cech: jakościowe, porządkowe i ilościowe (rys. 1).

Rys 1.

Cechy jakościowe (niemierzalne) to takie, których nie można jednoznacznie
scharakteryzować za pomocą liczb (czyli nie można zmierzyć). Możemy je tylko opisać
słowami. Możliwa jest zatem jedynie zupełna i rozłączna klasyfikacja zbioru wyników.
Podstawową operacją pomiarową jest identyfikacja kategorii, do której należy zaliczyć
wynik. Prowadzi to do podziału zbioru wyników na podzbiory rozłączne. Do cech
jakościowych zaliczamy np. płeć, grupę krwi, kolor włosów, zgon lub przeżycie, stan
uodpornienia przeciwko ospie (zaszczepiony lub nie) itp. W przypadku grupy krwi rezultat
pomiaru będzie następujący: n1 pacjentów ma grupę krwi A, n2 pacjentów - grupę krwi B, n3
pacjentów - grupę AB i n4 - grupę O.

Cechy porządkowe umożliwiają porządkowanie (lub uszeregowanie) wszystkich elementów
zbioru wyników. Cechy takie najlepiej określa się przymiotnikami i ich stopniowaniem.
Każdemu ze stanów można również przypisać liczbę według wzrostu natężenia. Proces ten
nazywa się rangowaniem. Na przykład, badając wzrost osoby, możemy użyć określeń:
"niski", "średni" lub "wysoki". Podobnie, badając liczbę krwinek białych i używając określeń

"poniżej normy", "w normie" lub "powyżej normy" - mamy do czynienia ze skalą
porządkową.

Cechy ilościowe (mierzalne) to takie, które dadzą się wyrazić za pomocą jednostek miary w
pewnej skali. Cechami mierzalnymi są na przykład: wzrost (w cm), waga (w kg), stężenie
hemoglobiny we krwi (w g/dl), wiek (w latach) itp. Wśród cech mierzalnych wyróżniamy
dwie podgrupy: cechy ciągłe i cechy skokowe.

Cecha ciągła to zmienna, która może przyjmować każdą wartość z określonego skończonego
przedziału liczbowego, np. wzrost, masa ciała czy temperatura.
Cechy skokowe mogą przyjmować wartości ze zbioru skończonego lub przeliczalnego
(zwykle całkowite), na przykład: liczba łóżek w szpitalu, liczba krwinek białych w 1 ml krwi.

Z podziałem cech na jakościowe i ilościowe wiąże się również stosowanie różnych
statystycznych metod badania. Po wytypowaniu cech, które będą nas interesować w badaniu,
musimy podjąć decyzję, jak będziemy mierzyć wartości tych cech (bądź określać ich
odmiany, jeśli są niemierzalne) w trakcie obserwacji. Badając liczbę krwinek białych,
możemy ją określić jako "poniżej normy", "w normie" lub "powyżej normy", lub podać ich
liczbę w 1 ml krwi. Podobnie, badając wzrost pacjentów, możemy podać go w centymetrach
albo używać określeń: "niski", "średni", "wysoki". Wybór takiego czy innego pomiaru zależy
oczywiście od celu badania. Pamiętajmy jednak, że w trakcie opracowywania zgromadzonych
informacji możemy przejść od bardzo ścisłych i dokładnych pomiarów do określeń ogólnych,
natomiast odwrotna droga nie jest możliwa.

Rodzaje statystyk opisowych

Po zakończeniu etapu obserwacji, tzn. zebraniu wszystkich interesujących nas wyników,
otrzymujemy "surowy" materiał statystyczny. Zebrany materiał powinien być
usystematyzowany i odpowiednio opisany. Materiał liczbowy należy odpowiednio opisać
statystycznie.

Opis statystyczny to obliczenie pewnych charakterystyk liczbowych (zwanych
parametrami) badanych cech. Stanowi on punkt wyjścia do wnioskowania w przypadku
badania grupy losowej. Natomiast przeprowadzenie badania na skończonej zbiorowości
generalnej eliminuje konieczność użycia metod wnioskowania statystycznego, czyli
uogólniania wyników z grupy na całą populację. W przypadku badania pełnego mówimy o
parametrach populacji, natomiast w przypadku badania częściowego - o parametrach
próby (statystykach). Parametry tak charakteryzują zbiorowość, że porównywanie różnych
zbiorowości statystycznych można sprowadzić do porównań tych parametrów. Podstawowe
zadania parametrów opisowych to:
- określenie przeciętnej wielkości i rozmieszczenia wartości zmiennej - dokonujemy tego
przez obliczenie miar położenia;
- określenie granic obszaru zmienności wartości zmiennej - dokonujemy tego przez obliczenie
miar zmienności;
- określenie skupienia i spłaszczenia (w stosunku do kształtu krzywej normalnej) oraz stopnia
zmiany od idealnej symetrii - dokonujemy tego przez obliczenie miar asymetrii i
koncentracji.

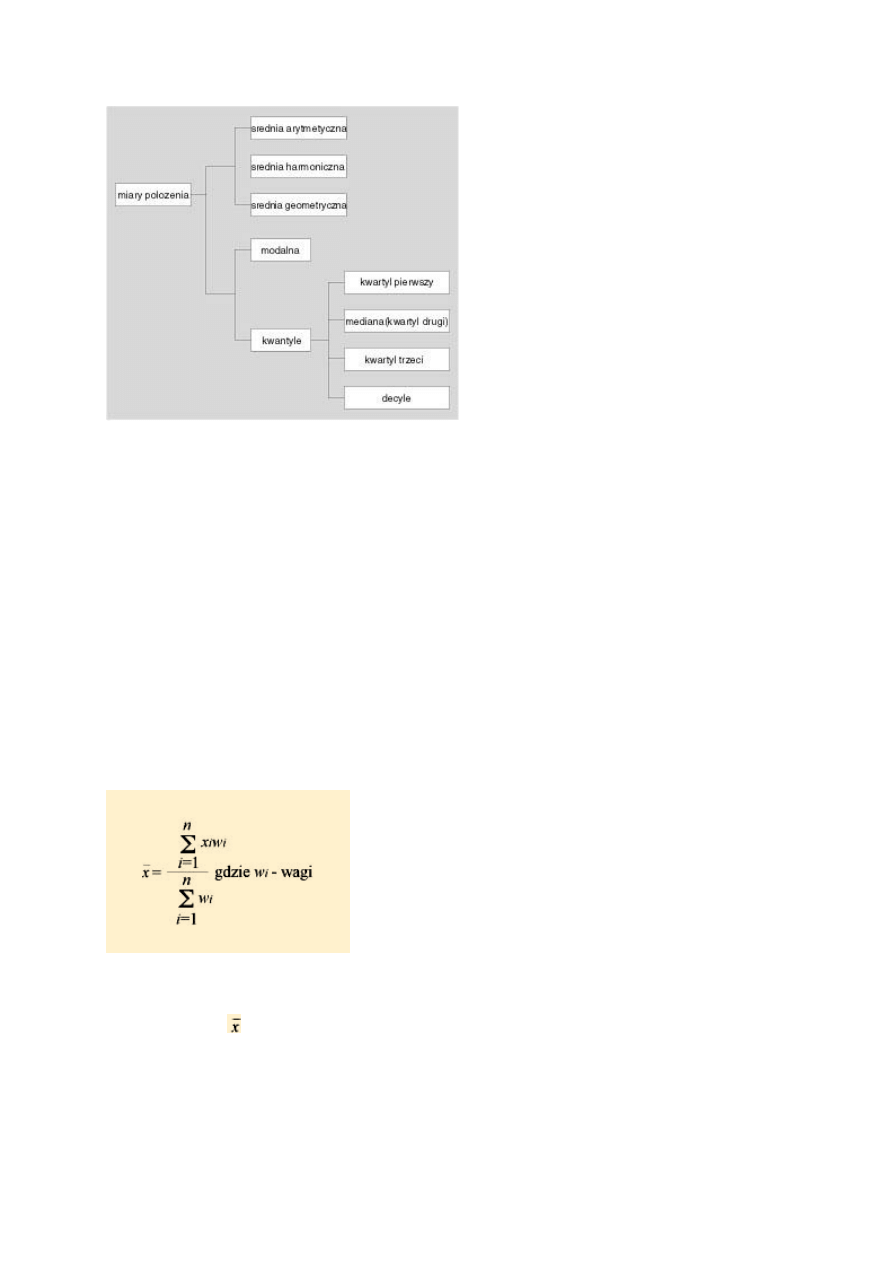
Rys 2. Miary położenia

Miary położenia

Dokładniejsze poznanie rodzajów i sposobów obliczania parametrów statystycznych
zaczniemy od miar położenia. Podział miar położenia przedstawia rysunek 2. Ich nazwa
wywodzi się stąd, że wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości
zmiennej. Miary przeciętne charakteryzują średni lub typowy poziom wartości zmiennej
(cechy), czyli mówią o przeciętnym poziomie rozważanej cechy. Miary te bywają też
nazywane miarami tendencji centralnej.

Średnie

Średnią arytmetyczną znamy oczywiście wszyscy. Średnia arytmetyczna jest najlepszą
miarą charakteryzującą rozkład cechy i dlatego jest najczęściej używana. Oblicza się ją ze
wszystkich uzyskanych winików pomiarów i ma ogromne znaczenie teoretyczne i praktyczne.
Często w praktyce (gdy pewnym pomiarom trzeba nadać większe znaczenie) oblicza się tzw.
średnią arytmetyczną ważoną według wzoru:

Przykład: wśród pacjentów przeprowadzono dwa testy psychomotoryczne - oba oceniane w
skali od 0 do 100. Psycholog uznał, że waga wyników testów powinna wynosić 2:3. Jeżeli
osoba otrzymała z pierwszego testu 40, a z drugiego 55 punktów, to średnia arytmetyczna
ważona wynosi: = (240+355)/(2+3) = 49 pkt.
Średnią możemy uważać za środek ciężkości lub punkt równowagi. Gdybyśmy wyniki
odmierzyli na jakimś pręcie i w każdym punkcie odpowiadającym wynikowi zawiesili takie
same odważniki, to średnia okazałaby się punktem w którym należałoby pręt podeprzeć, aby
zachować równowagę. Tak zinterpretował tę miarę belgijski astronom Lambret Quetelet,
nazywany ojcem statystyki. Przed nim statystykę stanowiło jedynie staranne i systematyczne

zapisywanie narodzin, zgonów i innych obserwacji, interesujących tylko urzędników. On
pierwszy zauważył, że te monotonne liczby są źródłem cennych informacji, gdy
zinterpretujemy je zgodnie z prawami rachunku prawdopodobieństwa.
Czasami spotykamy bardzo dokładnie obliczoną średnią (z dokładnością do kilku miejsc po
przecinku), ale trudniej z interpretacją, która czasami może wyglądać dziwnie. Zwłaszcza w
sytuacjach, gdy wartości początkowe są liczbami całkowitymi. Na przykład jesteśmy
informowani, że w miejskim szpitalu dziennie rodzi się średnio 5,56 zdrowych dzieci. Czy
ktoś widział 0,56 dziecka zdrowego? Ostrożnie ze zbędną dokładnością, której warto unikać.
Oprócz średniej arytmetycznej istnieją również inne rodzaje klasycznych miar tendencji
centralnej, w tym średnia geometryczna i średnia harmoniczna; są one rzadziej
wykorzystywane w medycynie. Wzory na ich obliczanie znajdzie Czytelnik w podręcznikach
statystyki. Obie te średnie są równe lub mniejsze od średniej arytmetycznej. Średnią
geometryczną stosujemy, gdy zjawiska są ujmowane dynamicznie (np. średnie tempo zmian).
Jedyną poważniejszą wadą średniej arytmetycznej jest to, że duży wpływ na nią wywierają
najmniejsza i największa wartość badanego szeregu, czyli tzw. skrajne wartości cechy. Na
przykład w pewnej firmie zarobki 8 zatrudnionych pracowników osiągnęły 500 zł
miesięcznie. Księgowa i kierownik otrzymali po 2000 zł, a właściciel wypłacił sobie 10 000
zł. Średnia zarobków w tej firmie wygląda zachęcająco (ok. 1636 zł); jakże jednak myląca i
niepełna jest ta informacja. I jeszcze inny przykład, gdzie użycie średniej wprowadzi nas w
błąd. Wyobraźmy sobie ciąg liczb: 30, 30, 30, 90, 90, 90, które odnoszą się do wzrostu (w
cm) zaginionych skrzatów domowych. Średnia wynosi tu 60. Jakże zdziwiony i rozczarowany
byłby ich odkrywca, gdyby wcześniej na podstawie informacji o średniej uszył im ubranka na
60 cm wzrostu. Sytuacje te lepiej opisują inne miary.

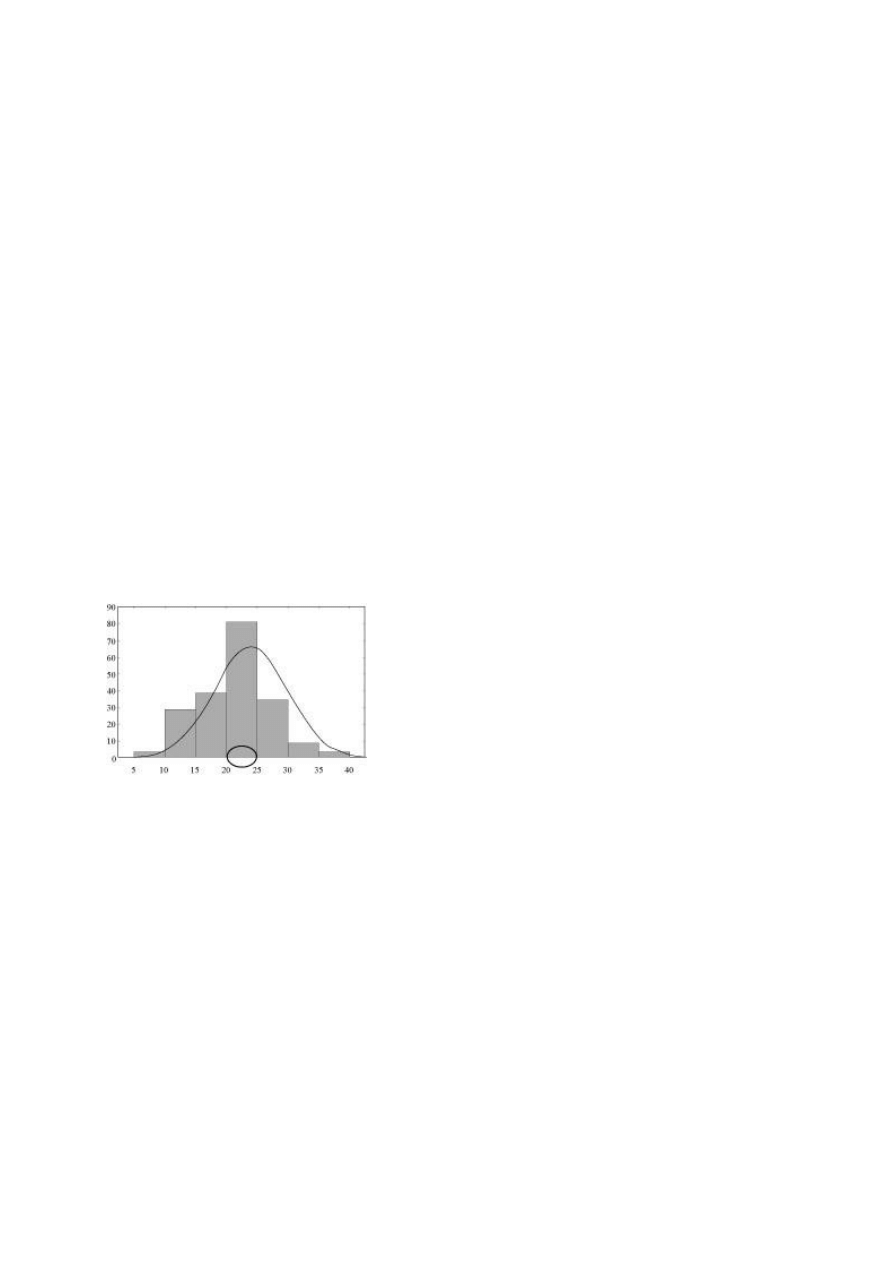
Rys 3. Histogram z zaznaczonym przedziałem modalnej

Modalna

Modalna (dominanta, moda, wartość najczęstsza, symbol - Mo) jest to wartość cechy
statystycznej, która w rozkładzie empirycznym występuje najczęściej (rys. 3). Dla podanego
wyżej przykładu modalna wynosi 500 zł i lepiej niż średnia odzwierciedla sytuację płacową w
firmie. W drugim przykładzie skrzaty miałyby lepiej dopasowane ubranka, gdyby krawiec
wiedział, że są dwie modalne wzrostu: 30 i 90 cm.
Zebrany materiał (duża liczba danych indywidualnych) przedstawiamy najczęściej w postaci
szeregu rozdzielczego. Szereg taki otrzymujemy, gdy zbiór danych podzielimy na klasy
według określonej cechy (jakościowej lub ilościowej) i podamy liczebność każdej z tych klas.
W szeregach takich modalna to wartość cechy, która znajduje się w klasie o największej
liczebności. Znalezienie takiej klasy, zwanej przedziałem modalnej, nie jest trudne, gdyż
wyróżnia ją jeden wyraźny punkt (szczyt) reprezentujący największą liczbę obserwacji (rys.
3). Jeśli histogram ma 2, 3 lub więcej szczytów, to mówimy, że jest bimodalny, trimodalny
itd.; świadczy to o niejednorodności badanej zbiorowości.
Modalna ma jednak słabe strony. Niestety jest miarą niestabilną. Weźmiemy następujące

liczby: 2, 2, 4, 6, 8, 20. Modalna wynosi tu 2. Wystarczy jednak zmienić 2 na 20 i modalna
przyjmie wartość 20. Widać więc, że zmiana tylko jednej liczby może znacznie zmienić
wartość modalnej. Jest to duża wada w porównaniu ze średnią i medianą, zmiany liczb nie
wpływają bowiem na ich wartość tak dramatycznie.

Kwantyle

Kwantyle to wartości cechy badanej zbiorowości (przedstawionej w postaci szeregu
statystycznego), które dzielą ją na określone części pod względem liczby jednostek. Części te
pozostają w określonych proporcjach. Do najczęściej stosowanych kwantyli należą: kwartyle
(podział na 4 części), decyle (podział na 10 części) oraz percentyle (podział na 100 części).
Omówimy najważniejsze - kwartyle (wartości ćwiartkowe) i wzory je wyznaczające dla
szeregów rozdzielczych.

Kwartyl pierwszy (Q1) jest to wartość jednostki, która dzieli zbiorowość w ten sposób, że
1/4 (25%) jednostek ma od niej wartości nie większe, a 3/4 (75%) - nie mniejsze.

Kwartyl drugi (mediana, wartość środkowa, symbol - Me) to wartość jednostki tak położonej
w zbiorowości, że dzieli ją na dwie równe części. Medianę wprowadził do praktyki
statystycznej K. Pearson w 1895 roku. Obok średniej arytmetycznej jest najczęściej
stosowanym parametrem statystycznym. Wartość mediany nie zależy od wartości
krańcowych (odstających). Gdy wartości te się pojawiają (często jako błąd przy zbieraniu
informacji), to średnia arytmetyczna może się zmienić znacznie, a mediana się nie zmieni.
Możemy ją wyznaczać nawet wtedy, gdy nie wszystkie obserwacje są dokładnie znane, np. z
szeregów, w których występują nie zamknięte przedziały klasowe. Nie sprawi więc nam
trudności w wyliczeniu mediany zastąpienie zamkniętego przedziału klasowego <35, 40>
zaznaczonego na rysunku 3. przedziałem <35, C>. Co więcej, w tym przypadku wartość
mediany nie ulegnie zmianie. Wszystko to powoduje, że mediana wysuwa się na czoło w
zastosowaniach do wszystkich wzrokowo uchwytnych, a trudno mierzalnych wielkości.
Mediany używamy też do analizy cech jakościowych.
W naukach medycznych mediana stosowana jest m.in. przy ustalaniu przeciętnej
przeżywalności pooperacyjnej (np. po operacjach z powodu nowotworu), ponieważ
pojedyncze przypadki przeżycia wielu lat po operacji nie wpływają znacząco na wartość
mediany (przeciwnie niż na średnią arytmetyczną). W naszym przykładzie zarobków w firmie
mediana, podobnie jak modalna, wynosi 500 zł. Innym ciekawym przykładem zastosowania
mediany jest historyczne już dziś opracowywanie danych z eksperymentu Evartsa i wsp., w
którym mierzono częstotliwość wyładowań wielu komórek nerwowych mózgu kota w czasie
snu i po przebudzeniu. Średnia i mediana częstotliwości wyładowań dla 90 komórek
nerwowych z obszaru wzrokowego wynosiły:

średnia

mediana

w czasie snu

7,30

5,20

po przebudzeniu

7,95

3,56

Jak widać średnia aktywności wzrasta po przebudzeniu kota, a mediana odwrotnie - maleje.
Wskazuje to na istnienie w mózgu neuronów dwóch typów: jednego zwiększające i drugiego
zmniejszającego częstotliwość wyładowań, gdy zwierzę czuwa, a wynikło stąd, że nie
wszystkie komórki mózgu wykonują tę samą pracę (tak uważano do czasu tego
eksperymentu), gdyż poszczególne komórki wyspecjalizowały się w różnych czynnościach.

Kwartyl trzeci (Q3) jest to wartość jednostki, która tak dzieli zbiorowość, że 3/4 (75%)
jednostek ma od niej wartości nie większe, a 1/4 (25%) - nie mniejsze.

Z kwartylami związany jest też charakterystyka zwana rozstępem kwartylowym. Jest to
różnica pomiędzy kwartylami trzecim i pierwszym (Q3-Q1). Rozstęp kwartylowy (odchylenie
ćwiartkowe) określa "długość" tej części przedziału zmienności cechy, w której znajduje się
50% "środkowych" obserwacji. Wprowadzone pojęcia przedstawia rysunek 4.

Rys 4. Kwartyle

Podsumowując: wszystkie trzy statystyki opisowe: średnia, modalna i mediana - "streszczają"
zbiór danych, co znacznie ułatwia nam jego wyobrażenie i dalszą analizę.

Więcej informacji znajdą Państwo na stronie http://www.mp.pl

Copyright © 1996 - 2009 Medycyna Praktyczna