Arkusz 12: Zginanie z siłą osiową. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Arkusz

Arkusz

12: Zginanie z siłą osiową

12: Zginanie z siłą osiową

Teoria dotycząca zginania z siłą osiową – z wykładów, ćwiczeń oraz książek: [1] i [2].

1. Zginanie z siłą osiową – definicja

Zginanie z siłą osiową (inaczej: rozciąganie lub ściskanie mimośrodowe) jest złożonym stanem mechanicznym –
moment zginający (M

y

lub M

z

lub częsciej oba) działa jednocześnie z siłą normalną F

x

.

Stan taki jest praktycznie realizowany w następujących warunkach:

•

pręt jest pryzmatyczny,

•

pręt poddany jest tylko obciążeniu działającemu równolegle do jego osi, jednak nie przyłożonemu dokładnie

w osi (czyli nie w środku ciężkości przekroju poprzecznego),

•

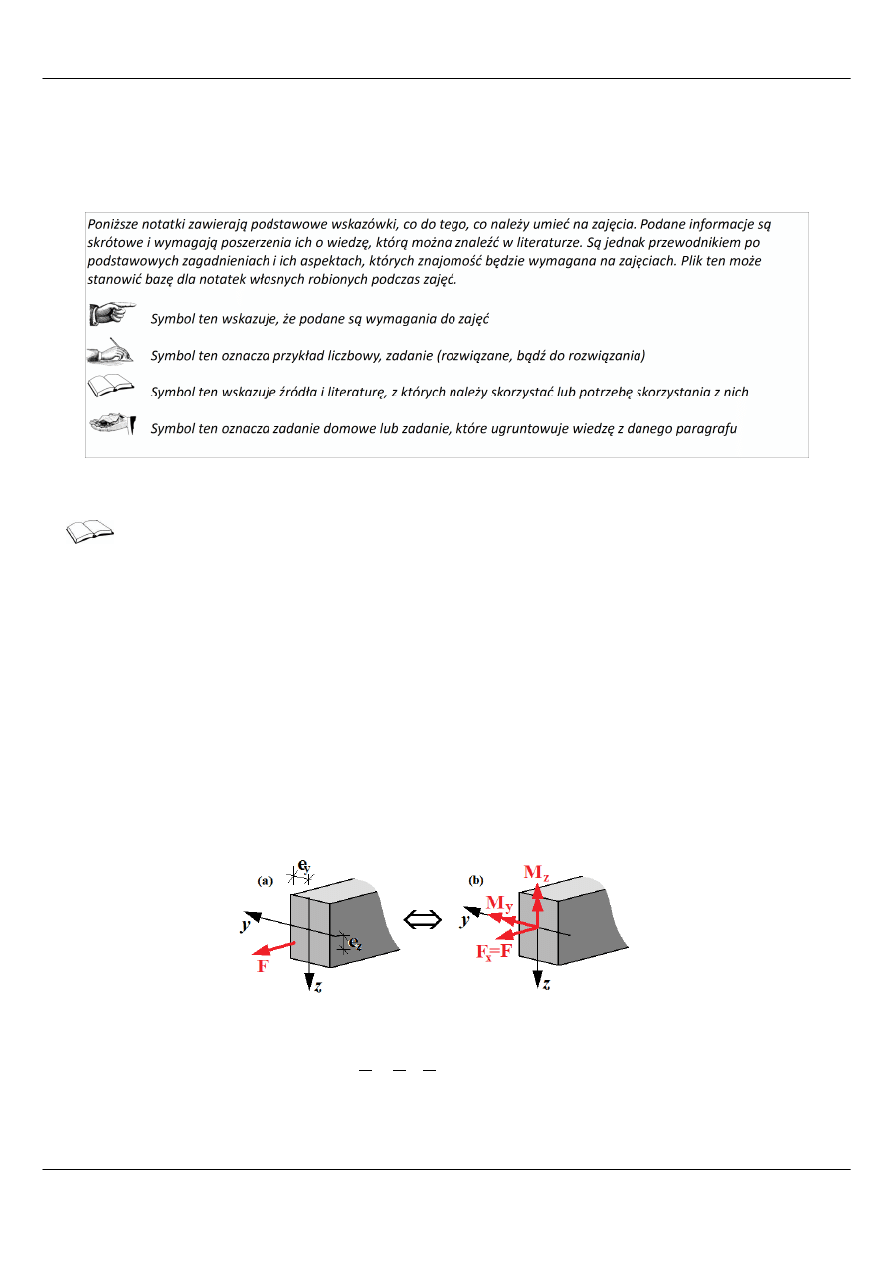
w wyniku redukcji takiego układu sił (czyli jednej siły F, rys. 1) do środka ciężkości jako bieguna redukcji,
otrzymujemy układ równoważny obciążeniu zewnętrznemu złożony z: F

x

, M

y

i M

z

.

Oczywiście:

F

x

= F ; M

y

= F⋅e

z

; M

z

= F⋅e

y

.

Natomiast tangens kąta nachylenia momentu

M

= M

y

+M

z

jest równy:

tg

β = e

y

/e

z

.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Rysunek 1: Siła działająca w rozciąganiu mimośrodowym (a) i układ odpowiadające

jej redukcji do środka ciężkości (b), (na podst. [3])

Arkusz 12: Zginanie z siłą osiową. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

2. Zginanie z siłą osiową – naprężenia

Tensory naprężenia i odkształcenia w zginaniu z siłą osiową mają następującą postać:

T

σ

=

[

σ

x

0

0

0

0

0

0

0

0

]

⇔

związki konstytutywne

T

ε

=

[

σ

x

1

E

0

0

0

σ

x

ν

E

0

0

0

σ

x

ν

E

]

Naprężenia normalne obliczane są jako superpozycja wszystkich działania wszystkich wpływów (F

x

, M

y

i M

z

):

σ

x

( x , y , z) =

F

x

(x)

A

( x)

+

M

y

(x)

I

y

( x)

⋅z

M

z

( x)

I

z

( x)

⋅ y

[

Nm

m

4

⋅m = Pa

]

gdzie: ▪ F

x

(x) jest siłą normalną przekrojową w przekroju o współrzędnej x;

▪ A(x) jest polem przekroju w przekroju o współrzędnej x;
▪ I

y

(x), I

z

(x) są głównymi centralnymi momentami bezwładności przekroju poprzecznego;

▪ M

y

(x), M

z

(x) są momentami zginającymi w przekroju o współrzędnej x (z odpowiednimi znakami).

3. Oś obojętna, promienie bezwładności

Podobnie, jak w pozostałych przypadkach zginania, które były omówione do tej pory, jest definiowana oś obojętna jako
prosta w przekroju poprzecznym, dla której naprężenia normalne wynoszą zero:

σ

x

( x , y , z) =

F

x

(x)

A

(x)

+

M

y

(x)

I

y

(x)

⋅ z

M

z

(x)

I

z

( x)

⋅ y = 0

Dla przekroju poprzecznego można zdefiniować promień bezwładności (jest to kolejna jego charakterystyka
geometryczna, obok np. momentów bezwładności):

i

y

=

√

I

y

/ A ⇔ i

y

2

=

I

y

A

,

i

z

=

√

I

z

/ A ⇔ i

z

2

=

I

z

A

.

Korzystając z powyższej definicji, oraz pamiętając, że

M

y

= F⋅e

z

; M

z

=

F

⋅e

y

, można przekształcić równanie osi

obojętnej do następującej postaci:

σ( x , y , z) =

F

x

(x)

A

⋅

[

1

+

e

z

⋅z

i

y

2

+

e

y

⋅y

i

z

2

]

= 0

,

skąd wynika dla mimośrodowego rozciągania lub ściskania (

F

x

≠0

):

1

+

e

z

⋅z

i

y

2

+

e

y

⋅y

i

z

2

= 0

.

Jeżeli wprowadzi się oznaczenie

a

=

i

z

2

e

y

oraz

b

=

i

y

2

e

z

,

równianie osi obojętnej przyjmie postać:

y

a

+

z

b

= 1

.

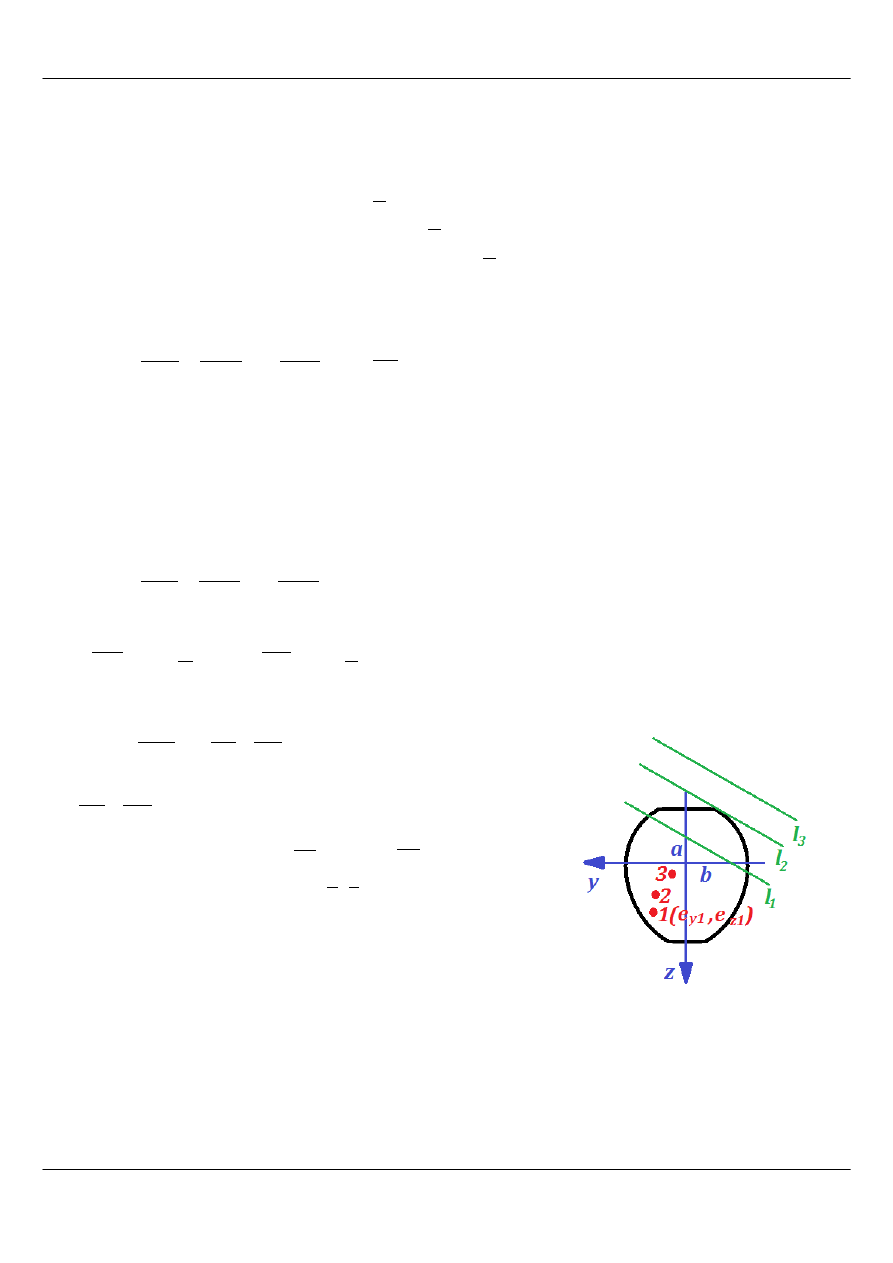
Jest to równanie odcinkowe prostej, w którym a i b są miejscami
przecięcia się tej prostej z odpowiednimi osiami układu współrzędnych.

Im bliżej środka ciężkości znajduje się miejsce przyłożenia siły
rozciągającej lub ściskającej, tym dalej od tego środka ciężkości znajduje
się oś obojętna. Należy pamiętać, że w przeciwieństwie do poprzednio
rozważanych przypadków zginania, dla zginania z siłą osiową, oś
obojętna nie przechodzi przez środek ciężkości.
Można dodać, dla porównania, że dla prostego zginania lub ściskania, gdy siła przyłożona jest w środku ciężkości, oś
obojętna znajduje się nieskończenie daleko od tego punktu.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

Rysunek 2: Punkty przyłożenia siły równoległej do

osi (czerwone) oraz odpowiadające im osie obojętne

(zielone)

Arkusz 12: Zginanie z siłą osiową. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

4. Rdzeń przekroju

Rdzeń przekroju definiowany jest jako miejsce geometryczne punktów
przekroju poprzecznego, w którym przyłożona siła daje naprężenia tego
samego znaku we wszystkich punktach tego przekroju poprzecznego.
Innymi słowy, dla każdego punktu rdzenia, jeżeli zostanie w nim
przyłożona siła normalna do przekroju, powstająca wówczas oś obojętna
znajduje się poza przekrojem lub co najwyżej jest do niego styczna.

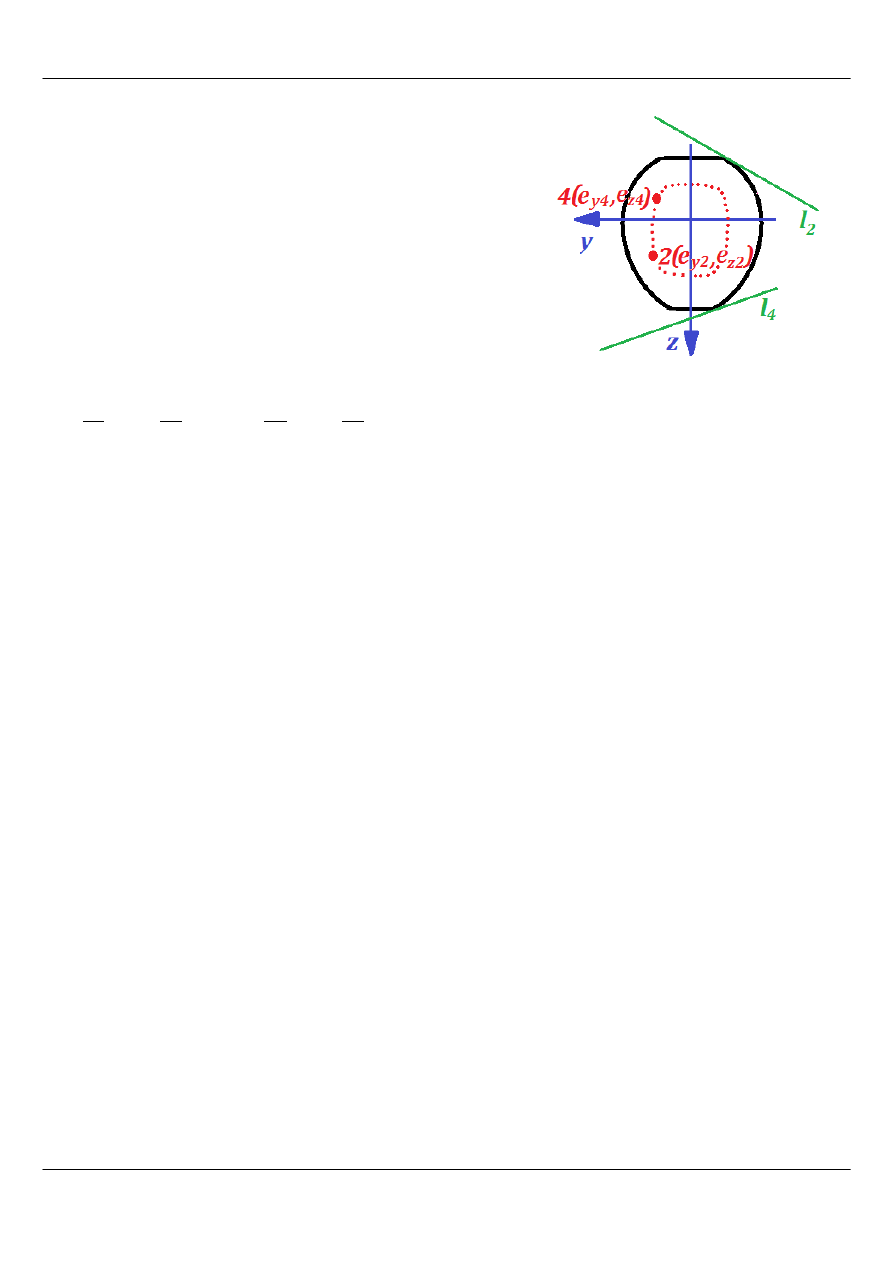
Algorytm wyznaczania położenia rdzenia przekroju polega na znalezieniu
wszystkich charakterystyk geometrycznych przekroju (pole, główne
centralne momenty i promienie bezwładności), a następnie dla stycznych
do konturu przekroju odnajduje się punkty odpowiadającego im
przyłożenia siły. Korzysta się tutaj z równania odcinkowego osi obojętnej
oraz zależności:

a

=

i

z

2

e

y

⇒ e

y

=

i

z

2

a

oraz

b

=

i

y

2

e

z

⇒ e

z

=

i

y

2

b

.

5. Warunek projektowy

Z powyższych wzorów widać, że naprężenia normalne mogą przyjmować wartości ujemne (ściskanie) i dodatnie
(rozciąganie), zależnie od znaku momentu zginającego oraz położenia rozważanego punktu względem kierunku
wysokości przekroju. Stąd, warunek maksymalnych naprężeń musi być rozważany zarówno dla ściskanej, jak i rozciąganej
części przekroju:

•

ściskanie:

| σ

x , c

max

| ⩽ k

g , c

lub

| σ

x , c

max

| ⩽ k

c

lub

| σ

x , c

max

|⩽ k

g

(gdzie c oznacza ściskanie, zaś g oznacza zginanie,

np. k

g,c

– dopuszczalne naprężenia ściskające przy zginaniu);

•

rozciąganie:

σ

x , t

max

⩽ k

g , t

lub

σ

x , t

max

⩽ k

t

lub

σ

x , t

max

⩽ k

g

(gdzie t oznacza rozciąganie, zaś g oznacza zginanie,

np. k

g,t

– dopuszczalne naprężenia rozciągające przy zginaniu).

Warto zaznaczyć, że choć rozważany obecnie stan mechaniczny jest stanem złożonym: rozciąganie lub ściskanie osiowe
oraz zginanie, nie ma potrzeby rozważania go względem hipotez wytężeniowych (

σ

red

⩽σ

dop

, gdzie

σ

red

oznaczają

naprężenia zredukowane, czyli pewną funkcję wszystkich naprężeń stycznych i normalnych wyznaczane wg hipotez
wytężeniowych). Dzieje się tak ponieważ występują tylko naprężenia normalne, które są już superponowane dla obu
podstawowych stanów mechanicznych rozciągania/ściskania osiowego oraz zginania.

Uwaga o ściskaniu mimośrodowym
Osobną i ważną kwestią jest ściskanie mimośrodowe przekrojów, ponieważ oprócz niebezpieczeństwa przekroczenia
dopuszczalnych naprężeń, zachodzi także niebezpieczeństwo związane z wyboczeniem konstrukcji. Ten temat będzie
analizowany podczas osobnych zajęć na kursie, należy jednak zasygnalizować w tym miejscu, że konieczne jest również
sprawdzenie wielkości dopuszczalnej siły, którą można działać na element ściskany ze względu na wyboczenie, jak i samej
geometrii konstrukcji (pręty krępe i smukłe). Przy okazji, powinno się dodać, że analiza prętów ściskanych mimośrodowo
wg podanej w tym rozdziale metody ma sens dla prętów krępych, czyli o małej wysokości w stosunku do wymiarów
przekroju poprzecznego właśnie ze względu na wyboczenie.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

Rysunek 3: Sposób konstrukcji geometrycznej rdzenia

przekroju - proste styczne do konturu oznaczające osie

obojętne i odpowiadające im punkty przyłożenia siły

równoległej do osi.

Arkusz 12: Zginanie z siłą osiową. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

6. Podsumowanie

• Rozwiązać zadania nr: 4.10 / str. 229; 4.12 / str. 231 z książki [1] oraz przykłady nr: 14.5.1, 14.5.2, 14.5.3,

14.5.5 z książki [2].

• Obliczanie rdzenia: rozwiązać przykłady 4.9 / str. 227z książki [1] oraz 14.5.7 do 14.7.10 z książki [2].

• Znajomość tensora naprężenia i odkształcenia w zginaniu z siłą osiową oraz wzoru na naprężenie.
• Umiejętność rozwiązywania zadań dla przypadków zginania z siłą osiową – wyznaczanie naprężeń w
punktach przekroju poprzecznego, rysowanie wykresów rozkładu naprężeń (bryły naprężeń) w przekrojach
poprzecznych, znalezienie osi obojętnej, wyznaczanie wymiarów konstrukcji z warunków projektowych,
określanie położenia rdzenia przekroju.
• Oś obojętna, promienie bezwładności, rdzeń przekroju – definicje, wzory, znaczenie.

7. Literatura

[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie

poszerzone i poprawione, Kraków 2004, rozdział 14

[3] dr inż. Paweł Szeptyński, ilustracje

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4