Każdemu planowi produkcji (x
1
,x
2
) na płaszczyźnie
O
(x
1
,x
2
) przyporządkowany jest w sposób
jednoznaczny punkt P o współrzędnych x
1
oraz x
2,
który zapisujemy jako P(x
1
,x
2
).
P
1
P
2
ZASOBY
S
1
2
2
14
S
2
1
2
8
S
3
4
0
16
ZYSK
2
3
I odwrotnie każdemu punktowi P(x
1
,x
2
) płaszczyzny
O
(x
1
,x
2
) odpowiada pewien plan produkcji (x
1
,x
2
).
Wyznaczanie dopuszczalnych planów produkcji –
rozwiązania dopuszczalne
Rozwiązaniem problemu optymalizacyjnego nazwiemy
rozwiązaniem dopuszczalnym
,
jeżeli spełnia ono wszystkie warunki ograniczające występujące w rozpatrywanym
problemie.
Należy zatem znaleźć część wspólną zbioru utworzonego wszystkich rozwiązań
dopuszczalnych która jednocześnie spełni wszystkie warunki ograniczające.
2x
1
+2x
2
≤ 14
x
1
+2x
2
≤ 8
4x
1
≤ 16
(1)
(2)
(3)
oraz warunek nieujemności zmiennych
x
1
≥ 0
X
2
≥ 0
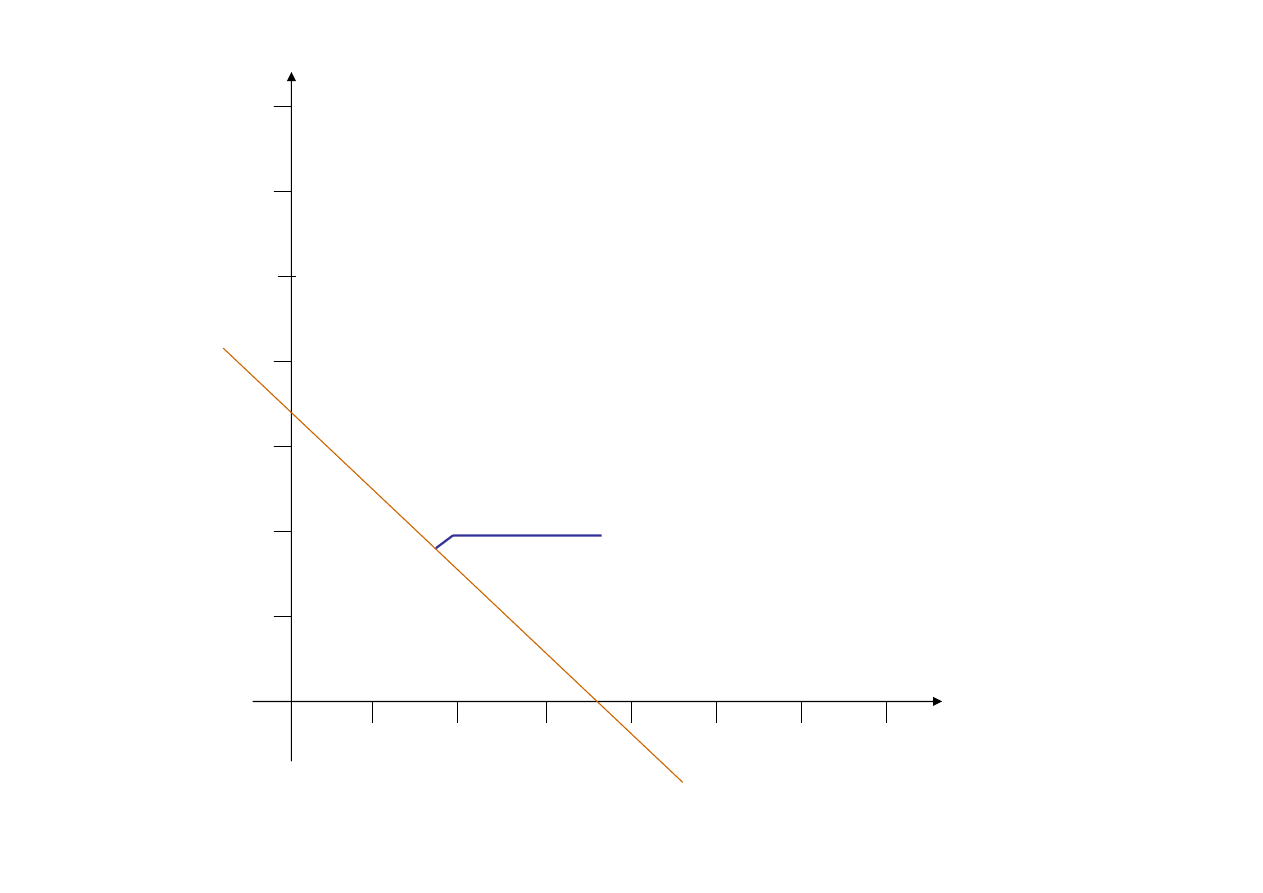
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,7)
(0,7)
(7,0)
2x
1
+2x
2
=14
X
1
X
2
Warunek ograniczający
(1)
-
2x
1
+2x
2
≤14
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,7)
(7,0)
X
2
X
1
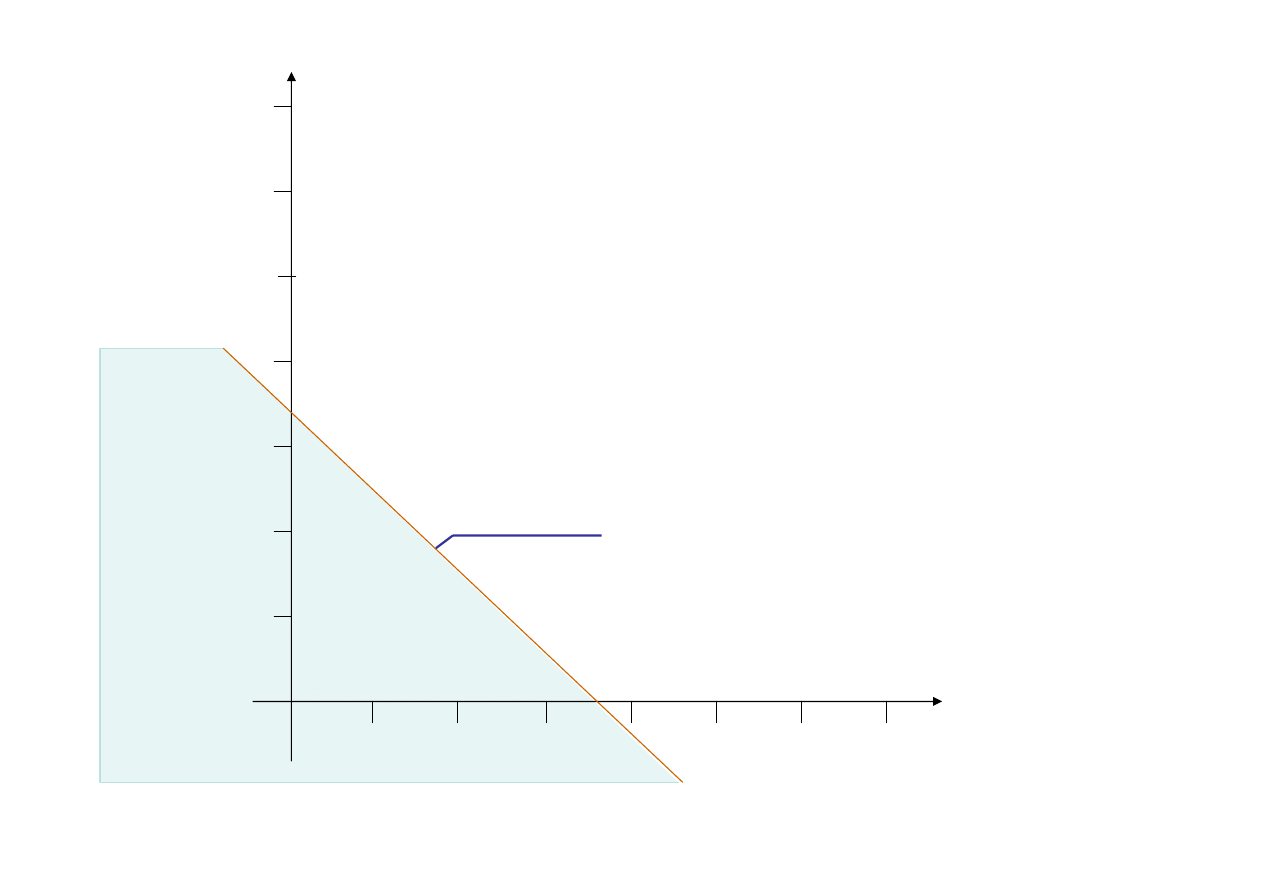
Warunek ograniczający
(1)
-
2x
1
+2x
2
≤14
2x
1
+2x
2
=14
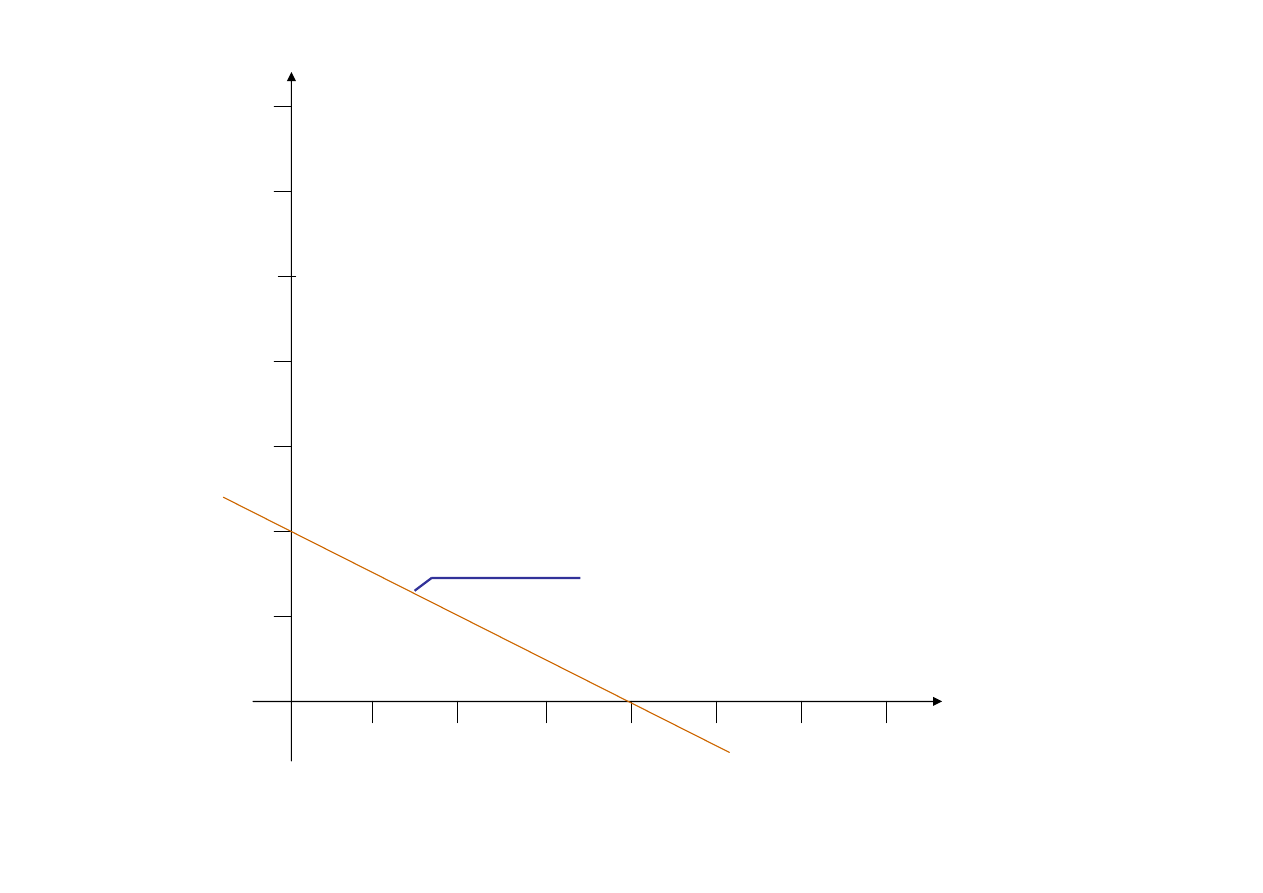
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,4)
(8,0)
x
1
+2x
2
=8
X
2
X
1
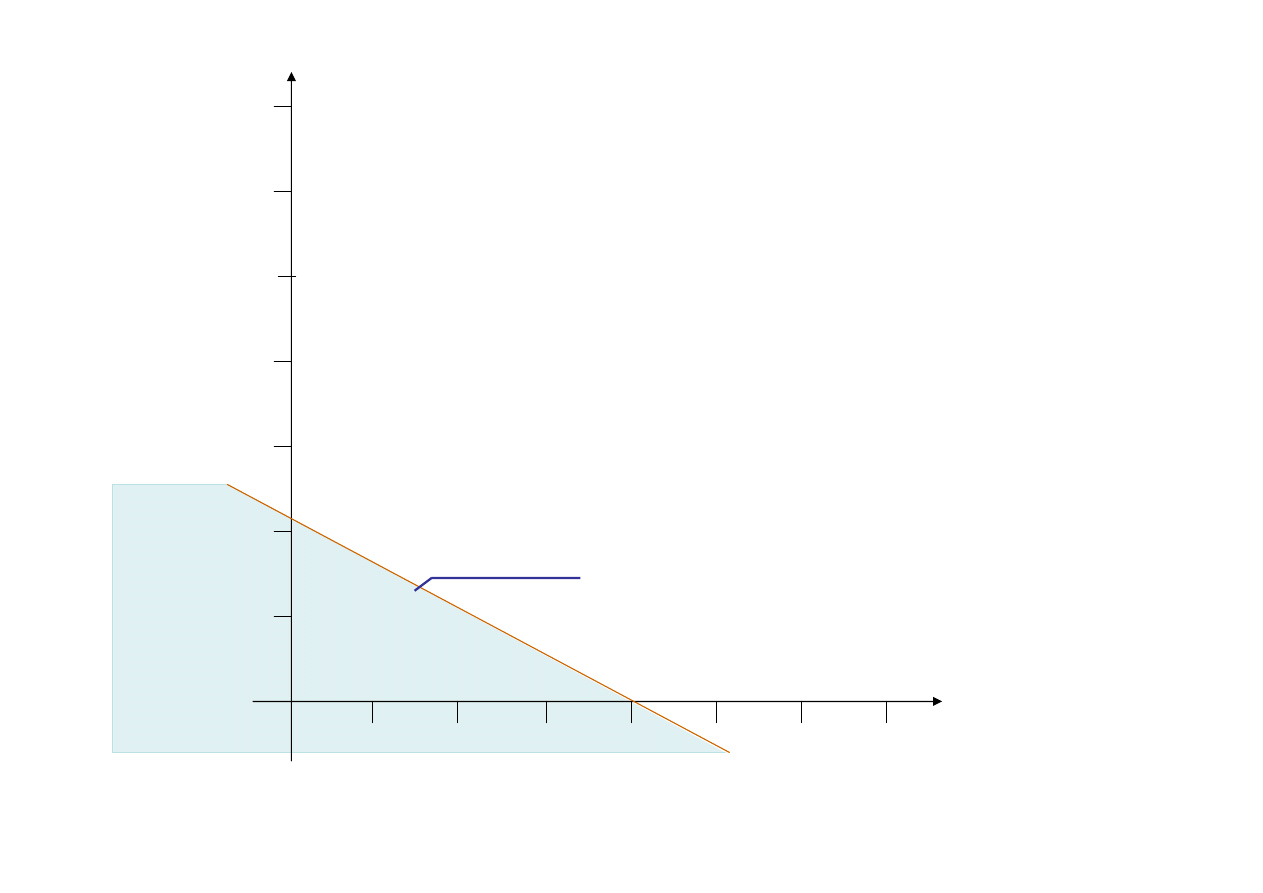
Warunek ograniczający
(2)
-
x
1
+2x
2
≤ 8
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,4)
(8,0)
x
1
+2x
2
=8
X
2
X
1
Warunek ograniczający
(2)
-
x
1
+2x
2
≤ 8
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,7)
4x
1
=16
X
2
X
1
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(0,7)
4x
1
=16
X
2
X
1
O
(0,0)
4
2
8
10
12
14
4
6
X
1
2
4
6
8
10
12
1
x
1
≥0
X
2
(0,7)
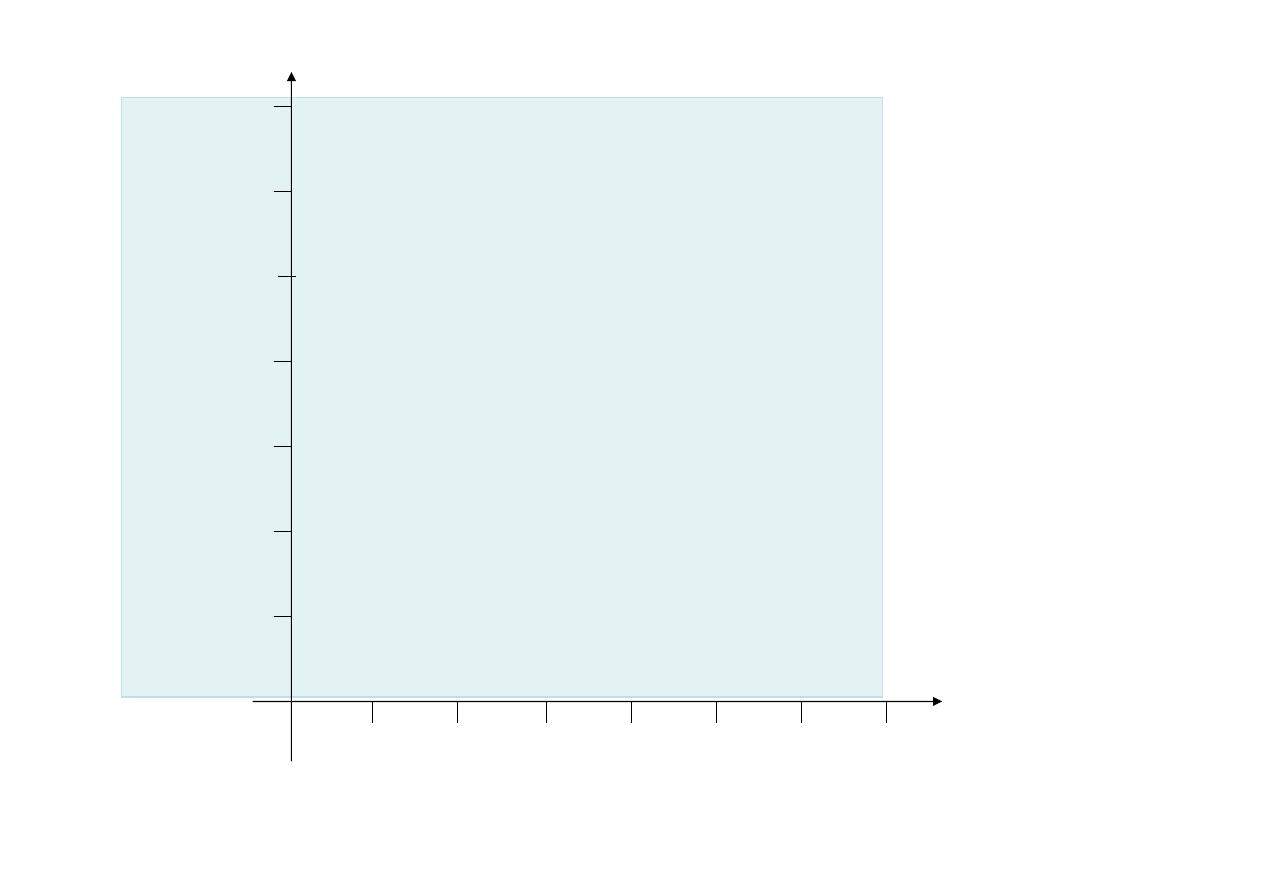
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
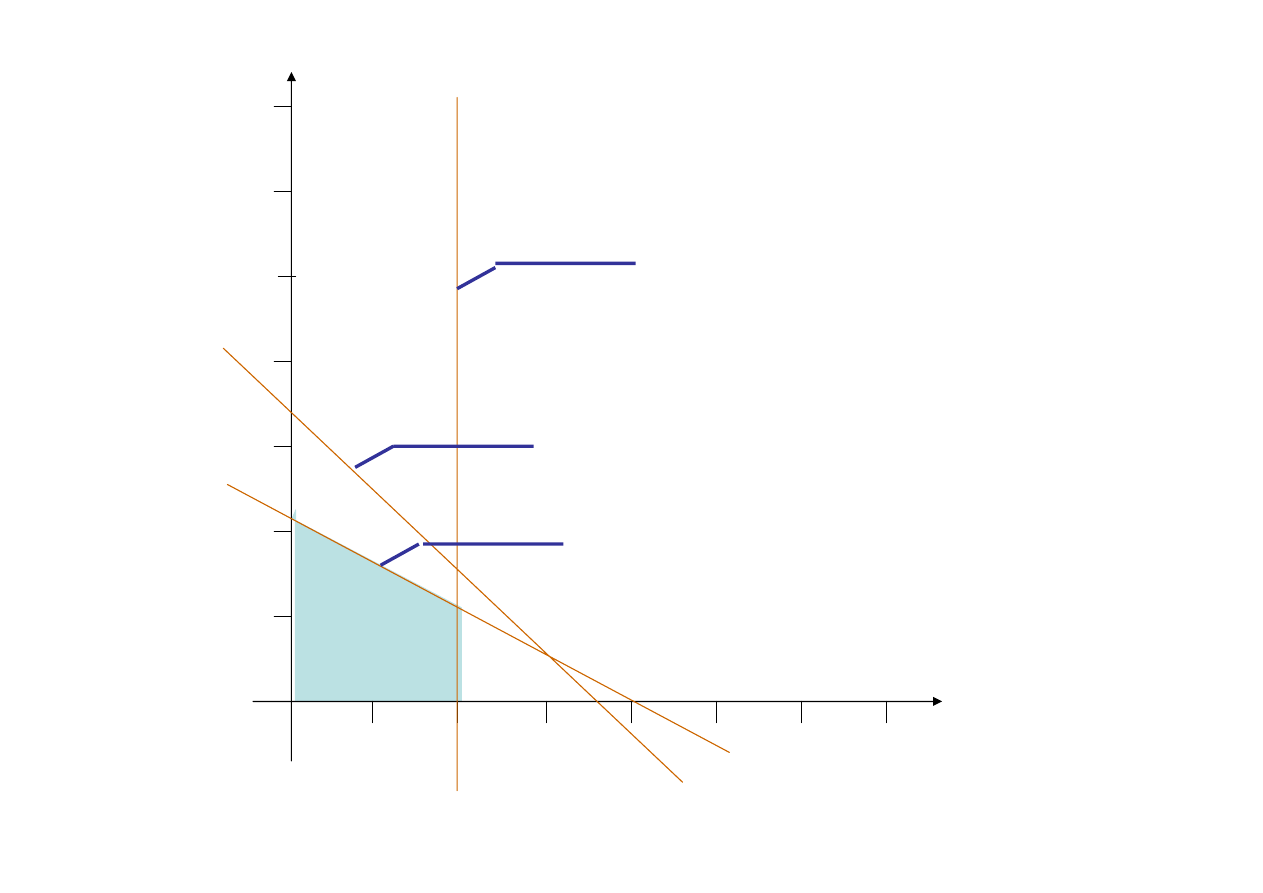
(0,7)
x
2
≥0
X
2
X
1
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
(7,0)
X
2
X
1
A
ograniczenie środka S
1
ograniczenie środka S
2
ograniczenie środka S
3
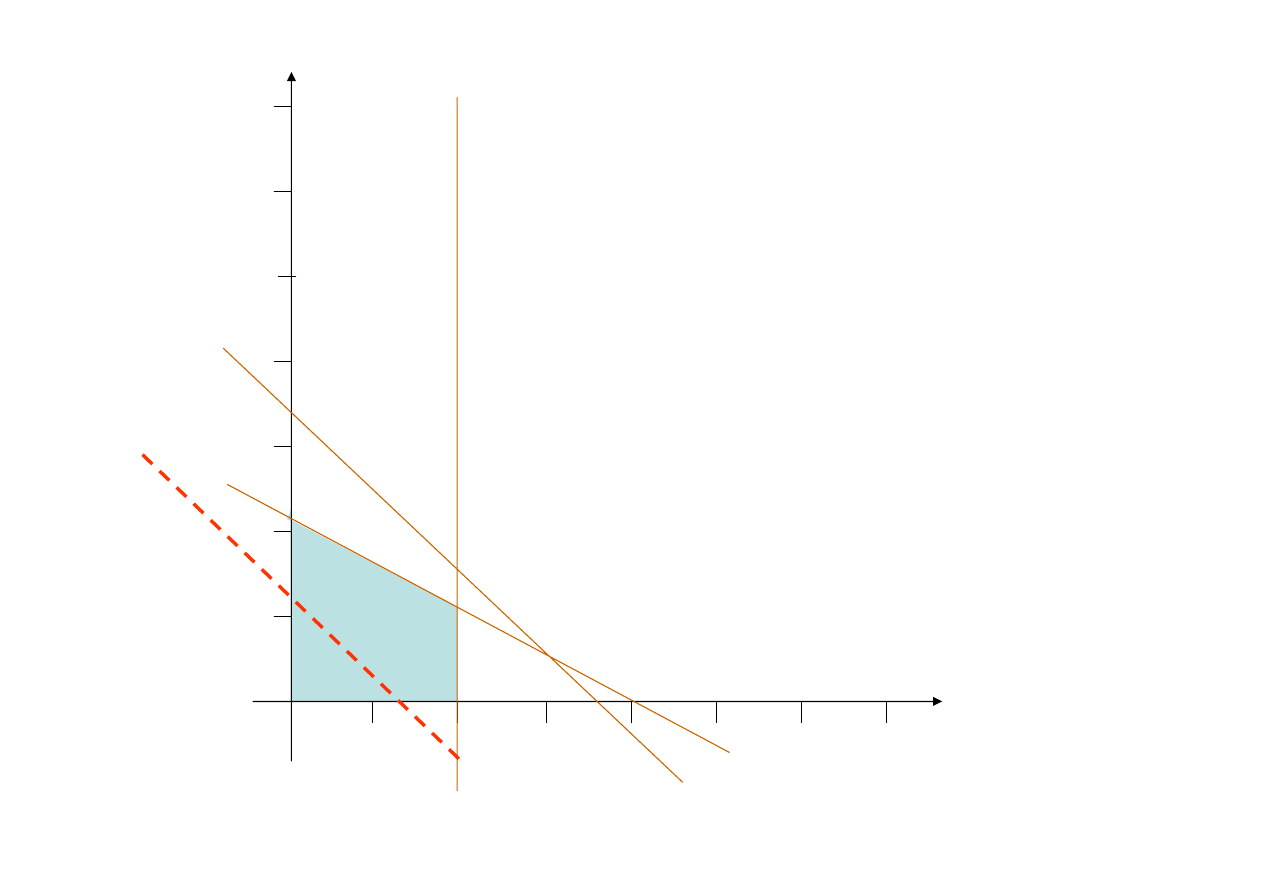
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
Do znalezienia rozwiązania optymalnego, w którym funkcja
celu
f(x
1
,x
2
)=2x
1
+3x
2
przyjmuje wartości największe
należy wykorzystać metodę „prób i błędów”.
Załóżmy, w pierwszym kroku, pewną wartość zysku np. 6
czyli wartość funkcji celu
2x
1
+3x
2
= 6
Czy istnieje
przynajmniej jedno rozwiązanie dopuszczalne pozwalające
zrealizować zysk na poziomie 6 jednostek?
2x
1
+3x
2
= 6
Istnieje nieskończenie wiele punktów tej prostej
leżących wewnątrz obszaru dopuszczalnego.
Odpowiedź na pytanie dotyczące istnienia
rozwiązania dopuszczalnego dającego wartość 6
jest pozytywna
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
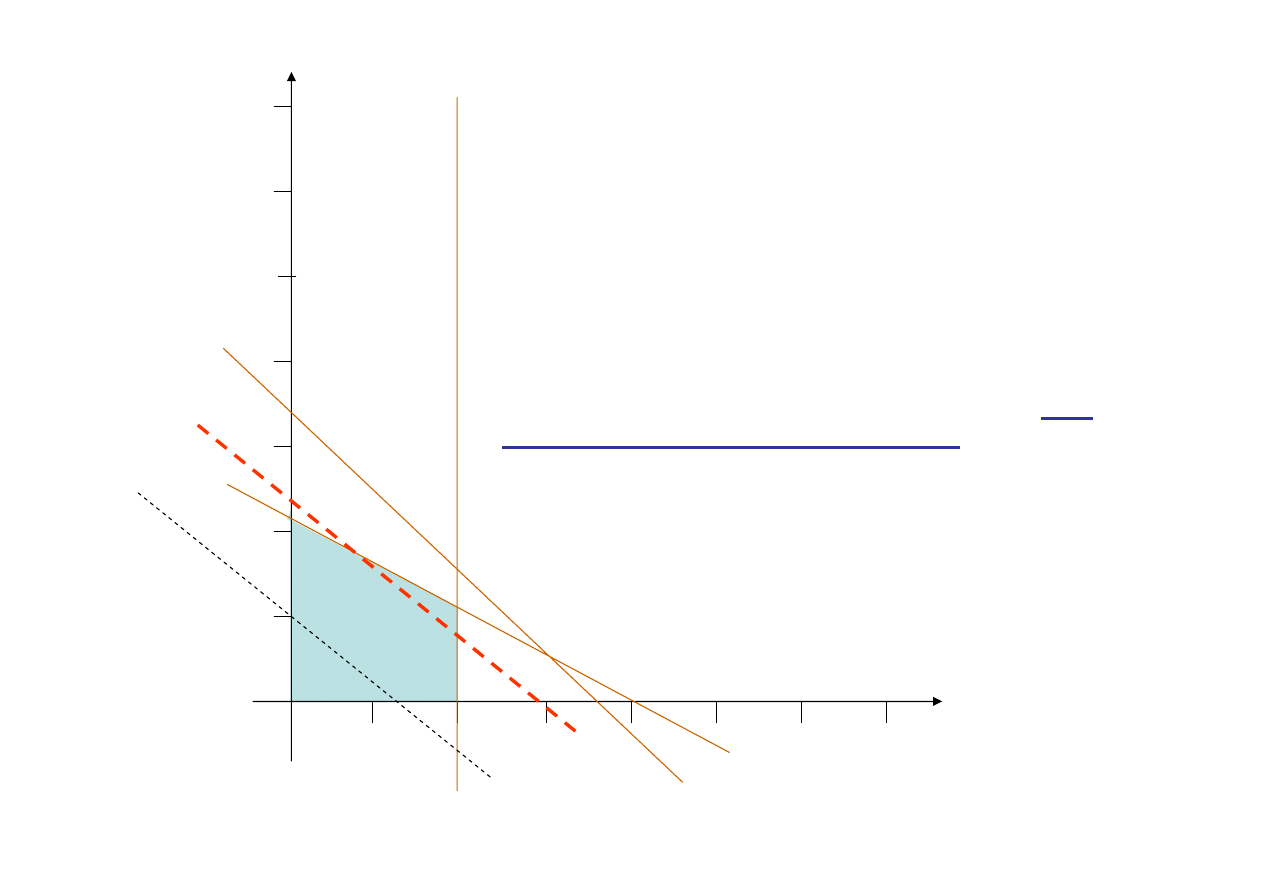
Podejmiemy teraz próbę znalezienia lepszych rozwiązań.,
Wybierzmy większą wartość zysku np. 12 wartość funkcji
celu
2x
1
+3x
2
= 12
2x
1
+3x
2
= 6
2x
1
+3x
2
= 12
Ponownie stwierdzamy, że istnieją wspólne punkty
prostej ze zbiorem rozwiązań dopuszczalnych- czyli
istnieje możliwość poprawy rozwiązania
Otrzymana prosta jest równoległa do rozpatrywanej
poprzednio. Przesuwając ją coraz wyżej, polepszamy
wartość funkcji celu
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
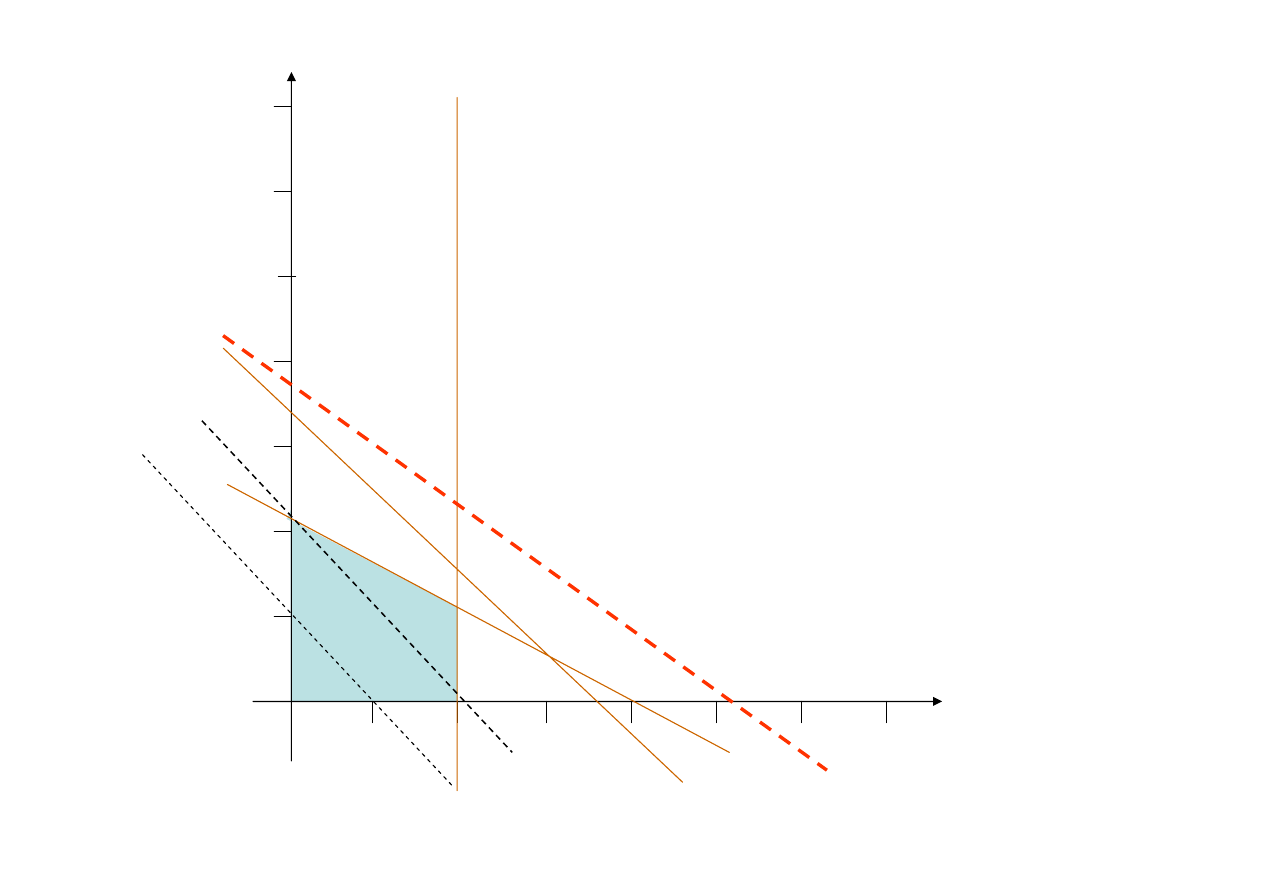
Rysując prostą przedstawiającą funkcję celu w postaci
2x
1
+3x
2
= 21
stwierdzamy, że nie istnieją punkty
wspólne tej prostej ze zbiorem rozwiązań dopuszczalnych
– nie istnieje więc taki plan produkcji, który dawałby zysk
równy
21
2x
1
+3x
2
= 6
2x
1
+3x
2
= 12
2x
1
+3x
2
= 21
Prosta przedstawiająca funkcję kryterium
została przesunięta zbyt daleko
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
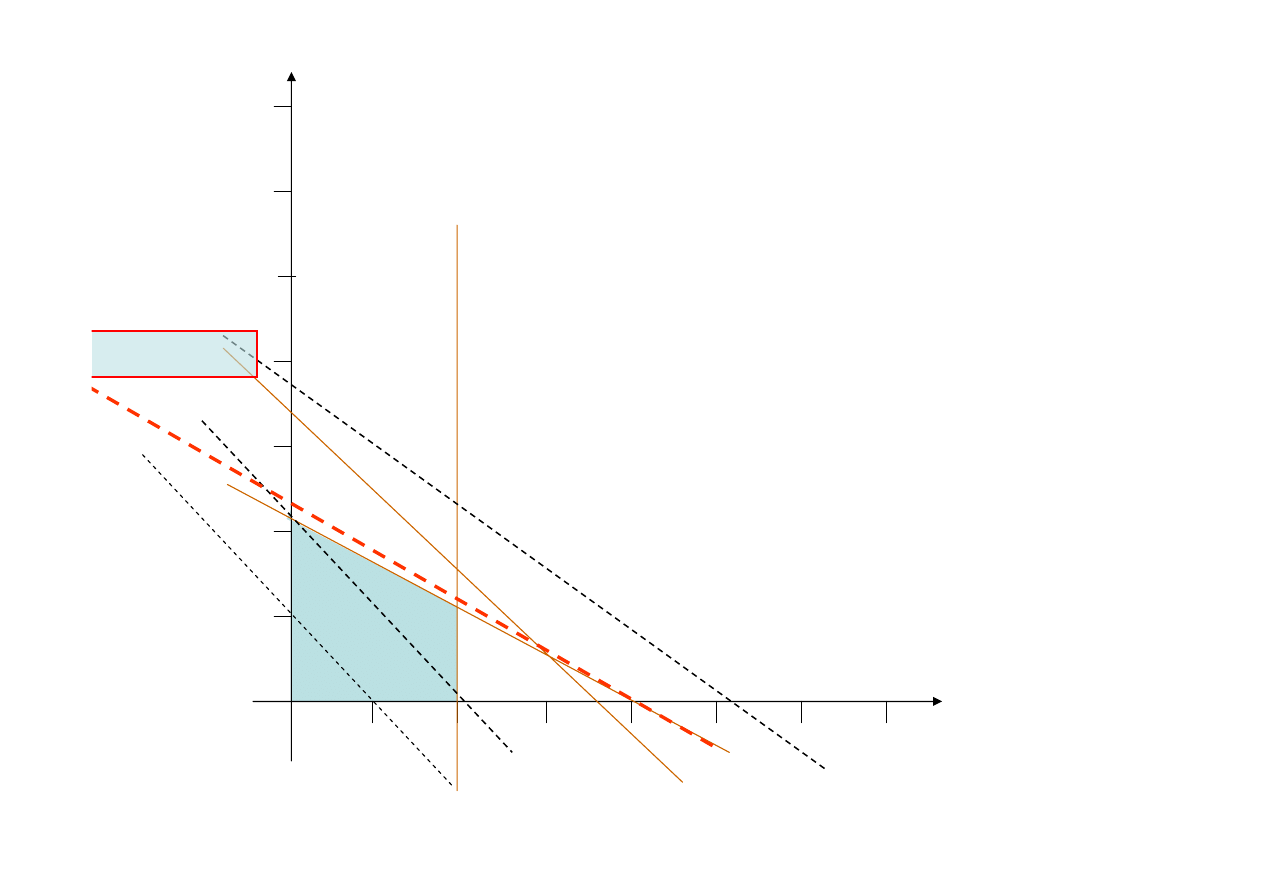
Wierzchołek
B
stanowi przecięcie prostych
x
1
+2x
2
=8
oraz
4
x
1
=16
.
Rozwiązując ten układ warunków, stwierdzamy, że
x
1
=4
i
x
2
=2
stąd
wartość funkcji celu w punkcie
B
wynosi
14
2x
1
+3x
2
= 6
2x
1
+3x
2
= 12
2x
1
+3x
2
= 21
W rozpatrywanym zagadnieniu optymalnym rozwianiem
jest wierzchołek
B
(4,2) zbioru dopuszczalnych
rozwiązań (
OABC
)
2x
1
+3x
2
= 14
Algorytm simpleks
Algorytm simpleks
Istota algorytmu simpleks polega na badaniu kolejnych
rozwiązań bazowych
(stanowiących wierzchołki zbioru rozwiązan dopuszczalnych) programu
liniowego o postaci kanonicznej (standardowej) w taki sposób, że:
1. znajdujemy (dowolne) rozwiązanie bazowe programu:
2. sprawdzamy, czy jest ono optymalne,
3. jeśli dane rozwiązanie nie jest optymalne, znajdujemy następne
rozwiązanie bazowe lepsze (lub przynajmniej nie gorsze od
poprzedniego)
Algorytm simpleks jest więc procedurą iteracyjną, etapową; w każdym etapie
wyznacza się rozwiązanie bazowe i sprawdza, czy można go jeszcze poprawić.
Postępowanie kończy się w momencie stwierdzenia, że aktualnego rozwiązania
bazowego nie można już poprawić, czyli że jest
optymalne
Sposób przechodzenia do kolejnych rozwiązan bazowych (kolejnych tablic
simpleks) oparty jest na przekształceniach macierzowych.
Każdy program liniowy, np.:
max
2
2
1
1
→
+
+
+
n
n
x
c
x
c
x
c
...
0
,
,
2
1
2
2
1
1
1
1
2
12
1
11
≥
≤
+
+
+
≤
+
+
+
n
m
n
mn
m
m
n
n
x
x
x
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
...
...
...
...
...
...
...
...
...
...
można zapisać w postaci macierzowej:
0
max
≥
≤
→
x
b
Ax
cx
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
mn
m
m
n
a
a
a
a
a
a
A
...
...
...
...
...
...
2
1
1
12
11
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
x
x
x
x
...
2
1
gdzie:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
m
b
b
b
...
1
[
]
n
c
c
c
...
1
=
Postać bazowa
Zadanie liniowe w postaci standardowej (kanonicznej)
ograniczenie zasobu
S
1
w postaci nierówności:
2x
1
+ 2x
2
≤ 14
ograniczenie zasobu
S
1
w postaci kanonicznej:
2x
1
+ 2x
2
+ x
3
= 14
dodając do lewej strony zmienną bilansującą
x
3
określoną jako
różnicę wartości lewej i prawej strony równania czyli:
x
3
= 14 - 2x
1
- 2x
2
≥ 0
Wartość
x
3
określa, jaka ilość środka
S
1
pozostanie niewykorzystana w
przypadku realizacji planu
Dwa pozostałe warunki ograniczające przekształcamy do postaci kanonicznych
przez wprowadzenie zmiennych bilansujących
x
4
i
x
5
Dla środka S
2
x
1
+ x
2
+ x
4
= 8
x
4
= 8 – x
1
– 2x
2
≥ 0
Dla środka S
3
x
1
+ x
5
= 16
x
5
= 16 – x
1
≥ 0
Wartości
x
4
i
x
5
określają jakie ilości środków, odpowiednio
S
2
i
S
3
pozostaną
niewykorzystane w przypadku realizacji planu (
x
1
, x
2
)
Oznacza to, rozpatrywane zadanie programowania liniowego jest
zadaniem w
postaci bazowej
, a
zmiennymi bazowymi
są zmienne
x
3
, x
4
i
x
5
.
Ponieważ wszystkie wartości zmiennych bazowych są nieujemne, jest to
bazowe rozwiązanie dopuszczalne
Przyjrzyjmy się rozwiązaniu bazowemu odpowiadającemu tej bazie
Przyjmując dla zmiennych niebazowych
x
1
i
x
2
wartości równe zeru, otrzymujemy
x
1
= 0, x
2
= 0, x
3
= 14, x
4
= 8, x
5
= 16
w rozwiązaniu tym wartość funkcji celu jest równa 0
max
3
2
)
,
,
,
,
(
2
1
5
4
3
2
1
→
+
=
x
x
x
x
x
x
x
f
W dalszych rozważaniach rozpatrzymy zadanie w postaci standardowej, w której
wszystkie warunki ograniczające (z wyjątkiem warunku nieujemności) są równaniami.
Dla rozpatrywanego zadania postać ta jest następująca:
max
3
2
)
,
,
,
,
(
2
1
5
4
3
2
1
→
+
=
x
x
x
x
x
x
x
f
0
,
,
,
,
16
4
8
2
14
2
2
5
4
3
2
1
5
1
4
2
1
3
2
1
≥
=
+
=
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
W dalszych rozważaniach rozpatrzymy zadanie w postaci standardowej, w której
wszystkie warunki ograniczające (z wyjątkiem warunku nieujemności) są równaniami.
Dla rozpatrywanego zadania postać ta jest następująca:
max
3
2
)
,
,
,
,
(
2
1
5
4
3
2
1
→
+
=
x
x
x
x
x
x
x
f
0
,
,
,
,
16
4
8
2
14
2
2
5
4
3
2
1
5
1
4
2
1
3
2
1
≥
=
+
=
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
współczynniki
funkcji celu
współczynniki
warunków
ograniczających
prawe strony
warunków
ograniczających
zmienne w
zadaniu
W rozpatrywanym przez nas zadaniu występuje
5
zmiennych i
3
warunki
ograniczające, stąd składowe wektorów i elementy macierzy są następujące
[
]
c
0
0
0
3
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
4
0
1
0
2
1
0
0
1
2
2
A
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
16
8
14
b
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
5
4
3
2
1
x
x
x
x
x
x
W rozpatrywanym przez nas zadaniu występuje
5
zmiennych i
3
warunki
ograniczające, stąd składowe wektorów i elementy macierzy są następujące
[
]
c
0
0
0
3
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
4
0
1
0
2
1
0
0
1
2
2
A
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
16
8
14
b
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
5
4
3
2
1
x
x
x
x
x
x
Widzimy, że wybierając z macierzy
A
kolumny trzecią, czwartą i piątą
otrzymujemy macierz jednostkową
Oznacza to, że układ równań odpowiadający warunkom ograniczającym
rozpatrywanego problemu jest w postaci bazowej
oraz, że zmiennymi bazowymi są zmienne
x
3
,
x
4
, i
x
5
, a zmiennymi niebazowymi
są zmienne pozostałe –
x
1
i
x
2
Ze względu na to, że przyjmując to rozwiązanie, nie uruchamiamy produkcji
(
x
1
= 0 i
x
2
= 0) zmienne bilansujące, określające niewykorzystane zasoby
środków
S
1
,
S
2
i
S
3
, są równe wielkościom zasobów tych środków.
w dalszych rozważaniach będziemy wykorzystywać
tablicę simpleksową
będącą
pewną modyfikacją
postaci macierzowej
zadania.
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
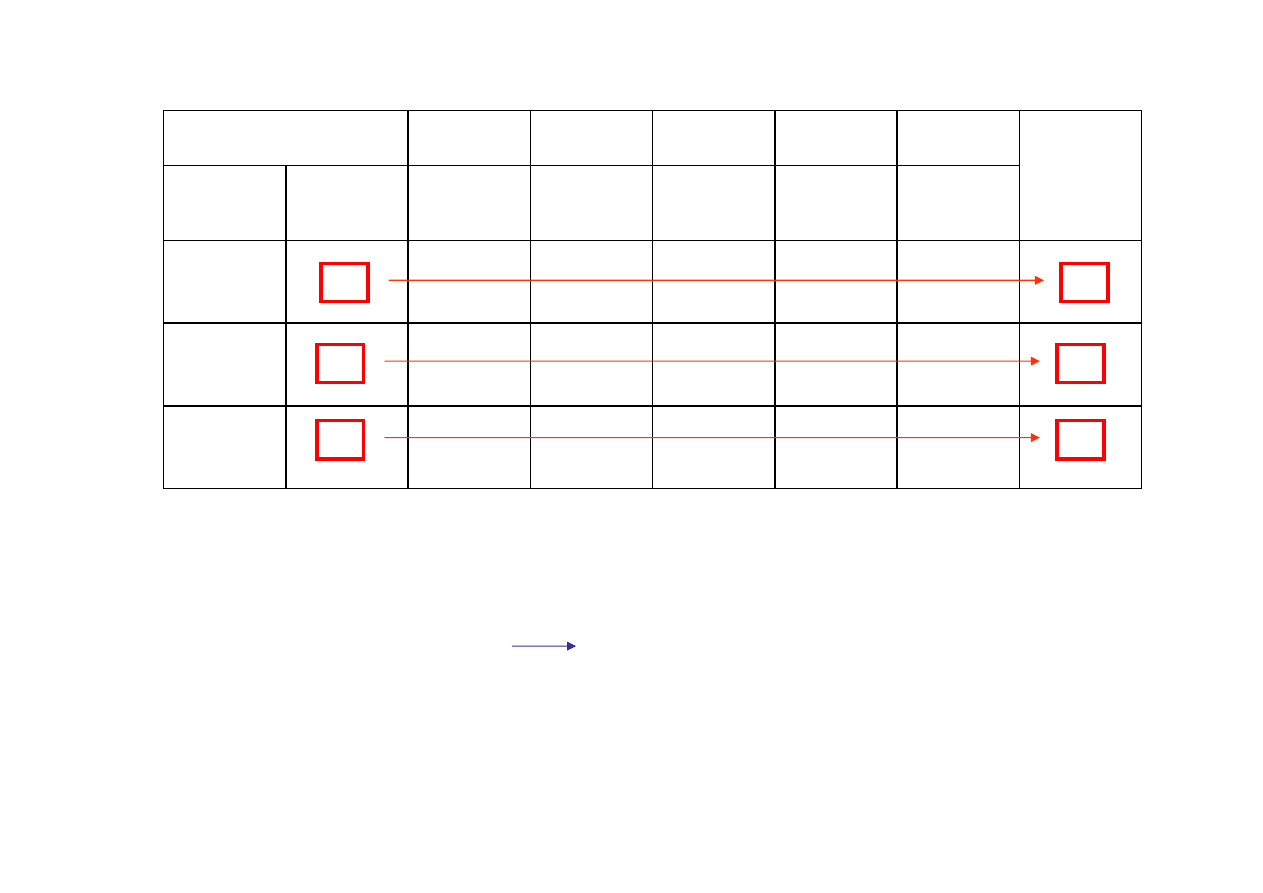
współczynniki funkcji celu c
nazwy zmiennych
macierz
współczynników A
wektor wyrazów
wolnych b
wykaz zmiennych
bazowych
wektor wartości
współczynników funkcji
celu c
B
odpowiadający
zmiennym bazowym
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
Z tablicy simpleksowej można odczytać wartość funkcji celu odpowiadającą
rozwiązaniu bazowemu, w którym zmiennymi bazowymi są
x
3
,
x
4
,
x
5
.
c
B
· b
wartość funkcji celu
0·14 + 0·8 + 0·16 = 0
Metoda simpleks
Metoda simpleks
Metoda simpleks polega na rozpatrzeniu ciągu
sąsiednich rozwiązań
bazowych
, czyli takich rozwiązań bazowych, dla których dwie kolejno
rozpatrywane bazy różnią się od siebie dokładnie o jedną zmienną.
Doboru
bazy sąsiedniej
dokonujemy w taki sposób aby zagwarantować
otrzymanie coraz lepszych (przynajmniej nie gorszych) wartości funkcji celu.
Przejście z jednej bazy do drugiej odbywa się przy wykorzystaniu
przekształceń
elementarnych
układu warunków ograniczających w postaci standardowej
(kanonicznej)
Przekształceniami elementarnymi
są: podzielenie dowolnie wybranego
warunku ograniczającego przez dowolną liczbę (różną od zera) oraz dodanie
do dowolnie wybranego warunku , pomnożonego przez dowolną liczbę (różną
od zera) innego warunku pomnożonego przez dowolna liczbę (różną od zera)
W wyniku przekształceń elementarnych układu warunków ograniczających
programowania liniowego otrzymujemy równoważny mu układ warunków,
generujących ten sam zbiór rozwiązań dopuszczalnych
Aby wykonać jeden krok (
iterację
) algorytmu metody simpleks należy:
1. stwierdzić czy rozwiązanie bazowe jest optymalne, czy też nie,
2. w przypadku gdy nie jest optymalne, wyznaczyć nową bazę sąsiednią,
3. przekształcić za pomocą przekształceń elementarnych macierz warunków
ograniczających do postaci bazowej względem bazy sąsiedniej.
Iteracja 1
Zbadamy jaki wpływ na dotychczasowe rozwiązanie (
x
3
, x
4
, x
5
, - zmienne
bazowe oraz
x
1
i
x
2
– zmienne niebazowe) miałoby przyjęcie przez jedną ze
zmiennych niebazowych np. zmienną
x
1
, wartości równej 1 (druga zmienna
niebazowa
x
2
przyjmuje cały czas wartość 0
Pierwszy warunek ograniczający w postaci kanonicznej:
Kryterium optymalno
Kryterium optymalno
ś
ś
ci
ci
14
2
2
3
2
1
=
+
+
x
x
x
14
2
3
=
+ x
ponieważ
x
1
= 1 oraz
x
2
= 0
12
3
=
x
wartość zmiennej bazowej
x
3
zmniejszyła się o 2 jednostki – z 14 do 12
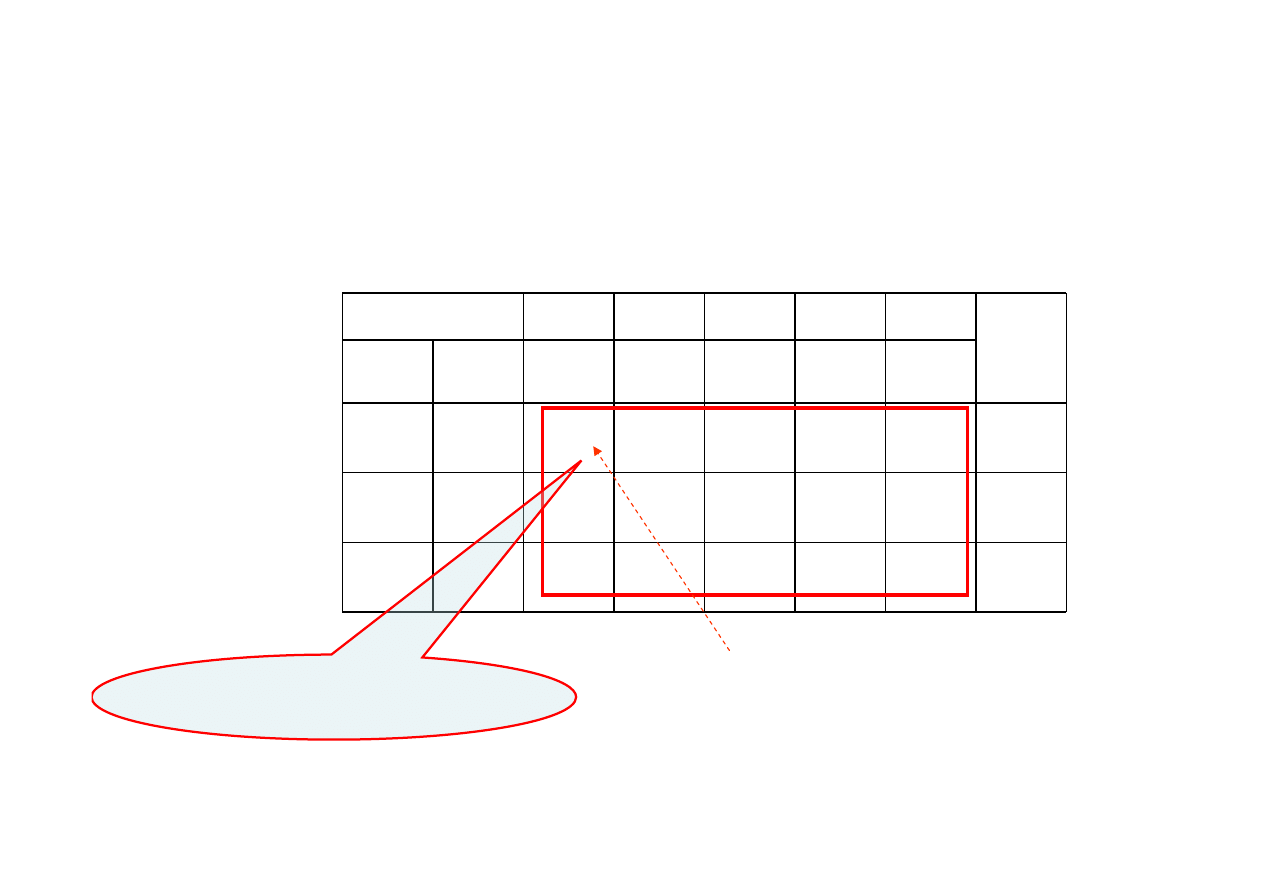
Wprowadzanie do rozwiązania coraz większych wartości zmiennej
x
1
będzie się odbywało kosztem zmiennej bazowej
x
3
każdej dodanej jednostce zmiennej
x
1
odpowiada spadek zmiennej bazowej
x
3
o 2 jednostki
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
macierz współczynników
warunków ograniczających A
Zmiana ta odpowiada wartości
współczynnika
a
11
= 2
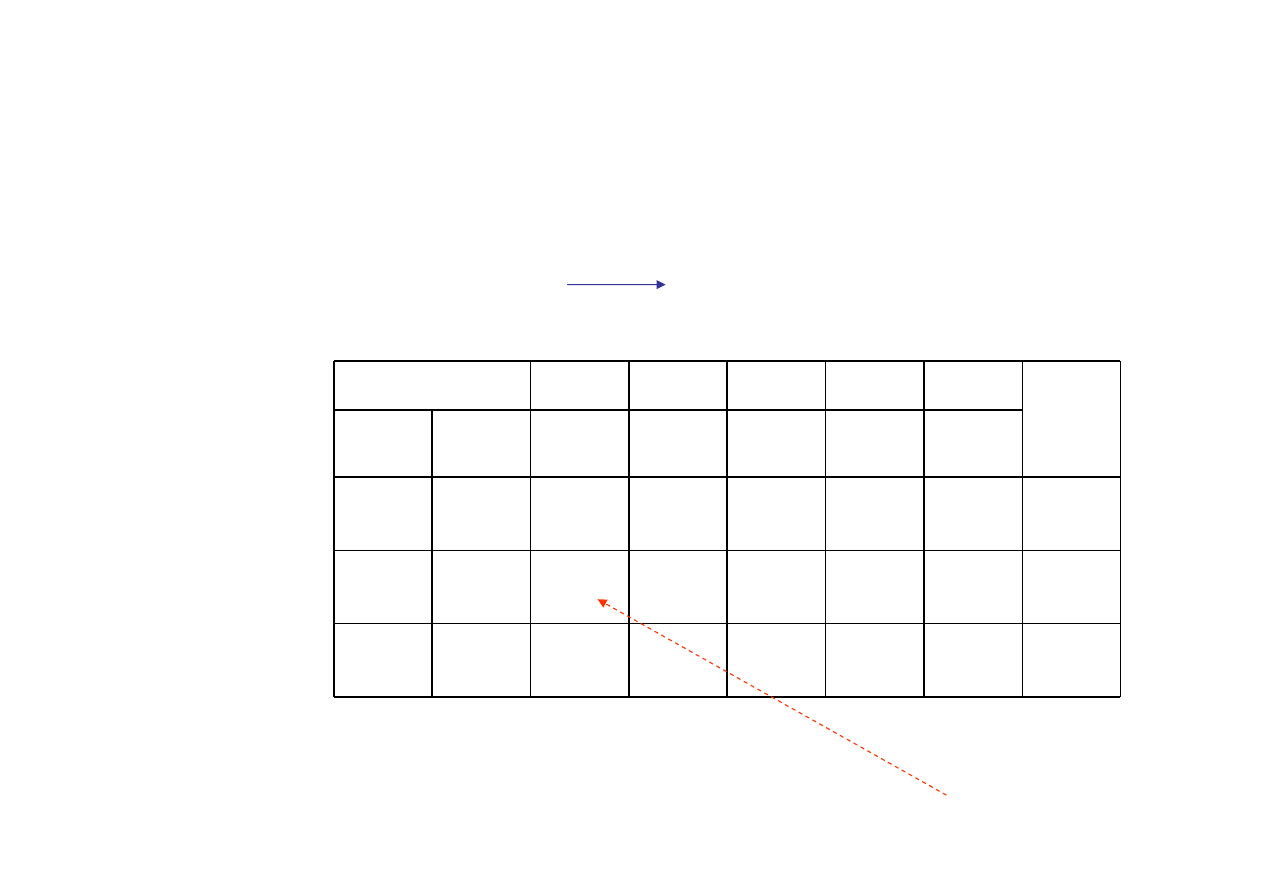
W podobny sposób sprawdźmy, jak na wartość zmiennej bazowej
x
4
wpłynie
przyjęcie założenia, że
x
1
= 1 – przy ciągłym trwaniu założenia, że
x
2
= 0
8
2
4
2
1
=
+
+
x
x
x
8
1
4
=
+ x
7
4
=
x
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
każdej zmianie wartości zmiennej
x
1
odpowiada spadek wartości
zmiennej
x
4
o wartość zapisaną w macierzy
A
(współczynnika
a
21
)
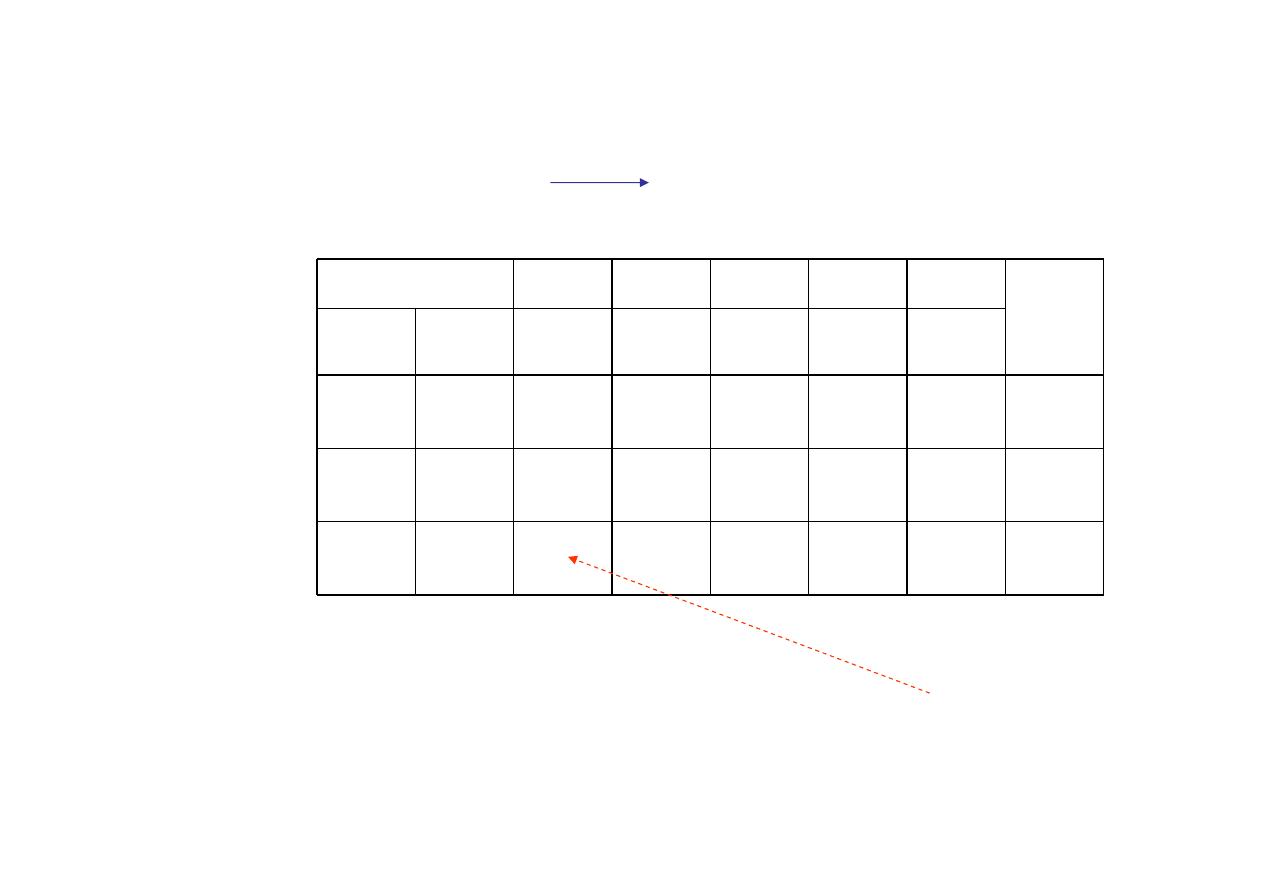
Rozpatrując w taki sam sposób trzeci warunek ograniczający, który ma postać:
16
4
5
1
=
+ x
x
16
4
5
=
+ x
12
5
=
x
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
każdej zmianie wartości zmiennej
x
1
odpowiada spadek wartości
zmiennej
x
5
o wartość zapisaną w macierzy
A
(współczynnika
a
31
)
Analogicznie możemy przeprowadzić rozważania dla drugiej zmiennej
niebazowej
x
2
przyjmując jej wartość równą jedności przy założeniu, że druga
zmienna niebazowa
x
1
jest równa 0
Zastanówmy się teraz w jaki sposób zmieni się
wartość funkcji celu
, która w
rozwiązaniu początkowym była równa 0.
ponieważ mamy
x
1
= 1 więc wzrost ten wyniesie:
2
1
2
1
1
=
⋅
=
⋅ x
c
0
2
0
11
3
=
⋅
=
⋅ a
c
Z drugiej strony możliwy jest
spadek
wartości funkcji celu związany z
obniżeniem dotychczasowych wartości przez zmienne bazowe.
Z pierwszym warunkiem ograniczającym związana jest zmiana:
0
1
0
21
4
=
⋅
=
⋅ a
c
0
4
0
31
5
=
⋅
=
⋅ a
c
Podobnie dla warunku drugiego i trzeciego
oraz
Dodając uzyskane wyniki, otrzymamy
łączną zmianę na poziomie 0
Z jednej strony spodziewamy się
wzrostu
wartość funkcji celu
związanego z tym, że współczynnik funkcji celu
c
1
= 2
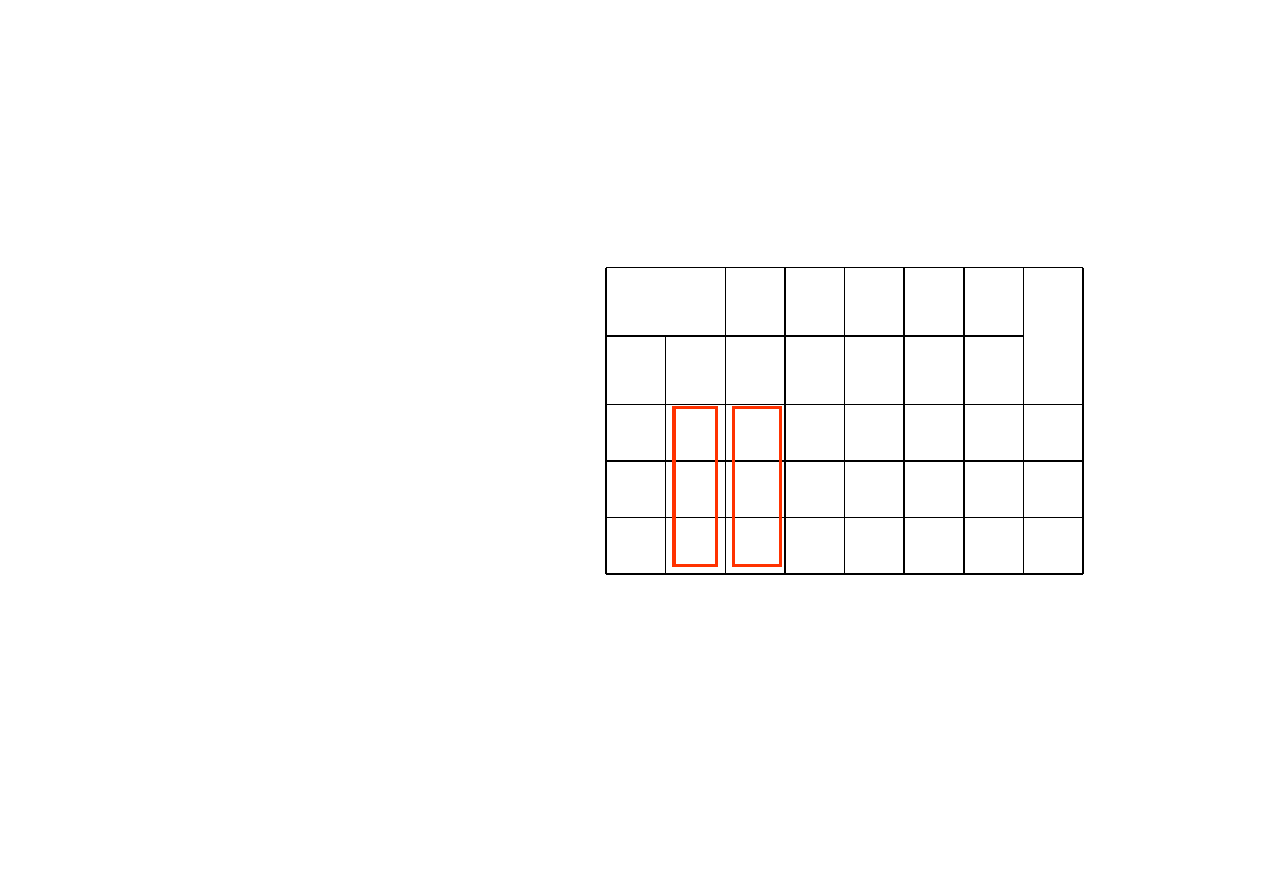
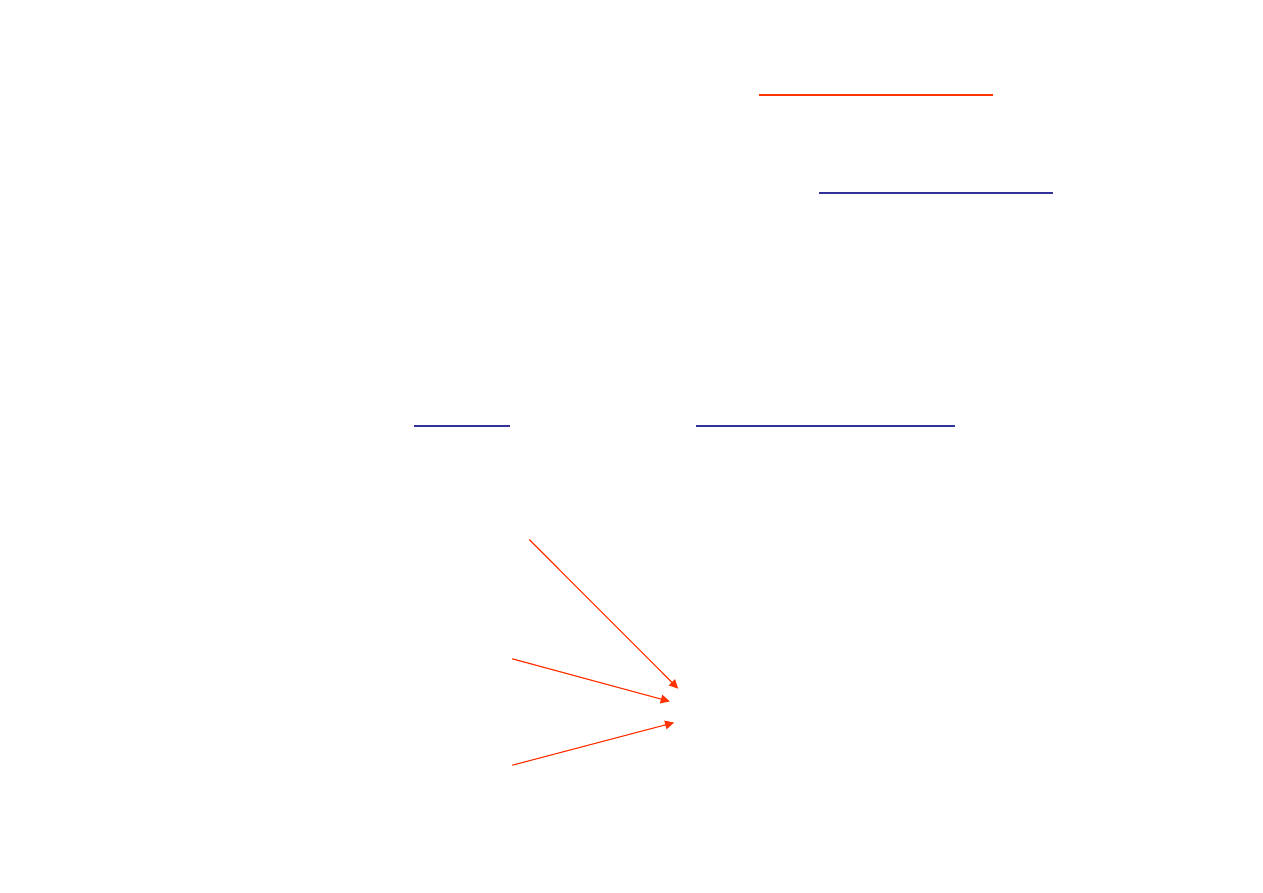
Zauważmy jednocześnie, że zmianę tę oznaczoną dla rozpatrywanej
zmiennej
x
j
symbolem
z
j
obliczyliśmy jako iloczyn skalarny dwóch
wektorów będących kolumnami tablicy simpleksowej:
cx
→max
2
3
0
0
0
Ba
za
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
Oznaczmy zmianę wartości funkcji celu spowodowaną zmianami w
wartościach zmiennych bazowych przez
z
j
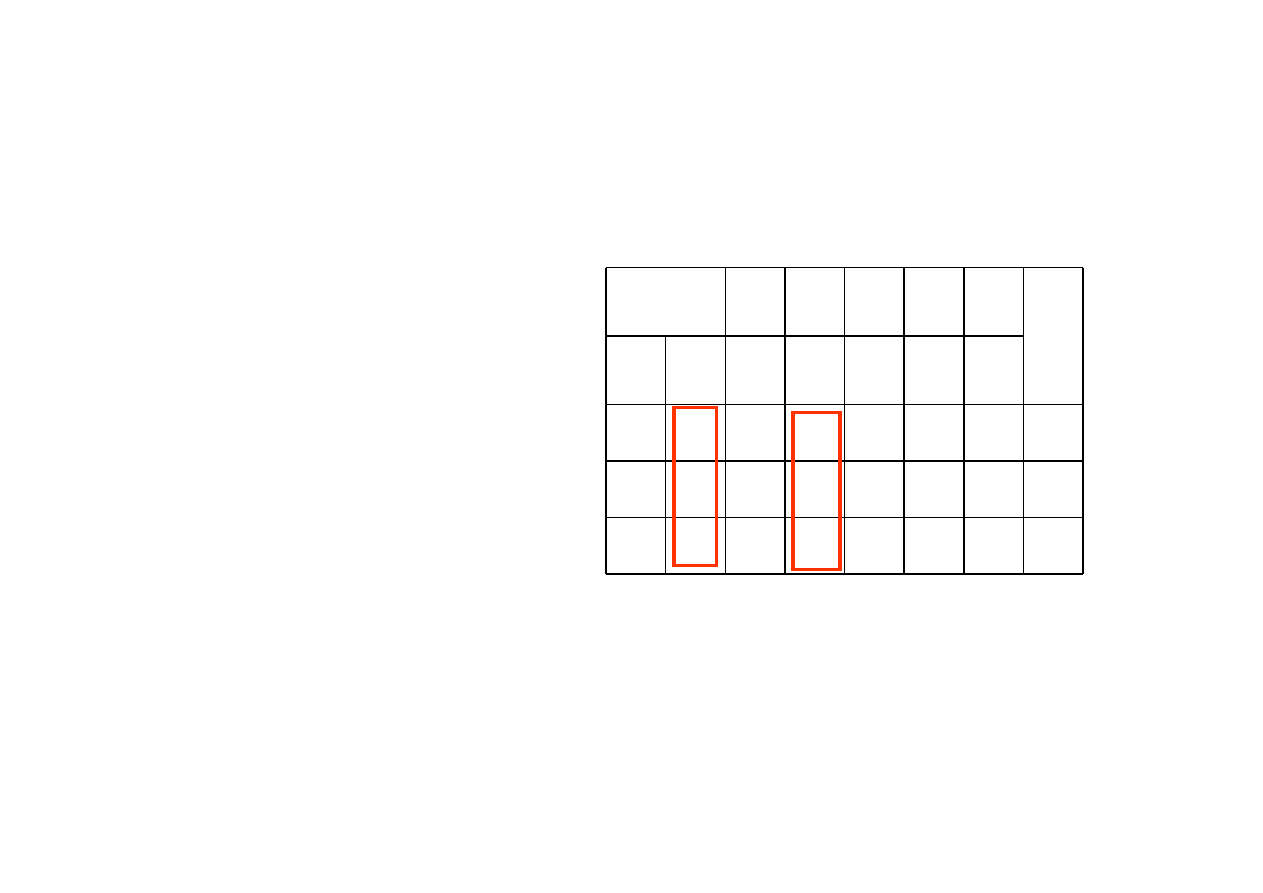
Zauważmy jednocześnie, że zmianę tę oznaczoną dla rozpatrywanej
zmiennej
x
j
symbolem
z
j
obliczyliśmy jako iloczyn skalarny dwóch
wektorów będących kolumnami tablicy simpleksowej:
cx
→max
2
3
0
0
0
Ba
za
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
Oznaczmy zmianę wartości funkcji celu spowodowaną zmianami w
wartościach zmiennych bazowych przez
z
j
W taki sam sposób obliczamy zmiany wartości funkcji celu przy
wprowadzeniu do rozważania zmiennej niebazowej
x
2
=1
(pamiętamy, że wówczas zmienna niebazowa
x
1
= 0)
0·2 + 0·2 + 0·4 = 0
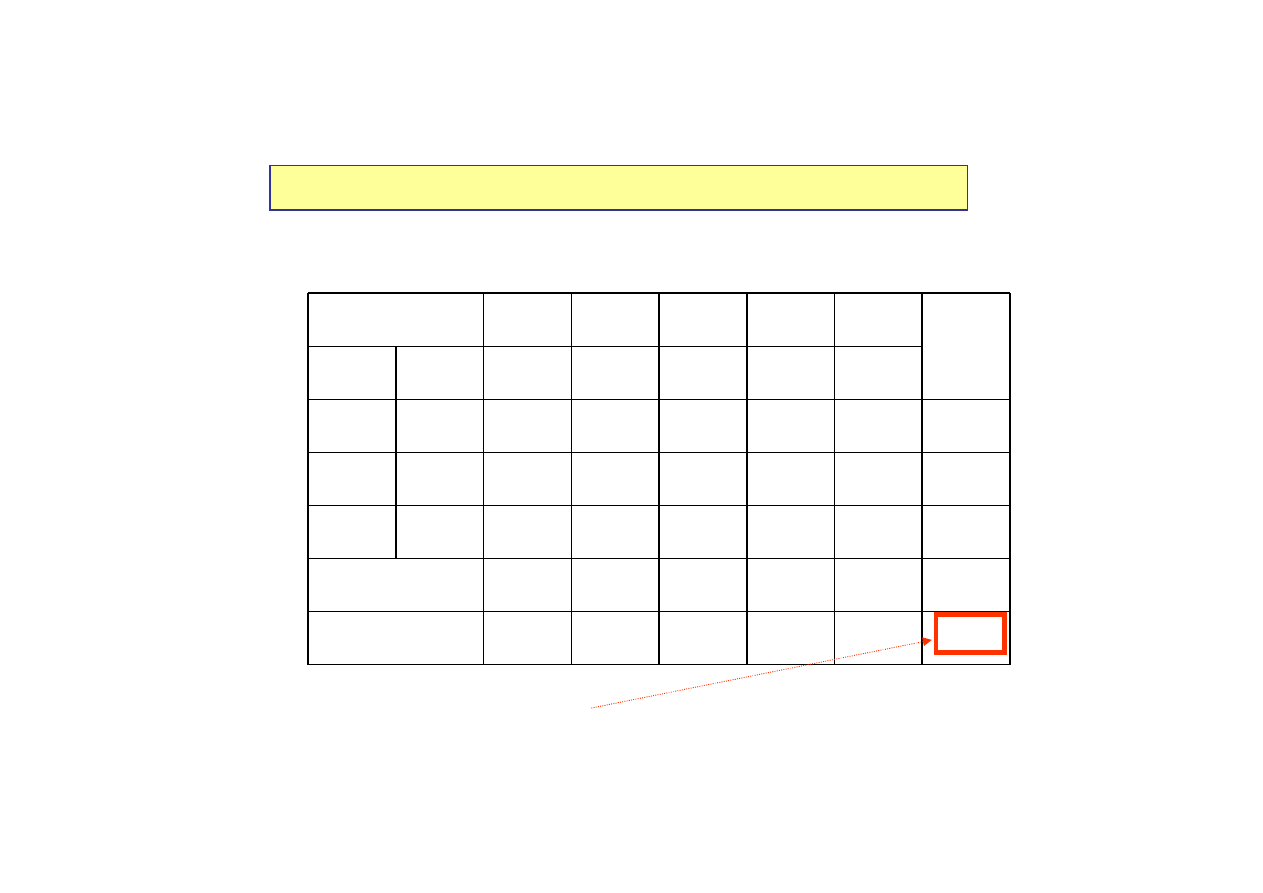
Różnica
c
j
– z
j
określa zmiany netto w wartościach funkcji celu, jeżeli
jedna jednostka zmiennej
x
j
zostanie wprowadzona do aktualnie
rozpatrywanego rozwiązania bazowego.
Wartości
c
j
– z
j
nazywamy
wskaźnikiem optymalności
wartości te dopisujemy jako ostatni wiersz tablicy simpleksowej.
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
zj
0
0
0
0
0
c
j
- z
j
2
3
0
0
0
0
ostatnim elementem w tym wierszu jest wartość funkcji celu
odpowiadająca rozpatrywanemu rozwiązaniu bazowemu
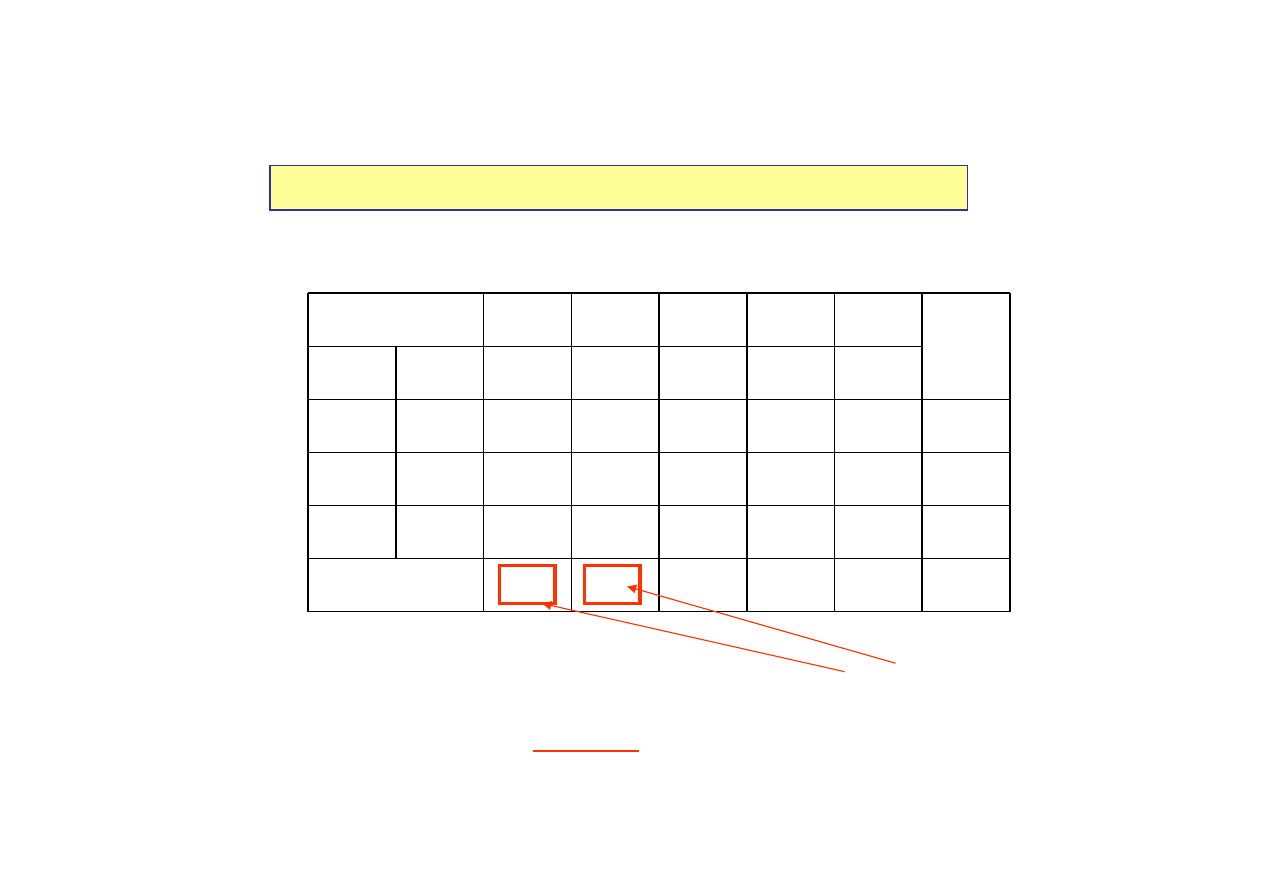
Różnica
c
j
– z
j
określa zmiany netto w wartościach funkcji celu, jeżeli
jedna jednostka zmiennej
x
j
zostanie wprowadzona do aktualnie
rozpatrywanego rozwiązania bazowego.
Wartości
c
j
– z
j
nazywamy
wskaźnikiem optymalności
wartości te dopisujemy jako ostatni wiersz tablicy simpleksowej.
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
c
j
- z
j
2
3
0
0
0
0
Wartości wskaźników optymalności dla zmiennych
x
1
i
x
2
są dodatnie, co
oznacza, ze jeżeli wprowadzimy którąkolwiek z tych zmiennych do bazy, to
wartość funkcji celu będzie
wzrastać
Kryterium optymalno
Kryterium optymalno
ś
ś
ci dla zadania maksymalizacji
ci dla zadania maksymalizacji
Je
Je
ż
ż
eli warto
eli warto
ść
ść
wszystkich wska
wszystkich wska
ź
ź
nik
nik
ó
ó
w optymalno
w optymalno
ś
ś
ci s
ci s
ą
ą
niedodatnie, to
niedodatnie, to
rozpatrywane rozwi
rozpatrywane rozwi
ą
ą
zanie jest optymalne.
zanie jest optymalne.
Je
Je
ż
ż
eli cho
eli cho
ć
ć
jeden ze wska
jeden ze wska
ź
ź
nik
nik
ó
ó
w optymalno
w optymalno
ś
ś
ci jest dodatni, to istnieje
ci jest dodatni, to istnieje
mo
mo
ż
ż
liwo
liwo
ść
ść
poprawy tego rozwi
poprawy tego rozwi
ą
ą
zania
zania
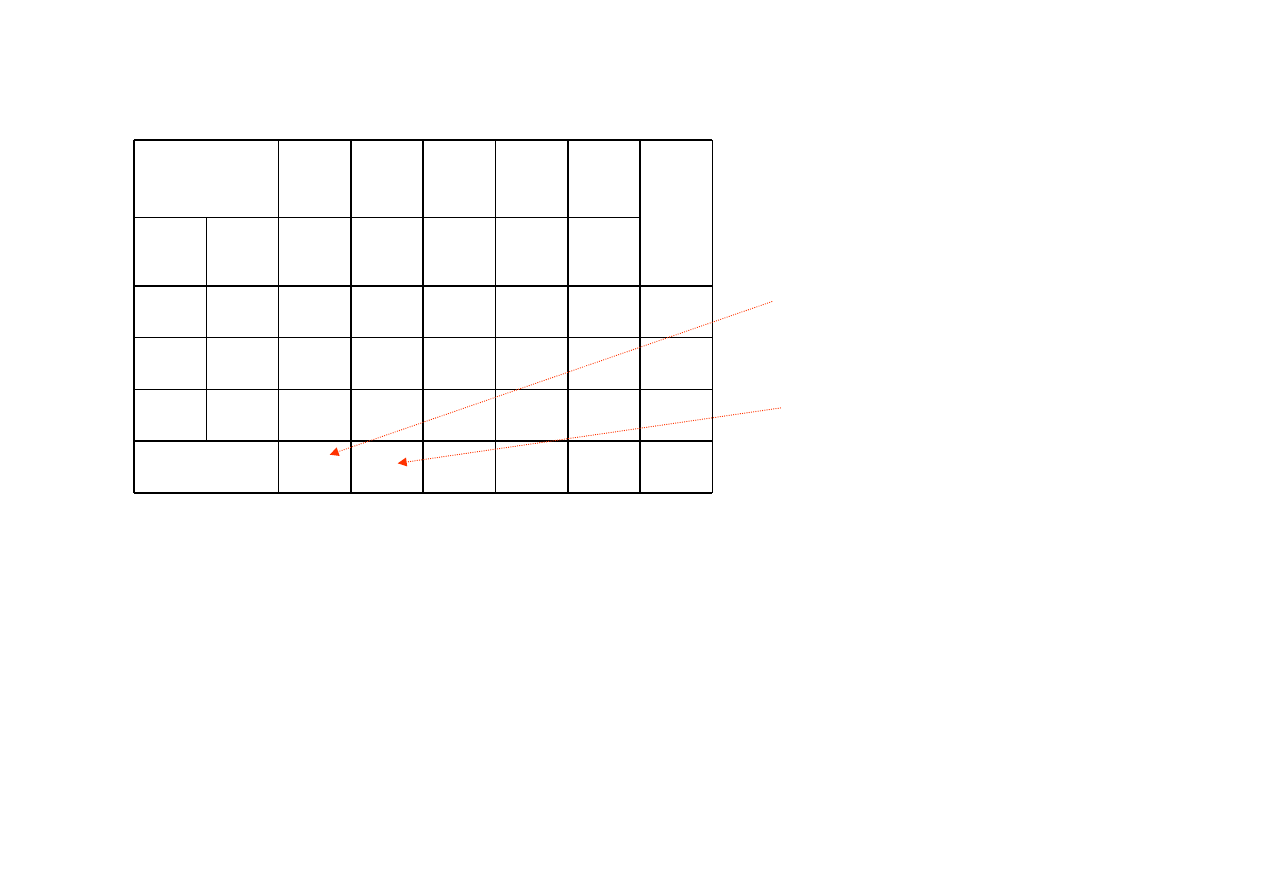
Wyb
Wyb
ó
ó
r zmiennej wprowadzanej do bazy
r zmiennej wprowadzanej do bazy
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
c
j
- z
j
2
3
0
0
0
0
wprowadzając do początkowego
rozwiązania bazowego zmiennej
x
1
= 1 powoduje wzrost
funkcji celu o
2
jednostki
x
2
= 1 powoduje wzrost
funkcji celu o
3
jednostki
Kryterium wej
Kryterium wej
ś
ś
cia
cia
Wybieramy największą wartość wskaźnika optymalności. Odpowiadająca mu
zmienną wprowadzamy do nowej bazy.
Jeśli największej wartości wskaźnika optymalności odpowiada więcej niż jedna
zmienna, to do nowej bazy wprowadzamy zmienną o najniższym numerze.
w rozpatrywanym prze nas przypadku do
nowej bazy wprowadzimy zmienną
x
2
Wyb
Wyb
ó
ó
r zmiennej
r zmiennej
opuszczaj
opuszczaj
ą
ą
cej baz
cej baz
ę
ę
14
2
2
3
2
1
=
+
+
x
x
x
14
2
3
2
=
+ x
x
Zastanówmy się teraz jaką największa wartość może przyjąć zmienna
x
2
,
którą zdecydowaliśmy się wprowadzić do nowej bazy.
Musi ona być tak dobrana aby były spełnione wszystkie warunki ograniczające
Pierwszy warunek ograniczający
14
2
2
=
x
ponieważ zmienna
x
1
jako niebazowa jest równa zeru, więc:
Zwiększając wartość
x
2
, możemy doprowadzić do tego, że dotychczasowa
zmienna bazowa
x
3
przyjmie wartość zero. Będzie tak wówczas, gdy:
7
2
=
x
czyli
dalsze zwiększanie wartości zmiennej
x
2
doprowadziłoby do tego, że
x
3
byłoby
ujemne, co jest niedopuszczalne.
Największa dopuszczalna wartość zmiennej
x
2
dla pierwszego warunku
ograniczającego jest równa 7
Drugi warunek ograniczający
8
2
4
2
1
=
+
+
x
x
x
8
2
4
2
=
+ x
x
8
2
2
=
x
4
2
=
x
W związku z tym, że mamy
x
1
= 0 otrzymujemy:
Zwiększając wartość
x
2
,
możemy doprowadzić do tego, że dotychczasowa
zmienna bazowa
x
4
przyjmie wartość zero. Będzie tak wówczas, gdy
czyli
Największa dopuszczalna wartość zmiennej
x
2
ze względu na drugi
warunek ograniczający wynosi 4
Trzeci warunek ograniczający
16
0
4
5
2
1
=
+
+
x
x
x
Ponieważ współczynnik przy
x
2
jest równy 0, zwiększanie wartości zmiennej
x
2
nie ma żadnego wpływu na zmienną
x
5
, tak więc zmiennej
x
5
nie możemy
wyprowadzić z bazy poprzez wprowadzenie do bazy zmiennej
x
2
Największa dopuszczalna wartość zmiennej
x
2
musi być tak dobrana, aby były
spełnione wszystkie warunki ograniczające. Ponieważ warunek drugi
ogranicza ją najbardziej (
x
2
= 4 ). Odpowiadająca temu warunkowi zmienna
x
4
przyjmie wartość 0, stając się zmienną niebazową.
Kryterium wyj
Kryterium wyj
ś
ś
cia
cia
Obliczamy ilorazy kolejnych wyraz
Obliczamy ilorazy kolejnych wyraz
ó
ó
w wolnych przez odpowiadaj
w wolnych przez odpowiadaj
ą
ą
ce im
ce im
elementy kolumny wchodz
elementy kolumny wchodz
ą
ą
cej do bazy dla tych element
cej do bazy dla tych element
ó
ó
w kolumny
w kolumny
wprowadzanej do bazy, kt
wprowadzanej do bazy, kt
ó
ó
re s
re s
ą
ą
dodatnie.
dodatnie.
Baz
Baz
ę
ę
opuszcza ta zmienna, dla kt
opuszcza ta zmienna, dla kt
ó
ó
rej odpowiadaj
rej odpowiadaj
ą
ą
cy jej iloraz jest
cy jej iloraz jest
najmniejszy. Je
najmniejszy. Je
ż
ż
eli minimum jest przyjmowane przez wi
eli minimum jest przyjmowane przez wi
ę
ę
cej ni
cej ni
ż
ż
jeden
jeden
raz, to jako zmienn
raz, to jako zmienn
ą
ą
opuszczaj
opuszczaj
ą
ą
c
c
ą
ą
baz
baz
ę
ę
wybieramy zmienn
wybieramy zmienn
ą
ą
o
o
najni
najni
ż
ż
szym numerze.
szym numerze.
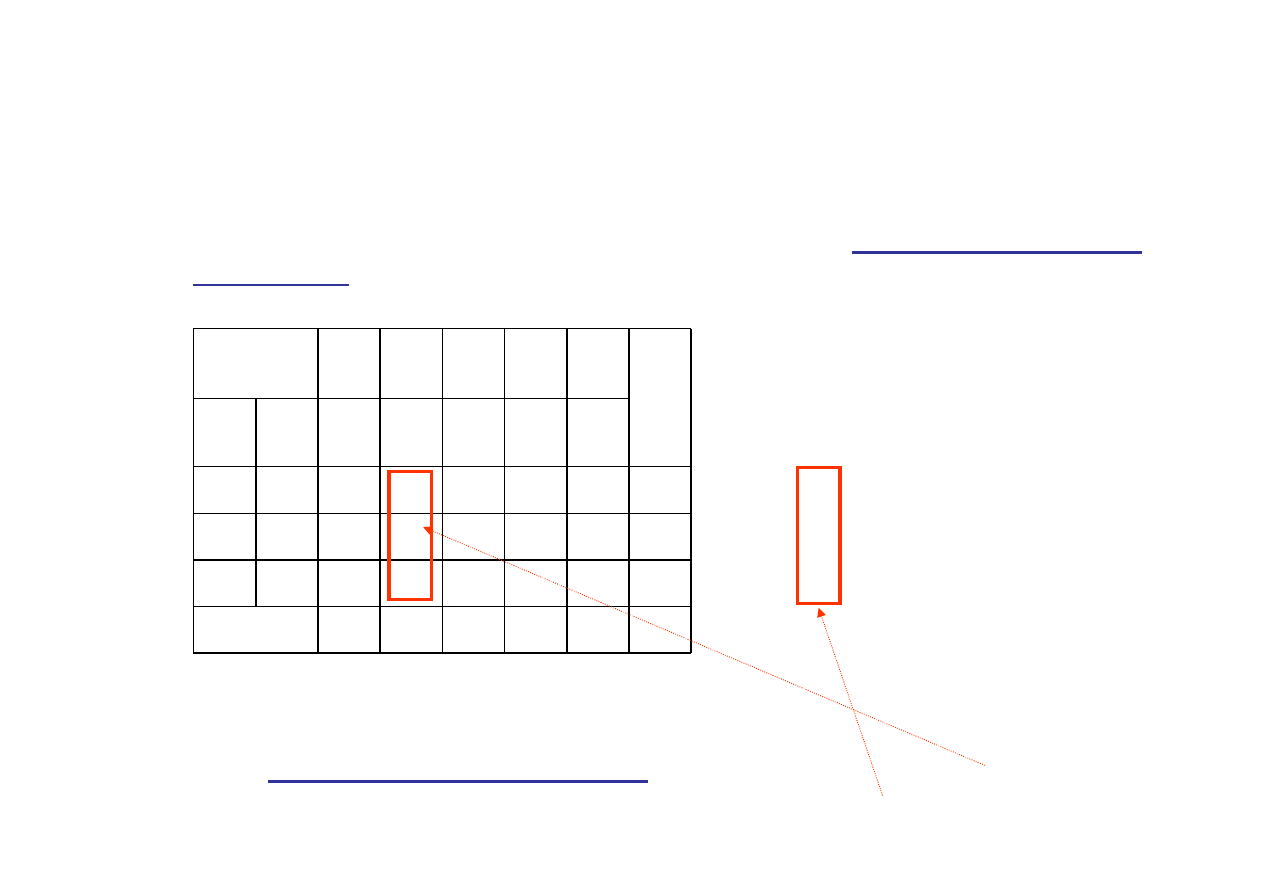
Przej
Przej
ś
ś
cie do rozwi
cie do rozwi
ą
ą
zania bazowego s
zania bazowego s
ą
ą
siedniego
siedniego
Ponieważ doszliśmy do wniosku, że z dotychczasowej bazy (
x
3
,
x
4
, i
x
5
) należy
usunąć zmienną
x
4
oraz na jaj miejsce wprowadzić zmienną
x
2
, naszym celem
jest obecnie otrzymanie odpowiadającego nowej bazie rozwiązania bazowego
sąsiedniego
cx →max
2
3
0
0
0
Ba
za
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
c
j
- z
j
2
3
0
0
0
0
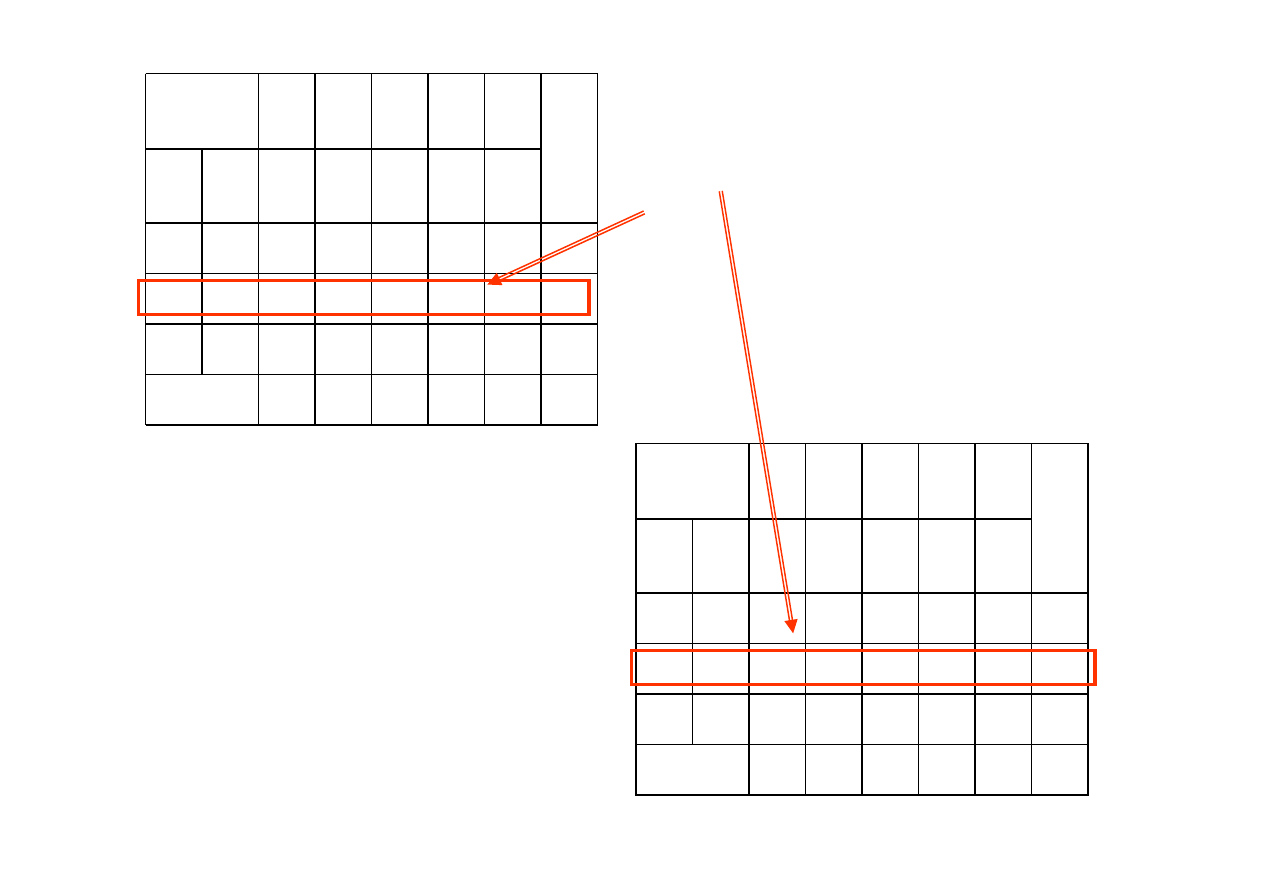
Ze względu na to, że zmienna
x
2
staje się zmienna bazową, musimy wykonać
operacje przekształceń elementarnych w taki sposób aby druga kolumna
przekształconej macierzy warunków ograniczających miała postać
0
1
0
cx
→max
2
3
0
0
0
Ba
za
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
c
j
- z
j
2
3
0
0
0
0
0
0
0
0
3
2
c
j
- z
j
16
1
0
0
0
4
0
x
5
4
0
0,5
0
1
0,5
3
x
2
14
0
0
1
2
2
0
x
3
x
5
x
4
x
3
x
2
x
1
c
B
Ba
za
b
0
0
0
3
2
cx
→max
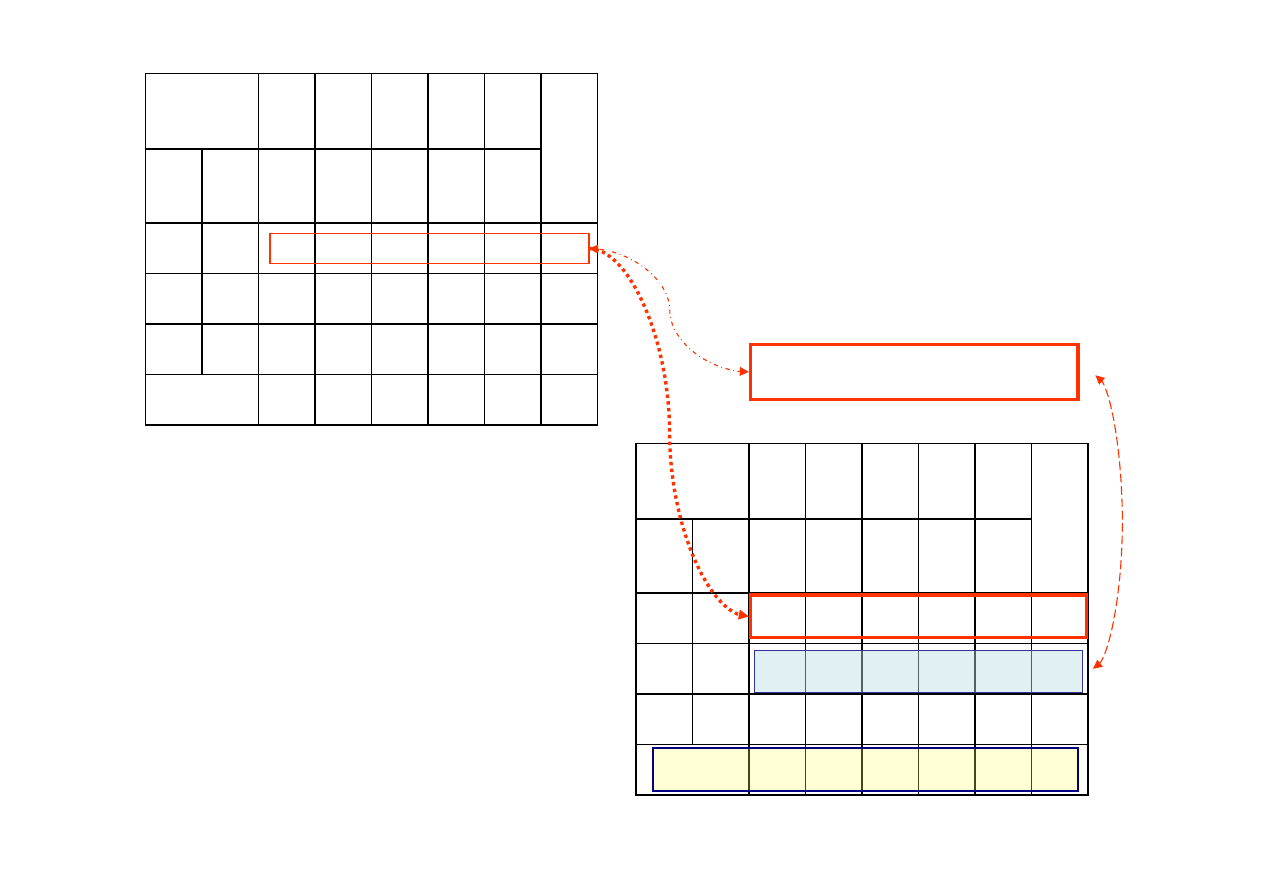
W tym celu drugi wiersz tabeli simpleksowej
dzielimy przez 2 i zapisujemy go w nowej
tabeli
4
0
0,5
0
1
0,5
0
0
0
0
3
2
c
j
- z
j
16
1
0
0
0
4
0
x
5
8
0
1
0
2
1
0
x
4
14
0
0
1
2
2
0
x
3
x
5
x
4
x
3
x
2
x
1
c
B
Ba
za
b
0
0
0
3
2
cx
→max
12
0
-1,5
0
0
0,5
c
j
- z
j
16
1
0
0
0
4
0
x
5
3
x
2
6
0
-1
1
0
1
0
x
3
x
5
x
4
x
3
x
2
x
1
c
B
Ba
za
b
0
0
0
3
2
cx
→max
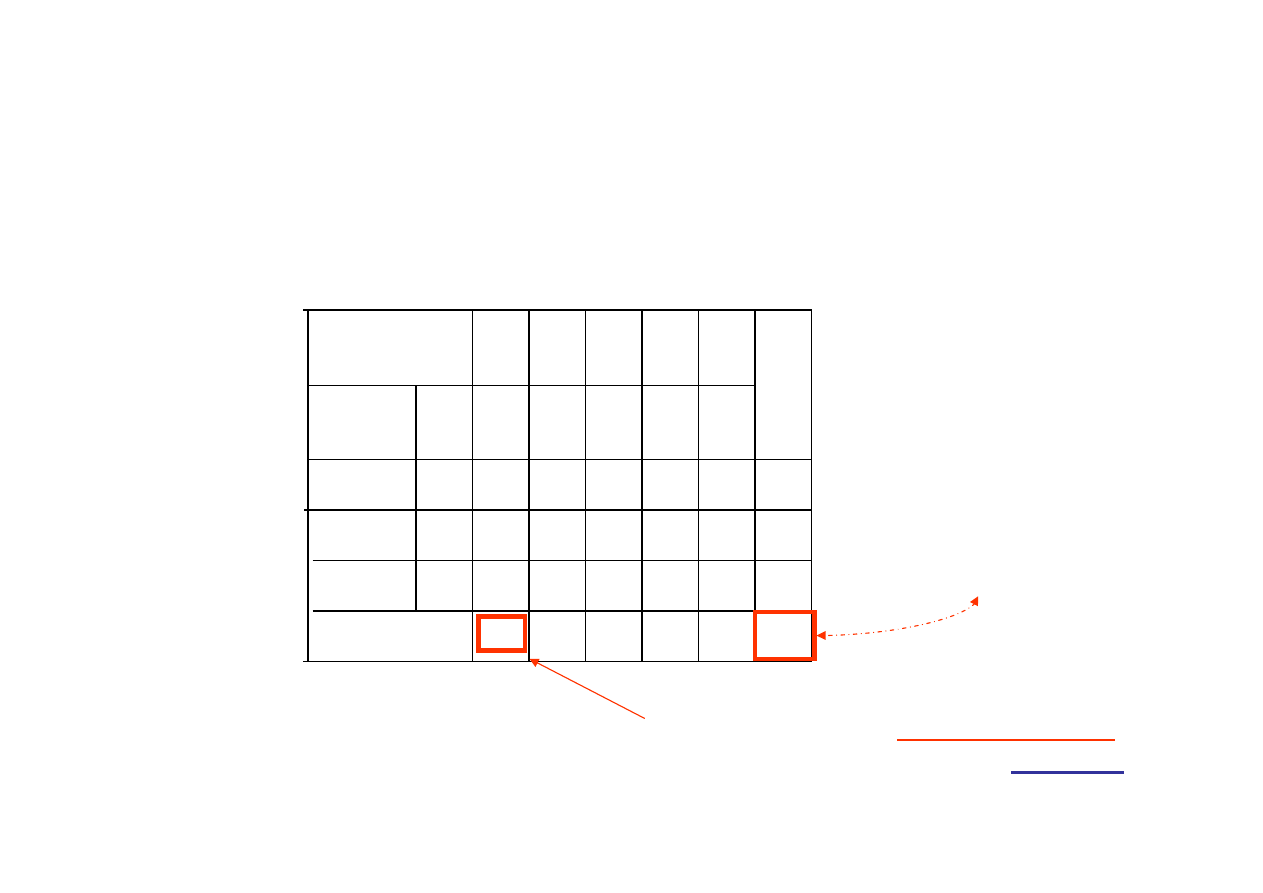
z koli przekształcony wiersz mnożymy przez
-2 i dodajemy do wiersza pierwszego z
pierwszej tablicy simpleksowej.
Wynik zapisujemy w tablicy simpleksowej II
x(
-2)
8
0
-1
0
-2
-1
(+)
4
0
0,5
0
1
0,5
12
0
-1,5
0
0
0,5
c
j
- z
j
16
1
0
0
0
4
0
x
5
3
x
2
6
0
-1
1
0
1
0
x
3
x
5
x
4
x
3
x
2
x
1
c
B
Baza
b
0
0
0
3
2
cx →max
Tablica simpleksowa po I iteracji
Tablica simpleksowa po I iteracji
wartość funkcji celu
po I iteracji
Zgodnie z kryterium optymalności otrzymane rozwiązanie
nie jest optymalne
,
ponieważ wartość współczynnika optymalności dla zmiennej
x
2
jest dodatnia
Iteracja 2
Kryterium wejścia dla metody simpleks wskazuje, że istnieje tylko jedna
możliwość wprowadzenia do bazy nowej zmiennej, aby poprawić wartość
funkcji celu w nowym rozwiązaniu. Tą zmienną jest
x
1
przyrost funkcji celu odpowiadający jednostce wprowadzanej zmiennej
x
1
wynosi
0,5
Stosując kryterium wyjścia, obliczamy odpowiednie ilorazy,
otrzymując:
dla wiersza 1 –
dla wiersza 2 –
6:1 = 6
4:(0,50) = 8
dla wiersza 3 –
16:4 = 4
Minimalną wartość otrzymujemy dla wiersza 3, co oznacza, że z bazy
należy usunąć zmienną
x
5
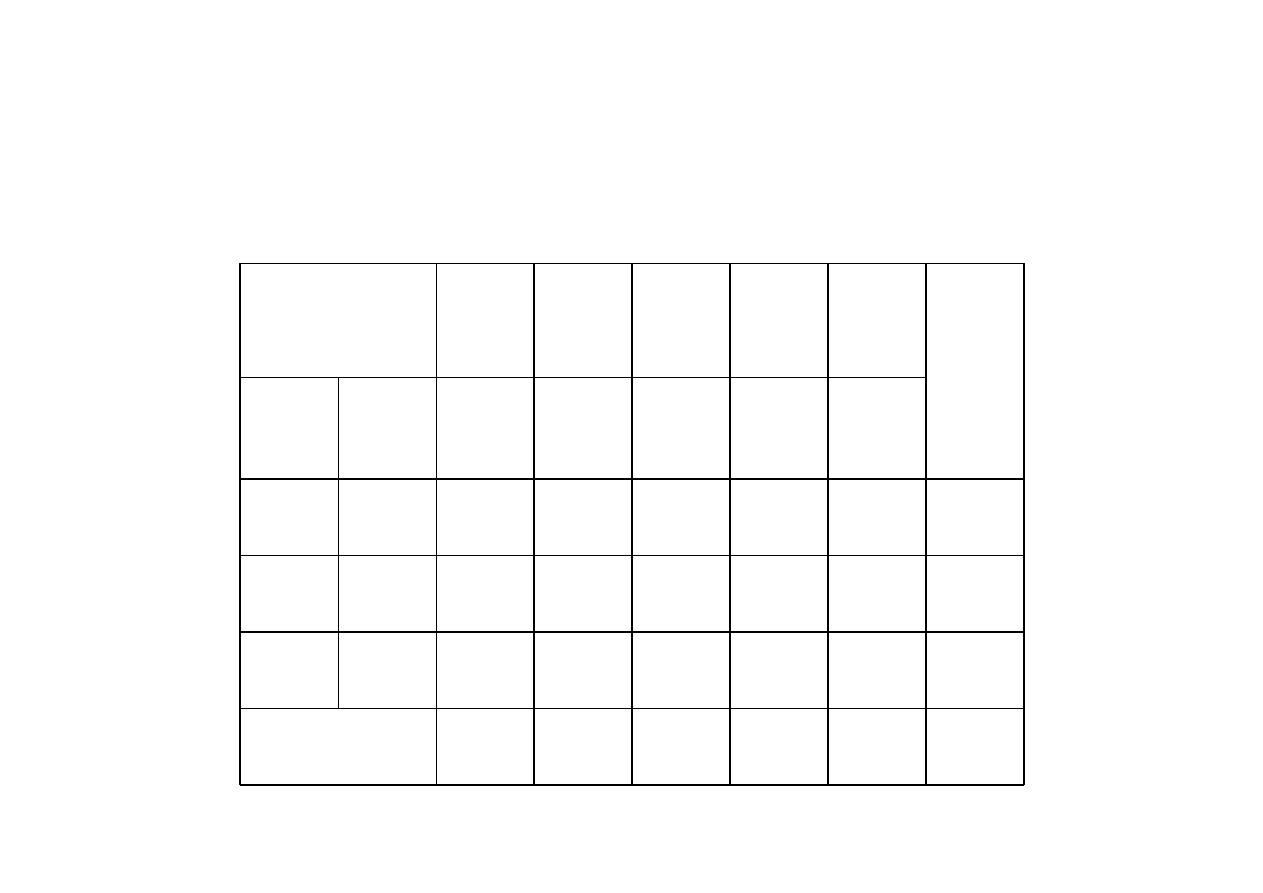
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
0
0
1
-1
-0,25
2
x
2
3
0
1
0
0,5
-0,125
2
x
1
2
1
0
0
0
0,25
4
c
j
- z
j
0
0
0
-1,5
-0,125
14
Tablica simpleksowa po II iteracji
Tablica simpleksowa po II iteracji
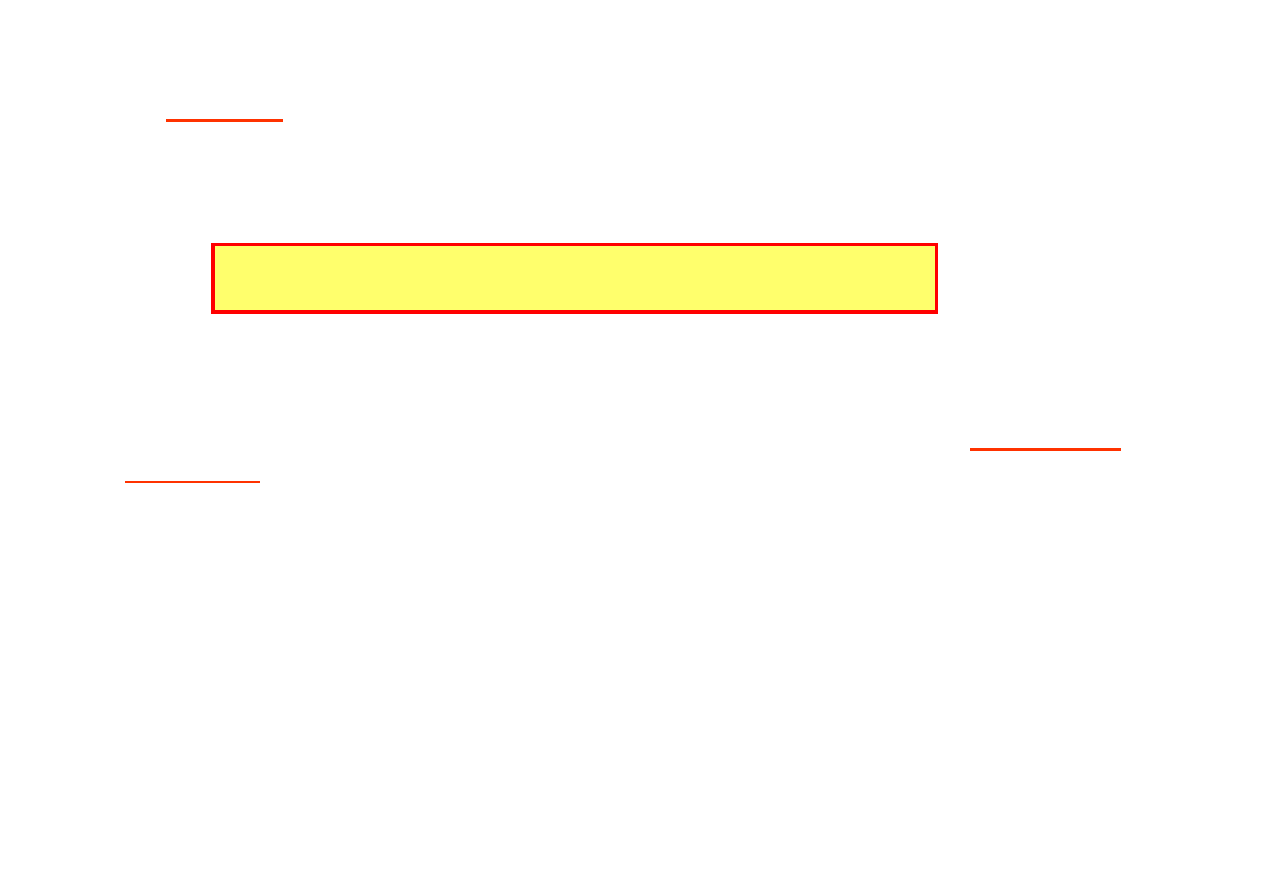
Iteracja 3
Sprawdzamy, czy otrzymane rozwiązanie bazowe jest optymalne;
0
0
2
2
4
5
4
3
2
1
=
=
=
=
=
x
x
x
x
x
,
,
,
,
Ponieważ wszystkie wskaźniki optymalności zapisane w ostatnim wierszu tablicy
simpleksowej są
niedodatnie
, zgodnie z kryterium optymalności jest to
rozwiązanie
optymalne
– co kończy procedurę optymalizacji.
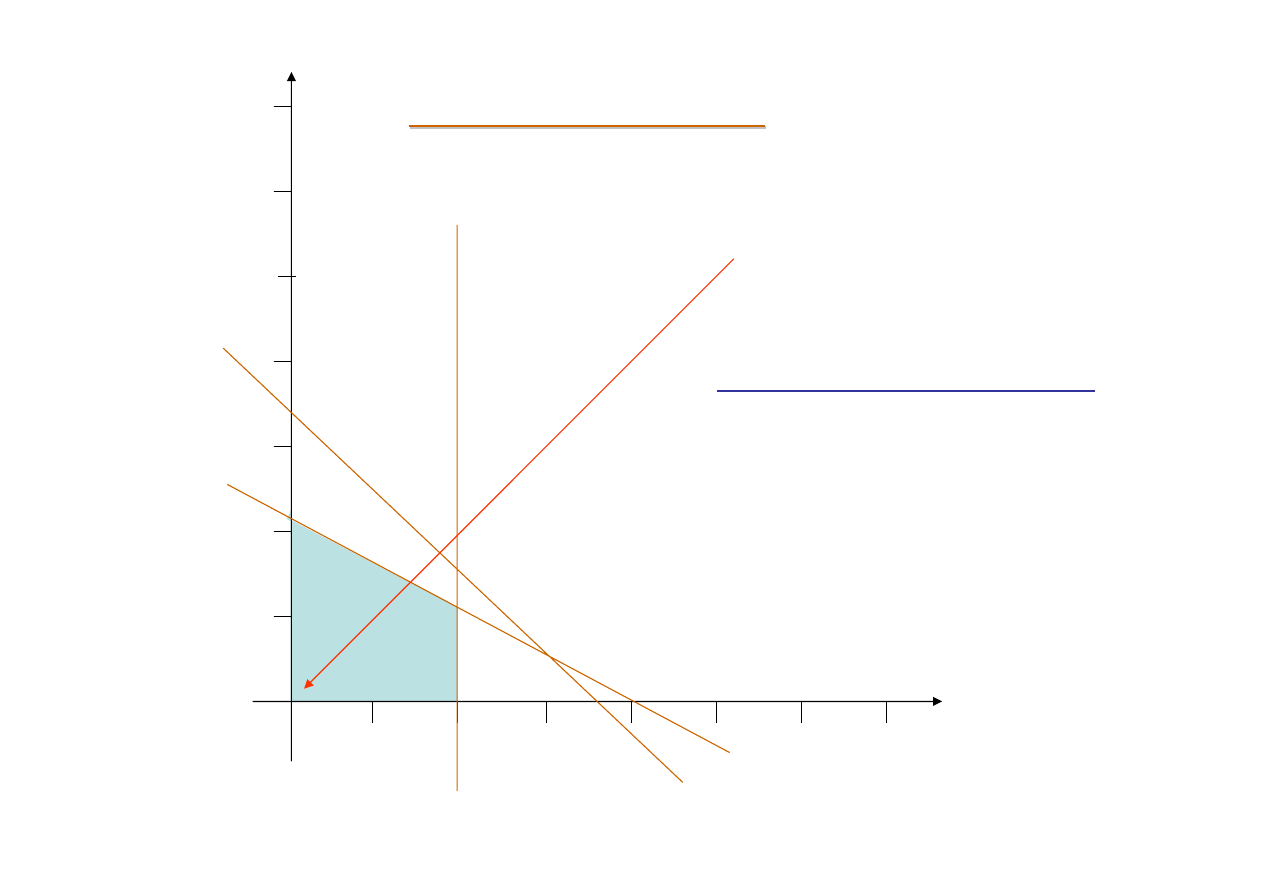
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
Interpretacja graficzna
Interpretacja graficzna
Rozwiązanie początkowe:
x
1
=0, x
2
=0, x
3
=14, x
4
=8, x
5
=16
Rozwiązanie nie jest optymalne
warunek ograniczający III
warunek
ograniczający II
warunek
ograniczający I
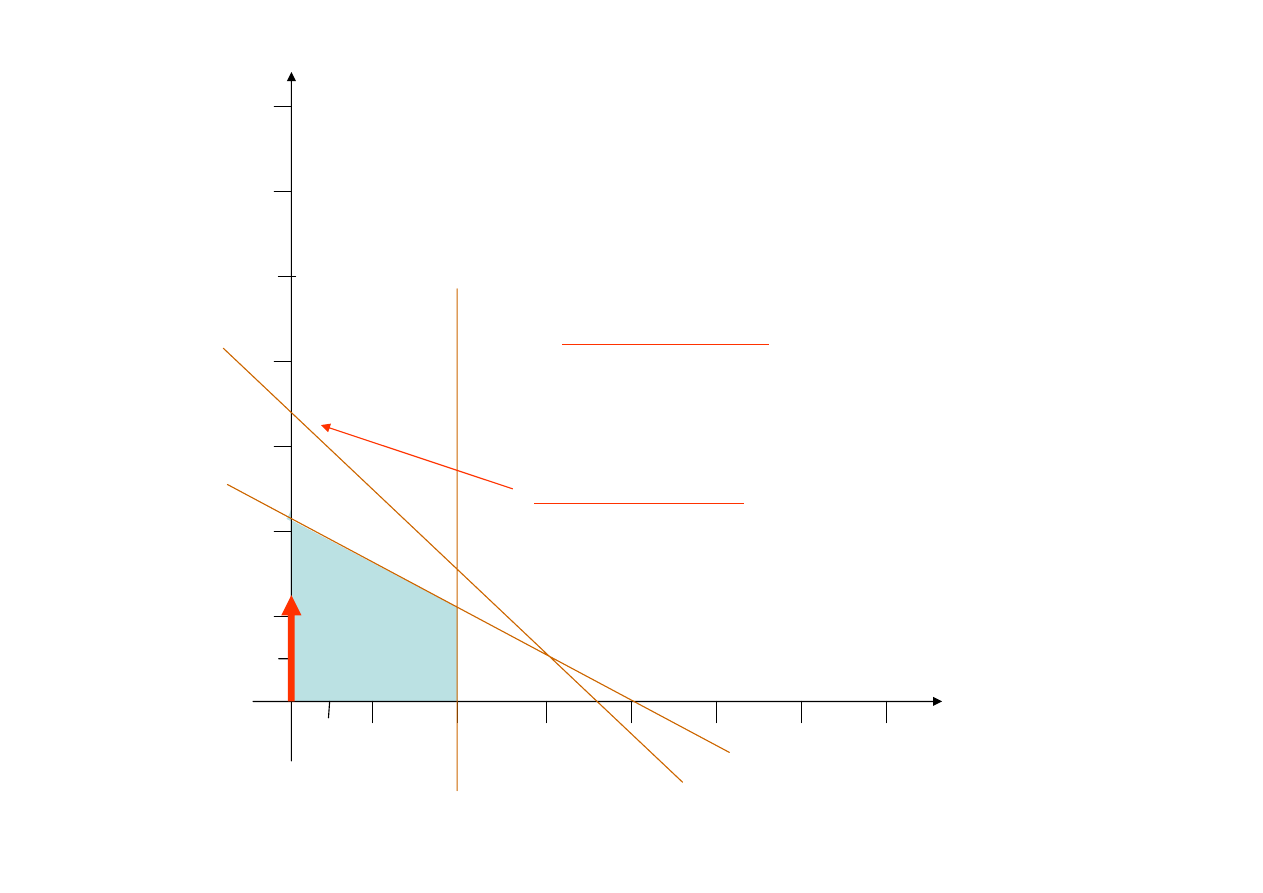
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
wprowadzając do I rozwiązania bazowego
za x
1
=1 otrzymujemy punkt
P
1
(1,0)
za x
2
=1 otrzymujemy punkt
P
2
(0,1)
P
1
(1,0)
P
2
(0,1)
warunek
ograniczający II
warunek
ograniczający I
warunek ograniczający III
Z
kryterium wejścia
wiemy, że
x
2
powoduje
szybszy wzrost funkcji celu zatem wprowadzamy
ją do bazy i poruszamy się w kierunku jej wzrostu
Kryterium wyjścia
podpowiada jak daleko
możemy się posunąć po osi x
2
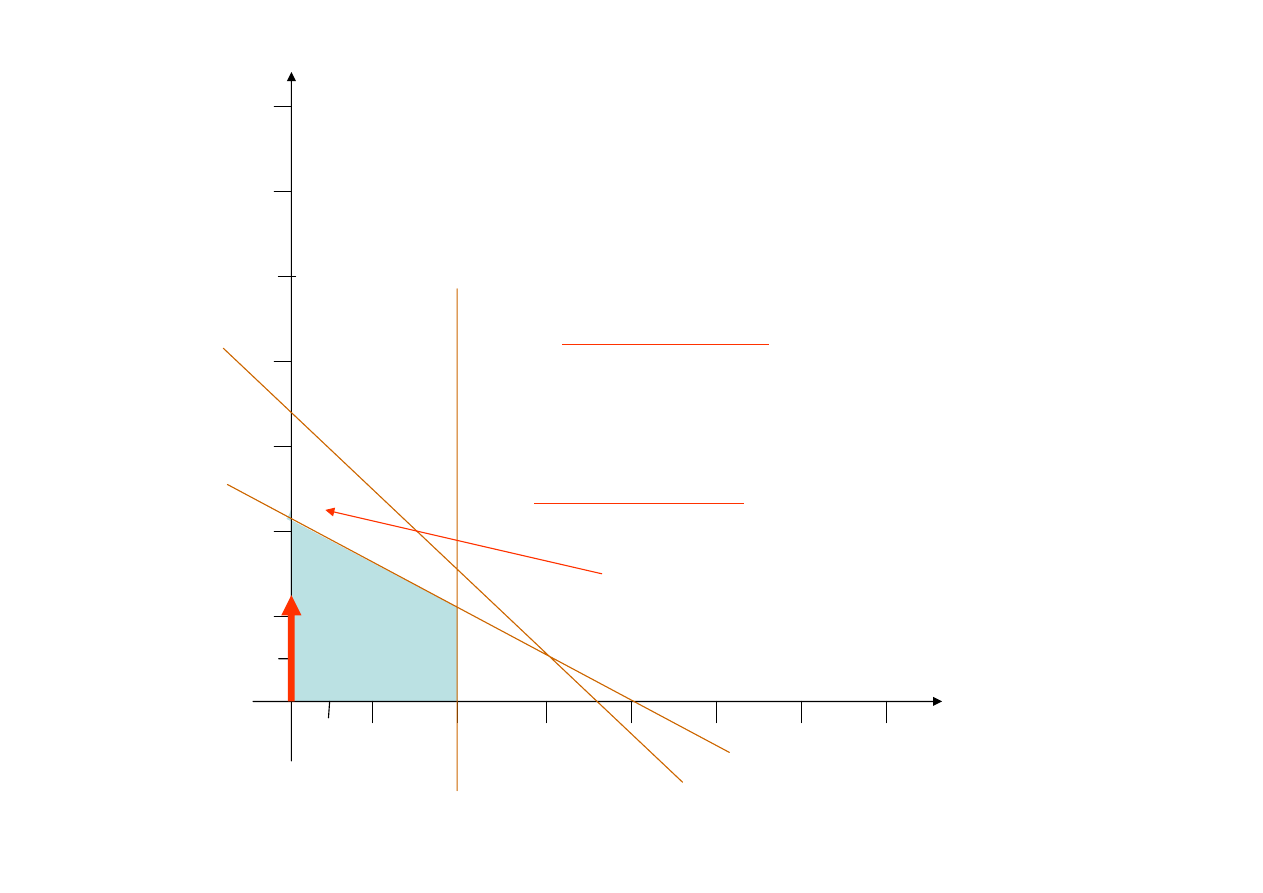
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
wprowadzając do I rozwiązania bazowego
za x
1
=1 otrzymujemy punkt
P
1
(1,0)
za x
2
=1 otrzymujemy punkt
P
2
(0,1)
P
1
(1,0)
P
2
(0,1)
warunek
ograniczający II
warunek
ograniczający I
warunek ograniczający III
Z
kryterium wejścia
wiemy, że
x
2
powoduje
szybszy wzrost funkcji celu zatem wprowadzamy
ją do bazy i poruszamy się w kierunku jej wzrostu
Kryterium wyjścia
podpowiada jak daleko
możemy się posunąć po osi x
2
x
1
=0, x
2
=4, x
3
=6, x
4
=0, x
5
=0
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
P
1
(1,0)
P
2
(0,1)
warunek
ograniczający II
warunek
ograniczający I
warunek ograniczający III
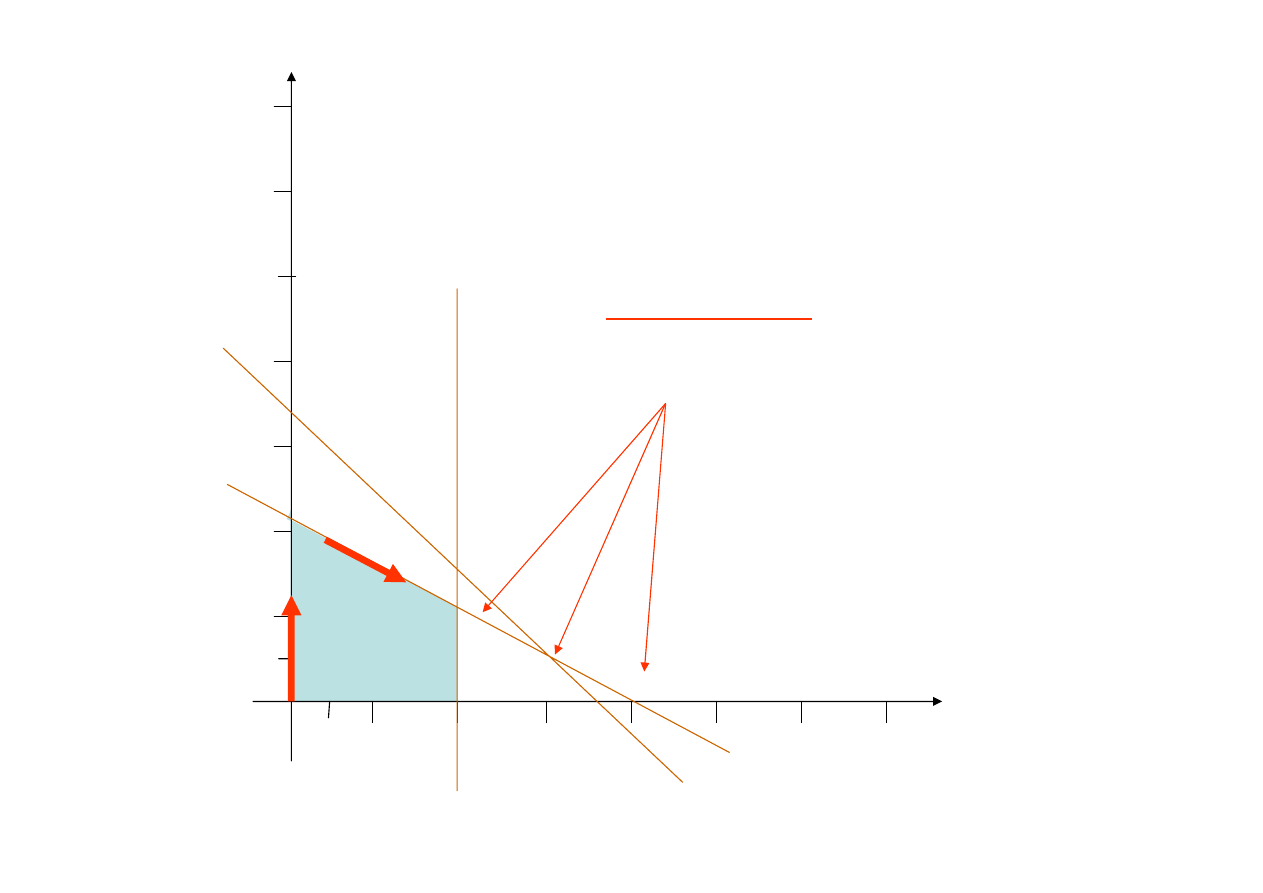
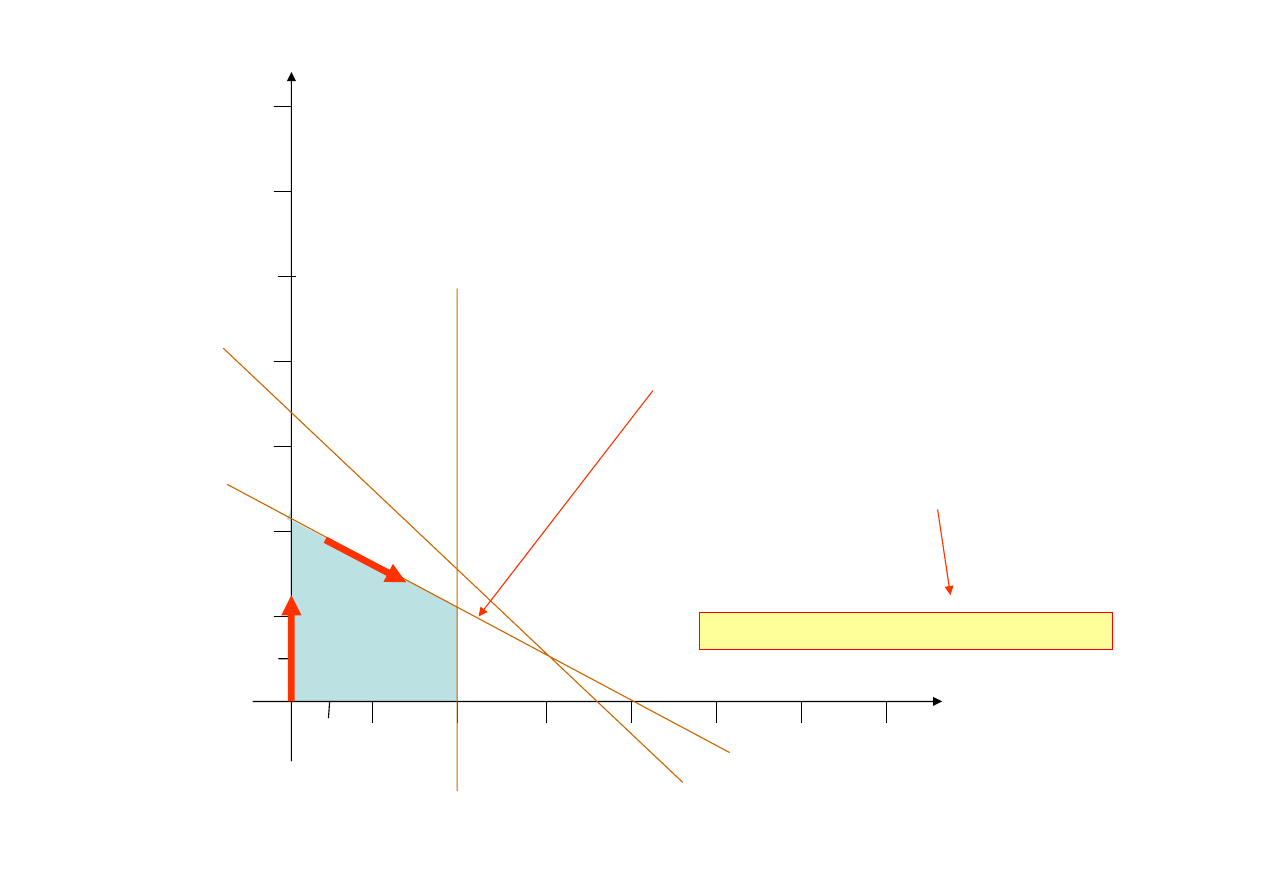
Po drugiej iteracji wiemy, że należy wprowadzić
do nowej bazy zmienną
x
1
Nowe
kryterium wyjścia
podpowiada jak daleko
możemy się posunąć po osi x
2
Rozpatrywane są
wierzchołki
H
O
(0,0)
2
4
6
8
10
12
14
2
8
10
12
14
4
6
F
X
2
X
1
A
B
C
D
E
P
1
(1,0)
P
2
(0,1)
warunek
ograniczający II
warunek
ograniczający I
warunek ograniczający III
Po drugiej iteracji wiemy, że należy wprowadzić
do nowej bazy zmienną
x
1
H
Wierzchołki
F
i
H
pozostają poza obszarem rozwiązań
dopuszczalnych pozostaje więc wierzchołek
B
x
1
=2, x
2
=4, x
3
=3, x
4
=0, x
5
=0
Wierzchołkowi
B
w pięciowymiarowej
przestrzeni odpowiada rozwiązanie
Algorytm simpleks polega na badaniu rozwiązań bazowych programu o
postaci
kanonicznej
(wszystkie warunki ograniczające maja postać równości), zatem przed
przystąpieniem do budowy pierwszej tablicy simpleksowej (postaci bazowej) należy
zmienić wszystkie nierówności na równania przez wprowadzenie pewnych
dodatkowych
zmiennych bilansujących
.
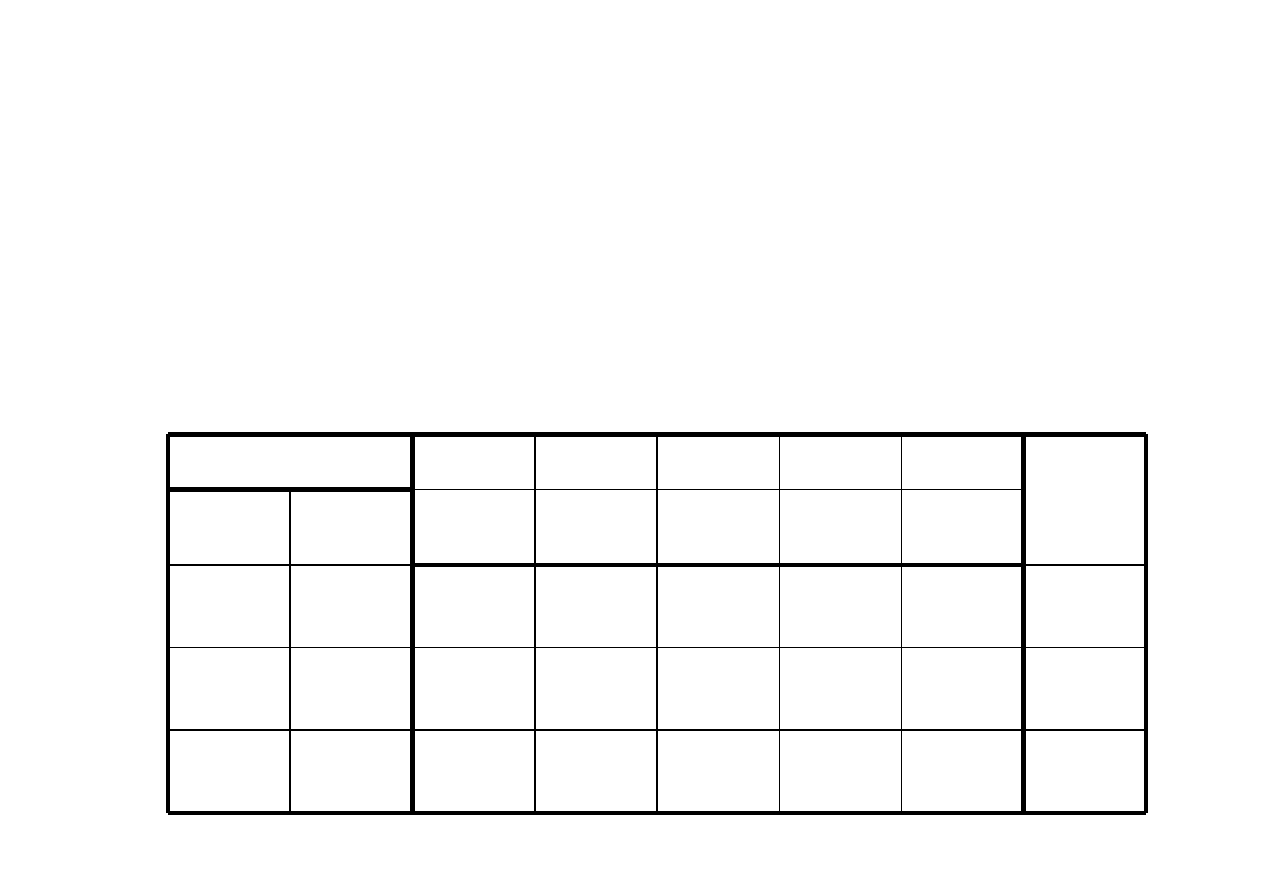
Wykorzystując zapis macierzowy, pierwszą tablicę simpleks można zapisać
następująco:
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
b
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
Algorytm simpleks polega na badaniu rozwiązan bazowych programu o
postaci
kanonicznej
(wszystkie warunki ograniczające maja postać równości), zatem przed
przystąpieniem do budowy pierwszej tablicy simpleksowej (postaci bazowej) należy
zmienić wszystkie nierówności na równania przez wprowadzenie pewnych
dodatkowych
zmiennych bilansujących
.
Wykorzystując zapis macierzowy, pierwszą tablicę simpleks można
zapisać następująco:
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
A
– jest macierzą współczynników występujących po lewej stronie
warunków ograniczających
b
– jest wektorem wyrazów wolnych warunków ograniczających
c
– jest wektorem wierszowym współczynników funkcji celu (zdefiniowanej
po wprowadzeniu zmiennych bilansujących)
x
b
– jest wektorem zmiennych bazowych
c
b
– jest wektorem kolumnowym współczynników funkcji celu dla zmiennych
bazowych
I
– jest macierzą jednostkową o wymiarach (
m x m) –
macierz
ą
współczynników
przy zmiennych występujących w pierwszej bazie
0
– jest wektorem zer
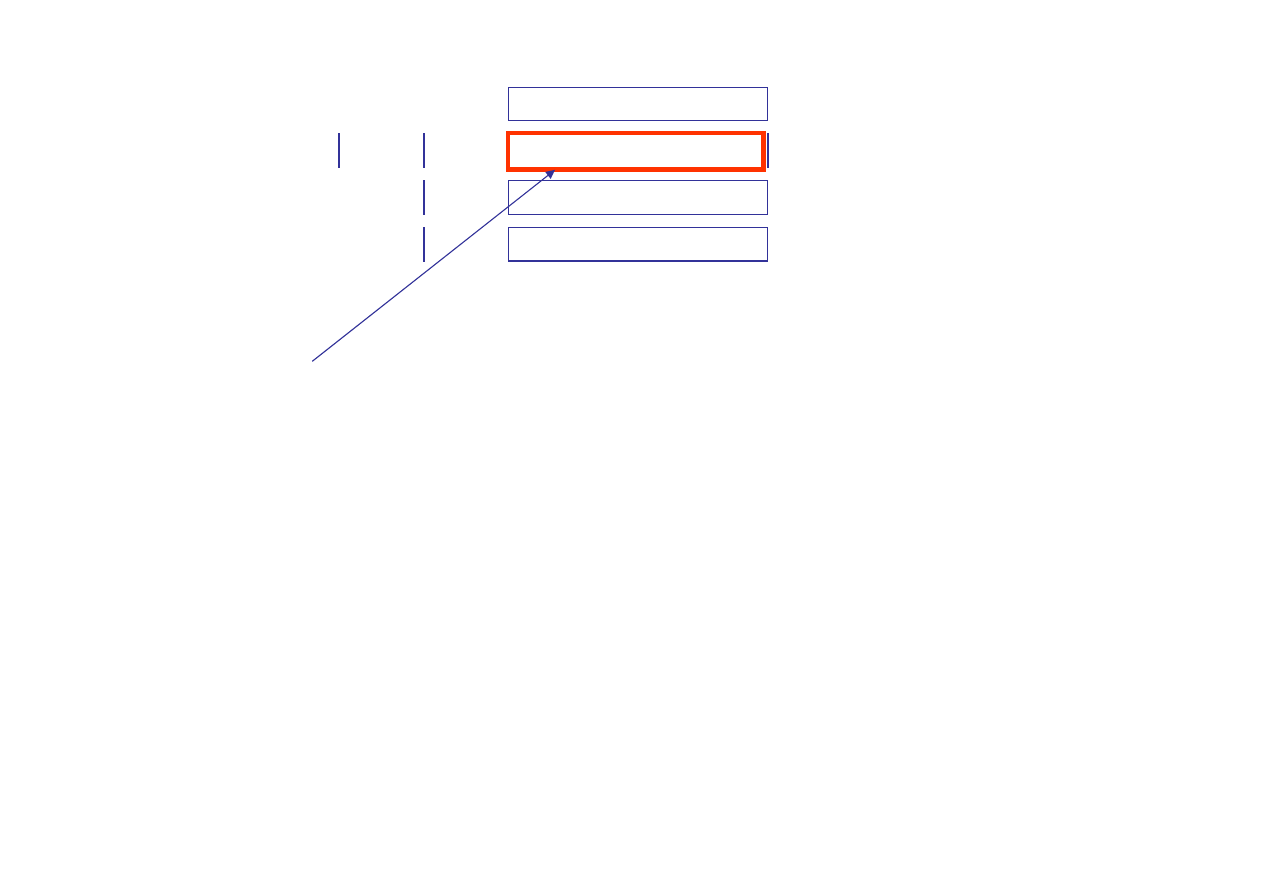
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
Zasadnicza część tablicy składa się z
m
wierszy (
m
jest liczba warunków
ograniczających i z tylu właśnie zmiennych skład się każde rozwiązanie
bazowe)
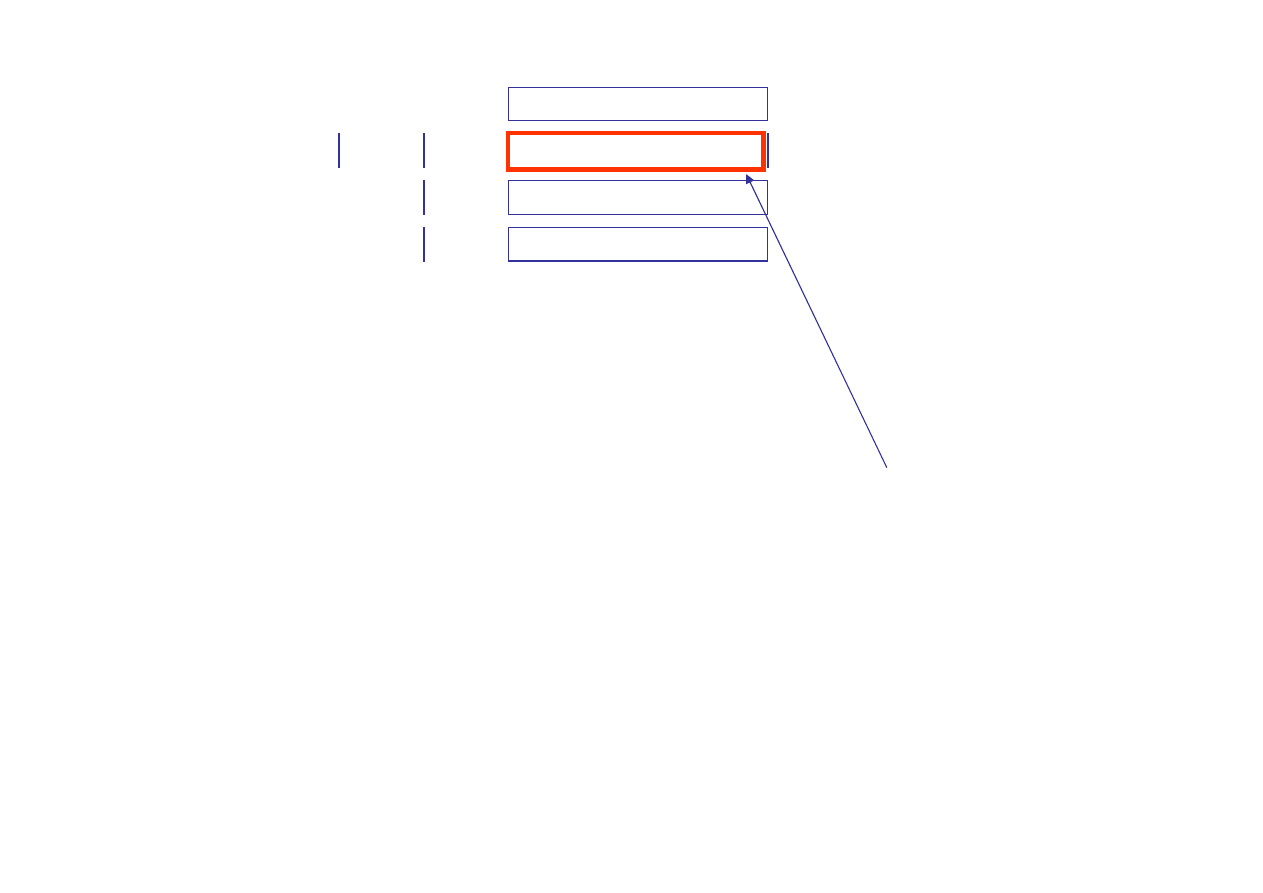
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
Zasadnicza część tablicy składa się z
m
wierszy (
m
jest liczba warunków
ograniczających i z tylu właśnie zmiennych skład się każde rozwiązanie
bazowe)
Liczba kolumn odpowiada łącznej liczbie zmiennych w modelu w postaci
kanonicznej (decyzyjnych i bilansujących) przy czym współczynniki przy
zmiennych bazowych tworzą macierz jednostkową
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
Zasadnicza część tablicy składa się z
m
wierszy (
m
jest liczba warunków
ograniczających i z tylu właśnie zmiennych skład się każde rozwiązanie
bazowe)
Liczba kolumn odpowiada łącznej liczbie zmiennych w modelu w postaci
kanonicznej (decyzyjnych i bilansujących) przy czym współczynniki przy
zmiennych bazowych tworzą macierz jednostkową
Wartość
z
j
dla poszczególnych zmiennych (kolumn tablicy) oblicza się jako
sumę iloczynów współczynników odpowiadających poszczególnym
zmiennym (
a
ij
) i współczynników funkcji celu dla zmiennych bazowych (
c
b
i
)
czyli
∑
=
=
m
i
bi
ij
j
c
a
z
1
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
Zasadnicza część tablicy składa się z
m
wierszy (
m
jest liczba warunków
ograniczających i z tylu właśnie zmiennych skład się każde rozwiązanie
bazowe)
Liczba kolumn odpowiada łącznej liczbie zmiennych w modelu w postaci
kanonicznej (decyzyjnych i bilansujących) przy czym współczynniki przy
zmiennych bazowych tworzą macierz jednostkową
Wartość
z
j
dla poszczególnych zmiennych (kolumn tablicy) oblicza się jako
sumę iloczynów współczynników odpowiadających poszczególnym
zmiennym (
a
ij
) i współczynników funkcji celu dla zmiennych bazowych (
c
b
i
)
czyli
∑
=
=
m
i
bi
ij
j
c
a
z
1
Ostatni wiersz tablicy simpleksowej c
j
– z
j
zwany jest wierszem zerowym
lub
kryterium simpleks
.
Elementy wiersza zerowego (kryterium simpleks) odpowiadające poszczególnym
zmiennym (kolumnom) informują, o ile zmieni się aktualna w danej iteracji wartość
funkcji celu, jeżeli jedną jednostkę tej zmiennej wprowadzimy do nowej (kolejnej)
bazy.
Innymi słowy służy on do sprawdzenia, czy aktualne rozwiązanie bazowe jest
rozwiązaniem optymalnym.
W przypadkach, gdy funkcja celu jest maksymalizowana, rozwiązanie dotąd nie
będzie optymalne, dopóki w wierszu zerowym będą występować liczby nieujemne
.
(dodatnie liczby świadczą, iż wprowadzenie do bazy zmiennej, której odpowiada
dodatni współczynnik zwiększy wartość funkcji celu)
wartość zmiennych
bazowych
wartość funkcji celu
zmienne
bazowe
rozwiązanie
A
B
l
1
−
1
−
l
B
b
B
l
1
−
A
B
c
b
T
b
1
−
1
−
b
T
b
B
c
b
B
c
b
T
b
1
−
A
B
c
c
b
T
b
1
−
−
1
−
−
b
T
b
B
c
j
j
z
c
−
j
z
bl
x
bl
c
c
l
B
Macierz jest macierz współczynników ograniczających stojących przy aktualnych
(w
l
-tej iteracji) zmiennych bazowych
Odwrotność tej macierzy w postaci zajmuje pozycję macierzy jednostkowej w
tablicy początkowej. Ponieważ zmienne bazowe zmieniają się w każdej iteracji,
również macierz a tym samym jej odwrotność macierz są w każdej iteracji
inne, stąd indeks
l
.
1
−
l
B
l
B
1
−
l
B
Również każdą pośrednią i każdą końcową tablice simpleks można przedstawić za
pomocą zapisu macierzowego.
W
l
-tej iteracji algorytmu tablica simpleks może być zapisana następująco:
zmienne
bazowe
rozwiązanie
A
V
l
l
V
b
V
l
A
V
c
l
T
b
l
T
b
V
c
b
V
c
l
T
b
A
V
c
c
l
T
b
−
l
T
b
V
c
−
j
j
z
c
−
j
z
bl
x
bl
c
c
Oznaczmy dla uproszczenia, macierz odwrotną
przez
Zatem w
l
-tej iteracji algorytmu tablica simpleks może być zapisana następująco:
1
−
l
B
l
V
Macierz jest macierzą odwrotną współczynników ograniczających
stojących przy aktualnych zmiennych bazowych ( w
l
-tej iteracji )
l
V
Document Outline