Robert Turos WM-32 [e-mail]

Zadanie II.4.3
Parametry stanu w punktach charakterystycznych obiegu Otto oraz prace bezwzględne

objętościowe są odpowiednio równe: przed zagęszczaniem adiabatycznym ciśnienie p

1

=1[at],

temperatura T

1

=300 [K], zasób objętości V

1

=1[m

3

], zaś po zagęszczeniu ciśnienie p

2

=12[at],

temperatura T

2

=

]

[

181

,

610

1

1

1

2

K

T

p

p

k

k

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

,

zasób objętości V

2

=

169495

,

0

1

2

1

=

•

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

V

p

p

k

[m

3

]

praca bezwzględna objętościowa L

1-2

=

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

−

k

k

p

p

k

V

p

1

1

2

1

1

1

(

)

1

(

= -253,573 [kJ].

Po przemianie izochorycznego sprężania ciśnienie p

3

=

75931

,

2

)

1

(

2

1

1

2

1

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

•

Δ

−

p

p

p

V

Qd

k

k

[MPa],

temperatura T

3

=

24

,

1430

)

1

(

1

1

1

2

1

1

=

•

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

Δ

−

−

T

p

p

V

p

Qd

k

k

k

[K], zasób objętości V

3

=V

2

, praca

bezwzględna objętościowa L

2-3

=0. Po przemianie adiabatycznego rozgęszczania

p

4

=

229943

,

0

)

1

(

1

1

2

1

1

=

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

−

−

p

p

p

V

Qd

k

k

k

[MPa], temperatura

T

4

=

189

,

703

1

)

1

(

1

1

2

1

1

1

=

•

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

−

−

T

p

p

V

p

Qd

k

k

k

[K], zasób objętościowy V

4

=V

1

, zaś praca bezwzględna

objętościowa L

4-1

=0. Podczas przemiany izochorycznego sprężania do obiegu doprowadzono

przyrost ilości ciepła

160

=

ΔQd

[kcal]. Zakładamy, że przemiany obiegu są przemianami

odwracalnymi oraz, że czynnikiem pracującym w obiegu jest powietrze traktowane tak jak gaz

doskonały dla którego indywidualna stała gazowa R=287,04

⎥

⎦

⎤

⎢

⎣

⎡

kgK

J

, zaś wykładnik izentropy

k=1,4. Obliczyć przyrosty ilości ciepła przemian obiegu Otto.

Rozwiązanie
1.

Wykresy obiegu termodynamicznego Otto dla powietrza we współrzędnych pV i TS z

zaznaczonymi przepływami przyrostów ilości ciepła.

T

p

T

3

p

3

T

2

p

4

T

4

p

2

T

1

p

1

S =S

1

2

V =V

2

3

Q =Q

2-3

d

Q

d

Q

w

δQ=0

δQ=0

Q =Q

2 -3

w

S =S

3

4

V =V

1

4

S

V

1

1

2

4

3

3

4

2

2.

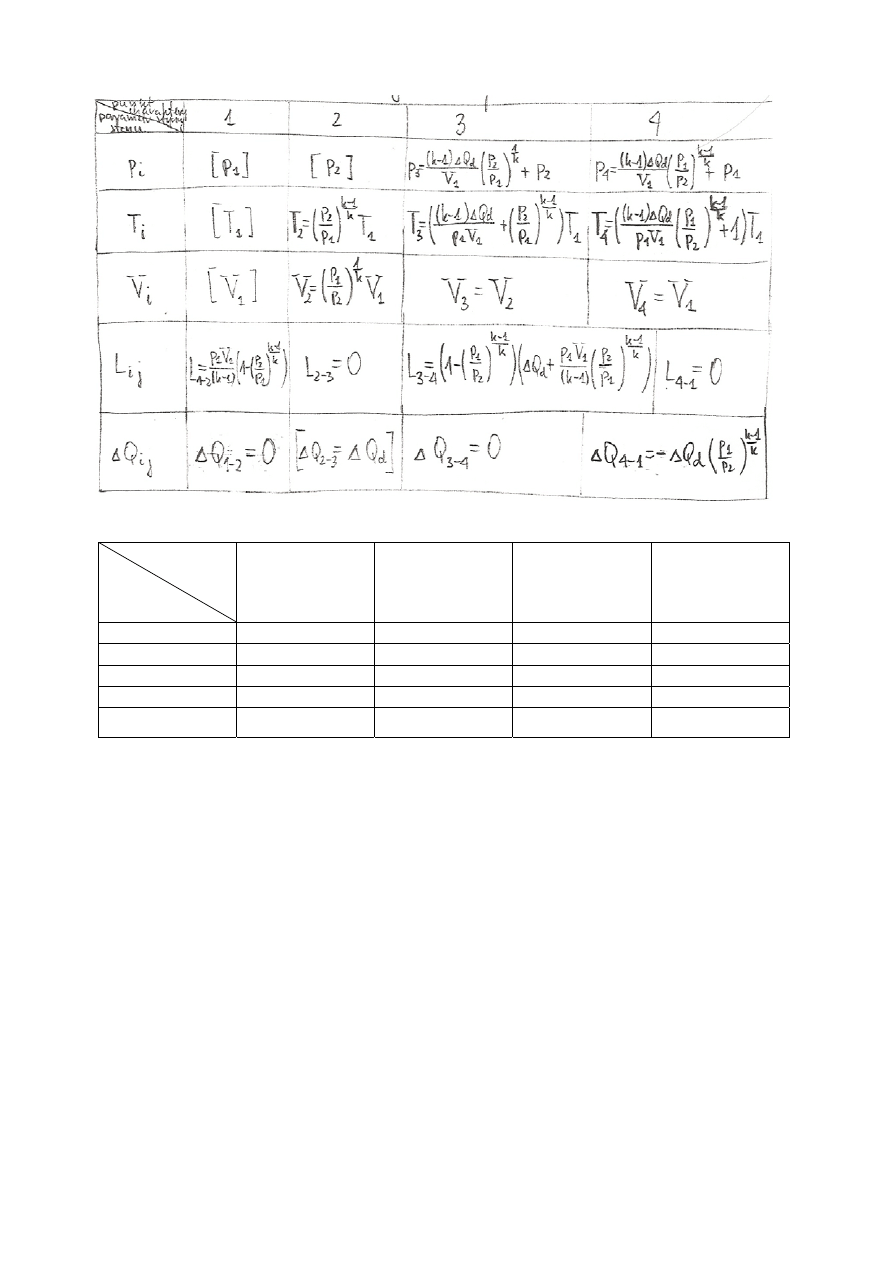
Tabela zestawienia danych i wyników obliczeń

Punkty

charaktery-
-tyczne

Parametry
stanu

1

2

3

4

p

i

1 [at]

12 [at]

2,75931 [MPa]

0,229943 [MPa]

T

i

300 [K]

610,181 [K]

1430,24 [K]

703,189 [K]

V

i

1 [m

3

] 0,169495

[m

3

] 0,169495

[m

3

] 1

[m

3

]

L

ij

-253,573 [kJ]

0

1116,25 [kJ]

0

ij

Q

Δ

0

=

ΔQd 670,4 [kJ]

0 -329,6[kJ]

3. Obliczam przyrosty ciepła przemian
3.1 Obliczam przyrosty ilości ciepła przemiany izochorycznej
Bilans energii dla przemiany odwracalnej
dE

I

=

L

Q

δ

δ

−

δ L= pdV

Zasób energii zewnętrznej określony jest związkiem:
E

I

= C

v

mT

C

v

= const. – gaz doskonały

m= const. – układ konstancjalny
dE

I

= C

v

mdT

Przemiana izochoryczna
V= const.

dV=0

δ L=0

Zatem bilans energii wewnętrznej wynosi:
dE

I

=

δ Q

Całkując równanie:

δ Q= C

v

mdT

Otrzymamy:

∫

∫

−

Δ

=

1

4

1

4

0

Q

T

T

v

dT

m

C

Q

δ

Z równania Mayera(?)

C

p

-C

v

=R

Oraz z definicji składnika izentropy

V

C

k

p

=

obliczamy:

1

−

=

k

R

C

v

Z równania stanu gazu doskonałego obliczam zasób masy gazu w obiegu:

1

1

1

RT

V

p

m

=

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

•

Δ

−

−

−

=

−

•

•

−

=

Δ

−

−

1

)

1

(

1

1

)

(

1

1

2

1

1

1

1

4

1

1

1

1

1

4

k

k

p

p

V

p

Qd

k

k

V

p

T

T

RT

V

p

k

R

Q

Ostatecznie:

k

k

p

p

Qd

Q

1

2

1

1

4

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

−

=

Δ

Obliczam wartość przyrostów ciepła przemian w obiegu:

4

,

670

160

19

,

4

=

•

=

ΔQd

[kJ]

607

,

329

1

4

−

=

Δ

−

Q

[kJ]

3.

Obliczam ….. Otto

k

k

w

w

ob

p

p

Qd

Q

Q

Qd

Q

Qd

Q

1

2

1

3

2

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

Δ

=

Δ

Δ

=

Δ

Δ

−

Δ

=

Δ

Obliczam sprawność teoretyczną obiegu

Qd

Q

w

Δ

Δ

−

= 1

η