Zad. II- 8,3 Marchewka Robert IZM 51
Wydajność sprężarki idealnej określana jest przez strumień wymiany masy tłoczonego
powietrza równy
⎥⎦
⎤
⎢⎣
⎡
=
•
s
kg
m
35434
,
0
. Sprężarka idealna tłoczy powietrze z otoczenia o
parametrach stanu
]
[
2
,
1
1
at
p
=
oraz t
1
=20[c] i zgęszcza je do ciśnienia p
2
=6[at] Zgęszczenie
przebiega w przemianie politropowej z wykładnikiem politropy n=1,25, zaś wykładnik
izentropy k=1,4. Indywidualna stała gazowa R=287,04[J/kgK]. Moc napędowa sprężarki
określona jest zaleznością
•
−
−
−
=
m
p
p
T
n
nR
N
n
n
n
)
)
(
1
(
1
1
1
2
1
|. Zaś strumień ciepła przekazywany
przez układ sprężarki idealnej do otoczenia
•
−
−
•
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
−
=
m
p
p
T
k
k
n
R
k
n
Q
n
n
n
)
1
(
)
1
)(
(
)
(
1
1
2
1
2
1
.
Obliczyć strumień wody
•
m
n
chłodnicy sprężarki idealnej, wiedząc, że temperatura wody
chłodzącej wzrosła od
]
[
40
,
]
[
15
2
1
C
do
C
t
t
w
w
o
o
=
=
zaś ciepło właściwe wody
]
[
1
gK
cal
c
w
=
.
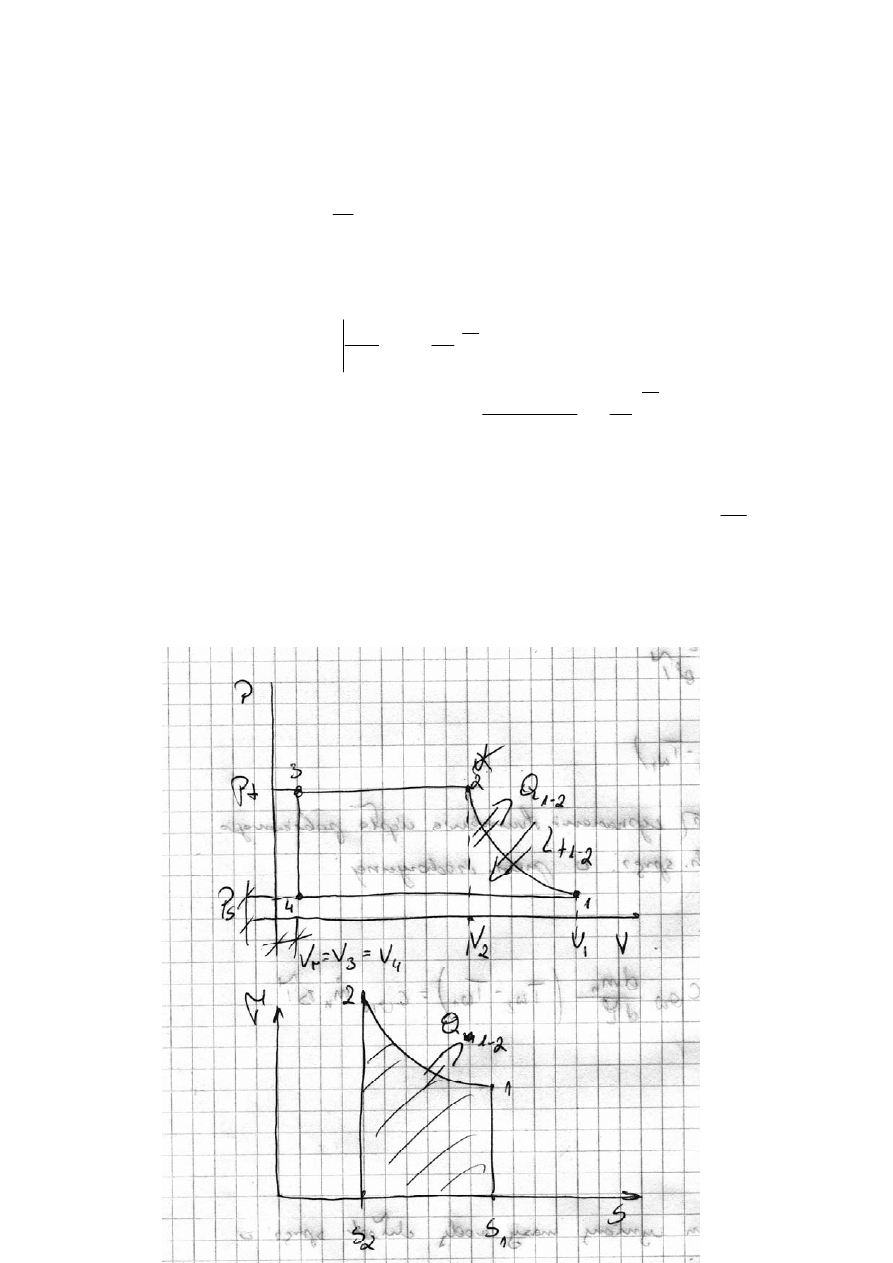
1) wykres odwracalnego biegu lewobierznego we współrzędnych PV i TS.
2) wyznaczenie ilości ciepła pobranego przez wode chłodzącą w jednym cyklu w
przemianie izochorycznej
2.1) I postać I zasady termodynamiki
I
I
dE
Q
L
dV
const
V
pdV
L
L
Q
dE
=
∂
=
∂
=
⇒
=
=
∂
∂
−
∂
=
0
zasób energii wewnętrznej wody
)
(
1
2
2
1
0
2
1
2
1
W
W
n
W
Q
T
T
n
W
n
W
n
W
I
n
n
W
I
T
T
m
C
Q
dT
m
C
dQ
dT
m
C
Q
dT
m
C
dE
const
m
T
m
C
E
w
w
−
=
=
=
∂
=
=
=
−
∫
∫
−
ϑ
ϑ
ϑ
ϑ
ϑ
3) wyznaczenie strumienia ciepła pobieranego przez wodę chłodzącą sprężarkę w
przemianie izochorycznej
τ
τ
τ
ϑ
ϑ
Δ
=
−
=
=
∂
•
•
−
=
n
W
W
W
n
W
m
C
T
T
d
dm
C
Q
d
Q
)
(
1
2
2
1
2
1
4) wyznaczam strumień wymiany masy wody chłodzącej sprężarkę w przemianie
politropowej
•
−
•
•
−
•
−
•
−
•
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
Δ
−
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
−
=
Δ
=
1
1
1
2
1
1
1
1
2
1
2
1
2
1
1
)
(
)
1
)(
1
(
)
(
1
)
(
)
1
)(
1
(
)
(
m
p
p
TC
T
k
n
R
k
n
m
m
p
p
T
n
k
k
n
R
T
m
C
Q
Q
n
n
W
n
n
n
n
W
n
ϑ
ϑ
5) obliczam wartość strumienia wymiany masy wody chłodzącej sprężarkę
⎥⎦
⎤
⎢⎣
⎡
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
Δ
−
−
−
=
•
−
•
s
kg
m
p
p
TC
T
k
n
R
k
n
m
n
n
W
n
166012
,
0
35434
,
0
1
)
2
,
1
2
,
6
(
25
*
10
*
19
,
4
16
,
293
4
,
0
*
25
,
0
)
4
,
1
25
,
1
(
04
,
287
1
)
(
)
1
)(
1
(
)
(
25
,
1
25
,
0
3
1
1
1
2
1
ϑ
