
6. Kinematyka odwrotna
W poprzednim wykładzie omówiliśmy, jak określić pozycję i orientację końcówki
roboczej w zależności od zmiennych przegubowych. Treść tego wykładu jest skoncentrowana
na problemie odwrotnym, tzn. znalezieniu zmiennych przegubowych w zależności od pozycji
i orientacji końcówki roboczej. Jest to zadaniem kinematyki odwrotnej i w ogólności jest ono
trudniejsze niż zadanie kinematyki prostej. Ogólnie problem kinematyki odwrotnej można
postawić następująco. Dana jest jednorodna macierz przekształcenia 4x4
)
3
(
1
0
d
R
H
E
∈
=
(209)
gdzie R
∈
SO(3). Należy znaleźć (jedno lub wszystkie) rozwiązania równania
H
)
,...,
(
T
6
1
0
=
q
q
n
(210)
gdzie
n
n
q
q
A
...
A
)
,...,
(
T
1
6
1
0
⋅
⋅
=
(211)
Równanie (210) daje 12 nieliniowych równań z n niewiadomymi, które mogą być
zapisane jako
4
3
2
1
3
2
1
)
,...,
(
T
,
6
1
,
,
,
; j
,
,
i
gdzie
h
q
q
j
i
i,j
=
=
=
(212)
gdzie T
ij
, h
ij
oznaczają 12 nietrywialnych elementów macierzy, odpowiednio
T
0
n
i
H.
(Ponieważ dolne wiersze obu macierzy
T
0
n
i
H wynoszą (0.0.0.1), więc spośród 16 równań
reprezentowanych przez zależność (210) cztery są trywialne).
Przykład 18.
Wróćmy do manipulatora stanfordzkiego z poprzedniego wykładu. Załóżmy, że
pozycja i orientacja ostatniego układu współrzędnych są określone przez macierz
=
⋅
⋅
⋅
⋅
⋅
=
1
0
0
0
A
A
A
A
A
A
T
33
32
31
23
22
21
13
12
11
6
5
4
3
2
1
6
0
z
y
x
d
r
r
r
d
r
r
r
d
r
r
r
(213)
W celu znalezienia odpowiednich zmiennych przegubowych
θ
1
,
θ
2
,
θ
3
,
θ
4
,
θ
5
i
θ
6
należy
rozwiązać następujący układ nieliniowych równań trygonometrycznych
−
+
=
+
+
+
+
=
−
+
+
−
=
+
−
=
+
+
=
−
+
=
+
+
=
+
−
+
+
+
−
=
+
−
−
+
+
−
=
−
−
−
=
+
+
−
−
=
+
−
−
−
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
]
)
(
[
)
(
]
)
(
[
)
(
)
(
]
)
(
[
)
(
]
)
(
[
5
2
4
5
2
6
2
3
2
1
5
5
1
4
2
5
4
1
6
1
2
2
1
3
5
4
1
2
5
1
5
4
2
1
6
1
2
2
1
3
5
2
5
4
2
33
5
4
1
5
2
5
4
2
1
23
5
4
1
5
2
5
4
2
1
13
6
5
2
6
4
6
5
4
2
32
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
22
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
12
6
5
2
6
4
6
5
4
2
31
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
21
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
11
s
s
c
c
c
d
c
d
d
s
s
c
s
s
c
c
s
s
c
d
c
d
s
s
d
d
s
s
s
s
c
c
s
c
c
c
d
s
d
s
c
d
d
c
c
s
c
s
r
s
s
c
c
s
s
c
c
s
r
s
s
s
c
s
s
c
c
c
r
s
s
c
c
s
s
c
c
s
r
c
c
s
c
s
c
s
s
s
c
s
s
c
c
c
s
r
c
c
s
c
s
s
s
s
s
c
s
s
c
c
c
c
r
c
s
c
s
s
c
c
c
s
r
s
c
c
c
s
c
c
s
s
s
s
c
c
c
c
s
r
s
c
c
c
s
s
c
s
s
s
s
c
c
c
c
c
r
z
y
x
ϕ
(214)

Równania te są zbyt skomplikowane, aby je rozwiązywać wprost, otrzymując wynik w
postaci zamkniętych, analitycznych wzorów. Potrzebujemy tu specjalnej efektywnej i
systematycznej techniki rozwiązywania, która wykorzysta szczególną strukturę kinematyczną
manipulatora. Bowiem podczas gdy zadanie kinematyki prostej ma zawsze jednoznaczne
rozwiązanie, które można otrzymać w prosty sposób przez przeliczenie równań, to zadanie
kinematyki odwrotnej może w ogóle nie mieć rozwiązania. Jeśli zaś rozwiązanie istnieje, to
może ono nie być jednoznaczne. W dodatku, ponieważ równania kinematyki prostej są
przeważnie skomplikowanymi nieliniowymi funkcjami zmiennych przegubowych, więc
rozwiązanie zadania odwrotnego, nawet gdy istnieje, może być trudne do otrzymania.
Podczas rozwiązywania zadania kinematyki odwrotnej jesteśmy zainteresowani raczej
znalezieniem zamkniętej postaci rozwiązania równań niż rozwiązaniem numerycznym.
Znalezienie rozwiązania w postaci zamkniętej oznacza podanie następującej zależności
q
k
= f
k
(h
11
, …, h
34
), gdzie k = 1, …, n
(215)
Rozwiązania w postaci zamkniętej są wygodniejsze z dwóch powodów. Po pierwsze, w
pewnych zastosowaniach, takich jak np. śledzenie spoiny, której położenie jest określane
przez system wizyjny, równania kinematyki odwrotnej muszą być rozwiązywane bardzo
szybko, powiedzmy co 20 milisekund. W tym celu praktycznie niezbędne jest posiadanie
gotowych równań, a nie korzystanie z metod iteracyjnych. Po drugie, równania kinematyki
mają na ogół wiele rozwiązań. Mając rozwiązanie w postaci zamkniętej, można przygotować
zasady wyboru konkretnych rozwiązań spośród wielu istniejących.
W praktyce, aby odpowiedzieć na pytanie o istnienie rozwiązań równań kinematyki
odwrotnej, należy przeprowadzić zarówno rozważania matematyczne, jak też inżynierskie.
Przykładowo, ruch przegubu obrotowego może być ograniczony do zakresu mniejszego niż
pełne 360°. W ten sposób nie wszystkie matematyczne rozwiązania równań kinematyki będą
odpowiadały fizycznie realizowalnym konfiguracjom manipulatora. Będziemy zakładać, że
dana pozycja i orientacja są takie, że istnieje co najmniej jedno rozwiązanie równania (210).
Gdy zostanie wyznaczone rozwiązanie matematyczne równań, należy jeszcze sprawdzić, czy
spełnia ono wszystkie ograniczenia dotyczące zakresów możliwych ruchów. Dla potrzeb
naszych rozważań będziemy odtąd zakładać, że dana w równaniu (210) macierz jednorodna H
odpowiada konfiguracji wewnątrz przestrzeni roboczej manipulatora z osiągalną orientacją.
To zagwarantuje, że otrzymane rozwiązanie matematyczne odpowiada konfiguracji
osiągalnej.
6.1. Odsprzężenie kinematyczne
Chociaż ogólnie problem kinematyki odwrotnej jest raczej trudny, jednak okazuje się, że dla
manipulatorów o sześciu stopniach swobody, których ostatnie trzy osie przecinają się w
jednym punkcie (tak jak we wcześniej opisanym manipulatorze stanfordzkim) jest możliwe
odsprzężenie powodujące podział kinematyki odwrotnej na dwa prostsze zadania, nazywane
odpowiednio kinematyką odwrotną pozycji i kinematyką odwrotną orientacji. Można wyrazić
to inaczej. Dla manipulatora z kiścią sferyczną i o sześciu stopniach swobody zadanie
kinematyki odwrotnej można podzielić na dwa prostsze zadania, mianowicie na znalezienie
najpierw położenia punktu przecięcia osi kiści, zwanego dalej środkiem kiści, a następnie
znalezienie orientacji kiści.
Załóżmy, że mamy dokładnie sześć stopni swobody i że trzy ostatnie osie przecinają
się w punkcie O. Wyrazimy zależność (210) w postaci układu dwóch równań
reprezentujących równania obrotu i równania położenia
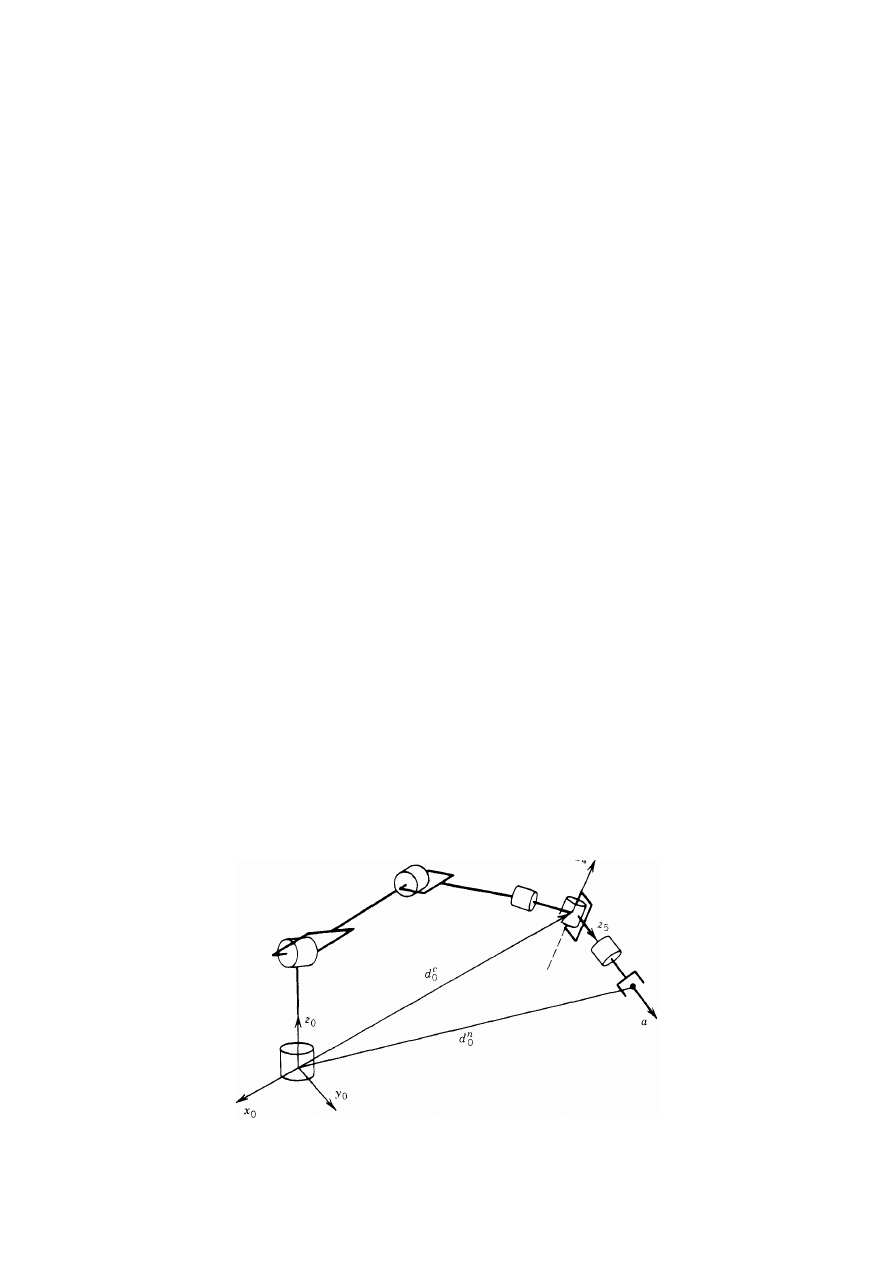
R
)
,...,
(
R
6
1
6
0
=
q
q
(216)
d
)
,...,
(
T
6
1
0
=
q
q
n
(217)
gdzie
d i R opisują odpowiednio daną pozycję i orientację układu narzędzia.
Założenie o kiści sferycznej oznacza, że osie
z
4
,
z
5
,
z
6
przecinają się w punkcie
O, a
stąd początki układów
O
4
i
O
5
umieszczonych zgodnie z konwencją Denayita-Hartenberga
będą zawsze w środku kiści
O. Często początek O
3
będzie również w początku
O, ale to nie
jest konieczne do dalszych rozważań. Ważnym punktem tego założenia dla kinematyki
odwrotnej jest to, że ruch ostatnich trzech osi nie zmienia położenia punktu
O. Tak więc
położenie środka kiści jest funkcją tylko pierwszych trzech zmiennych przegubowych.
Ponieważ początek
O
6
układu narzędzia jest po prostu przesunięty o odległość
d
6
wzdłuż osi
z
5
od punktu
O (patrz tab. 3), zatem wektor o
6
w układzie
O
0
x
0
y
0
z
0
można zapisać w postaci
zależności
o
6
–
o = -d
6
R k
(218)
Niech
p
c
oznacza wektor od początku układu bazowego do środka kiści. Wówczas do
uzyskania pozycji końcówki roboczej w punkcie reprezentowanym przez wektor
d z
orientacją opisaną macierzą
R = (r
ij
) jest konieczne i wystarczające, aby środek kiści
O był
zlokalizowany w punkcie wyznaczonym z równania
p
c
=
d – d
6
R k
(219)
oraz aby orientacja układu
O
6
x
6
y
6
z
6
względem układu bazowego była opisana macierzą
R.
Jeśli współrzędne wektora położenia
d są oznaczone przez d
x
,
d
y
,
d
z
a współrzędne wektora
ś
rodka kiści
p
c
są oznaczone przez
p
x
,
p
y
,
p
z
to równanie (219) opisuje zależność
−
−
−
=
33
6
23
6
13
6
r
d
d
r
d
d
r
d
d
p
p
p
z
y
x
z
y
x
(220)
Teraz, korzystając z równania (220), można znaleźć wartości pierwszych trzech
zmiennych przegubowych. Określą one macierz obrotu
R
0
3
która zależy tylko od tych trzech
pierwszych zmiennych. Następnie z wyrażenia
R = R
0
3
R
3
6
(221)
można teraz określić orientację końcówki roboczej względem układu
O
3
x
3
y
3
z
3
jako
R
3
6
= (
R
0
3
)
-1
R = (R
0
3
)
T
R
(222)
Ostatnie trzy kąty przegubowe są obliczane jako zbiór kątów Eulera odpowiadających
przekształceniu
R
3
6
.
Zauważmy, że prawa strona równania (222) jest całkowicie znana,
ponieważ macierz
R jest dana, a macierz R
0
3
może być obliczona, gdy będą znane pierwsze 3
zmienne przegubowe. Idea odsprzężenia kinematycznego została przedstawiona na rys. 49.
Rys. 49. Odsprzężenie kinematyczne

Podsumowanie powyższych rozważań
Dla omówionej klasy manipulatorów rozwiązanie zadania kinematyki odwrotnej może
być przedstawione w postaci następującego algorytmu.
Krok l: Znaleźć zmienne przegubowe q
1
, q
2
, q
3
takie, że środek kiści o wektorze p
c
jest
zlokalizowany równaniem
p
c
= d – d
6
R k
(223)
Krok 2: Wykorzystując zmienne przegubowe wyznaczone w kroku l, obliczyć macierz R
0
3
Krok 3: Znaleźć zestaw kątów Eulera odpowiadających macierzy obrotu
R
3
6
= (R
0
3
)
-1
R = (R
0
3
)
T
R
(224)
6.2. Kinematyka odwrotna pozycji – podejście geometryczne
W rozważanych przez nas układach kinematycznych do znalezienia zmiennych
q
1
, q
2
, q
3
odpowiadających wektorowi p
c
danemu wzorem (219) możemy wykorzystać
podejście geometryczne. Nasz sposób postępowania ograniczymy do podejścia
geometrycznego z dwóch powodów. Po pierwsze, jak już powiedzieliśmy, większość
projektowanych obecnie manipulatorów ma prostą kinematykę, składającą się zwykle z jednej
spośród pięciu przedstawionych we wcześniejszych wykładach konfiguracji oraz z kiści
sferycznej. W rzeczywistości to, że projekty manipulatorów rozwinęły się do takiego, a nie
innego stanu obecnego, spowodowane było częściowo właśnie trudnościami z ogólnym
zadaniem kinematyki odwrotnej. Po drugie, istnieją techniki, które można stosować do
rozwiązywania problemów kinematyki odwrotnej w różnych konfiguracjach. Ponieważ
jednak Czytelnik najczęściej spotka się z konfiguracjami robotów tutaj rozważanymi, dodanie
utrudnień związanych z analizą ogólnego przypadku wydaje się nieuzasadnione. Ogólne
metody rozwiązywania przedstawianych problemów Czytelnik znajdzie w obszernej
literaturze dotyczącej tego tematu.
Ogólnie można powiedzieć, że stopień skomplikowania zadania kinematyki odwrotnej
wzrasta wraz ze wzrostem liczby niezerowych parametrów kinematycznych. Dla większości
manipulatorów wiele parametrów spośród a
i
d
i
jest równych zeru, wartości parametrów
α
i
wynoszą 0 lub ±
π
/2 itd. Właśnie w takich przypadkach podejście geometryczne jest
najprostsze i najbardziej naturalne.
6.3. Konfiguracja stawowa
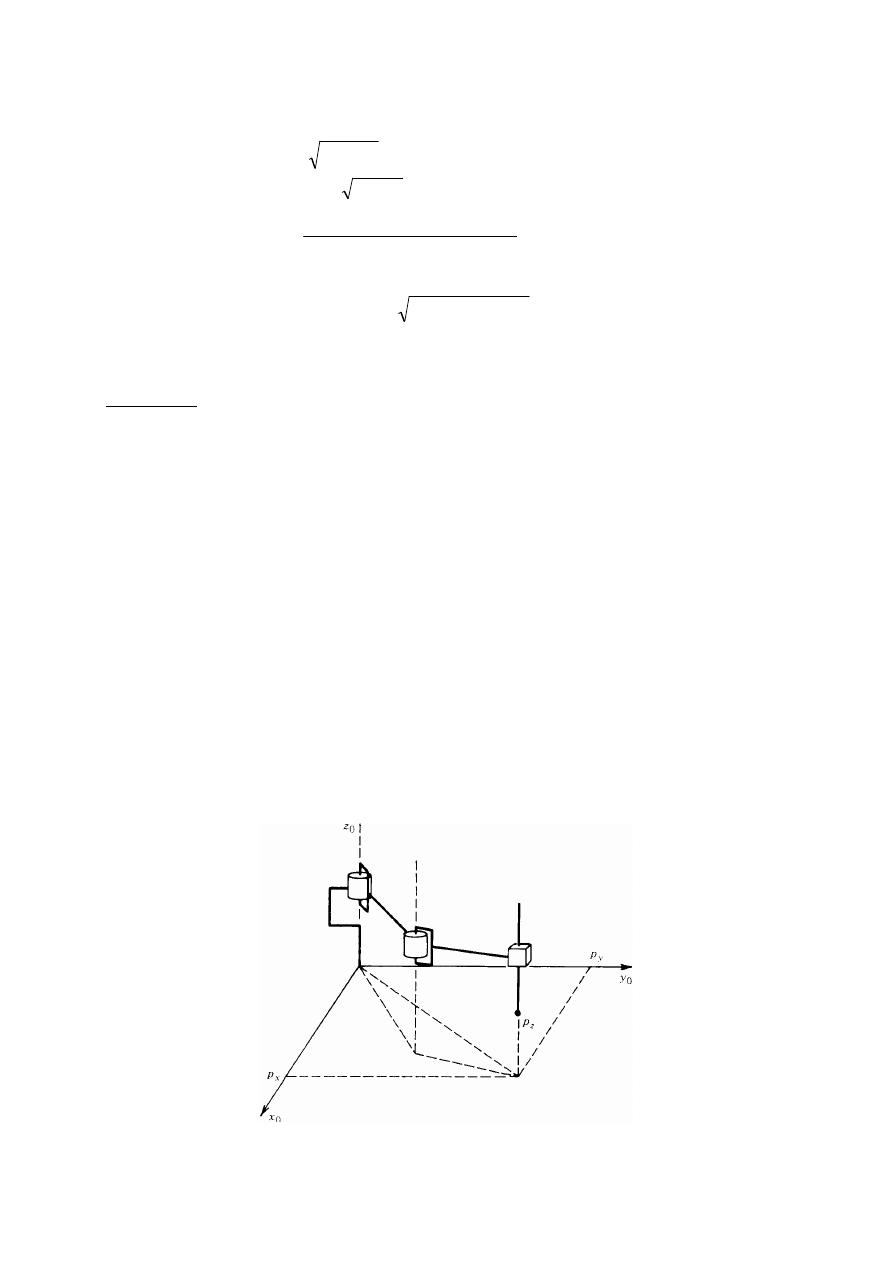
Rozważmy manipulator z łokciem przedstawiony na rys. 50. Elementy składowe
wektora p
c
oznaczamy przez p
x
, p
y
, p
z
. Rzutujemy wektor p
c
na płaszczyznę x
0
y
0
jak to
pokazano na rys. 51. Z tego rzutowania widzimy, że
θ
1
= arctan(p
x
, p
y
)
(225)
gdzie arctan (p
x
, p
y
) oznacza dwuargumentową funkcję arcus tangens zdefiniowaną dla
wszystkich (x, y) ≠ 0, wyznaczającą jednoznacznie kąt
θ
taki, że
2
2
2
2
sin
,
cos
y
x
y
y
x
x
+
=
+
=
θ
θ
(226)

Na przykład arctan(1, -1) = -
π
/4, a arctan(-1, 1) = +3
π
/4.
Rys. 50. Manipulator z łokciem
Rys. 51. Rzut środka kiści na płaszczyznę x
0
y
0
Zauważmy, że drugim dopuszczalnym rozwiązaniem dla kąta
θ
1
jest
θ
1
=
π
+ arctan(p
x
, p
y
)
(227)
gdy rozwiązanie
θ
2
odpowiadające równaniu (225) zostanie zastąpione przez
π
–
θ
2
.
Rozwiązania dla kąta
θ
1
istnieją, chyba że p
x
= p
y
= 0. W tym przypadku równanie
(225) nie jest określone, a manipulator znajduje się w pozycji osobliwej przedstawionej na
rys. 52. W pozycji tej środek kiści opisany wektorem p
c
leży na osi z
0
, a więc dla każdej
wartości kąta
θ
1
położenie środka jest stałe. Mamy więc do czynienia z nieskończoną liczbą
rozwiązań dla
θ
1
.
Rys. 52. Konfiguracja osobliwa
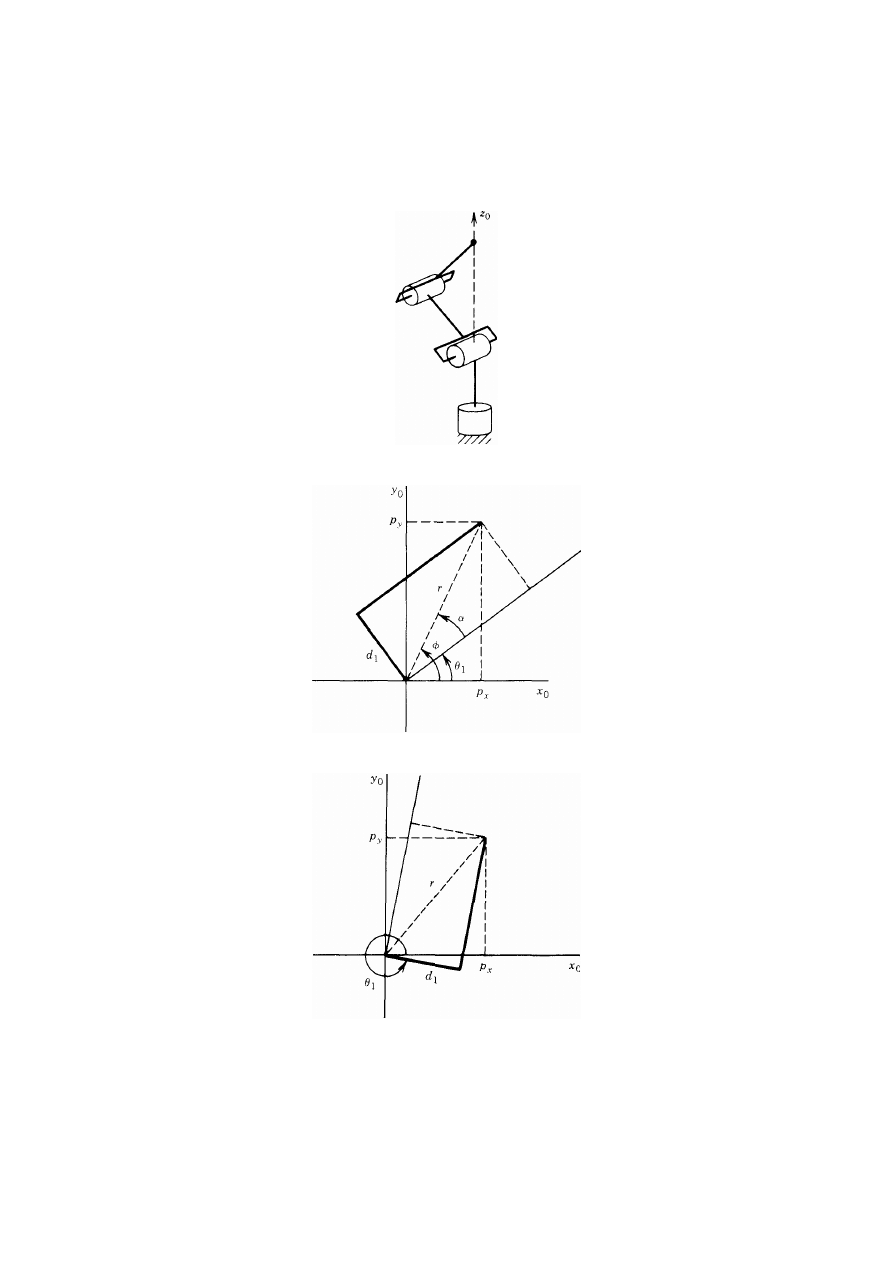
Jeżeli w omawianym manipulatorze wprowadzi się przesunięcie d
1
≠ 0, jak na rys. 53,
to wtedy środek kiści nie może leżeć na osi
Z
0
. Ogólnie w tym przypadku będą istniały dwa
rozwiązania dla kąta
θ
1
. Będą one odpowiadać tzw. konfiguracjom lewego i prawego
ramienia, przedstawionym na rys. 54 i rys. 55.
Rys. 53. Manipulator z łokciem z przesuniętym barkiem
Rys. 54. Konfiguracja lewego ramienia
Rys. 55. Konfiguracja prawego ramienia
Rysunek 54 ilustruje konfigurację lewego ramienia. Widzimy zależność tutaj
następującą zależność geometryczną
θ
=
φ
–
α
(228)
gdzie
φ
= arctan(p
x
, p
y
)
(229)
(
)
(
)
2
1
2
2
1
2
1
2
1
,
arctan
,
arctan
d
p
p
d
d
r
d
y
x
−
+
=
−
=
α
(230)
Drugie rozwiązanie, dla konfiguracji prawego ramienia, pokazanej na rys. 55, jest
następujące
(
)
2
1
2
2
1
1
,
arctan
)
,
arctan(
d
p
p
d
p
p
y
x
y
x
−
+
−
−
=
θ
(231)
W celu znalezienia kątów
θ
2
,
θ
3
dla manipulatora z łokciem, mając dany kąt
θ
1
,
rozważmy płaszczyznę utworzoną przez człony 2 i 3, jak to przedstawiono na
rys. 56.
Rys. 56. Rzutowanie na płaszczyznę utworzoną przez człony 2 i 3
Ponieważ ruchy tych członów są płaskie, rozwiązanie jest analogiczne do rozwiązania
dla dwuczłonowego manipulatora, omawianego podczas pierwszego wykładu. Zatem na
podstawie tych można stwierdzić, że
D
a
a
a
a
d
p
p
p
a
a
a
a
s
r
z
y
x
=
−
−
−
+
+
=
−
−
+
=
:
2
)
(
2
cos
3
2
2
3
2
2
2
1
2
2
3
2
2
3
2
2
2
2
3
θ
(232)
a stąd kąt
θ
3
jest równy
)
1
,
arctan(
2
3
D
D
−
±
=
θ
(233)
Podobnie otrzymujemy kąt
θ
2
w postaci
)
sin
,
cos
arctan(
)
,
arctan(
)
sin
,
cos
arctan(
)
,
arctan(
3
3
3
3
2
1
2
2
3
3
3
3
2
2
θ
θ
θ
θ
θ
a
a
a
d
p
p
p
a
a
a
s
r
z
y
x
+
−
−
+
=
=
+
−
=
(234)
Dwa rozwiązania dla
θ
2
odpowiadają dolnej i górnej pozycji łokcia. Przykładem
manipulatora z łokciem z przesunięciem jest manipulator PUMA zilustrowany na rys. 57. Jak
widać, możliwe są cztery rozwiązania zadania kinematyki odwrotnej. Odpowiadają one
sytuacjom: ramię z lewej strony u góry, ramię z prawej strony u góry, ramię z lewej strony u
dołu, ramię z prawej strony u dołu. Zobaczymy dalej, że dla orientacji kiści istnieją dwa
rozwiązania, co daje w sumie aż osiem możliwych rozwiązań kinematyki odwrotnej dla
manipulatora PUMA.
Rys. 57. Cztery rozwiązania kinematyki odwrotnej pozycji manipulatora PUMA: a) ramię
z lewej strony u góry, b) ramię z prawej strony u góry, c) ramię z lewej strony u dołu, d)
ramię z prawej strony u dołu
6.4. Konfiguracja sferyczna
Teraz zajmiemy się rozwiązaniem kinematyki odwrotnej pozycji dla manipulatora
sferycznego o trzech stopniach swobody przedstawionego na rys. 58.
Rys. 58. Manipulator sferyczny
b)
c)
d)

Tak jak w przypadku manipulatora z łokciem pierwsza zmienna przegubowa jest
obrotem podstawy i można ją wyznaczyć z równania
θ
1
= arctan(p
x
, p
y
)
(235)
przy założeniu, że składowe p
x
i p
y
nie są jednocześnie równe zeru. Jeśli p
x
i p
y
są równe zeru,
to podobnie jak poprzednio konfiguracja jest osobliwa i kąt
θ
1
może mieć dowolną wartość.
Kąt
θ
2
na podstawie rys. 58, jest dany wzorem
θ
2
= arctan(r, s)
(236)
gdzie r
2
= p
x
2
+ p
y
2
, s -= p
z
– d
1
. Tak jak w przypadku manipulatora z łokciem drugie
rozwiązania dla kątów
θ
1
,
θ
2
są postaci
θ
1
=
π
+ arctan(p
x
, p
y
)
(237)
θ
2
=
π
– arctan(r, s)
(238)
Odległość liniową d
3
można wyznaczyć ze wzoru
(d
3
+ a
2
)
2
= r
2
+ s
2
(239)
jako
2
2
1
2
2
2
2
2
3
)
(
a
d
p
p
p
a
s
r
d
z
y
x
−
−
+
+
=
−
+
=
(240)
Rozwiązania, w których argument pierwiastka jest ujemny, są pomijane. W sumie
otrzymujemy dwa rozwiązania kinematyki odwrotnej pozycji, oczywiście jeśli środek kiści
nie leży na osi z
0
. Jeżeli dodamy przesunięcie, to podobnie jak w omawianym manipulatorze z
łokciem otrzymamy konfigurację lewego i prawego ramienia.
6.5. Kinematyka odwrotna orientacji
W poprzednich wykładach wykorzystaliśmy podejście geometryczne do rozwiązania
problemu kinematyki odwrotnej pozycji. Daje nam to wartości trzech pierwszych zmiennych
przegubowych, odpowiadające danej pozycji środka kiści. Teraz zajmiemy się problemem
kinematyki odwrotnej orientacji, czyli znalezieniem dla ostatnich trzech zmiennych
przegubowych wartości odpowiadających danej orientacji względem układu O
3
x
3
y
3
z
3
. Dla
kiści sferycznej można to zinterpretować jako problem znalezienia kątów Eulera
odpowiadających danej macierzy obrotu R, jak to już wcześniej omawialiśmy.
6.6. Kąty Eulera
Załóżmy, że dana jest macierz U = u
ij
∈
SO(3) oraz przekształcenie R
3
6
kątów Eulera
zgodne z wzorem (83). Zadaniem jest znalezienie kątów Eulera
φ
,
θ
,
ψ
spełniających
równanie macierzowe
=
−
+
−
+
−
−
−
33
32
31
23
22
21
13
12
11
u
u
u
u
u
u
u
u
u
c
s
s
c
s
s
s
c
c
s
c
s
s
c
c
c
s
s
c
c
s
s
c
c
s
s
c
c
c
θ
ψ
θ
ψ
θ
θ
φ
ψ
φ
ψ
θ
φ
ψ
φ
ψ
θ
φ
θ
φ
ψ
φ
ψ
θ
φ
ψ
φ
ψ
θ
φ
(241)
Załóżmy, że elementy u
13
, u
23
nie są oba równe zeru. Wtedy z powyższego równania
widać, że s
θ
≠
0 i stąd elementy u
13
, u
23
nie są jednocześnie równe zeru. Jeśli oba elementy ^
u
13
, u
23
są równe zeru, to u
33
≠ ±1 i wówczas
C
θ
=
u
33
, a s
θ
=
±(1 – u
33
2
)
1/2
, a więc
)
1
,
arctan(
2
33
33
u
u
−
=
θ
(242)
lub
)
1
,
arctan(
2
33
33
u
u
−
−
=
θ
(243)

Jeśli wybierzemy pierwszą wartość kąta
θ
, to s
θ
> 0 oraz
)
,
arctan(
23
13
u
u
=
φ
(244)
)
,
arctan(
32
31
u
u
−
=
ψ
(245)
Natomiast gdy wybierzemy drugą wartość kąta
θ
, to s
θ
< 0 oraz
)
,
arctan(
23
13
u
u
−
−
=
φ
(246)
)
,
arctan(
32
31
u
u
−
=
ψ
(247)
Mamy więc dwa rozwiązania w zależności od wybranego znaku zmiennej
θ
.
Jeśli u
13
= u
23
= 0, to fakt, że macierz U jest ortogonalna, implikuje równości u
33
= ±1 i
u
13
= u
32
= 0. W ten sposób U ma postać
±
=
1
0
0
0
0
U
22
21
12
11
u
u
u
u
(248)
Gdy u
33
= 1, wtedy
C
θ
= l i s
θ
= 0, a więc
θ
= 0. W tym przypadku równanie (241)
przyjmuje postać
=
−
=
+
−
+
−
−
−
+
+
+
+
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
22
21
12
11
u
u
u
u
c
s
s
c
c
c
s
s
s
c
c
s
c
s
s
c
s
s
c
c
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
ψ
φ
(249)
Suma
φ
+
ψ
może być wyznaczona jako
φ
+
ψ
= arctan(u
11
, u
21
) = arctan(u
11
, -u
12
)
(250)
Ponieważ można wyznaczyć tylko sumę
φ
+
ψ
, w tym przypadku istnieje
nieskończenie wiele rozwiązań. Możemy przyjąć jako zasadę
φ
= 0 i zdefiniować
ψ
na
podstawie wzoru (248).
Gdy u
33
= -1, wtedy
C
θ
= -l i s
θ
= 0, tak więc
θ
=
π
.
W tym przypadku otrzymujemy
równanie (241) w następującej postaci
−
=
−
−
−
−
−
−
−
1
0
0
0
0
1
0
0
0
0
22
21
12
11
u
u
u
u
c
s
s
c
ψ
φ
ψ
φ
ψ
φ
ψ
φ
(251)
W ten sposób rozwiązaniem jest
φ
–
ψ
= arctan(-u
11
, -u
12
) = arctan(-u
21
, -u
22
)
(252)
Przykład 19.
Manipulator stawowy
Macierz
R
0
3
dla manipulatora stawowego lub z łokciem łatwiej jest policzyć, gdy
zapiszemy ją w postaci
−
−
−
−
−
=
0
R
23
23
1
23
1
23
1
1
23
1
23
1
3
0
c
s
c
s
s
c
s
s
s
c
c
c
(253)
Macierz
R
3
6
=
A
4
A
5
A
6
jest dana wzorem
−
−
−
−
+
−
+
=
5
6
5
6
5
5
4
6
4
6
5
4
6
4
6
5
4
5
4
6
4
6
5
4
6
4
6
5
4
6
3
R
c
s
s
c
s
s
s
c
c
s
c
s
c
c
c
c
s
s
c
c
s
c
c
c
s
s
c
c
c
(254)
Równanie, które należy rozwiązać dla trzech ostatnich zmiennych, jest więc
następującej postaci

R
3
6
= (R
0
3
)
T
R := U
(255)
i do jego rozwiązania może być zastosowane poprzednie rozwiązanie dla kątów Eulera. Na
przykład elementy (l, 3) i (2, 3) w powyższym równaniu macierzowym są równe
33
23
23
23
1
13
23
1
5
4
13
r
s
r
c
s
r
c
c
s
c
u
−
+
=
=
(256)
33
23
23
23
1
13
23
1
5
4
23
r
c
r
s
s
r
s
c
s
s
u
−
−
−
=
=
(257)
oraz
23
1
13
1
33
r
c
r
s
u
−
=
(258)
Stąd, gdy oba wyrażenia (256) i (257) nie są jednocześnie równe zeru, wtedy z
wzorów (242) i (243) otrzymujemy
θ
5
w postaci
(
)
2
23
1
13
1
23
1
13
1
5
)
(
1
,
arctan
r
c
r
s
r
c
r
s
−
−
±
−
=
θ
(259)
Jeśli w równaniu (259) zostanie wybrana dodatnia wartość pierwiastka, to kąty
θ
4
i
θ
6
obliczamy na podstawie wzorów (244) i (245) odpowiednio jako
33
23
23
23
1
13
23
1
33
23
23
23
1
13
23
1
4
,
arctan(
r
c
r
s
s
r
s
c
r
s
r
c
s
r
c
c
−
−
−
−
+
=
ϕ
θ
(260)
)
,
arctan(
22
1
12
1
21
1
11
1
6
r
c
r
s
r
c
r
s
+
−
=
θ
(261)
Inne rozwiązania są otrzymywane analogicznie. Jeśli s
5
= O, to osie przegubów 3 i 5
są współliniowe. Jest to konfiguracja osobliwa i można wtedy wyznaczyć jedynie sumę
θ
4
+
θ
6
. Jednym z możliwych działań w takiej sytuacji jest wybranie dowolnej wartości kąta
θ
4
i wyznaczenie
θ
6
z wzoru (250) lub (252).
6.7. Podsumowanie rozwiązania dla manipulatora z łokciem
W celu podsumowania wcześniejszych wyników spiszemy teraz pełne rozwiązanie
kinematyki odwrotnej dla manipulatora z łokciem o sześciu stopniach swobody,
przedstawionego na rys. 50, który nie ma przesunięcia przegubów i ma zamontowaną kiść
sferyczną.
Jeśli są dane
=
z
y
x
d
d
d
d
(262)
=
33
32
31
23
22
21
13
12
11
R
r
r
r
r
r
r
r
r
r
(263)
oraz
−
−
−
=
33
6
23
6
13
6
r
d
d
r
d
d
r
d
d
p
p
p
z
y
x
z
y
x
(264)
to zmienne przegubowe w notacji D-H wynikają z zależności określonych poniższym wzorem
(
)
+
−
=
−
−
±
−
=
−
−
−
−
+
=
−
−
−
+
+
=
−
±
=
+
−
−
+
=
=
)
,
arctan(
)
(
1
,
arctan
)
,
arctan(
2
)
(
),
1
,
arctan(
)
,
arctan(
)
,
arctan(
)
,
arctan(
22
1
12
1
21
1
11
1
6
2
23
1
13
1
23
1
13
1
5
33
23
23
23
1
13
23
1
33
23
23
23
1
13
23
1
4
3
2
2
3
3
2
2
1
2
2
2
3
3
3
3
3
2
1
2
2
2
1
r
c
r
s
r
c
r
s
r
c
r
s
r
c
r
s
r
c
r
s
s
r
s
c
r
s
r
c
s
r
c
c
a
a
a
a
d
p
p
p
M
gdzie
M
M
s
a
c
a
a
d
p
p
p
p
p
z
y
x
z
y
x
y
x
θ
θ
ϕ
θ
θ
θ
θ
(265)
Przykład 20.
Manipulator SCARA
Jako inny przykład rozważmy manipulator SCARA, którego kinematyka prosta jest
określona przez macierz
T
0
4
z równania (207). Kinematyka odwrotna jest dana jako zbiór
rozwiązań równania
−
−
−
+
−
−
−
+
+
−
+
=
1
0
0
0
1
0
0
0
0
1
0
d
R
4
3
12
2
1
1
4
12
4
12
4
12
4
12
12
2
1
1
4
12
4
12
4
12
4
12
d
d
s
a
s
a
c
c
s
s
s
c
c
s
c
a
c
a
c
s
s
c
s
s
c
c
(266)
Zauważmy na początku, że ponieważ manipulator SCARA ma tylko cztery stopnie
swobody, nie wszystkie elementy macierzy
H
∈
E(
3) dopuszczają rozwiązanie równania
(266). Rzeczywiście, łatwo można stwierdzić, że równanie (266) nie ma rozwiązania, chyba
ż
e macierz
R jest postaci
1
0
0
0
0
R
−
−
=
α
α
α
α
c
s
s
c
(267)
W tym przypadku suma
θ
1
+
θ
2
–
θ
4
jest określona wzorem
θ
1
+
θ
2
–
θ
4
=
α
= arctan(r
12
, r
11
)
(268)
Po zrzutowaniu ramion manipulatora na płaszczyznę x
0
y
0
otrzymujemy postać jak na rys. 59.
Rys. 59. Manipulator SCARA

Widać stąd, że
)
,
1
arctan(
2
2
r
r
−
±
=
θ
(269)
2
1
2
2
2
1
2
2
2
2 a
a
a
a
d
d
r
y
x
−
−
+
=
(270)
)
,
arctan(
)
,
arctan(
2
2
2
2
1
1
s
a
c
a
a
d
d
y
x
+
−
=
θ
(271)
Możemy teraz wyznaczyć kąt
θ
4
z zależności (268)
θ
4
=
θ
1
+
θ
2
–
α
=
θ
1
+
θ
2
– arctan(r
12
, r
11
)
(272)
Na koniec d
3
dane jest wzorem
d
3
= d
z
+ d
4
(273)
Wyszukiwarka
Podobne podstrony:
4 Kinematyka odwrotna
Kinematyka odwrotna, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów
wykład 5 +matlab, W SPR nr 03 04 Kinematyka Odwrotna
6 Kinematyka odwrotna
Kinematyka odwrotna id 235013 Nieznany
kinematyka odwrotna
Kinematyka odwrotna
odwrotna kinematyka manipulatoa
Odwrotne zadanie kinematyki
Wykł 1B wstępny i kinematyka
Wyklad 06 kinematyka MS
Wyklad 05 kinematyka MS
3 Rodzaje jednorodnych transformacji stosowanych w kinematy
więcej podobnych podstron