Przedmiot i metodologia

fizyki

- KINEMATYKA

Dr hab. inż. Jerzy

ZIELIŃSKI prof. WAT

Zakład Fizyki i Technologii

Kryształów bud 5, pok. 218

Tel. [phone]

Email: [e-mail]

Wykład 1B

PROGRAM

Wykład – 16 godz. semestr I + 20 semestr II
Ćwiczenia – 14 godz. semestr I + 22

semestr II

Laboratoria -

18 godz. semestr

II

Kurs
Wykład – 10 godzin
Ćwiczenia – 20 godzin

Zasady zaliczania w semestrze I



Przedmiot jest zaliczany na ostatnich
zajęciach



Zaliczanie w formie pracy pisemnej polega
na od-powiedzi na 6 pytań definicyjnych i
jedno opisowe.



Podstawą

przystąpienia

do

zaliczenia

przedmiotu jest wcześniejsze zaliczenie
ćwiczeń rachun-kowych i kursu.

Literatura

1975 

1997
1997
1994
2003
1994 

2002 

1991

2001

 Fizyka dla inżynierów cz. I i cz.. II, WNT

 

Fizyka, WNT

Fizyka cz. I i cz. .II, WNT
Podstawy fizyki dla elektroników Skrypt WAT
Krótki kurs fizyki dla inżynierów, Skrypt
Fizyka ogólna. Przykłady i zadania z fizyki cz. I.
Rozwiązania i odpowiedzi do zadań z fizyki cz. .II.

Skrypt WAT
Wybrane przykłady zadań do wykładu z fizyki dla
inżynierów,
Fizyka ogólna – ćwiczenia laboratoryjne cz. I i II. Skrypt
WAT

Wybrane zagadnienia z fizyki skrypt WAT

J. Massalski
M. Massalska

Cz. Bobrowski

J. Orear,
A. Rogalski
M. Demianiuk
Z. Raszewski i
inni

M Demianiuk 

S. Bartnicki i
inni

Z. Raszewski, J.
Zieliński, T.
Kostrzyński

Rok
wydania

Literatura

autor

Istota fizyki

poszukiwanie i poznawanie

podstawowych praw przyrody

ścisły związek fizyki z techniką

fizyka jest nauką ścisłą –

matematyczny opis praw

fizycznych

fizyka opiera się na pomiarach

PODSTAWY

KINEMATYKI

Kinematyka – klasyfikacja i
porównywanie różnych ruchów
(jak zmiany ruchu zależą od
czasu?)

Ruch mechaniczny



Ruch mechaniczny – zmiana położenia ciała  konieczne

wskazanie innych ciał względem, których ruch się odbywa

(względne przemieszczanie się ciał)



Ruch – zmiana w przestrzeni i w czasie



Układ odniesienia – zbiór nieruchomych względem siebie ciał

służący do rozpatrywania ruchu innych ciał i zegar odmierzający

czas



Ruch tego samego ciała względem różnych układów

odniesienia  różny charakter (pasażer w pociągu)



opis ruchu – podanie położenia dla każdej chwili czasu



Punkt materialny – ciało o znikomo małych rozmiarach w

warunkach danego zagadnienia, o danej masie i położeniu, które

można określić jak położenie punktu geometrycznego

Wektory

operacje na wektorach

ruch w dwóch i trzech

wymiarach

Wektory
i skalary



dla ruchu jednowymiarowego kierunek wyróżniamy

znakiem



do opisu ruchu w przestrzeni trójwymiarowej stosujemy

pojęcie wektora



wektor posiada wartość i kierunek



działania na wektorach podlegają prawom rachunku

wektorowego



wielkości wektorowe: przemieszczenie, prędkość,

przyspieszenie, siła



wielkości skalarne: temperatura, ciśnienie, energia, masa,

czas – nie wykazują żadnego kierunku w przestrzeni

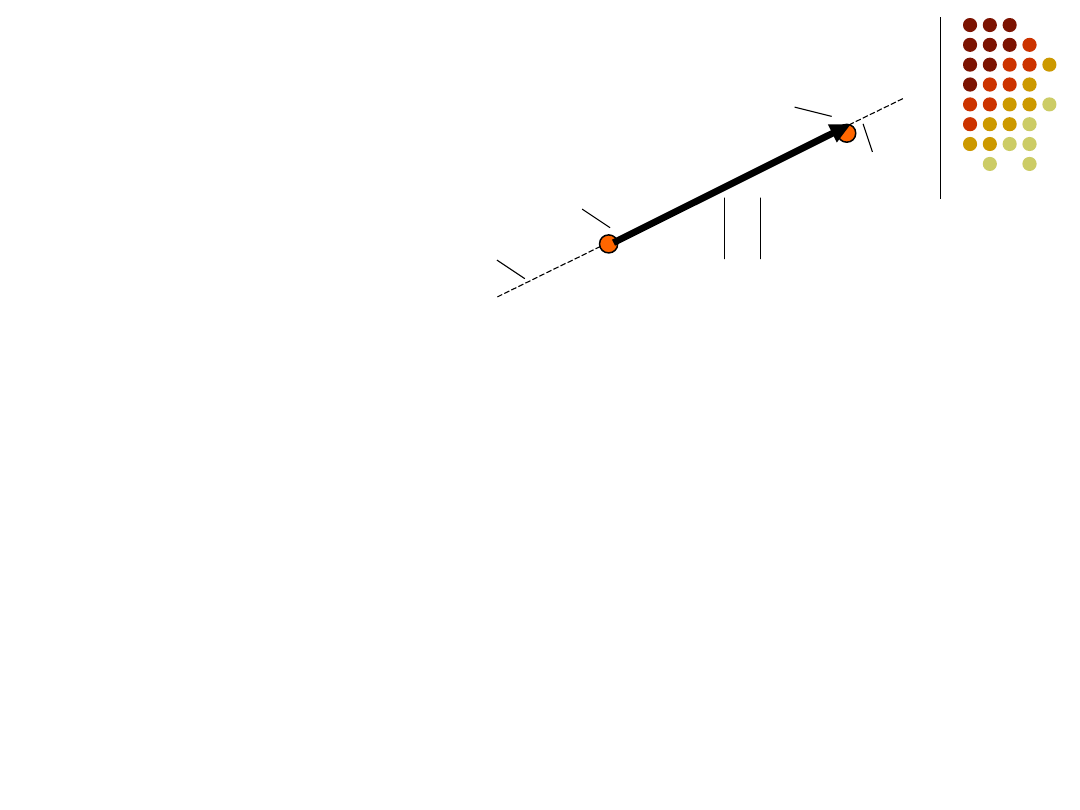
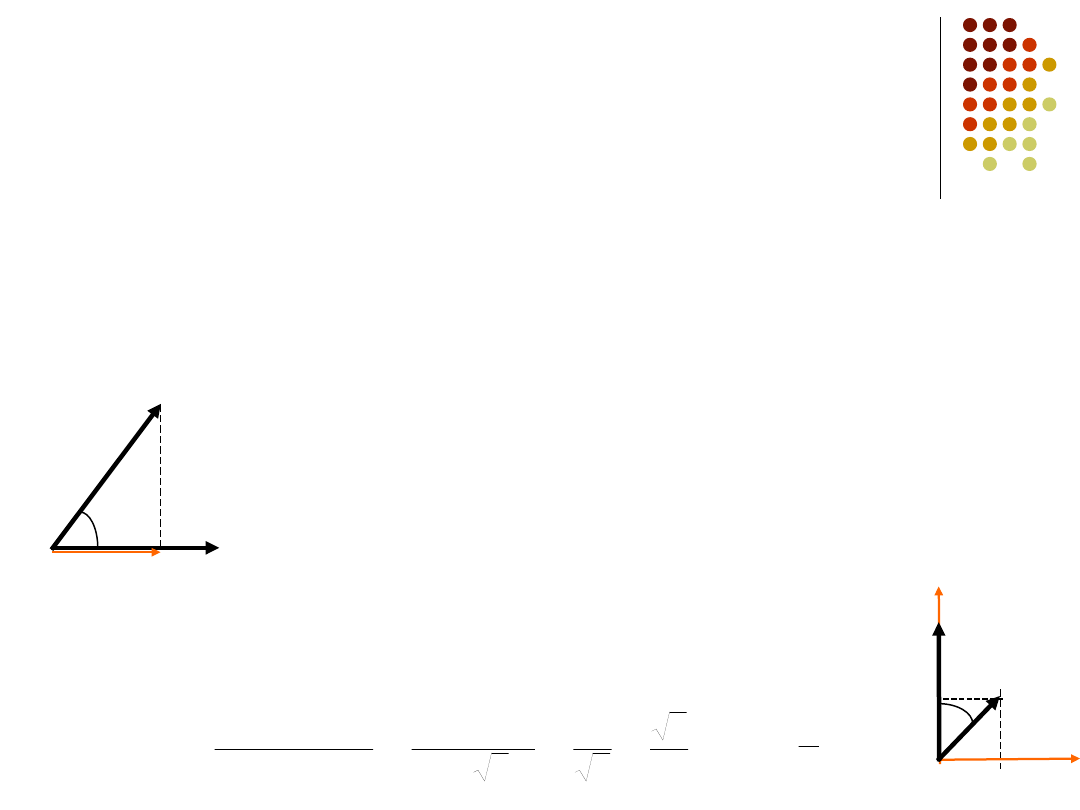
A

B

a

a

a ,



początek

koniec

moduł

zwrot

kierunek

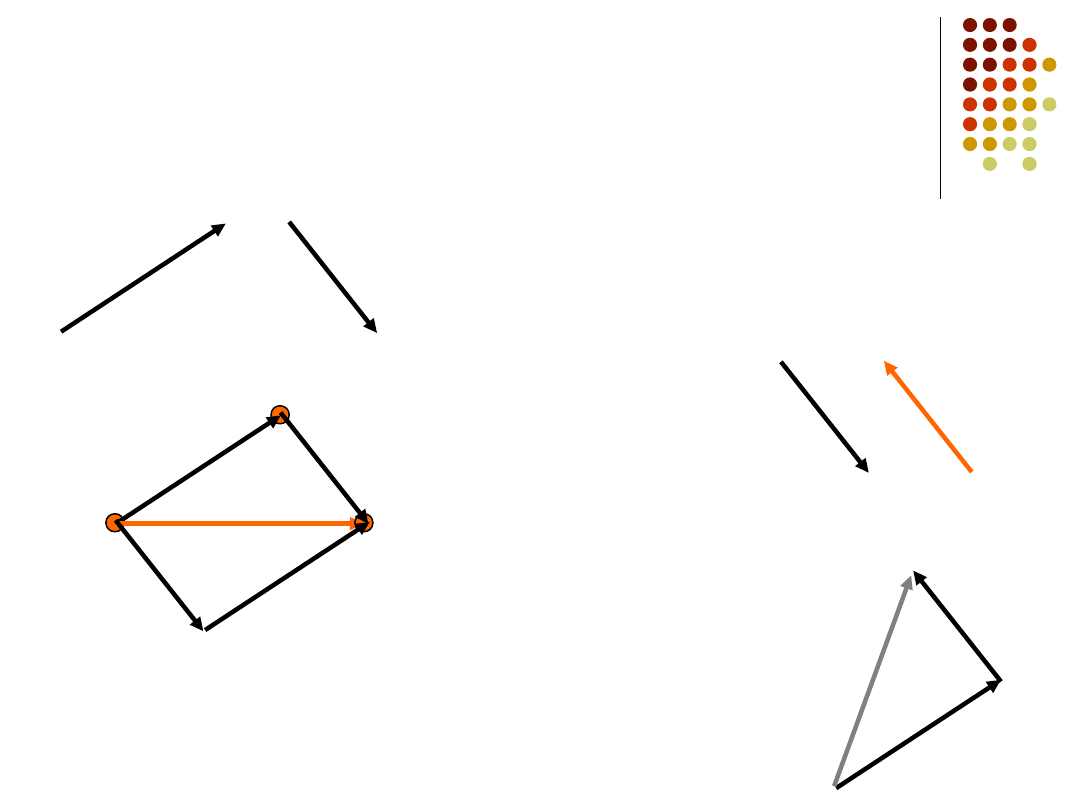
Działanie na wektorach



geometryczne dodawanie wektorów



składowe wektorów



wektory jednostkowe



dodawanie wektorów na składowych



mnożenie wektorów:



iloczyn skalarny



iloczyn wektorowy

Geometryczne dodawanie
wektorów

a

b



s

a

b



Szukamy sumy tych wektorów

Prawa dodawania:
przemienność
łączność

a

b

b

a























c

b

a

c

b

a























b



b





Odejmowanie wektorów to
dodawanie wektora przeciwnego

 

b

a

b

a

d





















a

b





d



A

B

c

łączne
przemieszczenie
jest sumą
wektorową
przemieszczeń
składowych

b



a

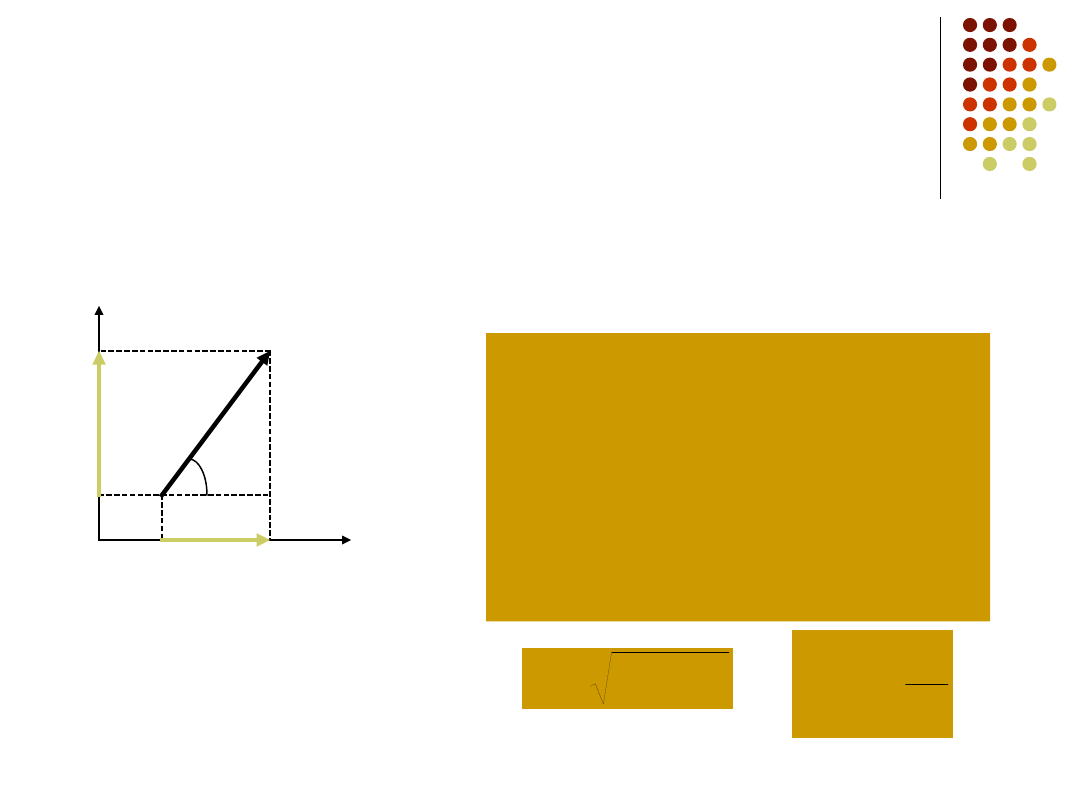
Składowe wektorów

Składową wektora nazywamy jego rzut na
wybraną oś np. x, y prostokątnego układu
współrzędnych

a

x

a

y

a

x

y





cos

a

a

x





sin

a

a

y



Dany wektor jest
jednoznacznie określony przez:

• wielkości a i , lub
• składowe a

x

i a

y

Wielkości te są powiązane
zależnościami:

a

2

2

y

x

a

a

a





x

y

a

a

tg 



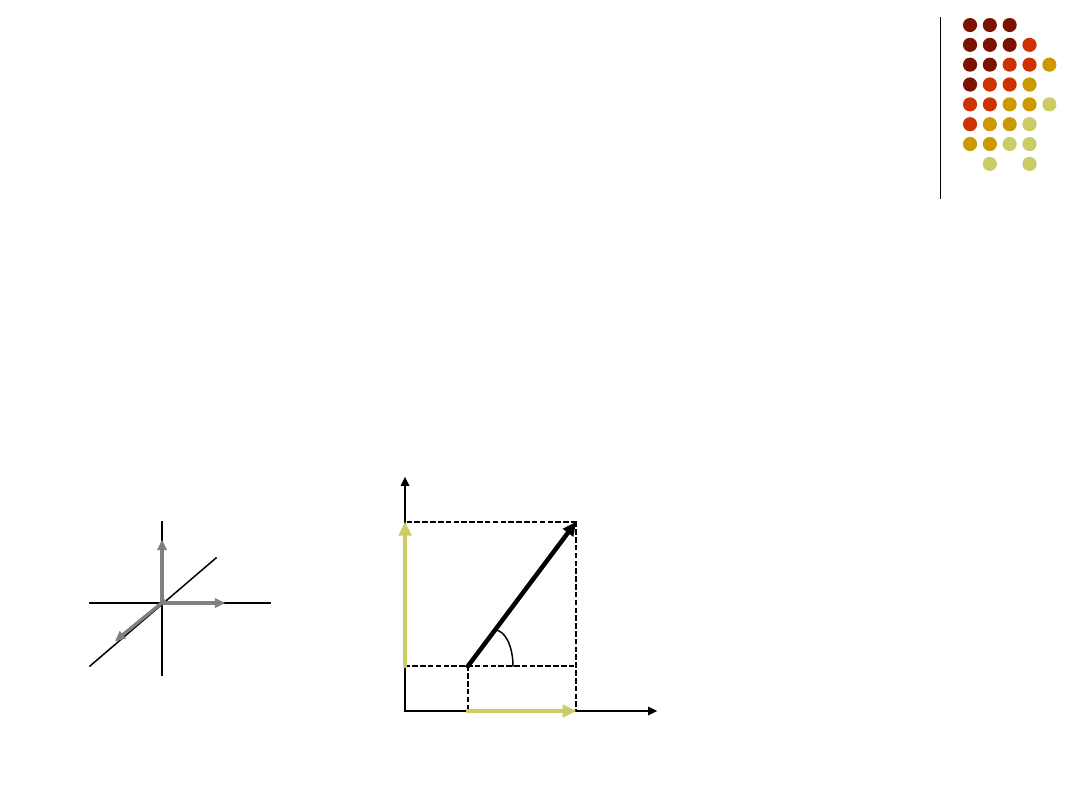
Wektory jednostkowe

Wektorem jednostkowym nazywamy wektor o długości
równej 1, skierowany w określonym kierunku.

W przypadku prawoskrętnego układu współrzędnych wektory
jednostkowe dodatnich kierunków osi x, y i z oznaczmy

k

j

i

ˆ

,

ˆ

,

ˆ

x

y

z

jˆ

iˆ

kˆ

a

i

a

x

ˆ

j

a

y

ˆ

x

y



y

x

a

a

a











j

a

i

a

a

y

x

ˆ

ˆ 









y

x

a

a

a

,





Dodawanie wektorów na
składowych





z

y

x

a

a

a

a

,

,









z

y

x

b

b

b

b

,

,









z

y

x

r

r

r

r

,

,





b

a

r











skoro wektor jest taki sam jak wektor to

i ich składowe muszą być jednakowe

x

x

x

b

a

r





y

y

y

b

a

r





z

z

z

b

a

r





r





b

a











3

1

2 ,

,



a





3

2

1 



,

,

b







0

1

3 ,

,



r

Obliczyć kąt pomiędzy
wektorami:

Mnożenie wektorów



iloczyn skalarny

jest wielkością skalarną iloczynowi modułu jednego wektora i
składowej drugiego wektora w kierunku pierwszego z nich



cos

ab

b

a









z

z

y

y

x

x

b

a

b

a

b

a

b

a













Jeśli znamy współrzędne
wektorów to iloczyn skalarny
równy jest sumie iloczynów
odpowiednich składowych

a

b







cos

a

 

2

0,



a

 

1

1,



b



2

2

2

1

2

2

1

2

1

0





















b

a

b

a

b

a

y

y

x

x



cos

4







a

b





x

y

1

0

2

1

Mnożenie wektorów



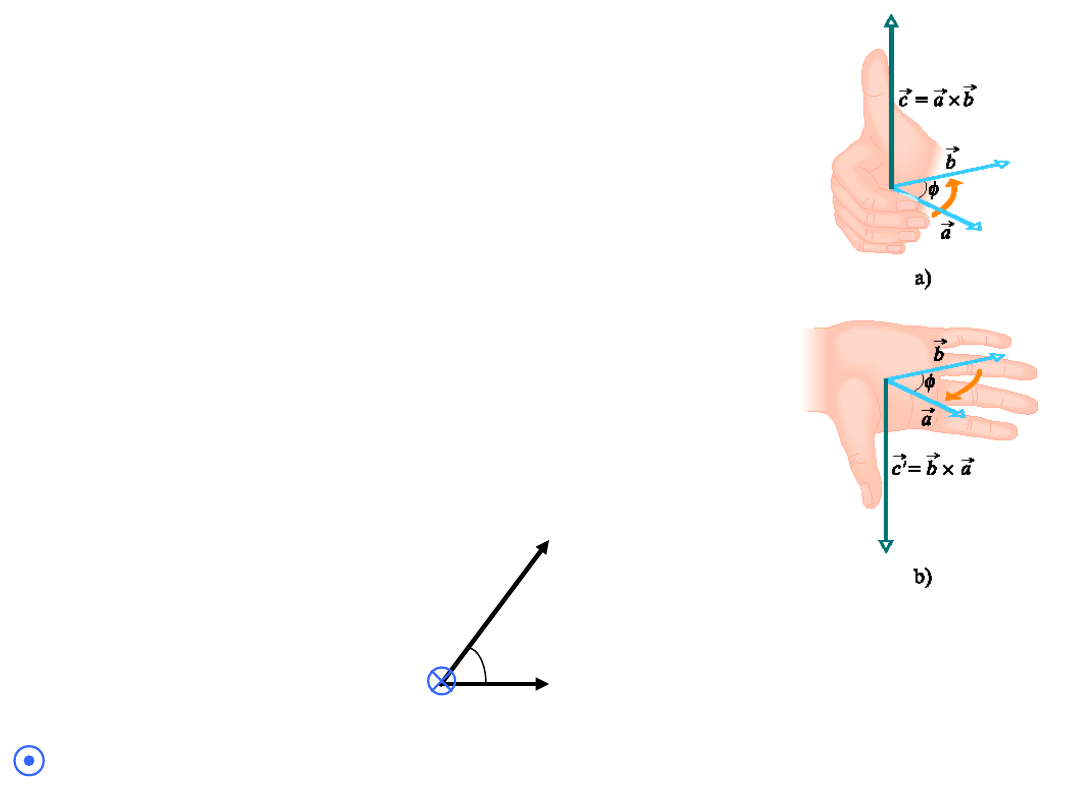
iloczyn wektorowy

b

a

c













sin

ab

c 

jest to wektor prostopadły do
płaszczyzny w której leżą ,
o zwrocie wyznaczony przez regułę
prawej dłoni i długości równej

c

b

i

a





wektor prostopadły do
ekranu i skierowany w głąb

a

b





c

c













z

a

b

b

a

j

a

b

b

a

i

a

b

b

a

b

a

y

x

y

x

x

z

x

z

z

y

z

y





























skierowany
do nas





0

2

1 ,

,



a





0

0

1 ,

,



b















z

j

i

b

a











2

1

0

1

1

0

1

0

0

0

0

2



































2

0

0









,

,

b

a

c







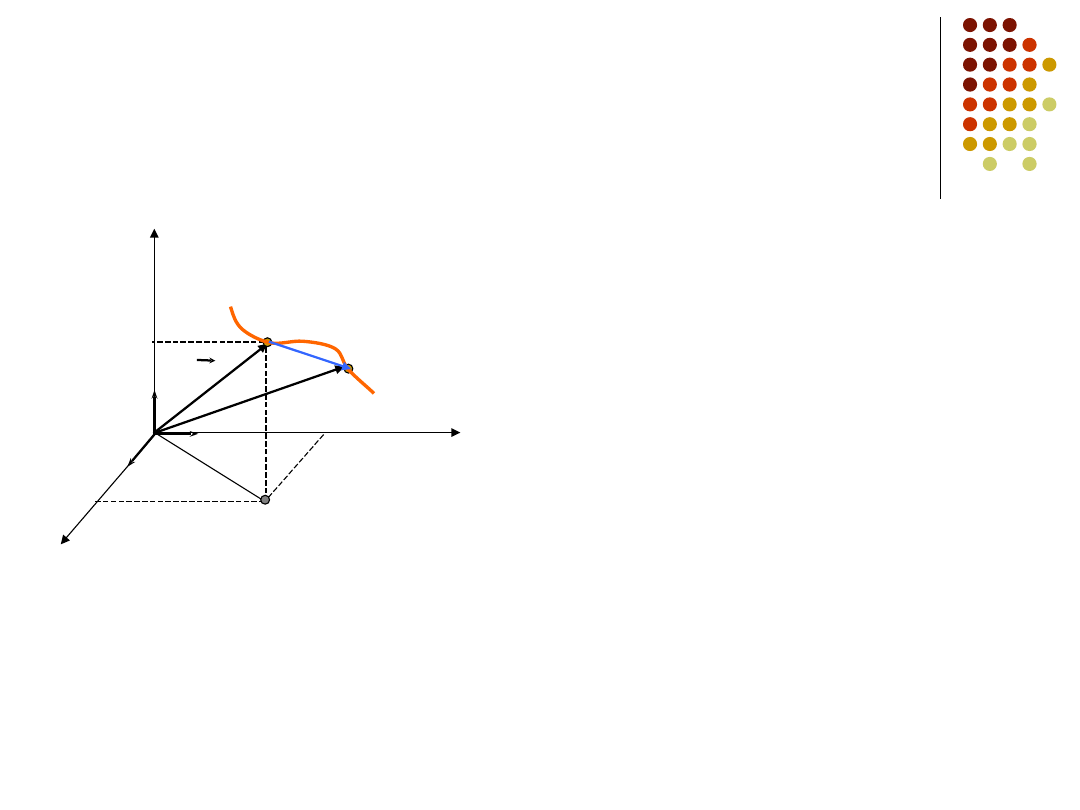
Ruch w trzech wymiarach



układ odniesienia - kartezjański
układ współrzędnych prostokątnych



położenie cząstki – podanie
współrzędnych cząstki (wektor
położenia)



ruch – zmiana położenia względem
układu odniesienia



tor (trajektoria) cząstki – linia którą
zakreśla poruszająca się cząstka



przemieszczenie

k

z

j

y

i

x

z

y

x

r























)

,

,

(

X

Y

Z

A

r

z

A

y

A

x

A

k



j



i



A

B

r

r

r













B

)

,

,

(

)

.

,

,

(

2

4

1

5

2

3

2





B

A

r

r







 



)

.

,

,

.

,

,

5

0

1

1

5

2

2

3

4

2

1





















A

B

r

r

r











0

0

1 ,

,



i







0

1

0 ,

,



j







1

0

0 ,

,



k



wektory jednostkowe

r



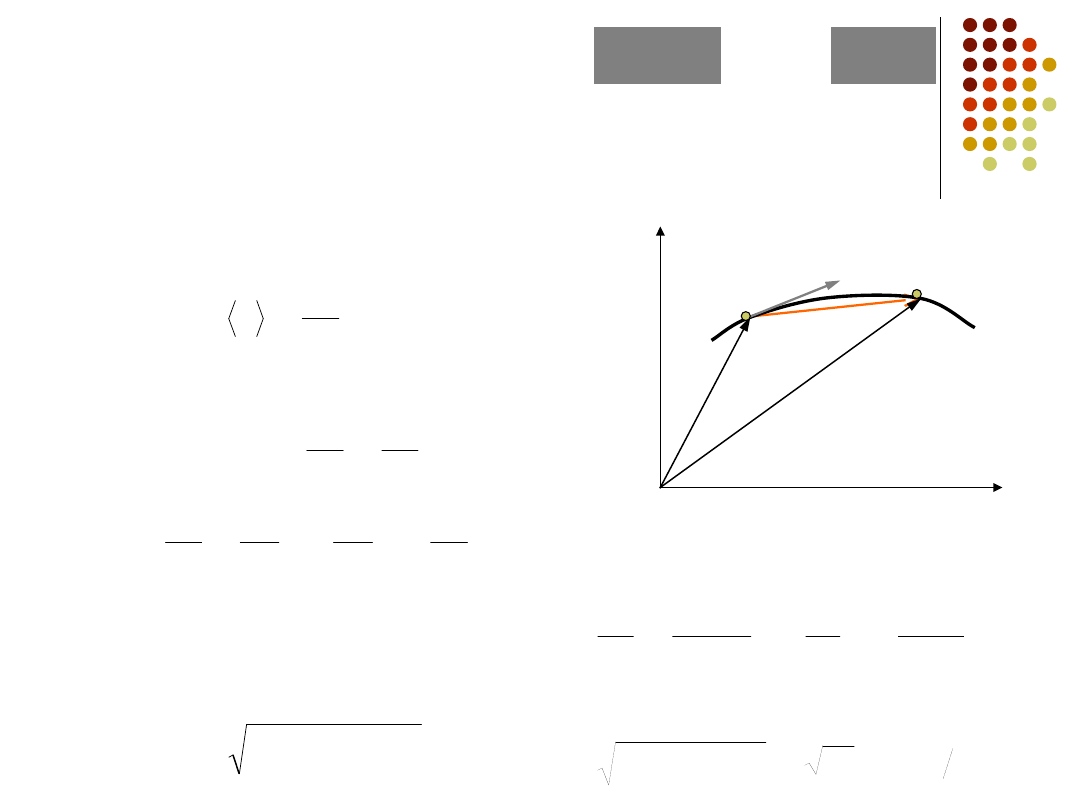
Prędkość

cząstka porusza się po krzywoliniowym torze z
punktu A do B w czasie t przebywając drogę

s



prędkość średnia



prędkość chwilowa

t

r

v











dt

r

d

t

r

v

t



















lim

0

k

dt

dz

j

dt

dy

i

dt

dx

dt

r

d

v



















k

v

j

v

i

v

v

z

y

x















2

2

2

z

y

x

v

v

v

v







y

x

A

B

 

t

r







r

r

t

t

r

















r





s



v



tor

ProjKinematics.s wf

RacingBalls.s wf





z

y

x

v

v

v

v

,

,









 

m

t

t

r

3

3

2

2

,

,





 

 

k

dt

t

d

j

dt

d

i

dt

t

d

dt

r

d

v











3

3

2

2









Przykład:





3

0

4

,

,

t

v 



s

t

Dla

1



  



3

0

4

1

,

,



s

v

s

m

v

5

25

3

0

4

2

2

2











wartość
prędkości

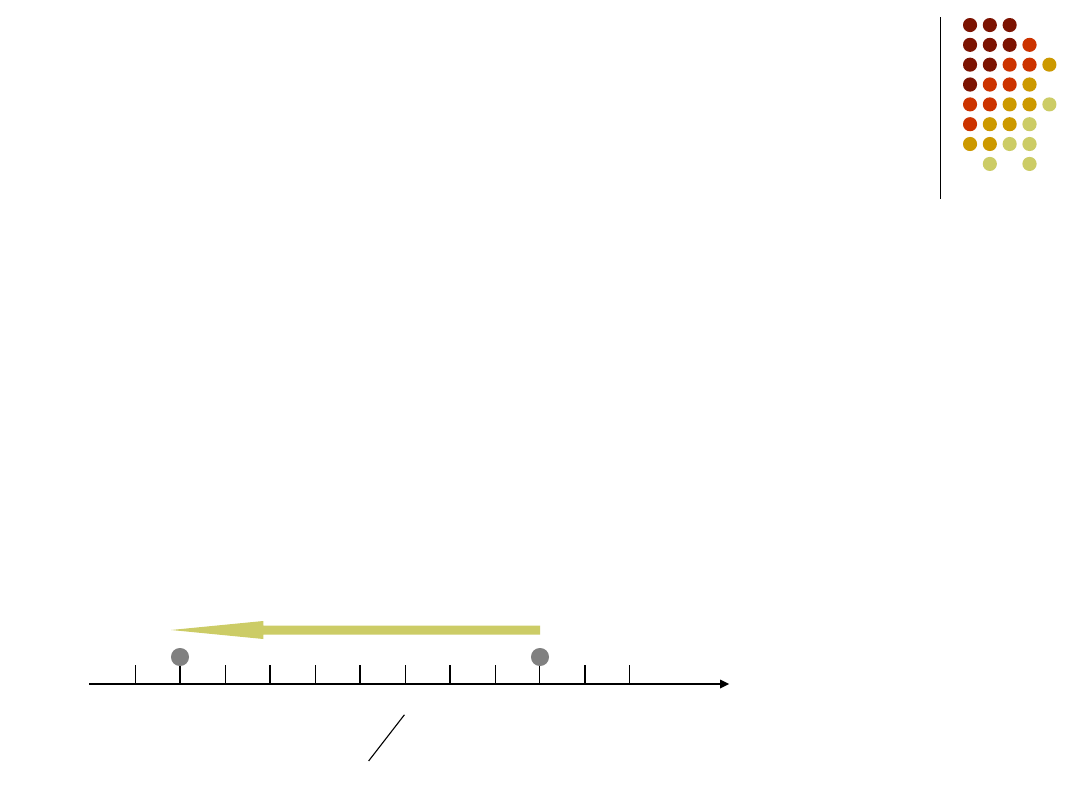
Ruch prostoliniowy



ruch zachodzący tylko wzdłuż linii prostej



położenie ciała, czyli współrzędną punktu w jakim się ono
znajduje, wyznaczamy względem punktu odniesienia
(początku osi) podając współrzędną punktu



przemieszczenie, zmiana położenia punktu materialnego



znak przemieszczenia określa kierunek ruchu

1

2

x

x

x







m

x

m

x

5

2

2

1







,

0 1 2 3 4 5

x [m]

-1

-2

-3

-4

-5

-6

początek osi

m

x

8

3

5













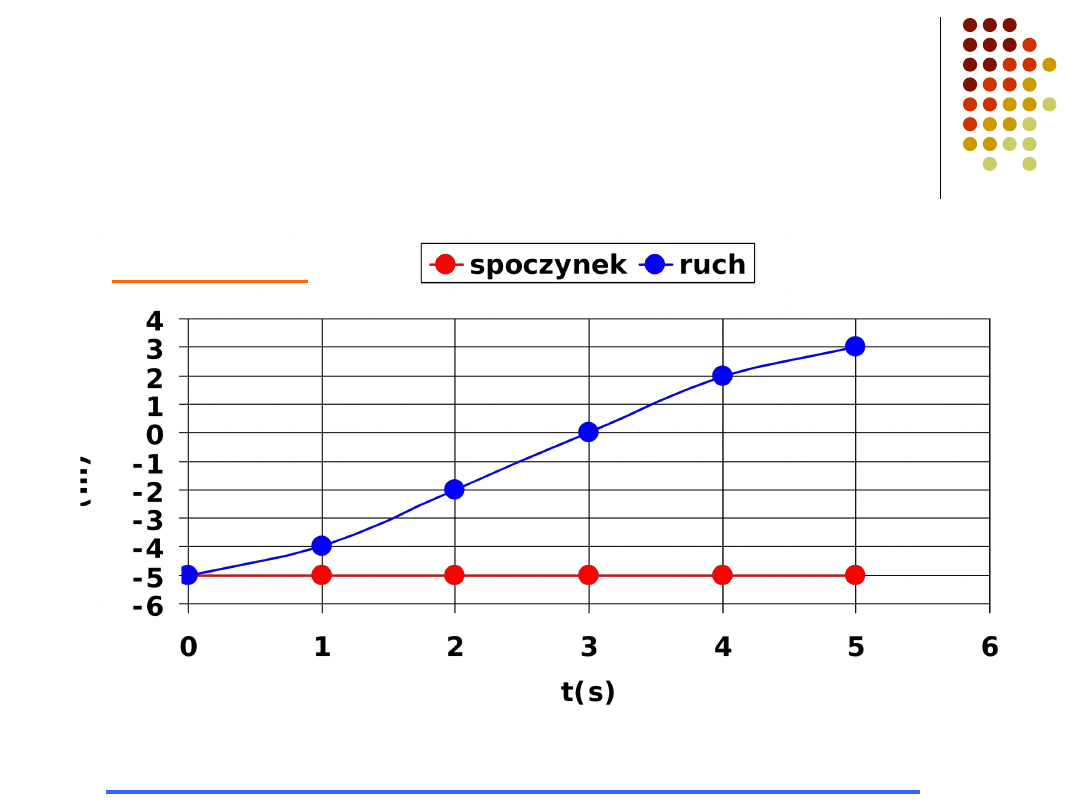
Sposób przedstawiania
ruchu – wykres x(t)

 

t

f

x 

5





x

5

5

0

7

0

1

0

2

3

















t

t

t

x

,

,

,

Prędkość średnia



jak szybko porusza się cząstka?



prędkość średnia

jednostka (m/s)



średnia wartość bezwzględnej prędkości

t

zenie

przemieszc

t

t

x

x

t

x

v

v

v

śr





















1

2

1

2

t

droga

calkowita

t

s

v

śr











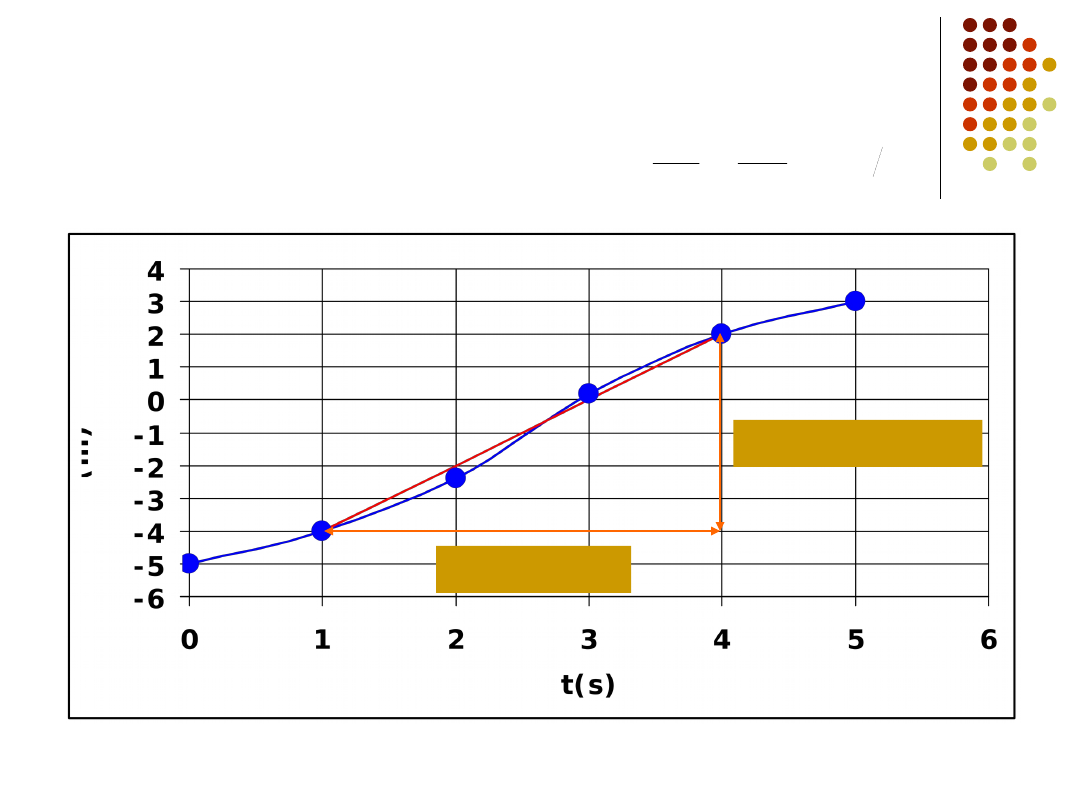
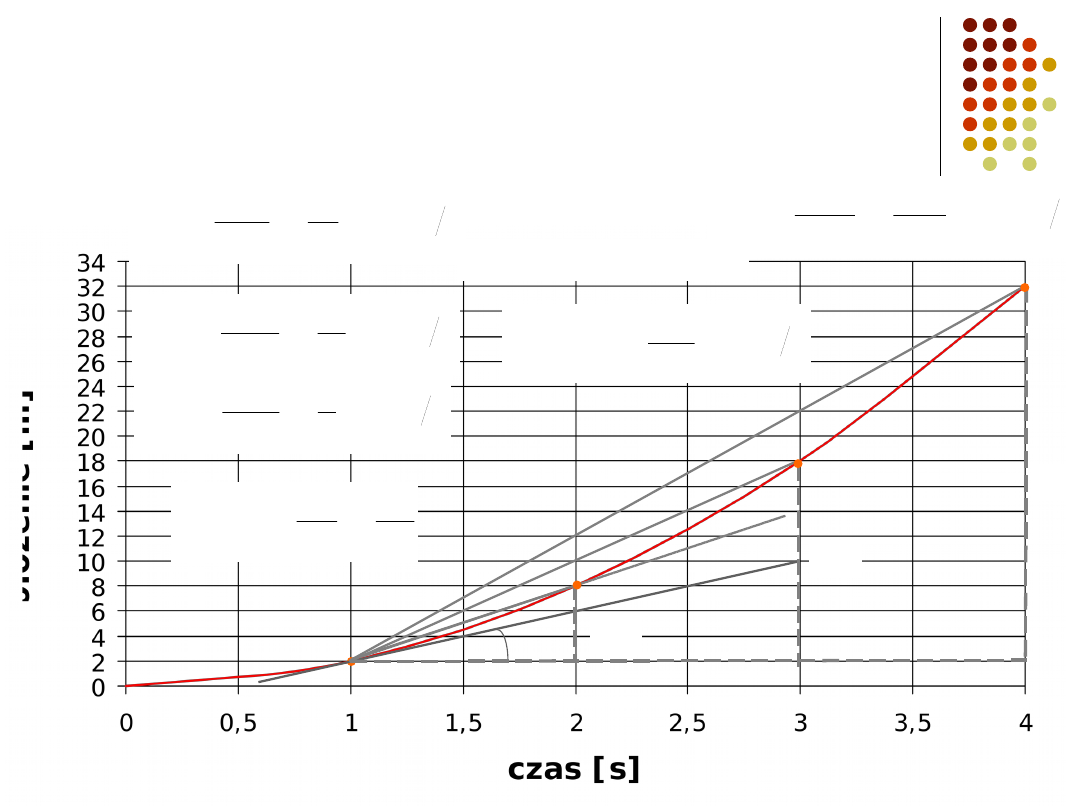
Wyznaczanie prędkości
średniej

x=2-(-4)=6 m

t=4-1=3 s

s

m

s

m

t

x

v

śr

2

3

6











prędkość średnia jako nachylenie prostej (współczynnik kierunkowy)

Prędkość chwilowa
czyli po prostu
„prędkość”



jak szybko porusza się cząstka w danej chwili



v – jest szybkością zmiany położenia cząstki

przy zmianie czasu w danej chwili (v jest

pochodną x względem t)



wartość v jest równa nachyleniu prostej

stycznej do wykresu x=f(t)

dt

dx

t

x

v

t













lim

0

Przy zmniejszaniu się t średnia prędkość dąży do granicy,

którą jest prędkość w danej chwili

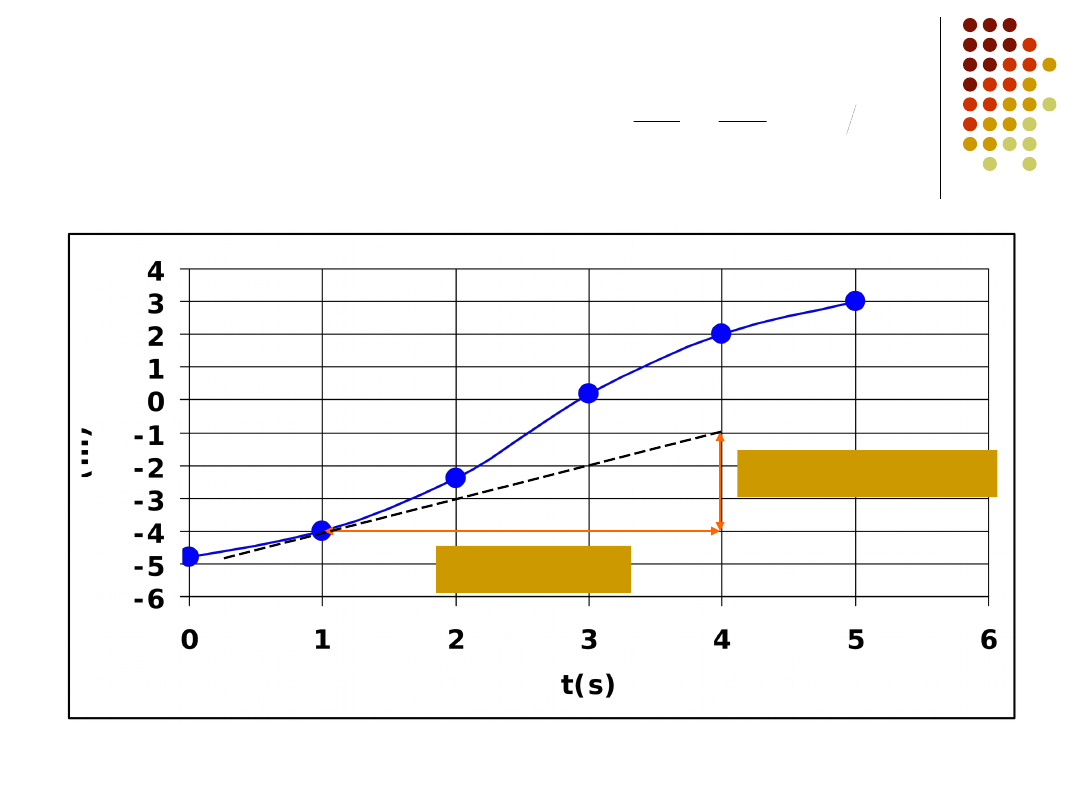
prędkości
chwilowa

 

s

m

s

m

t

x

s

v

1

3

3

1











prędkość chwilowa jako nachylenie stycznej do wykresu x(t)

x=-1-(-4)=3 m

t=4-1=3 s

Pochodna - graficznie

funkcja x=2t

2

pochodna x’=4t [v(t=1)=4]



s

m

t

x

tg

v

4













s

m

t

x

v

śr

10

3

30

1

1

1











1

x



s

m

t

x

v

śr

8

2

16

2

2

2











2

x



s

m

t

x

v

śr

6

1

6

3

3

3











3

x



dt

dx

t

x

v

t













lim

0

s

t

1

0,





s

m

t

x

v

n

n

śrn

1

4

1

0

41

0

,

,

,











41

0

2

1

1

2

2

,

,









x

Pochodna funkcji

Funkcja

f(x)

Pochodna

f’(x)

stała

0

x

n

nx

n-1

sin(x)

cos(x)

cos(x)

- sin(x)

e

ax

ae

ax

ln(x)

1/x

 

x

dt

t

df

dt

dx

ozn







.

 

y

dx

x

df

dx

dy

ozn







.

Właściwości pochodnej:

(ax)’=ax’

(x+y)’=x’+y’

(x·y)’=x’·y+x·y’

(x/y)’= (x’·y-x·y’)/y

2

 





dt

dx

dx

dy

dt

t

x

dy





Przykład

Położenie cząstki, poruszającej się wzdłuż osi x, jest
opisane równaniem (x-w metrach, t- w sekundach):

3

1

2

2

9

8

7

t

t

x

,

,

,







Ile wynosi prędkość cząstki w chwili t = 3,5 s?

Czy ciało porusza się wówczas ze stałą prędkością, czy
zmienną?





3

1

2

2

9

8

7

t

t

dt

d

dt

dx

v

,

,

,









   

2

1

2

3

2

9

0

t

v

,

, 





 

  

s

m

v

68

5

3

3

6

2

9

5

3

2









,

,

,

,

Cząstka porusza się w ujemnym kierunku osi x z prędko-
ścią o wartości bezwzględnej 68 m/s.

W równaniu v zależy od czasu, a więc prędkość nie
jest stała.

Rachunek całkowy

Całkowanie jest działaniem odwrotnym względem
różniczkowania. Polega na znalezieniu dla badanej funkcji
f(x) tzw. funkcji pierwotnej F(x) która w każdym punkcie
badanego przedziału spełnia równość F’(x) = f(x)

Funkcja pierwotna jest wyznaczana z dokładnością do
dowolnej stałej C, gdyż (F(x)+C)’=f(x)

Sumę F(x)+C nazywamy całką nieoznaczoną f(x) i
oznaczamy symbolem



dx

x

f

)

(



dx

......

symbol całkowania

funkcja zmienna
podcałkowa całkowania

Całka oznaczona

Jeżeli F(x) jest funkcją pierwotną funkcji f(x) to całką
oznaczoną funkcji f(x) w przedziale [a,b] nazywamy

)

(

)

(

)

(

)

(

a

F

b

F

x

F

dx

x

f

b

a

b

a









górna

dolna

granica
całkowania

Przykład:





5

7

1

4

2

1

2

1

2

2

4

1

2

4

1

,











x

dx

x

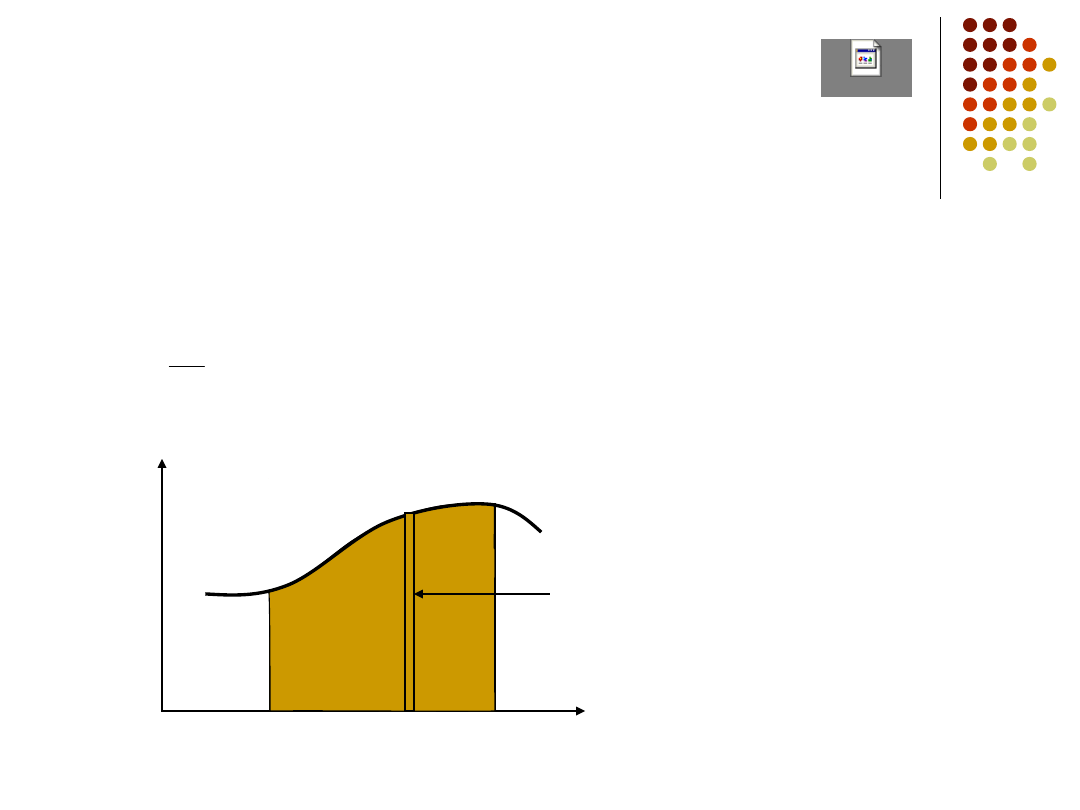
Całka jako suma

znajomość prędkości pozwala obliczyć drogę
przebytą przez punkt materialny

dt

ds

v 

dt

v

ds 





2

1

t

t

dt

v

s

v

t

t

1

t

2

s

v(t)

całka oznaczona

t

i

s

i













i

i

i

i

i

t

v

s

s

v

i

całka oznaczona
równa jest polu pod
krzywą

Integrals.s wf

Podstawowe wzory









C

x

dx

x

cos

sin







C

x

dx

1







C

ax

dx

a











C

n

x

dx

x

n

n

1

1







C

x

dx

x

ln

1

...

,

,

718

2









e

C

e

dx

e

x

x



C

dx

0







C

x

dx

x

sin

cos

Przykłady:

2

3

3

2

3

1

3

1

x

C

x

bo

C

x

dx

x

l























,

C

y

C

y

dy

y

dy

y























1

1

1

1

2

2









C

t

dt

t

5

5

1

5

cos

sin

Równanie różniczkowe typu ma rozwiązanie
ogólne postaci

Równania różniczkowe

 

x

f

dx

dy



 

dx

x

f

y





 

dx

x

f

dy 

 







dx

x

f

dy

 





dx

x

f

y

Przykład:

t

e

y

2



'

t

e

dt

dy

2







dt

e

y

t

2

C

e

y

t





2

2

1