PODSTAWY

KINEMATYKI

Wykład 2

PODSTAWY

KINEMATYKI

Kinematyka – klasyfikacja i
porównywanie różnych ruchów
(jak zmiany ruchu zależą od czasu?)

Wykład – 2 -

Ruch mechaniczny – zmiana położenia ciała 

konieczne wskazanie innych ciał względem, których

ruch się odbywa (względne przemieszczanie się ciał)

Ruch – zmiana w przestrzeni i w czasie

Układ odniesienia – zbiór nieruchomych względem

siebie ciał służący do rozpatrywania ruchu innych ciał i

zegar odmierzający czas

Ruch tego samego ciała względem różnych układów

odniesienia  różny charakter (pasażer w pociągu)

opis ruchu – podanie położenia dla każdej chwili czasu

Punkt materialny – ciało o znikomo małych rozmiarach

w warunkach danego zagadnienia, o danej masie i

położeniu, które można określić jak położenie punktu

geometrycznego

Ruch mechaniczny

3

Wektory

i skalary

• dla ruchu jednowymiarowego kierunek wyróżniamy

znakiem

• do opisu ruchu w przestrzeni trójwymiarowej stosujemy

pojęcie wektora

• wektor posiada wartość i kierunek
• działania na wektorach podlegają prawom rachunku

wektorowego

• wielkości wektorowe: przemieszczenie, prędkość,

przyspieszenie, siła

• wielkości skalarne: temperatura, ciśnienie, energia, masa,

czas – nie wykazują żadnego kierunku w przestrzeni

A

B

a

a

a ,



początek

koniec

moduł

zwrot

kierunek

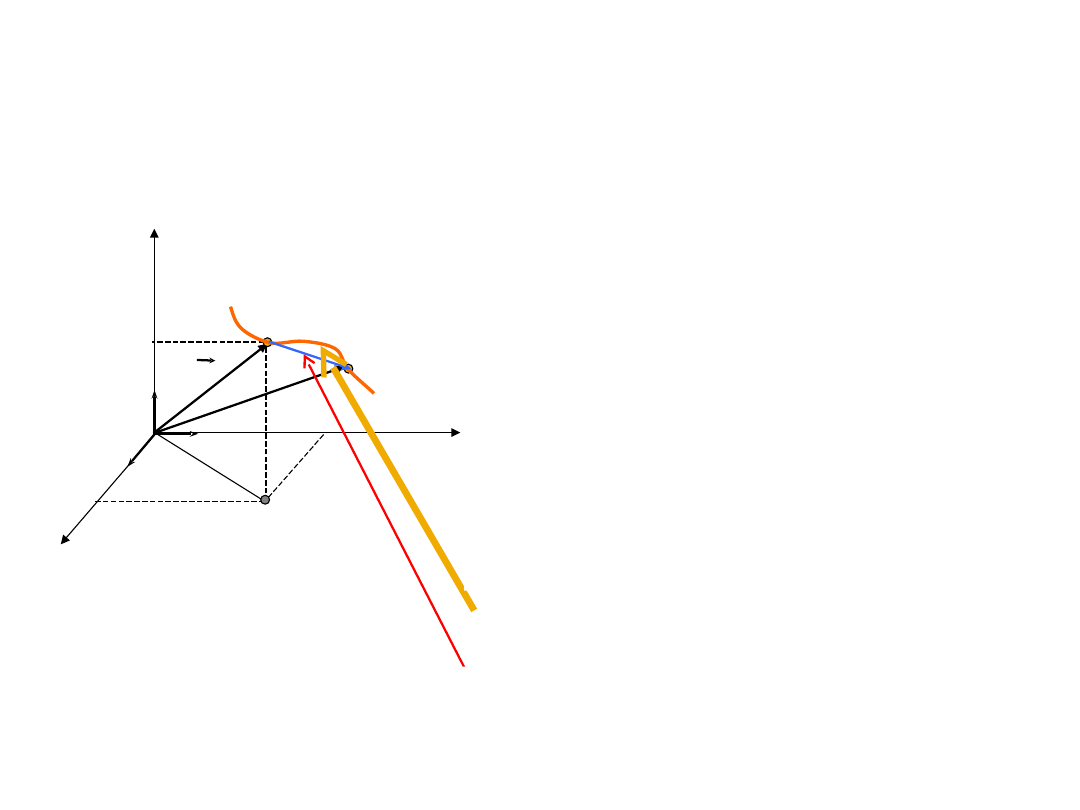
Ruch w trzech wymiarach

•

układ odniesienia

układ odniesienia - kartezjański
układ współrzędnych prostokątnych

•

położenie cząstki

położenie cząstki – podanie
współrzędnych cząstki (wektor
położenia)

•

ruch

ruch – zmiana położenia względem
układu odniesienia

•

tor (trajektoria) cząstki

tor (trajektoria) cząstki – linia którą
zakreśla poruszająca się cząstka

•

przemieszczenie

przemieszczenie

k

z

j

y

i

x

z

y

x

r























)

,

,

(

X

Y

Z

A

r

z

A

y

A

x

A

k



j



i



A

B

r

r

r













B

)

,

,

(

)

.

,

,

(

2

4

1

5

2

3

2





B

A

r

r







 



)

.

,

,

.

,

,

5

0

1

1

5

2

2

3

4

2

1





















A

B

r

r

r











0

0

1 ,

,



i







0

1

0 ,

,



j







1

0

0 ,

,



k



wektory jednostkowe

r



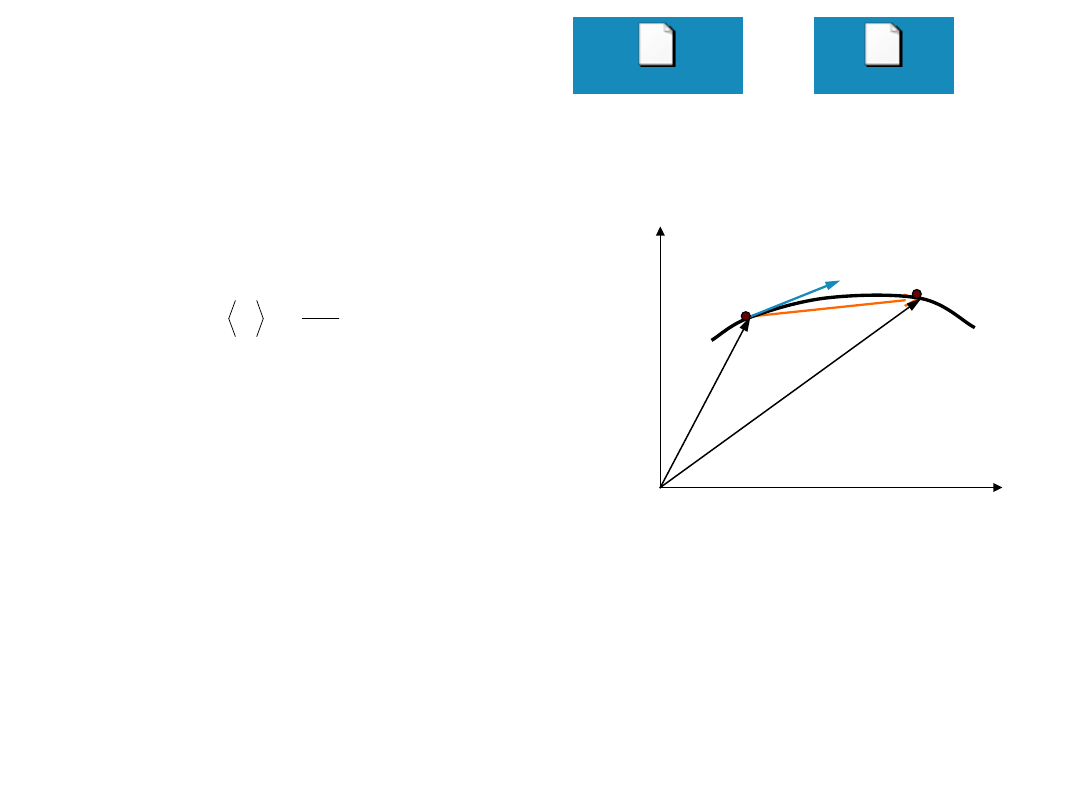
Prędkość

cząstka porusza się po krzywoliniowym torze z
punktu A do B w czasie t przebywając drogę s

• prędkość średnia

• prędkość chwilowa

t

r

v











dt

r

d

t

r

v

t



















lim

0

k

dt

dz

j

dt

dy

i

dt

dx

dt

r

d

v



















k

v

j

v

i

v

v

z

y

x















2

2

2

z

y

x

v

v

v

v







y

x

A

B

 

t

r







r

r

t

t

r

















r





s



v



tor

ProjKinematics.swf

RacingBalls .swf





z

y

x

v

v

v

v

,

,









 

m

t

t

r

3

3

2

2

,

,





 

 

k

dt

t

d

j

dt

d

i

dt

t

d

dt

r

d

v











3

3

2

2









Przykład:





3

0

4

,

,

t

v 



s

t

Dla

1



  



3

0

4

1

,

,



s

v

s

m

v

5

25

3

0

4

2

2

2











wartość
prędkości

Ruch prostoliniowy

• ruch zachodzący tylko wzdłuż linii prostej
• położenie ciała, czyli współrzędną punktu w jakim

się ono znajduje, wyznaczamy względem punktu
odniesienia (początku osi) podając współrzędną
punktu

• przemieszczenie, zmiana położenia punktu

materialnego

• znak przemieszczenia określa kierunek ruchu

7

1

2

x

x

x







m

x

m

x

5

3

2

1







,

0 1 2 3 4 5

x [m]

-1

-2

-3

-4

-5

-6

początek osi

m

x

8

3

5













Sposób przedstawiania

ruchu – wykres x(t)

 

t

f

x 

5





x

5

5

0

7

0

1

0

2

3

















t

t

t

x

,

,

,

Prędkość średnia

• jak szybko porusza się cząstka?

– prędkość średnia

jednostka (m/s)

– średnia wartość bezwzględnej prędkości

t

zenie

przemieszc

t

t

x

x

t

x

v

v

v

śr





















1

2

1

2

t

droga

calkowita

t

s

v

śr











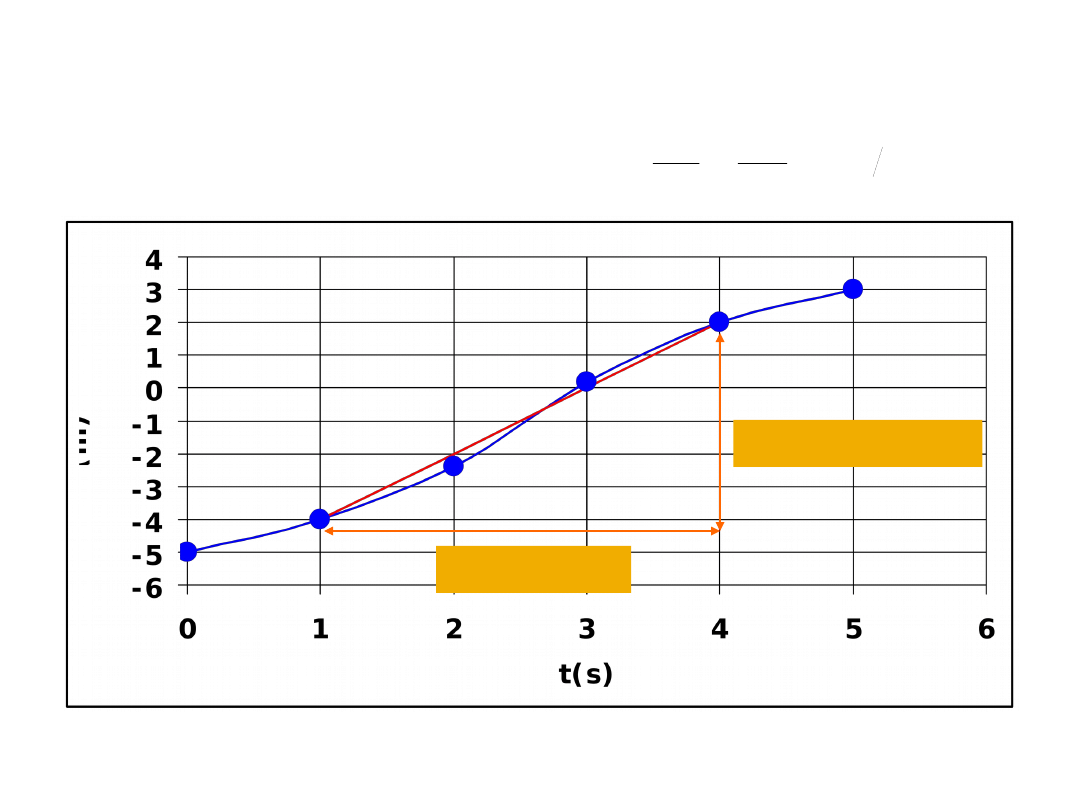
Wyznaczanie prędkości

średniej

x=2-(-4)=6 m

t=4-1=3 s

s

m

s

m

t

x

v

śr

2

3

6











prędkość średnia jako nachylenie prostej (współczynnik kierunkowy)

Prędkość chwilowa

czyli po prostu „prędkość”

• jak szybko porusza się cząstka w danej chwili

• v – jest szybkością zmiany położenia cząstki

przy zmianie czasu w danej chwili (v jest

pochodną x względem t)

• wartość v jest równa nachyleniu prostej

stycznej do wykresu x=f(t)

dt

dx

t

x

v

t













lim

0

Przy zmniejszaniu się t średnia prędkość dąży do granicy,

którą jest prędkość w danej chwili

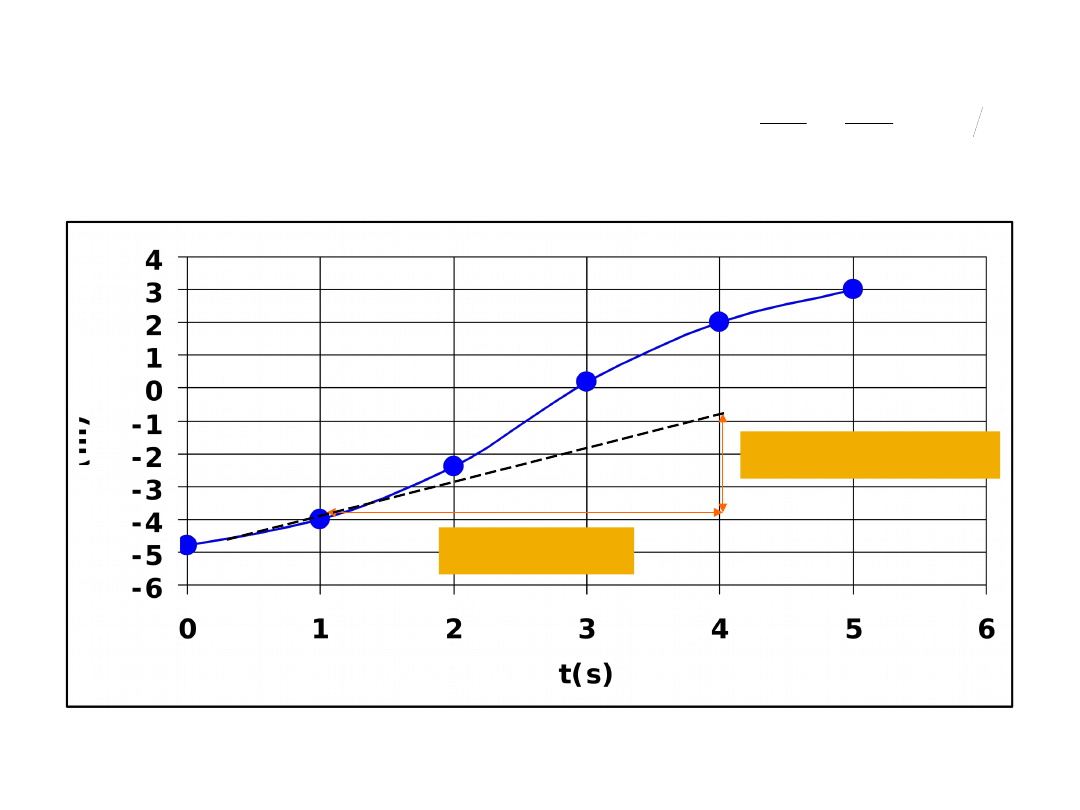
prędkość

chwilowa

 

s

m

s

m

t

x

s

v

1

3

3

1











prędkość chwilowa jako nachylenie stycznej do wykresu x(t)

x=-1-(-4)=3 m

t=4-1=3 s

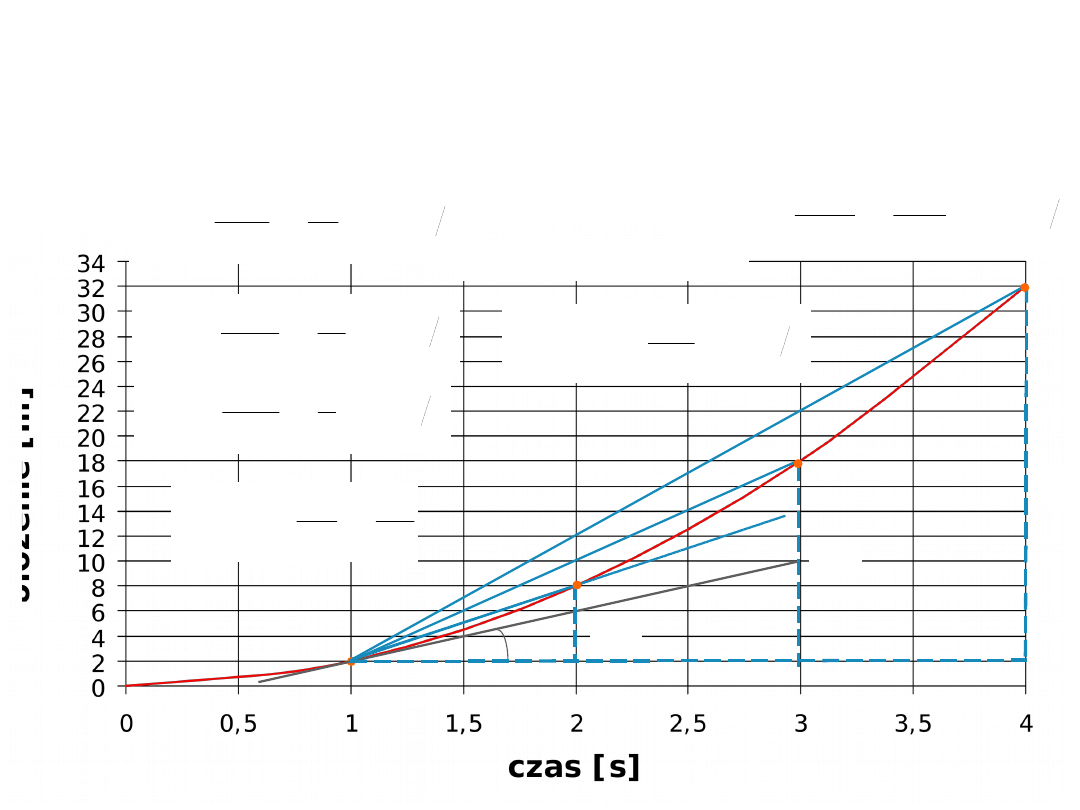
Pochodna - graficznie

funkcja x=2t

2

pochodna x’=4t [v(t=1)=4]



s

m

t

x

tg

v

4













s

m

t

x

v

śr

10

3

30

1

1

1











1

x



s

m

t

x

v

śr

8

2

16

2

2

2











2

x



s

m

t

x

v

śr

6

1

6

3

3

3











3

x



dt

dx

t

x

v

t













lim

0

s

t

1

0,





s

m

t

x

v

n

n

śrn

1

4

1

0

41

0

,

,

,











41

0

2

1

1

2

2

,

,









x

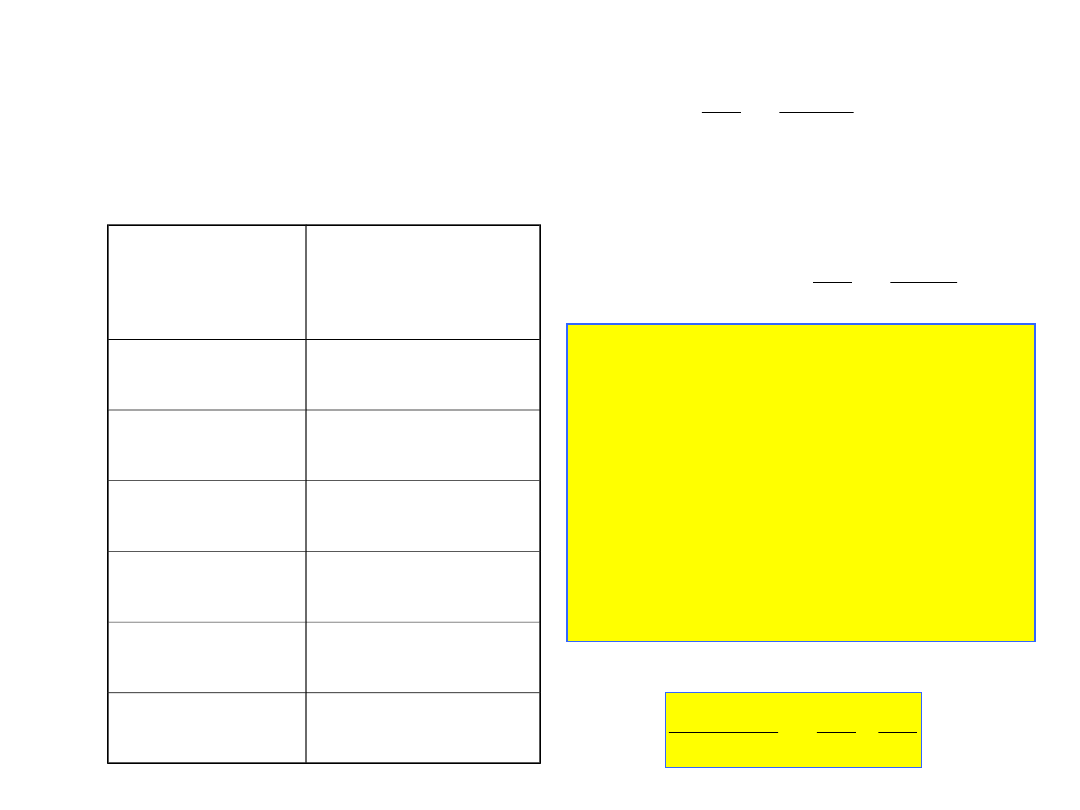
Pochodna

funkcji

Funkcja

f(x)

Pochodna

f’(x)

stała

0

x

n

nx

n-1

sin(x)

cos(x)

cos(x)

- sin(x)

e

ax

ae

ax

ln(x)

1/x

 

x

dt

t

df

dt

dx

ozn







.

 

y

dx

x

df

dx

dy

ozn







.

Właściwości pochodnej:

(ax)’=ax’

(x+y)’=x’+y’

(x·y)’=x’·y+x·y’

(x/y)’= (x’·y-x·y’)/y

2

 





dt

dx

dx

dy

dt

t

x

dy





Przykład

Położenie cząstki, poruszającej się wzdłuż osi x, jest
opisane równaniem (x-w metrach, t- w sekundach):

3

1

2

2

9

8

7

t

t

x

,

,

,







Ile wynosi prędkość cząstki w chwili t = 3,5 s?

Czy ciało porusza się wówczas ze stałą prędkością, czy zmienną?





3

1

2

2

9

8

7

t

t

dt

d

dt

dx

v

,

,

,









   

2

1

2

3

2

9

0

t

v

,

, 





 

  

s

m

v

68

5

3

3

6

2

9

5

3

2









,

,

,

,

Cząstka porusza się w ujemnym kierunku osi x z prędkością o
wartości bezwzględnej 68 m/s.

W równaniu v zależy od czasu, a więc prędkość nie jest stała.

Przyspieszenie

• gdy prędkość cząstki się zmienia tzn. że

doznaje ona przyspieszenia

– przyspieszenie średnie

– przyspieszenie chwilowe

16

dt

dv

t

v

a

t













lim

0

2

2

dt

x

d

dt

dx

dt

d

dt

dv

a



















t

v

t

t

v

v

a

śr













1

2

1

2

jednostka









2

s

m

Klasyfikacja ruchów

• tor:

• prostoliniowe
• krzywoliniowe (po okręgu, rzut poziomy)
• przestrzenne i płaskie

• wartość prędkości:

• jednostajne

v=const.

a=0

• jednostajnie zmienne v  const. a=const.
• niejednostajne

v  const. a  const.

17

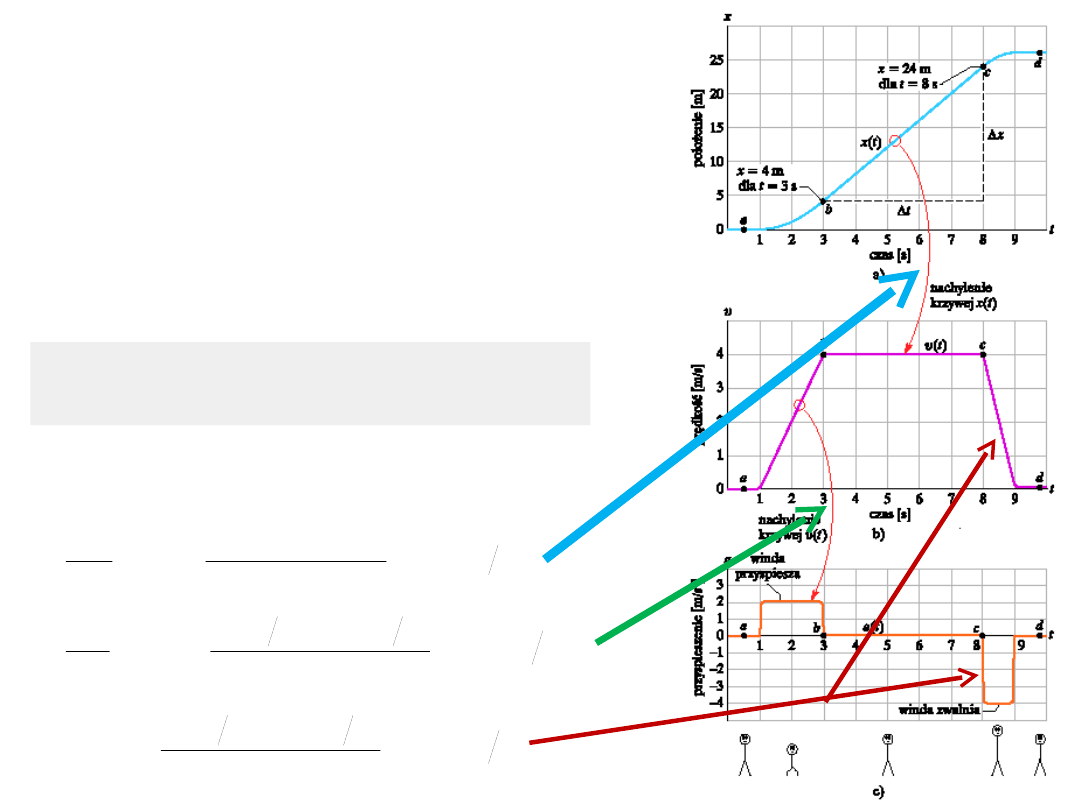
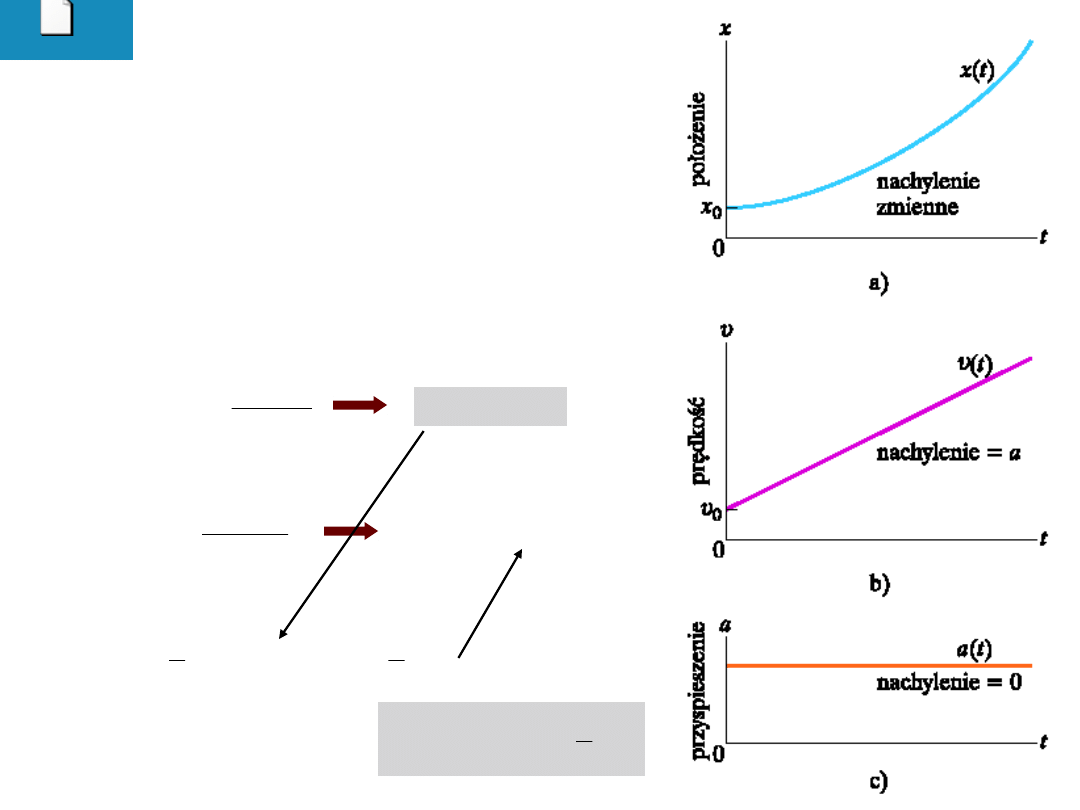
Przykład: winda

18

Na podstawie położenia windy w funkcji
czasu x(t) sporządzić wykres v(t) i a(t).

Winda początkowo nieruchoma jedzie
do góry i następnie zatrzymuje się.

Wybór układu:

dodatni kierunek x – do góry



 



   

s

m

s

s

m

m

v

t

x

4

3

8

4

24



















 



   

2

1

2

1

3

0

4

s

m

s

s

s

m

s

m

a

t

v



















 



   

2

2

4

8

9

4

0

s

m

s

s

s

m

s

m

a











Ruch ze stałym

przyspieszeniem

19

Gdy przyspieszenie jest stałe (a=const.)
to przyspieszenie średnie równe jest
chwilowemu:

0

0









t

v

v

a

a

śr

at

v

v





0

Podobnie:

0

0







t

x

x

v

śr

t

v

x

x

śr





0

Prędkość zmienia się liniowo w czasie, więc:





at

v

v

v

v

śr

2

1

2

1

0

0









2

0

0

2

1

at

t

v

x

x







Podstawowe równania
ruchu ze stałym
przyspieszeniem

ConstantAccel.swf

Spadek

swobodny

20

MonkeyHunter.swf

Każde ciało rzucone w górę lub w
dół w pobliżu powierzchni Ziemi
doznaje przyspieszenia o stałej
wartości skierowanego w dół.
Przyspieszenie to nazywamy

przyspieszeniem ziemskim

, a jego

wartość bezwzględna wynosi

g = 9,8 m/s

2

.

Przyspieszenie swobodnego
spadku ciała jest więc równe
a = -g = -9,8 m/s

2

.

Nie zależy ono od właściwości
przedmiotu: masy, kształtu.

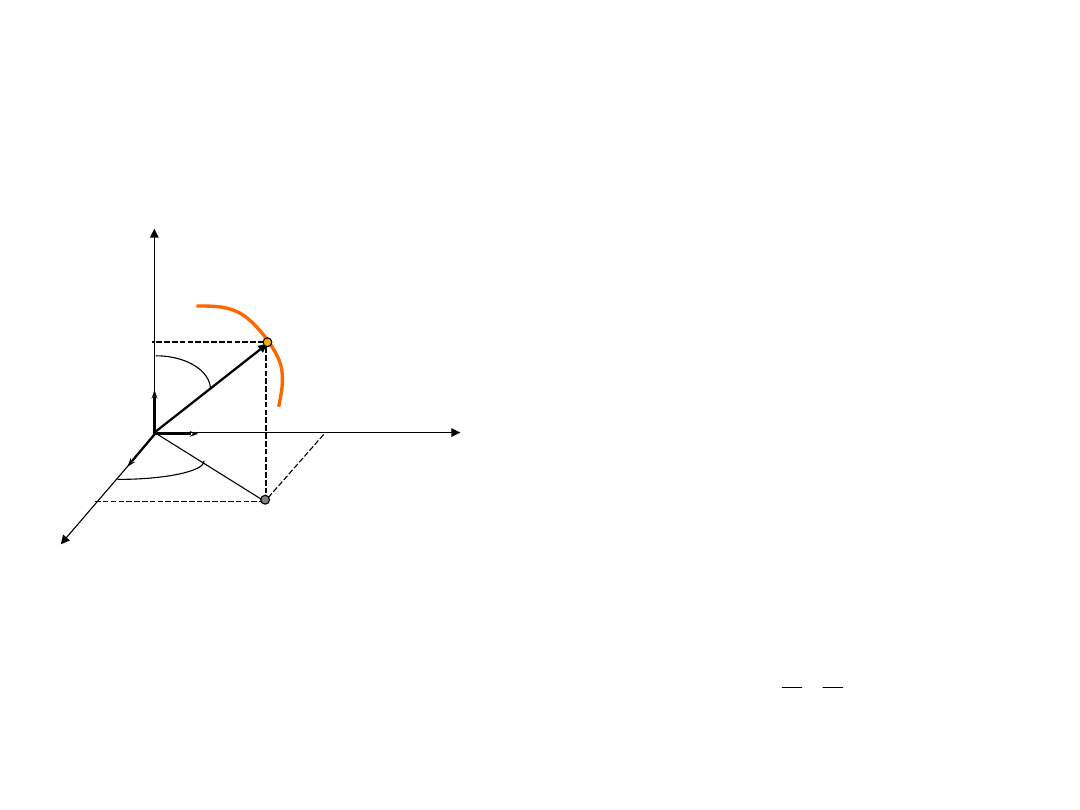
Układ sferyczny

• w układzie sferycznym

położenie cząstki określamy
przez podanie:

– odległości od środka układu r
– kąta azymutalnego  w

płaszczyźnie XY

– kąta biegunowego  jaki tworzy

wektor r dodatnią półosią OZ

21

)

,

,

(





r

r 







X

Y

Z

A

r

z

y

x

k



j



i







cos

sin

r

x 





sin

sin

r

y 



cos

r

z 

związek pomiędzy
współrzędnymi układu
kartezjańskiego i
sferycznego

)

,

,

(

4

4

3







A

r

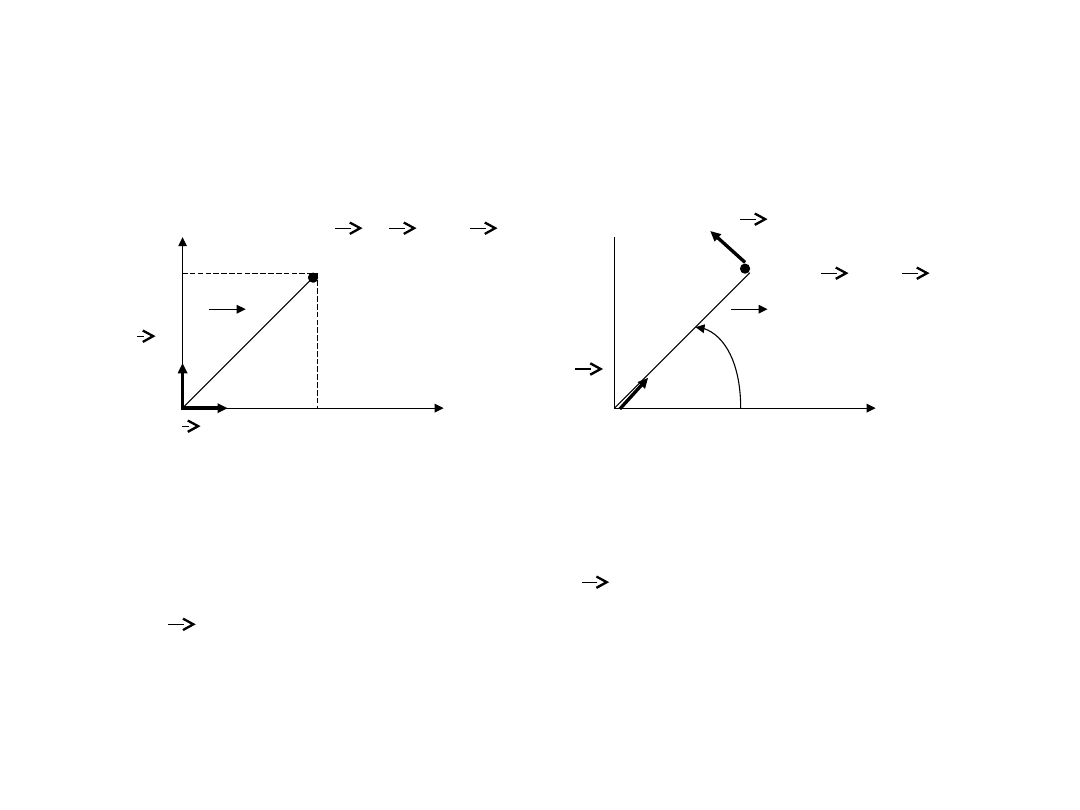
Układy odniesienia na

płaszczyźnie

• położenie punktu – wektor położenia r (współrzędne

wektora r (x,y) lub r(r, )

• wersory osi układu – wektory o jednostkowej długości,

skierowane zgodnie ze zwrotem osi współrzędnych

22

e

r

0

Y

j

X

i

r

+

r

x

y

e



r

r = i x + j y

r =

r

e

r

kartezjański układ
współrzędnych prostokątnych

układ biegunowy

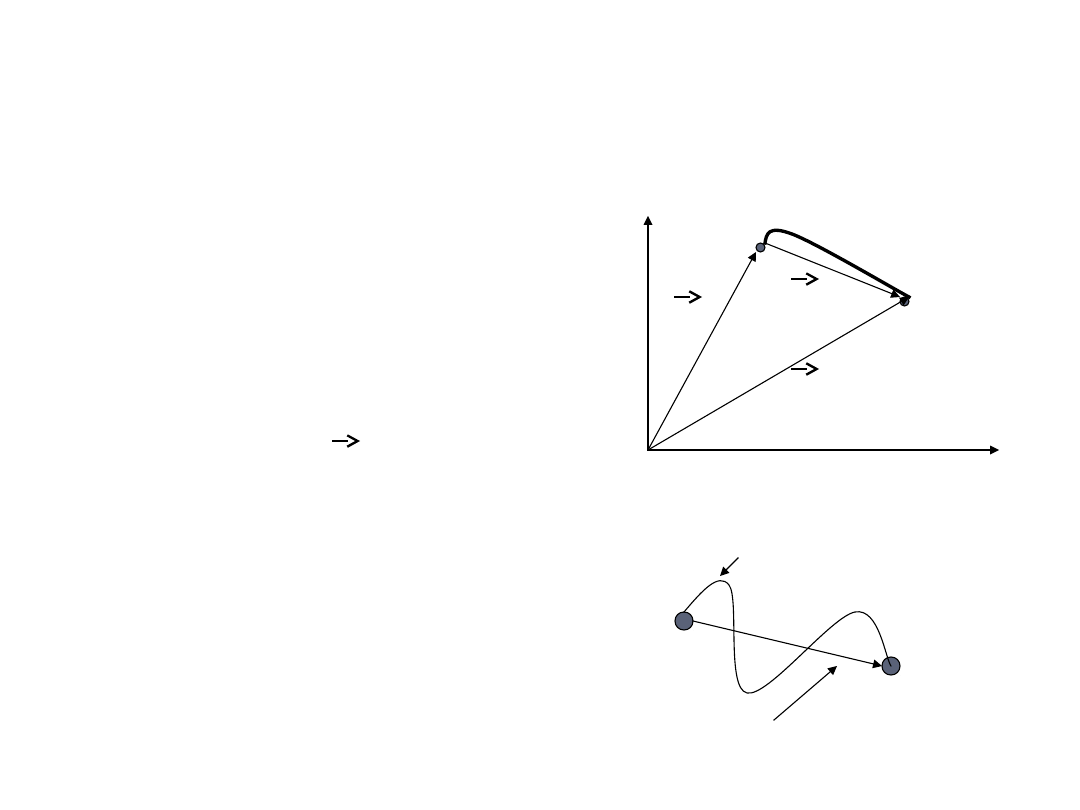
Tor a przemieszczenie

• tor (trajektoria) cząstki – linia

którą zakreśla poruszające się
ciało

• droga s – odległość pomiędzy

położeniem początkowym i
końcowym mierzona wzdłuż toru

• przemieszczenie r – wektor o

początku w punkcie początkowym
(1) i końcowym (2)

23

1

2

tor

przemieszczenie

r

1

r

12

r

2

X

Y

0

j

y

y

i

x

x

r

r

r











)

(

)

(

1

2

1

2

1

2

12













Prędkość

cząstka porusza się po krzywoliniowym torze z punktu A

do B w czasie t przebywając drogę s

• prędkość średnia

• prędkość chwilowa

24

t

r

v











dt

r

d

t

r

v

t



















lim

0

k

dt

dz

j

dt

dy

i

dt

dx

dt

r

d

v



















k

v

j

v

i

v

v

z

y

x















2

2

2

z

y

x

v

v

v

v







y

x

A

B

 

t

r







r

r

t

t

r

















r





s



v



tor

ProjKinematics.s wf





z

y

x

v

v

v

v

,

,









 

m

t

t

r

3

3

2

2

,

,





 

 

k

dt

t

d

j

dt

d

i

dt

t

d

dt

r

d

v











3

3

2

2









Przykład:





3

0

4

,

,

t

v 



s

t

Dla

1



  



3

0

4

1

,

,



s

v

s

m

v

5

25

3

0

4

2

2

2











wartość
prędkości

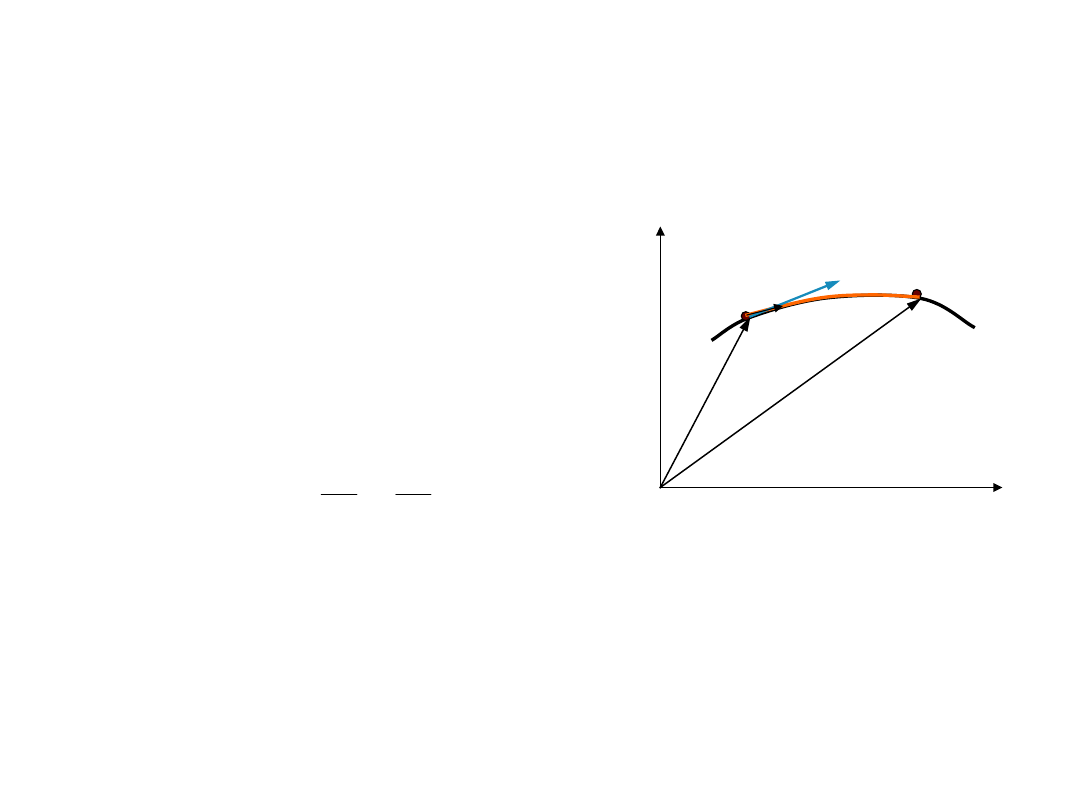
Prędkość

cząstka porusza się po krzywoliniowym

torze z punktu A do B w czasie t

przebywając drogę s

• wartość liczbowa prędkości

jest równa pochodnej drogi
względem czasu

25

dt

ds

t

s

v

t













lim

0

y

x

A

B

 

t

r







r

r

t

t

r

















r





s



v



tor

t

i

v

v







t

i



toru

do

styczny

wektor

i

t





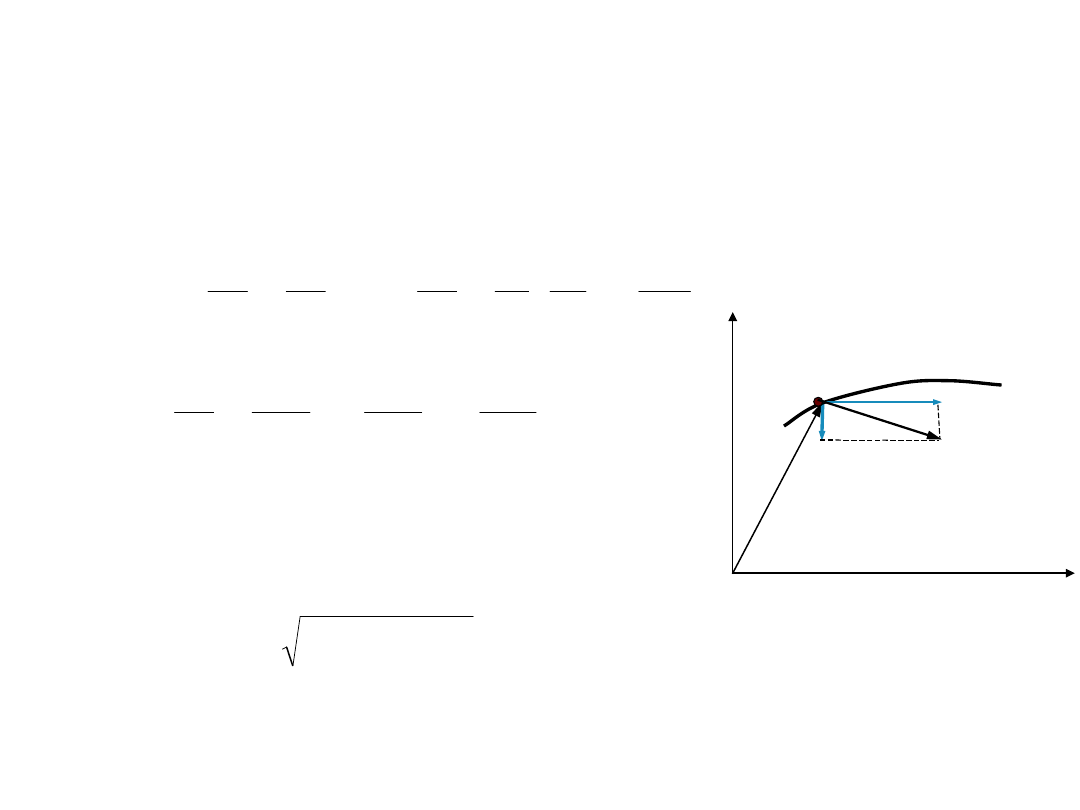
Przyspieszenie

26

dt

v

d

t

v

a

t



















lim

0

2

2

dt

r

d

dt

r

d

dt

d

dt

v

d

a



























y

x

 

t

r



a



x

a

tor

y

a

k

dt

dv

j

dt

dv

i

dt

dv

dt

v

d

a

z

y

x



















k

a

j

a

i

a

a

z

y

x















2

2

2

z

y

x

a

a

a

a











z

y

x

a

a

a

a

,

,





wartość
przyspieszenia





y

x

a

a

a

,









6

2

4

,

cos t

a











2

3

2 t

t

r

,

cos









t

t

v

6

2

2

,

sin







Przykład:

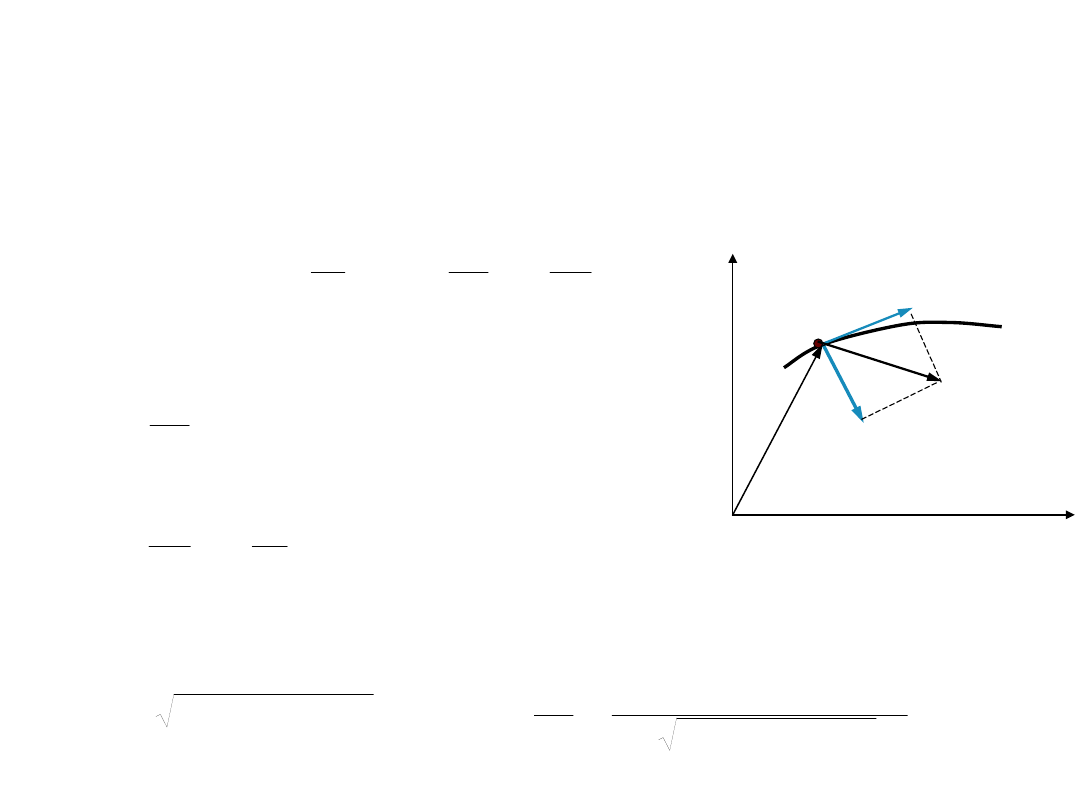
Przyspieszenie styczne i

normalne

27

t

i

v

v







 

v

dt

i

d

i

dt

dv

i

v

dt

d

a

t

t

t















n

t

a

a

a











dt

dv

a

t



R

v

v

dt

di

a

t

n

2





przyspieszenie styczne
szybkość zmiany wartości v

przyspieszenie normalne
szybkość zmiany kierunku ruchu
(R – promień krzywizny)

y

x

 

t

r



a



t

a



tor

n

a







2

3

2 t

t

r

,

cos









t

t

v

6

2

2

,

sin







Przykład:

2

2

36

2

2

t

t

v





sin

2

2

36

2

2

2

72

2

2

2

4

t

t

t

t

t

dt

dv

a

t











sin

cos

sin

Ruch jednostajny

po okręgu

28

Ruch po okręgu - przypadek ruchu

krzywoliniowego, gdy promień jest stały

r=const. i wartość prędkości nie zmienia się



 



j

v

i

v

j

v

i

v

v

y

x















cos

sin











r

x





cos

r

y





sin

j

r

x

v

i

r

y

v

v































 



j

v

r

v

i

v

r

v

j

dt

dx

r

v

i

dt

dy

r

v

dt

v

d

a

x

y





































 



























 





j

r

v

i

r

v

a











































sin

cos

2

2



 



r

v

r

v

a

a

a

y

x

2

2

2

2

2

2















sin

cos

Przyspieszenie

dośrodkowe

Ruch jednostajny

po okręgu

29

Ruch po okręgu – obliczmy
przyspieszenie styczne i normalne



 



j

v

i

v

j

v

i

v

v

y

x















cos

sin











v

v

v

v











2

2

2

2

cos

sin

0





dt

dv

a

t

r

v

v

dt

di

a

t

n

2













sin

,

cos r

r

r 













 











cos

,

sin

dt

d

r

dt

d

r

v

dt

r

d

v



 



d

r

ds 











 







cos

,

sin

dt

ds

dt

ds

v









cos

,

sin v

v

v







dt

d

r

v







r

v 

r

v

s





r

v













r

v

r

r

v

r

a

n

2

2

2

2

















 - prędkość kątową

Przyspieszenie liniowe:

tożsamość

Przyspieszenie normalne (dośrodkowe)

a

t

a

n

dt

d







 





dt

r

d

dt

r

d

dt

v

d

a







































r

r

r

r

v

dt

r

d



































2

0

















































r

s











r

v







W układzie biegunowym do opisu ruchu stosujemy:

 - położenie kątowe

Ruch jednostajny
po okręgu

30

r

d

ds







)

(

)

(

)

(

b

a

c

c

a

b

c

b

a































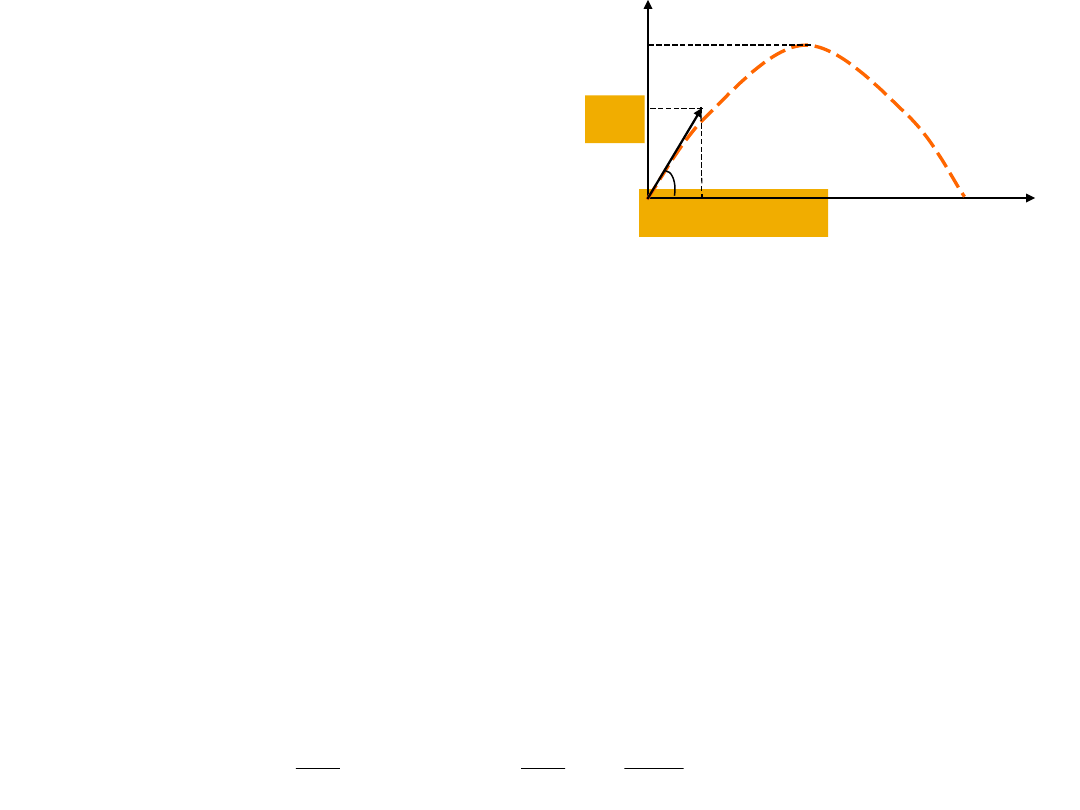
v

0x

Rzut ukośny

31

ruch w płaszczyźnie pionowej z prędkością początkową v

0

i z

przyspieszeniem ziemskim g

w rzucie ukośnym ruch cząstki w kierunku poziomym i kierunku
pionowym można traktować jako niezależne – żaden z nich nie
wpływa na drugi

ruch w poziomie: v

0x

= const. x = x

0

+ v

0x

t x

0

=0

ruch w pionie: a = -g y = y

0

+ v

0y

t –gt

2

/2 y

0

=0

wektor prędkości początkowej możemy przedstawić w postaci
sumy jego składowych w kierunku poziomym x i pionowym y

gdzie v

0x

=v

0

cos

0

v

0y

=v

0

sin

0

y

x

x

max

v

0y

y

max



0

j

v

i

v

v

y

x







0

0

0





x

v

x

t

0



2

0

2

0

0

2

x

x

y

v

x

g

v

x

v

y





jest to równanie toru

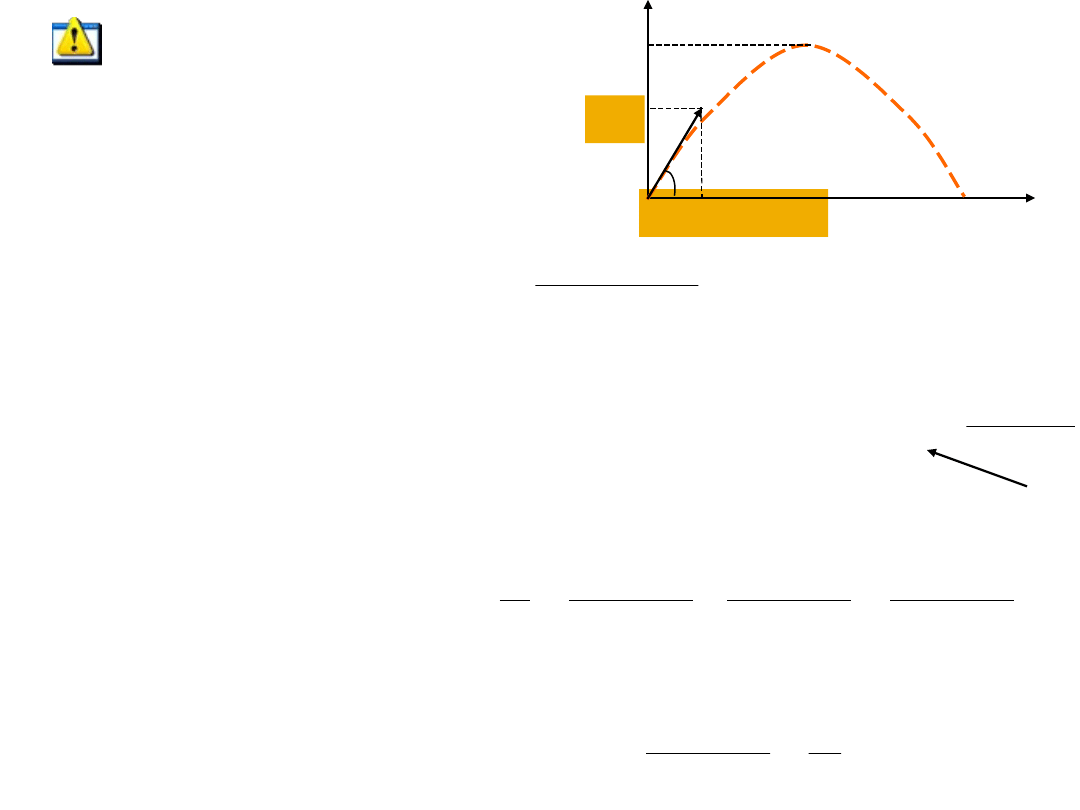
v

0x

Rzut ukośny

32

ruch w poziomie: v

x

= v

0x

=v

0

cos 

0

ruch w pionie: v

y

= v

0y

– gt = v

0

sin

0

– gt

równanie toru:

równanie paraboli









2

0

0

2

0

2





cos

v

gx

x

tg

y





zasięg rzutu:

 

0

2

0

0

0

0

0

2

2







sin

sin

cos

max

g

v

g

v

v

t

x

x

c







y

x

x

max

v

0y

y

max



0

maksymalna wysokość: y

max

gdy v

y

= 0 czyli 0 = v

0

sin

0

– gt

w

g

v

t

w

0

0



sin



 

g

v

g

v

g

v

t

g

t

v

t

y

y

w

w

w

2

2

2

0

2

2

0

0

2

2

0

0

2

2

0

2

0

0









sin

sin

sin

sin

max













ponieważ t

w

=t

s

to t

c

=2t

w

Rzut.exe

Rachunek całkowy

Rachunek całkowy

Całkowanie jest działaniem odwrotnym względem
różniczkowania. Polega na znalezieniu dla badanej funkcji
f(x) tzw. funkcji pierwotnej F(x) która w każdym punkcie
badanego przedziału spełnia równość F’(x) = f(x)

Funkcja pierwotna jest wyznaczana z dokładnością do
dowolnej stałej C, gdyż (F(x)+C)’=f(x)

Sumę F(x)+C nazywamy całką nieoznaczoną f(x) i
oznaczamy symbolem



dx

x

f

)

(



dx

......

symbol całkowania

funkcja zmienna
podcałkowa całkowania

Całka oznaczona

Jeżeli F(x) jest funkcją pierwotną funkcji f(x) to całką
oznaczoną funkcji f(x) w przedziale [a,b] nazywamy

)

(

)

(

)

(

)

(

a

F

b

F

x

F

dx

x

f

b

a

b

a









górna

dolna

granica
całkowania

Przykład:





5

7

1

4

2

1

2

1

2

2

4

1

2

4

1

,











x

dx

x

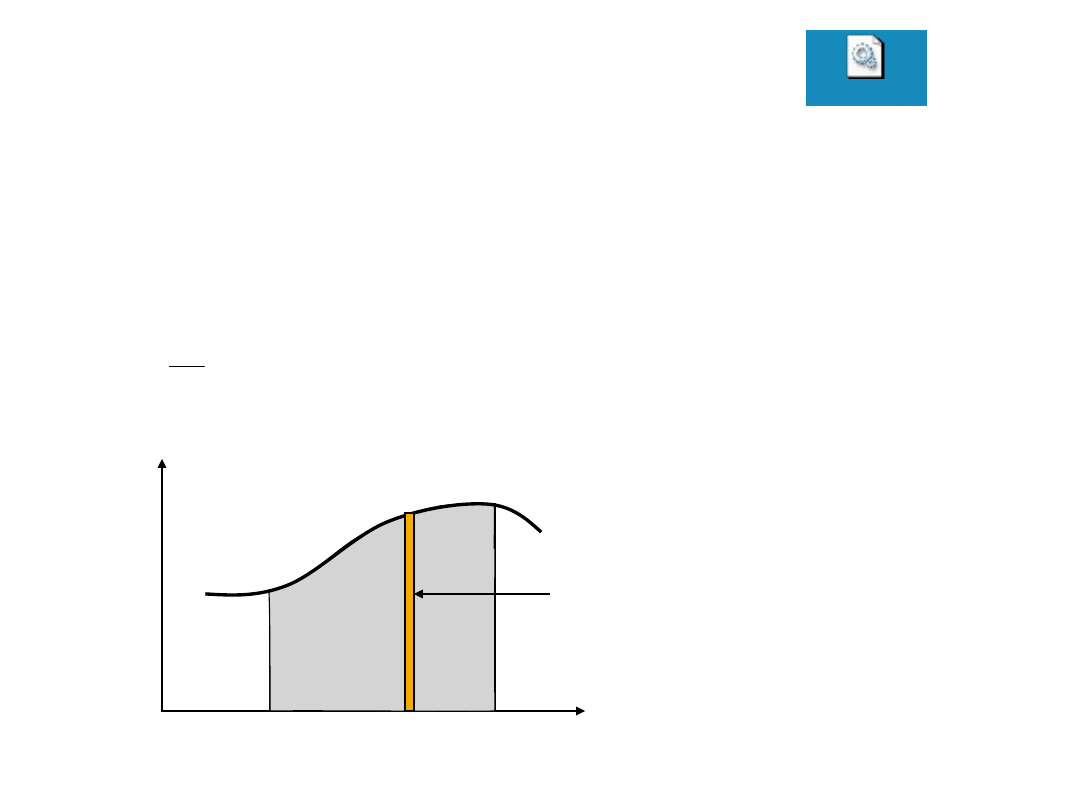
Całka jako suma

znajomość prędkości pozwala obliczyć drogę
przebytą przez punkt materialny

dt

ds

v 

dt

v

ds 





2

1

t

t

dt

v

s

v

t

t

1

t

2

s

v(t)

całka oznaczona

t

i

s

i













i

i

i

i

i

t

v

s

s

v

i

całka oznaczona
równa jest polu pod
krzywą

Integrals.swf

Podstawowe wzory









C

x

dx

x

cos

sin







C

x

dx

1







C

ax

dx

a











C

n

x

dx

x

n

n

1

1







C

x

dx

x

ln

1

...

,

,

718

2









e

C

e

dx

e

x

x



C

dx

0







C

x

dx

x

sin

cos

Przykłady:

2

3

3

2

3

1

3

1

x

C

x

bo

C

x

dx

x

l























,

C

y

C

y

dy

y

dy

y























1

1

1

1

2

2









C

t

dt

t

5

5

1

5

cos

sin

Równanie różniczkowe typu ma rozwiązanie
ogólne postaci

Równania różniczkowe

Równania różniczkowe

 

x

f

dx

dy



 

dx

x

f

y





 

dx

x

f

dy 

 







dx

x

f

dy

 





dx

x

f

y

Przykład:

t

e

y

2



'

t

e

dt

dy

2







dt

e

y

t

2

C

e

y

t





2

2

1