Dynamika

Dynamika - dział mechaniki



związek między wzajemnym

oddziaływaniem ciał

a zmianami ich ruchu.

Podstawy dynamiki



Zasady dynamiki



Siły



Praca, moc, energia

Podstawy dynamiki



opis ruchu za pomocą wektorów



podejście

geometryczne



przyczyny ruchu



dynamika



mechanika klasyczna

a

r







,

v

,



poznanie rodzaju i pochodzenia siły działającej na ciało



skutki działania siły



oddziaływania występujące w przyrodzie

.

Podstawy dynamiki –

wiadomości wstępne



p - pęd

– iloczyn jego masy i prędkości (wektor!)

v

m









p



m - masa punktu materialnego

– dodatnia wielkość

skalarna, miara bezwładności ciała


nie zależy od stanu ruchu tego ciała



wielkość addytywna



zasada zachowania masy,



F - siła

- miara oddziaływania na dane ciało ze

strony innych ciał (wektor!)

Zasady dynamiki

Podstawowa teoria, która pozwala nam przewidywać

ruch ciał



zasady dynamiki Newtona (1687 r)

Newton Isaac Sir (1643-1727), fizyk,

matematyk, filozof i astronom angielski.

Profesor fizyki i matematyki uniwersytetu

w Cambridge 1669-

1701, członek Royal

Society od 1672 i jego prezes od 1703,

członek paryskiej Akademii Nauk od 1699.

W

1705 otrzymał tytuł szlachecki.

S

iła wypadkowa jest sumą wektorową wszystkich sił

działających na ciało

wyp

F



I zasada dynamiki

Wnioski

Ciało, na które nie działa żadna siła (lub gdy siła
wypadkowa jest równa zeru) pozostaje w spoczynku
lub porusza się ze stałą prędkością po linii prostej.

(Zasada bezwładności)

0



wyp

F



0



a





Jeżeli to również przyspieszenie ciała

a to oznacza, że nie zmienia się ani wartość ani kierunek prędkości,

tzn. ciało jest w stanie spoczynku lub porusza się ze stałą co do

wartości prędkością po linii prostej.

I zasada dynamiki



Jeżeli na ciało nie działają siły zewnętrzne to istnieje taki układ

odniesienia, w którym to ciało spoczywa lub porusza się ruchem
jednostajnym prostoliniowym



układ inercjalny.



Nie ma rozróżnienia między ciałami spoczywającymi i

poruszającymi się ze stałą prędkością.



Nie ma też różnicy pomiędzy sytuacją, gdy nie

działa żadna siła i przypadkiem, gdy wypadkowa

wszystkich sił jest równa zeru.



Każdy ruch musi być opisany względem pewnego układu

odniesienia.



We wszystkich układach inercjalnych ruchami ciał

rządzą

dokładnie te sama prawa.

II zasada dynamiki

Szybkość zmiany pędu ciała równa jest wpadkowej

sile działającej na to ciało (siła działająca na ciało

jest równa pochodnej pędu względem czasu)

dt

p

d

F

wyp







a

m

t

d

d

m

t

d

m

d

t

d

p

d

F

const

m

wyp



























v

)

v

(

gdy

II zasada dynamiki



R

ównania ruchu

Wnioski

dt

p

d

F

wyp







m

F

a

wyp









Przyspieszenie ciała jest proporcjonalne do działającej

na ciało siły wypadkowej (współczynnik proporcjonalności

to odwrotność masy).



Im większa jest masa, tym mniejsze przyspieszenie

wywołane przez siłę.

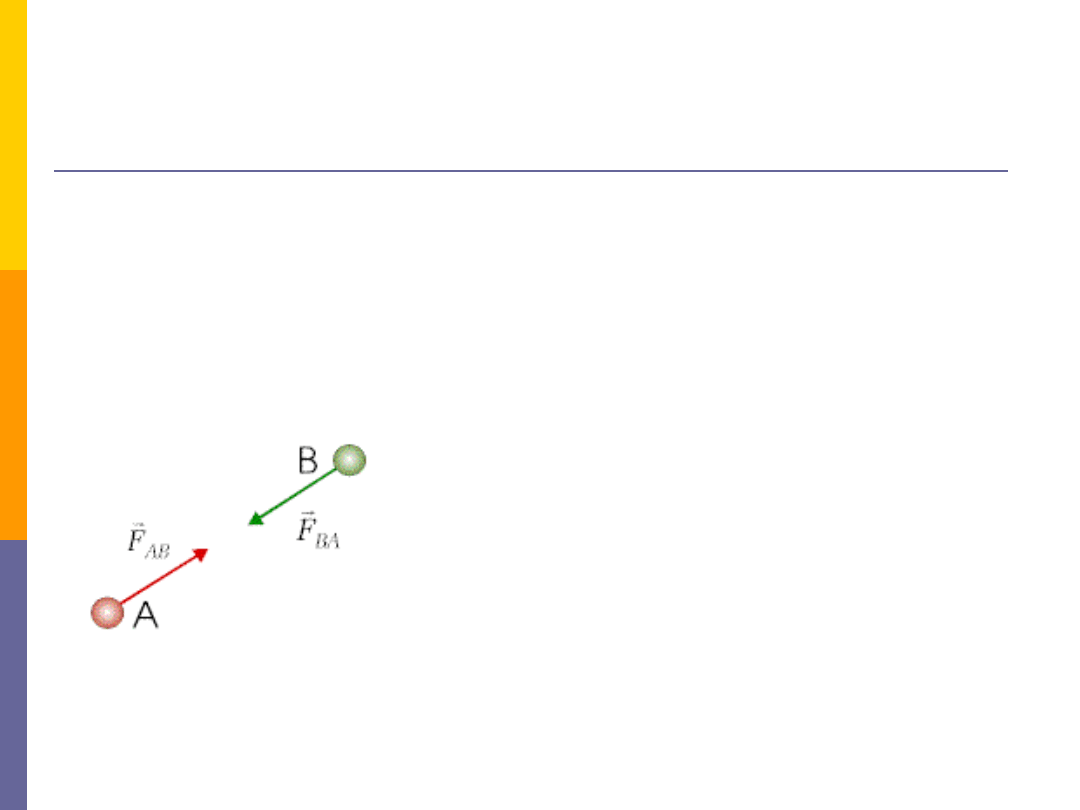
III zasada dynamiki

Gdy dwa ciała oddziałują wzajemnie, to siła

wywierana przez ciało drugie na ciało pierwsze jest

równa i przeciwnie skierowana do siły, jaką ciało

pierwsze działa na drugie.

A

B

B

A

F

F













III zasada dynamiki



Oddziaływania wzajemne dwóch ciał są zawsze

równe co do wartości, ale przeciwnie skierowane.

Wnioski



Każdej akcji towarzyszy zawsze równa co do wartości, lecz

przeciwnie skierowana reakcja.



Siły zawsze występują parami, ale są przyłożone do

różnych ciał.



Gdyby były przyłożone do jednego ciała, to znosiłyby się

i w naszym świecie nie byłoby ruchów zmiennych.

Siła ciężkości

Siła ciężkości (grawitacji)

-

siła, z jaką dane ciało jest

przyciągane przez inne ciało.

g

F





Ciężar ciała W

-

wartość bezwzględna siły potrzebnej do

zapobieżenia spadkowi ciała, mierzonej przez obserwatora na Ziemi.

Ciężar

W

jest równy wartości bezwzględnej siły ciężkości

F

g

działającej na

to ciało

W = mg

Ważenie ciała - wyznaczenie jego ciężaru

mg

F

g



W przypadku

Ziemi

, przy założeniach:

- Ziemia -

układ inercjalny

- brak oporu powietrza

gdzie

g

-

przyspieszenie ziemskie

g = 9,80665 m/s

2

Jednostka siły

w układzie SI

1 niuton (N)

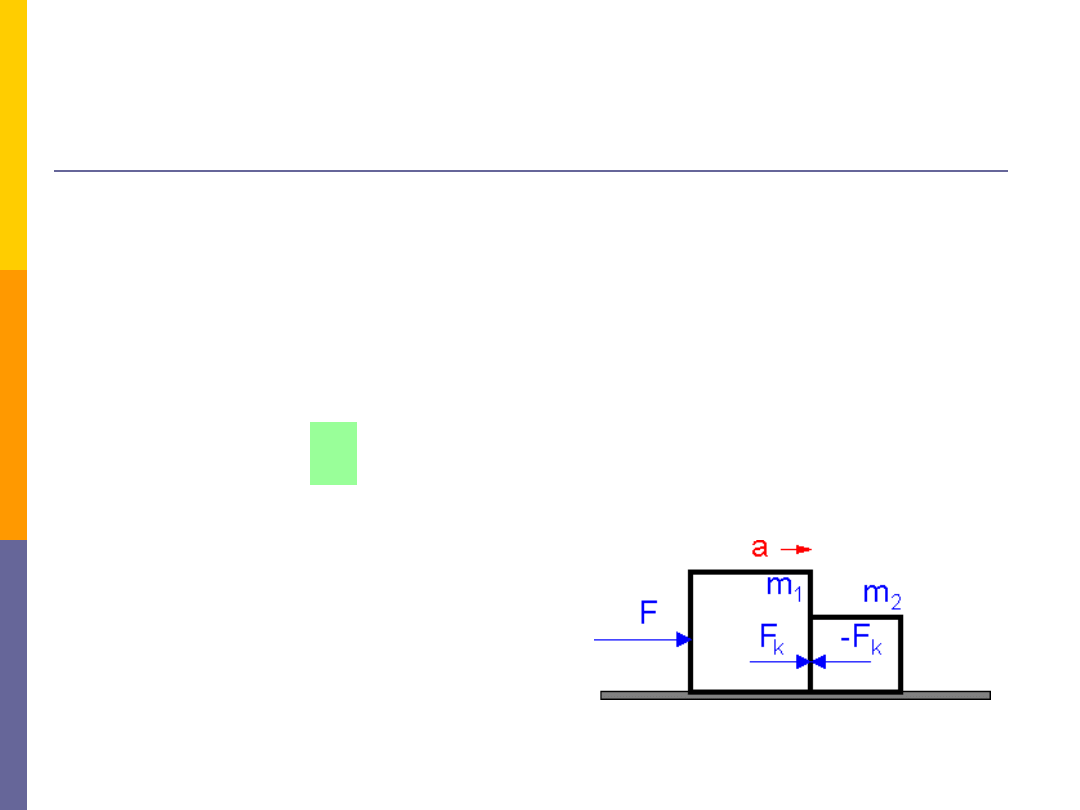
F





Si

ła

przy

ło

ż

ona jest tylko do ciała

m

1

,

ale nadaje przyspieszenie obu klockom.



Siła kontaktowa

, z jaką klocek o masie

m

1

działa na klocek o masie

m

2

,

nadaje

przyspieszenie klockowi

m

2

.

k

F



Siły kontaktowe



Występują przy dociskaniu do siebie dwóch ciał.



Źródłem tych sił jest odpychanie pomiędzy atomami.

a

m

F

k









2



Warto

ść siły kontaktowej

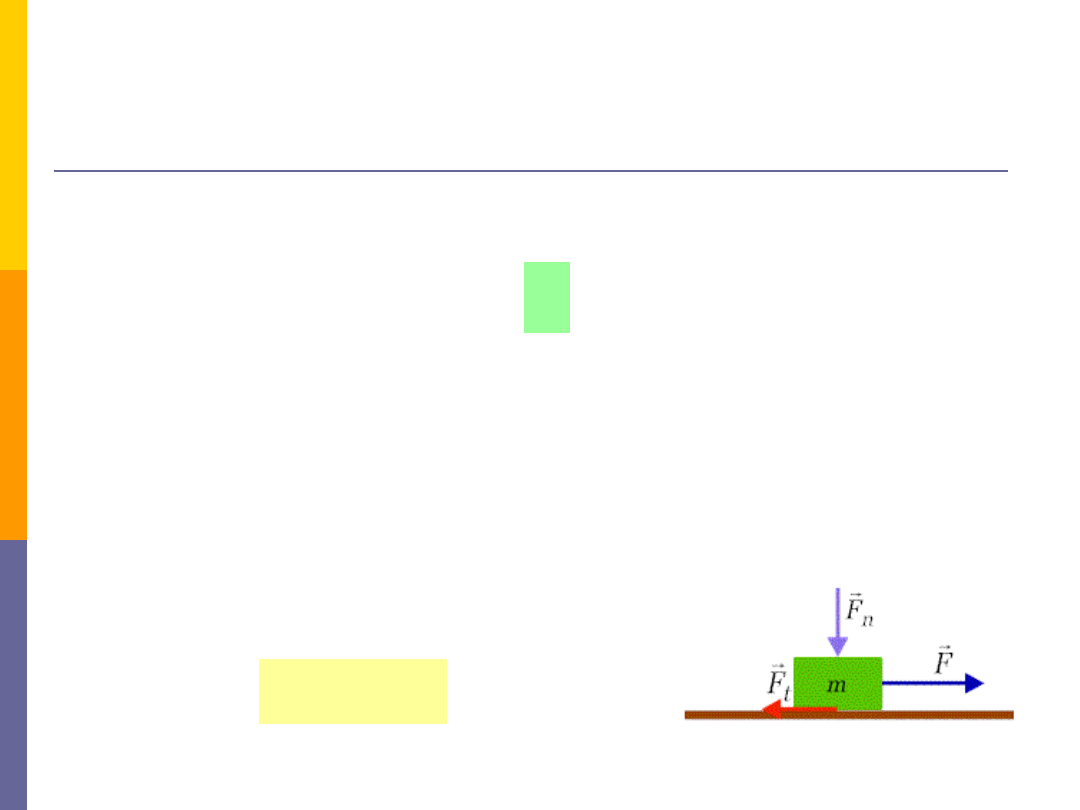
Siły tarcia



t

F

n

F



si

ła

jest proporcjonalna do si

ły nacisku

oraz współczynnika tarcia poślizgu



współczynnik tarcia statycznego lub dynamicznego

(w przypadku ruchu) zależy od rodzaju powierzchni trących

t

F





ciała poruszające się napotykają na opór ze strony

ośrodka, w którym się poruszają,



jedną z sił oporu jest siła tarcia

n

t

F

F









warto

ść siły tarcia jest równa

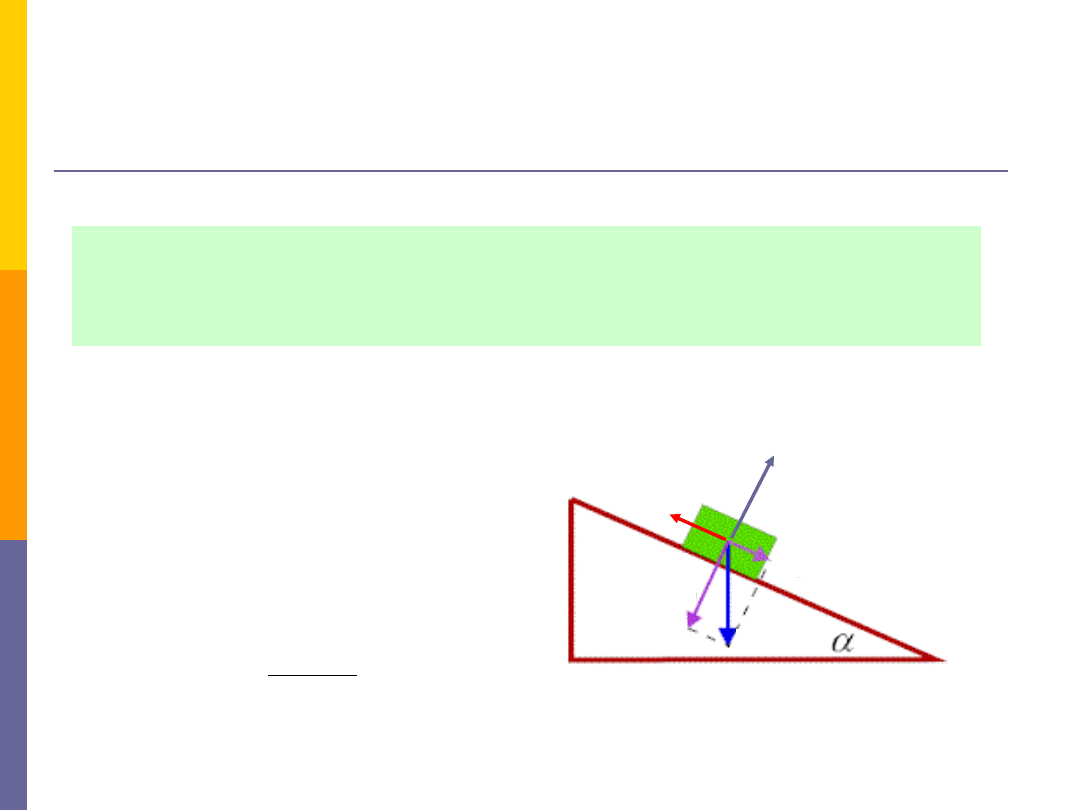
Siły tarcia -

przykład

Napisz równanie ruchu dla ciała o masie

m

zsuwającego się z

równi pochyłej o kącie nachylenia



. Współczynnik tarcia między

ciała a równia wynosi



.

Q

n

Q



s

Q



s

n

Q

Q

Q











R

F

Q

F

T

wyp















m

F

a

wyp







T

F



R



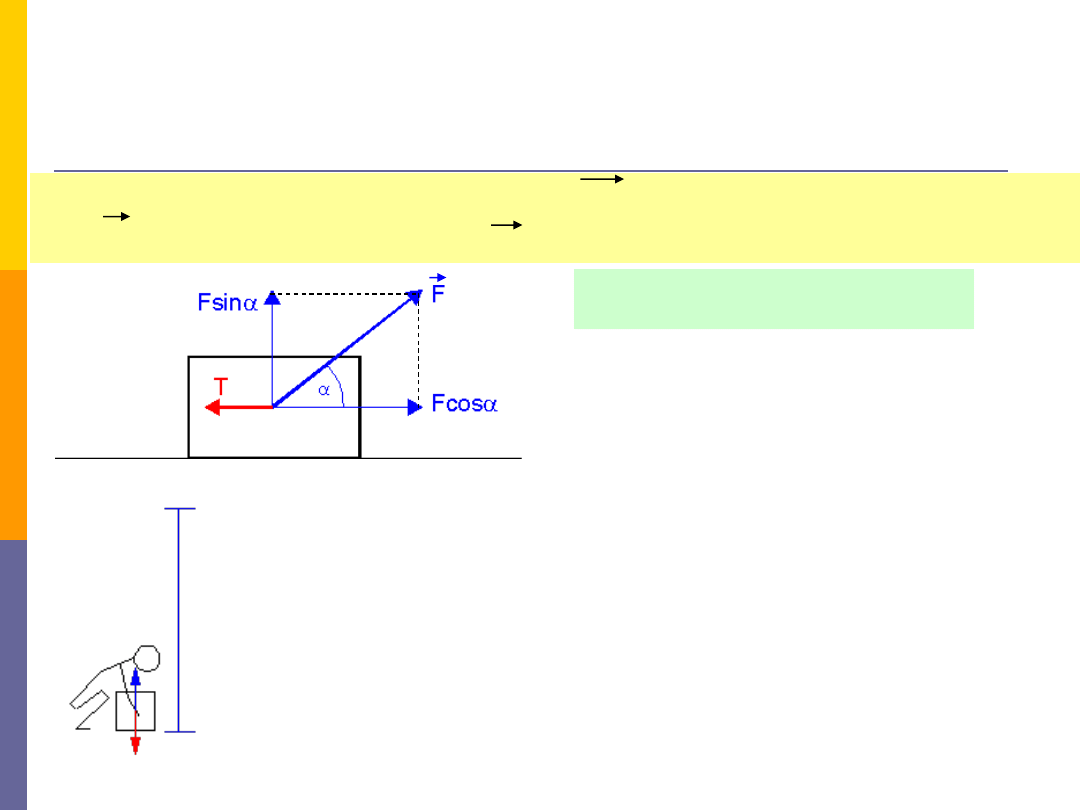
Praca, moc, energia –

praca



cos









s

F

s

F

W









W > 0 gdy

α < 90°,



W < 0 gdy

α > 90°,



W = 0 gdy

α = 90°.

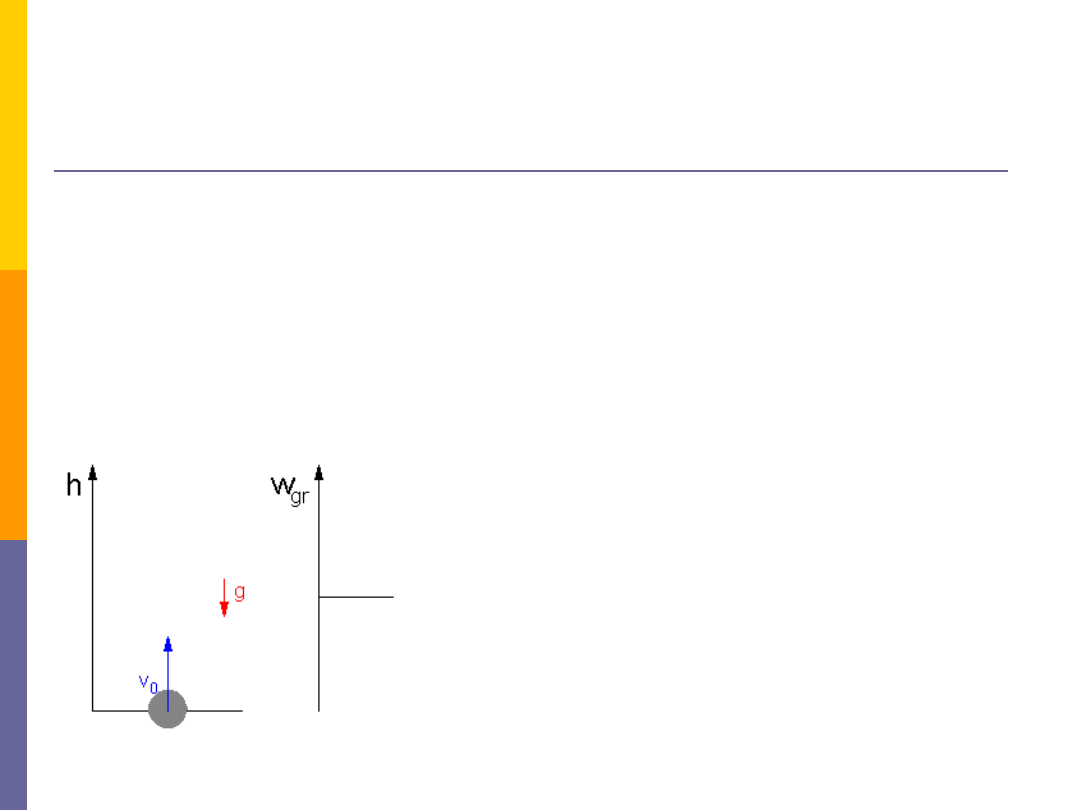
W trakcie podnoszenia ciała na wysokość

h

,

człowiek działa

siłą

F

równą ciężarowi ciała ale przeciwnie skierowaną, więc

wykonuje "dodatnią" pracę

W = mgh

• Praca wykonana przez człowieka jest równa co do
wartości "ujemnej" pracy wykonanej przez sił

ę

ciężkości.

h

F



Q



Praca W

wykonana przez stałą siłę F jest iloczynem skalarnym tej

siły

F

i wektora przesunięcia

s

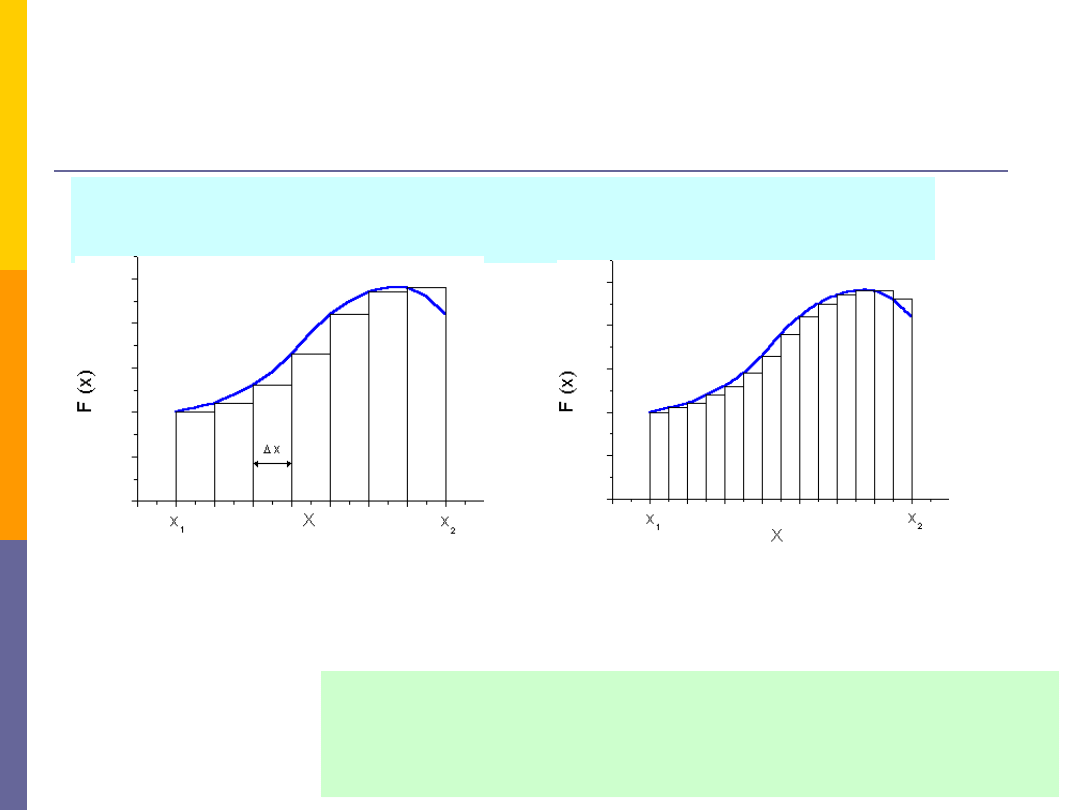
Praca, moc, energia –

praca

x

F

W

n

i

i











1

Praca wykonana przez siłę zmienną -

ruch prostoliniowy

x

F

W

i

i



























2

1

)

(

lim

1

0

x

x

n

i

i

x

dx

x

F

x

F

W

Jednostką pracy w układzie SI - dżul (J);
1J = 1N·m.
W fizyce atomowej powszechnie używa się jednostki
elektronowolt

(eV); 1eV = 1.6·10

-19

J.

Praca, moc, energia –

praca

–

przykład













x

x

x

kx

kx

x

kx

x

F

W

0

0

2

0

2

2

2

d

)

(

d

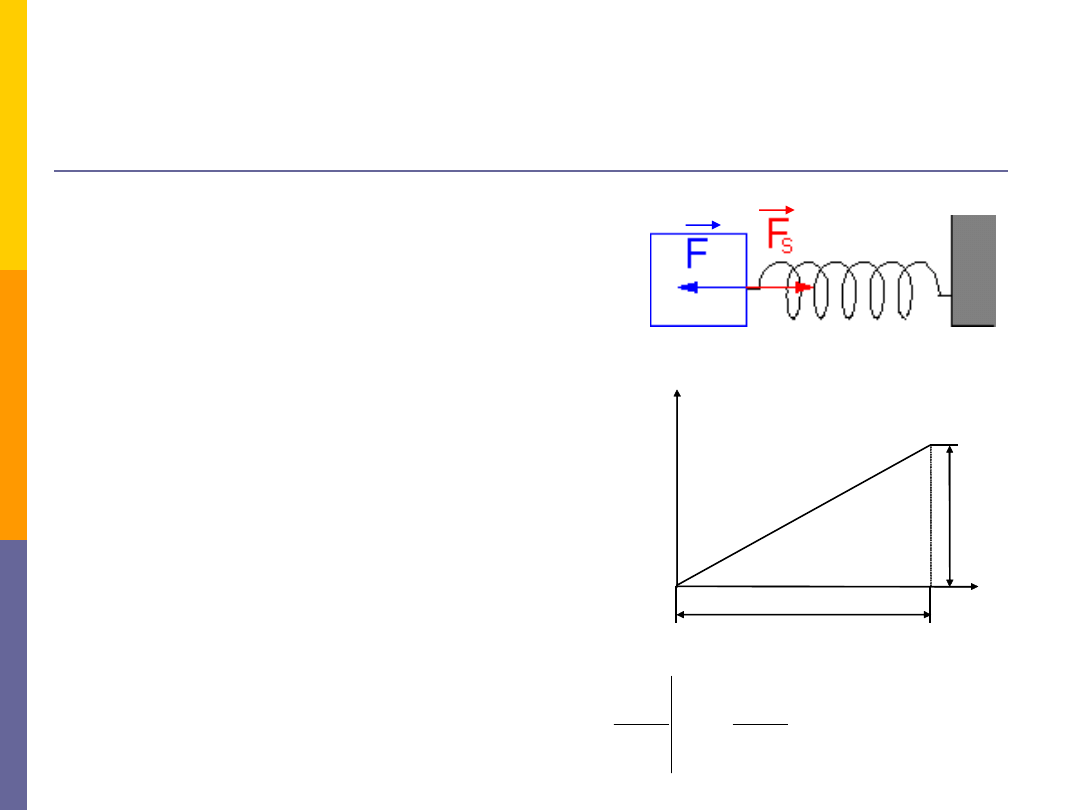
Siła wywierana przez sprężynę jest siłą
przywracającą równowagę:

F = -k x

Aby rozciągnąć sprężynę, musimy przyłożyć
siłę równą co do artości, lecz przeciwnie
skierowaną:
F = k x.

F(x)

x

F=kx

kx

x

Praca:

Sprężyna zamocowana jednym końcem i
rozciąganą siłą F tak, że jej koniec
przemieszcza się o x.

Praca, moc, energia –

moc

Moc

P

definiujemy jako ilość wykonanej pracy

do czasu

w jakim została ona wykonana.

Jeżeli praca W została wykonana w czasie



t

to

średnia moc

jest dana wzorem:

t

W

P







v











F

dt

s

d

F

dt

dW

P









Dla stałej siły F wzór ten przyjmuje postać:

dt

dW

t

W

P

t













lim

0

Dla przedziału czasu



t



O

mówimy o

mocy chwilowej:

Jednostką mocy w układzie SI - wat
(W)
1W = 1J/1s.

Praca, moc, energia –

energia



Energia kinetyczna



określona przez masę i prędkość ciała



Energia potencjalna



określona przez masy ciał i ich wzajemne położenie

2

v

2





m

E

k

Energią kinetyczna

- i

loczyn masy ciała i kwadratu prędkości podzielony

przez 2

Zależność między pracą i energią kinetyczną

Praca wykonana przez wypadkową siłę F działającą na punkt
materialny jest równa zmianie energii kinetycznej tego punktu.

W = E

k

– E

k0

Praca, moc, energia –

energia

Energia potencjalna

jest energią, którą dane

ciało, podlegające działaniu pewnej siły,
ma dzięki swemu położeniu w przestrzeni.

Pole jednorodne

-

działa na ciało siłą o stałej wartości, kierunku i zwrocie

niezależnie od położenia ciała.

Energia potencjalna w jednorodnym polu grawitacyjnym

Energią potencjalną ciała w punkcie P względem punktu
O nazywamy pracę, jaką wykonuje siła zachowawcza
przy przesunięciu tego ciała od punktu P do punktu O.

0

E

h

g

m

E

p









Grawitacyjną energię potencjalną
(przy powierzchni Ziemi) określamy
jako pracę siły ciężkości

mg

na pionowym

torze o wysokości

h

:

O

1

2

P

Praca, moc, energia –

energia

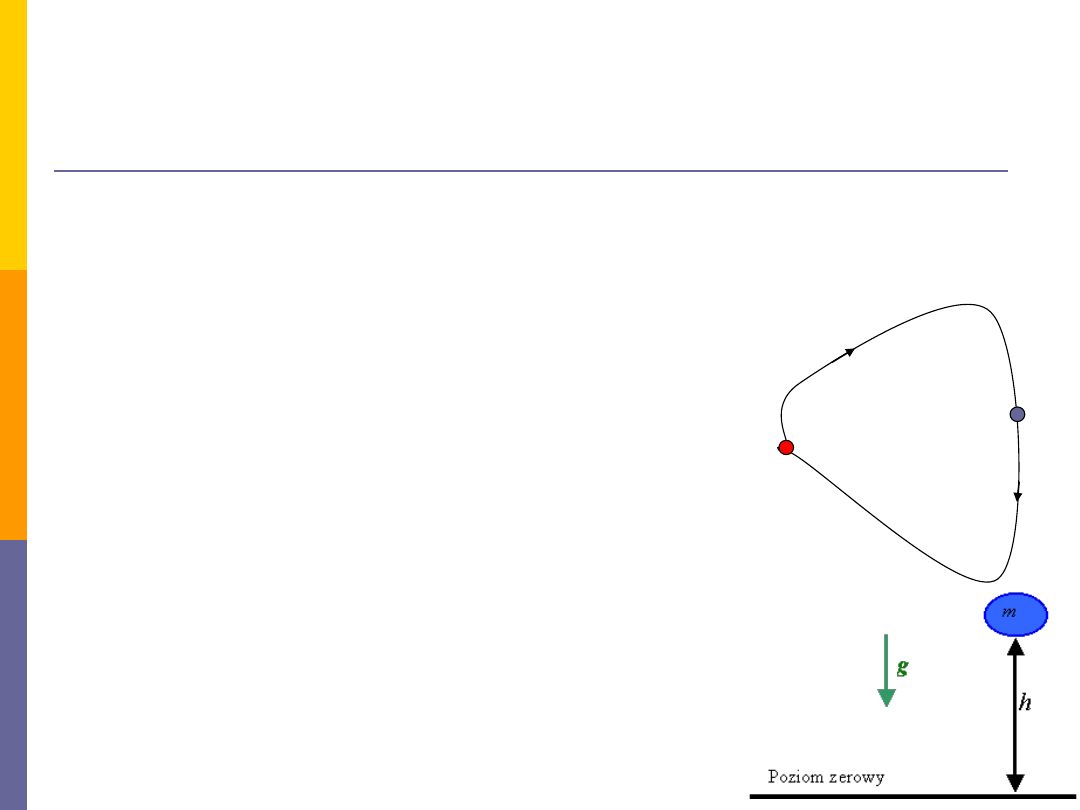
Siłę jest zachowawcza, jeżeli praca wykonana przez nią nad punktem
materialnym poruszającym się między dwoma punktami zależy tylko od tych
punktów, a nie od łączącej je drogi.

Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punktem
materialnym, który porusza się po dowolnej drodze zamkniętej jest równa
zeru.

Energia potencjalna jest wielkością
niekierowaną, czyli skalarem. Może
przybierać wartości ujemne.

Praca siły ciężkości

mg

na drodze

zamkniętej jest równa zeru.

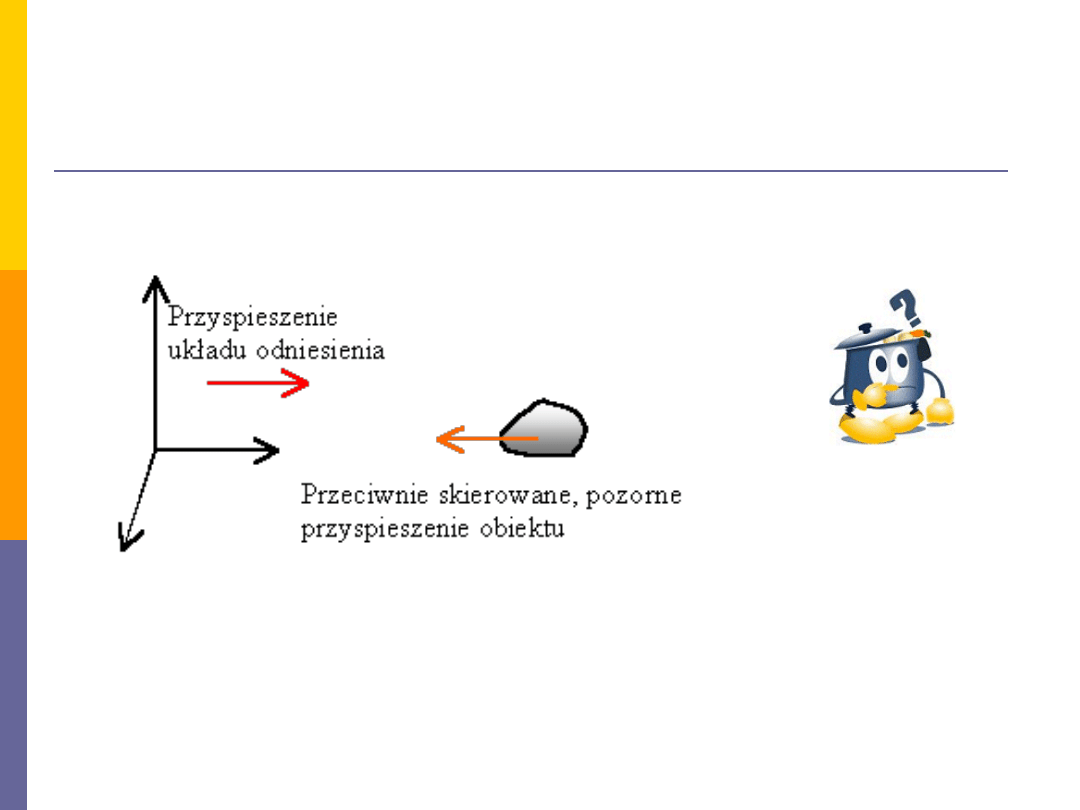
Siły bezwładności

Jeżeli układ odniesienia porusza się ruchem przyspieszonym względem
otoczenia (

układ nieinercjalny), to dla obserwatora w tym układzie ciała też

poruszają się ruchem przyspieszonym, lecz w przeciwnym kierunku. Wygląda to
tak samo jakby działała na nie jakaś siła



siła bezwładności

Czy wszystkie zagadnienia możemy rozwiązać

w inercjalnych układach odniesienia?

Siły bezwładności -

przykłady

Siła bezwładności podczas ruszania pojazdu - gdy samochód
rusza do przodu siła bezwładności wciska pasażerów w fotel,

Siła bezwładności podczas hamowania pojazdu - gdy samochód
(lub inny pojazd) nagle hamuje, wtedy siła bezwładności rzuca
pasażerem do przodu,






Siła odśrodkowa - gdy siedzimy na wirującej karuzeli siła
bezwładności (nazywana w tym przypadku "siłą odśrodkową")
wypycha nas i przedmioty przez nas trzymane na zewnątrz okręgu,
faktycznie działającą siłą na ciało jest „siła dośrodkowa”.

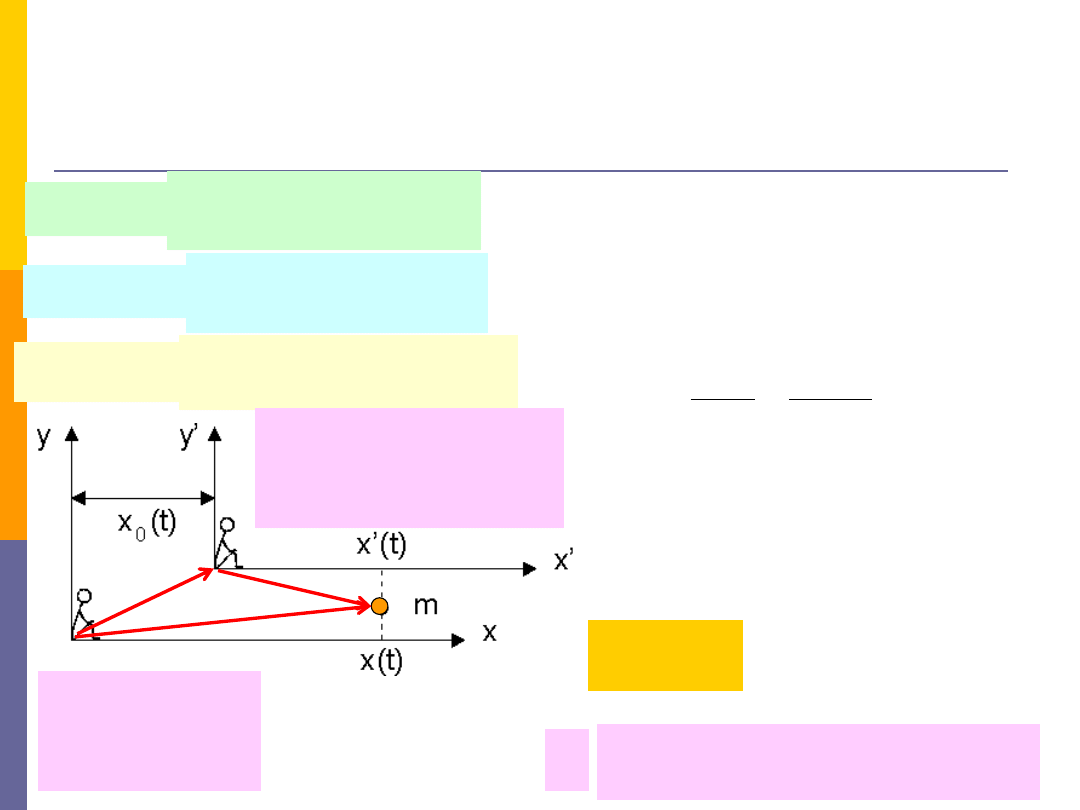
Siły bezwładności

w ruchu prostoliniowym

nieinercjalnego układu odniesienia

)

(

)

(

)

(

0

t

x

t

x

t

x







Związek między położeniem punktu

m

w obu układach odniesienia:

2

2

)

(

v(t)

dt

t

x

d

dt

d

a





Ponieważ przyspieszenie:

stąd:

0

a

a

a







siła bezwładności

.

0

a

m

F

B











a zatem:

i ostatecznie:

B

F

F

a

m

ma

ma

a

m













0

0

`

0

)

(t

x

r





położenie punktu

m

w układzie XOY

)

(t

x

r









położenie punktu

m

w układzie X`O`Y`

)

(

0

0

t

x

r





położenie punktu O

`

w układzie XOY

0

a



przyspieszenie unoszenia

ciała

m

w układzie X`O`Y`

Układ XOY –
„nieruchomy”

inercjalny

Układ X`O`Y` -
ruchomy wzgl.XOY

nieinercjalny

0

r



r



r





)

(

)

(

)

(

0

t

r

t

r

t

r













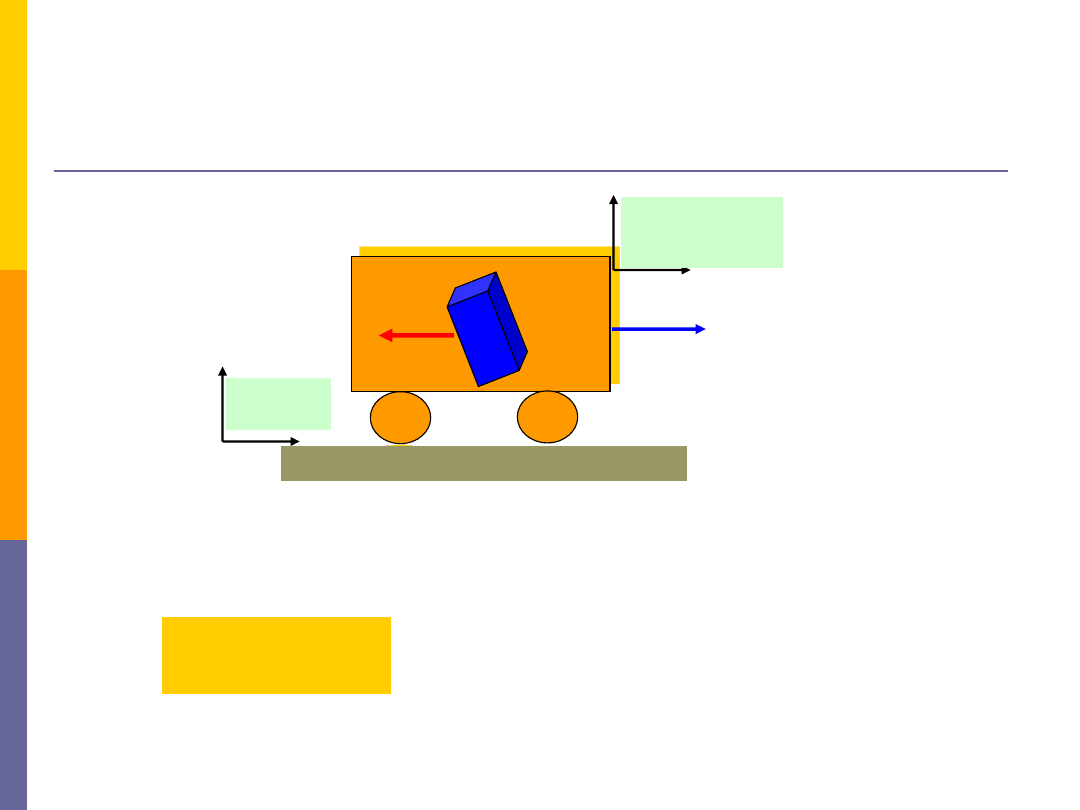
Siły bezwładności

- przykład

0

a

m

F

B











niezrównoważona siła bezwładności
działająca na klocek w układzie X`O`Y`

0

a



B

F



m

0



a



Y

X

Układ
inercjalny

0

0

a

a

a

















Gdy:

0

a

a











Y`

X`

Układ
nieinercjalny

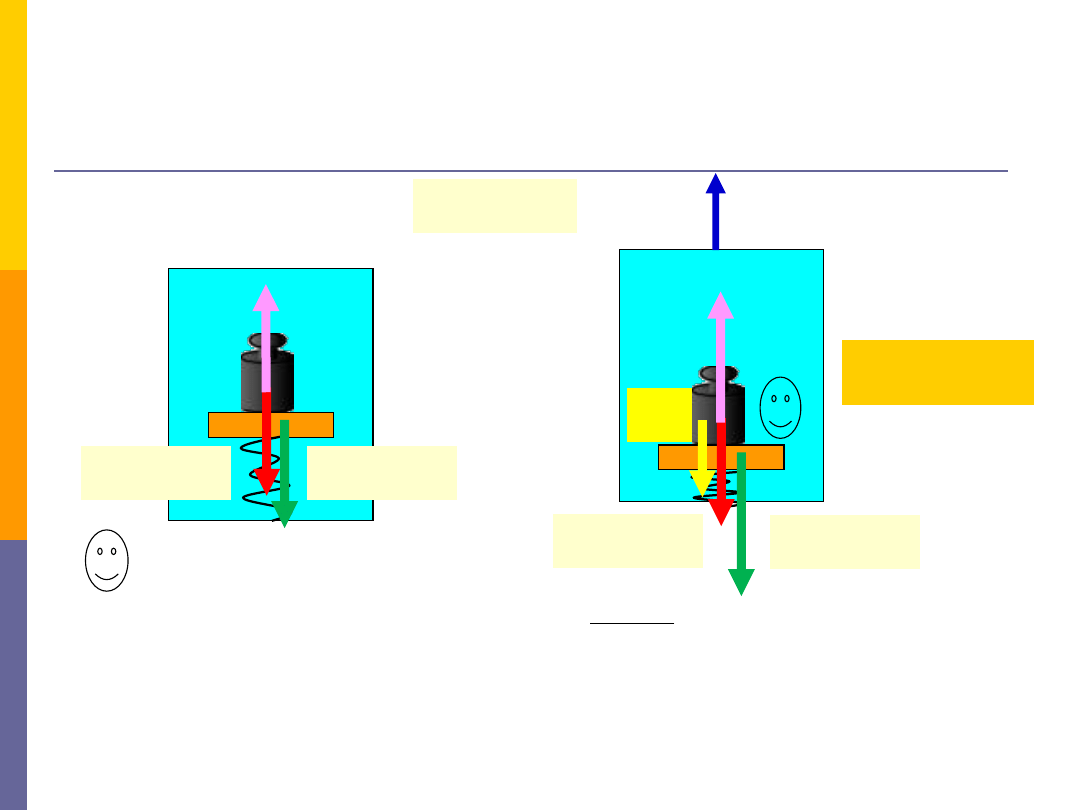
Siły bezwładności

- przykłady

Q=mg

R`=mg

R=mg

W układzie inercjalnym Ziemi:

m

Q

R

a





`

0

WINDA

0



o

a



wskazanie wagi:

mg

ma

R

R







0

`

W układzie nieinercjalnym windy:

0

`







Q

F

R

B







0

`

0









mg

ma

R

wskazanie wagi:

mg

ma

R

R







0

`

o

a



Q=mg

R > mg

F

B

0

a

m

F

B











R` > mg

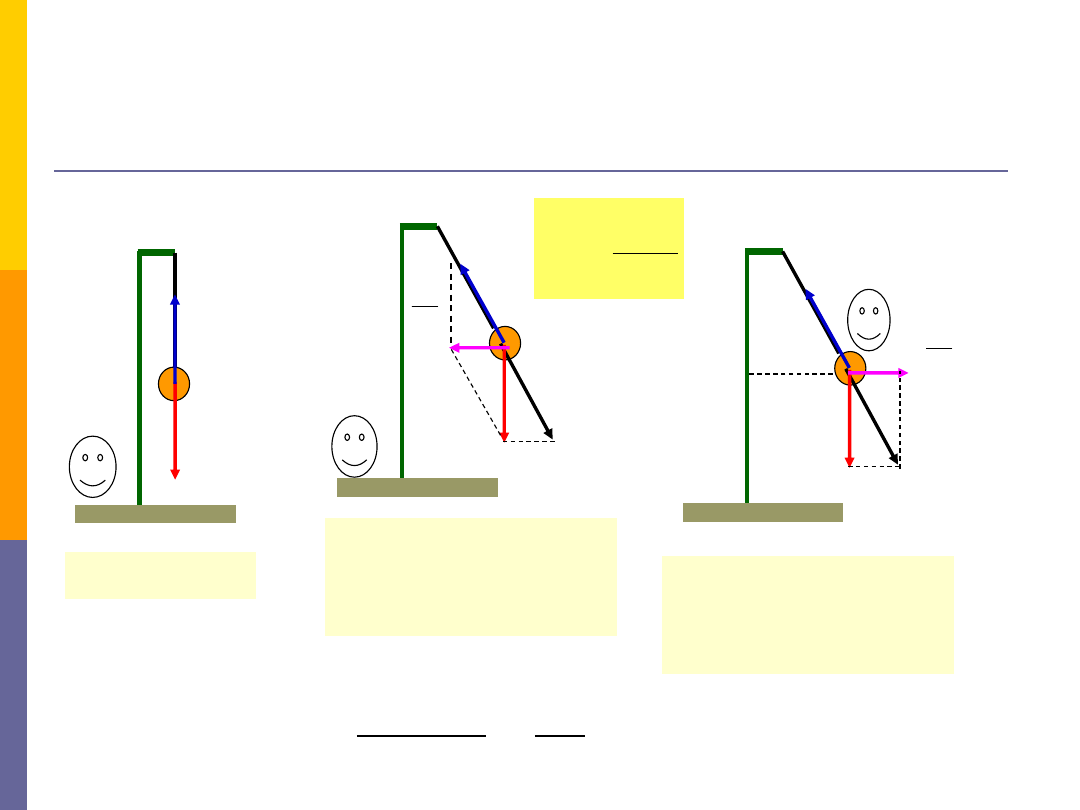
Q



N



Równowaga

0





N

Q





Siły bezwładności w ruchu obrotowym

Siła bezwładności odśrodkowa

– przykład

0







o

F

N

Q







Układ nieinercjalny
-

siła bezwładności

odśrodkowa F

O

Q



N



o

F



r

r

v

2

m

F

o



m

F

m

N

Q

a

d















Układ inercjalny -
siła przyłożona

dośrodkowa F

d

Q



N



d

F



Przy ruchu w kierunkach na północ lub
południe, kierunek odchylenia zależeć będzie
od półkuli:
-

na półkuli północnej F

C

działa „w prawo”

względem kierunku prędkości
-

na półkuli południowej – odwrotnie



Silniejsza erozja prawych brzegów rzek na

półkuli północnej i lewych na półkuli
południowej.

)

v

(

2





















m

F

C

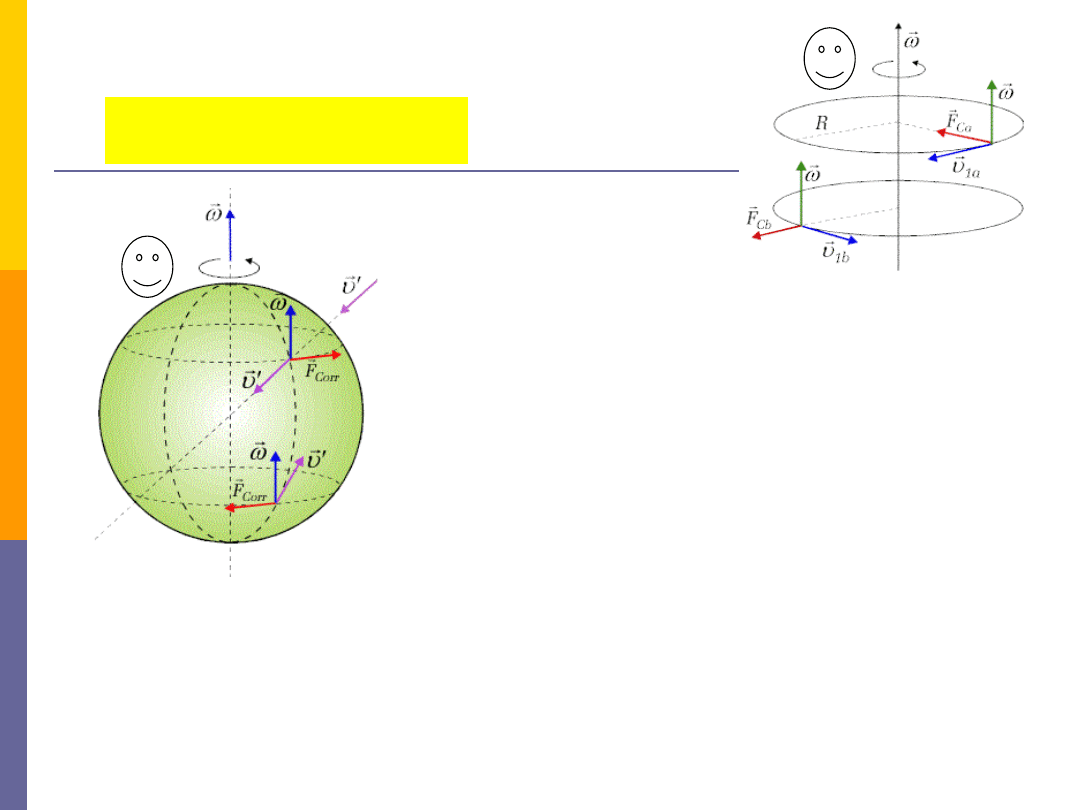
Siła bezwładności Coriolisa

Ciało spadające swobodnie (z wysokiej
wieży) z prędkością v

`

, pod wpływem

działania siły Coriolisa doznaje
odchylenia w kierunku wschodnim.

Kiedy poruszamy się wzdłuż równika
w kierunku wschodnim lub zachodnim
doznajemy siły działającej odpowiednio
„w górę” lub „w dół”.

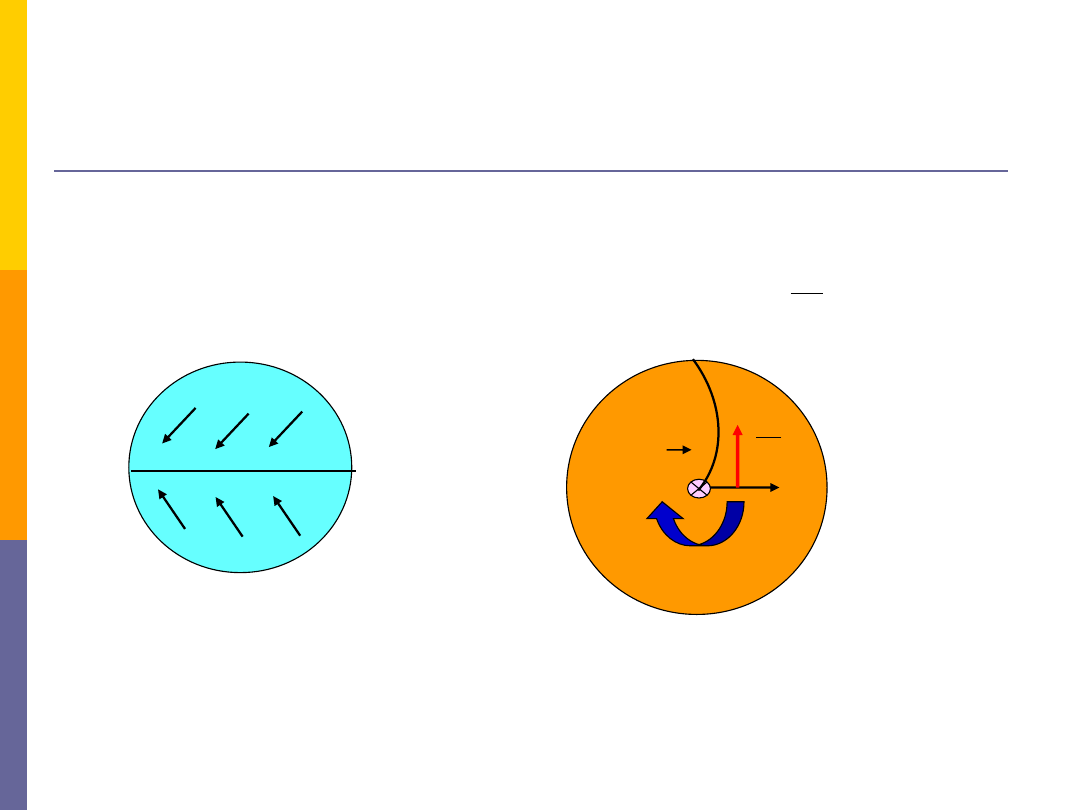
Wpływ na ruch mas powietrza - wiatr

passaty

równik

pn.-

wschód

pd.-

wschód

v



C

F



v







C

F

Siła bezwładności Coriolisa

Siła bezwładności Coriolisa
- wahadło Foucaulta

Zmiana płaszczyzny ruchu wahadła
względem Ziemi dowodzi jej obrotu
wokół własnej osi.

Jean Bernard Léon Foucault -
demonstracja wahadła w lutym
1851 roku w Paryskim
Obserwatorium Astronomicznym.

Siła bezwładności Coriolisa
- wahadło Foucaulta

Dziedziniec Politechniki Gdańskiej

Szybkość obrotu płaszczyzny wahań zależy od szerokości geograficznej φ
i wynosi 15

°·sin(φ) na godzinę.

C

F

F

F

a

m



















0

Druga zasada dynamiki w układach nieinercjalnych

Jeżeli w układzie nieinercjalnym ciało spoczywa to:

0





B

F

F





zasada d`Alamberta

C

B

F

F

F











0

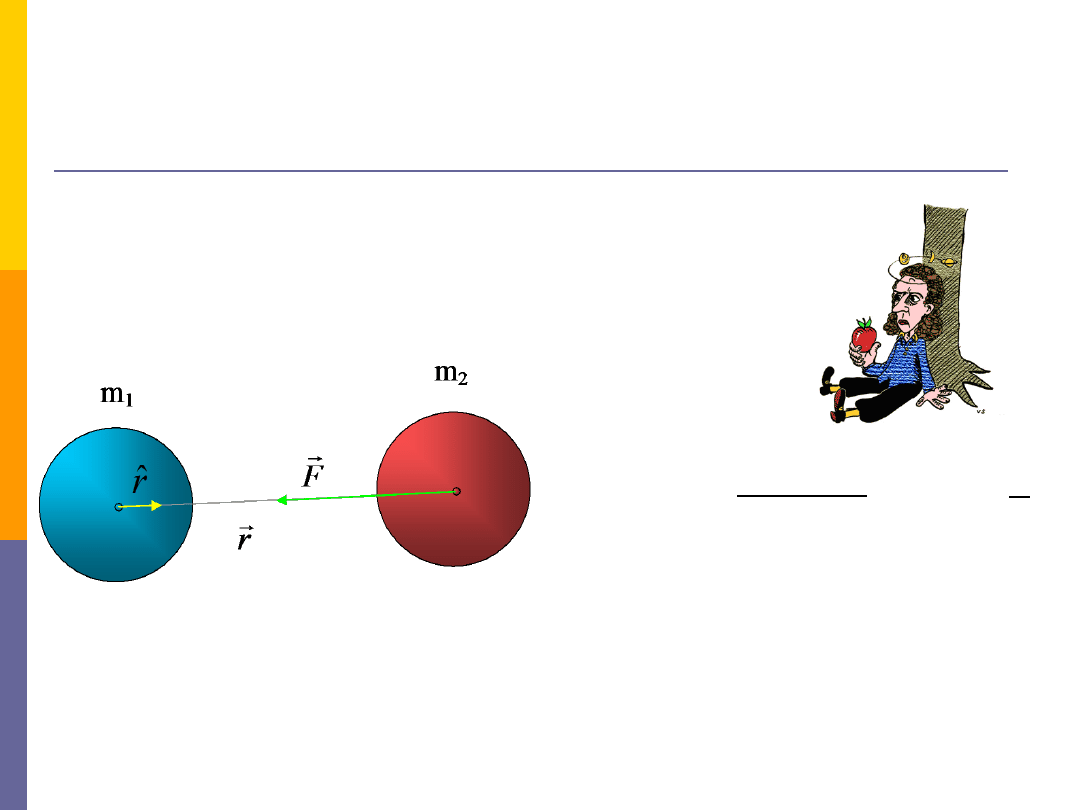
Grawitacja –

prawo powszechnego ciążenia

r

r

m

m

G

F

ˆ

2

2

1













Każde dwa ciała o masach m

1

i m

2

przyciągają się

wzajemnie siłą grawitacji wprost proporcjonalną
do iloczynu mas, a odwrotnie proporcjonalną do
kwadratu odległości między nimi.

Wartość współczynnika proporcjonalności G, nazywanego stałą
grawitacji wynosi 6.67·10

-11

Nm

2

/kg

2

i jest równa liczbowo sile, z jaką

oddziaływają na siebie dwa kilogramowe ciała z odległości jednego
metra.

r

r

r





ˆ

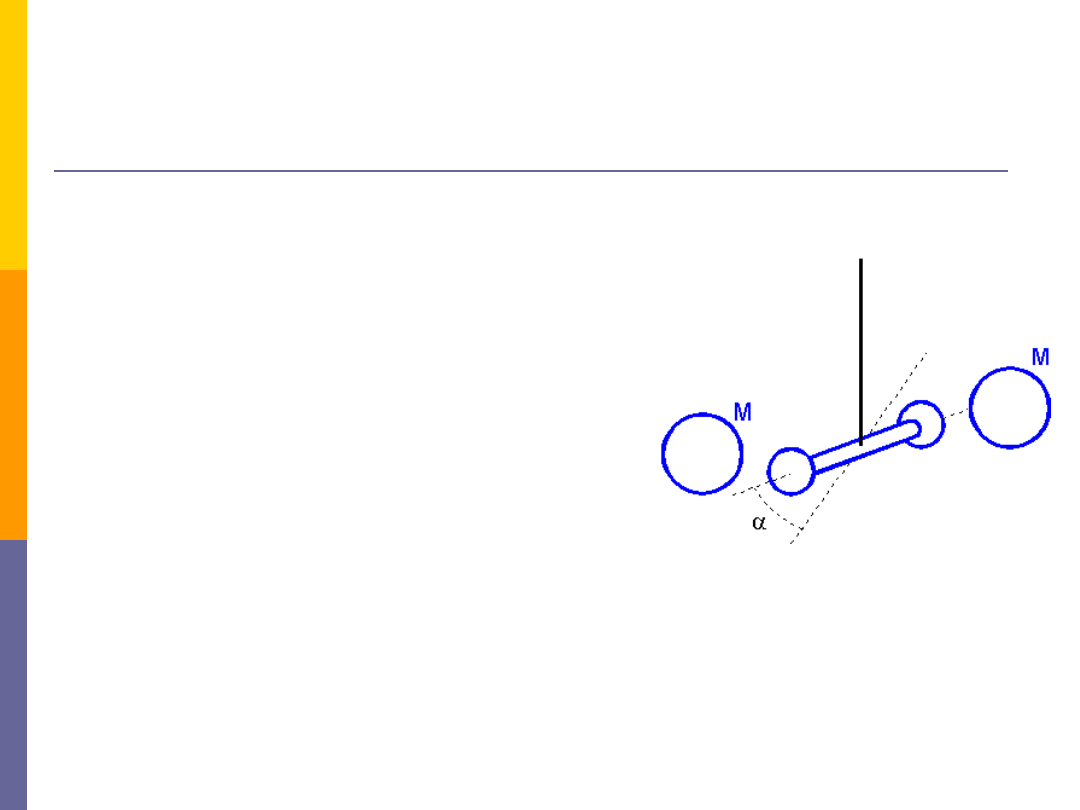
Grawitacja –

stała grawitacji

Doświadczenie Cavendisha (1798 r.)

W swoim pomiarze Cavendish wykorzystał fakt,
że siła potrzebna do skręcenia długiego,
cienkiego włókna kwarcowego jest bardzo mała.
Na takim włóknie zawiesił pręt z dwiema małymi
kulkami ołowianymi (m) na końcach. Następnie
w pobliżu każdej z kulek umieścił większą kulę
ołowianą (M) i zmierzył precyzyjnie kąt α o jaki
obrócił się pręt.













r

F

M

F

Grawitacja –

ciężar ciała

Siła ciężkości Q



Ciężar ciała

g = 9,80665 m/s

2



siła ciężkości (ciężar)



wyrażana w niutonach (N)



masa



wyrażana w kilogramach (kg)



masa bezwładna



popychamy ciało po płaskiej powierzchni,



masa grawitacyjna



utrzymujemy klocek uniesiony w górę

w stanie spoczynku,



masa bezwładna jest równa masie grawitacyjnej 

zasada

równoważności.

g

m

Q









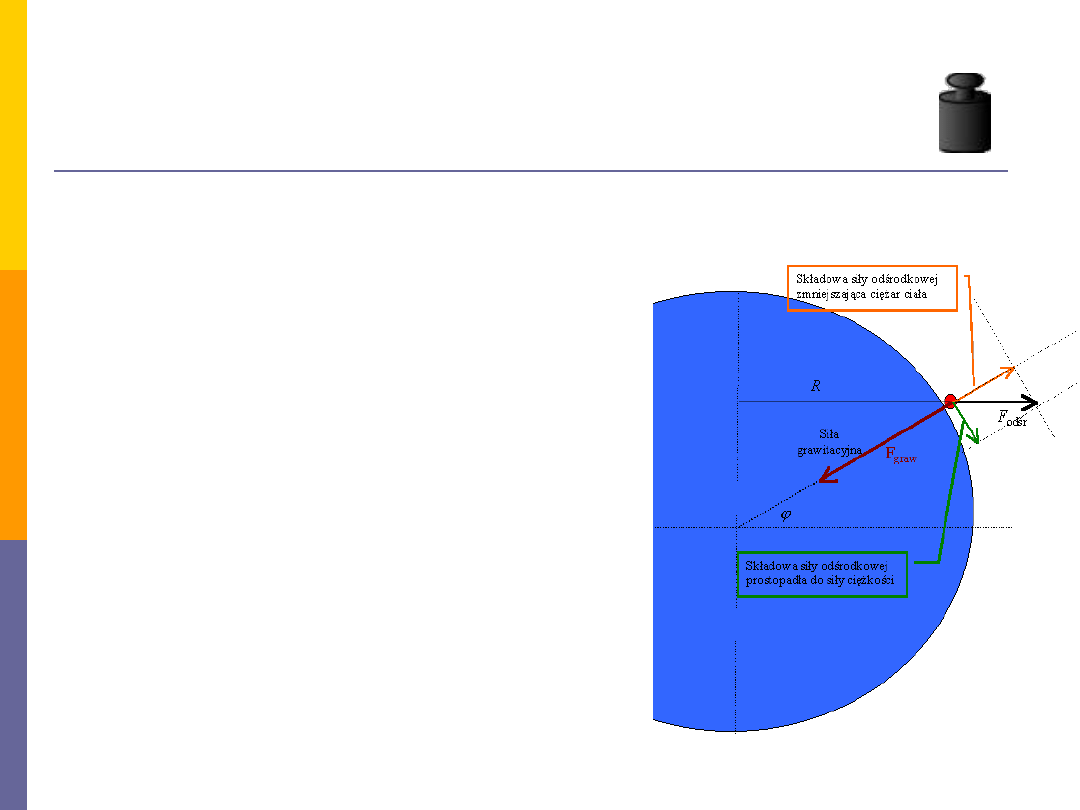
Grawitacja

–

ciężar ciała

wpływ ruchu wirowego Ziemi na wartość ciężaru ciała



największą wartość siła

odśrodkowa ma na równiku,



na biegunach ma wartość zero,



na równiku siła ta najefektywniej

zmniejsza ciężar,



tylko składowa siły odśrodkowej

równoległa do promienia powoduje

zmniejszanie ciężaru.