

Bryła sztywna



Środek masy:



definicja,



ruch środka masy,



Zasada zachowania pędu



Zderzenia:



sprężyste, niesprężyste,



centralne, niecentralne,

Podstawy dynamiki

Ruch środka masy







n

i

i

i

s

m

M

1

1

r

r







rozważmy układ punktów materialnych o masach

m

1

, m

2

, …, m

n

o stałej

masie całkowitej

M

. Środek masy jest równy:



różniczkując względem czasu otrzymamy:



co zapisujemy następująco:











n

i

i

i

s

m

M

1

r

r













n

i

i

i

s

dt

r

d

m

dt

r

d

M

1

















n

i

i

i

s

v

m

v

M

1







ponownie różniczkując względem czasu otrzymamy:









n

i

i

i

s

dt

v

d

m

dt

v

d

M

1

















n

i

i

i

s

a

m

a

M

1













n

i

i

s

F

a

M

1





zew

n

i

i

F

F











1

zew

s

F

a

M











środek masy układu

punktów materialnych

porusza się w taki sposób,

jakby cała masa układu

była skupiona w

środku

masy

i jakby wszystkie

siły zewnętrzne nań

działały

Zasada zachowania pędu



jeżeli nie działają siły zewnętrzne (lub wypadkowa jest równa zero):

dt

p

d

F

zew









0

const

p







Jeżeli

wypadkowa

sił

zewnętrznych

działających na układ jest równa zeru, to
całkowity wektor pędu układu jest stały.

Jeżeli

wypadkowa

sił

zewnętrznych

działających na układ jest równa zeru, to
pęd układu w stanie początkowym jest
równy

pędowi

układu

w

stanie

końcowym.

Zderzenia



zderzenie

– krótkotrwałe oddziaływanie dwóch ciał,

Podział:



zderzenia bezpośrednie – (mechaniczne),



zderzenia „bezstykowe” –

za pośrednictwem wszelkiego rodzaju pól,



zderzenia sprężyste (elastyczne) – spełniona jest

zasada zachowania pędu i energii kinetycznej



zderzenia niesprężyste (nieelastyczne) –

spełniona jest zasada zachowania pędu:



idealnie niesprężyste – ciała łączą się,



zderzenia centralne

– ciała poruszają się

wzdłuż linii łączącej środki



zderzenia niecentralne

– ukośne

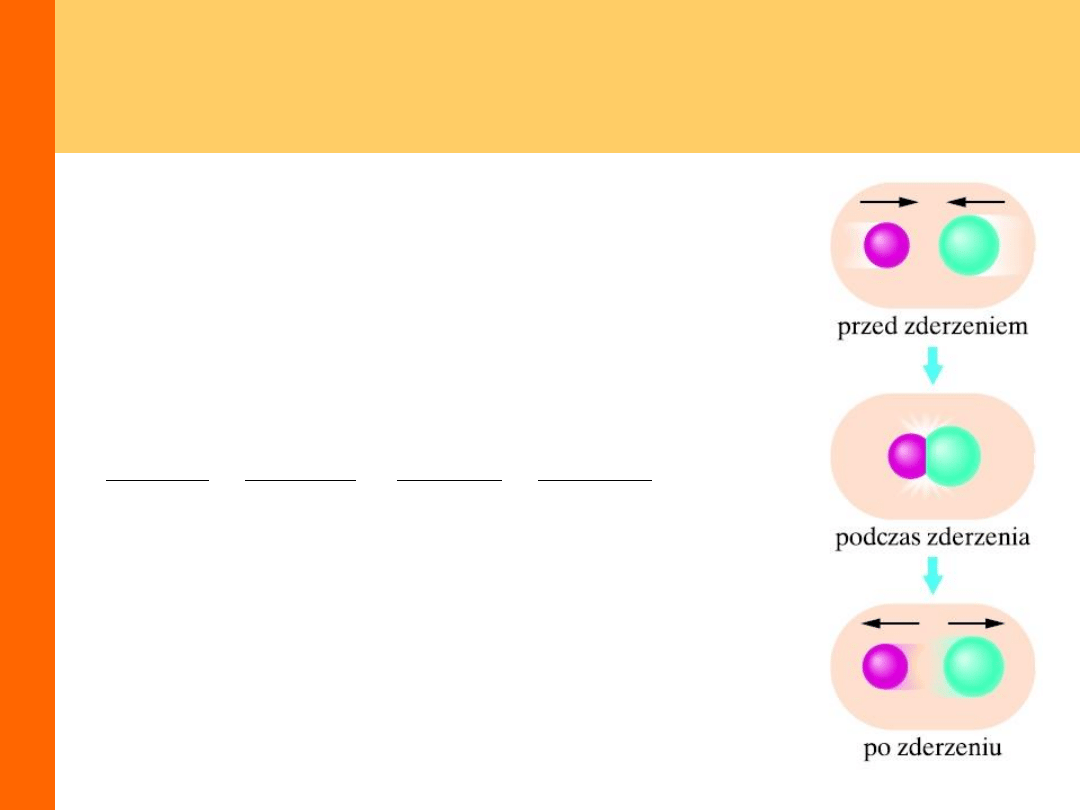
Zderzenia sprężyste













































2

2

1

1

2

2

1

1

2

2

2

2

1

1

2

2

2

2

1

1

2

2

2

2

u

m

u

m

v

m

v

m

u

m

u

m

v

m

v

m

















Rozpatrzymy zderzenia

sprężyste dla kul o masach

m

1

i

m

2

oraz ich

prędkości przed zderzeniem

v

1

i

v

2

. Chcemy

obliczyć prędkości

u

1

i

u

2

obu kul po zderzeniu. Zderzenie

sprężyste charakteryzuje się tym, że energia kinetyczna
przed

zderzeniem

równa się energii kinetycznej po

zderzeniu, a

traktując kule jako układ odosobniony wiemy,

że pęd układu przed zderzeniem jest równy pędowi po
zderzeniu:

zasada zachowania pędu

zasada zachowania energii kinetycznej

m

2

m

2

m

2

m

1

m

1

m

1

v

1

v

2

u

1

u

2

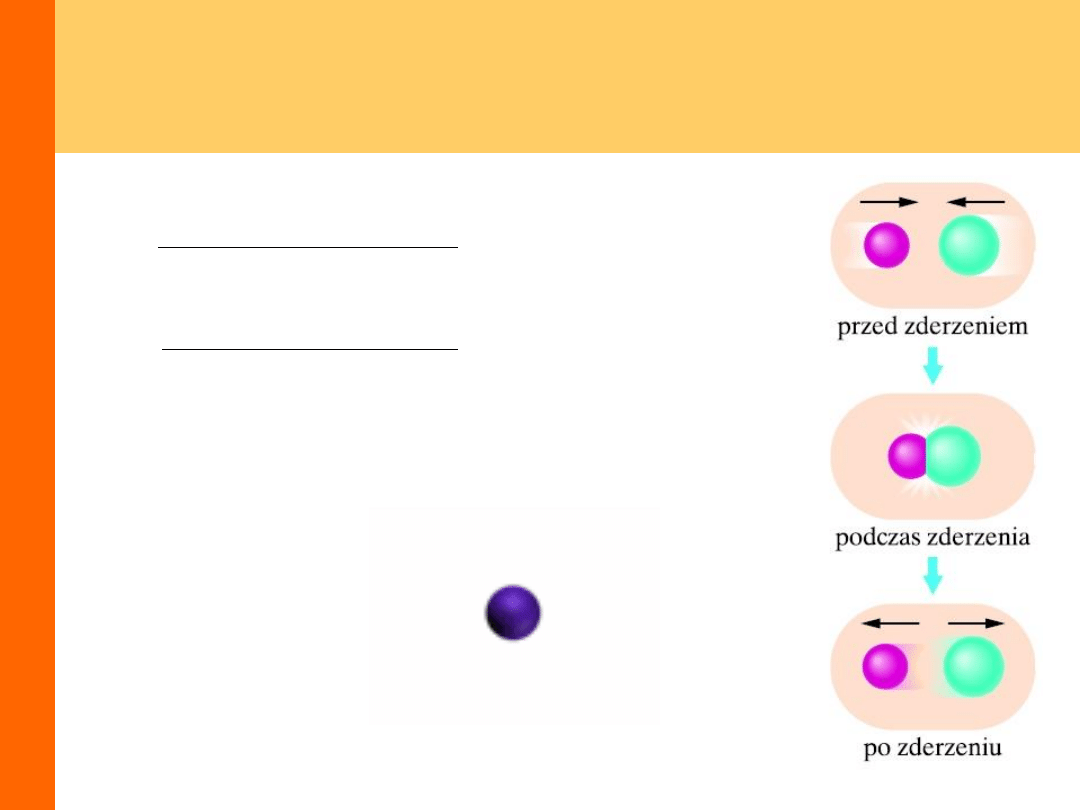
Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u

i ostatecznie:

Zbadajmy zachowanie się prędkości końcowych
w zależności od mas i prędkości początkowych:



niech

m

1

=

m

2











1

2

2

1

v

u

v

u

czyli kule o jednakowych masach
wymieniają wzajemne swe prędkości

m

2

m

2

m

2

m

1

m

1

m

1

v

1

v

2

u

1

u

2

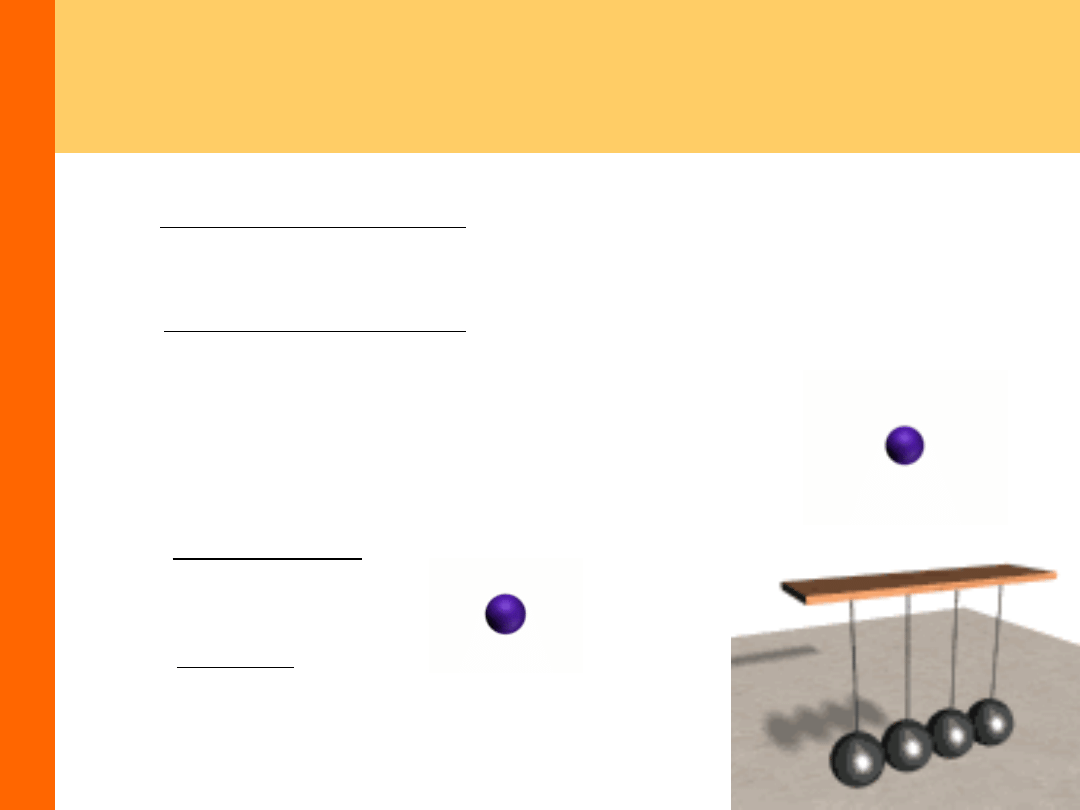
Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u



niech

v

2

= 0

wtedy:


























2

1

1

1

2

2

1

1

2

1

1

2

)

(

m

m

v

m

u

m

m

v

m

m

u

jeśli dodatkowo

m

1

=

m

2











1

2

1

0

v

u

u

Zderzenia sprężyste




































2

1

2

1

2

1

1

2

2

1

1

2

1

2

2

1

)

(

2

)

(

2

m

m

v

m

m

v

m

u

m

m

v

m

m

v

m

u



gdy druga kula ma masę znacznie większą od pierwszej i jest nieruchoma

jeśli dodatkowo
(odbicie od ściany)

0

2

2

1





v

i

m

m

1

2

1

2

1

2

1

2

1

2

1

1

1

2

1

1

v

m

m

m

m

u

v

m

m

m

m

u





















2

m

0

lim

2

1

2







m

m

m













0

2

1

1

u

v

u

Zderzenia niesprężyste

Rozpatrzymy zderzenie

niesprężyste kul o masach

m

1

i

m

2

poruszających się

z

prędkościami przed zderzeniem

v

1

i

v

2

. Niech obie

prędkości mają te same

kierunki i niech

v

1

>

v

2

. Po zderzeniu

następuje trwałe odkształcenie i ciała

poruszają się razem (zderzenie idealnie niesprężyste). Chcemy obliczyć wspólną
prędkości

u

.

2

1

2

2

1

1

2

1

2

2

1

1

)

(

m

m

v

m

v

m

u

u

m

m

v

m

v

m























zasada zachowania pędu

zasada zachowania energii kinetycznej

nie obowiązuje

–

zmiany energii wewnętrznej – odkształcenie, nagrzewanie ciał