1
Mechanika ogólna
Wykład nr 8
Podstawy dynamiki
Dynamika
n
Dział mechaniki zajmujący się
badaniem związków między ruchem
punktów materialnych i ciał sztywnych
oraz sił go wywołujących.
n
Dynamika bada zależności między
takimi wielkościami jak: siła,
przyspieszenie, prędkość, pęd, kręt,
praca, energia itd.
2
Pierwsza zasada
dynamiki Newtona
n
Prawo bezwładności:
– Z punktu widzenia dynamiki jest wszystko
jedno, czy ciało się porusza ruchem
jednostajnym prostoliniowym, czy jest w
spoczynku.
– W obu przypadkach siły działające na
ciało są w równowadze.
– Można zawsze założyć istnienie
nieruchomego układu odniesienia.
3
Druga zasada dynamiki
Newtona
n
Pod działaniem stałej siły punkt materialny
porusza się ruchem jednostajnie
przyspieszonym po linii prostej.
n
Przyspieszenie z jakim porusza się punkt
jest wprost proporcjonalne do działającej
siły (wypadkowej układu sił), a odwrotnie
proporcjonalne do masy ciała.
4
m
=
P
a
P
a
m
Trzecia zasada dynamiki
Newtona
n
Siły wzajemnego oddziaływania dwóch
punktów materialnych równoważą się,
tj. mają jednakowe moduły i kierunki,
zaś zwroty przeciwne.
5
P
1
P
2
2
1
P
P
=
2
1
P
P
−
=
Prawo grawitacji
n
Dwa ciała działają na siebie wzajemnie
jednakowymi co do wartości i
przeciwnie zwróconymi siłami o wartości
odwrotnie proporcjonalnej do kwadratu
odległości między ich środkami i wprost
proporcjonalnej do iloczynu mas tych
ciał.
6
1
2
2
m m
r
⋅
=
P
G
Zasada superpozycji
n
Efekt działania kilku wpływów na ciało
można wyrazić jako sumę efektów ich
działania.
n
Przyspieszenie z jakim porusza się ciało
pod wpływem układu sił (siły
wypadkowej) może zostać obliczone
jako suma przyspieszeń powodowanych
przez każdą z sił składowych.
7
1
2
...
...
n
n
m
m
m
m
=
+
+ +
=
+
+ +
=
1
2
a
a
a
a
P
P
P
P
Równania ruchu punktu
materialnego
n
Dynamiczne równanie różniczkowe ruchu
punktu materialnego:
n
Dynamiczne różniczkowe równania ruchu
we współrzędnych prostokątnych:
8
d
d
m
m
m
dt
dt
= ⋅ = ⋅ =
r
r
a
P
&&
x
ix
i
m x
m a
P
⋅ = ⋅ =
∑
&&
z
iz
i
m z
m a
P
⋅ = ⋅ =
∑
&&
y
iy
i
m y
m a
P
⋅ = ⋅
=
∑
&&
Skalarne równania ruchu
n
Rzutowanie przyspieszenia na osie
normalną, styczną i binormalną:
n
Wektor przyspieszenia całkowitego leży
na płaszczyźnie ściśle stycznej do toru.
9
2
n
in
i
v
m a
m
P
ρ
⋅
=
=
∑
t
it
i
dv
m a
m
P
dt
⋅ =
=
∑
b
ib
i
m a
P
⋅ =
∑
0
b
a
=
Pierwsze i drugie zadanie
dynamiki
n
Pierwsze zadanie dynamiki:
– Dana jest masa i równania ruchu punktu
materialnego, należy wyznaczyć siły
działające na ten punkt;
n
Drugie zadanie dynamiki:
– Dana jest masa i siły działające na punkt
materialny, należy wyznaczyć równania
ruchu tego punktu.
10
Pierwsze zadanie
dynamiki
n
Równanie ruchu:
n
Składowe wypadkowej we współrzędnych
prostokątnych:
n
Wartość i kierunek wypadkowej:
11
m
m
⋅ = ⋅ =
a
r
P
&&
x
P
mx
=
&&
y
P
my
=
&&
x
P
mz
=
&&
2
2
2
x
y
z
P
P
P
P
=
+
+
( )
cos
,
x
P
P
=
P i
S
( )
cos
,
y
P
P
=
P j
S
(
)
cos
,
z
P
P
=
P k
S
Drugie zadanie dynamiki
n
Ruch punktu pod działaniem siły:
– Stałej co do wartości i kierunku;
–
Zależnej od czasu;
–
Zależnej od prędkości;
– Zależnej od położenia.
12
const
=
P
( )
t
=
P
P
( )
v
=
P
P
( )
x
=
P
P
Ruch pod działaniem
stałej siły
(1)
n
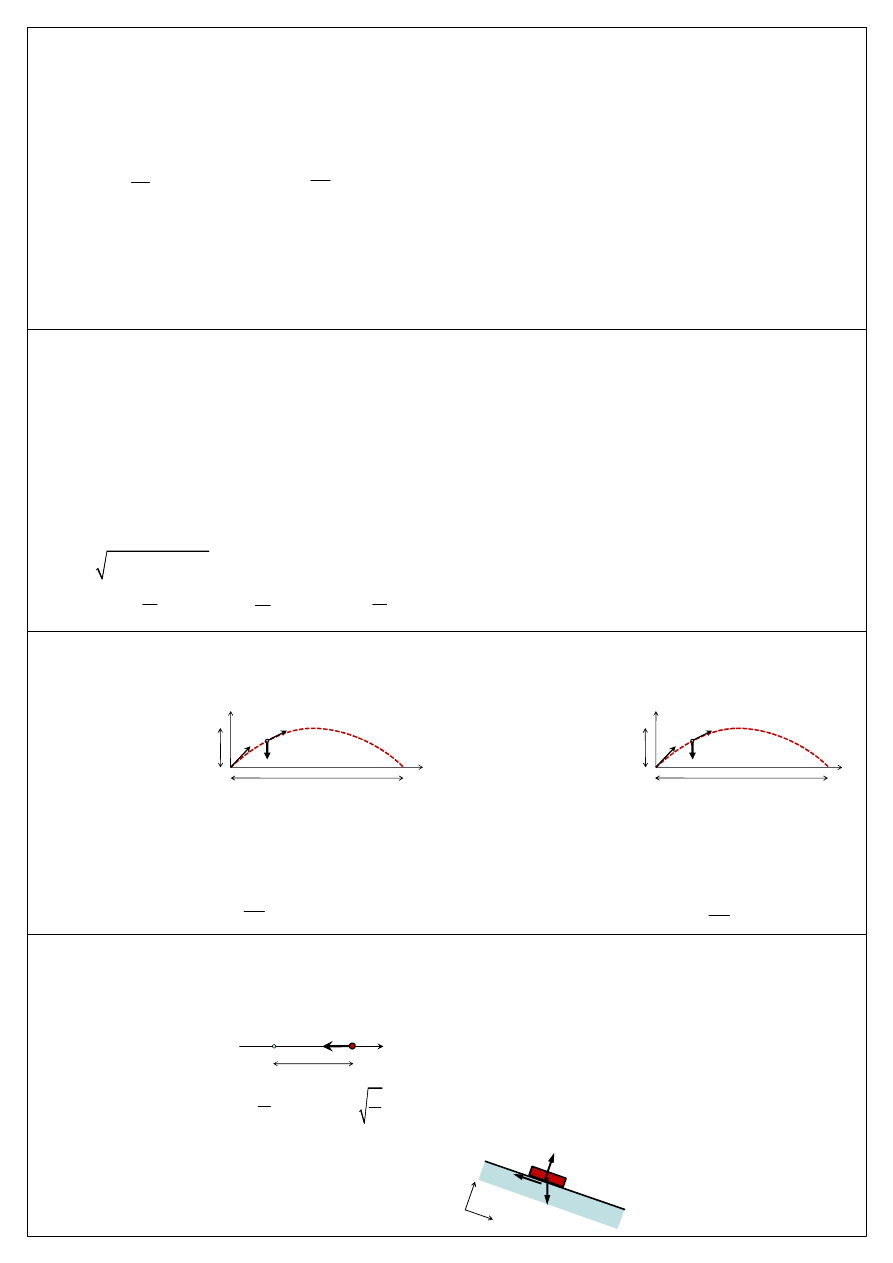
Rzut ukośny:
n
Równania ruchu:
n
Składowe przyspieszeń:
n
Składowe prędkości:
n
Równania ruchu:
13
( )
2
y
v
t
gt
C
= − +
( )
1
3
x t
C t
C
=
+
0
v
0
mx
=
&&
my
mg
= −
&&
0
x
a
=
y
a
g
= −
1
x
v
C
=
( )
2
2
4
2
gt
y t
C t
C
= −
+
+
mg
v
max
x
max
y
Ruch pod działaniem
stałej siły
(2)
n
Warunki brzegowe:
n
Stałe całkowania:
n
Równania prędkości:
n
Równania ruchu
14
1
0
cos
C
v
α
=
( )
0
sin
v t
gt
v
α
= − +
0
0
(
0)
cos
x
x
v t
v
v
α
=
=
=
0
0
(
0)
sin
y
y
v t
v
v
α
=
=
=
(
0)
0
x t
=
=
(
0)
0
y t
=
=
2
0
sin
C
v
α
=
3
0
C
=
4
0
C
=
0
cos
x
v
v
α
=
( )
0
cos
x t
v t
α
=
( )
2
0
sin
2
gt
y t
v t
α
= −
+
0
v
mg
v
max
y
max
x
Ruch pod działaniem siły
zależnej od położenia
n
Drgania liniowe:
n
Różniczkowe
równanie ruchu:
n
Rozwiązanie ogólne:
(Równanie ruchu harmonicznego prostego)
15
0
x
P
m
x
x
x
P
ma
mx
kx
=
=
= −
&&
0
k
x
x
m
+
=
&&
k
m
ω =
1
2
sin
cos
x
C
t
C
t
ω
ω
=
+
(
)
0
sin
x
a
t
ω ϕ
=
+
1
0
cos
C
a
ϕ
=
2
0
sin
C
a
ϕ
=
Ruch nieswobodnego
punktu materialnego
n
W przypadku, gdy warunki zewnętrzne
ograniczają swobodę ruchu, w
równaniu ruchu należy uwzględnić
także siły bierne (reakcje więzów):
16
m
m
=
= +
a
r
P
R
&&
X
Y
N
m
=
G
g
µ
=
T
N
x
x
m
=
∑
a
P
0
y
y
m
=
=
∑
a
P
Siła bezwładności
n
Równanie ruchu:
n
Siła bezwładności
(d’Alemberta):
n
Zasada d’Alemberta:
– Siły rzeczywiste działające na
punkt materialny równoważą
się z siłą bezwładności tego
punktu.
17
m
=
P
a
0
m
−
=
P
a
m
= −
B
a
0
+ =
P
B
0
r
v
n
a
0
r
P
0
t
a
=
const
=
v
2
n
v
a
r
=
m
m
B
Zasady zachowania w
dynamice
n
Zasada:
– zachowania pędu;
– zachowania momentu pędu (krętu);
– równoważności energii i pracy;
– zachowania energii mechanicznej.
18
Pęd,
zasada zachowania pędu
n
Zgodnie z drugim prawem Newtona:
– Pochodna pędu punktu materialnego
względem czasu równa jest sumie sił
działających na ciało.
n
Pęd (ilość ruchu) pozostaje wielkością
stałą, jeżeli siły działające na ciało
pozostają w równowadze:
19
( )
d m
d
m
m
dt
dt
=
=
=
v
v
P
a
m
const
=
v
Moment pędu, zasada
zachowania krętu
n
Momentem pędu (kręt) punktu
materialnego względem bieguna jest
iloczyn wektorowy promienia wodzącego
punktu względem bieguna i pędu:
n
Kręt punktu materialnego względem
bieguna jest wielkością stałą, jeśli moment
sił działających na punkt materialny
względem tego bieguna jest równy 0.
20
0
m
= ×
K
r
v
0
r
m
mv
Praca
n
Praca stałej siły na prostoliniowym
przesunięciu równa jest iloczynowi wartości
bezwzględnej przesunięcia przez miarę
rzutu siły na kierunek przemieszczenia.
n
Praca wypadkowej układu sił działających
na ciało równa jest sumie prac
poszczególnych sił działających na ciało.
21
α
m
P
α
m
P
l
W
P l
= ⋅
cos
W
Pl
α
=
Zasada równoważności
energii i pracy
n
Energia kinetyczna:
n
Zasada równoważności energii i pracy:
– Przyrost energii kinetycznej punktu
materialnego (ciała) równy jest pracy
wykonanej przez siły działającej na ciało.
22
2
2
mv
E
=
2
1
E
E
E
W
∆
=
−
=
Zasada zachowania
energii mechanicznej
n
Potencjalne pole sił:
– Praca wykonana przez siły w potencjalnym
polu sił nie zależą od drogi po której
wykonane zostało przemieszczenie a jedynie
od położeń początkowego i końcowego.
n
Energia mechaniczna ciała w
potencjalnym polu sił pozostaje
wielkością stałą.
23
1
1
2
2
E
V
E
V
+ =
+
Zasada zachowania
energii – przykład
(1)
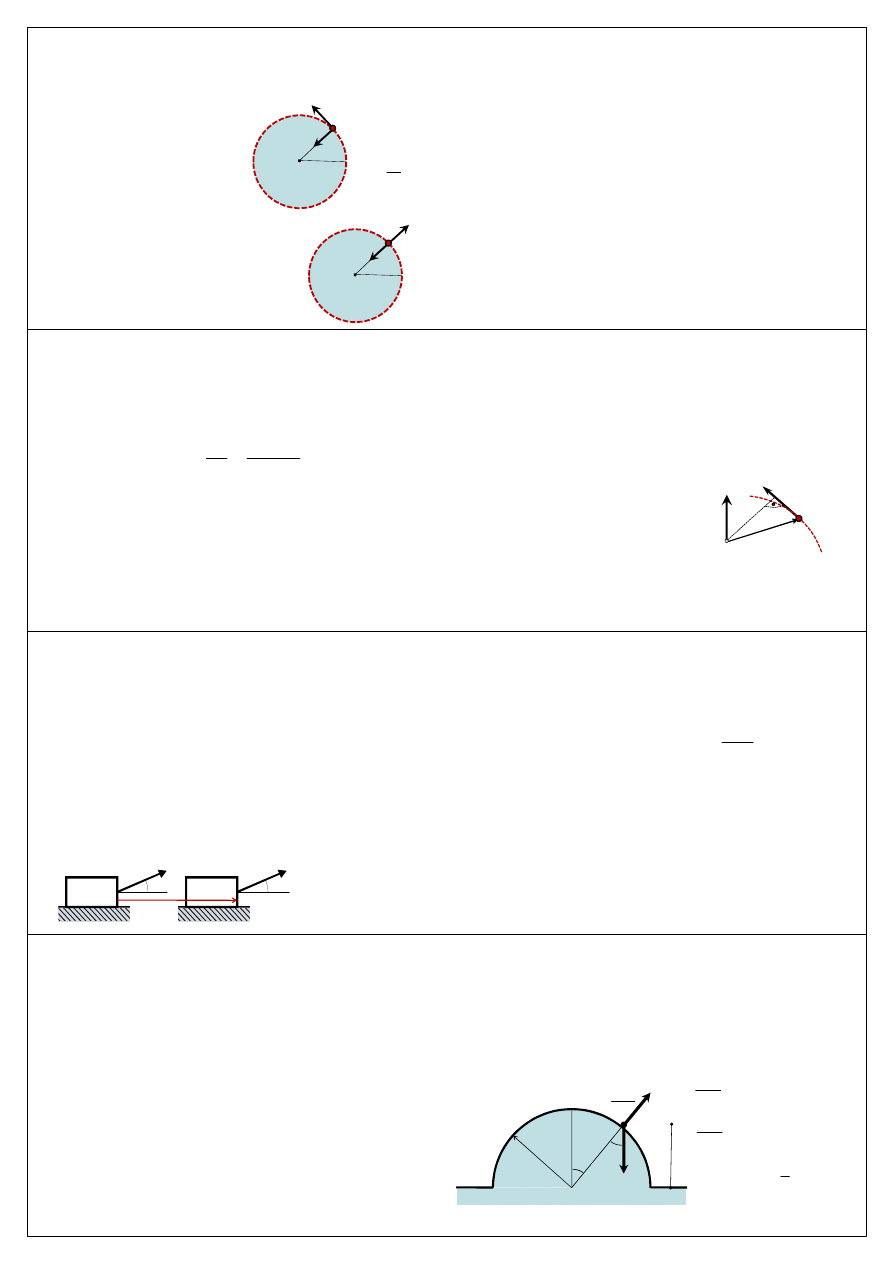
n
Wyznaczyć miejsce oderwania punktu
materialnego zsuwającego się po
gładkiej półkuli:
24
2
cos
mv
mg
r
ϕ
=
2
mv
r
(
)
2
cos
2
mv
mg r
r
ϕ
=
−
2
cos
3
ϕ =
r
mg
ϕ
ϕ
r
cos
ϕ
Zasada zachowania
energii – przykład
(2a)
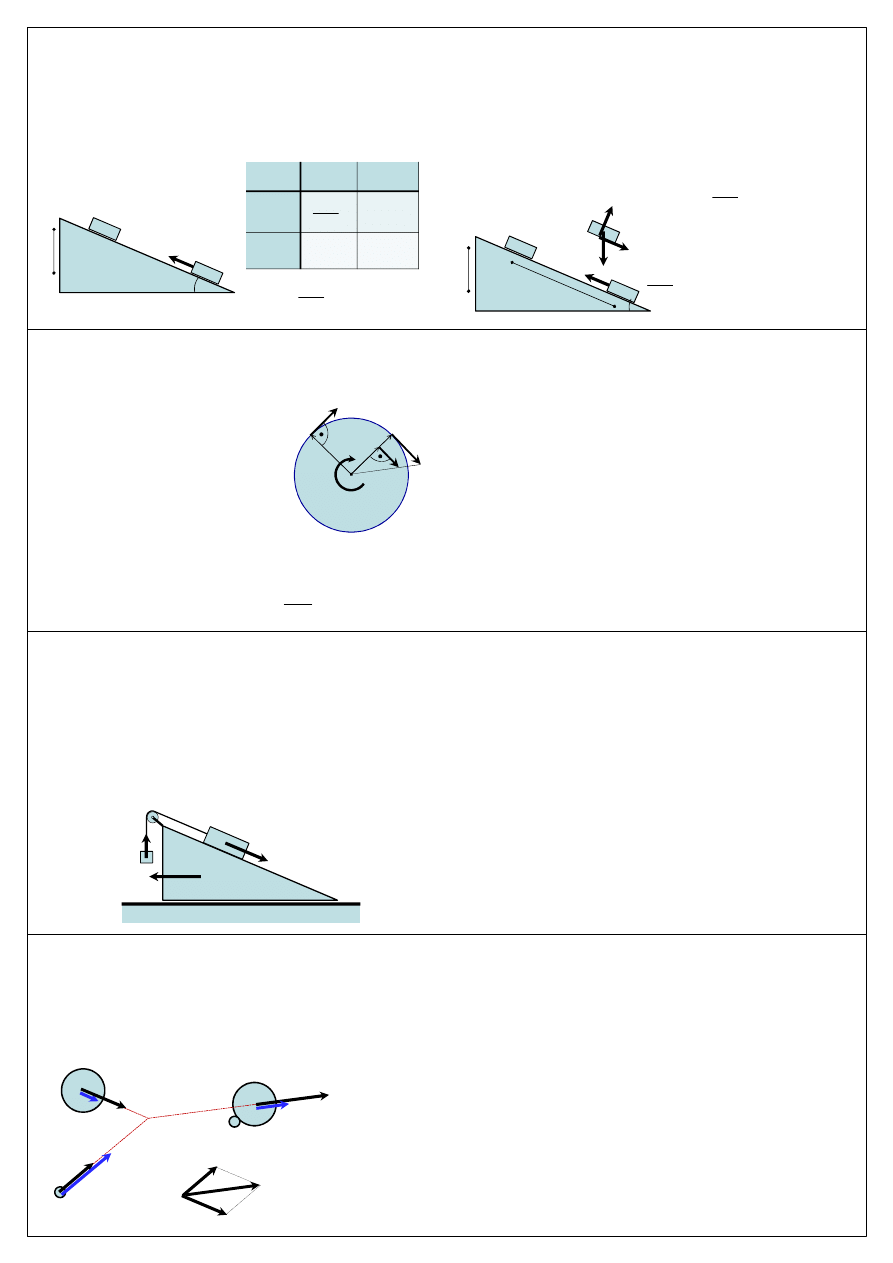
n
Na jaką wysokość po gładkiej równi
wjedzie ciało, któremu nadano
prędkość
początkową v:
25
h
v
2
2
mv
mgh
=
α
Energia
kinetyczna
Energia
potencjalna
Początek
Koniec
2
2
mv
0
0
mgh
Zasada zachowania
energii – przykład
(2b)
n
Na jaką wysokość po równi wjedzie
ciało, któremu nadano prędkość
początkową v (z uwzględnieniem tarcia):
– Praca siły tarcia:
26
h
N
2
2
mv
mgh Ts
=
+
µ
mg
T
W
Ts
=
s
v
α
T
N
µ
=
cos
N
mg
α
=
2
cos
sin
2
mv
mgh
mg
h
µ
α
α
=
+
⋅
Dynamika ruchu obrotowego
bryły sztywnej
n
Druga zasada dynamiki w
ruchu obrotowym bryły
sztywnej:
n
Kręt w ruchu obrotowym:
n
Energia kinetyczna:
27
t
I
ω
=
K
2
2
I
E
ω
=
0
R
r
v
r
ω
R
v
R
v
0
M
I
ε
=
Dynamika układu
punktów materialnych
n
Zasady zachowania w ruchu układu
punktów materialnych:
– Ruchu środka masy;
– Zachowania pędu;
– Zachowania krętu;
– Zasada d’Alemberta;
– Zachowania energii mechanicznej.
28
Zasada ruchu środka masy
n
Jeżeli siły zewnętrzne działające na układ
ciał równoważą się, to środek masy
układu pozostaje w spoczynku lub porusza
się ruchem jednostajnym prostoliniowym.
29
Zasada zachowania pędu
n
Pęd układu punktów materialnych –
suma wektorowa pędów wszystkich
punktów.
n
Przyrost pędu układu punktów
materialnych jest równy popędowi
wypadkowej sił zewnętrznych.
n
Pęd układu punktów materialnych
pozostaje niezmienny, jeżeli siły
działające na układ równoważą się.
30
Zasada zachowania pędu
– przykład
n
Określić prędkość ciała po uderzeniu
kuli:
31
2 2
m v
1 1
m v
(
)
1
2
m
m
v
+
(
)
1
2
m
m
v
+
2 2
m v
1 1
m v
2
v
1
v
v
Zasada zachowania
momentu pędu
n
Moment pędu (kręt) układu punktów
materialnych – suma wektorowa krętów
wszystkich punktów układu względem
bieguna.
n
Pochodna krętu układu punktów po
czasie równa jest wypadkowemu
momentowi sił względem bieguna.
n
Kręt układu punktów materialnych
pozostaje niezmienny, jeżeli wypadkowy
moment sił względem bieguna jest równy
zero.
32
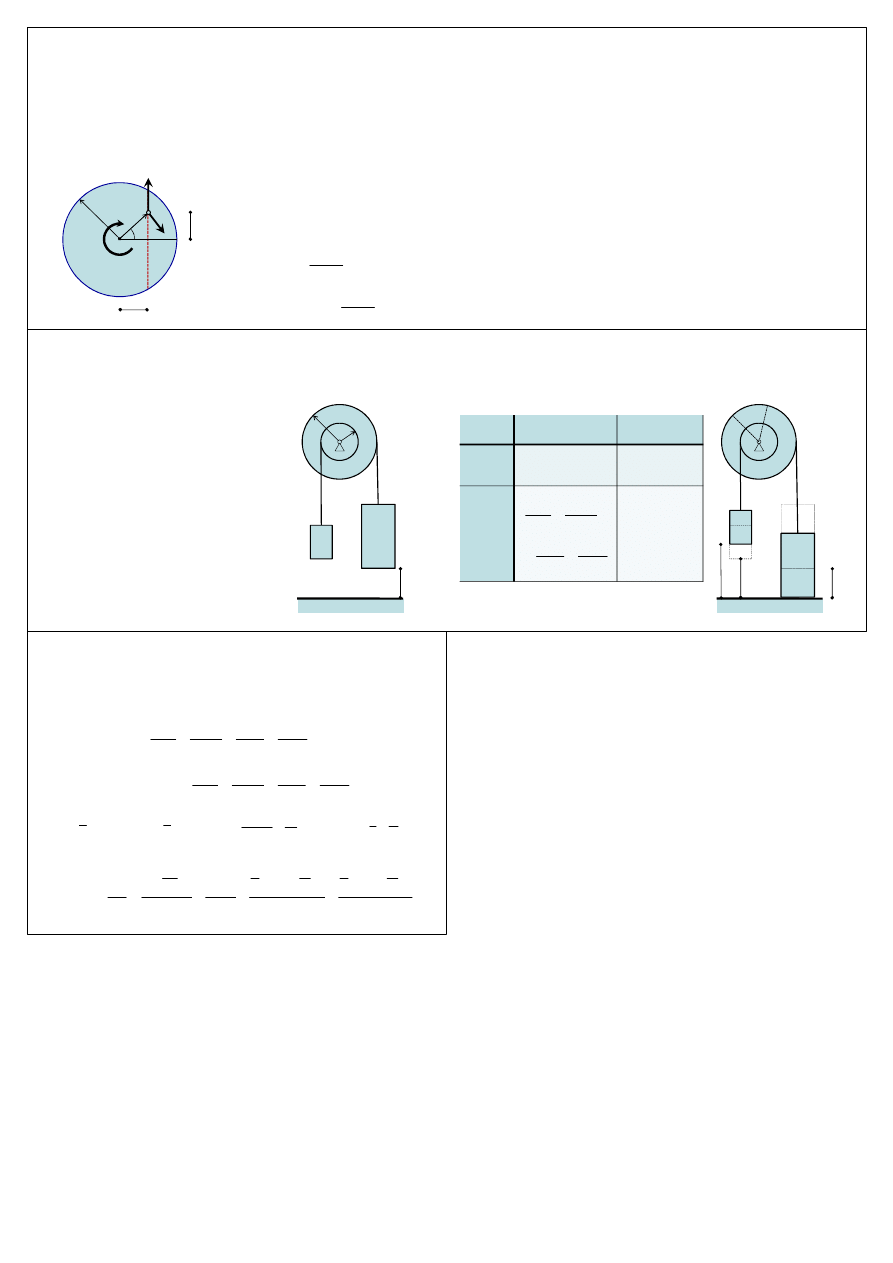
Zasada zachowania krętu
– przykład
n
Po cięciwie tarczy zaczyna poruszać się punkt
materialny z prędkością v. Z jaką prędkością
kątową poruszać się będzie tarcza?
33
0
m
α
R
w
r
v
r
M
ω
x
(t
)=
wt
d
0
=
K
t
I
ω
=
K
p
mwd
mur
=
−
K
0
mwd
mur
I
ω
−
−
=
2
2
0
2
MR
mwd
m r
ω
ω
−
−
=
(
)
2
2
2 2
0
2
MR
mwd
m
d
w t
ω
ω
−
+
−
=
Zasada zachowania energii
mechanicznej
n
Energia mechaniczna układu punktów
materialnych w potencjalnym polu sił
pozostaje niezmienna.
n
Przyrost energii kinetycznej układu
punktów materialnych równy jest
sumie prac wykonanych przez
wszystkie siły (zewnętrzne i
wewnętrzne) działające na ten układ.
34
Zasada zachowania energii
mechanicznej
(1)
n
Na dwa współśrodkowe
walce o masach m
1
i m
2
nawinięte są nieważkie
nici na których
zawieszono dwa ciała.
Obliczyć z jaką
prędkością uderzy o
ziemię ciało M.
35
1
m
R
r
2
m
m
M
H
Zasada zachowania energii
mechanicznej
(2)
36
1
m
2
m
m
M
h
2
H
h
1
Energia kinetyczna
Energia
potencjalna
Początek
Koniec
0
1
MgH
mgh
+
2
2
2
2
1
2
2
2
2
2
mv
MV
I
I
ω
ω
+
+
+
+
2
mgh
φ
Zasada zachowania energii
mechanicznej
(3)
37
2
2
2
2
1
2
1
2
2
2
2
2
I
I
mv
MV
MgH
mgh
mgh
ω
ω
+
=
+
+
+
+
(
)
2
2
2
2
1
2
2
1
2
2
2
2
I
I
mv
MV
MgH
mg h
h
ω
ω
−
−
=
+
+
+
2
1
1
1
2
I
m R
=
2
2
2
1
2
I
m r
=
2
1
h
h
H
r
R
φ
−
=
=
v
V
r
R
ω = =
2
2
2
2
2
2
1
2
1
1
2
2
2
2
2
2
Vr
V
V
m
m R
m r
Hr
MV
R
R
R
MgH
mg
R
−
=
+
+
+