AGH, Wydział EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych				Nazwisko i Imię: Chanowski Sławomir
LABORATORIUM TEORII SEROWANIA I TECHNIK REGULACJI				Semestr: IV
Rok szkolny: 1998/99		Rok studiów: II		Grupa: I
Kierunek: Elektrotechnika				Nr ćwiczenia: II, IX
Temat ćwiczenia: Charakterystyki dynamiczne podstawowych członów.
Data wykonania: 10-03-1999, 17-04-1999	Data oddania: 27-05-99		Data zaliczenia sprawozdania:

I. Wprowadzenie:

Analiza i synteza układów sterowania automatycznego opiera się na wykorzystaniu charakterystyk dynamicznych. Charakterystyki te opisują zachowanie się układu sterowania jako całości lub poszczególnych jego elementów w stanach dynamicznych, tj. podczas trwania procesów przejściowych. Rozróżniamy dwa rodzaje charakterystyk dynamicznych:

1. charakterystyki czasowe,

2. charakterystyki częstotliwościowe.

Charakterystyka czasowa jest to przebieg w czasie odpowiedzi y(t) układu dynamicznego na ściśle określone wymuszenie u(t). Odpowiedzią jednostkową (odpowiedzią skokową) obiektu jednowymiarowego, liniowego nazywamy sygnał, jaki występuje na wyjściu tego obiektu po przyłożeniu do jego wejścia, przy zerowych warunkach początkowych, sygnału będącego funkcją jednostkową 1(t). Jednostronną transformatę Laplace'a odpowiedzi jednostkowej otrzymuje się po pomnożeniu transmitancji obiektu G(s) przez transformatę funkcji jednostkowej
:

.

Odpowiedzią impulsową obiektu jednowymiarowego, liniowego nazywamy sygnał, jaki występuje na wyjściu tego obiektu po przyłożeniu do jego wejścia, przy zerowych warunkach początkowych, sygnału będącego funkcją impulsową Diraca δ(t). Jednostronną transformatę Laplace'a odpowiedzi impulsowej otrzymuje się po pomnożeniu transmitancji obiektu G(s) przez transformatę funkcji impulsowej Diraca δ(s)=1:

g(s)=G(s).

Po odwrotnej transformacie Laplace'a h(s) i g(s) otrzymujemy odpowiedzi w dziedzinie czasu, na podstawie których wykreślamy charakterystyki i wyznaczamy parametry obiektu.

Charakterystyki częstotliwościowe są to krzywe przedstawiające transmitancję widmową G(jω) w funkcji częstotliwości kątowej (pulsacji). Ponieważ transmitancja widmowa wiąże się z operatorową G(C)=G(s) a dla układów liniowych odpowiedz impulsowa g(t)=L^-1[G(s)] i skokowa h(t)=L^-1[G(s)/s], zatem na podstawie charakterystyk częstotliwościowych można wyznaczyć charakterystyki czasowe i odwrotnie. Transmitancja widmowa G(jω) jest funkcją zespoloną postaci ω i parametrów układu. Można ją przedstawić w postaci algebraicznej G(jω)=P(ω)+Q(ω), lub wykładniczej G(jω)=A(ω)e^jϕ(ω)

gdzie:

P(ω) - część rzeczywista transmitancji widmowej - charakterystyka rzeczywista,

Q(ω) - część urojona transmitancji widmowej - charakterystyka urojona,

A(ω) - moduł transmitancji widmowej - charakterystyka amplitudowa,

ϕ(ω) - argument transmitancji widmowej - charakterystyka fazowa.

Wykres transmitancji we współrzędnych (P,Q), nosi nazwę charakterystyki amplitudowo-fazowej (nazywana charakterystyką Nyquist'a).

Charakterystyki Bode'go:

Logarytmiczna charakterystyka modułu jest to krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy pulsację w skali logarytmicznej a na osi rzędnych moduł transmitancji widmowej wyrażony w dB odkładany w skali liniowej:

M(ω)=20log| G(jω)|

Logarytmiczna charakterystyka fazy jest to krzywa we współrzędnych prostokątnych, gdzie na osi odciętych jest pulsację w skali logarytmicznej a na osi rzędnych faza ϕ(ω) wyrażona w radianach odkładana w skali liniowej:

ϕ(ω)=arg[G(jω)]=arctg[Q(ω)/P(ω)]

I. Przebieg ćwiczenia:

1. Bezinercyjny człon proporcjonalny.

Człon bezinercyjny proporcjonalny opisany jest równaniem:

gdzie:

y - wyjście,

u - wejście,

k - współczynnik wzmocnienia.

Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

a w dziedzinie czasu:

Charakterystyka skokowa:

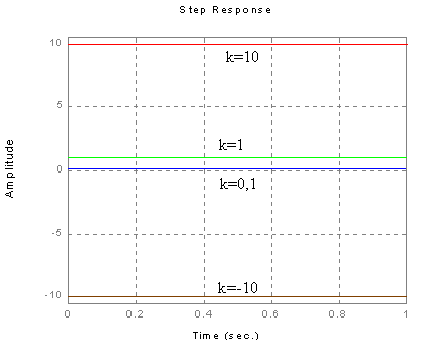
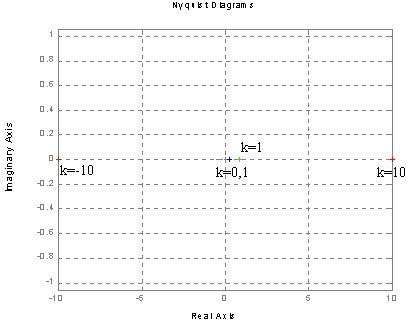
Charakterystyka Nyquist'a .

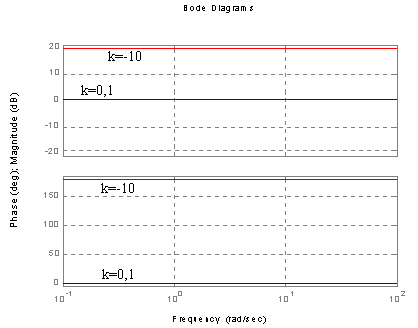
Charakterystyka Bode'go (amplitudowa, fazowa).

2. Człon całkujący idealny

W członie całkującym idealnym sygnał wyjściowy jest proporcjonalny do całki sygnału wejściowego:

k - współczynnik wzmocnienia równy stosunkowi pochodnej sygnału wyjściowego do sygnału wejściowego w stanie ustalonym. Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

a w dziedzinie czasu:

Podobnie odpowiedź impulsowa:

;

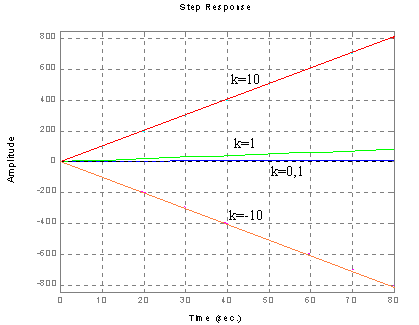
Charakterystyka skokowa:

Charakterystyka Nyquist'a .

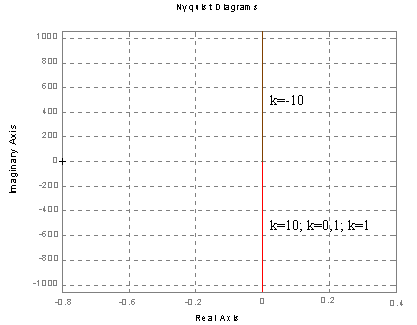
Charakterystyka Bode'go (amplitudowa, fazowa).

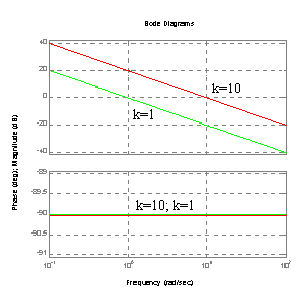
3. Człon różniczkujący idealny.

Człon różniczkujący idealny opisany jest równaniem różniczkowym:

gdzie:

y - wyjście,

u - wejście,

k - współczynnik wzmocnienia.

Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

a w dziedzinie czasu:

δ(t) - delta Diraca.

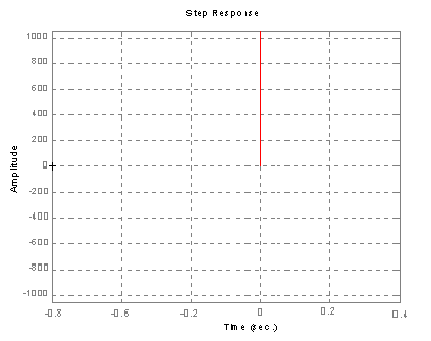
Charakterystyka skokowa:

Charakterystyka Nyquist'a .

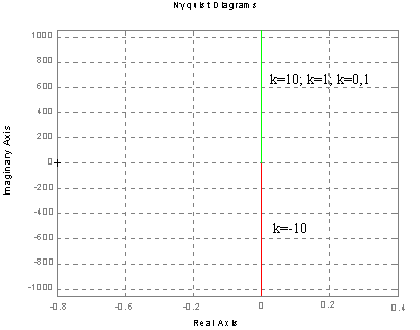
Charakterystyka Bode'go (amplitudowa, fazowa).

4. Człon różniczkujący z inercją

Człon różniczkujący z inercją w dziedzinie czasu jest dany równaniem różniczkowym:

T - stała czasowa; k - współczynnik wzmocnienia równy stosunkowi - w stanie ustalonym - sygnału wyjściowego do pochodnej sygnału wejściowego. Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

a w dziedzinie czasu:

Podobnie odpowiedź impulsowa:

;

Charakterystyka skokowa:

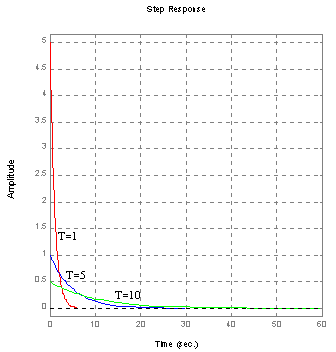
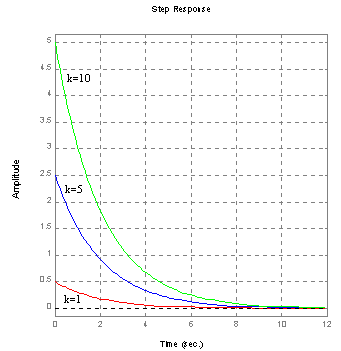
T=2 k=5

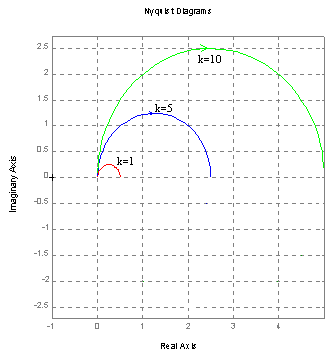
Charakterystyka Nyquist'a .

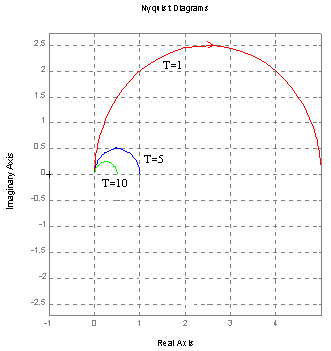
T=2 k=5

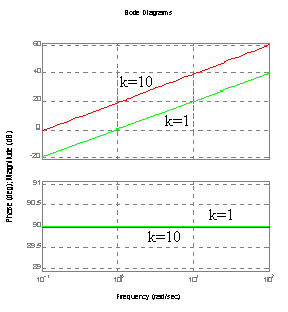
Charakterystyka Bode'go (amplitudowa, fazowa).

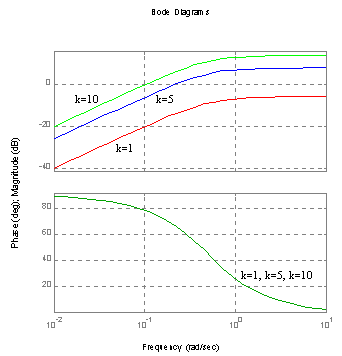
T=2 k=5

Na charakterystyce fazowe wykresy się pokrywają.

5. Człon inercyjny pierwszego rzędu.

Człon inercyjny pierwszego rzędu jest opisany równaniem różniczkowym:

w którym: T - stała czasowa; k - współczynnik wzmocnienia równy w elemencie inercyjnym I-go rzędu stosunkowi wartości ustalonej sygnału wyjściowego do wartości ustalonej sygnału wejściowego. Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

a w dziedzinie czasu:

Podobnie odpowiedź impulsowa:

;

Charakterystyka skokowa:

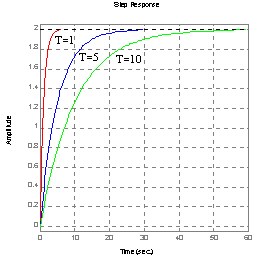
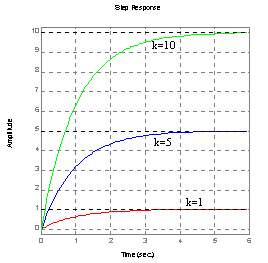
dla T=1 dla k=2

Charakterystyka Nyquist'a .

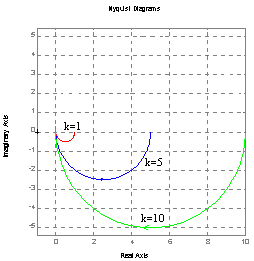
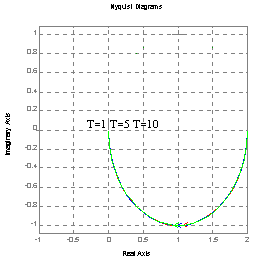
dla T=1 dla k=2

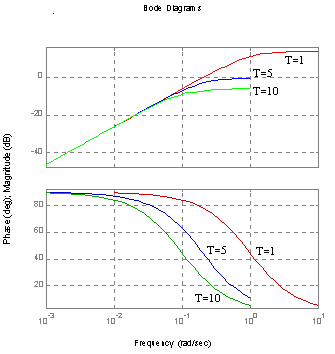
Charakterystyka Bode'go (amplitudowa, fazowa).

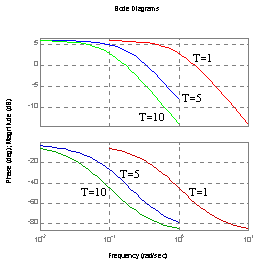
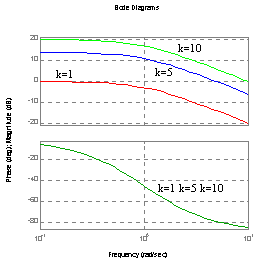
dla T=1 dla k=2

6. Człon oscylacyjny drugiego rzędu.

Człon oscylacyjny drugiego rzędu jest opisany równaniem różniczkowym:

Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

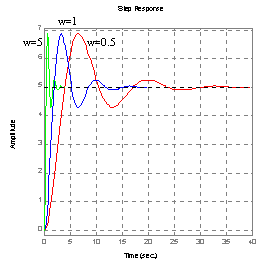
Charakterystyka skokowa:

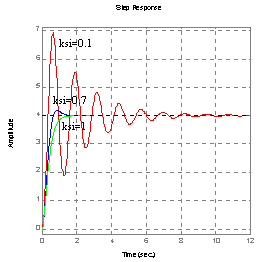
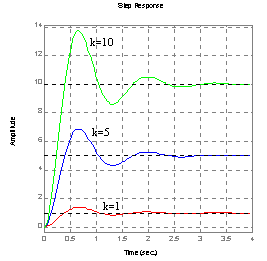
ω_n=5, k=4 ksi=0.3, ω_n=5

ksi=0.3, k=5

Charakterystyka Nyquist'a (amplitudowo-fazowa).

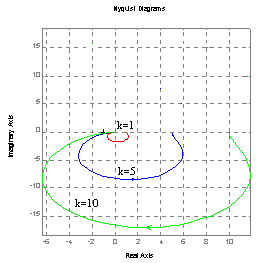
ksi=0.3, k=5 ksi=0.3, ω_n=5

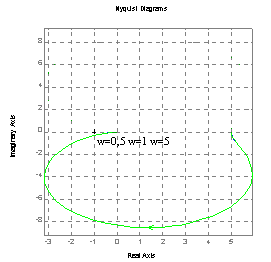
ω_n=0.3, k=5

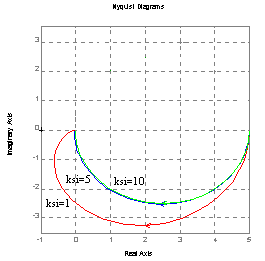
Charakterystyka Bode'go (amplitudowa, fazowa).

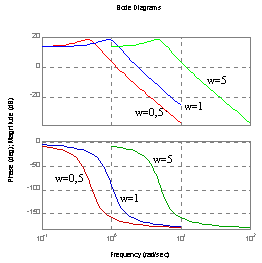
ksi=0.3, k=5 ksi=0.3, ω_n=5

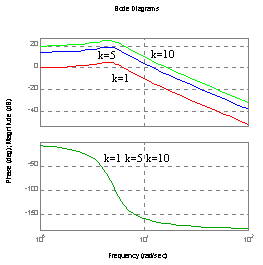
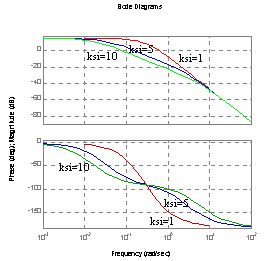
ω_n=0.3, k=5

7. Człon opóźniający.

Człon opóźniający jest opisany równaniem różniczkowym:

Po wykonaniu transformaty Laplace'a obu stron równania i założeniu zerowych warunków początkowych otrzymujemy transmitancję operatorową:

Odpowiedź jednostkową członu można wyrazić wzorem:

Charakterystyka skokowa:

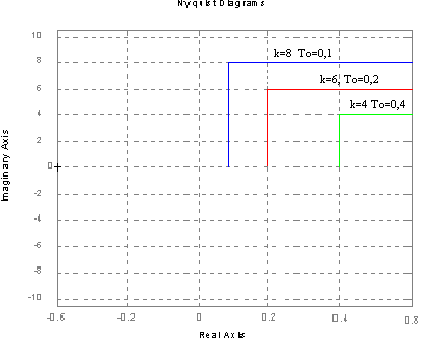
Charakterystyka Nyquist'a.

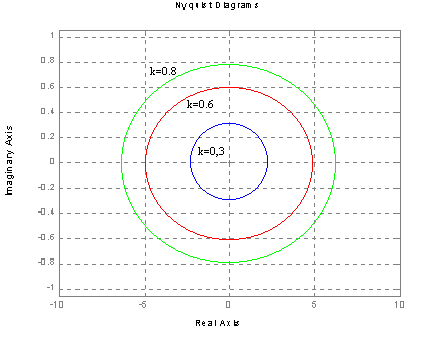
Charakterystyka Bode'go (amplitudowa, fazowa).

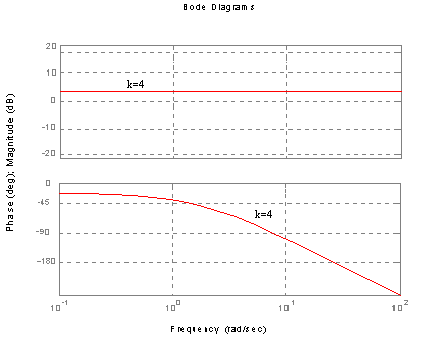
Wnioski:

W przypadku członów liniowych, które były obiektem badań, można wyróżnić trzy podstawowe wielkości charakteryzujące obiekt. Pierwszą z nich jest stała wzmocnienia k. Najogólniej można powiedzieć, że jest to stosunek - w stanie ustalonym - wartości sygnału wyjściowego do sygnału wejściowego. W przypadku członów inercyjnych i oscylacyjnego decyduje on o wartości amplitudy w stanie ustalonym dla odpowiedzi jednostkowej. Współczynnik tłumienia ξ występujący w opisie obiektów drugiego rzędu, decyduje o szybkości zaniku drgań oscylacyjnych (człon oscylacyjny) lub o czasie trwania stanu nieustalonego (człon inercyjny). Im wartość bezwzględna współczynnika ξ jest bliższa 1 to stan nieustalony obiektu jest krótszy. Trzecim parametrem opisującym obiekty liniowe jest stała czasowa T. Decyduje ona o inercyjności danego układu, czyli o czasie trwania stanu nieustalonego. Im jest ona większa tym układ dłużej osiąga stan ustalony. Na wykresach podane są charakterystyki dla kilku wartości k i ξ, preferowanych przez prowadzącego, co lepiej obrazuje zachowanie się członów podczas zmiany tych parametrów.

1

17

---