AGH, Wydział EAIiE Katedra Automatyki Napędu i Urządzeń Przemysłowych				Nazwisko i Imię: Chanowski Sławomir
LABORATORIUM TEORII SEROWANIA I TECHNIK REGULACJI				Semestr: IV
Rok szkolny: 1998/99		Rok studiów: II		Grupa: 11
Kierunek: Elektrotechnika				Nr ćwiczenia: III
Temat ćwiczenia: Badanie dynamiki podstawowych członów dyskretnych.
Data wykonania: 24-03-1999	Data oddania: 05-05-99		Data zaliczenia sprawozdania:

1. Wprowadzenie:

Układami dyskretnymi nazywamy układy z kwantowaniem sygnału w czasie. W liniowych układach impulsowych, wartości sygnałów w chwilach dyskretnych są związane ze sobą zależnościami liniowymi. Jeśli oprócz kwantowania sygnału w czasie zachodzi kwantowanie w poziomie, to taki układ nazywamy cyfrowym układem impulsowym. Cyfrowy układ impulsowy jest układem nieliniowym.

Funkcją dyskretną (impulsową) nazywamy funkcję nie ciągłą o wartościach rozpatrywanych jedynie w momentach

t=nT

zwanych chwilami kwantowania, gdzie:

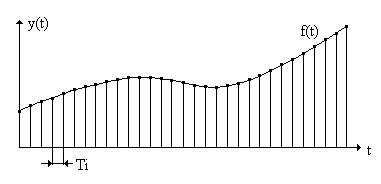
n - liczba całkowita,

T - okres próbkowania (kwantowania) - czas impulsowania.

Funkcję dyskretną otrzymujemy z funkcji ciągłej f(t) dokonując kwantowania w czasie.

Przekształceniem (transformacją) Z^* dyskretnej (impulsowej) funkcji czasu, nazywamy przekształcenie operatorowe Z[f(nT)]=F(z) określone wzorem:

gdzie:

f(nT) - oryginał,

F(z) - transformata Z funkcji f(nT).

Oryginał f(nT) można wyznaczyć (jedynie w chwilach impulsowania) na podstawie transformaty F(z) stosując odwrotne przekształcenie Z,

F(nT)=Z^-1[F(z)]

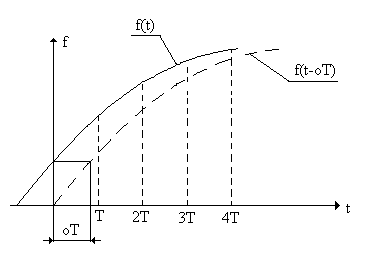
W przekształceniu Z można wyznaczyć funkcją czasu jedynie w chwilach próbkowania. Pomiędzy tymi chwilami nie wiemy nic o wartościach funkcji poszukiwanej. Jest to poważną wadą przekształcenia Z. Z tego powodu metoda przekształcenia Z nie jest adekwatna do badań układów impulsowo-ciągłych, zwłaszcza przy zbyt długim czasie próbkowania. Wady tej nie ma zmodyfikowane przekształcenie Z, oznaczane jako Z_m. Przekształcenie to pozwala wyznaczyć funkcję czasu również w czasie pomiędzy chwilami impulsowania. Dzieje sią tak dzięki fikcyjnemu opóźnieniu funkcji f(t) o odcinek ΔT. Po skwantowaniu funkcji przesuniętej mamy f(nT-ΔT).

2. Zasilanie badanych członów.

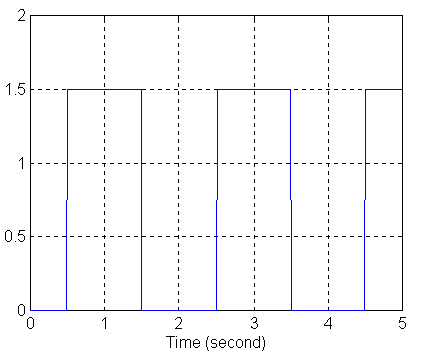
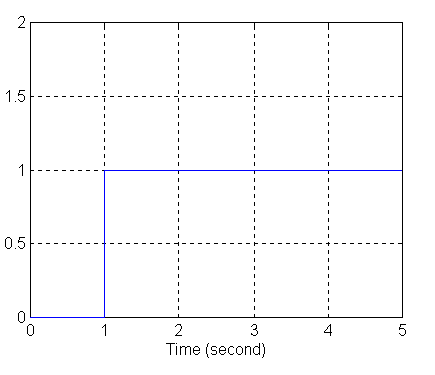
Każdy z badanych członów będzie zasilany z generatora sygnału prostokątnego (Pulse Generator) i z generatora skoku jednostkowego (Step Input).

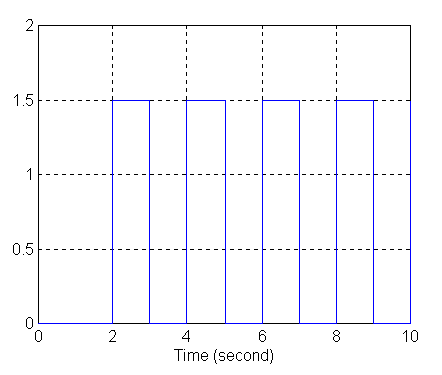
Wykres sygnału z generatora prostokątnego (Pulse Generator):

Wykres sygnału z generatora skoku jednostkowego (Step Input):

3. Badanie zachowania się członu opóźniającego G(z)=1/z

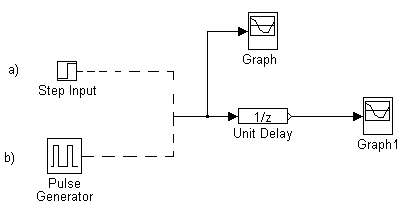
Schemat układu pomiarowego:

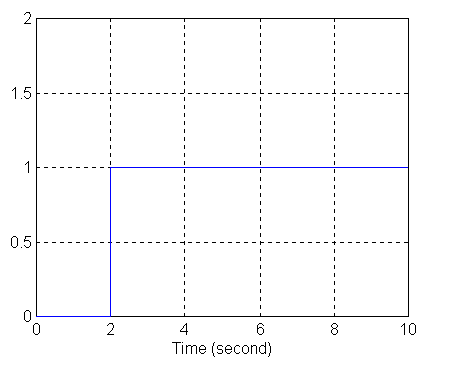
a) wykres sygnału wyjściowego przy zasilaniu z generatora skoku jednostkowego (Step Input):

b) wykres sygnału wyjściowego z generatora prostokątnego (Pulse Generator):

4. 
   Badanie zachowania się członu różniczkującego o transmitancji:

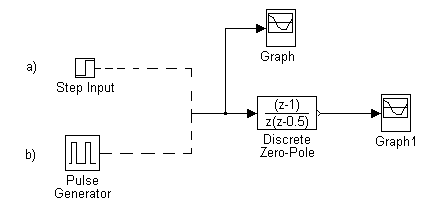
Schemat układu pomiarowego:

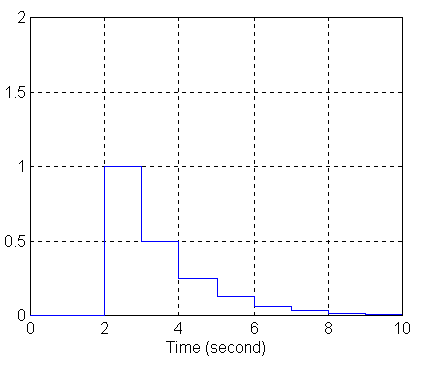
a) wykres sygnału wyjściowego przy zasilaniu z generatora skoku jednostkowego (Step Input):

b) wykres sygnału wyjściowego z generatora prostokątnego (Pulse Generator):

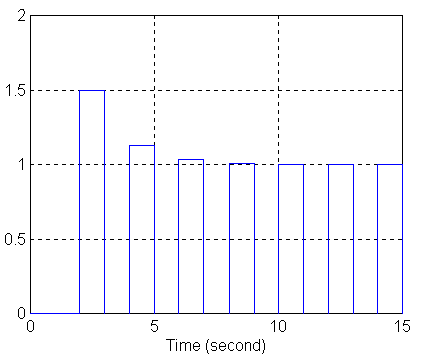
5. Badanie zachowania się członu oscylacyjnego o transmitancji:

Schemat układu pomiarowego:

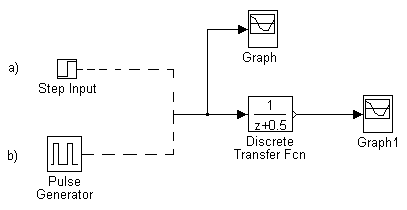
a) wykres sygnału wyjściowego przy zasilaniu z generatora skoku jednostkowego (Step Input):

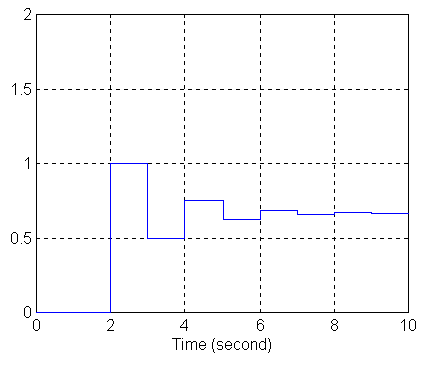
b) wykres sygnału wyjściowego z generatora prostokątnego (Pulse Generator):

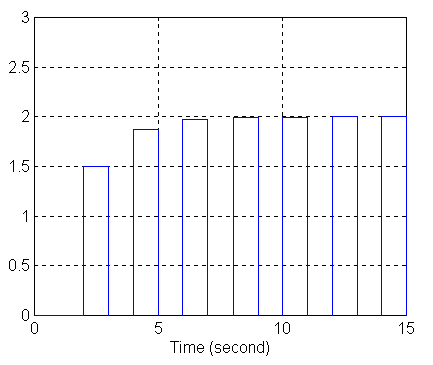
6. Badanie zachowania się członu całkującego o transmitancji:

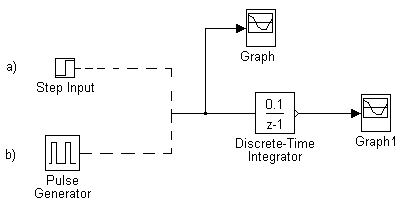
Schemat układu pomiarowego:

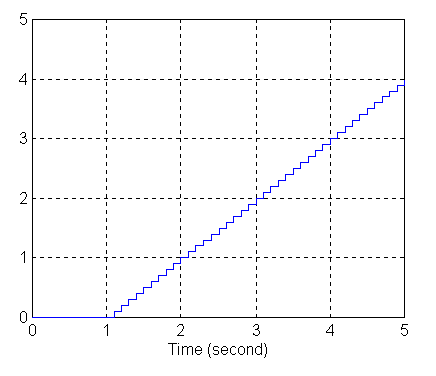
a) wykres sygnału wyjściowego przy zasilaniu z generatora skoku jednostkowego (Step Input):

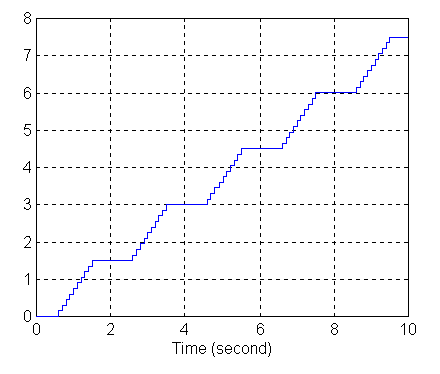
b) wykres sygnału wyjściowego z generatora prostokątnego (Pulse Generator):

7. Wnioski:

Nieliniowość otrzymanych charakterystyk spowodowane jest zadaną dyskretną transmitancją członu. Po aproksymowaniu charakterystyk, będących odpowiedzią na skok jednostkowy i sygnał prostokątny, do lini ciągłych zauważamy iż są one takie same jak charakterystyki czasowe zdejmowane w sposób ciągły. Dokładność wyznaczonych charakterystyk rośnie (bardziej przypominają charakterystyki liniowe) gdy krok kwantowania maleje. Przy nieodpowiednim (zbyt długim) czasie impulsowania np.: funkcji okresowej równym okresowi tej funkcji, metoda przekształcenia Z wyznaczania oryginałów prowadzi do błędnych wniosków wewnątrz przedziałów próbkowania. Natomiast wyniki prawidłowe zapewnia metoda zmodyfikowana przekształcenia Z_m przy dowolnym okresie próbkowania. Obecnie w technice pomiarowej i przy analizie układów najczęściej stosowane jest kwantowanie równomierne, dlatego różnice pomiędzy sąsiednimi stanami kwantowania są jednakowe w całym zakresie i równe jednemu kwantowi. Wartość kwantu można dowolnie regulować. Z niezmienności wartości kwantu wynika bardzo mały błąd kwantowania. W naszym przypadku proces kwantowania najlepiej widać na charakterystykach dla członu całkującego są to widoczne „schodki”. Wszelkie układy pomiarowe, sterowania, analizy, coraz to częściej opierają się na technice cyfrowej (dyskretnej). Technika ta jest stosowana ze względu na swe zalety:

• łatwość przesyłania sygnału cyfrowego,

• mniejsze zakłócenia występujące przy przesyłaniu,

• coraz częstsze wykorzystanie komputerów w technice ,

• szybkość przetwarzania A/C i C/A.

W rzeczywistych układach dynamicznych liniowych, zależności dyskretnej funkcji wyjściowej y(t) od dyskretnej funkcji wejściowej u(t) jest opisana liniowym równanie różnicowym. Rozwiązywanie równań różnicowych jest znacznie łatwiejsze od rozwiązywania równań różniczkowych (Laplace'a), co skraca czas i ułatwia analizę układów. Każde równanie różniczkowe układu dynamicznego można przekształcić w równanie różnicowe dokonując kwantowania sygnałów w czasie i przybliżając różniczki różnicami. Dokładność tego przybliżenia rośnie gdy okres próbkowania T maleje.

1

10

---