AKADEMIA GÓRNICZO - HUTNICZA W KRAKOWIE			Grupa B Rafał Szemraj
EAIiE	2001/2002		Rok II Semestr IV	Elektrotechnika		Rok B Grupa 8
Temat: Charakterystyki dynamiczne podstawowych członów - część druga
Data wykonania: 2002-03-14		Data zaliczenia:			Ocena:

1. Wstęp teoretyczny:

W automatyce przyjęto zwyczajowo opisywać i przedstawiać wszelkiego rodzaju układy sterowania i regulacji za pomocą schematów blokowych. Podstawowymi elementami takich schematów są elementy (bloki, człony) służące do odpowiedniego przekształcania (transformacji) sygnałów. Każdy taki element opisuje pewna formuła matematyczna na podstawie której określa się zależność pomiędzy sygnałem wejściowym elementu (wymuszeniem) a sygnałem wyjściowym (odpowiedzią układu).Niektóre z takich elementów są dość skomplikowane, ale nawet takie można przedstawić jako złożenie kilku tzw. członów elementarnych. Ogólnie rzecz biorąc każdy schemat blokowy stacjonarnego układu liniowego można przedstawić jako kombinację trzech podstawowych członów: proporcjonalnego, różniczkującego i całkującego połączonych w odpowiedni sposób węzłami zaczepowymi i sumacyjnymi. W praktyce niektóre elementy nieco bardziej złożone niż wymienione wyżej, które również można przedstawić jako złożenie członów podstawowych, także zostały zaliczone do członów elementarnych. Ogólnie rzecz biorąc do członów elementarnych zaliczamy:

• Proporcjonalny

• Całkujący

• Różniczkujący idealny

• Różniczkujący rzeczywisty

• Inercyjny

• Oscylacyjny

Jak wspomniałem wcześniej każdy z członów podstawowych opisany jest funkcją matematyczną określającą związek pomiędzy wymuszeniem i odpowiedzią układu. Jakkolwiek układy takie realizują operacje na sygnałach będących funkcjami czasu to do opisu matematycznego tychże elementów posługujemy się tzw. transformatą Laplace'a . Upraszcza to w znaczny sposób opis zarówno pojedynczego elementu jak również układu bardziej złożonego.

Jako cechy charakterystyczne danego elementu przedstawia się jego charakterystyki będące graficznym przedstawieniem działania. Do takich charakterystyk należą:

• Ch-ka czasowa, będąca odpowiedzią na skok jednostkowy
  ,
  

• Ch-ka Bodego (ch-ka amplitudowa i częstotliwościowa)

• Ch-ka Nyquista (ch-ka amplitudowo - częstotliwościowa na płaszczyźnie zespolonej

Do podstawowych wielkości opisujących dany element zaliczamy:

• Transmitancję operatorową:
  

• Transmitancję widmową:
  

• Moduł transmitancji widmowej:
  

• Faza transmitancji widmowej:
  

• Wzmocnienie (w decybelach [dB]):
  

2. Opis członu proporcjonalnego:

Człon inercyjny opisujemy takim oto równaniem czasowym:

,, gdzie:

- odpowiednio sygnał wejściowy i wyjściowy.

T - stała czasowa układu.

Po dokonaniu transformaty Laplace'a powyższego równania otrzymujemy:

Stąd transmitancja operatorowa układu:

Zbadajmy odpowiedź układu na wymuszenie w postaci skoku jednostkowego
, czyli
:

Mamy:
, a w dziedzinie czasu:
.

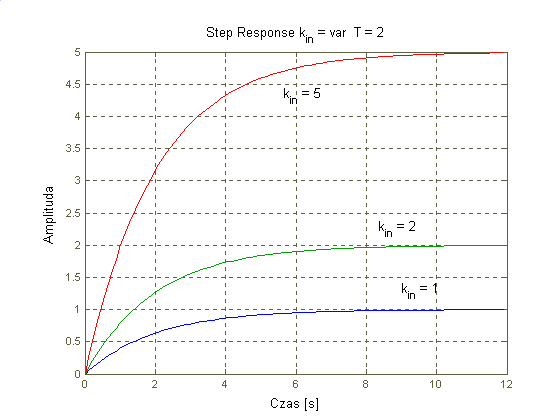
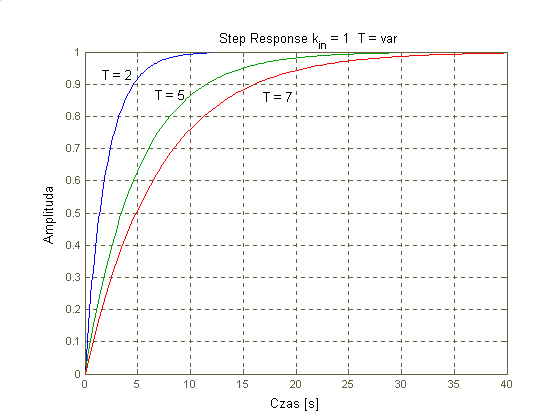
Widać więc, że odpowiedzią układu na wymuszenie skokiem jednostkowym jest krzywa wykładnicza narastająca od zera do wartości k_in. Im wieksza wartość stałej czasowej T tym czas ustalania się odpowiedzi jest dłuższy. Transmitancja widmowa:

⇒
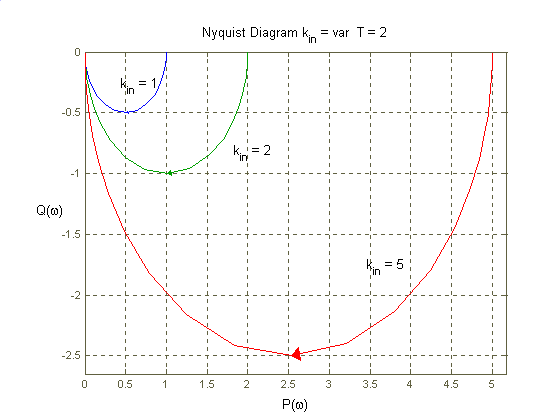
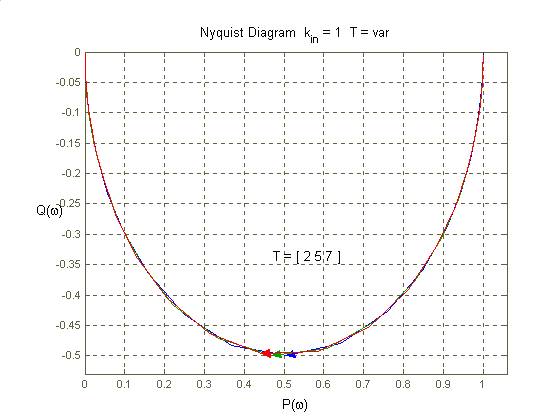
, Ch-ka Nyquista ma postać paraboli. Przyjrzyjmy się dla jakich wartości
amplituda transmitancji widmowej jest największa:

Widzimy więc, że dla zerowej pulsacji amplituda jest największa i wynosi
. Na płaszczyźnie ch-ki Nyquista sytuacji tej odpowiada punkt o współrzędnych
i
. Tak jak dla członu różniczkującego rzeczywistego tak i tutaj punktowi wierzchołka paraboli odpowiadaja sytuacja gdy
Wtedy
i
, a amplituda transmitancji widmowej maleje
razy (czyli wzmocnienie zmniejsza się o 3 dB).

Kwestie do rozważenia:

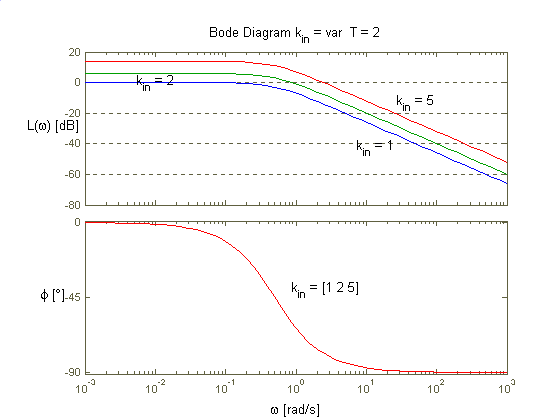
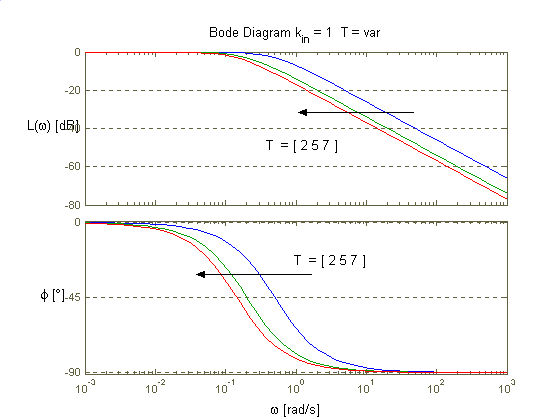
• Człon inercyjny jest filtrem dolnoprzepustowym, ponieważ ma największe wzmocnienie dla zerowej częstotliwości. Dla pulsacji równej odwrotności stałej czasowej wzmocnienie maleje o 3dB. Wyższe częstotliwości są coraz silniej tłumione.

• Dla dużych wartości pulsacji ch-ka bodego dla członu inercyjnego w dość dobrym stopniu przybliża ch-kę Bodego członu całkującego. Można więc założyć, że dla zakresu dużych częstotliwości (odpowiednio większych od odwrotności stałej czasowej) układ działa jak integrator. Również dla bardzo małej czasowej i w krótkim przedziale czasu wykres odpowiedzi na skok jednostkowy obu układów jest zbliżony.

• Im większa stała czasowa T tym próg częstotliwości od której układ możemy uznać za integrator obniża się.

• Im większy współczynnik k_in tym kształt odpowiedzi układu jest bardziej zbliżony do prostej (czyli do kształtu odpowiedzi członu całkującego).

4. 
   Opis członu oscylacyjnego:

Człon oscylacyjny możemy opisać następującym równaniem:

gdzie:

- odpowiednio sygnał wejściowy i wyjściowy.

T - okres drgań rezonansowych członu.

ξ - współczynnik tłumienia członu.

Po dokonaniu transformaty Laplace'a otrzymujemy:

a stąd
.

Przyjrzyjmy się biegunom tej transmitancji:

Widzimy więc, że od wartości współczynnika tłumienia zależy ilość i charakter biegunów transmitancji. Ogólnie rzecz biorąc bieguny możemy przedstawić za pomocą wzorów:

gdzie

Odpowiedź na wymuszenie skokiem jednostkowym ma postać:

. Po przejściu na dziedzinę czasu mamy:

,

Jak zauważymy dla ξ = 0 (brak tłumienia) odpowiedź ma kształt cosinusa:

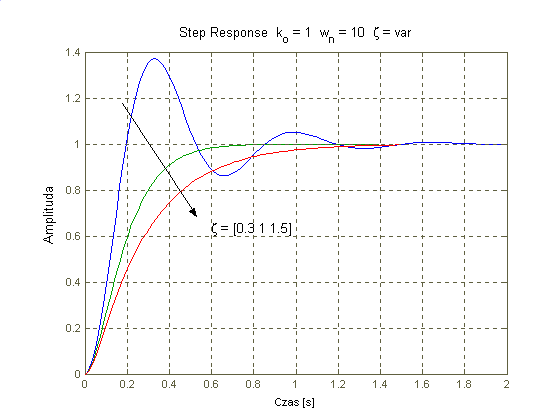
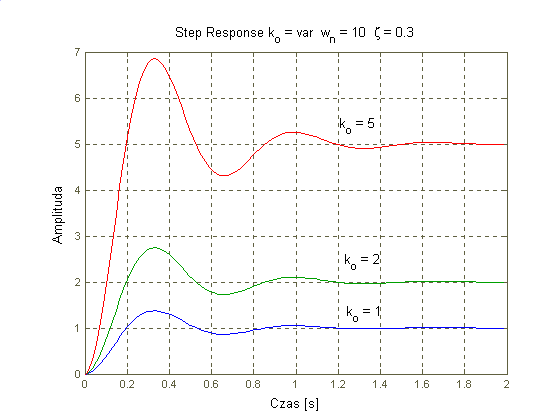
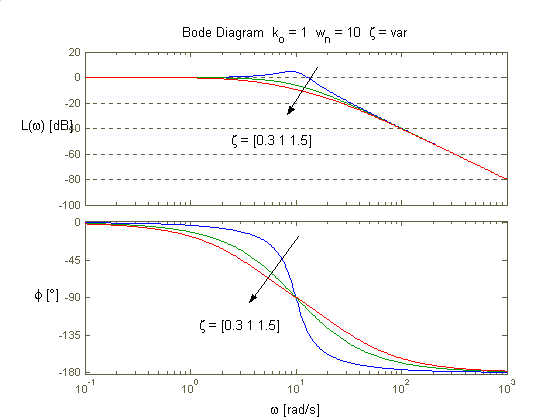
Dla wartości równych i większych od jedynki tłumienie jest tak duże, że oscylacje nie występują i układ zachowuje się jak człon inercyjny. Dla tłumienia z zakresu od 0 do 1 odpowiedź układu oscyluje wokół wartości wzmocnienia k (im wartość ξ bardziej zbliżona do 1 oscylacje są tłumione w bardziej widoczny sposób). Dla wartości mniejszych od zera układ jest niestabilny (oscylacje zamiast wytłumieniu ulegają wzmocnieniu) a dla wartości ξ ≤ -1 układ oprócz niestabilności charakteryzuje się zanikiem oscylacji.

Postać transmitancji widmowej:

Mamy więc :

Obrazem charakterystyki Nyquista są krzywe zamknięte na płaszczyźnie liczb zespolonych o początku w punkcie
i końcu
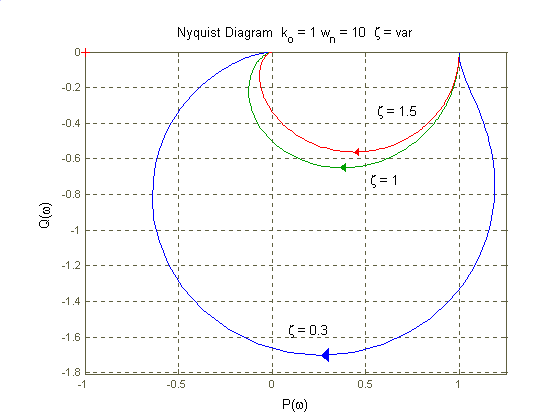
. Promień krzywizny zależy przede wszystkim od wartości współczynnika tłumienia (im jest on większy tym promień mniejszy). Przyjrzyjmy się dla jakiej pulsacji moduł transmitancji jest największy - dla zerowej pulsacji jest on równy k₀. Dla pulsacji równej

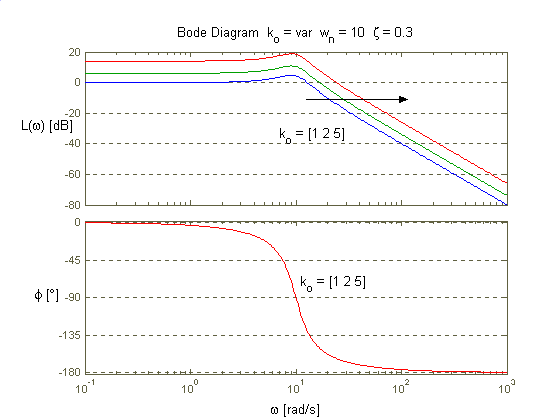
. Zauważmy zatem, że jeżeli spełniony jest warunek ξ ≤ 0,5 to wzmocnienie układu jest największe dla pulsacji równej pulsacji drgań własnych układu oscylacyjnego. Dla wartości większych wzmocnienie maleje wraz ze wzrostem pulsacji od zera do nieskończoności. Dla tejże charakterystycznej wartości omegi przesunięcie fazowe członu wynosi -90⁰ i nie zależy od współczynnika tłumienia. Dla innej wartości kształt charakterystyki fazowej zależy od współczynnika tłumienia. Im bardziej jest on większy przebieg tej ch-ki jest bardziej płynny.

• Charakter członu zależy od współczynnika tłumienia. W zależności od jego wartości układ może być oscylacyjny, mieć charakter członu inercyjnego lub charakteryzować się niestabilnością.

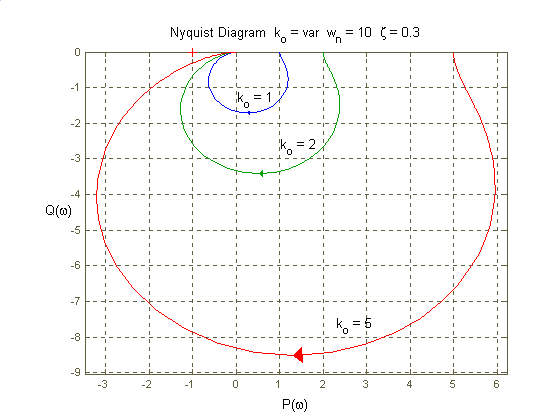
• Odpowiedź układu na wymuszenie skokiem jednostkowym po ustaleniu osiąga wartość współczynnika wzmocnienia k₀. Wzmocnienie jest odpowiednio do niego proporcjonalne a jego wartość wyznacza charakterystyczny punkt na osi rzeczywistej ch-ki Nyquista.

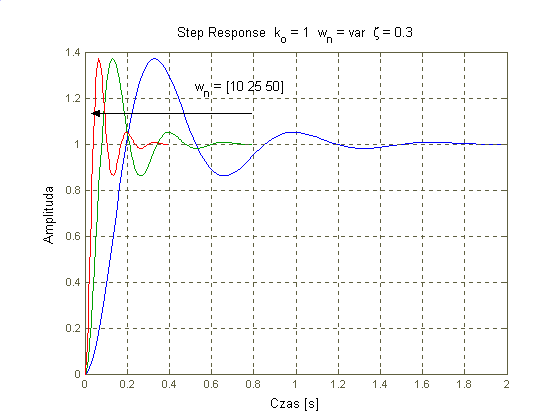
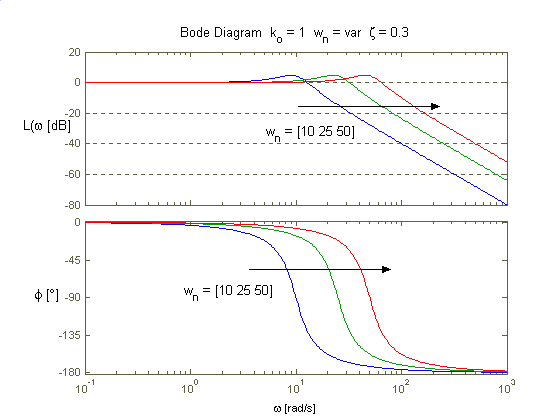
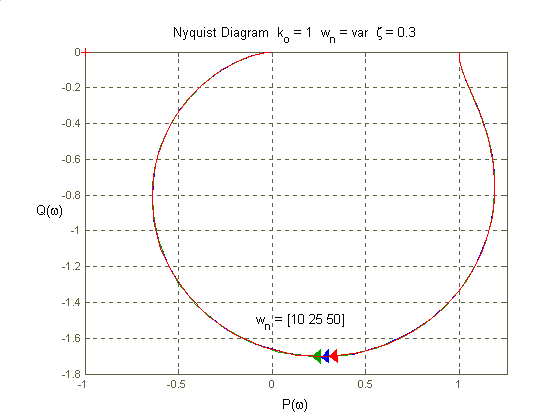
• Im mniejszy okres drgań własnych tym układ szybciej osiąga stan ustalony i częstotliwość drgań (w przypadku obecności oscylacji) jest większa. Punkt na charakterystyce fazowej dla którego przesunięcie wynosi -90⁰ przesuwa się w prawo gdy T maleje. Na ch-kę Nyquista zmiana okresu drgań własnych nie ma wpływu.

• Od wartości współczynnika tłumienia zależy charakter odpowiedzi (oscylacje, brak oscylacji, niestabilność) jak również obecność maksimum modułu transmitancji widmowej (obecne dla ξ ≤ 0,5). Im większa wartość współczynnika tym bardziej łagodna ch-ka fazowa oraz promień ch-ki Nyquista ulega skróceniu (sygnał zostaje w większym stopniu tłumiony).

Charakterystyka dynamiczna podstawowych członów2

Rafał Szemraj Strona 8

---