4.5. Przekształcenia jednorodne
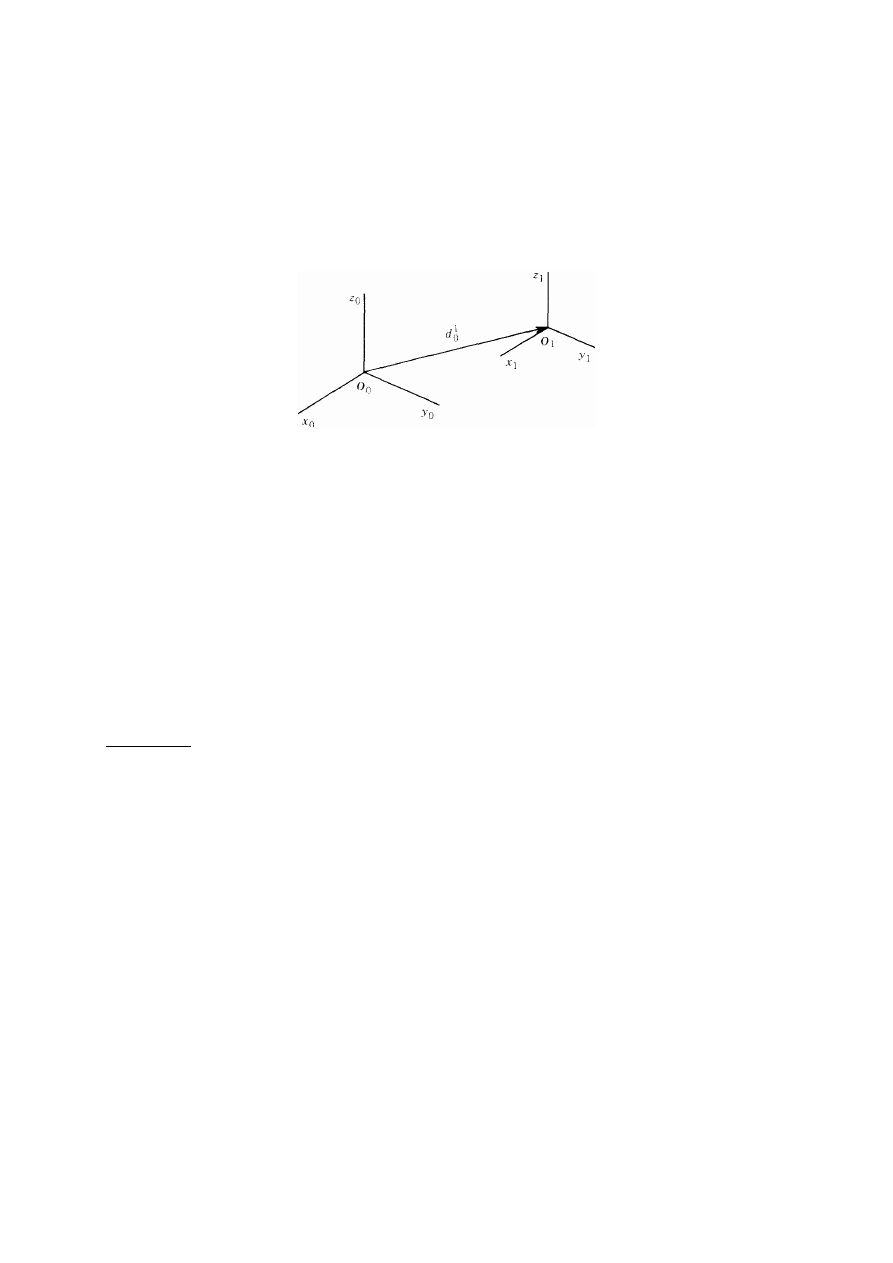
Rozważmy teraz układ współrzędnych Ox
1
y
1
z
1
otrzymany z układu Ox
0
y
0
z
0
przez
przesunięcie równoległe o odległość |d|, jak to pokazano na rys. 37. Wówczas wektory
jednostkowe i
0
, j
0
, k
0
są równoległe odpowiednio do wektorów i
1
, j
1
, k
1
. Wektor d jest
wektorem o początku w punkcie O
0
, a końcu w punkcie O
1
wyrażonym w układzie
współrzędnych Ox
0
y
0
z
0
.
Rys. 37. Układ przesunięty
Dowolny punkt P ma reprezentacje p
0
i p
1
jak poprzednio. Ponieważ odpowiednie osie
współrzędnych w tych dwóch układach są równoległe, więc wektory p
0
i p
1
są powiązane
zależnością
p
0
= p
1
+ d
0
1
(85)
lub
p
0x
= p
1x
+ d
0x
1
(86)
p
0y
= p
1y
+ d
0y
1
(87)
p
0z
= p
1z
+ d
0z
1
(88)
Najbardziej ogólnie związek między rozważanymi układami współrzędnych Ox
0
y
0
z
0
i
Ox
1
y
1
z
1
może być wyrażony przez kombinację czystego obrotu i czystego przesunięcia, co
jest określane jako ruch sztywny.
Definicja 1.
Przekształcenie
p
0
= Rp
1
+ d
(89)
definiuje ruch sztywny, jeżeli macierz R jest ortogonalna. Zauważmy, że ta definicja obejmuje
również odbicia, gdy det R = -l. W naszym przypadku nie będziemy potrzebować najbardziej
ogólnego ruchu sztywnego, przyjmujemy więc zawsze, że R
∈
SO(3).
Jeżeli zatem mamy dwa ruchy sztywne
p
0
= R
0
1
p
1
+ d
0
1
(90)
p
1
= R
1
2
p
2
+ d
1
2
(91)
to ich połączenie określa trzeci ruch sztywny, który możemy opisać przez podstawienie
wyrażenia dla p
1
z wzoru (91) do zależności (90). Otrzymujemy wtedy
p
0
= R
0
1
R
1
2
p
2
+ R
0
1
d
1
2
+ d
0
1
(92)
Ponieważ jednak związek między wektorami p
0
i p
1
jest także ruchem sztywnym, możemy go
opisać jako
p
0
= R
0
2
p
2
+ d
0
2
(93)
Z porównania równań (92) i (93) otrzymujemy równości
R
0
2
= R
0
1
R
1
2
(94)
d
0
2
= d
0
1
+ R
0
1
d
1
2
(95)
Równość (94) pokazuje, że przekształcenia orientacji mogą być po prostu mnożone, a
równanie (95) pokazuje, że wektor od początku O
0
do początku O
2
jest sumą wektorową

wektora d
0
1
od O
0
do O
1
i wektora R
0
1
d
1
2
od O
1
do O
2
wyrażonych w orientacji układu
współrzędnych Ox
0
y
0
z
0
.
Porównanie tego z równością macierzową
+
=
⋅
1
0
d
d
R
R
R
1
0
d
R
1
0
d
R
1
0
2
1
1
0
2
1
1
0
2
1
2
1
1
0
1
0
(96)
gdzie
0 oznacza (000), pokazuje, że ruchy sztywne mogą być reprezentowane przez zbiór
macierzy o postaci
)
3
(
R
;
1
0
d
R
H
SO
∈
=
(97)
Korzystając z faktu, że macierz
R jest ortogonalna, łatwo jest pokazać, że przekształcenie
odwrotne
H
-1
jest określone następująco
=
1
0
d
R
-
R
H
T
T
1
-
(98)
Macierze przekształceń postaci (97) są
nazywane przekształceniami jednorodnymi.
Aby przedstawić przekształcenie (89) jako mnożenie macierzy, trzeba rozszerzyć wektory
p
0
i
p
1
przez dodanie czwartego składnika równego jedności następująco:
Przyjmijmy, że
=
1
P
0
0
p
(99)
=
1
P
1
1
p
(100)
Wektory
P
0
i
P
1
są znane jako
reprezentacje jednorodne odpowiednio wektorów p
0
i
p
1
. Można teraz bezpośrednio zobaczyć, że przekształcenie (89) jest równoważne
(jednorodnemu) równaniu macierzowemu
P
0
=
H P
1
+
H
0
1
P
1
(101)
Zbiór wszystkich 4x4-macierzy
H postaci (97) jest oznaczany jako E(3). Zbiór
podstawowych przekształceń jednorodnych generujących grupę E(3) jest określony
związkami
=
1
0
0
0
0
1
0
0
0
0
1
0
0
0
1
,
a
Trans
a
x
(102)
=
1
0
0
0
0
1
0
0
0
1
0
0
0
0
1
,
b
Trans
b
y
(103)
=
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
,
c
Trans
c
z
(104)
dla przesunięcia oraz związkami
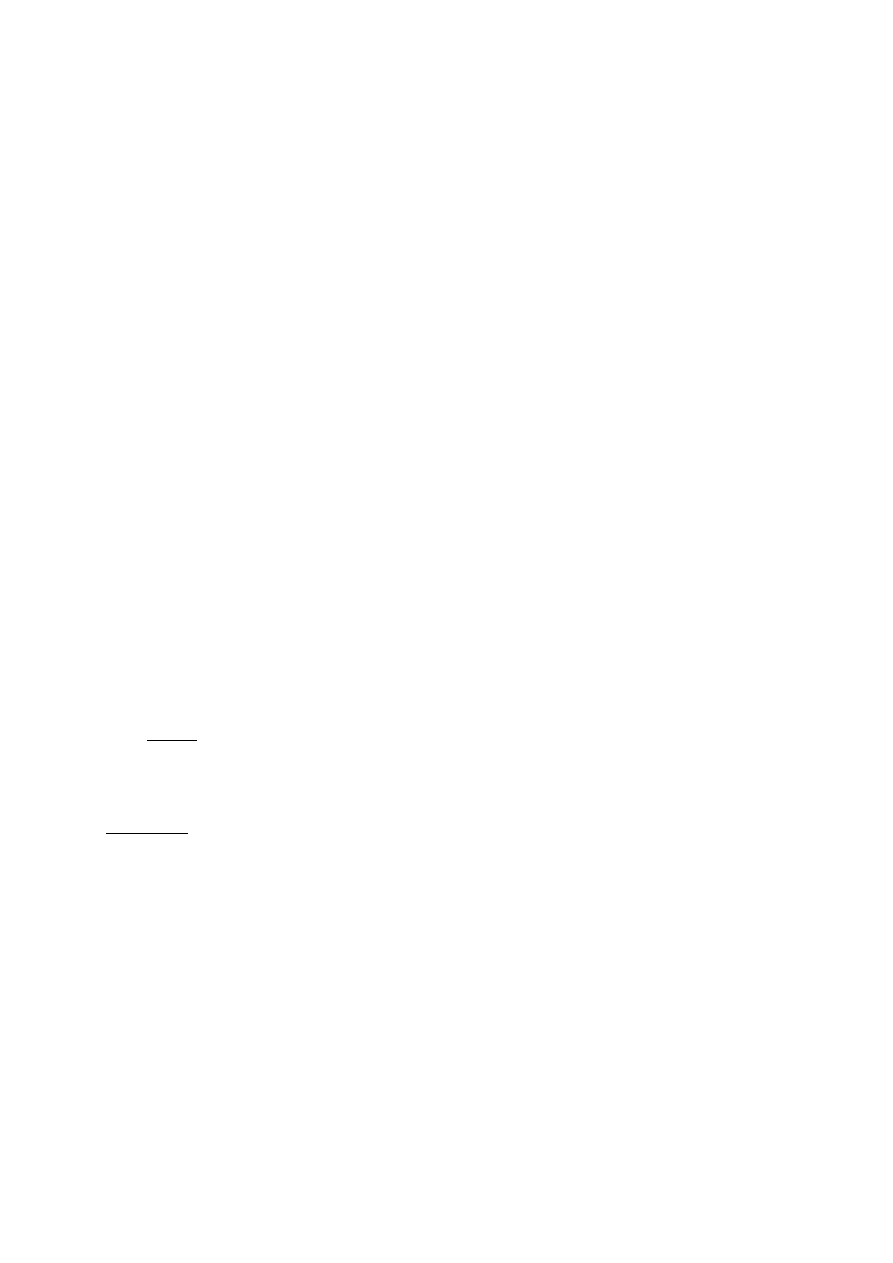
−
=
1
0
0
0
0
0
0
0
0
0
0
1
,
α
α
α
α
α
c
s
s
c
Rot
x
(105)
−
=
1
0
0
0
0
0
0
0
1
0
0
0
,
φ
φ
φ
φ
φ
c
s
s
c
Rot
y
(106)
−
=
1
0
0
0
0
1
0
0
0
0
0
0
,
θ
θ
θ
θ
θ
c
s
s
c
Rot
z
(107)
dla obrotu wokół osi x, y, z.
Najbardziej ogólne przekształcenie jednorodne, które będziemy rozważać, może zatem
być zapisane jako
=
=
1
0
0
0
d
a
s
n
1
0
0
0
T
z
z
z
z
y
y
y
y
x
x
x
x
d
a
s
n
d
a
s
n
d
a
s
n
(108)
W powyższym równaniu n = (n
x
, n
y
, n
z
)
T
jest wektorem reprezentującym kierunek osi
O
1
x
1
, w układzie Ox
0
y
0
z
0
, s = (s
x
, s
y
, s
z
)
T
reprezentuje kierunek osi O
1
y
1
, zaś a = (a
x
, a
y
, a
z
)
T
reprezentuje kierunek osi O
1
z
1
. Wektor d = (d
x
, d
y
, d
z
)
T
reprezentuje wektor od początku O
0
do
początku O
1
wyrażony w układzie Ox
0
y
0
z
0
. Powód wybrania liter n, s oraz a zostanie
wyjaśniony w rozdz. 3.
Uwaga: Dla przekształceń jednorodnych o wymiarach 4x4 obowiązuje taka sama
interpretacja dotycząca składania przekształceń oraz ich kolejności, jak dla obrotów o
wymiarach 3x3.
Przykład 8.
Macierz przekształcenia jednorodnego H, która reprezentuje obrót o kąt
α
wokół osi bieżącej
x; z następującymi potem: przesunięciem o b jednostek wzdłuż bieżącej osi x, przesunięciem
o d jednostek wzdłuż bieżącej osi z, obrotem o kąt
θ
wokół bieżącej osi z, jest określona
następująco
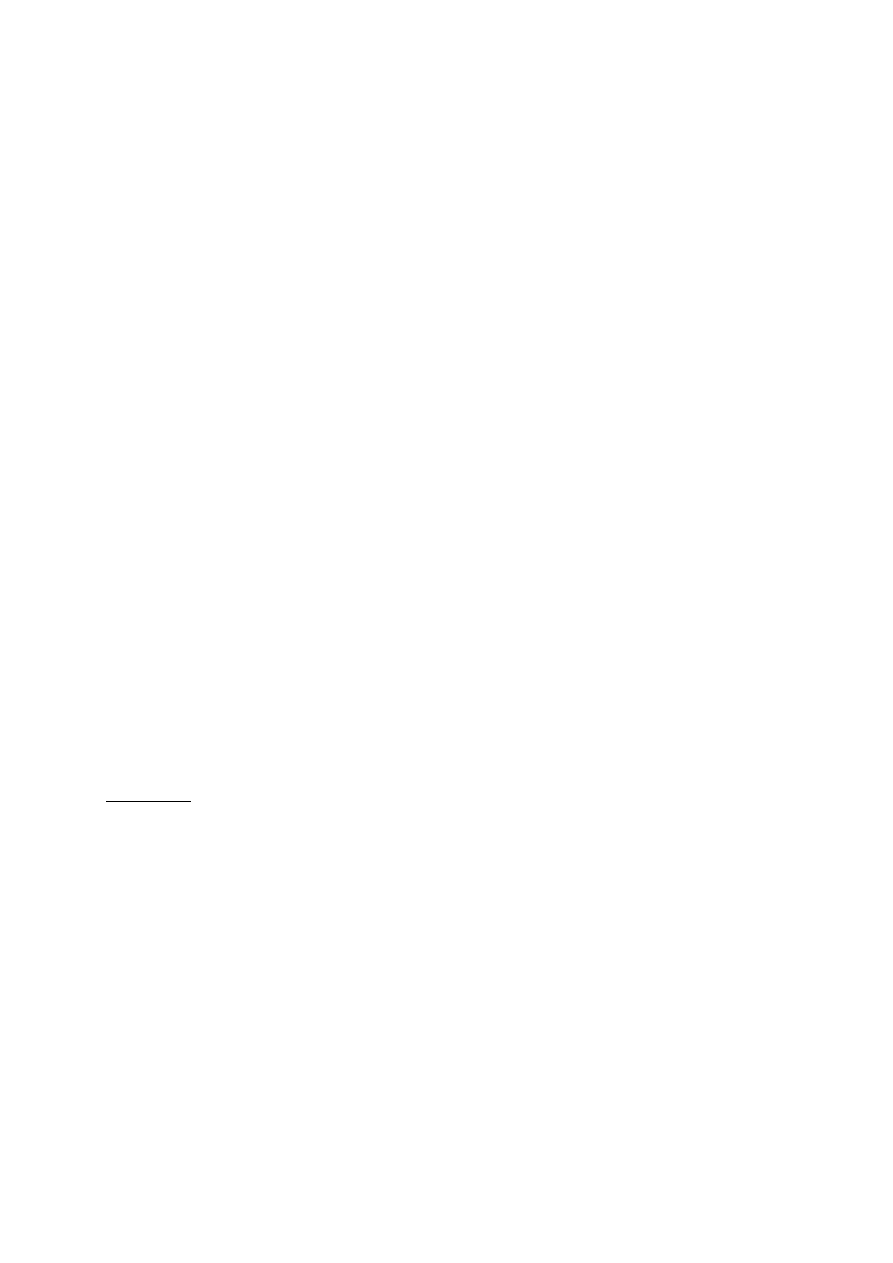
−
−
−
=
−
⋅
⋅
⋅
−
=
=
=
1
0
0
0
cos
cos
cos
sin
sin
sin
sin
sin
cos
cos
sin
cos
0
sin
cos
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
1
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
H
,
,
,
,
α
α
ϕ
α
ϕ
α
α
α
ϕ
α
ϕ
α
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
α
α
α
α
ϕ
α
d
d
b
d
b
Rot
Trans
Trans
Rot
z
d
z
b
x
x
(109)
Reprezentacja jednorodna (97) jest specjalnym przypadkiem współrzędnych
jednorodnych, które są szeroko stosowane w dziedzinie grafiki komputerowej . Dodatkowo
interesujące są tam przekształcenia skalowania i/lub perspektywy. Najbardziej ogólne
przekształcenie jednorodne przybiera postać
−
−
−
−
−
−
=
−
−
−
−
−
−
=
×
×
×
×
skalowanie
|
a
perspektyw
|
ie
przesunięr
|
obrót
s
|
f
|
d
|
R
H
1
1
3
1
1
3
3
3
(110)
Dla naszych celów zawsze przyjmujemy wektor w ostatnim wierszu macierzy
H
równy (0, 0, 0, l), chociaż ogólniejsza postać dana równaniem (110) może być użyteczna do
włączenia systemu wizyjnego w szerszy system zrobotyzowany lub do symulacji graficznej.
4.6. Macierze skośniesymetryczne
W tej części wykładów wyprowadzimy niektóre dalsze własności macierzy obrotów,
użyteczne do obliczania względnych przekształceń prędkości i przyśpieszeń między układami
współrzędnych. Takie przekształcenia są związane z obliczaniem pochodnych macierzy
obrotów. Dzięki wprowadzeniu zapisu macierzy skośniesymetrycznych możliwe jest
uproszczenie wielu obliczeń.
Definicja 2.
Macierz S jest nazywana
macierzą skośniesymetryczną wtedy i tylko wtedy, gdy
S
T
+
S = 0
(111)
Zbiór wszystkich macierzy skośniesymetrycznych o wymiarze 3x3 oznaczamy przez
SS(3).
Jeżeli
S
∈
SS(3) ma elementy s
ij
,
i, j = l, 2, 3, wtedy równanie (111) jest równoważne
dziewięciu równaniom postaci
s
ij
+
s
ji
= 0, oraz
i, j = 1, 2, 3
(112)
Z zależności (112) widzimy, że
s
ii
= 0, tzn. elementy na przekątnej macierzy
S są
równe zeru, a elementy poza przekątną
s
ij
dla
i ≠ j spełniają równość s
ij
= -s
ji
. Stąd macierz S
ma tylko trzy niezależne wiersze lub kolumny i każda skośniesymetryczna macierz 3x3 jest
postaci
−
−
−
=
0
0
0
S
3
2
3
1
2
1
s
s
s
s
s
s
(113)
Jeżeli natomiast
a = (a
x
,
a
y
,
a
z
)
T
, jest 3-wymiarowym wektorem, to macierz
skośniesymetryczną
S(a) definiujemy następująco

−
−
−
=
0
0
0
S(a)
x
y
x
z
y
z
a
a
a
a
a
a
(114)
Przykład 9.
Macierze skośniesymetryczne S(i), S(j) i S(k) otrzymane dla wektora a równego
odpowiednio jednostkowym wektorom normalnym i, j i k, są dane równościami
−
=
0
1
0
1
0
0
0
0
0
S(i)
(115)
−
=
0
0
1
0
0
0
1
0
0
S(j)
(116)
−
=
0
0
0
0
0
1
0
1
0
S(k)
(117)
Ważną własnością macierzy S(a) jest liniowość. Oznacza to, że dla dowolnych
wektorów a i b należących do przestrzeni R
3
oraz skalarów
α
i
β
jest spełniona równość
S(
α
a +
β
b) =
α
S(a) +
β
S(b)
(118)
Inną ważną własnością macierzy S(a) jest to, że dla dowolnego wektora p = (p
x
, p
y
, p
z
)
T
można napisać zależność
S(a) p = a
×
p
(119)
gdzie a
×
p określa iloczyn wektorowy. Równanie (119) może być sprawdzone przez
bezpośrednie obliczenie.
Jeżeli R
∈
SO(3) i a, b są wektorami w przestrzeni średnio przeliczając można
pokazać, że
R(a
×
b) = Ra
×
Rb
(120)
Równanie (120) nie jest prawdziwe w ogólności, jeżeli R nie jest macierzą ortogonalną.
Oznacza ono, że jeżeli najpierw obrócimy wektory a i b, używając obrotu R, a potem
utworzymy iloczyn wektorowy obróconych wektorów R(a) i R(b), to rezultat będzie taki sam,
jak otrzymany przez utworzenie najpierw iloczynu wektorowego a
×
b, a potem obrócenie do
wektora R(a
×
b).
Dla dowolnych przekształceń R, S
∈
SO(3) i dowolnych wektorów a, b
∈
R
3
z równań
(119) i (120) wynika, że
RS(a) R
T
b = R(a
×
R
T
b) = (R a)
×
(R R
T
b) = (R a)
×
b = S(R a) b
(121)
W ten sposób pokazaliśmy użyteczny fakt, że
RS(a) R
T
= S(R a)
(122)
Równanie (122) jest jednym z użyteczniej wyrażeń. Lewa strona tego równania reprezentuje
przekształcenie macierzy S(a) przez podobieństwo. Równanie (122) stwierdza, że
reprezentacja macierzy S(a) w układzie współrzędnych obróconym przez R jest taka sama jak
macierz skośniesymetryczna S(R a) odpowiadająca wektorowi a obróconemu przez R.

Załóżmy teraz, że macierz obrotu R jest funkcją jednej zmiennej
θ
. Stąd R = R(
θ
)
∈
SO(3) dla każdego kąta
θ
. Ponieważ macierz R jest ortogonalna dla wszystkich kątów
θ
, więc
R(
θ
) R(
θ
)
T
= I
(123)
Po zróżniczkowaniu obu stron równości (123) względem
θ
jako pochodną iloczynu
otrzymamy
0
d
dR
)
R(
)
R(
d
dR
=
+
θ
θ
θ
θ
T
T
(124)
Zdefiniujmy macierz:
T
)
R(
d
dR
S
θ
θ
=
(125)
Wówczas transpozycją macierzy
S jest macierz
θ
θ
θ
θ
d
dR
)
R(
)
R(
d
dR
S
T
T
T
T
=
=
(126)
Równanie (124) oznacza wówczas, że
S + S
T
= 0
(127)
Innymi słowy, macierz
S zdefiniowana wzorem (125) jest skośniesymetryczna. Mnożąc obie
strony równości (125) przez
R i wykorzystując fakt, że R
T
R = I, otrzymujemy
)
SR(
d
dR
θ
θ
=
(128)
Równanie (128) jest bardzo ważne. Oznacza ono, że obliczenie pochodnej macierzy
obrotu
R jest równoważne pomnożeniu tej macierzy przez macierz skośniesymetryczną S.
Najczęściej spotyka się sytuację, gdy
R jest podstawową macierzą obrotu lub iloczynem
podstawowych macierzy obrotu.
Przykład 10.
Jeżeli
R = R
x,
θ
jest podstawową macierzą obrotu określoną równaniem (52), to
bezpośrednie obliczenie pokazuje, że
S(i)
0
1
0
1
0
0
0
0
0
cos
sin
0
sin
cos
0
0
0
1
sin
cos
0
cos
sin
0
0
0
0
R
d
dR
S
=
−
=
⋅
−
−
=
=
θ
θ
θ
θ
θ
θ
θ
θ
θ
T
(129)
Stąd otrzymujemy
θ
θ
θ
,
x,
S(i)R
d
dR
x
=
(130)
a w wyniku podobnych obliczeń dostajemy pozostałe pochodne
θ
θ
θ
,
y,
S(j)R
d
dR
y
=
(131)
θ
θ
θ
,
z,
S(k)R
d
dR
z
=
(132)
Przykład 11.
Niech
R
k,
θ
będzie obrotem wokół osi zdefiniowanej przez wektor
k jak w zależności
(74). Można łatwo sprawdzić, że
S(k)
3
= -
S(k). Z tego faktu wynika, że
θ
θ
θ
,
k,
S(k)R
d
dR
k
=
(133)

4.7. Prędkość kątowa i przyspieszenie kątowe
W trakcie wykładów wyprowadziliśmy wyrażenia określające pozycję i orientację
różnych układów współrzędnych przez wprowadzenie przekształceń jednorodnych. W tej
części rozważamy prędkości i przyśpieszenia względne w tym samym kontekście.
Załóżmy, że macierz obrotu R jest zmienna w czasie, tak że R = R(t)
∈
SO(3) dla
każdego t
∈
R. Postępowanie identyczne z tym w poprzedniej części pokazuje, że pochodna
względem czasu R’(t) macierzy R(t) jest dana wzorem
R’(t) = S(t) R(t)
(134)
gdzie macierz S(t) jest skośniesymetryczna. Ponieważ macierz S(t) jest skośniesymetryczna,
więc może być jednoznacznie reprezentowana w postaci S(
ω
ωω
ω
(t)) przez pewien wektor
ω
ωω
ω
(t).
Wektor
ω
ωω
ω
(t) jest prędkością kątową układu obracającego się względem układu ustalonego w
chwili t.
Przykład 12.
Załóżmy, że R(t) = R
x,
θ
(t). Wówczas pochodna R’(t) = dR/dt jest obliczana jako
)
R(
))
S(ω(
)
R(
S(i)
d
d
d
dR
d
dR
t
t
t
t
t
⋅
=
⋅
⋅
=
=
θ
θ
θ
&
(135)
gdzie
ω
= i
θ
jest prędkością kątową wokół osi x.
Załóżmy, że p
1
reprezentuje wektor ustalony w układzie współrzędnych O
1
x
1
y
1
z
1
, a
układ O
1
x
1
y
1
z
1
obraca się względem układu O
0
x
0
y
0
z
0
. Wtedy współrzędne wektora p
1
w
układzie O
0
x
0
y
0
z
0
są określone zależnością
p
0
= R(t) p
1
(136)
zaś prędkość p
’
0
jest równa
p
’
0
= S(
ω
ωω
ω
) R(t) p
1
= S(
ω
ωω
ω
) p
0
=
ω
ωω
ω
××××
p
0
(137)
co jest znanym wyrażeniem dla prędkości w postaci iloczynu wektorowego. Załóżmy teraz,
ż
e ruch układu O
1
x
1
y
1
z
1
względem układu O
0
x
0
y
0
z
0
jest bardziej ogólny. Dokładniej,
przekształcenie jednorodne łączące te dwa układy jest zależne od czasu, tak że
=
1
0
)
(
d
)
(
R
)
(
H
1
0
1
0
1
0
t
t
t
(138)
Dla uproszczenia zapisu pomińmy argument t oraz wskaźniki dolne i górne przy
macierzy R
0
1
i wektorze d
0
1
Wtedy możemy napisać
p
0
= R p
1
+ d
(139)
a po zróżniczkowaniu powyższego równania i wykorzystaniu wzoru (135) otrzymujemy
p’
0
= R’ p
1
+ d’ = S(
ω
ωω
ω
) R p
1
+ d’ =
ω
ωω
ω
××××
r + v
(140)
gdzie r = R p
1
jest wektorem od początku 0
1
do punktu P wyrażonym w układzie O
0
x
0
y
0
z
0
, a v
jest prędkością, z jaką porusza się początek 0
1
.
Jeżeli wektor p
1
jest także zmienny względem układu O
1
x
1
y
1
z
1
, to musimy dodać do
członu v wyrażenie R(t) p’
1
, które jest prędkością zmiany p
1
wyrażoną w układzie O
0
x
0
y
0
z
0
.
Możemy również zróżniczkować wyrażenie dla uzyskania przyśpieszenia względnego
w dwóch układach współrzędnych, jak następuje. Po pierwsze, przypomnijmy, że iloczyn
wektorowy spełnia zasadę różniczkowania iloczynu, tzn.
dt
d
dt
d
dt
d
b
a
b
a
b)
(a
×
+
×
=
×
(141)

Jeśli teraz równanie (140) zapiszemy w postaci
p’
0
– d’ = R’ p
1
=
ω
ωω
ω
×
R p
1
(142)
i zróżniczkujemy obie strony względem czasu t, to otrzymamy
p’’
0
– d’’ =
ω
ωω
ω
’
×
(R’ p
1
) =
ω
ωω
ω
’
×
r +
ω
ωω
ω
×
(
ω
ωω
ω
×
r)
(143)
wówczas równanie (143) może być zapisane również jako
p’’
0
=
ω
ωω
ω
’
×
r +
ω
ωω
ω
×
(
ω
ωω
ω
×
r) + a
(144)
gdzie a jest przyśpieszeniem liniowym. Wyrażenie
ω
ωω
ω
×
(
ω
ωω
ω
×
r) opisuje przyśpieszenie
nazywane przyśpieszeniem normalnym lub dośrodkowym punktu materialnego. Jest ono
zawsze skierowane w kierunku osi obrotu i jest prostopadłe do tej osi. Wyrażenie
ω
ωω
ω
’
×
r
opisuje tzw. przyspieszenie styczne.
Ponownie, jeśli wektor p
1
porusza się względem układu O
1
x
1
y
1
z
1
, powyższe wyrażenie
trzeba odpowiednio zmodyfikować w następujący sposób
p’’
0
=
ω
ωω
ω
’
×
r +
ω
ωω
ω
×
(
ω
ωω
ω
×
r) + 2
ω
×
R p
1
+ a
(145)
gdzie a = R p’’
1
+ d’’. Wyrażenie 2
ω
×
R p
1
opisuje natomiast znane powszechnie
przyspieszenie Coriolisa.
4.8. Dodawanie prędkości kątowych
Często jesteśmy zainteresowani znalezieniem wypadkowej prędkości kątowej
wynikającej ze względnych obrotów kilku układów współrzędnych. Różniczkujemy wtedy
wyrażenia
na
składanie
prędkości
kątowych
w
dwóch
ruchomych
układach
O
1
x
1
y
1
z
1
i O
2
x
2
y
2
z
2
względem układu stałego O
0
x
0
y
0
z
0
.
Dla danego punktu P z reprezentacjami p
0
, p
1
, p
2
w odpowiednich układach mamy
związki
p
0
= R
0
1
p
1
+ d
0
1
(146)
p
1
= R
1
2
p
2
+ d
1
2
(147)
p
0
= R
0
2
p
2
+ d
0
2
(148)
gdzie jak poprzednio
R
0
2
= R
0
1
R
1
2
(149)
oraz
d
0
2
= d
0
1
+ R
0
1
d
1
2
(150)
Również jak wcześniej, wszystkie powyższe wielkości są funkcjami czasu. Biorąc pochodne
obu stron równania (149) otrzymamy
R’
0
2
= R’
0
1
R
1
2
+ R
0
1
R’
1
2
(151)
Wyrażenie R’
0
2
po lewej stronie wzoru (151) można zapisać jako
R’
0
2
= S(
ω
ωω
ω
0
2
) R
0
2
(152)
Pierwszy wyraz po prawej stronie równości (151) jest prosty
R’
0
1
R
1
2
= S(
ω
ωω
ω
0
1
) R
0
1
R
1
2
= S(
ω
ωω
ω
0
1
) R
0
2
(153)
Sprawdźmy drugi wyraz prawej strony. Równanie (122) umożliwia następujące obliczenia
R
0
1
R’
1
2
=R
0
1
S(
ω
ωω
ω
1
2
)R
1
2
=R
0
1
S(
ω
ωω
ω
1
2
)(R
0
1
)
T
R
0
1
R
1
2
=S(R
0
1
ω
ωω
ω
1
2
)R
0
1
R
1
2
=S(R
0
1
ω
ωω
ω
1
2
)R
0
2
(154)
Po połączeniu powyższych wyrażeń otrzymamy
S(
ω
ωω
ω
0
2
) R
0
2
= [S(
ω
ωω
ω
0
1
) + S(R
0
1
ω
ωω
ω
1
2
)] R
0
1
R
1
2
(155)
Ponieważ S(a) + S(b) = S(a + b), więc
(
ω
ωω
ω
0
2
) =
ω
ωω
ω
0
1
+ R
0
1
ω
ωω
ω
1
2
(156)
Innymi słowy, prędkości kątowe mogą być dodawane, jeśli są wyrażone względem tego
samego układu współrzędnych, w tym przypadku O
0
x
0
y
0
z
0
.
Powyższe wyrażenie może być rozszerzone na dowolną liczbę układów współrzędnych.
Na przykład jeżeli
R
0
n
= R
0
1
R
1
2
… R
n-1
n
(157)

wtedy
R’
0
n
= S(
ω
ωω
ω
0
n
) R
0
n
(158)
gdzie
ω
ωω
ω
0
n
=
ω
ωω
ω
0
1
+ R
0
1
ω
ωω
ω
1
2
+ R
0
2
ω
ωω
ω
2
3
+ R
0
3
ω
ωω
ω
3
4
+ … + R
0
n-1
ω
ωω
ω
n-1
n
(159)
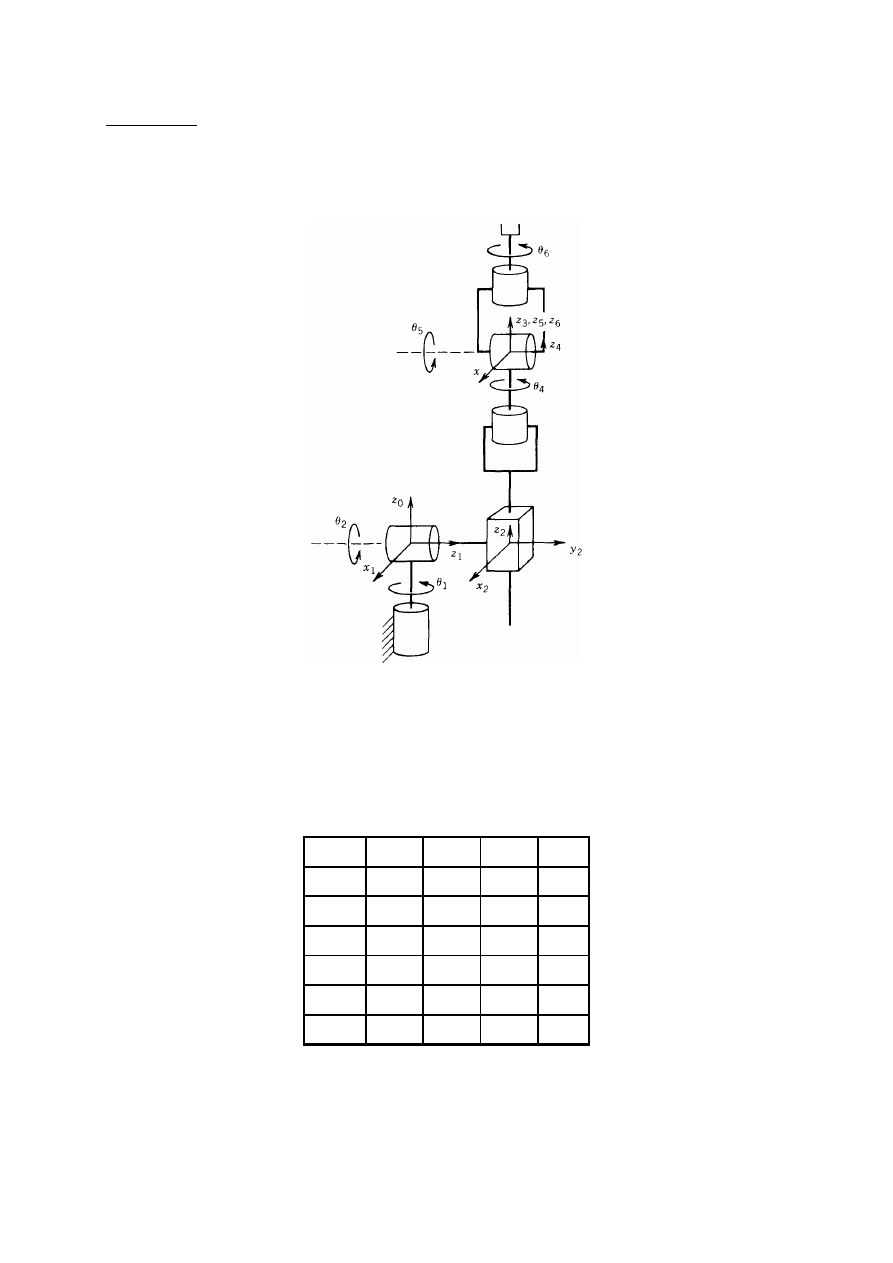
5. Kinematyka prosta: reprezentacja Denavita-Hartenberga
W tej rozdziale części wykładu wyprowadzimy równania kinematyki prostej, zwane
też równaniami kinematyki konfiguracji, dla robota sztywnego. Zadanie kinematyki prostej
można postawić następująco: Mając dane zmienne przegubowe robota, określić pozycję i
orientację końcówki roboczej. Dla przegubów obrotowych zmiennymi przegubowymi są kąty
między członami, natomiast dla przegubów pryzmatycznych – wysunięcia członów. Zadanie
kinematyki prostej jest przeciwieństwem zadania kinematyki odwrotnej, które zostanie
przeanalizowane w następnym rozdziale, a które można opisać następująco: Mając daną
pozycję i orientację końcówki roboczej robota, wyznaczyć zmienne przegubowe, które
zapewnią osiągnięcie docelowej pozycji i orientacji.
5.1. Łańcuchy kinematyczne
W celu przeprowadzenia analizy kinematyki wyobraźmy sobie robota jako ciąg
sztywnych członów, połączonych razem różnymi przegubami. Przeguby mogą być albo
bardzo proste, takie jak przeguby obrotowe lub pryzmatyczne, albo też bardziej
skomplikowane, takie jak przeguby kulowe lub kielichowe. (Przypominamy, że przegub
obrotowy jest podobny do zawiasu i umożliwia obrót wokół pojedynczej osi, natomiast
przegub pryzmatyczny pozwala na ruch liniowy wzdłuż pojedynczej osi, czyli na tzw.
wysunięcie lub wsunięcie). Różnica między tymi dwiema sytuacjami jest taka, że w
pierwszym przypadku przegub ma tylko jeden stopień swobody ruchu: kąt obrotu dla
przegubu obrotowego a wielkość przemieszczenia liniowego dla przegubu pryzmatycznego.
W przeciwieństwie do tego przeguby kulowe i kielichowe mają po dwa stopnie swobody. W
czasie wykładów założymy, że wszystkie przeguby mają jeden stopień swobody. Zauważmy,
ż
e to założenie nie pociąga za sobą zmniejszenia ogólności rozważań, ponieważ takie
przeguby, jak kulowy i kielichowy (z dwoma stopniami swobody) lub kiść sferyczna (z
trzema stopniami swobody), mogą być traktowane jako szereg przegubów o pojedynczych
stopniach swobody z zerową długością członów między nimi.
Przy założeniu, że każdy przegub ma jeden stopień swobody, działanie każdego
przegubu można opisać jedną liczbą rzeczywistą: kątem obrotu w przypadku członu
obrotowego lub przemieszczeniem w przypadku członu pryzmatycznego. Celem analizy
kinematyki prostej jest określenie wypadkowego efektu konkretnych wartości zmiennych we
wszystkich przegubach. Aby uczynić to w sposób systematyczny, trzeba wprowadzić pewne
konwencje. Możliwe jest oczywiście przeprowadzenie analizy kinematyki prostej bez
respektowania tych konwencji, tak jak to robiliśmy np. dla przykładowego dwuczłonowego
manipulatora płaskiego. Jednakże analiza kinematyki manipulatora o n członach jest
wyjątkowo skomplikowana, a proponowana poniżej konwencja znacznie upraszcza równania
kinematyki. Ponadto przyczynia się ona do rozwoju uniwersalnego języka, którym
porozumiewają się specjaliści robotyki.
Przypuśćmy, że robot ma n + l członów ponumerowanych od 0 do n,
zaczynając od
podstawy robota, którą oznaczymy jako człon 0. Przeguby są ponumerowane od l do n, przy
czym przegub i łączy człon i – 1 z członem i. Zmienna przegubowa dla przegubu i jest
oznaczona przez q
i
. W przypadku przegubu obrotowego q, jest kątem obrotu, a w przypadku
przegubu pryzmatycznego q
i
jest przemieszczeniem. Następnie do każdego członu w sposób

sztywny doczepiamy układ współrzędnych. W szczególności w podstawie zaczepiamy
nieruchomy układ oznaczony numerem 0. Dalej wybieramy układy od l do n tak, że układ i
jest na sztywno związany z członem i. To oznacza, że przy jakimkolwiek ruchu wykonanym
przez robota współrzędne każdego punktu członu i, jeśli wyrazimy je w układzie i, pozostaną
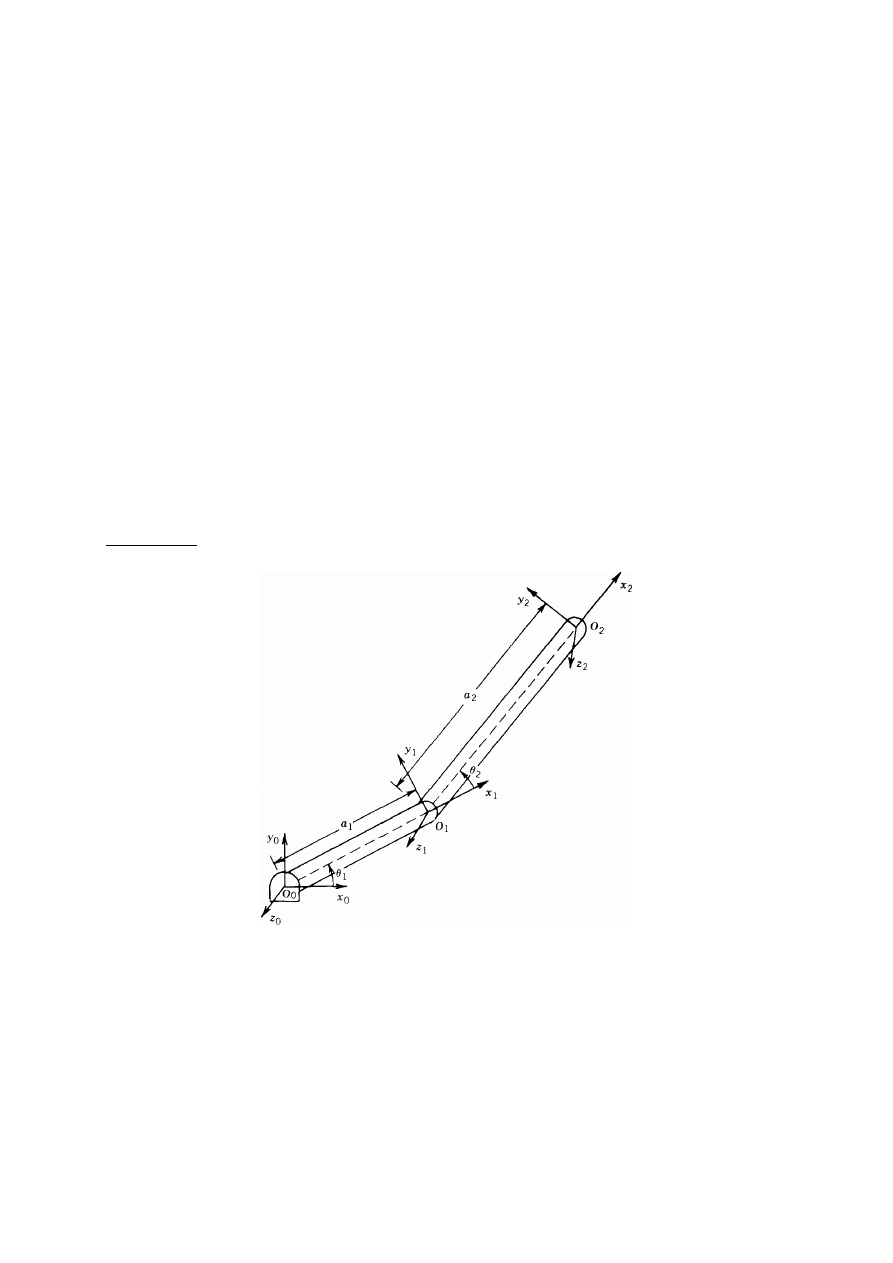
niezmienne. Rys. 38 ilustruje ideę sztywnego związania układu współrzędnych z członem dla
manipulatora z łokciem.
Rys. 38. Układy współrzędnych doczepione do manipulatora z łokciem
Załóżmy teraz, że A
i
jest macierzą przekształcenia jednorodnego, które przekształca
współrzędne punktu z układu i do układu i – 1. Macierz A
i
nie jest stała, lecz zmienia się wraz
ze zmianą konfiguracji robota. Założenie, że wszystkie przeguby są obrotowe lub
pryzmatyczne oznacza, że macierz A
i
jest funkcją tylko jednej zmiennej q
i
. Innymi słowy
A
i
= A
i
(q
i
)
(160)
Macierz jednorodna, która transformuje współrzędne punktu z układu j do układu i
jest nazywana w przedstawianej konwencji macierzą przekształcenia i jest zwykle oznaczana
jako T
i
j
, oraz jak już wcześniej pokazaliśmy
T
i
j
= A
i+1
A
i+2
… A
j-1
A
j
dla i < j
(161)
T
i
j
= I dla i = j
(162)
T
i
j
= (T
i
j
)
-1
dla j > i
(163)
Ze sposobu, w jaki przywiązaliśmy poszczególne układy współrzędnych do
odpowiadających im członów, wynika, że pozycja dowolnego punktu końcówki roboczej w
układzie n jest stała, niezależna od konfiguracji robota. Oznaczmy pozycję i orientację
końcówki roboczej względem układu bazowego (nieruchomego) odpowiednio jako 3
wymiarowy wektor d
0
n
i macierz obrotu R
0
n
o wymiarze 3 x 3 oraz zdefiniujmy macierz
jednorodną
=
1
0
d
R
H
n
0
n
0
(164)

Wówczas pozycja i orientacja końcówki roboczej w układzie bazowym robota jest wyrażona
jako
H = T
0
n
= A
1
(q
1
) … A
n
(q
n
)
(165)
A każde jednorodne przekształcenie A
i
ma postać
=
1
0
d
R
A
1
-
1
-
i
i
i
i
i
(166)
Stąd
=
⋅
⋅
=
+
1
0
d
R
A
...
A
T
1
j
i
j
i
j
i
j
i
(167)
Macierz R
i
j
opisuje orientację układu j względem układu i oraz jest wyznaczona przez części
obrotowe macierzy A, czyli
R
i
j
= R
i
i+1
… R
j-1
j
(168)
Wektory d
i
j
są obliczane rekurencyjnie ze wzoru
d
i
j
= d
i
j-1
+ R
i
j-j
d
j-1
j
(169)
Podsumowując – to jest wszystko, co dotyczy kinematyki prostej! Określ funkcje
A
i
(q
i
) i pomnóż je przez siebie tak, jak potrzeba. Można jednak znacznie uprościć i
uporządkować zagadnienie przez wprowadzenie dalszych konwencji, takich jak notacja
Denavita-Hartenberga do opisu przegubu. Jest to celem dalszej części niniejszego wykładu.
5.2. Reprezentacja Denavita-Hartenberga
Chociaż możliwe jest przeprowadzenie całej tutaj prezentowanej analizy, stosując
arbitralnie wybrane układy współrzędnych związane z kolejnymi członami, to jednak bardzo
pomocnym będzie systematyczny dobór tych układów.
W tym celu, tj. do wyboru układów współrzędnych, w robotyce stosuje się notację
Denavita-Hartenberga, zwaną w skrócie notacją D-H. W tej konwencji każde jednorodne
przekształcenie A
i
jest reprezentowane jako wynik czterech przekształceń „podstawowych”
−
−
=
=
−
−
=
⋅
⋅
⋅
=
1
0
0
0
cos
sin
0
sin
sin
cos
cos
cos
sin
cos
sin
sin
cos
sin
cos
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
1
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
A
,
,
,
,
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
x
a
x
d
z
z
i
d
a
a
a
d
Rot
Trans
Trans
Rot
i
i
i
i
α
α
θ
α
θ
α
θ
θ
θ
α
θ
α
θ
θ
α
α
α
α
θ
θ
θ
θ
α
θ
(170)
gdzie cztery wielkości
θ
i
, a
i
, d
i
;
α
i
, są parametrami członu i oraz przegubu i. Poszczególne
parametry w równaniu (170) są zwykle nazywane: a
i
– długością członu,
α
i
– skręceniem
członu, d
i
– odsunięciem przegubu,
θ
i
– kątem przegubu. Ponieważ macierz
A, jest funkcją
jednej zmiennej, więc trzy z powyższych czterech wielkości są dla danego członu stałe, a
czwarty parametr –
θ
i
dla przegubu obrotowego i d
i
dla pryzmatycznego – jest zmienną
przegubową.
Jak już wcześniej pokazano, dowolna macierz jednorodna może być opisana
sześcioma parametrami, np. trzema składowymi wektora przemieszczenia d i trzema kątami
Eulera zgodnymi z macierzą obrotu R. W notacji Denavita-Hartenberga mamy, dla odmiany,
cztery parametry. Jak to możliwe? Otóż, chociaż wymaga się, aby układ i był sztywno
związany z członem i, to jednak istnieje pewna swoboda w wyborze początku układu i jego
osi. Na przykład nie jest konieczne, aby początek O
i
układu i odpowiadał przegubowi i lub i +
l, czyli któremuś z końców członu i. W ten sposób, dzięki sprytnemu dobraniu położenia
początku układu i jego osi, można ograniczyć liczbę niezbędnych parametrów z sześciu do
czterech (a w niektórych przypadkach nawet mniej). Zobaczmy, jak to się robi.
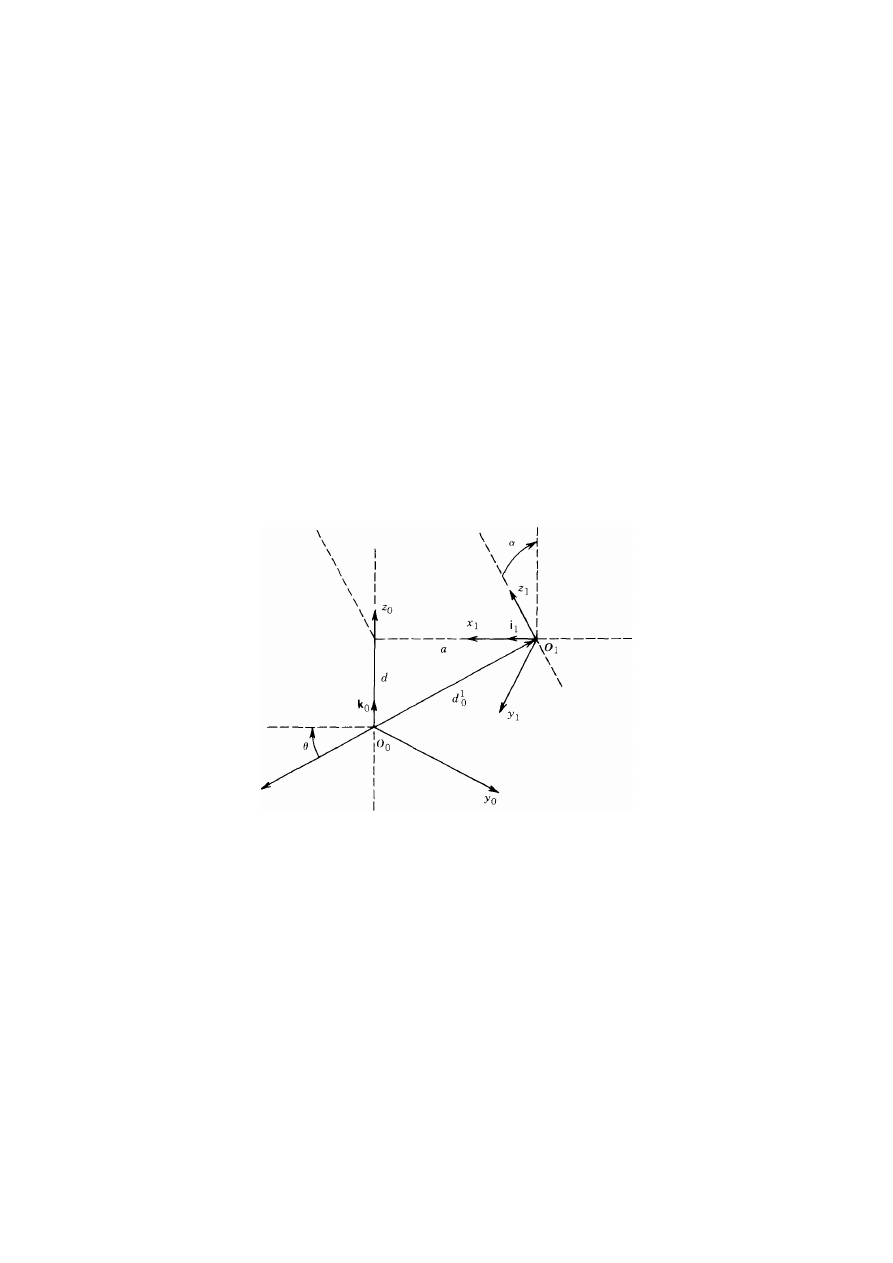
Zacznijmy od określenia, jakie właściwie przekształcenia jednorodne można wyrazić wzorem
(170). Przypuśćmy, że mamy dane dwa układy współrzędnych oznaczone odpowiednio przez
0 i 1. Istnieje jednoznacznie zdefiniowane przekształcenie jednorodne opisane macierzą A,
które przekształca współrzędne z układu l do układu 0. Przypuśćmy teraz, że te dwa układy
mają dodatkowo następujące właściwości:
(DH1) oś x
1
jest prostopadła do osi
Z
0
,
(DH2) oś x
1
przecina oś
Z
0
,
jak to pokazano na rys. 39.
Rys. 39. Układy współrzędnych zgodne z założeniami (DH1) i (DH2)
Przy tych warunkach żądamy, aby istniały jednoznacznie wyznaczone liczby a, d,
θ
,
α
takie,
ż
e
A = Rot
z,
θ
Trans
z,d
Trans
x,a
Rot
x,
α
(171)
Oczywiście, ponieważ
θ
i
α
są kątami, w rzeczywistości żądamy, aby były one określone
jednoznacznie z dokładnością do wielokrotności 2
π
.
Chcemy pokazać, że macierz A może być zapisana w tej postaci, więc przedstawmy A
jako
=
1
0
d
R
A
(172)

i niech r
i
oznacza kolumnę i macierzy obrotu R. Zgodnie z rys. 39 widać, że przyjęte
założenie (DH1) oznacza, że wektor r
1
(który reprezentuje wektor jednostkowy i
1
w układzie
0) jest ortogonalny do k
0
= [0, 0, 1]
T
, tzn. r
31
= 0. Stąd żądamy, abi istniały jednoznacznie
określone kąty
θ
i
α
takie, że
−
−
=
=
−
⋅
−
=
⋅
=
α
α
α
θ
α
θ
θ
α
θ
α
θ
θ
α
α
α
α
θ
θ
θ
θ
α
θ
cos
sin
0
sin
cos
cos
cos
sin
sin
sin
cos
sin
cos
cos
sin
0
sin
cos
0
0
0
1
1
0
0
0
cos
sin
0
sin
cos
R
R
R
x,
z,
(173)
Jedyną posiadaną informacją jest, że
r
31
= 0. Jednak to wystarczy. Po pierwsze, ponieważ
każdy wiersz i każda kolumna macierzy
R musi mieć jednostkową długość, więc warunek r
31
= 0 implikuje następujące równości
r
11
2
+
r
21
2
= 1
(174)
r
32
2
+
r
33
2
= 1
(175)
Stąd istnieją jedyne kąty
θ
i
α
takie, że
(
r
11
,
r
21
) = (cos
θ
, sin
θ
)
(176)
(
r
33
,
r
32
) = (cos
α
, sin
α
)
(177)
Skoro kąty
θ
i
α
zostały już znalezione, to formalnością jest pokazanie, że pozostałe elementy
macierzy
R muszą mieć postać określoną równaniem (173). Należy więc wykorzystać fakt, że
R jest macierzą obrotu.
Założenie (DH2) oznacza, że wektor
d = d
0
1
(który jest wektorem początku układu 1
wyrażonym w układzie 0) jest kombinacją liniową wektorów
k
0
i
Ri
1
. Ponieważ r
31
= 0, więc
możemy wyrazić
d
0
1
w sposób jednoznaczny jako
=
+
=
=
=
d
a
a
ar
dk
aRi
dk
d
θ
θ
sin
cos
1
0
1
0
1
0
(178)
Wstawiając
R z równania (173) i d z równania (178) do wzoru (172) otrzymujemy macierz
(170).
Teraz, gdy wykazaliśmy, że każda macierz jednorodna spełniająca wymienione wyżej
warunki (DH1) i (DH2) może być reprezentowana w postaci (170), możemy przedstawić
fizyczną interpretację każdej z czterech występujących w równaniu (170) wielkości. Parametr
a jest odległością między osiami z
0
i
z
1
mierzoną wzdłuż osi
x
1
. Kąt
α
jest kątem między
osiami
z
0
i
z
1
mierzonym w płaszczyźnie prostopadłej do osi
x
1
. Dodatni kierunek kąta
α
jest
określony przez osie
z
0
i
z
1
na podstawie reguły prawej ręki, jak to przedstawiono na rys. 40.
Natomiast parametr
d jest odległością między początkiem O
0
a przecięciem osi
x
1
z
Z
0
,
mierzoną wzdłuż osi
Z
0
.
Na koniec
θ
jest kątem między osiami osie
x
0
i
x
1
mierzonym w
płaszczyźnie prostopadłej do osi
z
0
.

Rys. 40. Dodatnie kierunki kątów
α
i
i
θ
i
Teraz pozostało jeszcze pokazać, że dla manipulatora robota można zawsze wybrać
układy współrzędnych 0,..., n w taki sposób, że dwa podane wyżej warunki są spełnione.
Trzeba przy tym zaakceptować możliwość, że środek O
i
układu i nie musi leżeć na przegubie
i. Przypomnijmy te dwa warunki: (DH1) oś x
i
jest prostopadła do osi z
i-1
oraz (DH2) oś x
i
przecina oś z
i-1
. Przy czytaniu materiału poniżej należy pamiętać, że wybór układów
współrzędnych nie jest jedynym możliwym, nawet jeśli ograniczy się go powyższymi
wymaganiami. Po przedstawieniu ogólnej procedury omówimy różne przypadki, w których
jest możliwe dalsze uproszczenie macierzy jednorodnych.
Na początku dobrze jest zidentyfikować wszystkie osie przegubów i oznaczyć je z
0
,...,
z
n-1
. Jeśli przegub i + l jest obrotowy, to z
i
jest jego osią obrotu, jeśli zaś pryzmatyczny, to z
i
jest osią przesunięcia w tym przegubie. Następnie należy wybrać początek O
0
układu
bazowego. Ten punkt może być wybrany dowolnie wzdłuż osi z
0
.
Na koniec wybierzmy
dowolnie x
0
, y
0
, pamiętając tylko, aby w efekcie otrzymać układ prawoskrętny. W ten sposób
ustaliliśmy układ 0.
Załóżmy, że układy 0, ..., i – 1 zostały ustalone. Dla lepszego zrozumienia dalszych
rozważań przeanalizujmy rys. 41.
Rys. 41. Przyporządkowanie układów współrzędnych zgodnie z notacją D-H
W celu ustalenia układu i niezbędne jest rozpatrzenie dwóch przypadków: a) osie z
i-1
, z
i
nie
leżą w jednej płaszczyźnie, b) należą one do jednej płaszczyzny.
W przypadku a), tzn. gdy osie z
i-1
, z
i
nie leżą w jednej płaszczyźnie, wtedy istnieje dokładnie
jeden odcinek prostopadły do obu osi, który łączy obie osie i ma najmniejszą długość. Prostą
zawierającą ten odcinek, a więc prostopadłą (normalną) do osi z
i-1
, z
i
należy obrać za oś x
i
, a
punkt jej przecięcia z osią z
i
przyjąć za początek O
i
układu współrzędnych. Sposób
konstrukcji tej prostej gwarantuje, że spełnione są oba warunki (DH1) i (DH2), a wektor z
punktu O
i-1
do O
i
jest kombinacją liniową wektorów jednostkowych osi z
i-1
, x
i
. Do pełnego
określenia układu i trzeba jeszcze przyjąć oś y
i
tak, aby układ był prawoskrętny. Ponieważ są
spełnione warunki (DH1) i (DH2), więc macierz jednorodna A
i
ma postać zgodną z
równaniem (170).
Rozważmy teraz przypadek b), tzn. gdy osie z
i-1
, z
i
leżą w jednej płaszczyźnie.
Oznacza to, że osie te albo są równoległe, albo przecinają się. Są to w rzeczywistości sytuacje
podobne, wymagające tak samo szczegółowej analizy. Jeśli osie z
i-1
, z
i
są równoległe, to
istnieje nieskończenie wiele wspólnych normalnych między nimi. Dlatego warunek (DH1) nie
wystarczy do dokładnego określenia osi x
i
. W takim przypadku wybieramy środek O
i
na
przegubie i tak, że x
i
jest tą normalną poprowadzoną z osi z
i-1
, która przechodzi przez O
i
.
Zauważmy, że w tym przypadku wybór punktu O
i
jest dowolny. Równie dobrze moglibyśmy
wybrać normalną przechodzącą przez punkt O
i-1
, jak też oś x
i
i wtedy odległość d
i
byłaby
równa zeru. To drugie podejście jest częściej spotykane w literaturze z dziedziny robotyki.
Ponieważ osie z
i-1
i z
i
są równoległe, więc kąt
α
i
, jest równy zeru. Gdy oś x
i
jest już ustalona,
przyjmuje się oś y
i
jak zwykle z zachowaniem reguły prawej ręki.
Na koniec rozważmy przypadek, gdy z
i
przecina oś z
i-1
. W tej sytuacji jako oś x
i
wybieramy normalną do płaszczyzny wyznaczonej przez osie z
i
, z
i-1
. Wybór dodatniego
kierunku osi jest dowolny. W tym przypadku najbardziej naturalnym wyborem początku
układu O
i
jest punkt przecięcia osi z
i
, z
i-1
jednakże wystarczy dowolny punkt osi z
i
.
Zauważmy, że w tym przypadku parametr
α
i
jest równy zeru.
Przedstawiona procedura konstrukcji jest użyteczna dla układów 0, ..., n – 1 w robocie
o n członach. Trzeba jeszcze określić układ n. Ostatni układ współrzędnych O
n
x
n
y
n
z
n
jest
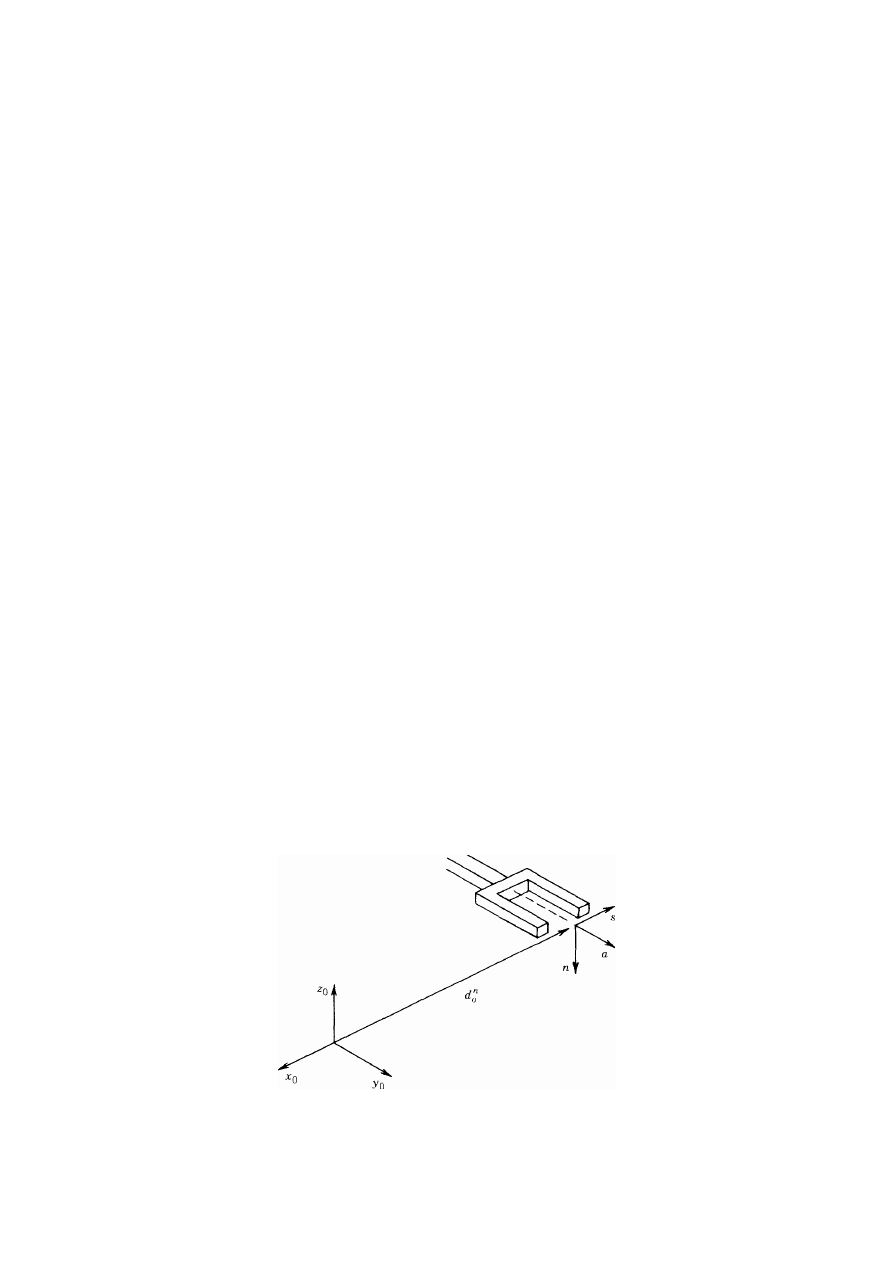
zwykle związany z układem końcówki roboczej lub narzędzia (rys. 42).
Rys. 42. Ustalenie układu końcówki roboczej

Początek układu O
n
jest najczęściej umieszczany symetrycznie między palcami chwytaka.
Wektory jednostkowe osi x
n
, y
n
, z
n
są oznaczane odpowiednio przez n, s, a, co wywodzi się ze
znaczenia poszczególnych osi. Tak więc a oznacza zbliżenie (z ang. approach), bowiem
chwytak robola zbliża się najczęściej do obiektu zgodnie z kierunkiem wektora a. Podobnie
kierunek wektora s oznacza kierunek przesuwania (z ang. sliding), w tym bowiem kierunku
przesuwają się palce typowego chwytaka podczas zamykania i otwierania. Oznaczenie n
określa kierunek normalny (z ang. normal) do płaszczyzny wyznaczonej przez wektory a i s.
We wszystkich współczesnych robotach ruch ostatniego przegubu jest obrotem
końcówki roboczej o kąt
θ
n
a dwie ostatnie osie przegubów z
n-1
, z
n
są zgodne. Dlatego też
transformacja między dwoma ostatnimi układami współrzędnych jest zawsze przesunięciem
wzdłuż osi z
n-1
o odległość d
6
zakończonym (lub poprzedzonym) obrotem o kąt
θ
6
wokół osi
z
n-1
.
Jest to ważna obserwacja, która ułatwi obliczenia związane z kinematyką odwrotną w
dalszej części wykładów.
Na zakończenie zauważmy następujący ważny fakt. We wszystkich przypadkach,
zarówno dla przegubu obrotowego, jak i pryzmatycznego, wielkości a
i
i
α
i
są zawsze stałe dla
wszystkich wskaźników i oraz są one charakterystyczne dla danego manipulatora. Jeśli
przegub i jest pryzmatyczny, wtedy wielkość
θ
i
jest również stała, podczas gdy d
i
jest
zmienną przegubową tego przegubu. Analogicznie, jeśli przegub i jest obrotowy, wtedy
wielkość d
i
jest stała, a
θ
i
jest zmienną przegubową.
5.3. Podsumowanie procedury zgodnej z notacją Denavita-Hartenberga
Przedstawioną powyżej procedurę, opartą na notacji Denavita-Hartenberga, możemy
zapisać w postaci następującego algorytmu, który rozwiązuje kinematykę prostą dla
dowolnego manipulatora:
Krok 1: Umieścić i oznaczyć osie przegubów z
0
, ..., z
n-1
.
Krok 2: Przyjąć bazowy układ współrzędnych. Jego początek umieścić dowolnie na osi z
0
.
Osie x
0
i y
0
wybrać tak, aby układ był prawoskrętny. Dla i = l, ..., n – l wykonać kroki 3, 4, 5.
Krok 3: Umieścić środek O
i
w miejscu, gdzie wspólna normalna do osi z
i
i z
i-1
przecina oś z
i
.
Jeśli oś z
i
przecina oś i z
i-1
, to umieścić początek O
i
w tym przecięciu. Jeśli z
i
i z
i-1
są
równoległe, to umieścić O
i
na przegubie i.
Krok 4: Przyjąć oś x
i
wzdłuż wspólnej normalnej osi z
i-1
i z
i
przechodzącej przez początek O
i
lub w kierunku normalnej do płaszczyzny obu tych osi, jeśli z
i-1
i z
i
przecinają się.
Krok 5: Wybrać oś y
i
tak, aby układ był prawoskrętny.
Krok 6: Ustalić układ współrzędnych końcówki roboczej O
n
x
n
y
n
z
n
. Zakładając, że oś n jest
obrotowa, przyjąć k
n
= a wzdłuż kierunku z
n-1
. Wybrać początek O
n
na osi z
n
;
preferowany
jest środek chwytaka lub czubek narzędzia, z którym pracuje robot. Przyjąć j
n
= s w kierunku
zamykania chwytaka oraz i
n
= n jako s x a. Jeśli narzędzie nie jest zwykłym chwytakiem,
przyjąć x
n
i y
n
według uznania, zachowując tylko zasady układu prawoskrętnego.
Krok 7: Utworzyć tabelę parametrów kinematycznych a
i
, d
i
,
α
i
,
θ
i
, gdzie
a
i
– odległość wzdłuż osi x
i
od początku O
i
do przecięcia osi x
i
i z
i-1
,
d
i
– odległość wzdłuż osi z
i-1
od początku O
i-1
do przecięcia osi x
i
i z
i-1
; jeśli przegub
jest pryzmatyczny, to di jest zmienną,
α
i
– kąt między osiami z
i-1
i z
i
mierzony wokół osi x
i
,
θ
i
–kąt między osiami x
i-1
i x
i
mierzony wokół osi z
i-1
; jeśli przegub jest obrotowy, to
θ
i
jest zmienną.
Krok 8: Zbudować macierze przekształceń jednorodnych A
i
wstawiając powyższe parametry
do równania (170).
Krok 9: Utworzyć macierz T
0
n
= A
1
… . A
n
; opisuje ona pozycję i orientację układu
narzędzia wyrażoną w bazowym układzie współrzędnych.
5.4 Wybrane przykłady
Ponieważ w notacji Denavita-Hartenberga jedyną zmienną kątową jest
θ
, więc w
niektórych przypadkach uprościmy zapis pisząc c
i
zamiast cos
θ
i
, itd. Oznaczymy także
θ
1
+
θ
2
przez
θ
12
oraz cos(
θ
1
+
θ
2
) przez c
12
i tak samo w innych tego typu przypadkach. W
następnych przykładach bardzo ważne jest, aby pamiętać, że notacja Denavita-Hartenberga,
aczkolwiek systematyczna, jednak umożliwia dość dużą swobodę w wyborze niektórych
parametrów manipulatora. Szczególnie dotyczy to przypadków równoległych przegubów
pryzmatycznych.
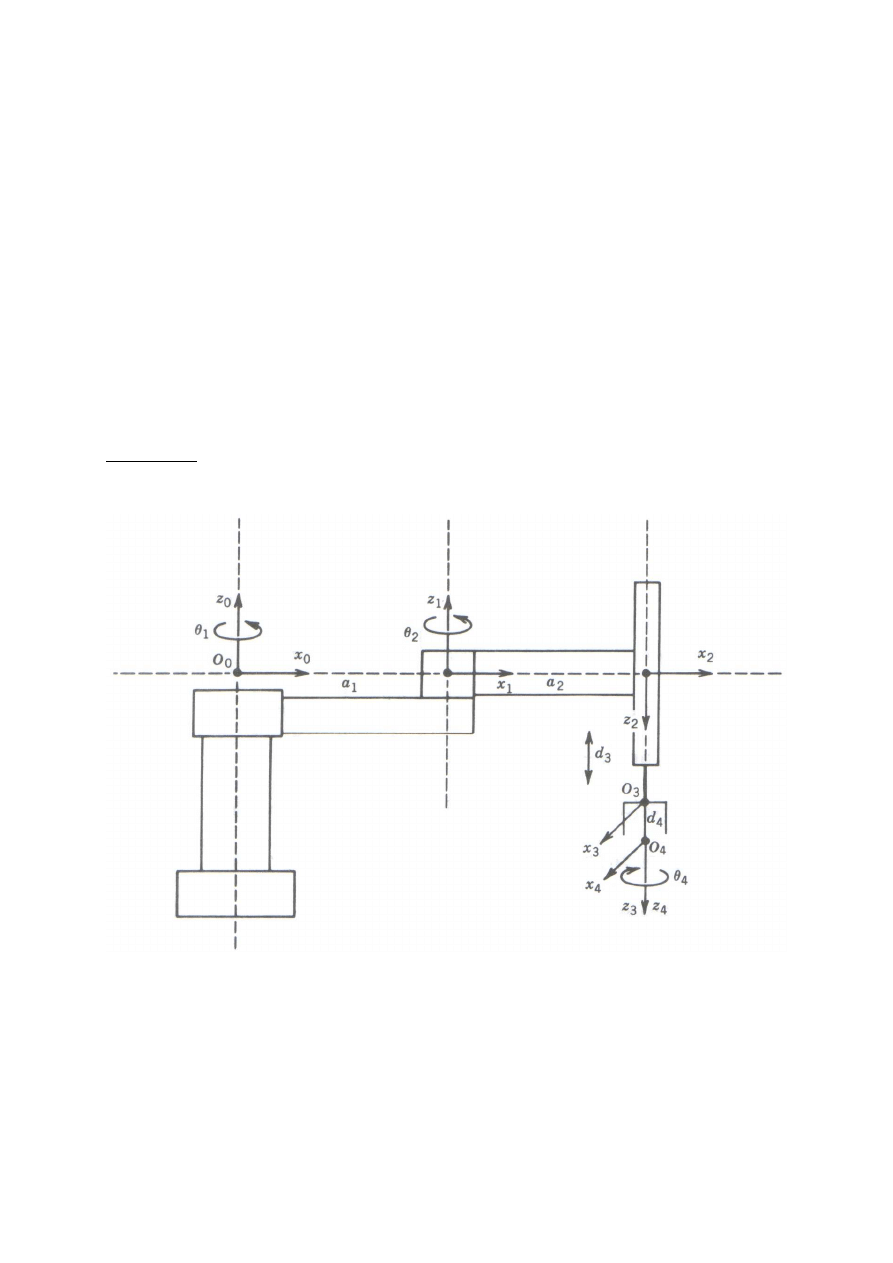
Przykład 13. Płaski manipulator z łokciem
Rozważmy dwuczłonowe ramię płaskie przedstawione na rys. 43.
Rys. 43. Dwuczłonowy manipulator plaski
Osie przegubów z
0
i z
1
są prostopadłe do strony. Przyjmujemy układ bazowy O
0
x
0
y
0
z
0
, jak to
pokazano na rysunku. Początek układu został wybrany w punkcie przecięcia osi z
0
ze stroną, a
kierunek osi x
0
jest całkowicie dowolny. Gdy już układ bazowy został przyjęty, układ O
1
x
1
y
1
z
1
ustalamy zgodnie z konwencją Denavita-Hartenberga, jak to pokazano na rysunku, gdzie
początek O
1
został umieszczony na przecięciu osi z
1
i strony. Ostatni układ O
2
x
2
y
2
z
2
jest
ustalony przez wybór jego początku O
2
na końcu członu 2. Parametry kinematyczne pokazano
w tab. 1. Macierze Wyznaczono z wzoru (170) w poniżej przedstawionej postaci

Tab. 1. Parametry kinematyczne dwuczłonowego manipulatora płaskiego
Parametr Człon 1
Człon 2
a
i
a
1
a
2
α
i
0
0
d
i
0
0
θ
i
θ
1
θ
2
−
=
1
0
0
0
0
1
0
0
sin
0
cos
sin
cos
0
sin
cos
A
1
1
1
1
1
1
1
1
1
θ
θ
θ
θ
θ
θ
a
a
(179)
−
=
1
0
0
0
0
1
0
0
sin
0
cos
sin
cos
0
sin
cos
A
2
2
2
2
2
2
2
2
2
θ
θ
θ
θ
θ
θ
a
a
(180)
Macierze T są równe
1
1
0
A
T
=
(181)
+
+
+
+
+
+
+
−
+
=
=
−
−
=
=
1
0
0
0
0
1
0
0
)
sin(
sin
0
)
cos(
)
sin(
)
cos(
cos
0
)
sin(
)
cos(
1
0
0
0
0
1
0
0
sin
0
cos
sin
cos
0
sin
cos
1
0
0
0
0
1
0
0
sin
0
cos
sin
cos
0
sin
cos
A
A
T
2
1
2
1
1
2
1
2
1
2
1
2
1
1
2
1
2
1
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
2
1
2
0
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
a
a
a
a
a
a
a
a
(182)
Zauważmy, że pierwsze dwa elementy ostatniej kolumny macierzy T
0
2
są współrzędnymi x i
y początku układu O
2
w układzie bazowym, tzn.
x = a
1
cos
θ
1
+ a
2
cos(
θ
1
+
θ
2
)
(183)
y = a
1
sin
θ
1
+ a
2
sin(
θ
1
+
θ
2
)
(184)
są współrzędnymi końcówki roboczej w bazowym układzie współrzędnych. Część obrotowa
macierzy T
0
2
opisuje orientację układu O
2
x
2
y
2
z
2
w stosunku do układu bazowego.
Przykład 13. Trójczłonowy robot cylindryczny
Rozważmy teraz trójczłonowy robot cylindryczny przedstawiony symbolicznie na rys. 44. Jak
to pokazano, początek O
0
został przyjęty na przegubie 1. Zauważmy, że zarówno punkt O
0
na
osi z
0
, jak również kierunek osi x
0
, są dowolne.
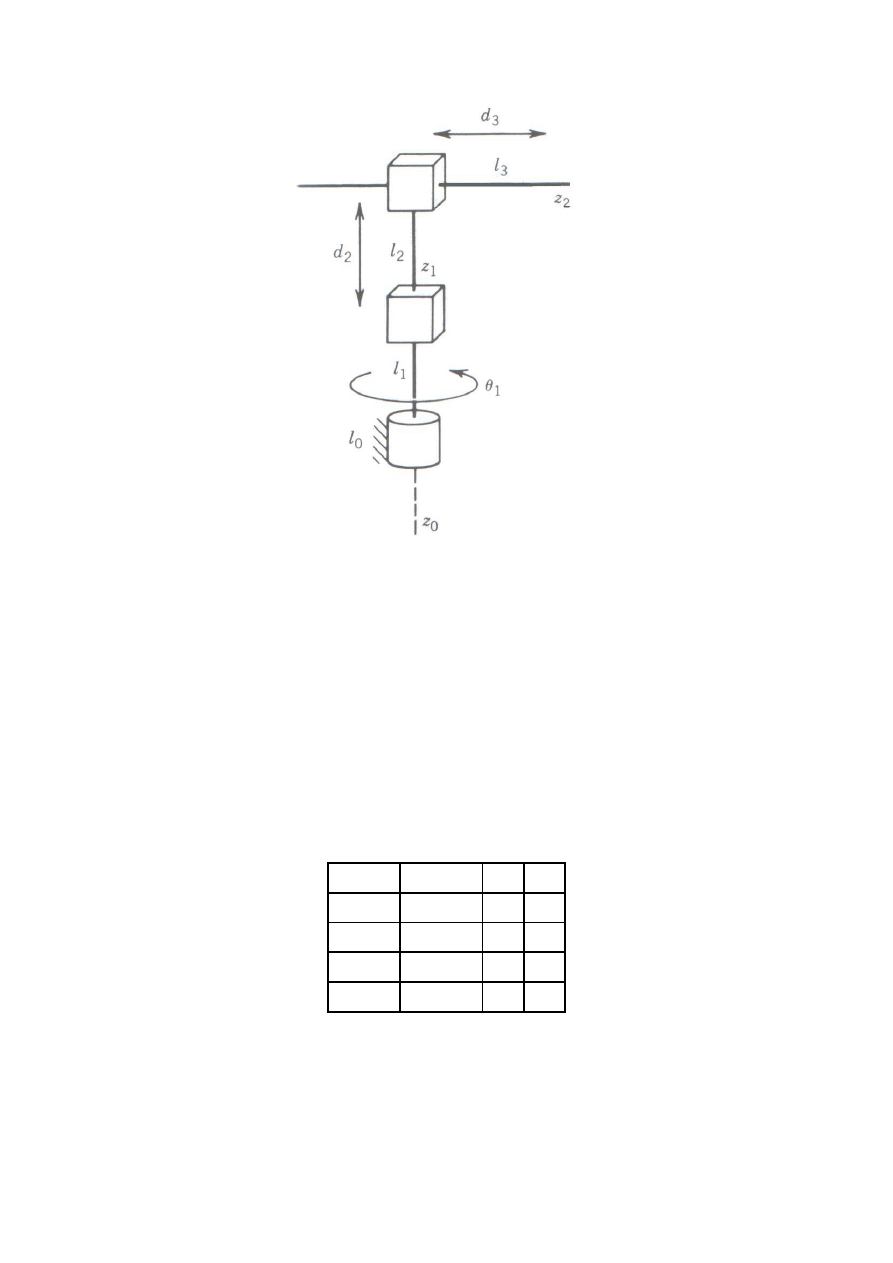
Rys. 44. Trójczłonowy manipulator cylindryczny
Nasz wybór początku O
0
jest najbardziej naturalny, ale O
0
może równie dobrze znajdować się
na przegubie 2. Oś x
0
jest wybrana jako prostopadła do płaszczyzny rysunku. Następnie,
ponieważ osie z
0
i z
1
są zgodne, początek O
1
został wybrany na przegubie 1, jak to pokazano
na rysunku. Oś x
1
jest prostopadła do płaszczyzny rysunku dla
θ
1
= 0, ale oczywiście jej
kierunek będzie się zmieniał, gdyż
θ
1
jest zmienną.
Ponieważ osie z
1
i z
2
przecinają się, więc początek O
2
umieszczono w punkcie ich
przecięcia. Oś x
2
została wybrana jako równoległa do osi x
1
, dzięki czemu kąt
θ
2
jest równy
zeru. Na koniec został ustalony trzeci układ współrzędnych na końcu członu 3, jak to
pokazano na rys. 44. Parametry kinematyczne przedstawiono w tab. 2.
Tab. 2. Parametry kinematyczne trójczłonowego manipulatora cylindrycznego
Człon
1
2
3
a
i
0
0
0
α
i
0
-90
0
d
i
d1=const d2
d3
θ
i
θ
1
0
0
A odpowiednie macierze A i T wyglądają następująco
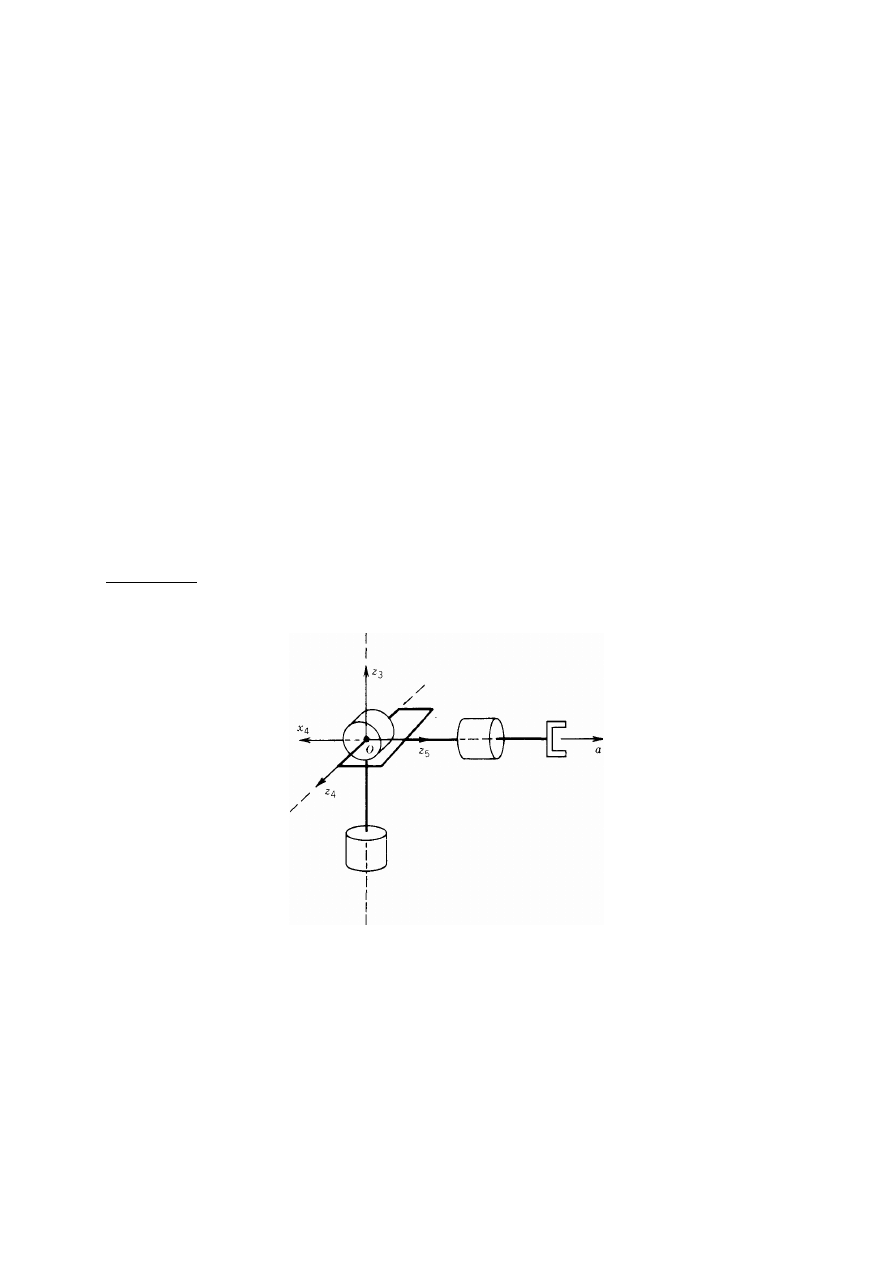
−
=
1
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
A
1
1
1
1
1
1
d
θ
θ
θ
θ
(185)
−
=
1
0
0
0
0
1
0
0
1
0
0
0
0
0
1
A
2
2
d
(185)
=
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
A
3
3
d
(186)
+
−
−
−
=
=
1
0
0
0
0
1
0
cos
cos
0
sin
sin
0
sin
cos
A
A
A
T
2
1
1
3
1
1
1
3
1
1
3
2
1
3
0
d
d
d
d
θ
θ
θ
θ
θ
θ
(187)
Przykład 14. Kiść sferyczna
Konfigurację kiści sferycznej ilustruje rys. 45.
Rys. 45 Przyporządkowanie układów współrzędnych w kiści sferycznej
Osie przegubów z
3
,
z
4
, z
5
przecinają się w punkcie O. Parametry Denavita-Hartenberga są
przedstawione w tab. 3. Przykładem robota z kiścią tego typu jest manipulator stanfordzki.
Dalsza analiza stosuje się oczywiście do wszystkich kiści sferycznych.
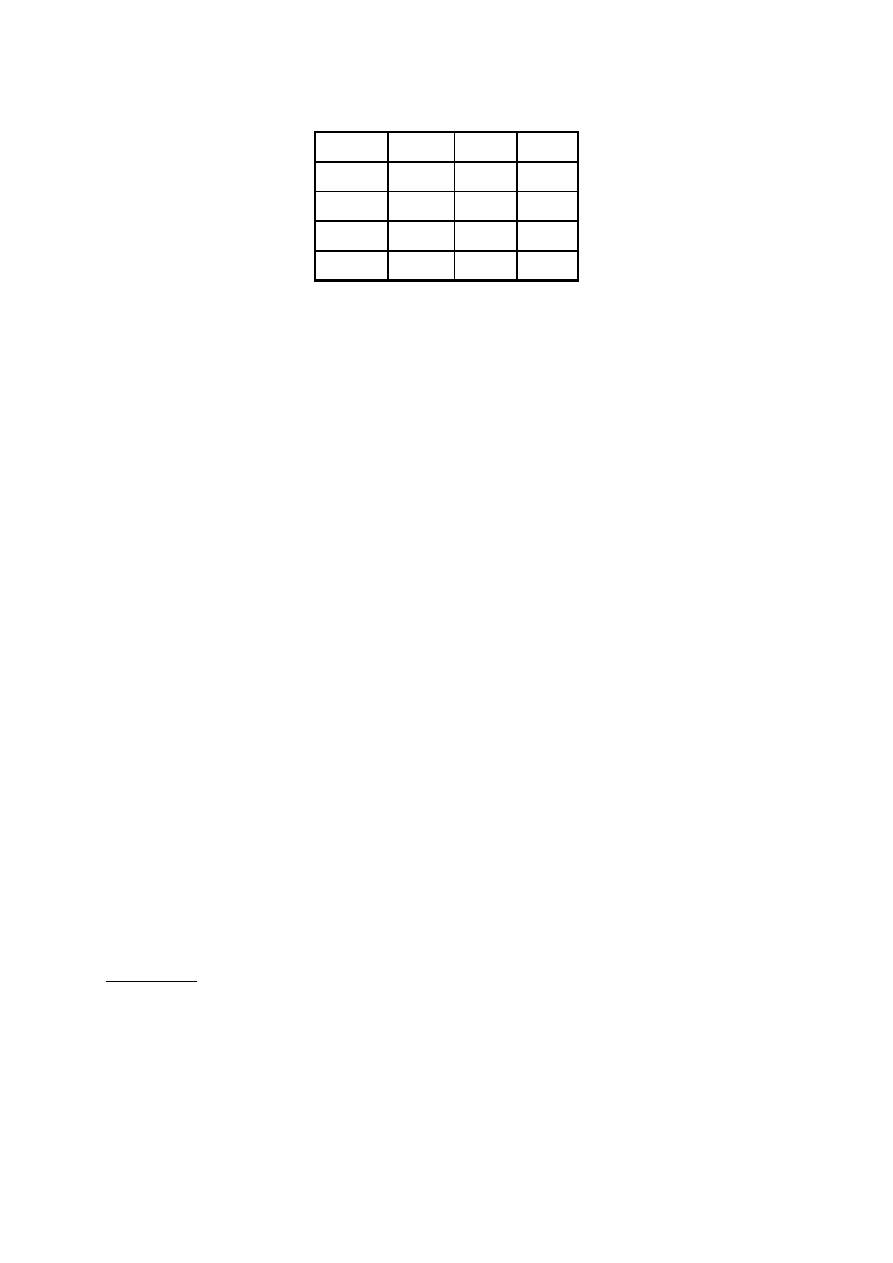
Tab. 3. Parametry Denavita-Hartenberga dla kiści sferycznej
Człon
4
5
6
a
i
0
0
0
α
i
-90
90
0
d
i
0
0
d
6
θ
i
θ
4
θ
5
θ
6
Pokażemy teraz, że ostatnie trzy zmienne przegubowe
θ
4
,
θ
5
i
θ
6
są odpowiednio
kątami Eulera
φ
,
θ
,
ψ
w odniesieniu do układu współrzędnych O
3
x
3
y
3
z
3
. Aby to zobaczyć,
potrzebujemy obliczyć macierze A
4
, A
5
i A
6
, wykorzystując tab. 3 i równanie (170). Wówczas
otrzymujemy
−
=
1
0
0
0
0
0
1
0
0
cos
0
sin
0
sin
0
cos
A
4
4
4
4
4
θ
θ
θ
θ
(188)
−
=
1
0
0
0
0
0
1
0
0
cos
0
sin
0
sin
0
cos
A
5
5
5
5
5
θ
θ
θ
θ
(189)
−
=
1
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
A
6
6
6
6
6
6
d
θ
θ
θ
θ
(190)
A po wymnożeniu tych macierzy, otrzymujemy
−
+
−
+
−
−
−
=
=
=
1
0
0
0
1
0
d
R
A
A
A
T
5
6
5
6
5
6
5
5
4
6
5
4
6
4
6
5
4
6
4
6
5
4
5
4
6
5
4
6
4
6
5
4
6
4
6
5
4
6
3
6
3
6
5
4
6
3
c
d
c
s
s
c
s
s
s
d
s
s
c
c
s
c
s
s
c
c
c
s
s
c
d
s
c
c
s
s
c
c
s
s
c
c
c
(191)
Porównanie części obrotowej
R
3
6
macierzy
T
3
6
z macierzą przekształcenia (83) przy obrocie
układu współrzędnych o kąty Eulera pokazuje, że kąty
θ
4
,
θ
5
i
θ
6
mogą rzeczywiście być
utożsamiane z kątami Eulera
φ
,
θ
,
ψ
w odniesieniu do układu współrzędnych O
3
x
3
y
3
z
3
.
Przykład 15.
Manipulator cylindryczny z kiścią sferyczną
Załóżmy teraz, że przymocowujemy kiść sferyczną do manipulatora cylindrycznego z
przykładu 13, jak to pokazano na rys. 46. Zauważmy, że oś obrotu w przegubie 4 jest
równoległa do osi z
2
i pokrywa się z osią z
3
z przykładu 13. Dzięki temu możemy
bezpośrednio połączyć dwa wcześniejsze wyrażenia (187) i (191), aby otrzymać równania
kinematyki prostej w postaci
T
0
6
=
T
0
3
T
3
6
(192)
gdzie macierz
T
0
3
jest określona równaniem (187), a macierz
T
3
6
– równaniem (191). Stąd
kinematyka prosta tego manipulatora jest opisana poniższym wzorem
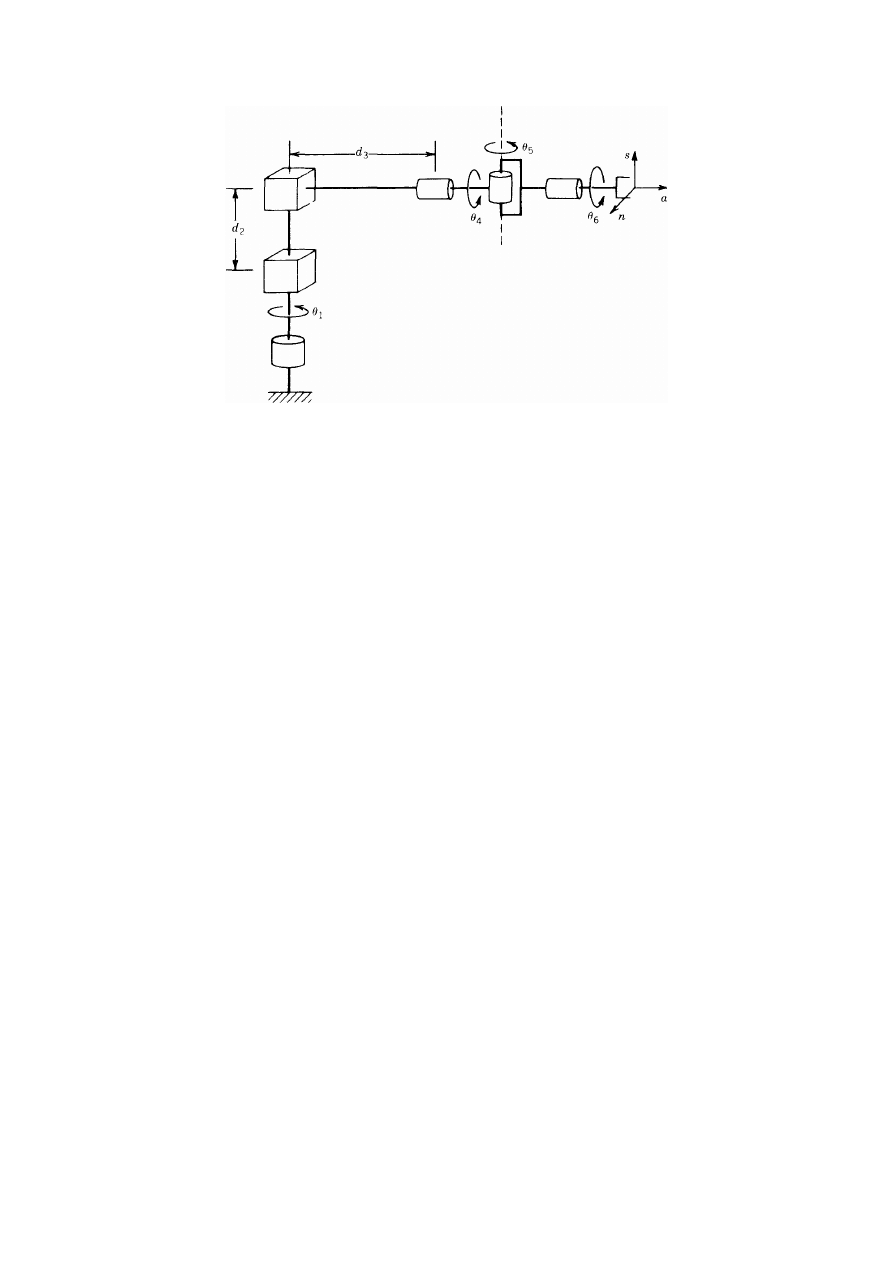
Rys. 46. Robot cylindryczny z kiścią sferyczną
=
−
+
−
+
−
−
−
⋅
+
−
−
−
=
⋅
=
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
T
T
T
33
32
31
23
22
21
13
12
11
5
6
5
6
5
6
5
5
4
6
5
4
6
4
6
5
4
6
4
6
5
4
5
4
6
5
4
6
4
6
5
4
6
4
6
5
4
2
1
1
3
1
1
1
3
1
1
6
3
3
0
6
0
z
y
x
d
r
r
r
d
r
r
r
d
r
r
r
c
d
c
s
s
c
s
s
s
d
s
s
c
c
s
c
s
s
c
c
c
s
s
c
d
s
c
c
s
s
c
c
s
s
c
c
c
d
d
c
d
c
s
s
d
s
c
(193)
gdzie
+
+
−
=
−
+
=
−
−
=
−
=
+
=
−
=
−
=
+
−
−
=
−
−
−
=
−
−
=
−
−
=
+
−
=
2
1
5
4
6
1
3
5
1
6
5
4
1
6
1
3
5
1
6
5
4
1
6
5
4
33
5
1
5
4
1
23
5
1
5
4
1
13
6
4
6
5
4
32
6
5
1
6
4
1
6
5
4
1
22
6
5
1
6
4
1
6
5
4
1
12
6
4
6
5
4
31
6
5
1
6
4
1
6
5
4
1
21
6
5
1
6
4
1
6
5
4
1
11
d
d
s
s
d
d
c
d
c
c
d
s
c
s
d
d
s
d
c
s
d
s
c
c
d
d
s
s
r
c
c
s
c
s
r
c
s
s
c
c
r
c
c
s
c
s
r
s
s
c
c
s
s
s
c
c
s
r
s
s
s
c
s
c
s
c
c
c
r
s
c
c
c
s
r
c
s
c
s
s
s
c
c
c
s
r
c
s
s
s
s
c
c
c
c
c
r
z
y
x
(194)
Zauważmy, jak bardzo wzrosło skomplikowanie równań kinematyki prostej tego
manipulatora po wprowadzeniu zorientowania końcówki roboczej, podczas gdy wyrażenia
(187) opisujące pozycję samego ramienia są stosunkowo proste. Przyjęcie kiści sferycznej nie
tylko upraszcza wyprowadzenie równań kinematyki prostej, ale pozwala także uprościć
rozwiązanie problemu kinematyki odwrotnej, czym zajmiemy się w dalszych wykładach.
Przykład 16. Manipulator stanfordzki
Rozważmy manipulator stanfordzki przedstawiony na rys. 47. Jest on przykładem
manipulatora sferycznego RRP z kiścią sferyczną. Manipulator ten ma przesunięcie w
przegubie barkowym, które trochę komplikuje zarówno zadanie kinematyki prostej, jak i
odwrotnej.
Rys. 47. Przyporządkowanie układów współrzędnych dla manipulatora stanfordzkiego
Na początku przyporządkujemy układy współrzędne przegubów, zgodnie z notacją
Denavita-Hartenberga, jak to pokazano na rys. 47. Parametry kinematyczne przedstawiono w
tab. 4.
Tab. 4. Parametry Denavita-Hartenberga dla manipulatora stanfordzkiego
Człon
a
i
α
i
d
i
θ
i
1
0
-90
0
θ
1
2
0
+90
d
2
θ
2
3
0
0
d
3
0
4
0
-90
0
θ
4
5
0
+90
0
θ
5
6
0
0
d
6
θ
6
Na tej podstawie można wyznaczy macierze A
i
które wyrażają się następującymi
wzorami

−
−
=
1
0
0
0
0
0
1
0
0
0
0
0
A
1
1
1
1
1
c
s
s
c
(195)
−
=
1
0
0
0
0
1
0
0
0
0
0
A
2
2
2
2
2
2
d
c
s
s
c
(196)
=
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
A
3
3
d
(197)
−
−
=
1
0
0
0
0
0
1
0
0
0
0
0
A
4
4
4
4
4
c
s
s
c
(198)
−
=
1
0
0
0
0
0
1
0
0
0
0
0
A
5
5
5
5
5
c
s
s
c
(199)
−
=
1
0
0
0
1
0
0
0
0
0
0
A
6
6
6
6
6
6
d
c
s
s
c
(200)
Wówczas macierz T
0
6
można zapisać jako
=
⋅
⋅
⋅
⋅
⋅
=
1
0
0
0
A
A
A
A
A
A
T
33
32
31
23
22
21
13
12
11
6
5
4
3
2
1
6
0
z
y
x
d
r
r
r
d
r
r
r
d
r
r
r
(201)
gdzie
−
+
=
+
+
+
+
=
−
+
+
−
=
+
−
=
+
+
=
−
+
=
+
+
=
+
−
+
+
+
−
=
+
−
−
+
+
−
=
−
−
−
=
+
+
−
−
=
+
−
−
−
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
]
)
(
[
)
(
]
)
(
[
)
(
)
(
]
)
(
[
)
(
]
)
(
[
5
2
4
5
2
6
2
3
2
1
5
5
1
4
2
5
4
1
6
1
2
2
1
3
5
4
1
2
5
1
5
4
2
1
6
1
2
2
1
3
5
2
5
4
2
33
5
4
1
5
2
5
4
2
1
23
5
4
1
5
2
5
4
2
1
13
6
5
2
6
4
6
5
4
2
32
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
22
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
12
6
5
2
6
4
6
5
4
2
31
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
21
6
4
6
5
4
1
6
5
2
6
4
6
5
4
2
1
11
s
s
c
c
c
d
c
d
d
s
s
c
s
s
c
c
s
s
c
d
c
d
s
s
d
d
s
s
s
s
c
c
s
c
c
c
d
s
d
s
c
d
d
c
c
s
c
s
r
s
s
c
c
s
s
c
c
s
r
s
s
s
c
s
s
c
c
c
r
s
s
c
c
s
s
c
c
s
r
c
c
s
c
s
c
s
s
s
c
s
s
c
c
c
s
r
c
c
s
c
s
s
s
s
s
c
s
s
c
c
c
c
r
c
s
c
s
s
c
c
c
s
r
s
c
c
c
s
c
c
s
s
s
s
c
c
c
c
s
r
s
c
c
c
s
s
c
s
s
s
s
c
c
c
c
c
r
z
y
x
ϕ
(202)
Przykład 17.
Manipulator typu SCARA
Jako inny przykład zastosowania ogólnej procedury rozważmy manipulator typu
SCARA, przedstawiony na rys. 48.
Rys. 48. Przyporządkowanie układów współrzędnych dla manipulatora SCARA
Manipulator ten, wzorowany na robocie AdeptOne, składa się z ramienia typu RRP i kiści o
jednym stopniu swobody, której ruchem jest obrót wokół pionowej osi. Pierwszym krokiem
jest umieszczenie i oznaczenie osi przegubów, jak to pokazano na rys48. Ponieważ wszystkie
osie są równoległe, mamy sporo swobody w rozmieszczaniu początków układów
współrzędnych. Zostały one wybrane jak na rysunku dla wygody w dalszych rozważaniach.
Oś
x
0
ustalono w płaszczyźnie rysunku. Jest to zupełnie dowolne i wpływa jedynie na
konfigurację zerową manipulatora, tzn. pozycję manipulatora dla
θ
1
= 0.
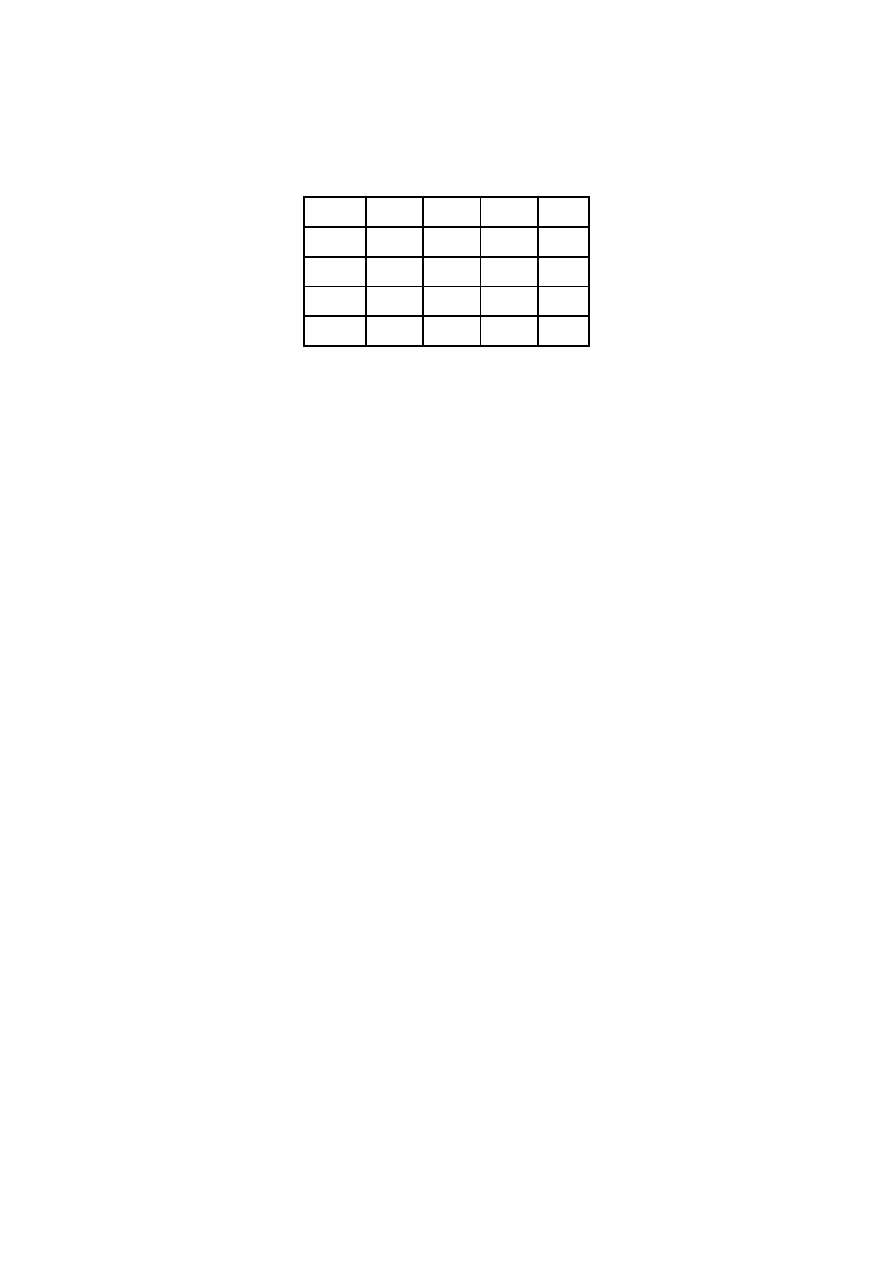
W tab. 5. przedstawiono parametry kinematyczne, a poniżej macierze A manipulatora
typu SCARA.
Tab. 5. Parametry Denavita-Hartenberga dla manipulatora typu SCARA
Człon
a
i
α
i
d
i
θ
i
1
a
1
0
0
θ
1
2
a
2
180
0
θ
2
3
0
0
d
3
0
4
0
0
d
4
θ
4
A macierze A
i
poniżej
−
=
1
0
0
0
0
1
0
0
0
0
A
1
1
1
1
1
1
1
1
1
s
a
c
s
c
a
s
c
(203)
−
−
=
1
0
0
0
0
1
0
0
0
0
A
2
2
2
2
2
2
2
2
2
s
a
c
s
c
a
s
c
(204)
=
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
A
3
3
d
(205)
−
=
1
0
0
0
1
0
0
0
0
0
0
A
4
4
4
4
4
4
d
c
s
s
c
(206)
Równania kinematyki prostej mają więc następującą postać
=
⋅
⋅
⋅
=
1
0
0
0
A
A
A
A
T
33
32
31
23
22
21
13
12
11
4
3
2
1
4
0
z
y
x
d
r
r
r
d
r
r
r
d
r
r
r
(207)
gdzie

−
−
=
+
=
+
=
=
=
=
=
−
=
−
−
=
−
=
+
−
=
+
=
4
3
12
2
1
1
12
2
1
1
32
31
23
13
33
4
12
4
12
22
4
12
4
12
21
4
12
4
12
12
4
12
4
12
11
0
,
0
,
0
,
0
1
d
d
d
s
a
s
a
d
c
a
c
a
d
r
r
r
r
r
c
c
s
s
r
s
c
c
s
r
c
s
s
c
r
s
s
c
c
r
z
y
x
ϕ
(208)
Wyszukiwarka
Podobne podstrony:
Materialy dla studentow OA 1 id Nieznany
materialy dla studentow 10 2 id Nieznany
materialy dla studentow polisac Nieznany
Materiały dla studentów OA W2
Programowanie liniowe material dla studenta id 396197
Biochemia materialy dla studentow id 8618
materialy dla studentow polisac Nieznany
Materiały dla studentów ENDOKRYNOLOGIA
materiały dla studentów 8
Socjalizm utopijny, Materiały dla studentów WSB DG
Test z Monitoringu Biologicznego, Materiały dla studentów, ochrona srodowiska
MATERIALY DO WYKLADU CZ V id 2 Nieznany
Materiały dla studentów Studiów Podyplomowych, Edukacja wczesnoszkolna, edukacja wczesnoszkolna, na
RYTMY BIOLOGICZNE, MATERIAŁY dla STUDENTÓW, 500 PRAC (pedagogika, psychologia, socjologia, filozofia
więcej podobnych podstron