Statystyka opisowa

dr Dorota Kałuża-Kopias

Zakład Demografii i Gerontologii

społecznej

Informacje ogólne:

• kontakt e-mail:

[e-mail]

• dyżur: środa 15.00-16.30 pok. A.34
• obecność na zajęciach zwiększa

prawdopodobieństwo zaliczenia
przedmiotu....

• zaliczenie: pisemne w formie testu

Podstawowe pojęcia

statystyczne

• Termin statystyka [łac. Status- państwo] został

wprowadzony do powszechnego użytku w
połowie XVII w. przez niemieckiego uczonego
Gottfreda Achenwalla. Początkowo był to proces
gromadzenia i zestawiania danych liczbowych
wykorzystywanych później w procesie rządzenia
państwem. Obecnie nauka zajmuje się
badaniem i opisywaniem prawidłowości
występujących w zjawiskach masowych.

• Przedmiotem badań statystycznych jest

zbiorowość statystyczna. Pojęcie to ma
charakter uniwersalny ze względu na jego
zastosowanie do wszystkich badań
statystycznych dotyczących zarówno życia
społecznego, jak i gospodarczego.

• Zbiorowość statystyczna (populacja) –

zbiór jednostek (osób, przedmiotów,
faktów) podobnych do siebie pod
względem określonej cechy (cech) i
powiązanych ze sobą logicznie, ale nie
identycznych.

• Liczebność – ilość jednostek wchodzących w

skład zbiorowości statystycznej.

• Na przykład zbiorowością statystyczną w

przypadku badania płci są wszystkie osoby
będące obywatelami danego kraju.

• Z uwagi na wielkość zbiorowości statystycznej i

fakt, iż przeprowadzenie badania pełnego (całej
zbiorowości) jest zbyt kosztowne w praktyce
znacznie częściej bada się tylko część jednostek
wchodzących w skład zbiorowości statystyczne
(tzw. zbiorowość próbną, próbę statystyczną).

• Próbą statystyczną (zbiorowością

próbną) nazywamy cześć zbiorowości
statystycznej poddanej badaniu, która
została wyodrębniona ze zbiorowości w
określony sposób.

Cechy statystyczne i ich rodzaje

• Najczęściej cechy statystyczne są dzielone na:
• Cechy ilościowe (mierzalne) – są to te

właściwości jednostki statystycznej, które dadzą

się zmierzyć i wyrazić za pomocą liczb oraz
konkretnej jednostki, np. wzrost (cm), wiek (lata),
masa (kg), itd..

• Cechy jakościowe (niemierzalne) – są to te

właściwości jednostki statystycznej, których nie

można zmierzyć, a jedynie stwierdzić czy dany

wariant właściwości występuję bądź nie u danej

jednostki. Cechy te określane są najczęściej

słownie, np. pleć, wykształcenie, kategorie

zawodowe, narodowość, itd..

• W wyniku pogrupowania jednostek

zbiorowości statystycznej według cech
mierzalnych

możemy otrzymać podział

na cechy:

– Ciągłe – mogą przyjmować dowolną wartość

z określonego przedziału liczbowego, a zbiór

wartości takich cech jest nieprzeliczalny, np.
waga (40-120) kg.

– Skokowe (dyskretne) – mogą przyjmować

tylko niektóre wartości z określonego

przedziału liczbowego, np. ilość dzieci w
rodzinie.

• W przypadku cech niemierzalnych

rozróżniamy klasyfikację:

– Dwudzielną (dychotoniczną) – przyjmują

tylko dwa warianty, tzn. każda jednostka ma
daną własność lub nie, innych możliwości nie
ma np. płeć – kobieta i mężczyzna.

– Wielodzielną (politomiczną) – przyjmują

więcej niż dwa warianty, np. stan cywilny –
panna/kawaler, zamężna/żonaty,
rozwiedziona/rozwiedziony,
separowana/separowany, wdowa/wdowiec.

• Innym podziałem cech statystycznych jest

podział ze względu na przynależność jednostek

do danej zbiorowości statystycznej. W tym

przypadku rozróżniamy cechy:

• Stałe – wspólne wszystkim jednostkom

zbiorowości statystycznej, nie podlegają badaniu

statystycznemu, pomagają jedynie zaliczyć daną

jednostkę do określonej zbiorowości
statystycznej.

• Zmienne – właściwości, którymi poszczególne

jednostki różnią się od siebie, tzn. występują u

poszczególnych jednostek zbiorowości w postaci

możliwych wariantów cechy.

• W zależności od charakteru zbiorowości

statystycznej wśród cech stałych

wyróżnić można cechy:

• Rzeczowe – odnoszą się do pytania co?,

lub kogo badamy?,

• Czasowe – określają, jaki okres obejmuje

badanie?,

• Przestrzenne – określają, gdzie odbywa

się badanie.

• Rozpatrzmy na przykład zbiorowość, której

jednostkami statystycznymi są wszyscy studenci

studiujący na kierunku ekonomia w Łodzi w roku

akademickim 2010/2011. Stałą cechą rzeczową

jednostek tej zbiorowości jest to, że są to

studenci kierunku ekonomia, stałą cechą

przestrzenną jest to, że studenci ci są z łódzkich

uczelni, stałą cechą czasową jest zaś fakt, iż do

zbiorowości tej należą tylko ci, którzy byli
studentami politologii w roku akademickim
2010/2011.

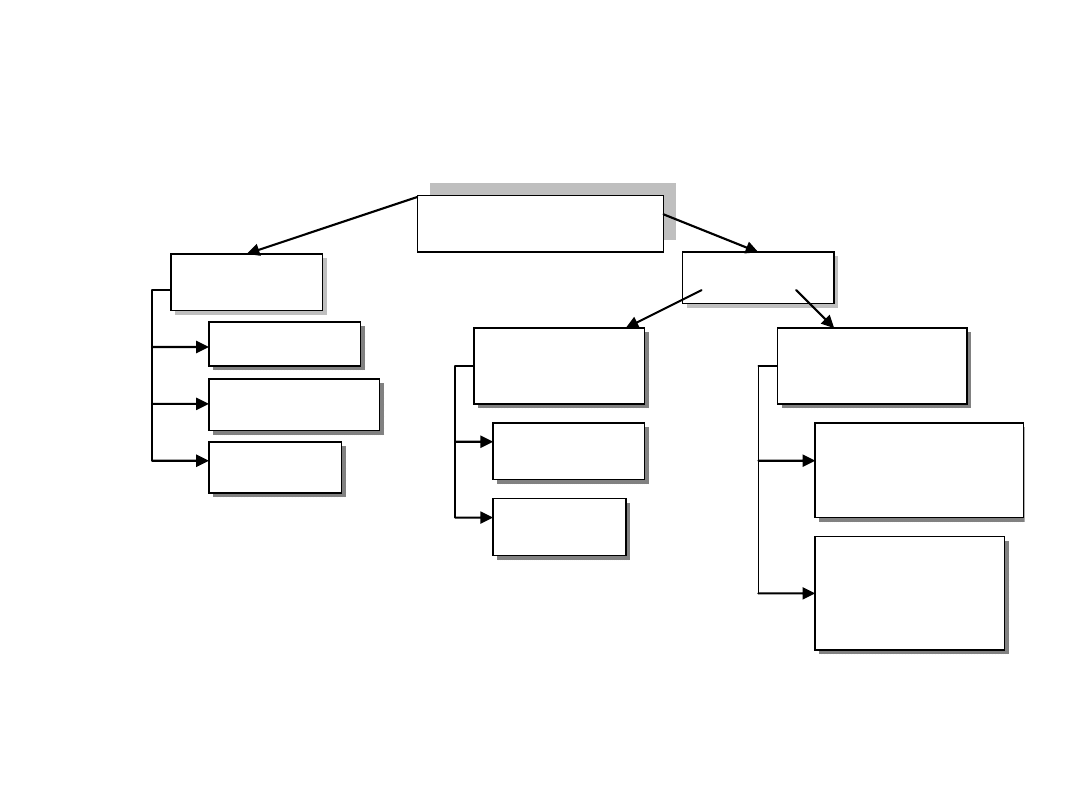
Rys. 1.1 Podział cech statystycznych

Źródło: Opracowanie własne

Cechy statystyczne

Zmienne

Stałe

Rzeczowe

Czasowe

Przestrzenne

Dwudzielne
(dychotoniczną)

Ciągłe

Skokowe

Jakościowe
(niemierzalne)

Ilościowe
(mierzalne)

Wielodzielną
(politomiczną)

Etapy badania statystycznego

• Badanie statystyczne polega na zebraniu

odpowiednich informacji dotyczących określonej

zbiorowości statystyczne, a następnie
przetworzeniu i analizie tych informacji.

• Wyróżnić można cztery etapy badania

statystycznego:

• Przygotowanie badania statystycznego;
• Obserwacja statystyczna;
• Opracowywanie zebranego materiału

statystycznego;

• Analiza zebranego materiału statystycznego;

• W pierwszym etapie badania należy:

– Sformułować cel badania i hipotezy

badawcze;

– Określić zbiorowość i jednostkę statystyczną

(ze względu na kryterium rzeczowe, czasowe,
przestrzenne);

– Określić listę cech statystycznych;
– Określić metodę badania statystycznego;

• Ze względu na kompletność badania

statystycznego wyróżniamy badania:

– Całkowite (pełne) – obserwacji poddane są wszystkie

jednostki statystyczne, np. spisy powszechne,
bieżąca rejestracja statystyczna (zgonów, urodzeń,
małżeństw);

– Częściowe – część zbiorowości poddana zostaje

badaniu statystycznemu, są to badania: ankietowe,
monograficzne, reprezentacyjne, np. kontrola jakości
wyrobów;

• Ze względu na ciągłość obserwacji

wyróżniamy badania:

– Jednorazowe – np. ustalenie przyczyny

zgonu;

– Okresowe (cykliczne) – np. spisy

powszechne;

– Ciągłe – np. rejestracja bieżąca urodzeń,

zgonów;

– Określić źródła informacji;

• Pierwotne – zbieramy informacje dla konkretnego

badania, np. ankieta informacja zaczerpnięta u
źródła;

• Wtórne – zbiór danych zgromadzonych dla celów

poza statystycznych, np. dla bieżącej działalności
jednostek gospodarczych;

• Opracować formularze statystyczne i przygotować

makiety tablic wynikowych oraz zapewnić
odpowiednią kontrolę zbieranych materiałów
statystycznych;

• Szkolenie osób zbierających materiał statystyczny

(tylko w przypadku materiału pierwotnego);

• Opracowywanie planu finansowego badania.

• Etap drugi – obserwacja statystyczna

czyli zbieranie

materiału statystycznego

przebiega zgodnie z

założeniami z

wcześniejszego

etapu

projektowania

badania.

• Etap trzeci – opracowywanie zebranego

materiału statystycznego.

• Na tym etapie mamy do wykonania

następujące czynności:

• Kontrolę formalną i merytoryczną;
• Grupowanie materiału statystycznego;
• Podliczanie (zliczanie) materiału

statystycznego;

• Prezentacja materiału statystycznego;

• Zebrany materiał statystyczny podczas drugiego

etapu nazywamy materiałem surowym, który

często zawiera różnego rodzaju braki i błędy.

Dlatego przed analizą statystyczną poddajemy

go kontroli zarówno pod kontem formalnym, jak i
merytorycznym.

• Kontrola formalna polega na sprawdzeniu

kompletności i zgodności rachunkowej materiału
statystycznego, natomiast kontrola
merytoryczna

sprawdza logiczną poprawność

zapisów.

• Do przeprowadzenia badania statystycznego oprócz

kontroli formalnej i merytorycznej należy dokonać

grupowania materiału statystycznego, które stanowi

przejście od materiałów informacyjnych o pojedynczych

jednostkach badanej zbiorowości statystycznej do

informacji dających obraz o całej zbiorowości. Inaczej

mówiąc grupowanie materiału statystycznego polega

na wyodrębnienie jednorodnych grup ze zbiorowości

statystycznej. Takim podziałem jest na przykład podział

ludności ze względu na płeć czy charakter miejsca

zamieszkania (miasto, wieś).

• Głównym i ostatecznym celem każdego

badania statystycznego jest analiza
zebranego materiału statystycznego,
która ma na celu możliwie wszechstronne
poznanie i zbadanie analizowanej
zbiorowości.

Sposoby prezentacji materiału

statystycznego

• Opracowanie materiału statystycznego

(tzn. grupowanie i zliczanie) sprowadza

się do prezentacji danych statystycznych
w odpowiedniej formie.

• Istnieją dwie podstawowe formy

prezentacji danych statystycznych:

• Szeregi statystyczne;
• metoda graficzna (histogramy, wykresy,

kartogramy, itd.).

• Sposób prezentacji zależny jest od

specyfiki i celu badania. Główną zasadą
jaką badacz kieruje się przy wyborze
formy prezentacji danych statystycznych
jest zapewnienie czytelności i
przejrzystości zebranych danych, a dzięki
temu uzyskanie możliwości analizy
prezentowanego materiału statystycznego.

Szeregi statystyczne

• Dane statystyczne uporządkowane według

wariantu jednej cechy zaprezentowane w
postaci tabelarycznej tworzą szereg
statystyczny.

• W zależności od rodzaju analizy badanych

zjawisk rozróżniamy szeregi

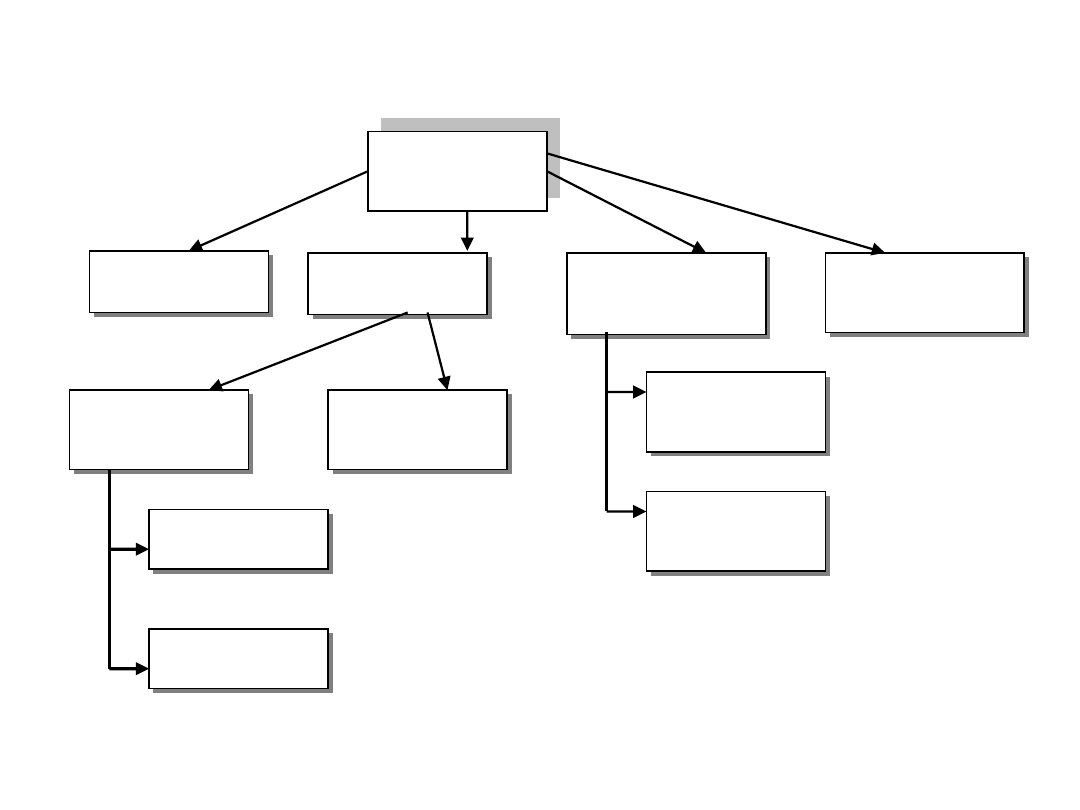
Rys. 1.2. Podstawowe rodzaje szeregów statystycznych

Źródło: Opracowanie własne

Szeregi
statystyczne

Okresów

Rozdzielcze

Czasowe
(dynamiczne)

Momentów

Z cechą
mierzalną

Szczegółowe

Przedziałowe

Geograficzne
(przestrzenne)

Punktowe

Z cechą
niemierzalną

1. Szereg szczegółowy (indywidualny, prosty, wyliczający) – ciąg liczbowych wielkości

statystycznych uporządkowanych według badanej cechy (rosnąco lub malejąco). W

praktyce ma zastosowanie przy małych zbiorowościach.

Nr badanej jednostki

1

2

3

4

n

Wariant badanej cechy (

i

x

)

1

x

2

x

3

x

4

x

n

x

gdzie:

i

x - oznacza wartość cechy dla i-tej jednostki zbiorowości statystycznej;

i= 1,2…,n

Przykład:

10 studentów kierunku politologia spytano ile palą dziennie papierosów. Uzyskano

następujące informacje (ilość wypalanych papierosów w sztukach):1,2,8,10,3,2,1,5,6,4.

Aby z powyższych informacji utworzyć szereg szczegółowy należy ułożyć liczbę

wypalanych papierosów niemalejąco.

Nr studenta

1

2

3

4

5

6

7

8

9

10

Liczba wypalanych papierosów (

i

x

) 1

1

2

2

3

4

5

6

8

10

• W przypadku gdy mamy do czynienia z dużymi

zbiorowościami statystycznymi stosujemy
szeregi rozdzielcze, które dzielą badaną
zbiorowość na klasy (części) według określonej
cechy.

• Szereg rozdzielczy – składa się z dwóch

kolumn (w pierwszej kolumnie znajdują się
warianty badanej cechy , w drugiej kolumnie
liczba jednostek zbiorowości statystycznej, która
dany wariant cechy posiada .

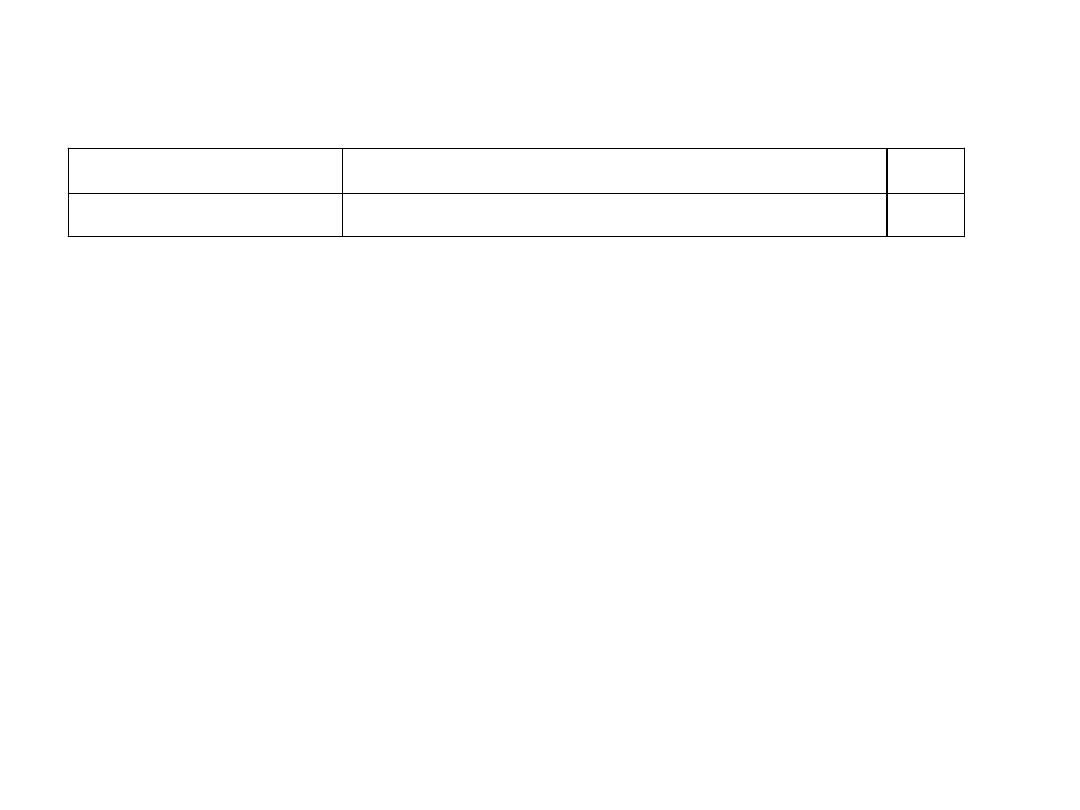
Wariant badanej cechy (

i

x

)

1

x

2

x

3

x

4

x

k

x



liczba jednostek (

i

n

)

1

n

2

n

3

n

4

n

k

n

n

gdzie:

i

x - oznacza i-ty wariant badanej cechy

i=1,2,…,k

i

n - liczba jednostek zbiorowości statystycznej o i-tym wariancie cechy (tzw. liczebności

cząstkowe);

k – liczba wariantów cechy (klas);

n – liczebność całkowita zbiorowości (próby);



-

znak sumy;

przy czym:







k

i

i

n

n

1

• Szeregi rozdzielcze dla cech

mierzalnych dzielą się na:

• Punktowe – stosujemy gdy liczba

wariantów cechy jest niewielka.

• Z przedziałami klasowymi – stosujemy

gdy jest duża liczba wariantów badanej
cechy.

• Ważne przy konstrukcji szeregów rozdzielczych

z przedziałami klasowymi jest ustalenie:

• Liczby klas (przedziałów), w praktyce wynosi

ona od 5 do 15 (w zależności od liczby
obserwacji i charakteru danych). Jednym ze
sposobów ustalenia liczby klas jest skorzystanie
z formuły:

• Długości przedziału klasowego (rozpiętość)

stanowi różnicę między górną a dolną krawędzią
przedziału (x dolne - x górne). W praktyce
staramy się aby rozpiętości poszczególnych
przedziałów były porównywalne.

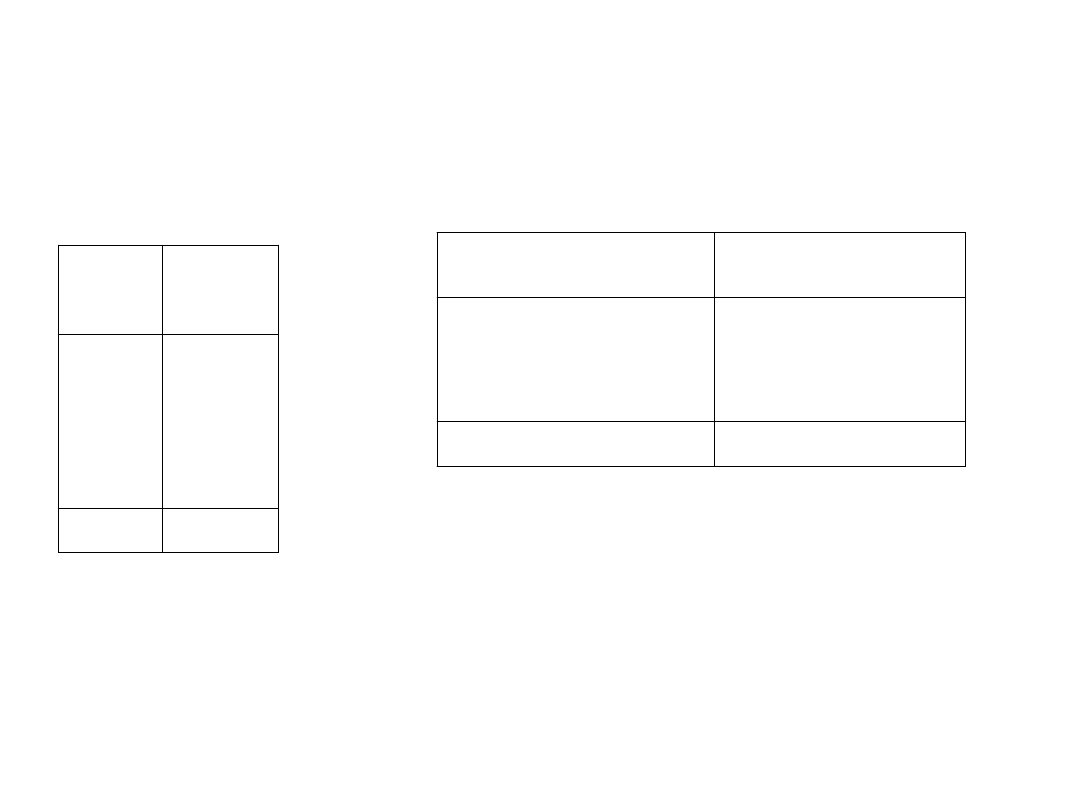
Szereg rozdzielczy punktowy (tab. 1.1)

Szereg rozdzielczy z przedziałami klasowymi (tab. 1.2)

Tab. 1.1 Wzrost dzieci

Tab. 1.2 Absencja chorobową pracowników firmy X

w klasie trzeciej szkoły podstawowej

Źródło: Dane umowne

Wzrost

(w cm)

i

x

Liczba

dzieci

i

n

150
151
152
153
154
155
156

25
35
40
45
40
30
20



235

Liczba dni nieobecności

i

x

Liczba pracowników

i

n

0 – 4
5 – 9

10 – 14
15 – 19
20 – 24

100
150
200
130
120



700

• Czasami mamy do czynienia z szeregami

statystycznymi rozdzielczymi o pierwszym
lub ostatnim przedziale kasowym
otwartym. Sytuacja taka występuje, np.
gdy w badanej zbiorowości statystycznej
występują ekstremalne wartości badanej
cechy (zarówno bardzo duże, jak i bardzo
małe).

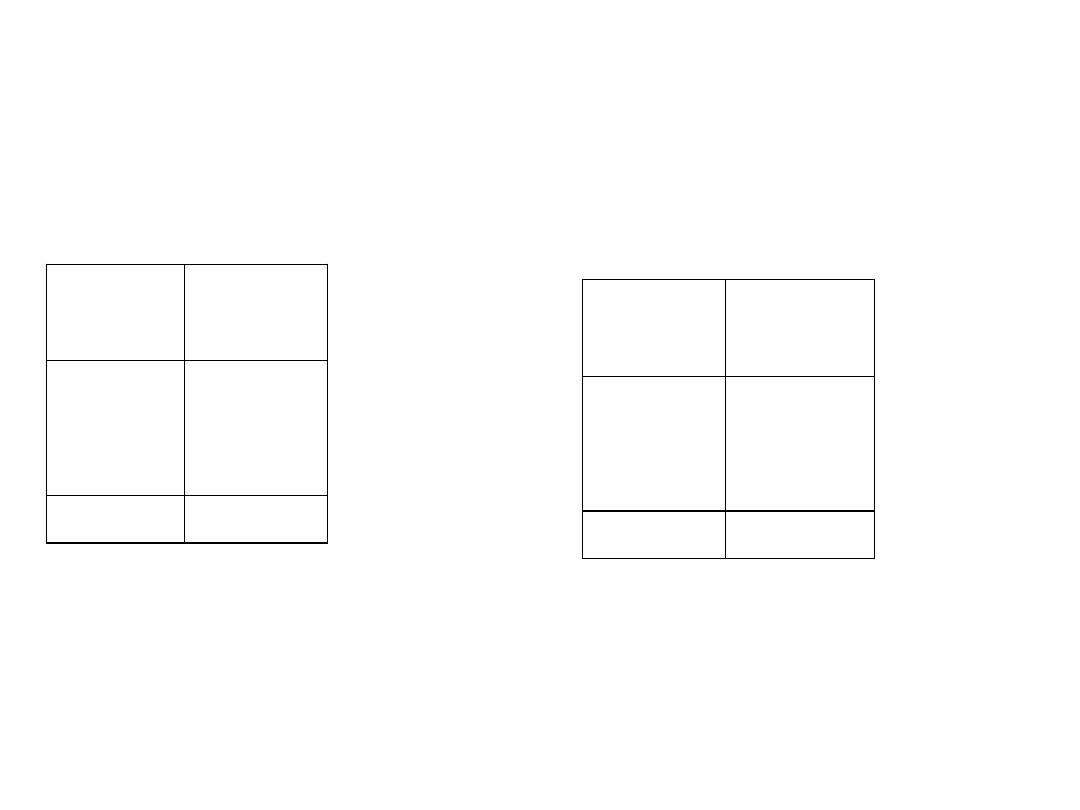
Szeregi rozdzielcze z otwartymi przedziałami klasowymi (tab. 1.3, 1.4)

Tab. 1.3

Tab. 1.4

Źródło: Dane umowne

Liczba dni

nieobecności

i

x

Liczba

pracowników

i

n

0 – 4
5 – 9

10 – 14
15 – 19

20 i więcej

100
150
200
130
120



700

Liczba dni

nieobecności

i

x

Liczba

pracowników

i

n

4 i mniej

5 – 9

10 – 14
15 – 19
20 – 24

100
150
200
130
120



700

Szereg rozdzielczy dla cechy niemierzalnej (tab. 1.5)

Tab. 1.5 Struktura ludności w wieku 15 lat i więcej według stanu cywilnego faktycznego w 2002 roku

Stan cywilny

i

x

Ludność (w tys.)

i

n

Mężczyźni

Kawalerowie

Żonaci i partnerzy

W tym partnerzy

Wdowcy

Rozwiedzieni

Separowani

Kobiety

Panny

Zamężne i partnerki

W tym partnerki

Wdowy

Rozwiedzione

Separowane

14962,1

4863,0
9145,7

198,0
424,7
394,2

9,6

16326,3

3869,0
9239,9

198,0

2446,3

635,8

13,7

Źródło: Rocznik Demograficzny 2007, s. 164



Szereg przestrzenny - (geograficzny)

–

prezentuje

strukturę

przestrzenną

badanego zjawiska. Konstrukcja szeregu
geograficznego polega na tym,

że w

pierwszej

kolumnie

zamieszczamy

jednostki terytorialne, a w drugiej badane
wielkości statystyczne.

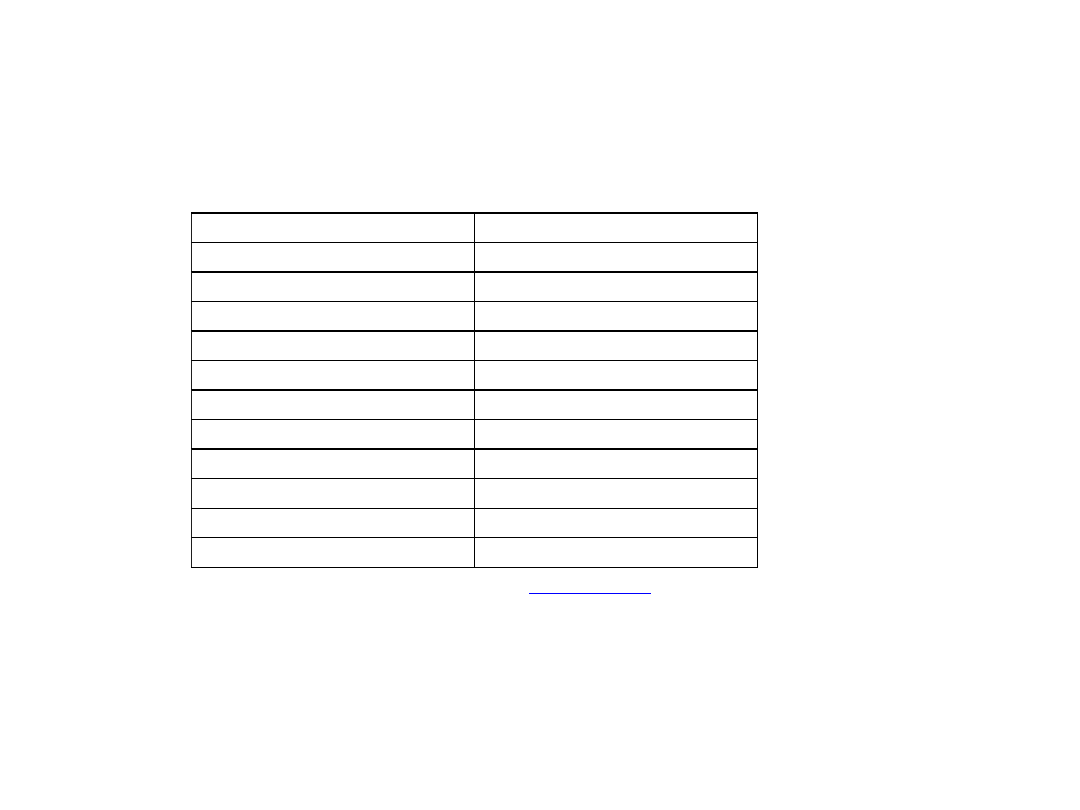
Szereg przestrzenny (tab. 1.6)

Tab. 1.6 Największe państwa świata w 2007 (w mln osób)

Kraj

Ludność

Chiny

1318

Indie

1132

USA

302

Indonezja

232

Brazylia

189

Pakistan

169

Bangladesz

149

Nigeria

144

Rosja

142

Japonia

128

Meksyk

107

Źródło: dane dostępne na stronie

www.un.org

• Zgrupowany materiał statystyczny przedstawiany jest

najczęściej w postaci tablic statystycznych, które

stanowią zbiór szeregów statystycznych. Każda tablica

statystyczna zaopatrzona jest w tytuł, kolumny i wiersze.

W zależności z ilu szeregów składa się tablica można je

podzielić na:

• Proste – składają się z jednego szeregu i zawierają

informacje o zbiorowości statystycznej z punktu widzenia
jednej cechy.

• Kombinowane – składają się z kilku szeregów i

zawierają informacje o jednej zbiorowości z punktu
widzenia kilku cech.

• W przypadku gdy z różnych przyczyn nie

możemy wypełnić jakiejś pozycji w tablicy to w
miejsce to wstawiamy jeden ze znaków:

• (-) zjawisko nie występuje;
• (.) brak informacji;
• (X) rubryka nie może być wypełniona ze

względu na układ tablicy;

• (0) wielkość mniejsza od minimum jednostki;

Analiza struktury zbiorowości

• Realizacji tego zadania służą odpowiednie miary

statystyczne (zwane parametrami). Do podstawowych

parametrów opisujących strukturę zbiorowości

statystycznych należą:

• wskaźnik natężenia;
• wskaźnik struktury;
• wskaźnik podobieństwa struktur;
• miary opisujące tendencję centralną (średnie);

– klasyczne,
– pozycyjne,

• miary dyspersji (rozproszenia, zróżnicowania, rozrzutu);

– klasyczne,
– pozycyjne,

• Wyniku obserwacji statystycznej

otrzymujemy informację o badanym
zjawisku w postaci liczb

bezwzględnych

(absolutnych),

które są zawsze

wielkościami mianowanymi (np. masa w
kg, liczba w sztukach, powierzchnia w ).
Wartości bezwzględne jednak nie nadają
się do porównań w czasie i w przestrzeni
badanych zbiorowości.

• Prawdziwy osąd o stanie badanego

zjawiska daje dopiero uwzględnienie
wartości bezwzględnych innego zjawiska
występującego wraz z badanym. Dlatego
w analizie statystycznej oprócz liczb
bezwzględnych wykorzystuje się liczby
względne (stosunkowe), które stanowią
stosunek (iloraz) liczb bezwzględnych
opisujących zjawiska ze sobą powiązane.

• Wskaźniki natężenia to liczby względne,

obliczane wówczas gdy chcemy
przedstawić badaną wielkość w
odniesieniu do innej, która jest z nią
logicznie powiązana.

Wartość wskaźnika natężenia (

n

W ) wyznaczamy na podstawie wzoru (1.1):

b

a

W

n



(1.1)

gdzie:

a - wielkość pierwsza;

b - wielkość druga logicznie powiązana z wielkością pierwszą;

• W opisie zjawisk demograficznych i

społeczno-ekonomicznych jest to miara
bardzo często wykorzystywana. Niektóre z
nich to: gęstość zaludnienia (liczba
ludności przypadająca na 1 km2),
współczynnik zawierania małżeństw
(odnoszący liczbę zawartych w danym
okresie małżeństw do populacji osób
zamieszkałych na danym obszarze), itd.

Wskaźnik struktury (frakcja),

wskaźnik podobieństwa struktur

• Struktura badanej zbiorowości często

przedstawiana jest w podziale na
podgrupy jednostek różniących się od
siebie wariantami analizowanej cechy.
Udział poszczególnych części zbiorowości
posiadających dany wariant cechy w całej
zbiorowości opisuje wskaźnik struktury
(frakcja), który może być wyrażony w
procentach albo w promilach.

Wartość wskaźnika struktury (

i

w ) wyznaczamy na podstawie wzoru (1.2):

n

n

w

i

i



(1.2)

przy czym







k

i

i

w

1

1 (lub 100 jeśli wyrażany jest w procentach, 1000 – jeśli w promilach)

i

1

0





i

w

(lub 100 jeśli wyrażany jest w procentach, 1000 – jeśli w promilach)

gdzie:

i = 1, 2,…, n;

k – liczba podgrup badanej zbiorowości;

n - liczebność całkowita zbiorowości;

i

n - liczebność cząstkowa zbiorowości;

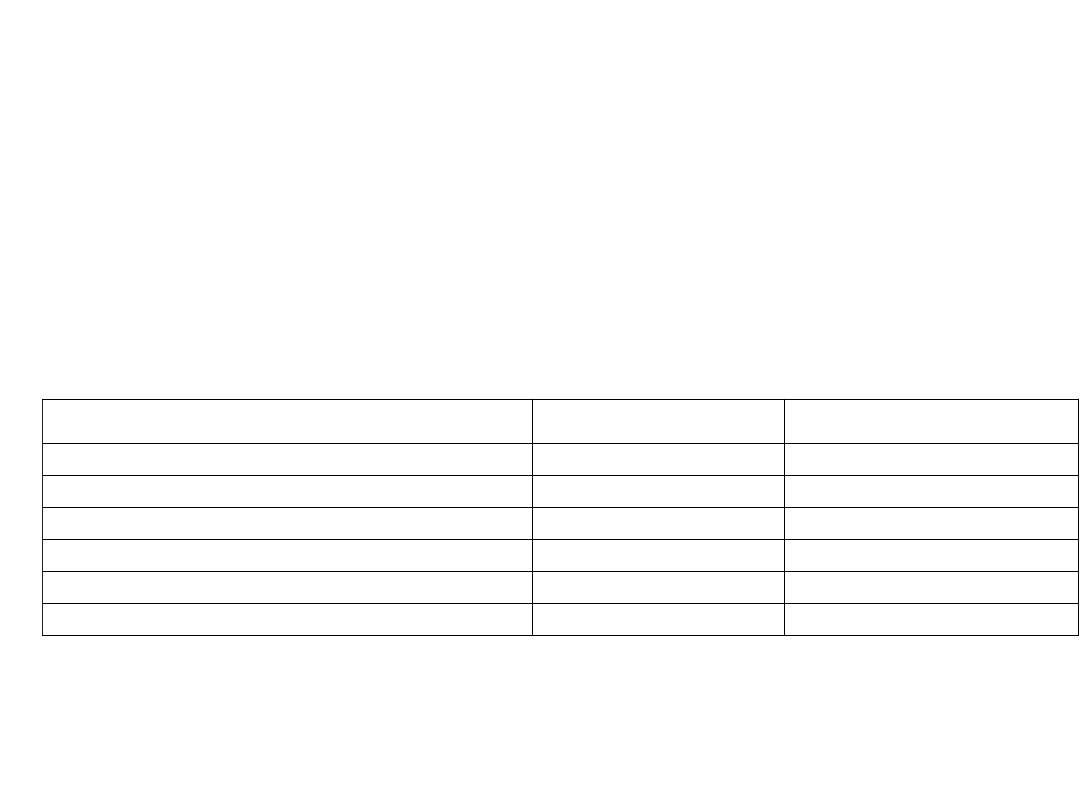
Przykład:

Tablica 1.7 przedstawia wydatki na grupy towarów w 2004 r. ponoszonych miesięcznie przez

gospodarstwa domowe. Aby określić, jaki był udział poszczególnych grup towarów w

wydatkach miesięcznych gospodarstw domowych, obliczono w kolumnie 3. wskaźniki

struktury.

Tab. 1.7 Wydatki na grupy towarów gospodarstw domowych w 2004 r.

grupy towarowe

miesięczne wydatki na os.

Wskaźniki struktury (

i

w

) w %

Żywność i napoje bezalkoholowe

181

46,06

Napoje alkoholowe i wyroby tytoniowe

19

4,83

Odzież i obuwie

39

9,92

Użytkowanie mieszkań i nośniki energii

129

32,82

Zdrowie

25

6,36

Suma

393

100,00

Źródło: Obliczenia własne na podstawie danych z Rocznika Statystycznego 2005, s. 203

• Do określenia podobieństwa struktur

badanych zbiorowości z punktu widzenia
określonej cechy w naukach społecznych
często jako miarę wykorzystuje się
wskaźnik podobieństwa struktur, który
wyznacza się według wzoru (1.3):





)

,

min(

iII

iI

p

w

w

w

(1.3)

przy czym

1

0





p

w

,

gdzie:

iII

iI

w

w ,

- oznaczają wskaźniki struktury dla dwóch porównywalnych zbiorowości (I i II).

Im wartość wskaźnika bliższa jedności tym struktury badanych zbiorowości są do siebie

bardziej podobne. Najczęściej miara ta wyrażana jest w procentach, wówczas

100

0





p

w

• W tab. 1.8 przedstawiono strukturę studentów według

płci na dwóch uczelniach (politechnice i uniwersytecie).

Chcąc odpowiedzieć na pytanie czy struktura studentów

ze względu na płeć jest do siebie podobna na obu

uczelniach, należy obliczyć wskaźnik podobieństwa

struktur, według wzoru (1.3). Jak wynika z danych

zawartych w tablicy wyższy udział kobiet wśród ogółu

studentów występuje na uniwersytecie (55%). Mimo to

obliczony w kolumnie 4., tab. 1.8 wskaźnik podobieństwa

struktur wynosi 0,7, co wskazuje na 70% podobieństwo

obu porównywanych struktur.

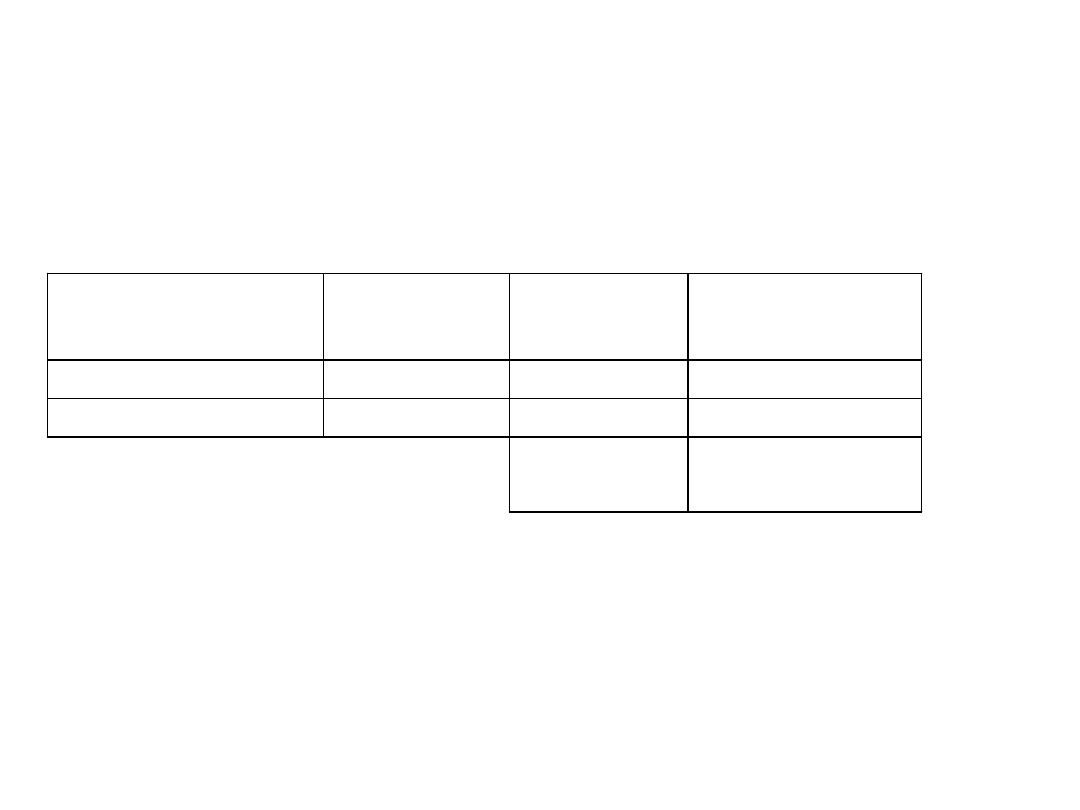
Tab. 1.8 Struktura studentów według płci

Płeć (studenta)

Politechnika

iI

w

I

Uniwersytet

iII

w

min (

iII

iI

w

w ,

)

Kobieta

0,25

0,55

0,25

Mężczyzna

0,75

0,45

0,45

p

w

0,70

Źródło: Dane umowne

Miary średnie

(klasyczne i pozycyjne)

• Średnie klasyczne – do obliczenia

których potrzebujemy wszystkich

jednostek zbiorowości statystycznej;

• Średnie pozycyjne – które są

konkretnymi wartościami jednostek

zbiorowości statystycznej, jednostek

wyróżnionych ze zbiorowości ze względu

na swoją pozycję w szeregu
statystycznym;

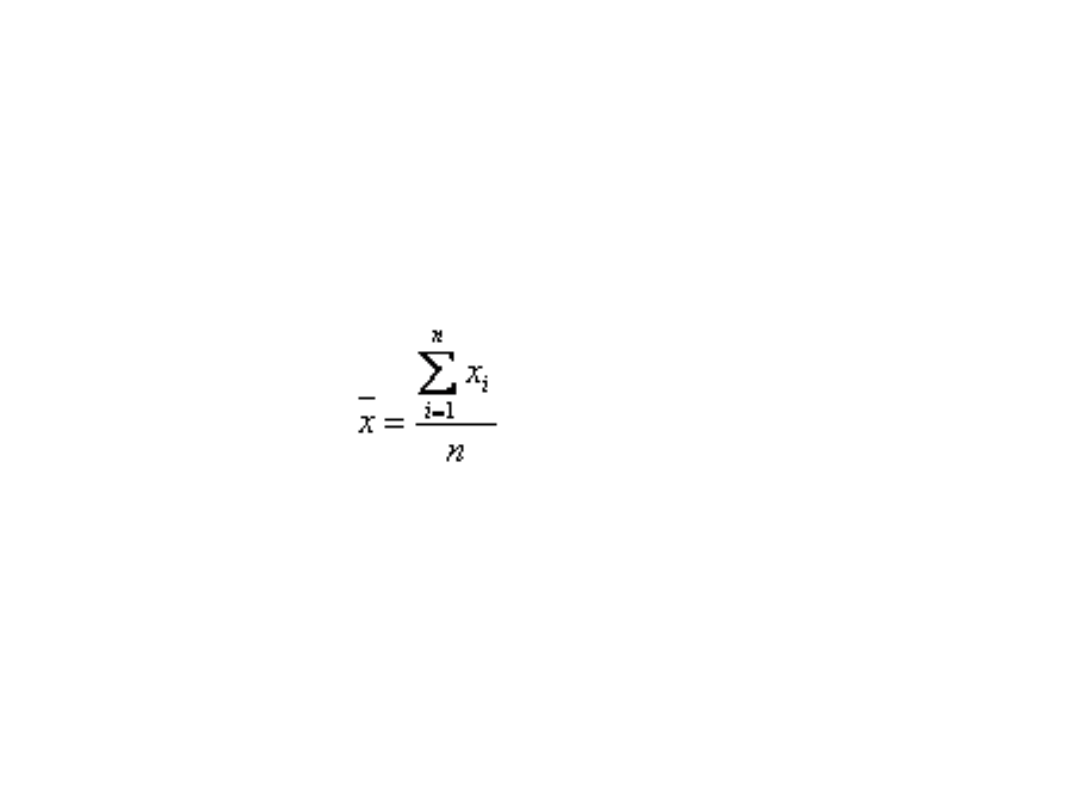
• Średnia arytmetyczna – otrzymujemy ją w wyniku

podzielenia sumy wartości cechy wszystkich jednostek

zbiorowości statystycznej przez liczebność zbiorowości.

gdzie:
• wartość cechy dla i-tej jednostki zbiorowości;
• i=1,2,…, n;
• n - liczebność całkowita zbiorowości (próby);
• Średnią arytmetyczną obliczoną według powyższego

wzoru nazywamy średnią arytmetyczną prostą i

wyznaczamy ją na podstawie szeregów szczegółowych.

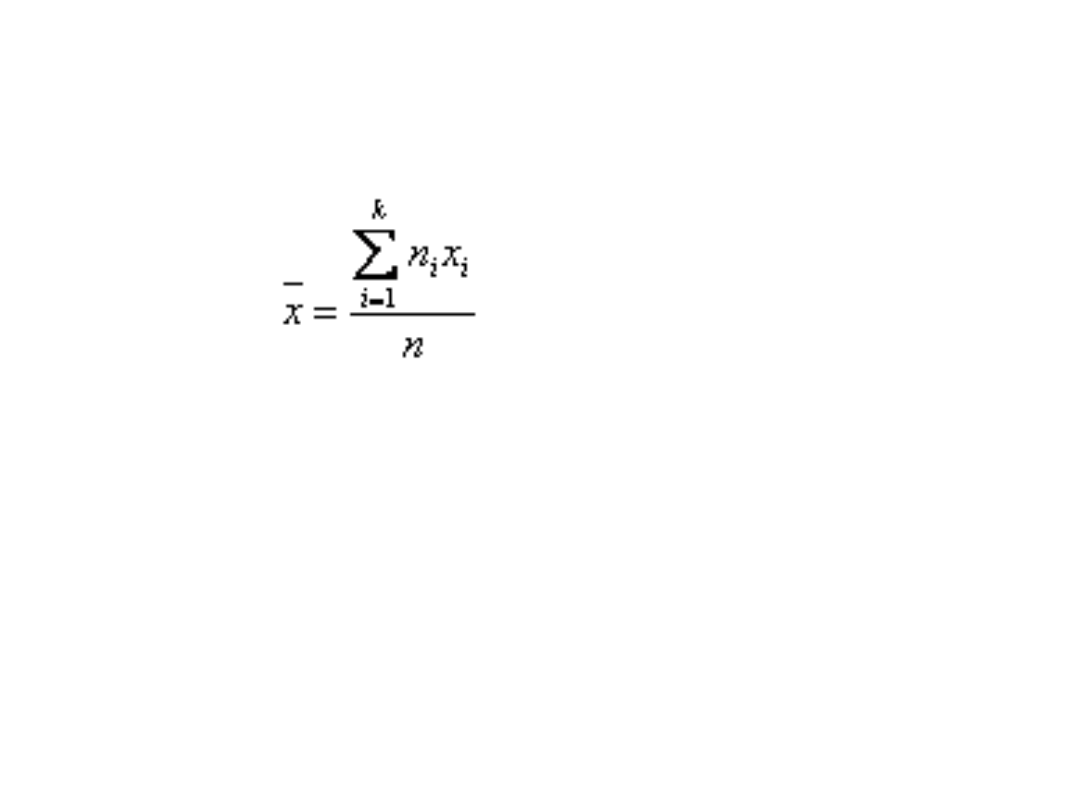
gdzie:

i

n

- liczba jednostek zbiorowości statystycznej o i-tym wariancie cechy

k – liczba wariantów cechy (klas);

• W przypadku szeregu rozdzielczego z

przedziałami klasowymi warianty cechy
wyrażone są za pomocą klas. W każdej
klasie występuje nie jeden wariant cechy
lecz wiele. W tym wypadku średnią
arytmetyczną ważoną wyznaczamy
według wzoru

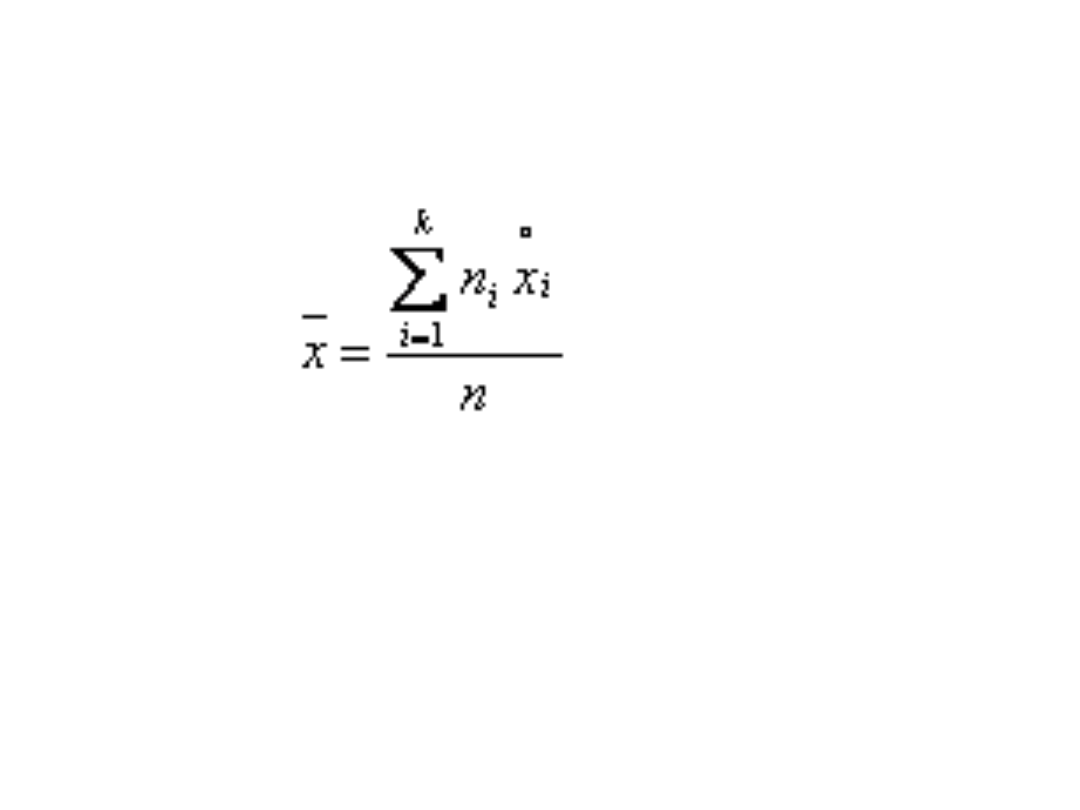
gdzie:

i

x



- środek przedziału klasowego, który wyznaczamy sumując dolny i górny kraniec

przedziału, a następnie tak obliczoną sumę dzielimy przez 2.

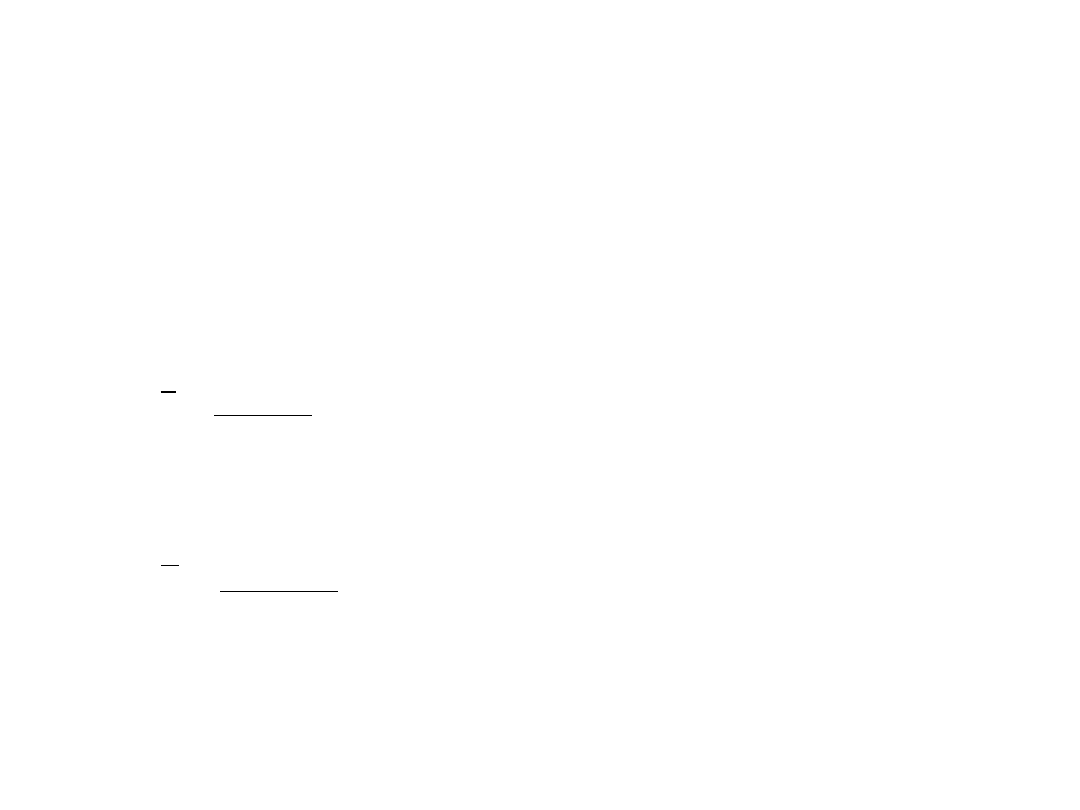
Jeśli w miejsce wagi

i

n

we wzorach podstawimy

wskaźnik struktury

i

w

, to średnie arytmetyczne ważone

przyjmą postać:













k

i

i

i

k

i

i

i

x

w

n

x

n

x

1

1













k

i

i

i

k

i

i

i

x

w

n

x

n

x

1

1





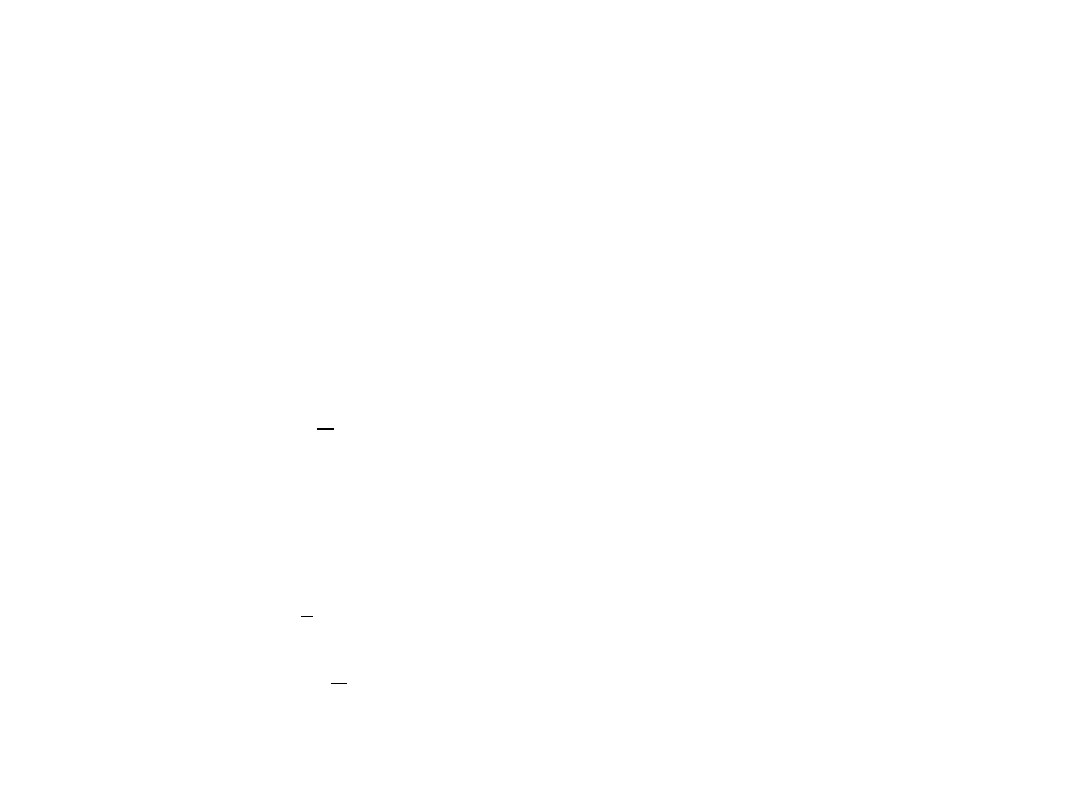
Wybrane własności średniej arytmetycznej:

1. Średnia arytmetyczna jest wielkością mianowaną, tzn.

wyrażona jest w takich samych jednostkach jak badana cecha;

2. Średnia arytmetyczna nie może przyjąć wartości niższej niż

minimalna wartość badanej cechy oraz wyższej niż

maksymalna wartość cechy,

czyli:

x

x

x

min

max

 

,

3. Suma odchyleń od średniej arytmetycznej poszczególnych

wartości cechy

x

i

równa jest zero,

czyli:





x

x

i







0

w szeregu szczegółowym

lub





x

x

n

i

i









0

w szeregu rozdzielczym.

Wady:

• Przede wszystkim jest ona wielkością

abstrakcyjną, tzn. może przyjąć wartość jaka nie

wystąpiła u żadnej badanej jednostki.

• W przypadku szeregów rozdzielczych o

otwartych przedziałach klasowych wyznaczenie

średniej arytmetycznej jest niemożliwe, ze

względu na niemożność obliczenia środka

przedziału klasowego.

• Ponadto nie powinno się jej wyznaczać dla

zbiorowości, w których występują nietypowe

wartości cechy.

Miary średnie pozycyjne

W odróżnieniu od średnich klasycznych, są

wielkościami, których wartości wyznaczane są
na podstawie tylko niektórych (konkretnych)
wyrazów szeregu statystycznego.

Tak więc są to rzeczywiste wartości cechy

występujące w badanej zbiorowości, wybrane ze
względu na swoje położenie w uporządkowanym
szeregu statystycznym. Do średnich
pozycyjnych zaliczamy dominantę oraz kwartyle.

• Dominanta (moda, wartość

najczęstsza, wartość modalna) – jest to
wartość cechy, która występuje
najczęściej (najliczniej) w badanej
zbiorowości statystycznej.

• W szeregach szczegółowych oraz

rozdzielczych punktowych dominantę
stanowi ta wartość cechy, która powtarza
się najczęściej (o największej liczebności)
u badanych jednostek zbiorowości
statystycznej.

0

1

0

1

0

1

0

0

0

*

)

(

)

(

h

n

n

n

n

n

n

x

D



















(1.9)

gdzie:

x

0

- dolna granica przedziału Do;

h

0

-rozpiętość przedziału Do – czyli różnica między dolnym i górnym krańcem przedziału Do;

n

0

- liczebność przedziału Do;

n

-1

– liczebność przedziału poprzedzającego przedział Do;

n

+1

– liczebność przedziału następującego po przedziale Do;

Warunki wyznaczania dominanty

• Rozpiętości przedziału dominanty i

sąsiadujących z nim przedziałów muszą
być równe;

• Nie należy wyznaczać dominanty w

przypadku gdy brak jest jednego wyraźnie
zaznaczonego maksimum liczebności;

• Kwartyle są to miary, które dzielą

zbiorowość na części, które pozostają w
stosunku do siebie w określonych
proporcjach. Jednym z najbardziej
znanych kwartyli jest kwartyl drugi zwany
medianą.

• Mediana Me (kwartyl drugi, wartość

środkowa) – jest to miara, która dzieli
zbiorowość na dwie równe części w ten sposób,
że liczba jednostek mających wartość nie
mniejszą od Me jest równa liczbie jednostek
mających wartość niewiększą od Me. Sposób
wyznaczenia mediany zależny jest od typu
szeregu statystycznego oraz liczby jednostek
wchodzących w skład zbiorowości statystycznej
(liczebności).

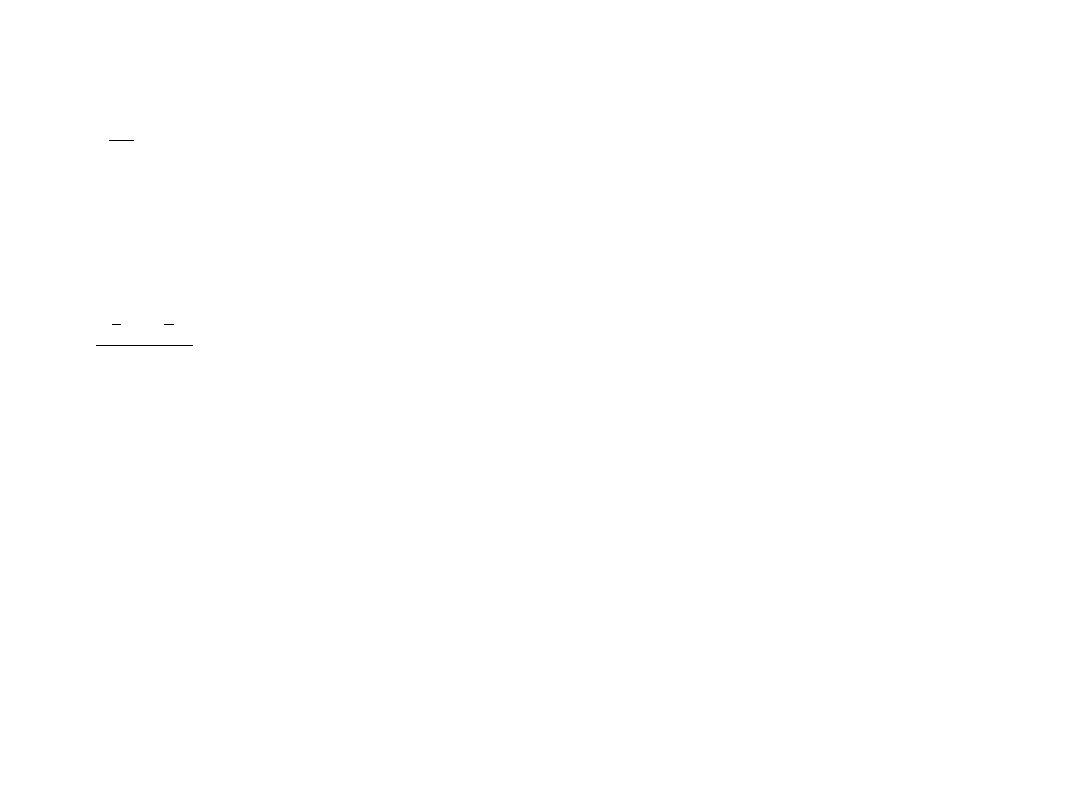
2

1





n

x

Me

(1.10)

W przypadku zbiorowości o parzystej liczebności mamy dwie wartości środkowe. W takim

wypadku medianę stanowi tu średnia arytmetyczna dwóch wartości środkowych (wzór 1.11).

2

1

2

2







n

n

x

x

Me

(1.11)

Liczebność skumulowana (

sk

n ) jest to suma liczebności cząstkowych od 1 do i-tego

wariantu cechy (klasy w przypadku szeregu rozdzielczego z przedziałami klasowymi),





k

i

i

n

1

(1.12)

W szeregu z przedziałami klasowymi medianę wyznaczamy ze wzoru 1.13:

)

(

*

1

0

0

0









sk

Me

n

Nr

n

h

x

Me

(1.13)

gdzie:

x

0

- dolna granica przedziału Me ;

h

0

-rozpiętość przedziału

Me

;

n

0

- liczebność przedziału

Me

;

n

sk-1

- liczebność skumulowana powyżej przedziału Me ;

Me

Nr - numer mediany (pozycja mediany), który jest zależny od liczebności całkowitej

zbiorowości (wzór 1.14).











 

2

2

1

n

n

Nr

Me

(1.14)

-dla n nieparzystego

-dla n parzystego

• Zaletą mediany jest to, iż może być ona

obliczana w przypadku, w którym nie
możemy lub nie powinniśmy wyznaczać
średniej arytmetycznej, która w
przeciwieństwie do mediany jest wrażliwa
na występowanie wartości nietypowych
cechy.

Kwartyl pierwszy i trzeci

• Kwartyl pierwszy jest to taka wartość

cechy, która dzieli zbiorowość w ten

sposób, że 25% jednostek ma od niej

wartość mniejszą, a 75% jednostek

większą, , zaś kwartyl trzeci to wartość tej

cechy, poniżej której znajduje się 75%, a

powyżej której 25% jednostek zbiorowości
statystycznej. Wyznaczenie tych miar

odbywa się na tej samej zasadzie, jak
wyznaczenie mediany.

• W szeregach szczegółowych

przyjmujemy, że zbiorowość jest dzielona

przez medianę na dwie równe części. Jeśli

wyznaczymy ponownie medianę dla

części pierwszej to jej wartość będzie

odpowiadała kwartylowi pierwszemu, jeśli

zaś drugiej połowie zbiorowości to
kwartylowi trzeciemu. Dla obu tych

podzbiorowości mediana jest wyznaczana

według wzoru 1.10 lub 1.11.

• W przypadku szeregu rozdzielczego

punktowego wyznaczenie kwartala
pierwszego i trzeciego polega na
wskazaniu w kolumnie wartości cechy
odpowiadającej liczebności skumulowanej
zawierającej zbiorowości w przypadku ,
natomiast dla -

zawierającej jednostek

zbiorowości.

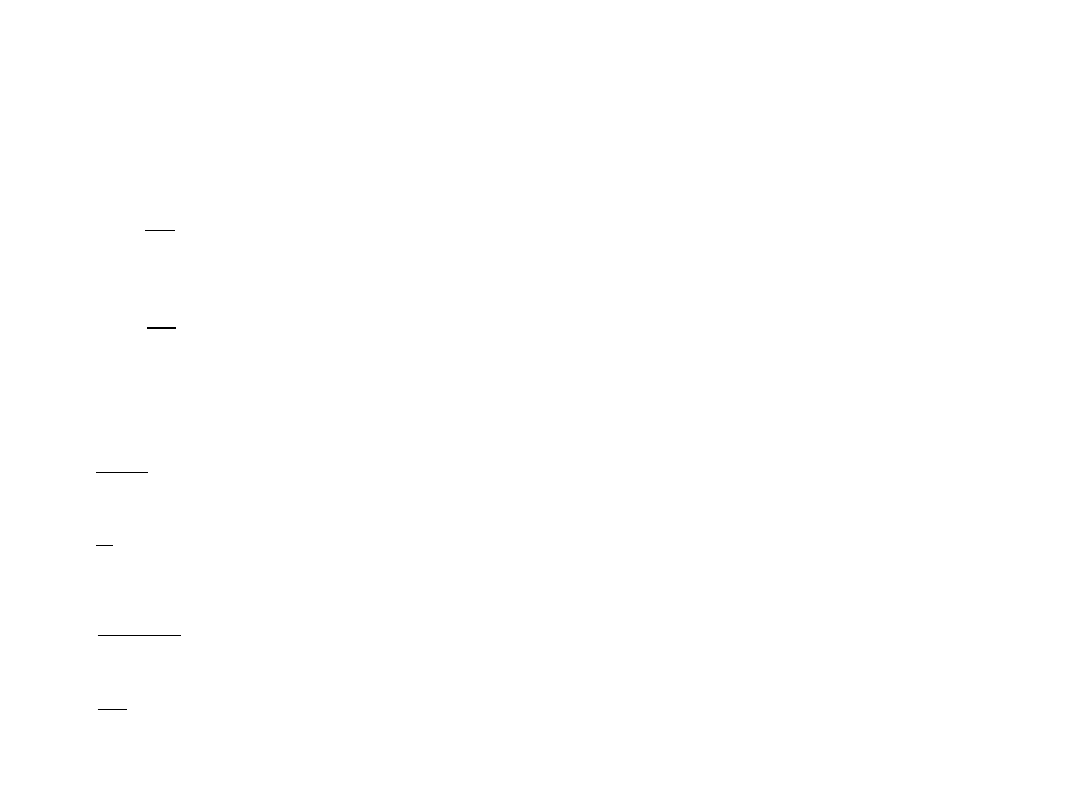
W przypadku szeregu rozdzielczego z przedziałami klasowymi kwartyl pierwszy i trzeci

wyznaczane są ze wzorów 1.15 i 1.16.

)

(

*

1

0

0

0

1

1









sk

Q

n

Nr

n

h

x

Q

(1.15)

)

(

*

1

0

0

0

3

3









sk

Q

n

Nr

n

h

x

Q

(1.16)

gdzie:











 

4

4

1

1

n

n

Nr

Q

(2.17)















4

3

4

)

1

(

3

3

n

n

Nr

Q

(2.18)

dla n nieparzystego

dla n parzystego

dla n nieparzystego

dla n parzystego

Miary zróżnicowania

(klasyczne i pozycyjne)

Miary klasyczne:
• Wariancja;
• Odchylenie standardowe;
• Współczynnik zmienności;
Miary pozycyjne:
• Rozstęp (obszar zmienności);
• Odchylenie ćwiartkowe;
• Współczynnik zmienności;

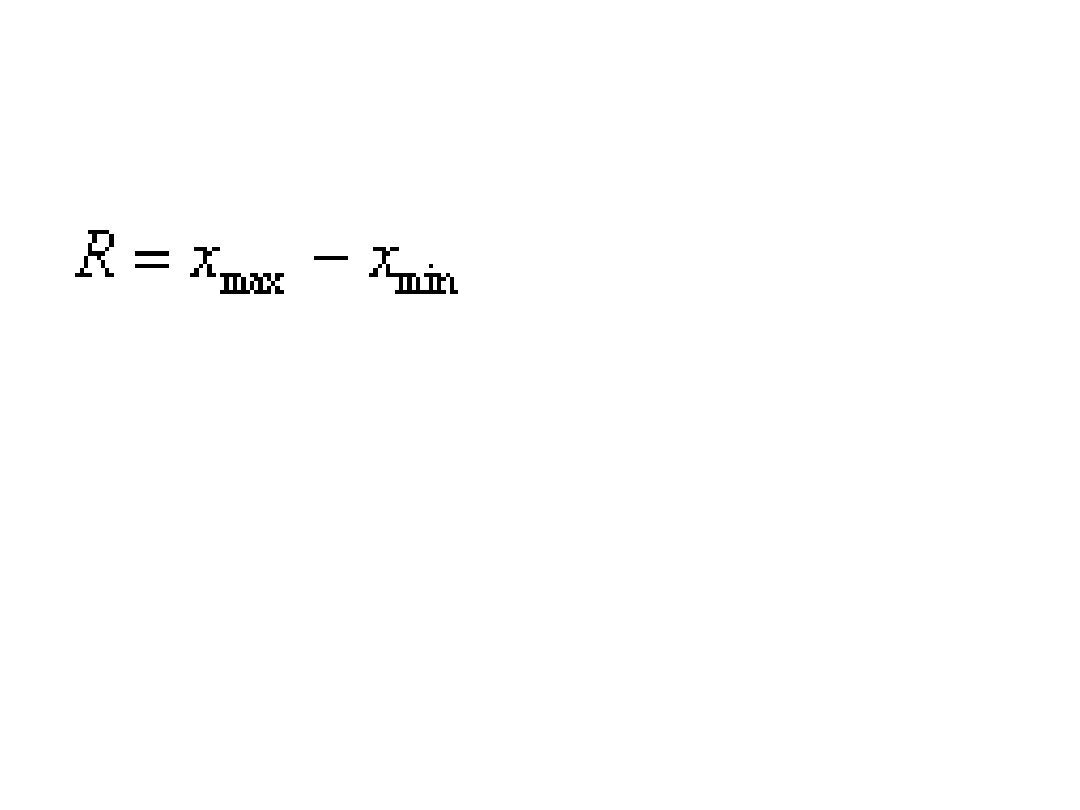
Rozstęp

Miara ta ma

niewielką wartość poznawczą, gdyż obszar zmienności

uzależniony jest tylko od dwóch wartości skrajnych, które często
różnią się istotnie od wszystkich pozostałych wartości badanej cechy,
tak

więc rozstęp wykorzystywany jest jedynie przy wstępnej ocenie

rozproszenia badanej cechy w

zbiorowości.

odchylenie ćwiartkowe (Q), które określa

średnie zróżnicowanie wartości cechy od

mediany

Q=

2

1

3

Q

Q



(1.20)

Miara ta stosowana jest zazwyczaj, gdy niemożliwe lub nie wskazane jest obliczanie miar
klasycznych zróżnicowania.

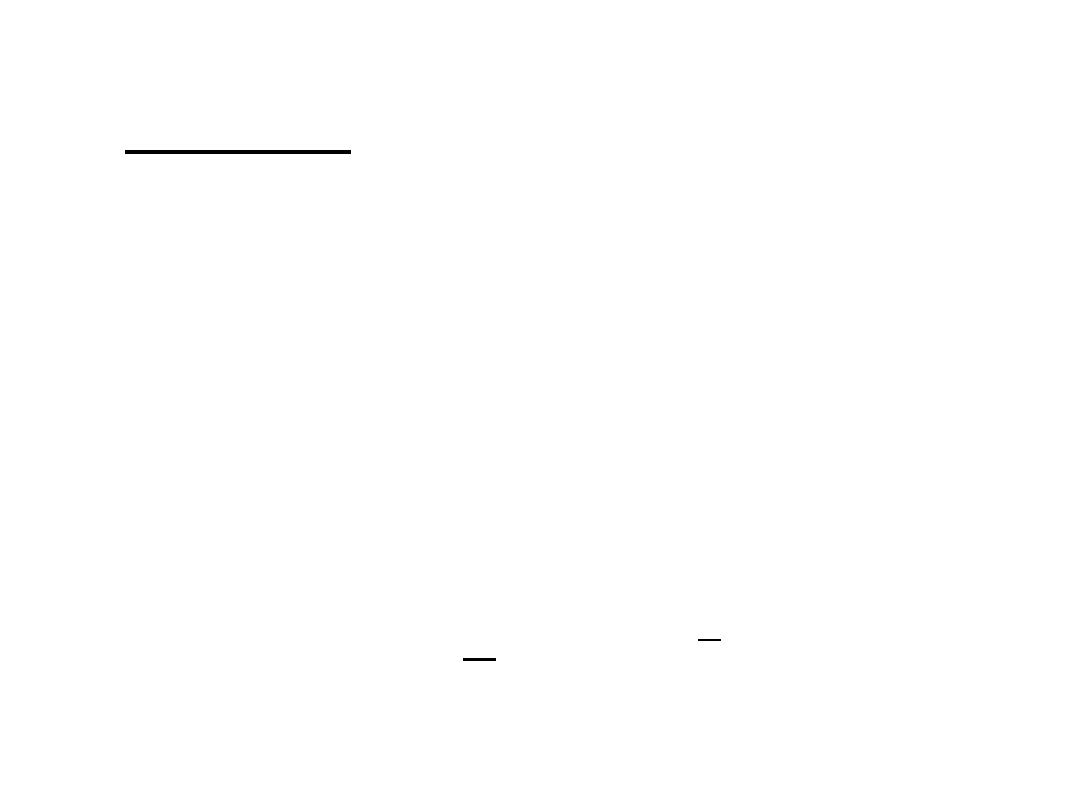
Wariancją określa się średnią

arytmetyczną z sumy kwadratów
odchyleń poszczególnych wartości cechy
statystycznej od średniej
arytmetycznej całej zbiorowości
statystycznej. Wariancję wyznacza się
z następujących wzorów:

-

dla szeregu szczegółowego:















n

i

i

x

x

n

s

1

2

2

1

2

s

-

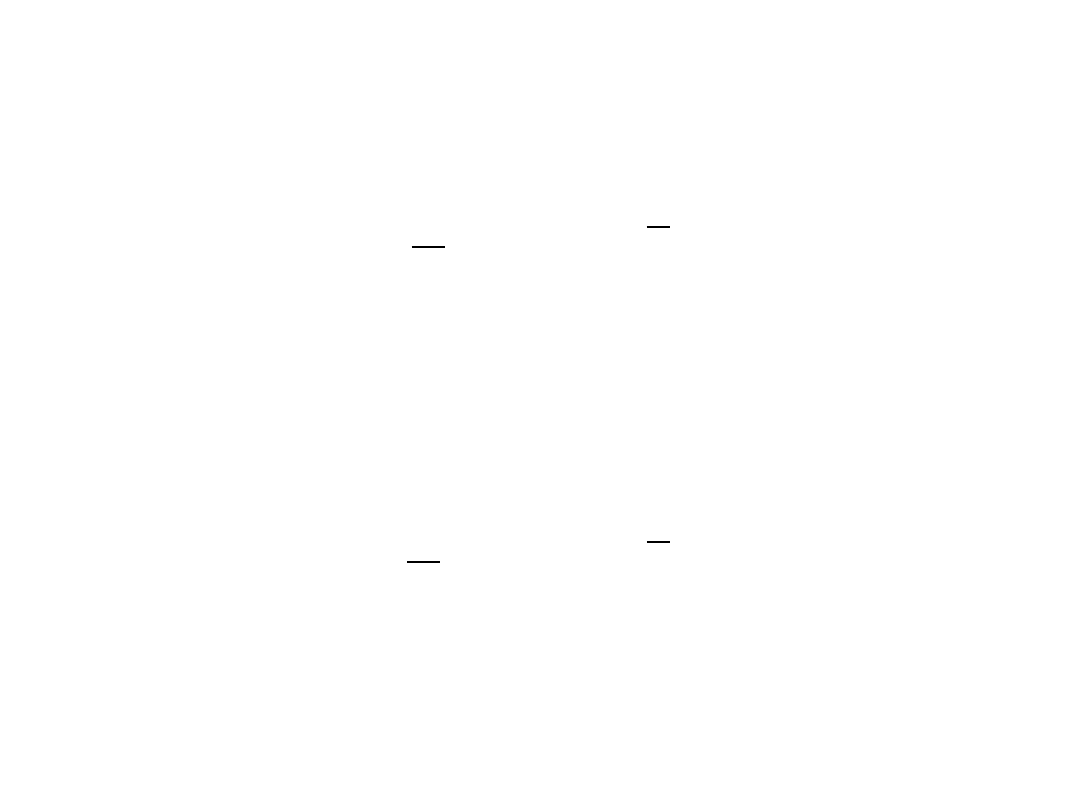
dla szeregu rozdzielczego punktowego:

-

dla szeregu rozdzielczego
przedziałowego:





i

n

i

i

n

x

x

n

s













1

2

2

1

i

n

i

i

n

x

x

n

s













 









1

2

0

2

1

Podstawowe właściwości wariancji:

1.

Jest zawsze liczbą nieujemną

2.

Jest zawsze wielkością mianowaną,
tzn. wyrażoną w jednostkach
badanej cechy statystycznej. Miano
wariancji zawsze jest kwadratem
jednostki fizycznej, w jakiej mierzona
jest badana cecha

3.

Im zbiorowość statystyczna jest
bardziej zróżnicowana, tym wartość
wariancji jest wyższa

Odchylenie standardowe jest

pierwiastkiem kwadratowym z wariancji:

gdzie:

- odchylenie standardowe

- wariancja.

Odchylenie standardowe określa, o

ile wszystkie jednostki statystyczne
danej zbiorowości różnią się średnio od
wartości średniej arytmetycznej
badanej zmiennej.

2

s

s



s

2

s

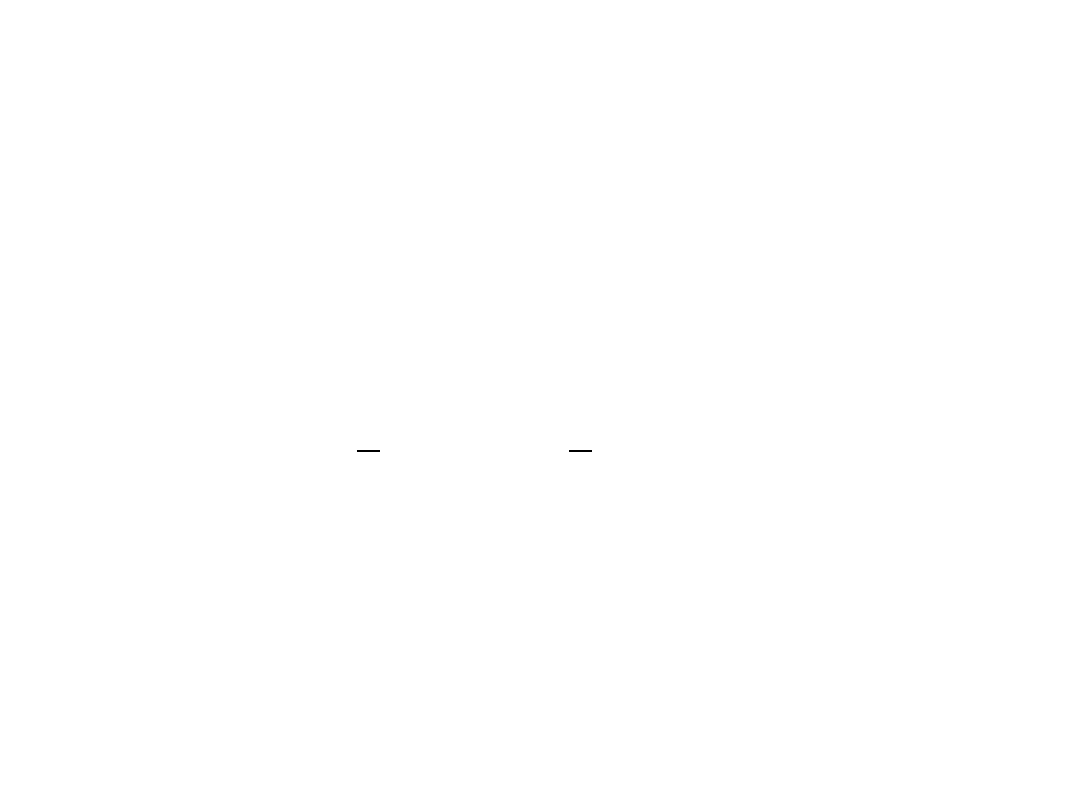
W statystyce odchylenie

standardowe wykorzystywane jest do

tworzenia typowego obszaru zmienności

statystycznej. W obszarze takim mieści

się około 2/3 wszystkich jednostek

badanej zbiorowości statystycznej.

Typowy obszar zmienności określa

wzór:

s

x

x

s

x

typ









Miary dyspersji (rozproszenia), jak i wartości

średnie są liczbami mianowanymi. Fakt ten
umożliwia bezpośrednie porównywania miar
dyspersji obliczonych dla różnych szeregów.

Jeżeli badane zjawisko mierzone jest w różnych

jednostkach miary lub kształtuje się na niejednakowym
poziomie, wówczas do oceny rozproszenia należy
stosować współczynnik zmienności.

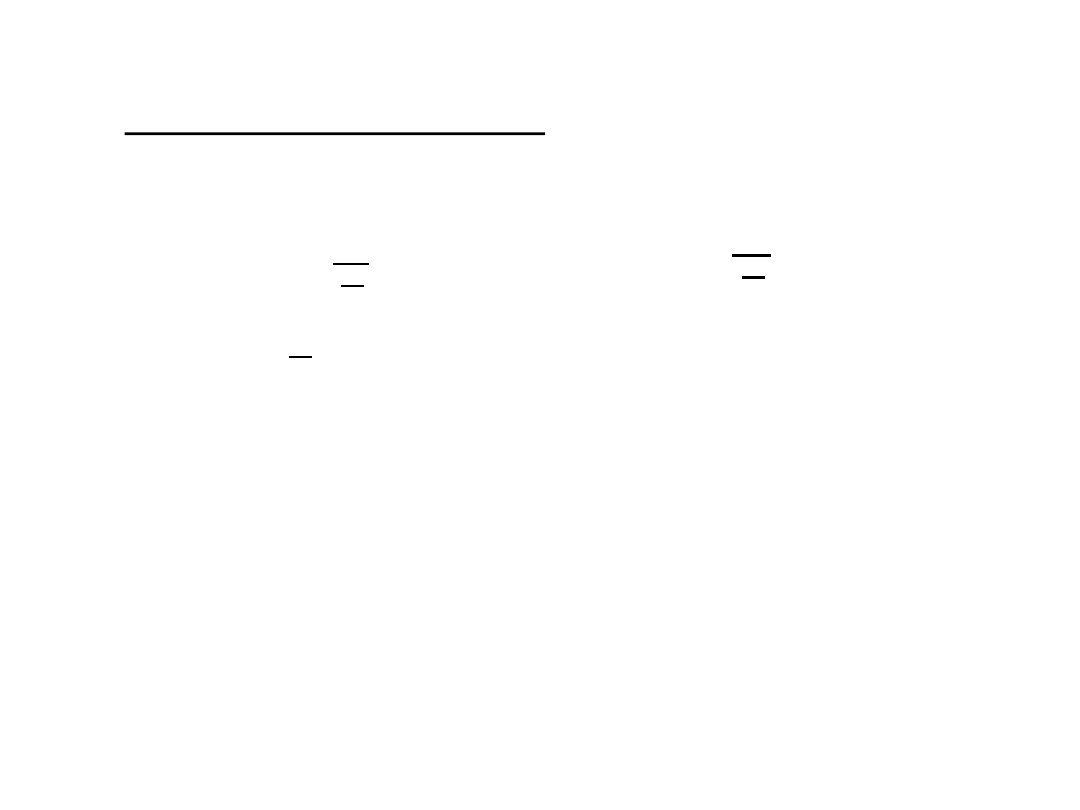
Współczynnik zmienności jest ilorazem odchylenia

przeciętnego lub odchylenia standardowego oraz średniej:

lub

(zamiast może być inna średnia, np. mediana)

Współczynnik zmienności może być wyrażony

w procentach. Współczynnik ten zastępuje bezwzględne
miary dyspersji.

x

s

V



x

d

V



x

Współczynnik zmienności pozwala porównywać

różne szeregi lub szeregi tego samego typu, ale o
różnej strukturze. Umożliwia on dokonanie analiz
zmienności w czasie i przestrzeni. Współczynnik
zmienności (obok odchylenia standardowego)
wykorzystywany jest jako miara ryzyka finansowego.