EWR - TERMODYNAMIKA FENOMENOLOGICZNA

1

TERMODYNAMIKA

FENOMENOLOGICZNA

Przedmiotem badań są właściwości układów
makroskopowych w zależności od temperatury.

•

Układ makroskopowy

np. 1 gram lub 1 mol substancji

1 mol

zwiera N

A

atomów lub cząsteczek,

czyli tyle, ile jest w 12 gramach węgla C

12

N

A

= 6,022

⋅

10

23

mol

-1

liczba Avogadra

•

Parametry makroskopowe:

właściwości układu, które można mierzyć
(ciśnienie p, objętość V, temperatura T, ...)

•

Związek właściwości makroskopowych
z mikrostrukturą opisuje termodynamika
statystyczna

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

2

ENERGIA WEWNĘTRZNA

Energią wewnętrzną układu nazywa się energię
zależną tylko od stanu termodynamicznego ciała.

W przypadku układu nieruchomego,
nie umieszczonego w żadnym polu zewnętrznym,
energia wewnętrzna jest równa energii całkowitej
układu.

Energia wewnętrzna jest sumą energii oddziaływań
międzycząsteczkowych i wewnątrzcząsteczkowych
układu, a także energii ruchu cieplnego cząsteczek oraz
wszystkich innych rodzajów energii występujących w
układzie.

Wartość energii wewnętrznej jest trudna do ustalenia ze
względu na jej złożony charakter.

W opisie procesów termodynamicznych istotniejsza jest
zmiana energii wewnętrznej, dlatego określając energię
wewnętrzną układu pomija się te rodzaje energii, które
nie zmieniają się w rozpatrywanym układzie
termodynamicznym. Na przykład dla gazu doskonałego
jedyną składową energii wewnętrznej, która może się
zmieniać, jest energia kinetyczna cząsteczek gazu. Stąd
zmiana energii wewnętrznej równa jest zmianie energii
kinetycznej cząsteczek.

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

3

RÓWNOWAGA

TERMODYNAMICZNA

Układy makroskopowe odizolowane od otoczenia

osiągają po pewnym czasie

stan

równowagi termodynamicznej.

•

stan układu jest wówczas ustalony

•

nie występują żadne przepływy

Fluktuacje - zasady równowagi szczegółowej

ZEROWA ZASADA TERMODYNAMIKI

Jeżeli ciało A i B są w stanie równowagi termo-
dynamicznej z trzecim ciałem C, to są one
również w stanie równowagi termodynamicznej
ze sobą nawzajem.

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

4

TEMPERATURA

Każdemu ciału można przyporządkować wielkość
fizyczną nazywaną temperaturą.

Temperatura jest jedną z podstawowych wielkości
fizycznych. Jednostką temperatury w skali
bezwzględnej jest 1 K ( jeden kelwin)

Kiedy dwa ciała są w stanie równowagi
termodynamicznej ich temperatury są równe.

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

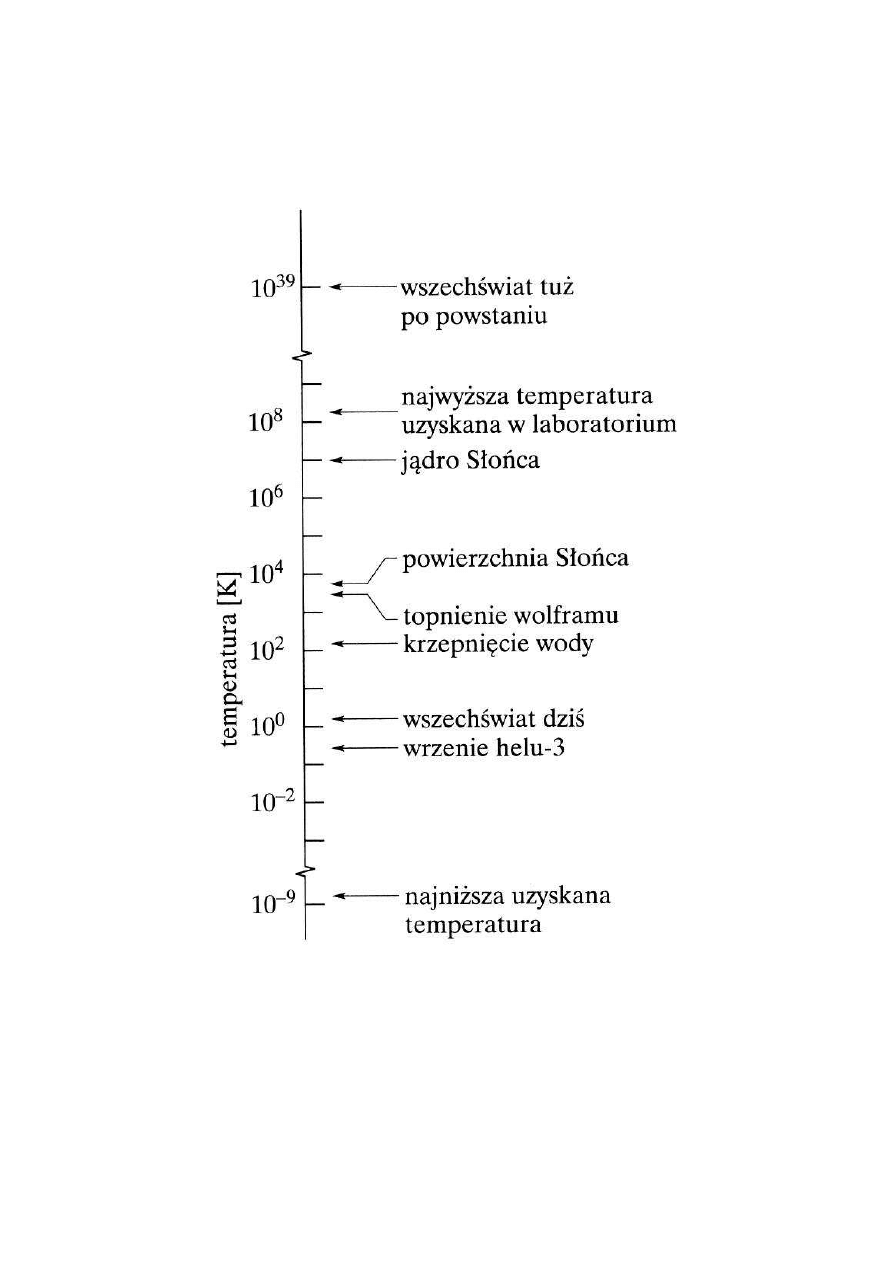
5

SKALA TEMPERATUR

Halliday, Resnick, Walker,
Podstawy fizyki,

PWN 2003 , tom 2

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

6

PARAMETRY EKSTENSYWNE

(proporcjonalne do ilości substancji)

Stany równowagi są całkowicie określone przez
wartości zespołu parametrów ekstensywnych
(U, V, N

1

, ..., N

r

)

1

Parametry ekstensywne są addytywne U = U

1

+ U

2

V = V

1

+ V

2

Przykład:
stany równowagi układu jednoskładnikowego
(składającego się z jednego rodzaju atomów lub
cząsteczek)

opisywane

są

przez

punkty

w trójwymiarowej przestrzeni parametrów stanu
(U, V, N)

1

U - energia wewnętrzna, V - objętość, N

i

- ilość moli

substancji „i”

V

N
p

U

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

7

STAN UKŁADU

Stan układu opisuje się w określonych warunkach

zewnętrznych

Oddziaływanie układu z otoczeniem odbywa się

poprzez ścianki.

Ś

cianki mogą być:

•

izolujące –

brak jakiejkolwiek formy oddziaływania

•

zamykające -

brak wymiany cząstek

•

adiabatyczne -

tylko możliwość wykonania pracy

•

diatermiczne -

tylko oddziaływanie termiczne

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

8

CIEPŁO

Energię przekazywaną w wyniku kontaktu
termicznego Q(A,B) nazywa się ciepłem
przekazanym układowi w procesie A – B

Ciepło jest to energia przekazywana między
dwoma układami na skutek istnienia między nimi
różnicy temperatur.

Praca i ciepło
zależą od przebiegu
procesów
– nie są funkcjami
stanu

V

p

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

9

I ZASADA TERMODYNAMIKI

•

Zasada zachowania energii dla układów
adiabatycznych

W

ad

(A,B) = U(B) – U(A)

Praca nad układem osłoniętym adiabatycznie wykonana
w procesie przejścia od stanu A do stanu B jest
całkowicie określona przez te stany i równa różnicy
energii wewnętrznej w stanie B i w stanie A.

•

Zasada zachowania energii dla układów
zamkniętych (nie adiabatycznych), czyli

Pierwsza Zasada Termodynamiki:

U(B) – U(A) = W (A,B) + Q(A,B)

Energia wewnętrzna układu wzrasta, jeżeli układ
pobiera energię w postaci ciepła Q lub gdy siła
zewnętrzna wykonuje nad układem pracę W.

Energia wewnętrzna układu maleje, gdy układ
przekazuje ciepło otoczeniu o niższej temperaturze
(wówczas Q < 0) lub gdy układ wykonuje pracę (wtedy
W < 0).

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

10

II ZASADA TERMODYNAMIKI

Dla każdego układu termodynamicznego istnieje
funkcja stanu

S

, zwana

entropią

, o następujących

właściwościach:

- S jest wielkością ekstensywną
-

w procesach zachodzących w układach
izolowanych entropia nigdy nie maleje.

S(B)

≥

S(A)

Wynika stąd nieodwracalny charakter procesów
w układach odizolowanych.

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

11

ENTROPIA

Entropia jest funkcją parametrów ekstensywnych

U, V, N

1

, N

2

, N

3

,… .

Równanie podstawowe dla układu jedno-
składnikowego (jeden rodzaj cząstek,

N

i

= N)

S = S(U, V, N)

Dla rzeczywistych układów fizycznych entropia
jest rosnącą funkcją energii wewnętrznej, można
więc to równanie przekształcić do postaci:

U = U(S, V, N)

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

12

PARAMETRY INTENSYWNE

(lokalne)

Energia wewnętrzna:

U = U(S, V, N

1

, N

2

, N

3

, … )

Zmiana energii wewnętrznej w układzie
jednoskładnikowym

U

U

U

dU

dS

dV

dN

S

V

N

∂

∂

∂

=

+

+

∂

∂

∂

współczynniki przy różniczkach parametrów
ekstensywnych nazywa się parametrami
intensywnymi.

Parametry intensywne (lokalne)

(∂U/∂S)

V,N

= T temperatura termodynamiczna

(∂U/∂V)

S,N

=

−

p ciśnienie

(∂U/∂N)

S,V

=

µ

potencjał chemiczny

dU = TdS

−−−−

pdV +

µ

dN

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

13

PARAMETRY INTENSYWNE

dU = TdS

−−−−

pdV +

µ

dN

T

- temperatura termodynamiczna

p

- ciśnienie

µ

-

potencjał chemiczny

Przykłady

•

zamiana ścianki izolującej ścianką diatermiczną

w wyniku przepływu ciepła ustala się taki podział
energii, że

T

1

= T

2

•

zamiana ścianki izolującej ścianką przepuszczającą

w wyniku przepływu cząstek ustala się taki podział

materii, że

µ

1

=

µ

2

•

zamiana ścianki izolującej ścianką adiabatyczną

w wyniku przesunięcia ścianki wyrównują się
ciśnienia

p

1

= p

2

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

14

PROCESY TERMODYNAMICZNE

Procesy odwracalne - układ przechodzi przez ciąg
kolejnych stanów równowagi termodynamicznej
w taki sposób, że entropia układu się nie zmienia.

przebieg jest kwazistatyczny

Przykład:

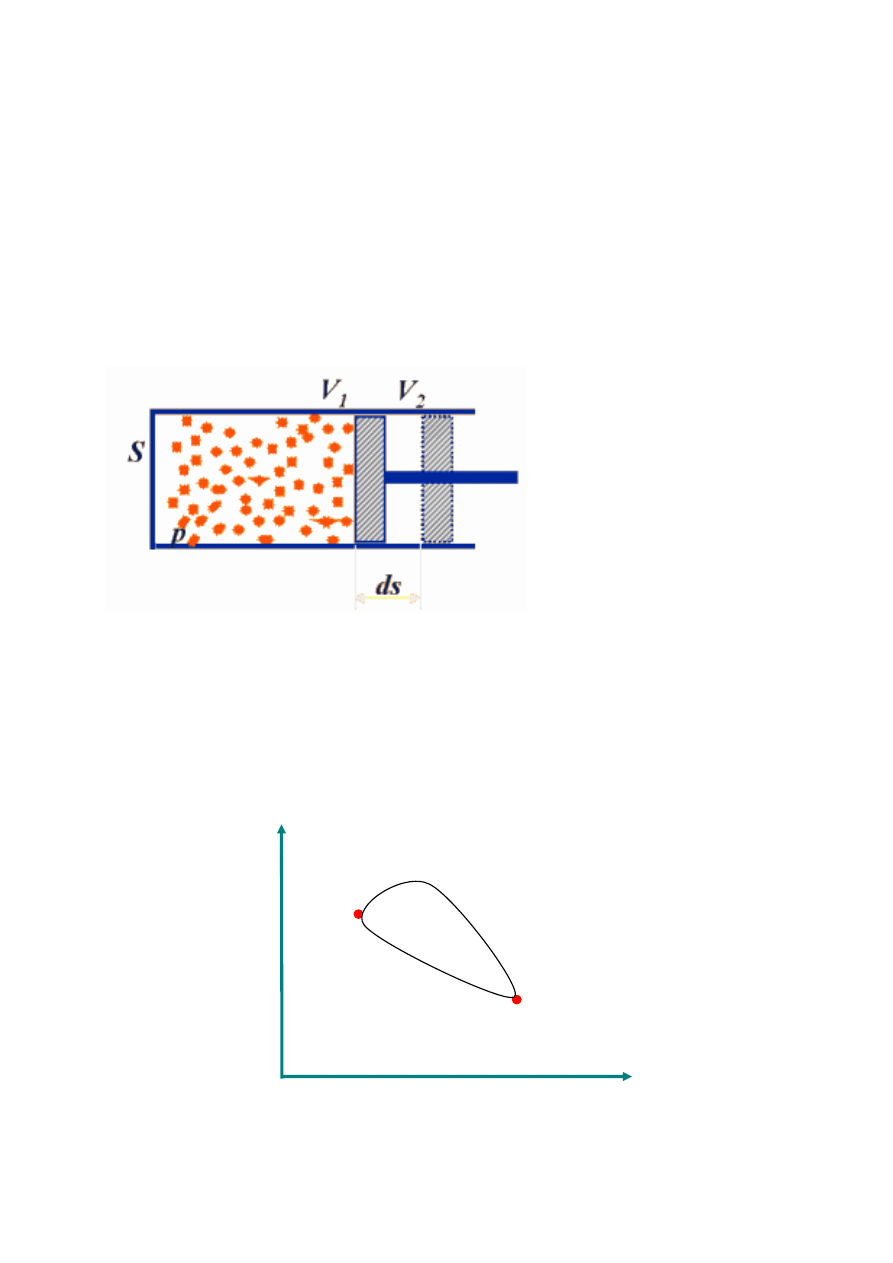
Układ zamknięty (N=const.) w kontakcie termicznym
i mechanicznym z otoczeniem o temperaturze T

0

i ciśnieniu p

0

.

W procesie odwracalnym

•

dU

= T

dS – p

dV

( bo d

Ν

= 0 )

z pierwszej zasady termodynamiki

•

dU =

δ

Q +

δ

W

stąd

δ

Q +

δ

W = T

dS – p

dV

Praca elementarna

δ

W = F dx =

−

pA dx =

−

p dV

δ

Q = T

dS

Jest to podstawowy związek łączący zmianę entropii z
energią wymienianą z otoczeniem przez kontakt
termiczny

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

15

POJEMNOŚĆ CIEPLNA

Dostarczenie ciepła powoduje wzrost temperatury
układu

δ

Q

→

dT

Pojemność cieplna C

, definiowana równaniem

δ

Q = CdT

zależy od rodzaju procesu:

1. dostarczanie ciepła przy stałej objętości (V = const.)

δ

Q = C

V

dT

dla gazu jednoatomowego C

V

=3/2 R

2.

dostarczanie ciepła przy stałym ciśnieniu (p = const.)

δ

Q = C

p

dT

dla gazu jednoatomowego C

p

= C

V

+R

RYS http://1lo-

epsilon.ovh.org/dokumenty%20PDF/CIEPLO_WLASCIWE_

GAZU_DOSKONALEGO.pdf

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

16

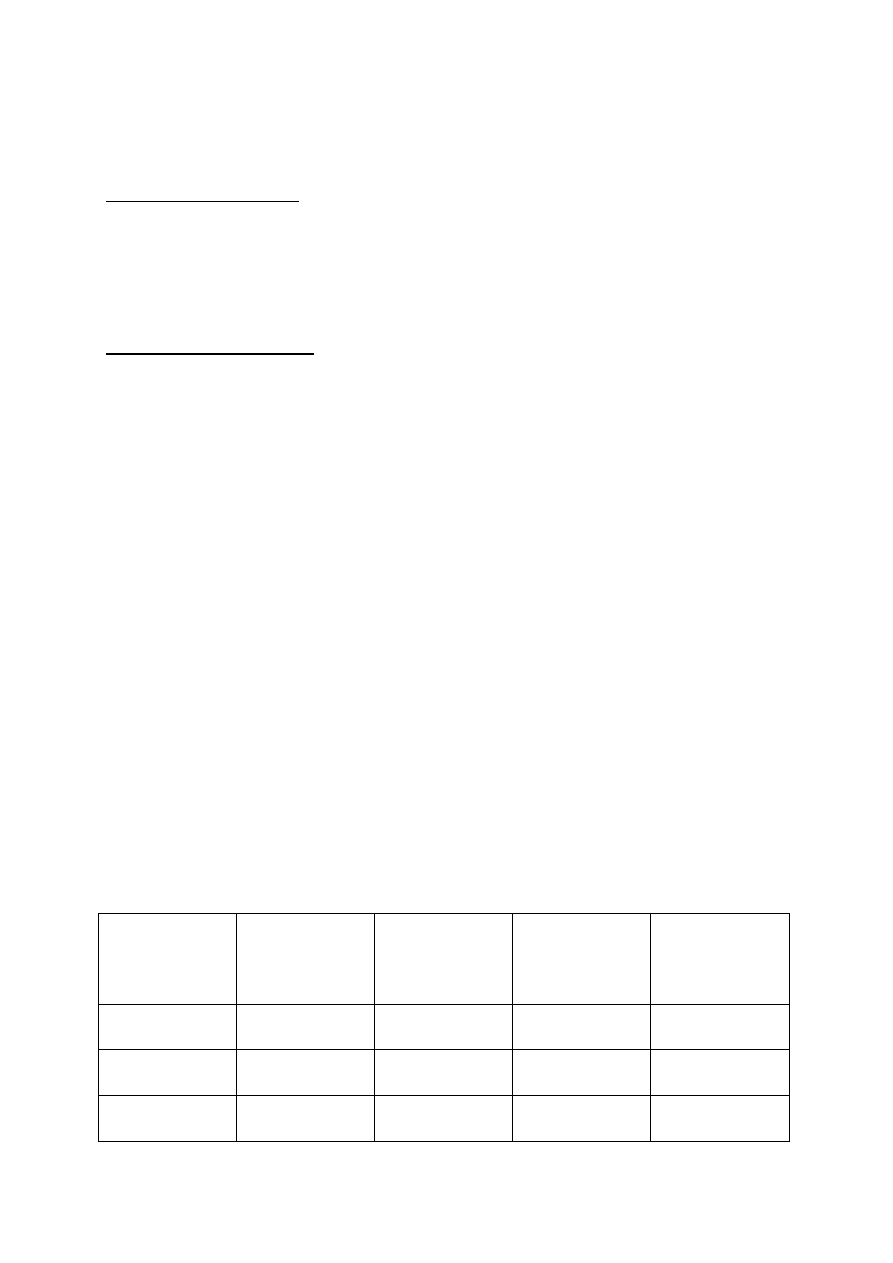
CIEPŁO WŁAŚCIWE

Ciepło molowe:
przy stałej objętości c

V

= C

V

/N

przy stałym ciśnieniu c

p

= C

p

/N

Ciepło właściwe:
przy stałej objętości c

wV

= C

V

/m

przy stałym ciśnieniu c

wp

= C

p

/m

Ciepło właściwe to ilość ciepła, której należy

dostarczyć, żeby podnieść temperaturę jednego

kilograma substancji o 1 K.

CIEPŁO PRZEMIANY

ciepło parowania

Q = c

PAR

m

ciepło topnienia

Q = c

TOP

m

T

TOP

[K]

c

TOP

kJ/kg

T

WRZ

[K]

c

PAR

kJ/kg

tlen

54,8

13,9

90,2

213

woda

273

333

373

2256

miedź

1356

207

2868

4730

Q = c

w

m

∆

T

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

17

CIEPŁO WŁAŚCIWE

1 mol = 6,02 x 10

23

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

18

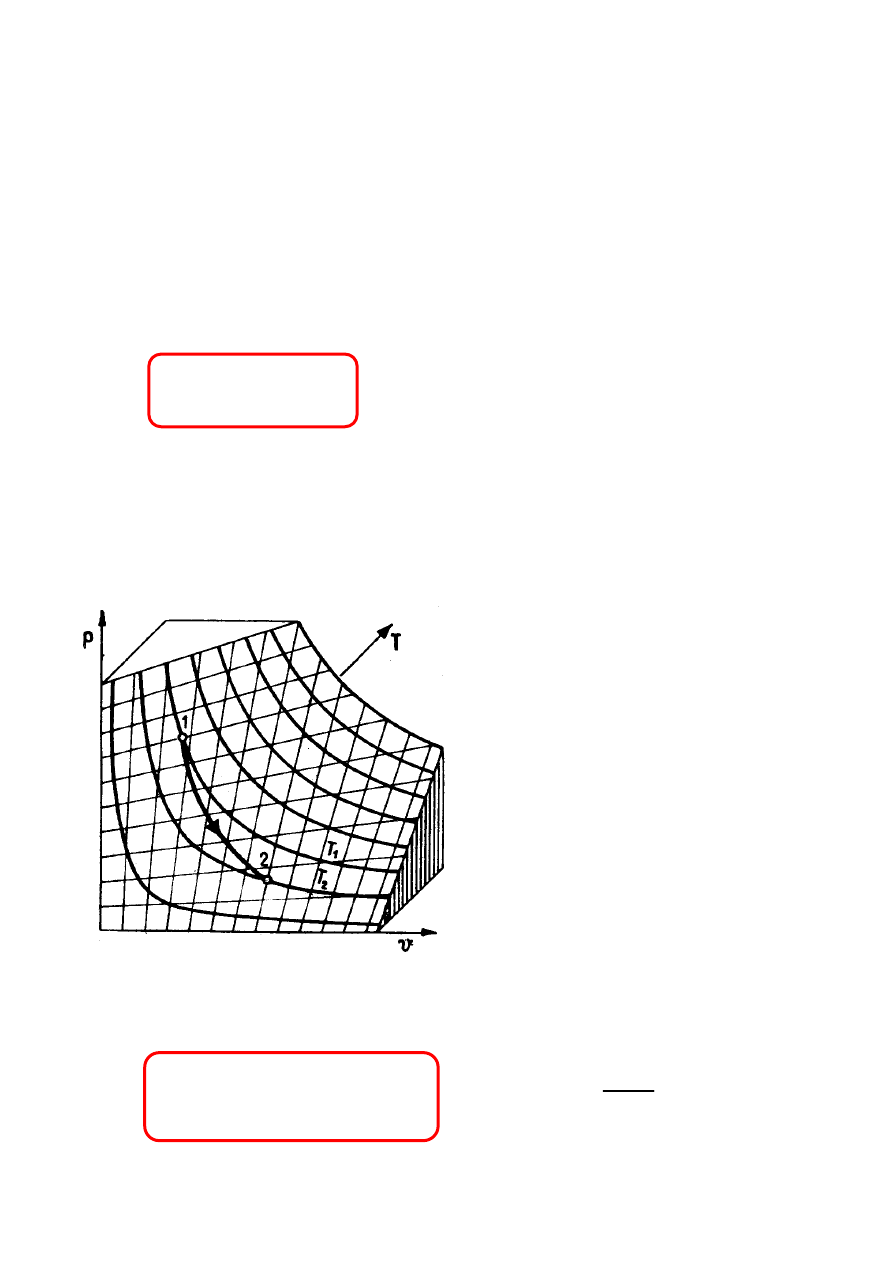
RÓWNANIA STANU

T = T(U, V, N

)

p = p(U, V, N

)

p = p(T , V, N

)

µ

=

µ

(U, V, N

)

Dla N = const.

p = p (V,T

)

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

19

RÓWNANIE STANU

GAZU DOSKONAŁEGO

Dla N = const. równanie stanu gazu doskonałego,
czyli równanie Clapeyrona

pV = NRT

- równanie Clapeyrona

R - stała gazowa R = k N

A

= 8,31 J K

-1

mol

-1

k – stała Boltzmanna k = 1,38·10

-23

J K

-1

T = const. – izotermy

p = const. – izobary

V = const. – izochory

Równanie Poissona (rówanie adiabaty):

.

pV

const

κ

=

1

>

=

V

p

C

C

κ

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

20

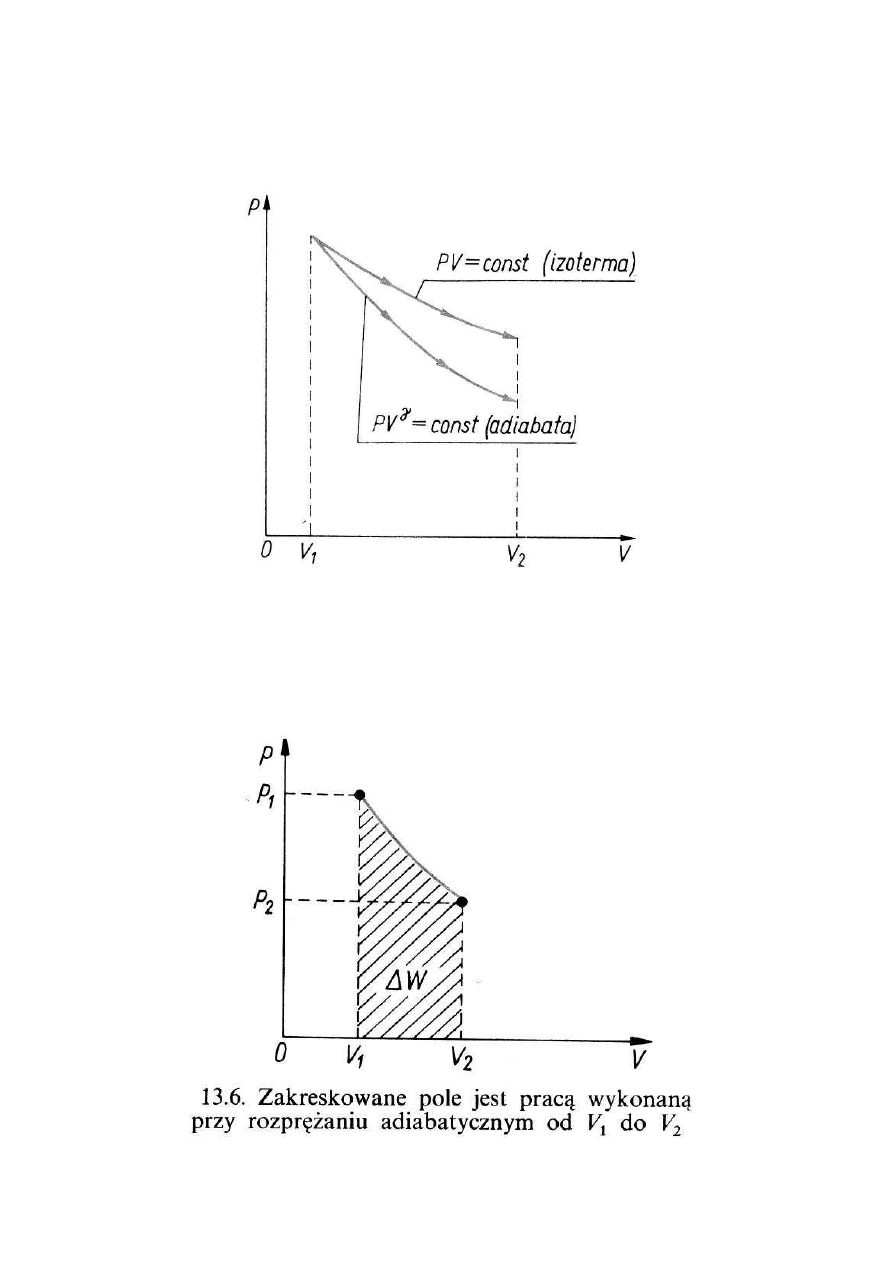
ADIABATA i IZOTERMA

Praca siły zewnętrznej

dW = F dx =

−

pA dx =

−

p dV

Praca wykonana

przez układ:

∫

=

pdV

W

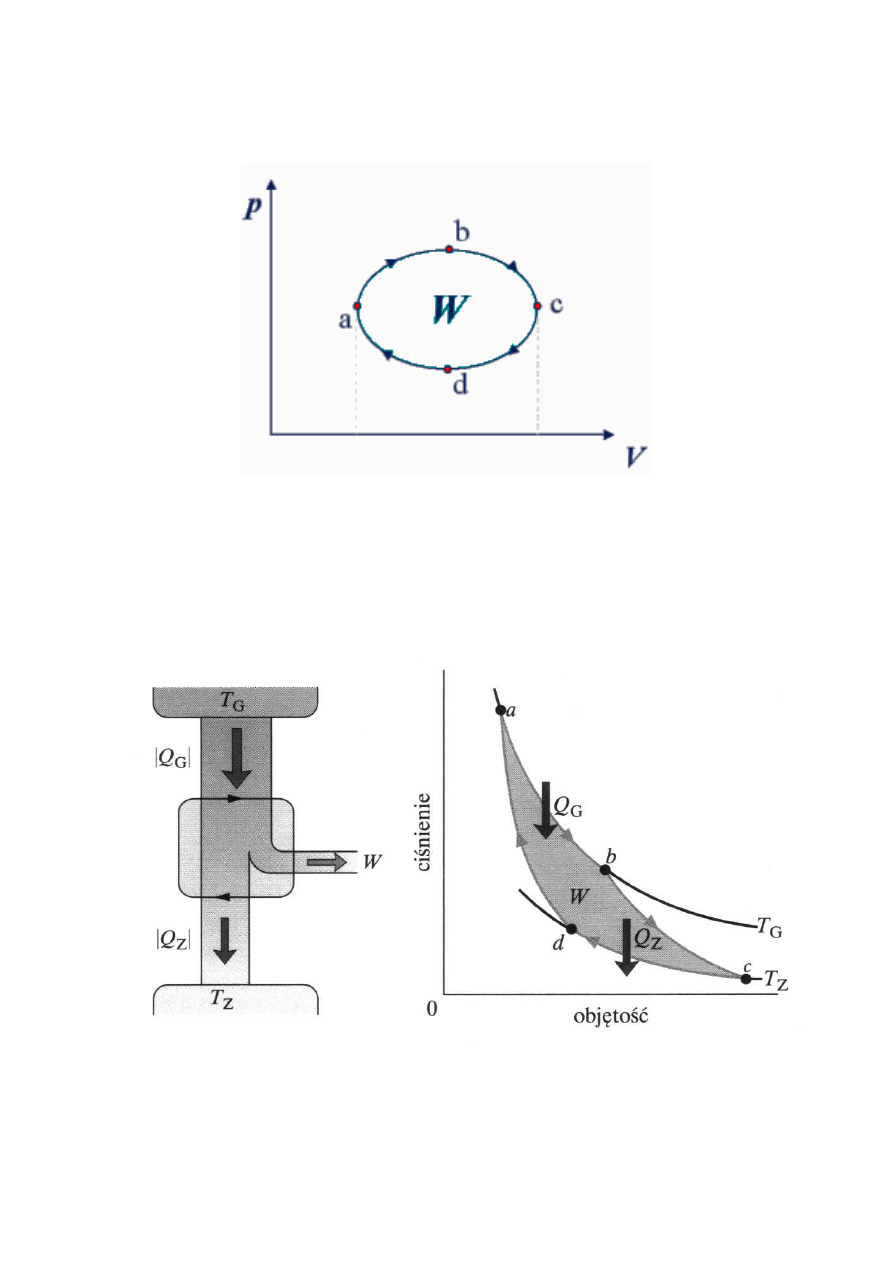
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

21

CYKLE TERMODYNAMICZNE

SILNIK CARNOTA

Halliday, Resnick, Walker, Podstawy fizyki, PWN 2003 , tom 2

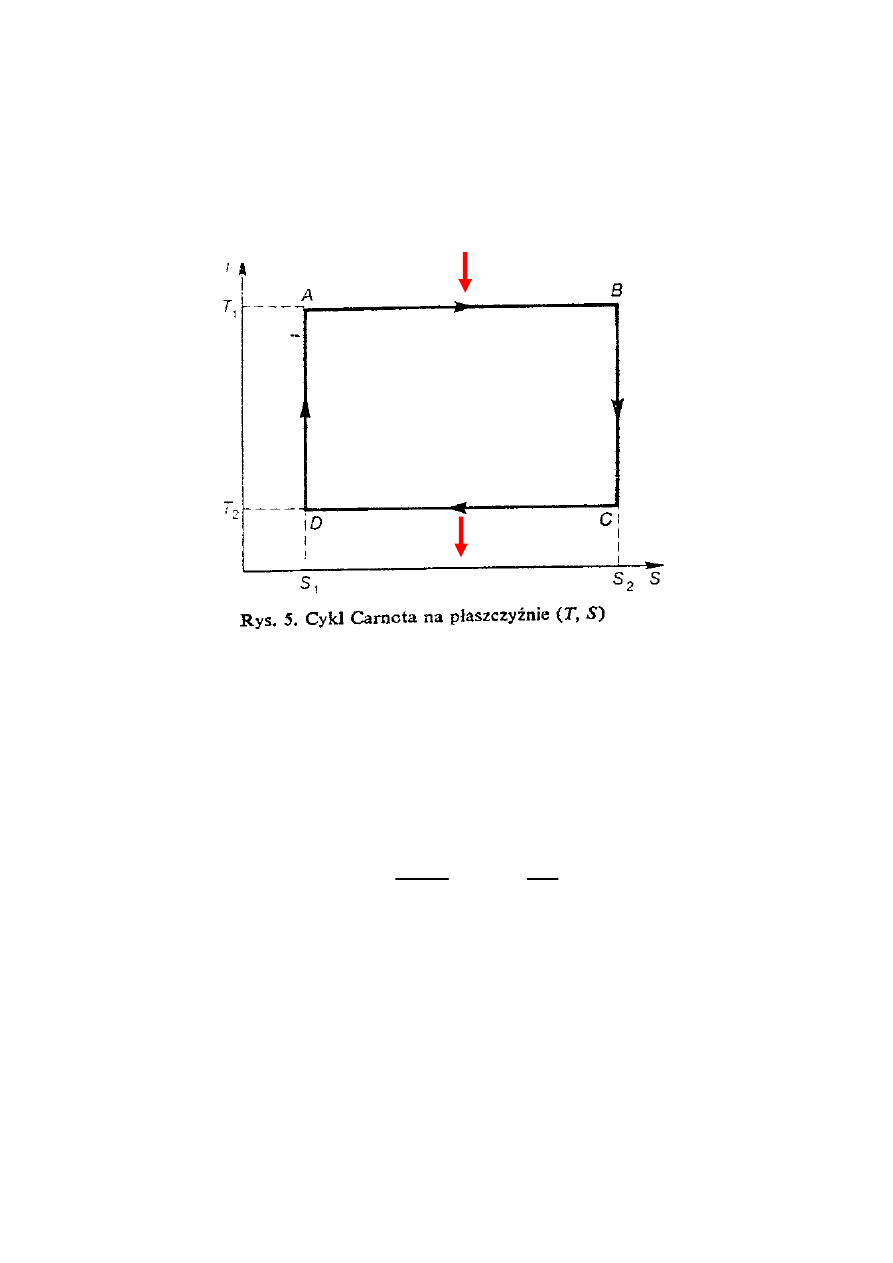
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

22

CYKL CARNOTA

Cykl Carnota na płaszczyźnie

(T, S)

∆

S = 0

∆

S = Q(A,B)/T

1

+ Q(C,D)/T

2

Sprawność silnika

1

2

1

T

T

Q

W

AB

−

=

=

η

W procesie przejścia od stanu A do B układ wykonuje
maksymalną możliwą pracę wtedy, gdy proces jest
odwracalny.

Zmianę entropii układu kompensuje zmiana entropii
otoczenia.

Q(A,B)

Q(C,D)

T

dS = dQ/T

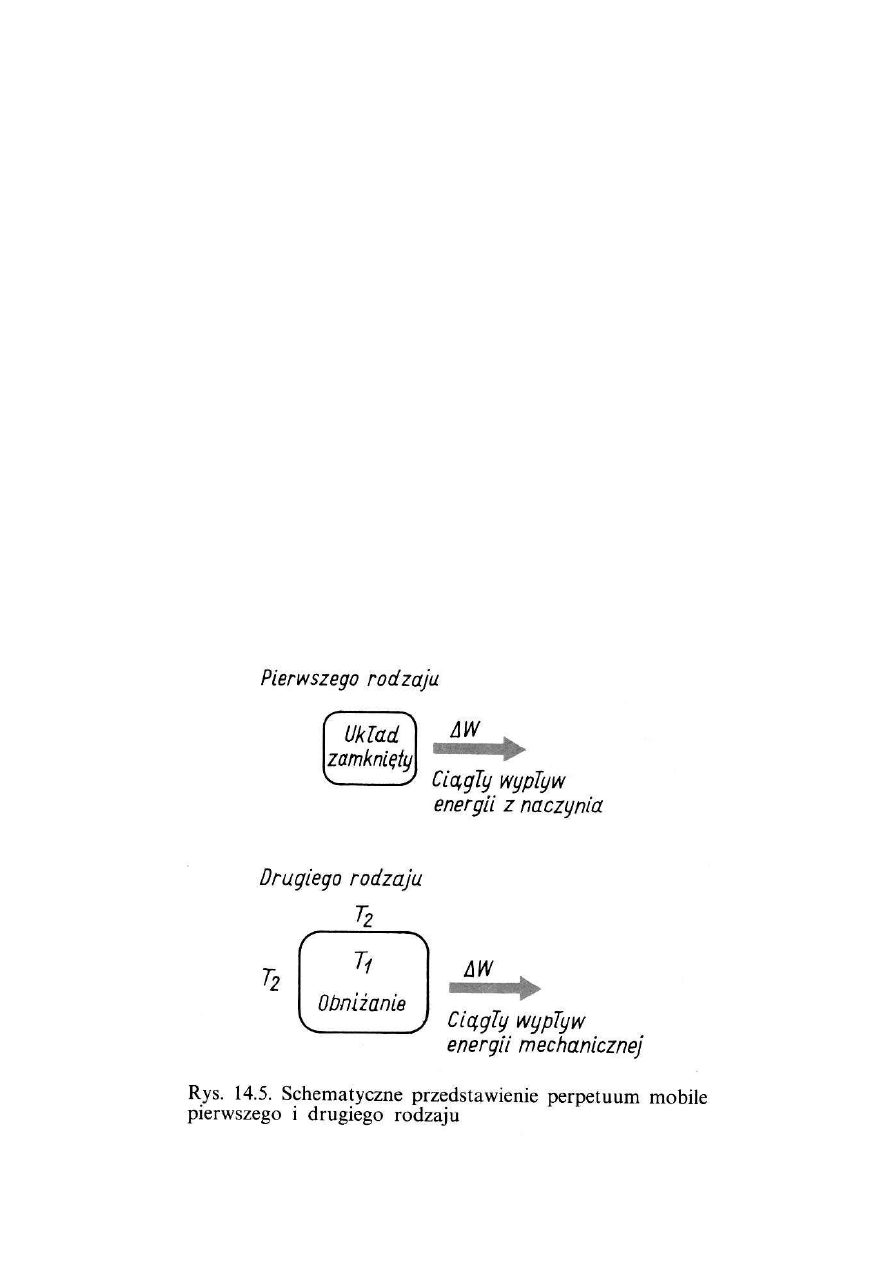
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

23

KONSEKWENCJE DRUGIEJ
ZASADY TERMODYNAMIKI

1.

nie można zbudować perpetuum mobile drugiego
rodzaju

2.

gdy dwa ciała o różnych temperaturach znajdują
się w kontakcie termicznym, to ciepło przepływa
z ciała o wyższej temperaturze do ciała o niższej
temperaturze

3.

ż

adna cykliczna maszyna cieplna, pracująca

między temperaturą górną T

1

i dolną T

2

nie

może mieć sprawności większej niż (T

1

-T

2

)/ T

1

4.

w układzie zamkniętym entropia nie może maleć

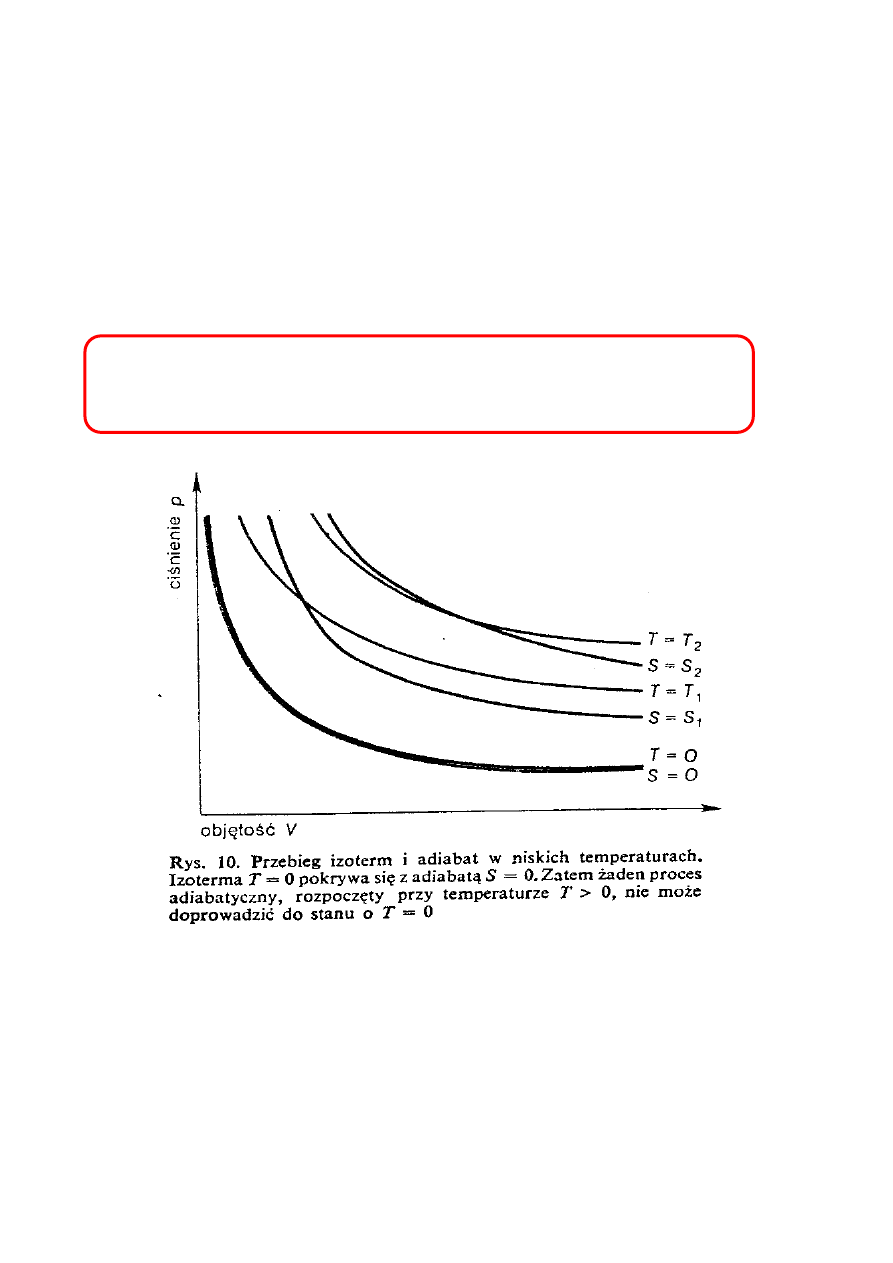
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

24

III ZASADA TERMODYNAMIKI

Opisuje podstawowe właściwości układów w niskich
temperaturach.

Sformułowanie Plancka

W stanach równowagi o zerowej temperaturze
wartość entropii wynosi zero.

Izoterma T = 0 i adiabata S = 0 pokrywają się

Ż

aden proces adiabatyczny rozpoczęty przy T > 0

nie może doprowadzić do T = 0.

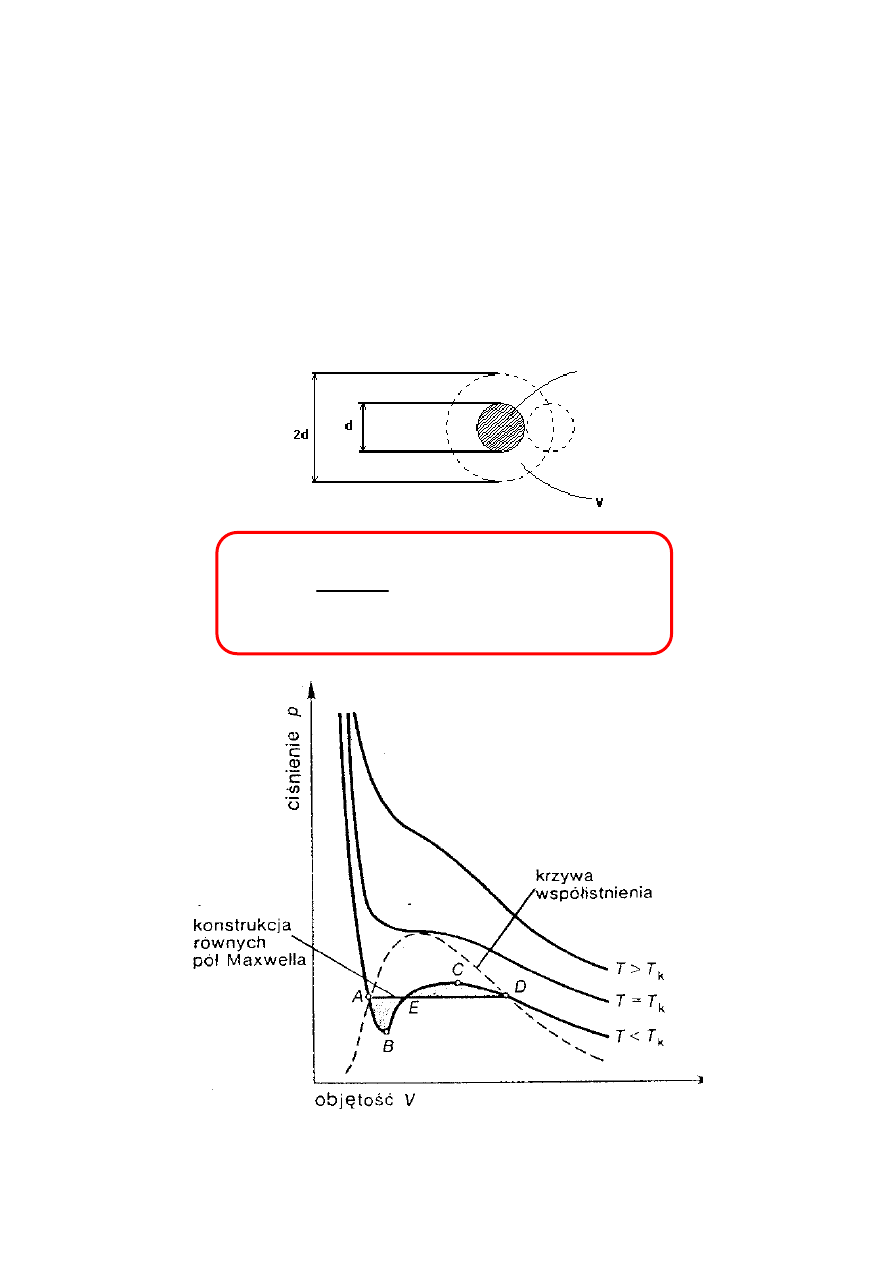
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

25

RÓWNANIE VAN DER WAALSA

•

GAZ DOSKONAŁY

pV = NRT

- równanie Clapeyrona

•

GAZ RZECZYWISTY

(

)

NRT

bN

V

V

aN

p

=

−













+

2

2

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

26

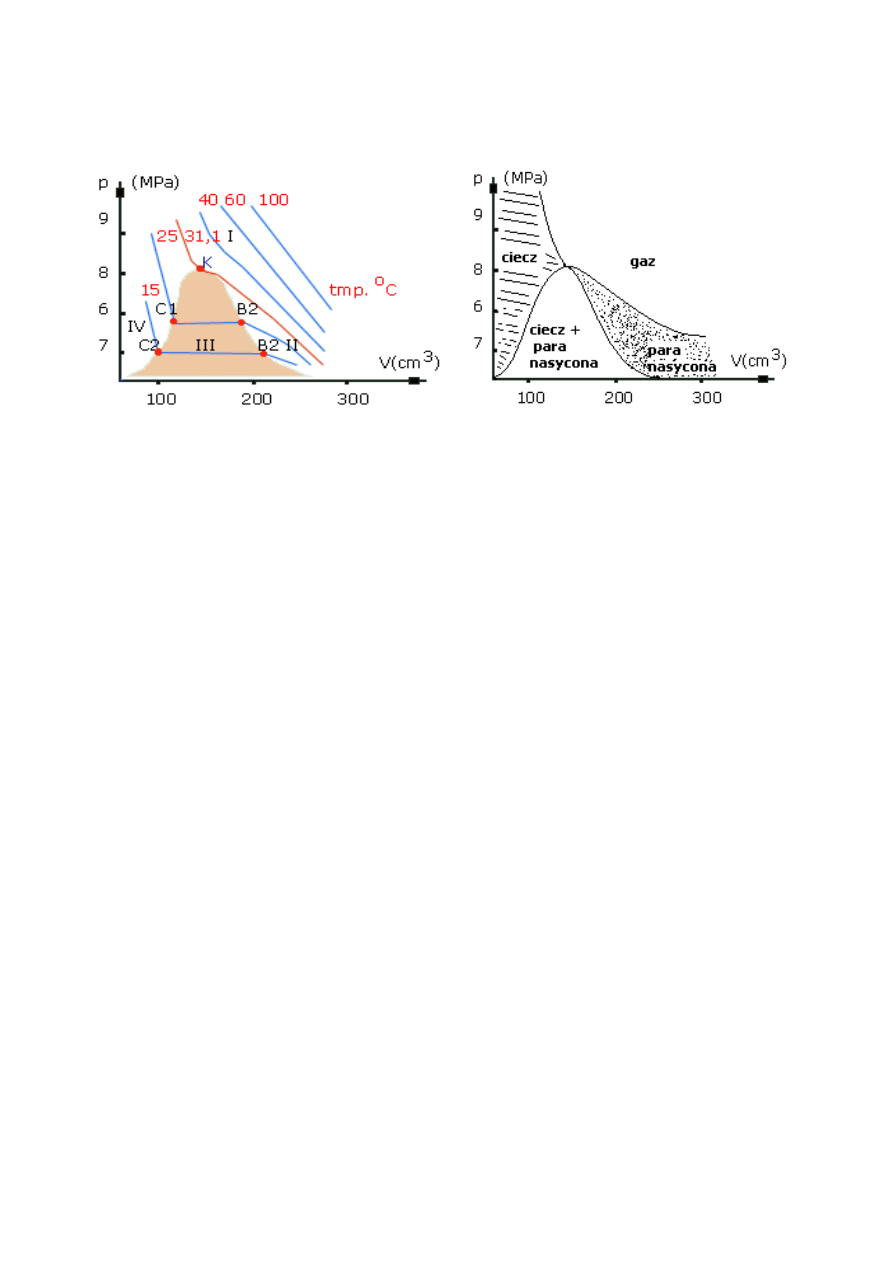
IZOTERMY DOŚWIADCZALNE

Izotermy doświadczalne CO

2

i podział na obszary fazowe,

gazu, pary nasyconej i cieczy

•

Izotermy dla 100, 60, 40

o

C przypominają kształtem

izotermy gazu doskonałego.

•

Dla +31,1

o

C izoterma krytyczna wykazująca punkt

przegięcia K.

•

Izotermy dla temperatur niższych zawierają stopniowo
coraz to dłuższe odcinki poziome, które odpowiadają
układowi zawierającemu ciecz i parę nasyconą.

Punkt K, zwany punktem krytycznym, jest określony
wartością

temperatury krytycznej, ciśnienia krytycznego

i objętości krytycznej

. Zaciera się w nim różnica między

cieczą i gazem.

W temperaturze powyżej temperatury krytycznej nie może
istnieć dana substancja w stanie ciekłym. Skroplenie
substancji (przejście w stan ciekły) następuje po oziębieniu
gazu poniżej temperatury krytycznej.

(

)

K

K

V

p ,

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

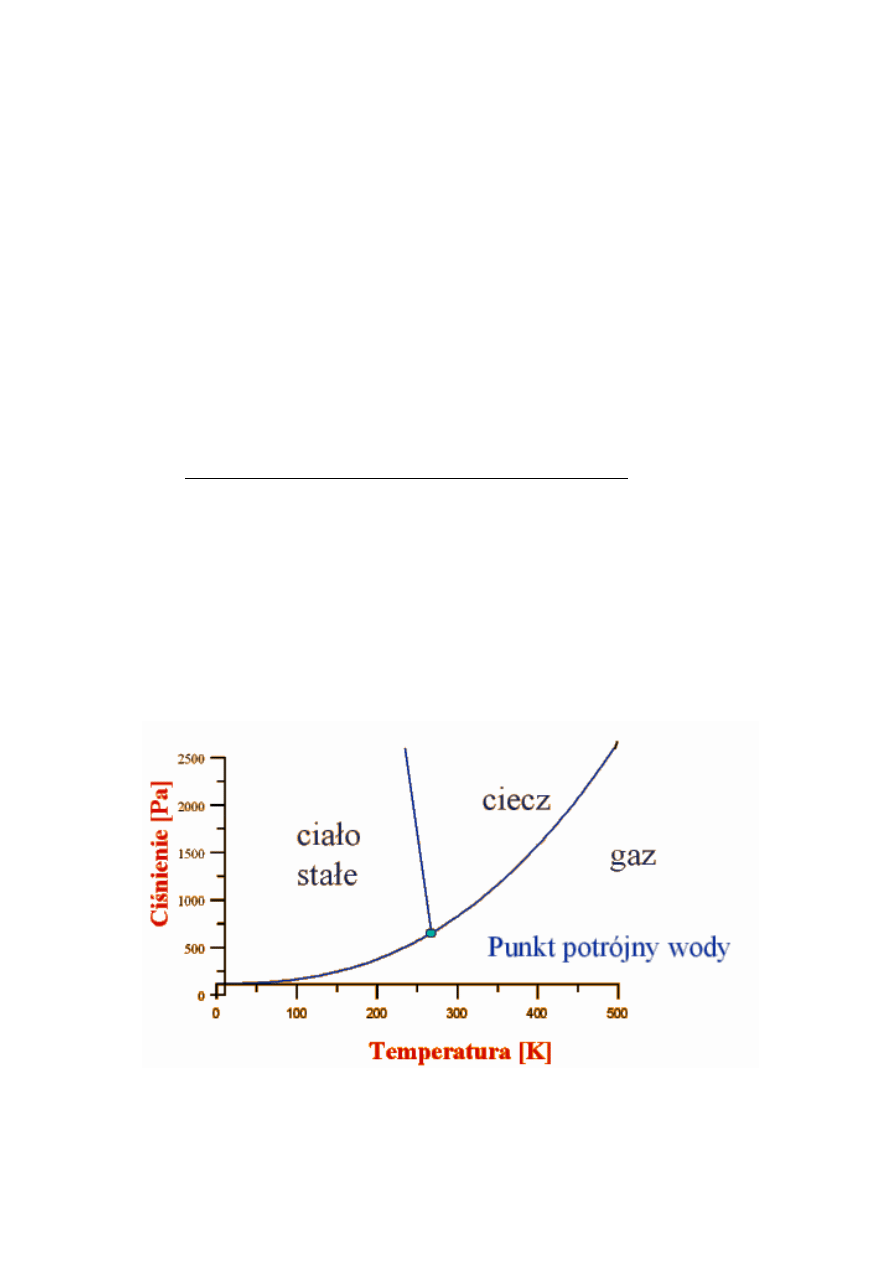
27

REGUŁA FAZ GIBBSA

Jeżeli układ

r

składnikowy znajduje się w kilku fazach

(na przykład w kilku stanach skupienia) - zawiera

α

faz, to równowaga termodynamiczna wymaga

równości potencjałów chemicznych każdego składnika
we wszystkich fazach:

µ

j

1

=

µ

j

2

=

...

=

µ

j

α

=

µ

j

j = 1,

2, ..., r

liczba termodynamicznych stopni swobody (liczba
parametrów intensywnych mogących zmieniać się
niezależnie) wynosi

f = r + 2 -

α

Ponieważ

f ≥ 0

więc w stanie równowagi może

współistnieć najwyżej

r + 2

faz

Punkt potrójny wody w temp.

273,16 K

Halliday, Resnick, Walker,

Podstawy fizyki,

PWN 2003 , tom 2

r

–

ilość składników

α

–

ilość faz

EWR - TERMODYNAMIKA FENOMENOLOGICZNA

28

ROZSZERZALNOŚĆ CIEPLNA

∆

L =

α

L

∆

T

∆

V =

β

V

∆

T

β

=3

α

T

1

T

2

Halliday, Resnick, Walker,

Podstawy fizyki,

PWN 2003 , tom 2

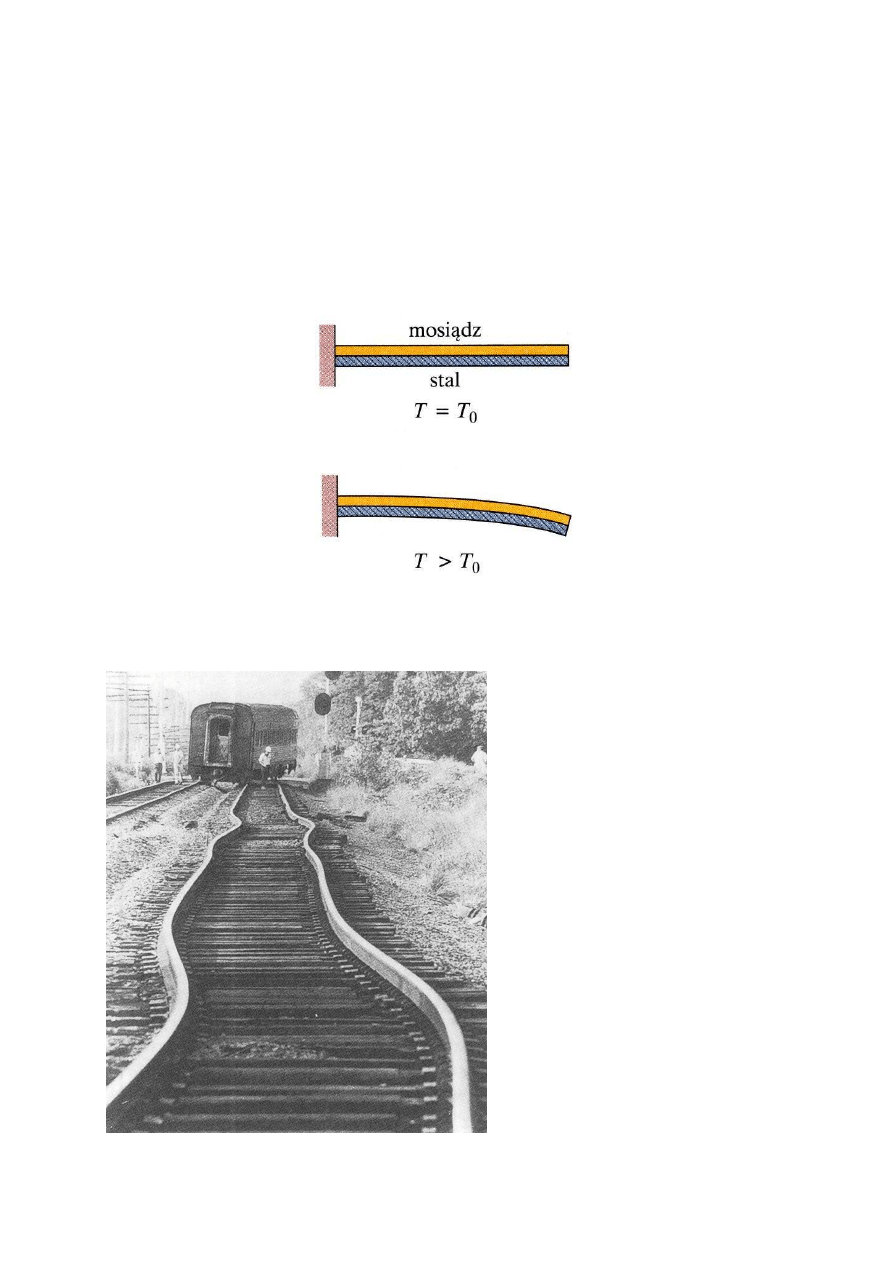
EWR - TERMODYNAMIKA FENOMENOLOGICZNA

29

ROZSZERZALNOŚĆ CIEPLNA

Przykład zastosowania rozszerzalności cieplnej
termometr
bimetal

Rysunki z

Halliday, Resnick, Walker,

Podstawy fizyki,

PWN 2003 , tom 2