FIZYKA

Termodynamika -

Zadania - Rozwiazania

ciesiolek

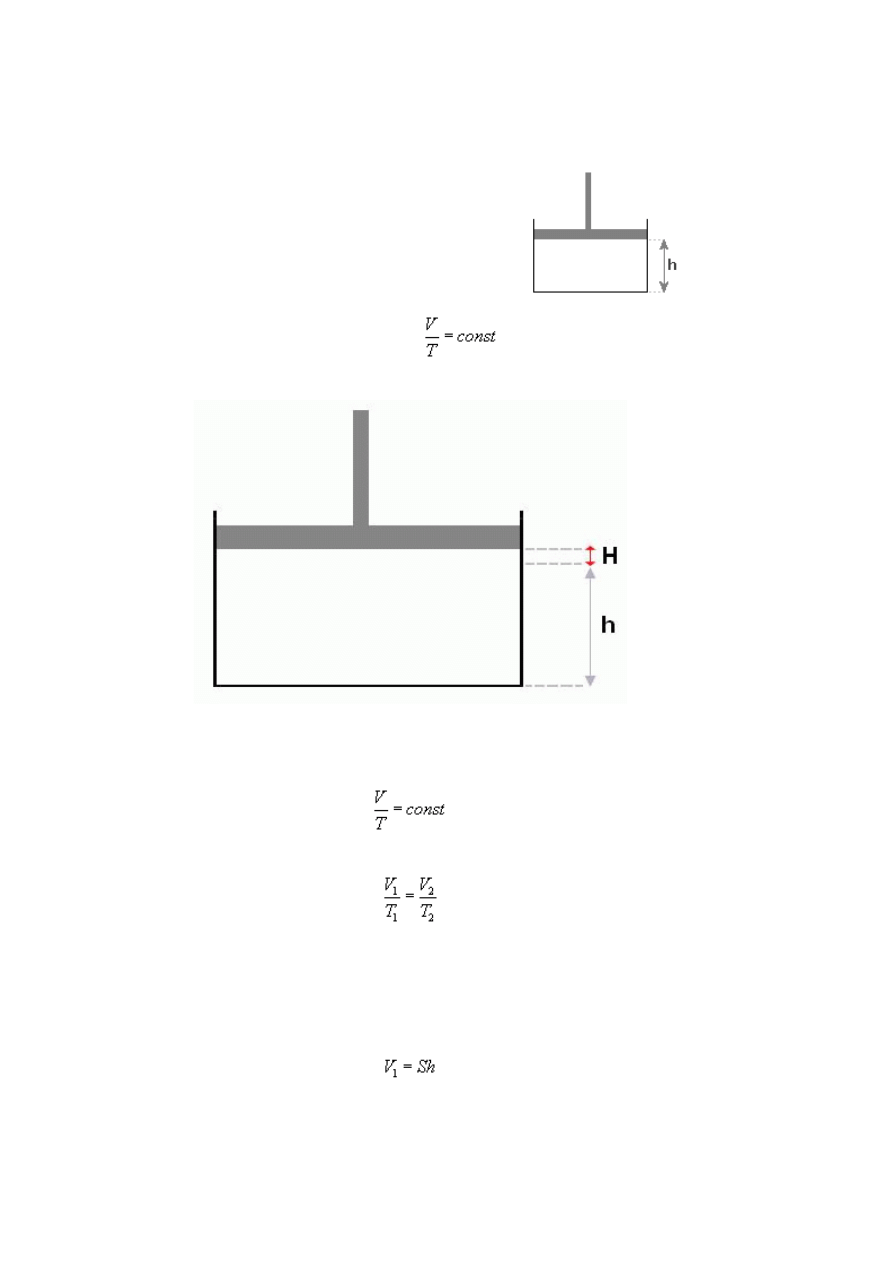
Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 1

Treść:
W naczyniu cylindrycznym, zamkniętym tłokiem, ogrzano
izobarycznie gaz od temperatury 300K do 400K, przy czym
tłok przesunął się o 2cm. Ile wynosiła wysokość słupa h
gazu przed podgrzaniem (patrz rysunek)?
Dane:
T

1

= 300 K

T

2

= 400 K

H = 2 cm

Szukane:
h = ?

Wzory:
1. Równanie stanu gazu -
przemiana izobaryczna

Rysunek:

Rozwiązanie:
W przemianie izobarycznej wartością stałą jest ciśnienie. Równanie gazu przyjmuje więc
postać:

To samo równanie w innej formie możemy zapisać w ten sposób:

gdzie V to objętość gazu, a T temperatura. T

1

i T

2

mamy podane w treści zadania,

pozostaje więc problem z objętością :)

Wiemy, że objętość to iloczyn wysokości i podstawy figury. Z tego wynika, że w przed
rozsunięciem tłoka objętość gazu wyraża się wzorem:

gdzie S to pole podstawy figury, w której znajduje się gaz, a h jest szukaną wysokością.

Po rozsunięciu tłoka, pole podstawy się oczywiście nie zmieni, ale do wysokości h

musimy dodać drugą H by otrzymać całkowitą wysokość tłoka po rozsunięciu, więc:

Wracamy teraz do równania stanu gazu.

I podstawiamy objętości:

Mnożymy "na krzyż":

W ten sposób widzimy, że nieznane pole podstawy możemy skrócić i dochodzimy do
postaci:

W tym momencie możemy podstawić dane temperatury.

H mamy dane, więc:

Warto zauważyć, że w większości zadań należy dokonać zamiany jednostek (cm na m) na
samym początku rozwiązywaniu zadania. W tym wypadku jednak nie było to konieczne.

Odpowiedź: Przed podgrzaniem wysokość słupa gazu wynosiła 6 cm.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 2

Treść:
Pocisk o masie m=30g mając prędkość v=144km/h wbił się w drzewo. Ile
wynosiło ciepło W wydzielone przy hamowaniu?
Dane:
m = 30 g
v = 144 km/h

Szukane:
Q = ?

Wzory:
Energia kinetyczna

Rozwiązanie:
Przed rozwiązaniem zadania zauważ, że dane z jego treści (masa i prędkość) są podane w
jednostkach nie należących do układu SI. Dlatego najpierw je przeliczymy:

Pocisk przed wbiciem się w drzewo posiada pewną prędkość, a co się z tym wiąże
energię kinetyczną. Po wbiciu się w drzewo i wyhamowaniu nie ma już żadnej energii.
Co się więc z nią stało? Cała została zamieniona na ciepło, które to właśnie musimy
znaleźć. Zapisując to wzorem matematycznym:

Policzmy w takim razie energię kinetyczną pocisku:

Sprawdźmy jednostkę:

Wszystko się zgadza, zatem przy hamowaniu pocisku wydzieliło się ciepło równe 24
dżule.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 3

Treść:
Młot parowy o masie m=4 ton uderza z prędkością v=3m/s w żelazną płytę o
masie m

p

=6kg i cieple właściwym c

w

=500J/kgK. O ile ogrzeje się podczas

jednego uderzenia ta płyta, jeżeli 80% energii wydzielonej przy uderzaniu młota
zostaje zużyte na ogrzewanie płyty?
Dane:
m = 4 t = 4000 kg
v = 3 m/s
m

p

= 6 kg

c

w

= 500 J/kgK

Szukane:
ΔT = ?

Wzory:
1. Energia kinetyczna

2. Ciepło
pobierane/oddawane

Rozwiązanie:
Młot, uderzając w płytę, posiada pewną prędkość, a co się z tym wiąże energię
kinetyczną. Przekazuje 80% swojej energii płycie. Co się stało z pozostałymi 20%?
Została zamieniona na np. pokonanie oporu powietrza czy na ogrzanie się młota, lecz to
nie jest obiektem naszego zainteresowania w tym zadaniu :).
Energia przekazana płycie zostaje zamieniona na ogrzanie płyty (ponieważ zakładamy, że
płyta pozostała w spoczynku):

Podczas ogrzewania (dostarczania energii) bez zmiany stanu skupienia ciała dochodzi do
wzrostu jego temperatury zgodnie ze wzorem:

Rozwiązując równanie ze względu na ΔT otrzymujemy:

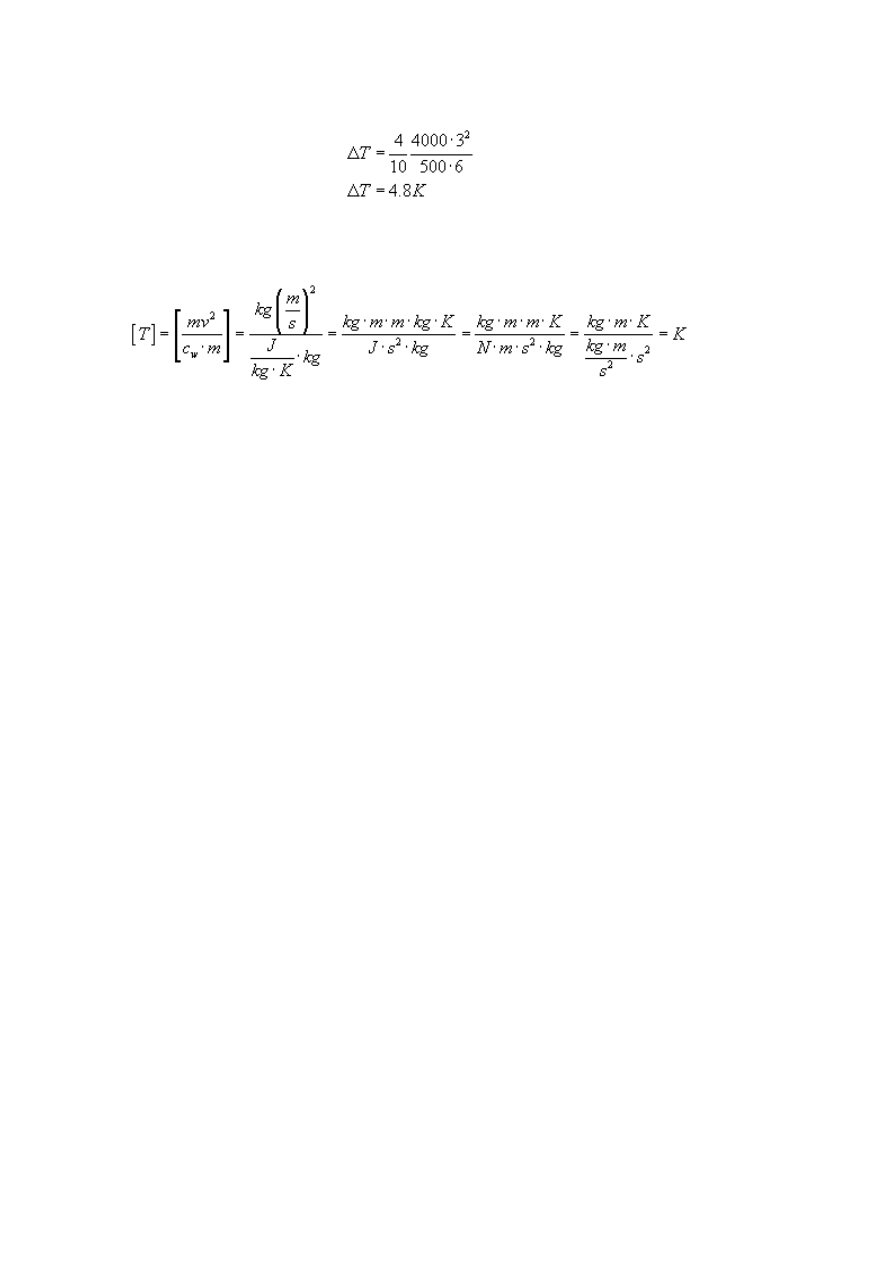
Podstawiając dane mamy:

Sprawdźmy na koniec jednostkę:

Ostatecznie wyliczyliśmy, że płyta ogrzeje się o 4.8 (stopni) Kelwina.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 4

Treść:
Ciału o masie m=2kg nadano prędkość v=36km/h. Siła tarcia zmniejsza prędkość
ciała o połowę na drodze s=100m. Ile wynosi przyrost energii wewnętrznej
układu?
Dane:
m = 2 kg
v = 36 km/h = 36000m/3600s = 10
m/s
s = 100 m

Szukane:
ΔU = ?

Wzory:
Energia kinetyczna

Rozwiązanie:
Ciału nadano pewną prędkość, więc tym samym posiada energię kinetyczną. Siła tarcia
wykonując pewną pracę W

T

zmniejsza o połowę prędkość ciała. Praca ta w formie energii

cieplnej zostaje przekazana na zwiększenie energii wewnętrznej układu.

Energia kinetyczna początkowa ciała:

Energia kinetyczna ciała po przebyciu 100 m:

Praca sił tarcia:

Praca sił tarcia zostaje zużyta na zwiększenie energii wewnętrznej ciała, więc:

Wykazaliśmy zatem, że przyrost energii wewnętrznej układu wynosi 75 dżuli.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 5

Treść:
Wodę o masie m=2.5kg i cieple właściwym c

w

=4000J/kgK ogrzano przy pomocy

palnika gazowego od t

1

=10

o

C do t

2

=100

o

C w ciągu t=10 minut. Jaka była moc

palnika, jeżeli woda otrzymała całe wydzielone ciepło?
Dane:
m = 2.5 kg
c

w

= 4000 J/kgK

t

1

= 10

o

C

t

2

= 100

o

C

t = 10 min = 600 s

Szukane:
P = ?

Wzory:
1. Ciepło pobrane/oddane

2. Moc palnika

3. Zależność między temperaturą w
stopniach Celsjusza a Kelwina

Rozwiązanie:
Aby zadanie policzyć prawidłowo, na samym początku musimy poprzekształcać
jednostki w danych zadaniach na jednostki z układu SI. Częściowo uczyniłem to przy
podawaniu danych powyżej, tu przeliczę jednak temperatury, które trzeba przeliczyć ze
stopni Celsjusza na Kelwiny zgodnie ze wzorem

gdzie:
t - temperatura w stopniach Celsjusza (nie mylić z czasem ;-) ),
T - temperatura w Kelwinach.

Tak więc:

Woda by się ogrzać od T

1

do T

2

pobiera z palnika ciepło Q zgodnie ze wzorem:

Palnik dostarcza ciepło wodzie w postaci energii W, a jego moc wyraża się wzorem:

a stąd:

Ciepło oddane przez palnik musi być równe ciepłu pobranemu przez wodę co możemy
zapisać jako:

Zatem zapisujemy powyższe w postaci wzorów i wyliczamy szukaną moc:

Podstawiając dane mamy:

Sprawdźmy jeszcze jednostkę:

Wszystko się zgadza, tak więc ostateczną odpowiedzią na pytanie o moc palnika jest
1500 watów.

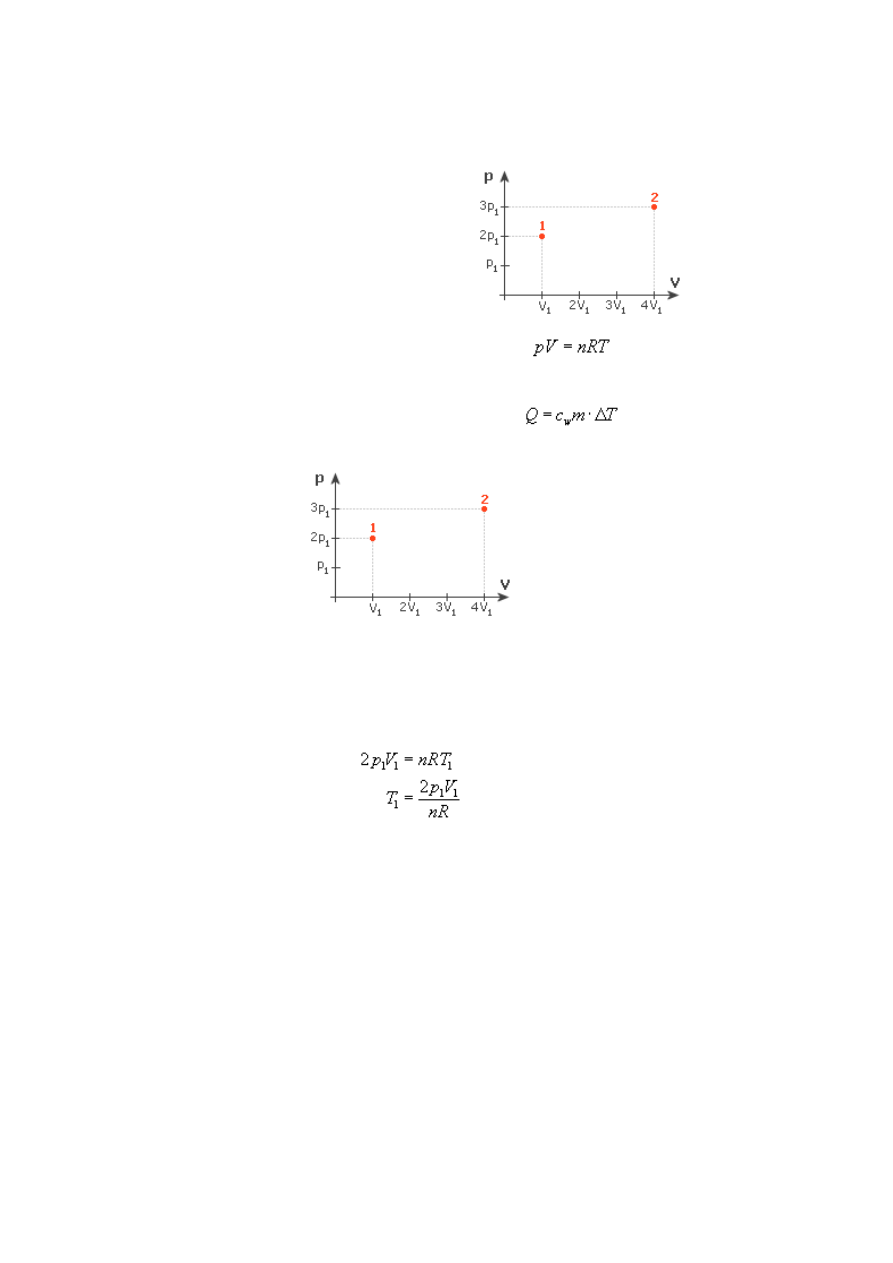
Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 6

Treść:
Jak zmieni się energia wewnętrzna gazu przy
przejściu ze stanu 1 do stanu 2 (patrz rysunek)?
Dane:
wykres

Szukane:
ΔU = ?

Wzory:
1.Energia wewnętrzna gazu

2.Równanie gazu
doskonałego

3.Ciepło pobierane/oddawane

Rysunek:

Rozwiązanie:
Na rysunku mamy przedstawiony wykres (zależność) ciśnienia od objętości. Zgodnie z
równaniem Clapeyrona (gazu doskonałego) dla ciśnienia 2p

1

i objętości V

1

(czyli dla

stanu pierwszego), możemy zapisać:

Oczywiście zakładamy, że liczba cząstek n i stała gazowa R są niezmienne (ktoś mógłby
mnie upomnieć o jakąś tautologię w sformułowaniu "stała niezmienna", ale weźmy na
przykład stałą Hubla, która mimo nazwy "stała" ma zmienne wartości ;) ).

Obliczmy teraz, ile będzie wynosić temperatura w drugim stanie:

Temperatura wzrosła 6-krotnie w porównaniu z pierwszym stanem. Lecz jak to się ma do
energii wewnętrznej gazu? A tak, że energia wewnętrzna gazu jest wprost proporcjonalna
do ciepła, które mu dostarczono (zakładamy, że nad gazem nie została wykonana żadna
praca, ani on sam jej nie wykonał).

Ciepło zaś jest wprost proporcjonalne do temperatury (na podstawie wzoru nr 3), a stąd:

Wykazaliśmy zatem, że energia wewnętrzna przy przejściu ze stanu 1 do 2 wzrosła 6 razy.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 7

Treść:
Gaz w cylindrze sprężono, działając na tłok siłą F=5N i przesuwając go o
d=10cm. W wyniku sprężania energia wewnętrzna gazu nie zmieniła się. Oblicz,
jaką ilość ciepła przekazał gaz w czasie sprężania do otoczenia.
Dane:
F = 5 N
d = 10 cm = 0.1 m
U = const.

Szukane:
Q = ?

Wzory:
1. Energia wewnętrzna gazu

2. Praca

Rozwiązanie:
Aby sprężyć gaz w cylindrze, wykonano nad nim pewną pracę. Energia wewnętrzna gazu
nie zmieniła się, więc zgodnie ze wzorem na energię wewnętrzną gazu oddał on do
otoczenia taką ilość energii równą co do wartości bezwzględnej pracy jaką nad nim
wykonano.

Praca wykonana nad gazem wynosi:

Wzór ten bierze się stąd, ponieważ wektor przesunięcia tłoka jest zgodny z wektorem siły
działającej na tłok (więc funkcja cosinus kąta zerowego równa jest 1).

Ciepło oddane do otoczenia przez gaz równa się:

Ciepło oddane do otoczenia w czasie sprężania wynosi 0.5 J.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 8

Treść:
Gaz doskonały ogrzano dostarczając ciepła Q. Temperatura bezwzględna wzrosła
wskutek tego od wartości T do 3T, a ciśnienie od wartości p do 3p. Ile wyniósł
przyrost energii wewnętrznej gazu?
Dane:
Q
ΔT
Δp

Szukane:
ΔU = ?

Wzory:
1. Równanie gazu doskonałego

2. Energia wewnętrzna gazu
doskonałego

Rozwiązanie:
Nim dostarczono ciepło parametry gazu wynosiły p, T. Zgodnie z pierwszym wzorem
równanie gazu na początku moglibyśmy zapisać jako :

gdzie:
n - to liczba cząsteczek gazu (w naszym zadaniu niezmienna),
R - stała gazowa,
V - objętość, jaką zajmował ten gaz.

Po dostarczeniu ciepła temperatura wzrosła do 3T, a ciśnienie do 3p. Zapiszmy równanie
gazu dla tych warunków:

Jak widzimy objętość gazu nie zmieniła się. Można by zapytać co to ma wspólnego z
przyrostem energii wewnętrznej gazu, który mamy określić? Ma, i to bardzo dużo :)

By obliczyć przyrost energii wewnętrznej gazu musimy znać ilość dostarczonego ciepła i
pracę jaką wykonano nad gazem, bądź jaką on wykonał. Ilość ciepła mamy podaną w
treści zadania, zaś jedyną niewiadomą jest praca. Jeśli wykonalibyśmy pracę nad gazem
musielibyśmy poruszyć tłokiem i sprężyć gaz, zaś jak gaz wykonałby pracę, musiałby
również "poruszyć" tłokiem. Wykazaliśmy, że objętość gazu przed i po dostarczeniu mu
ciepła nie zmieniła się więc tłok cały czas był w jednej pozycji, czyli:

Ostatecznie możemy odpowiedzieć, że przyrost energii wewnętrznej gazu wynosi Q.

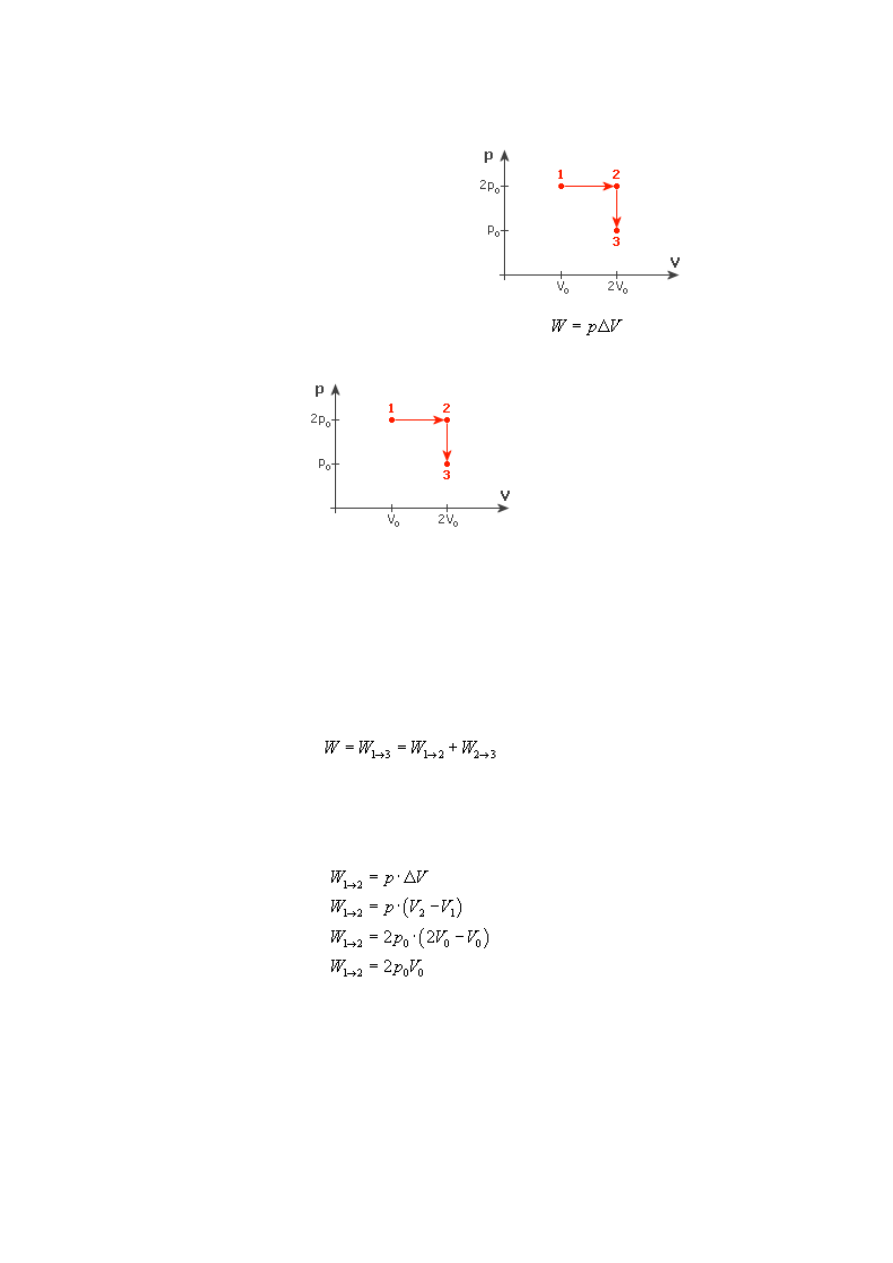
Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 9

Treść:
N moli idealnego gazu o temperaturze początkowej T
poddano przemianom (rysunek). Jaką pracę wykonał
gaz przy przejściu ze stanu 1 do 3?
Dane:
T
N

Szukane:
W = ?

Wzory:
1. Równanie Clapeyrona

2. Praca gazu idealnego

Rysunek:

Rozwiązanie:
Zanim do czegokolwiek się zabierzemy, spójrzmy na wykres. Wprawnym okiem można
zauważyć, iż przy przejściu gazu ze stanu 1 do stanu 2 nie zmienia się ciśnienie, a przy
przejściu ze stanu 2 do stanu 3 stała jest objętość. Oznacza to, że w przypadku stanu 1-2
mamy do czynienia z przemianą izobaryczną, a w stanach 2-3 izochoryczną.

Całkowita praca gazu przy przejściu ze stanu 1 do 3 to suma prac przejścia do
poszczególnych stanów:

Zajmijmy się najpierw przemianą izobaryczną. Gaz nie zmienia swojego ciśnienia,
zgodnie więc ze wzorem na pracę:

Przyjrzymy się teraz przemianie izochorycznej. Zauważ, że gaz przechodząc ze stanu 2
do stanu 3 nie zmienia swojej objętości - stąd ΔV = 0. Oznacza to, że praca wykonana
przez gaz w tej przemianie wynosi zero.
Całkowita praca wynosi więc:

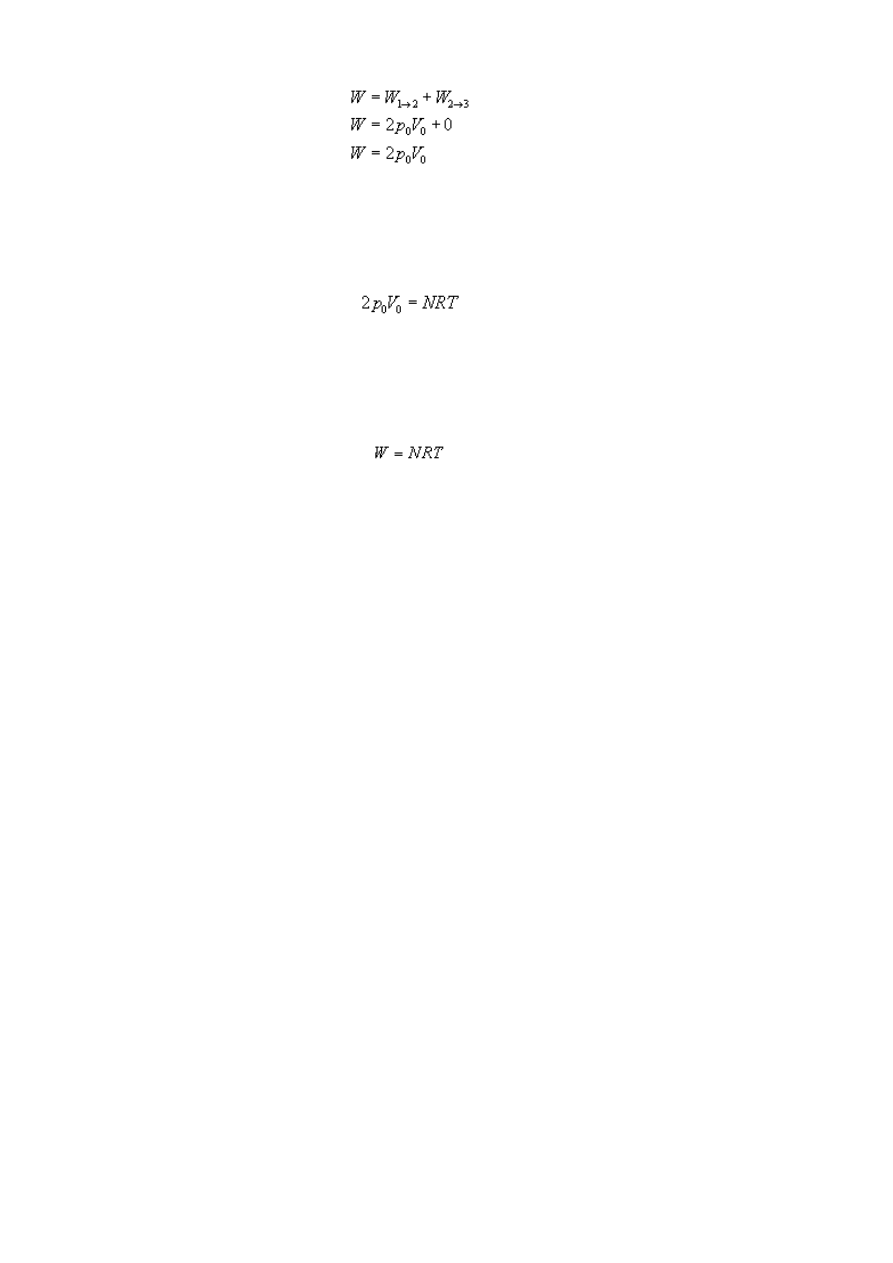
Niby wszystko fajnie, ale jak zapisać nasz wynik w postaci danych, które mamy w
zadaniu, czyli N i T? Przydać nam się może do tego równanie Clapeyrona, które to sobie
zapiszemy dla stanu 1 naszego gazu (bo dla tego stanu mamy podaną temperaturę T).

gdzie R to stała gazowa (do znalezienia w tablicach).

Porównując dwa powyższe wzory otrzymamy, że:

Gaz przy przejściu ze stanu 1 do stanu 3 wykonał pracę NRT.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 10

Treść:
Ile ciepła odda do chłodnicy silnik o sprawności η=20%, jeżeli pobierze Q

2

10kJ

ciepła?
Dane:
η = 20%
Q

1

= 10 kJ = 10000 J

Szukane:
Q

2

= ?

Wzory:
Sprawność silnika Carnota

Rozwiązanie:
Zadanie typu "podstaw do wzoru" :). Korzystając ze wzoru na sprawność idealnego
silnika cieplnego (Carnota) przekształcamy wzór ze względu na ciepło oddane do
chłodnicy:

gdzie Q

2

to szukane ciepło oddane do chłodnicy. Ktoś pewnie powie, że wzór można

przekształcić w prostszy sposób, my jednak pokazaliśmy ten najbardziej intuicyjny.
Podstawmy dane do naszego wzoru:

Silnik odda 8 kJ do chłodnicy.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 11

Treść:
W silniku Carnota stosunek temperatury grzejnika do temperatury chłodnicy
wynosi 4. Ile wynosi teoretyczna sprawność silnika? Jaką pracę wykona ten silnik,
jeżeli pobierze ciepło w ilości Q

2

=200J?

Dane:
Q

2

= 200 J

T

1

/ T

2

= 4

Szukane:
η = ?
W = ?

Wzory:
1. Sprawność silnika Carnota (pierwsza
postać wzoru)

2. Sprawność silnika Carnota (druga postać
wzoru)

3. Sprawność silnika Carnota (trzecia postać
wzoru)

Rozwiązanie:
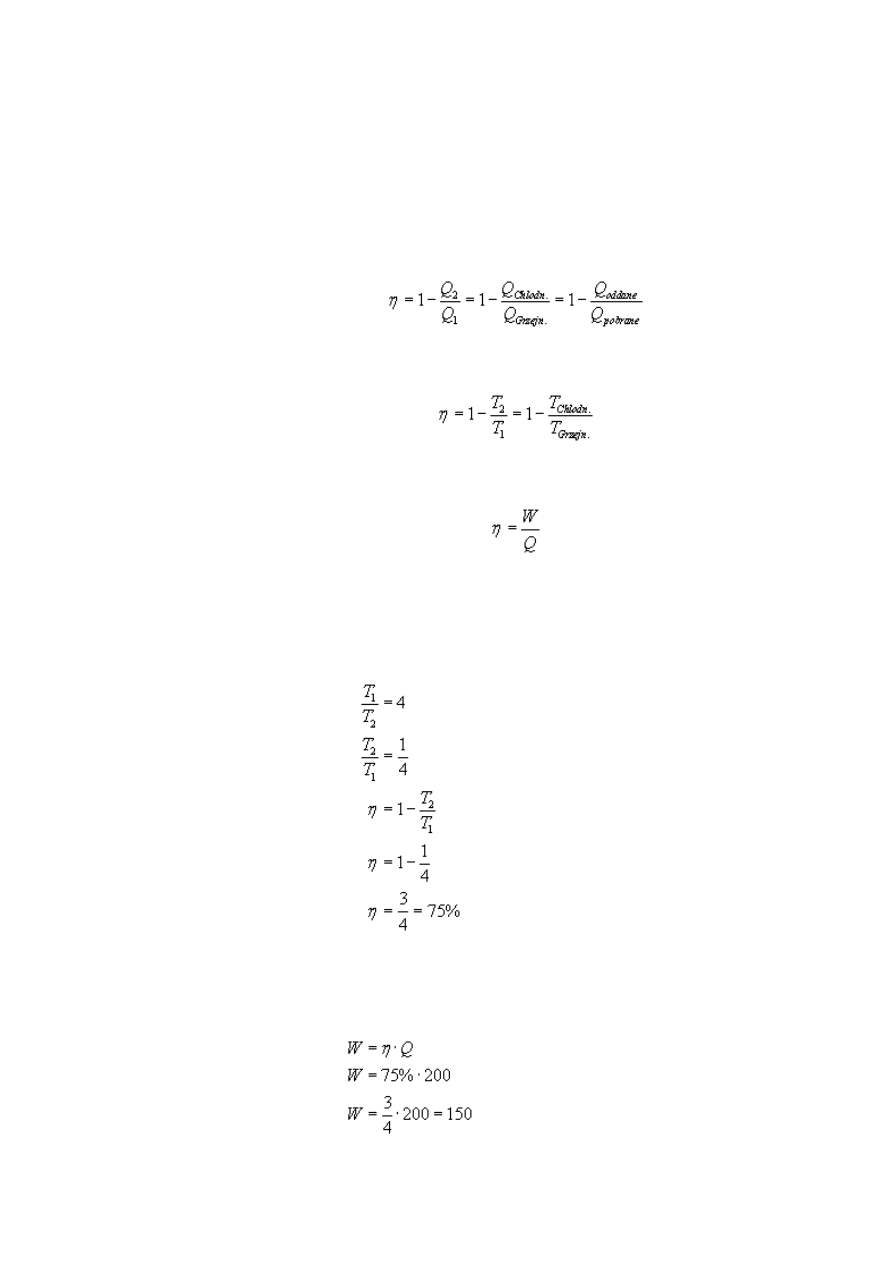
Korzystając z drugiej postaci wzoru na sprawność silnika cieplnego, obliczmy szukaną
sprawność, mając podany stosunek temperatury grzejnika do temperatury chłodnicy:

Znając sprawność i przekształcając trzeci wzór, możemy z łatwością obliczyć pracę jaką
wykona ten silnik:

Sprawność tego silnika wynosi 75%, zaś praca, jaką on wykona, wyniesie 150 J.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 12

Treść:
Silnik Carnota o sprawności η=20% ma różnicę temperatur pomiędzy źródłem
ciepła i chłodnicą wynoszącą ΔT=100K. Ile wynosi temperatura chłodnicy tego
silnika?
Dane:
η = 20%
ΔT = 100 K

Szukane:
T

2

= ?

Wzory:
Sprawność silnika cieplnego

Rozwiązanie:
Zadanie bardzo proste, gdyż wystarczy odpowiednio po przekształcić pierwszy wzór ze
względu na temperaturę chłodnicy. Zabieramy się do pracy! :)

Wiemy, że różnica temperatur wynosi 100 stopni, zapiszmy to...

...i włączmy do naszego wzoru:

Przekształcamy równanie, tak aby otrzymać szukane T

2

:

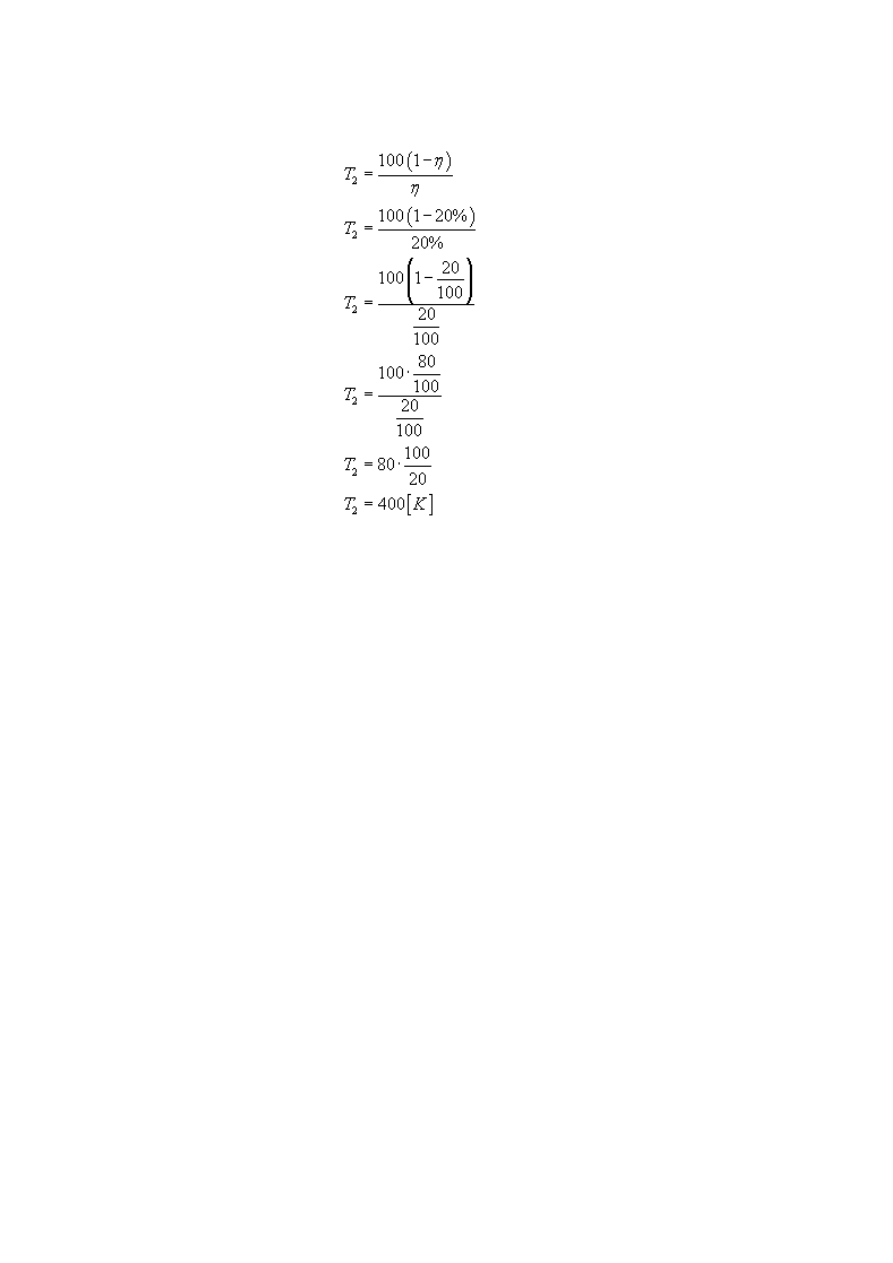
Ponieważ sprawność η mamy daną, podstawiamy ją, by otrzymać ostateczny wynik:

Temperatura chłodnicy wynosi 400 kelwinów.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 13

Treść:
Temperatura gazu idealnego wzrosła z T

1

=T do T

2

=nT. Jak zmieniła się średnia

prędkość cząsteczek tego gazu?
Dane:
T

1

= T

T

2

= nT

k - stała Boltzmanna

Szukane:
v

2

/ v

1

= ?

Wzory:
1. Energia kinetyczna

2. Średnia energia kinetyczna ruchu
postępowego cząsteczek gazu doskonałego

Rozwiązanie:
Kreseczka nad prędkością (v) oznacza, iż jest to średnia prędkość.
Pojawiająca się we wzorach literka k oznacza stałą Boltzmanna. Jej wartość można
sprawdzić w tablicach :)

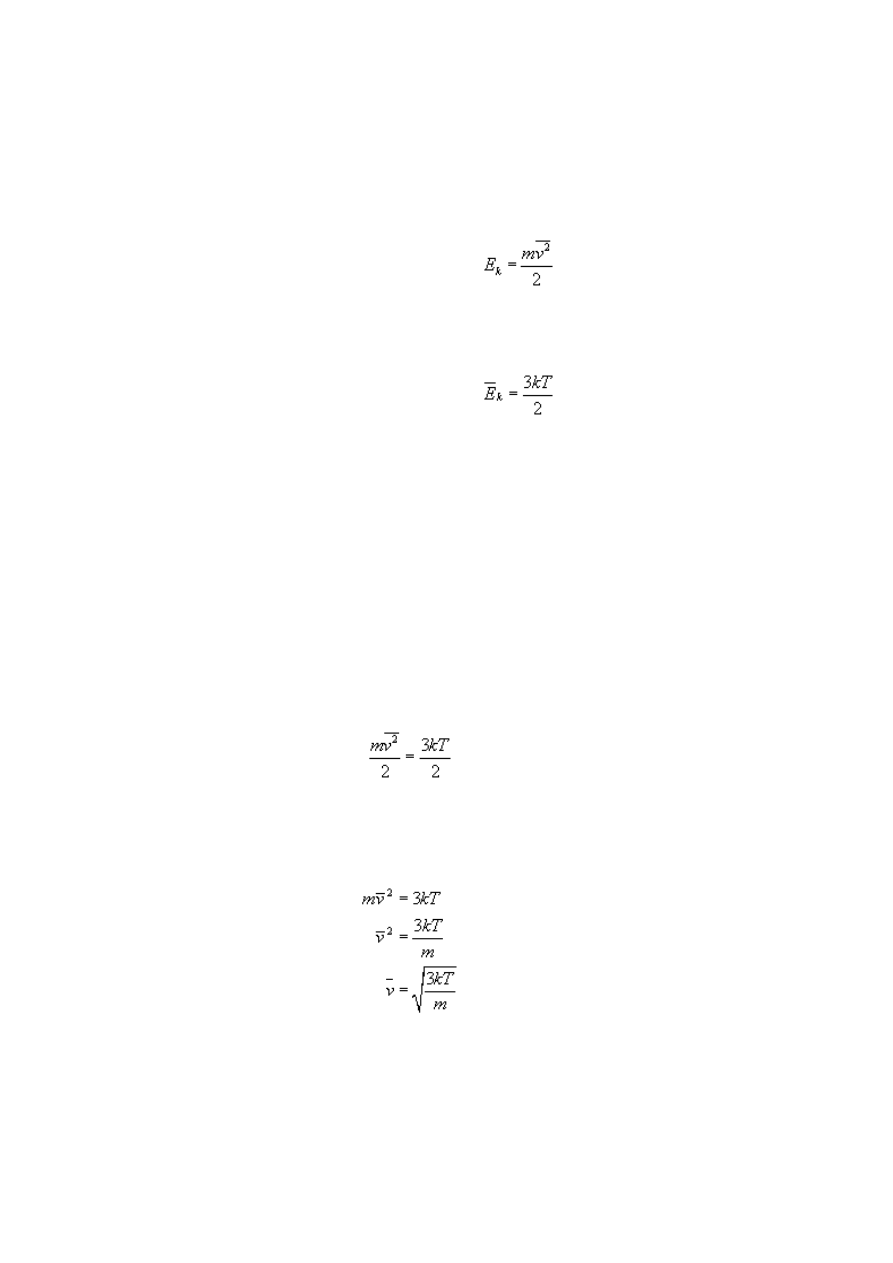
Aby obliczyć średnią prędkość cząsteczek gazu doskonałego, znając zmianę temperatury
tego gazu, musimy obie wielkości powiązać ze sobą za pomocą energii kinetycznych. W
przypadku gazu doskonałego, którego cząsteczki nie oddziałują ze sobą (z wyjątkiem
chwil, w których się zderzają), za energię wewnętrzną uważamy tylko energię kinetyczną
wszystkich rodzajów ruchu cząsteczek.
Skoro cząsteczki gazu posiadają jedynie energię ruchu postępowego (w tym przypadku
jest to gaz jednoatomowy), możemy porównać oba wzory na energię.

gdzie m to masa gazu.
Ze wzorów wyprowadzamy wzór na średnią prędkość cząsteczek gazu.

Mając już wyznaczoną prędkość wracamy do danych w zadaniu. Wiemy, że

Podstawiając, że T

1

=T i T

2

=nT otrzymujemy:

Z obu równań wyznaczamy prędkość (posługując się wcześniej otrzymanym wzorem):

Szukaną zmianę prędkości wyrazimy poprzez stosunek średnich prędkości:

Prędkość cząsteczek gazu idealnego wzrosła o pierwiastek z n.

Przemiany gazu doskonałego, zasady termodynamiki - Zadanie 14

Treść:
Ile cząsteczek tlenu znajduje się w 1cm

3

powietrza w warunkach normalnych?

Tlen zajmuje 20,95% objętości powietrza.
Dane:
V

p

= 1cm

3

V

t

= 20,95% * V

p

Szukane:
N = ?

Wzory:
1. Liczba Avogadro

2. Objętość 1 mola gazu w warunkach
normalnych

Rozwiązanie:
Objaśnienie:

N

A

- liczba Avogadro - liczba atomów, cząsteczek lub innych cząstek materii w jednym

molu substancji złożonej z tychże atomów lub cząsteczek lub cząstek.
N - szukana liczba cząsteczek.
L - pomocnicza szukana liczba, oznaczająca liczbę moli tlenu.
V

p

- objętość powietrza.

V

t

- objętość tlenu.

Na samym początku warto zauważyć, że objętość jednego mola gazu w warunkach
normalnych podana jest w dm

3

, a objętość tlenu mamy w cm

3

, więc od razu zamieniamy

jednostki. Robimy to w następujący sposób:

I dalej:

Z treści zadania wyliczamy objętość tlenu.

Z drugiej strony mamy podaną objętość jednego mola gazu i ilość cząsteczek w jednym
molu. Tworzymy więc proporcję, by obliczyć, ile moli zajmuje nasz tlen:

Mnożymy "na krzyż" i otrzymujemy, że

I ostatnie mnożenie :) Skoro wiemy ile moli ma nasz tlen i ile cząsteczek jest w 1 molu
(liczba Avogadro) wystarczy pomnożyć otrzymane L z N

A

by otrzymać liczbę

cząsteczek :)

W warunkach normalnych w 1cm

3

powietrza, którego 20,95% stanowi tlen, znajduje się

ok. 5,63

.

10

18

cząsteczek tlenu.

***

Bilans cieplny – przykład rachunkowy

Oto przykład praktycznego wykorzystania zasady

bilansu cieplnego

.

Rozwiążmy następujący problem:

Zadanie

Kowal zanurza do kadzi z 6 l wody rozgrzany stalowy pręt, w wyniku czego, w krótkim czasie
temperatura wody wzrasta od 20°C do 70°C. Masa pręta wynosi 2 kg. Jaką temperaturę miał pręt
przed zanurzeniem?

Rozwiązanie

W opisanej sytuacji mamy do czynienia z przekazywaniem ciepła od pręta do wody. Temperatury
pręta i wody - początkowo różne – po wymianie ciepła będą miały jedną temperaturę końcową
(oznaczymy ją przez t

k

). Temperatura ta będzie większa od początkowej temperatury wody, ale

mniejsza od początkowej temperatury pręta.
Zastosujemy tu

bilans cieplny

– w tej konkretnej sytuacji będzie on miał postać:

Q

pobrane_przez_wodę

= Q

oddane_przez_pręt

Zarówno ciepło pobrane, jak i oddane będzie wyliczane ze

wzoru na ciepło ogrzewania bez zmiany

stanu skupienia

:

Q = m·c

w

·

∆

t

Różne będą jednak substancje i różnice temperatur:

Q

pobrane_przez_wodę

= m

wody

·c

w_wody

· (t

k

– t

p_wody

)

Q

oddane_przez_pręt

= m

pręta

·c

w_stali

· (t

p_pręta

– t

k

)

Dane tu są:

m

wody

= 6 kg (bo litr wody waży 1 kg)

m

pręta

= 2 kg

c

w_stali

= 500 J/kg°C (dana odczytana z tablic)

c

w_wody

= 4200 J/kg°C (dana odczytana z tablic)

t

k

= 70°C

t

p_wody

= 20°C

Szukamy

t

p_pręta

= ?

Przekształcenia

Podstawiamy wyrażenia na ciepło pobrane i oddane do równania bilansu cieplnego:
m

wody

·c

w_wody

· (t

k

– t

p_wody

) = m

pręta

·c

w_stali

· (t

p_pręta

– t

k

)

W powyższym równaniu wszystko jest dane z wyjątkiem t

p_pręta

.

Dzielimy obie strony równania przez: m

pręta

·c

w_stali

, a następnie dodajemy do obu stron równania

t

k

. Ostatecznie otrzymamy wtedy wzór na szukane t

p_pręta

:

Po podstawieniu liczb otrzymamy wynik końcowy:
t

p_pręta

= 1330°C.