Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

1

Ćwiczenie 348

Badanie zjawiska Halla w germanie typu p

Przed zapoznaniem się z instrukcją i przystąpieniem do wykonywania ćwiczenia należy opanować następujący
materiał teoretyczny:
1. Podstawy modelu pasmowego ciał stałych. Rodzaje półprzewodników i ich modele pasmowe [1 lub 2].
2. Przewodnictwo półprzewodników, koncentracja i ruchliwość nośników prądu [1].
3. Efekt Halla w półprzewodnikach [1 lub 2 lub 3].

Cel ćwiczenia

Celem ćwiczenia jest:

1. Zbadanie efektu Halla w germanie.
2. Określenie typu przewodnictwa, wyznaczenie stałej Halla oraz ruchliwości i koncentracji nośników

większościowych w badanym półprzewodniku.

Opis zjawiska

Jeśli półprzewodnik, w którym płynie prąd umieścić w polu magnetycznym o indukcji B skierowanym

prostopadle do tego prądu, to pojawia się w nim siła elektromotoryczna prostopadła zarówno do prądu, jak i do pola
magnetycznego. Zjawisko to znane jest jako efekt Halla.

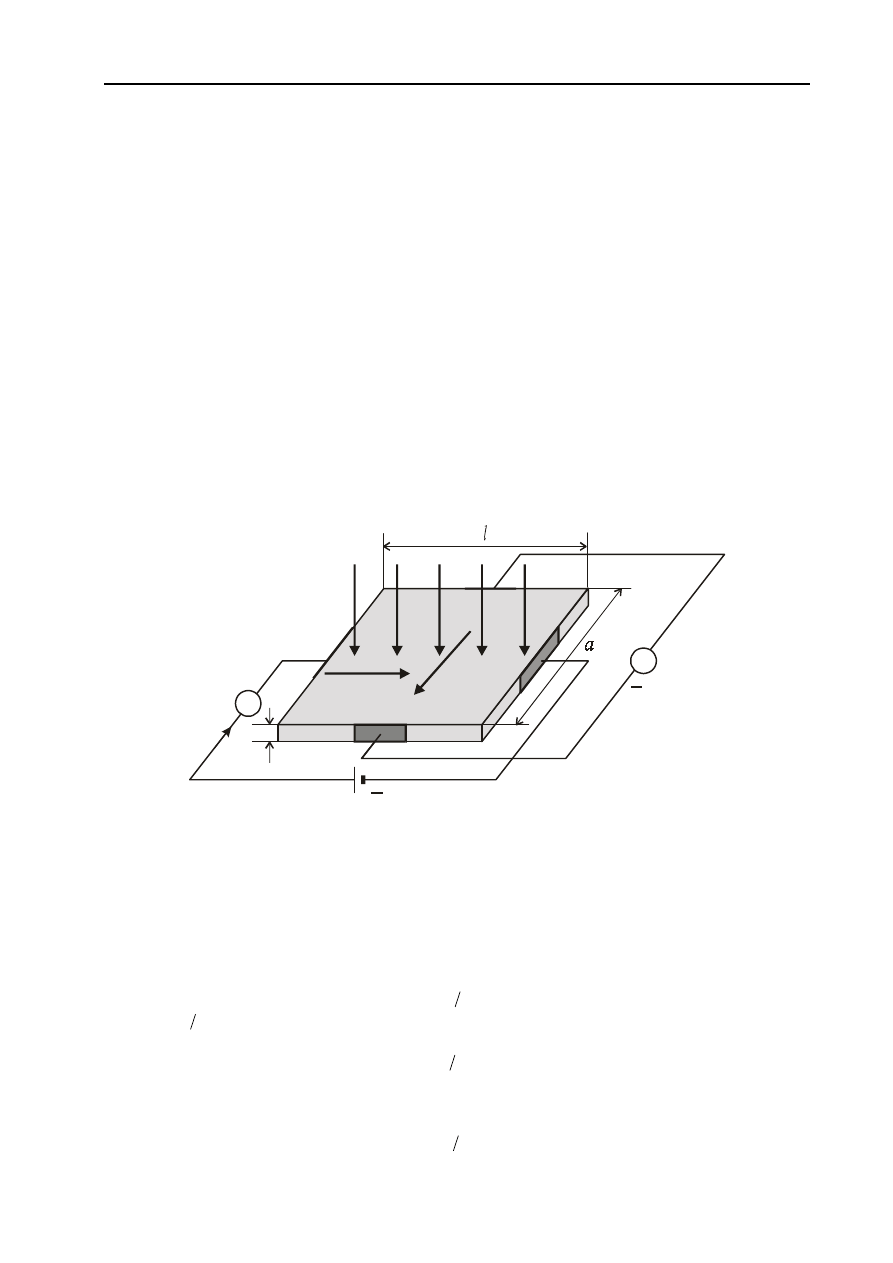
W ćwiczeniu bada się półprzewodnik akceptorowy, w którym nośnikami prądu są dziury o koncentracji p.

Próbka jest wycięta z monokryształu germanu i ma kształt płasko-równoległej płytki o szerokości a, grubości d i
długości l.

U

H

+

+

d

I

A

V

B

E

E

H

Rys. 1. Efekt Halla w półprzewodniku typu p

Przez próbkę płynie prąd o gęstości j pod wpływem pola elektrycznego E wytworzonego przez źródło stałego
napięcia (rys. 1). Przy ustalonym kierunku wektora indukcji pola magnetycznego B na dziury poruszające się w
półprzewodniku z prędkością v działa siła Lorentza, która odchyla je ku tylnej ściance. Wskutek tego na przedniej
ściance występuje ich niedostatek. W wyniku rozdziału ładunku powstaje poprzeczne pole elektryczne E

H

. Proces

rozdzielania ładunku trwa dopóki siła z jaką pole E

H

działa na swobodne nośniki ładunku nie zrównoważy siły

Lorentza. W stanie równowagi siły te mają równe wartości tzn. eE

H

= evB, a ponieważ j = epv i E

H

= U

H

/a, to

hallowska różnica potencjałów U

H

między przeciwległymi ścianami próbki wynosi:

( )

jBa

ep

U

H

1

=

, (1)

gdzie

ep

R

H

1

=

jest tzw. współczynnikiem Halla. Znajomość współczynnika Halla pozwala na potwierdzenie

znaku nośników ładunku oraz obliczenie ich koncentracji i ruchliwości

µ:

(

)

H

eR

p 1

=

, (2)

H

R

σ

=

µ

. (3)

We wzorze (3)

σ jest przewodnictwem badanej próbki, które można wyznaczyć na podstawie jej oporności R i

wymiarów

Rda

l

=

σ

. (4)

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

2

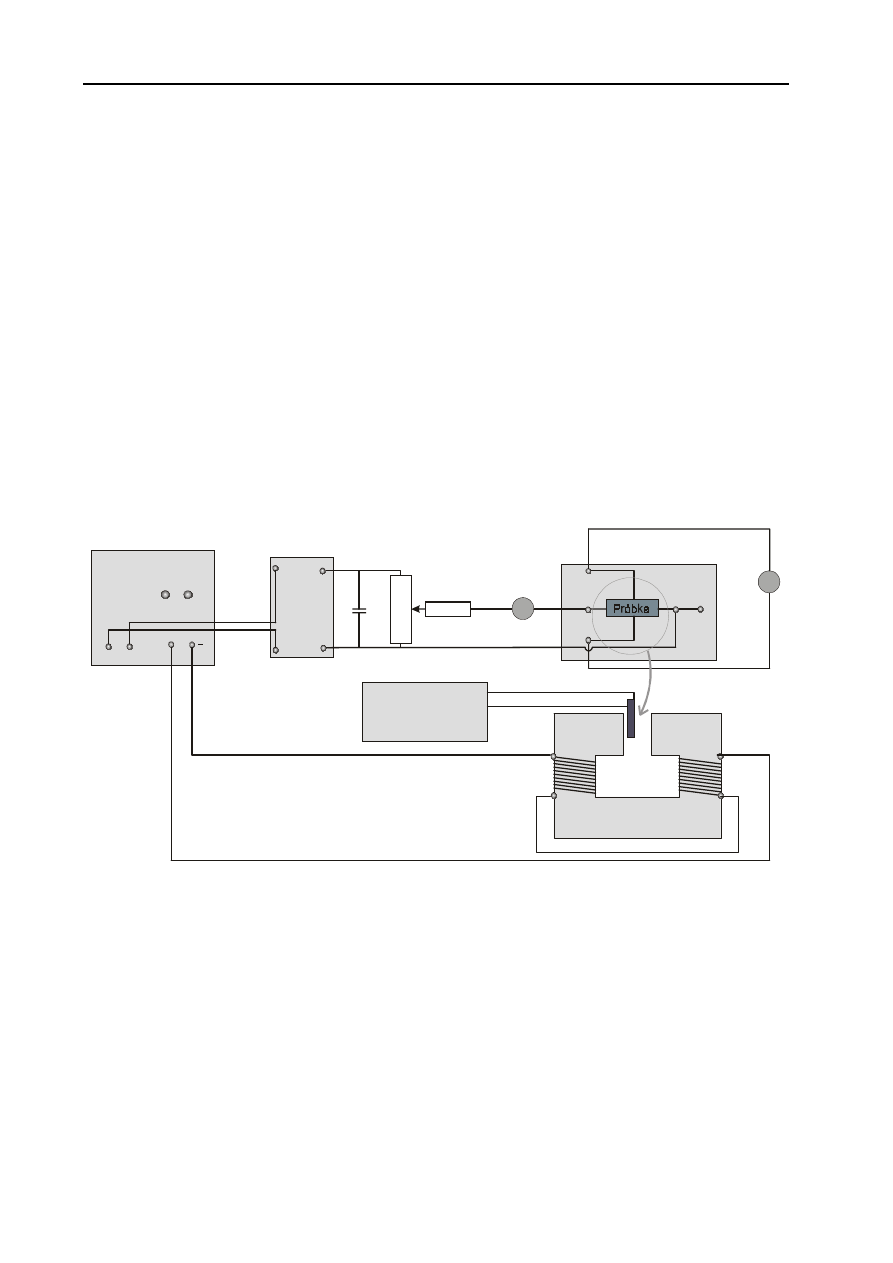
Opis układu pomiarowego

W skład zestawu do badania efektu Halla wchodzą (rys. 2):

1. Zasilacz.

Z jego wyjścia zmiennonapięciowego dostarczany jest prąd sterujący próbką. Z wyjścia stałoprądowego zasilany
jest elektromagnes.

2. Prostownik.

Połączony jest do gniazd zasilacza oznaczonych symbolami 0 i 12 V

∼. W celu wygładzenia prądu zasilającego,

do wyjścia wzmacniacza podłączony jest kondensator elektrolityczny (C = 2000

µF).

3. Potencjometr (P).

Połączony jest z prostownikiem i służy do regulacji prądu I płynącego przez próbkę. W szereg z potencjometrem
podłączony jest opornik 330

Ω zabezpieczający przed przekroczeniem maksymalnej dozwolonej wartości prądu

płynącego przez próbkę (50 mA).

4. Miliamperomierz do pomiaru natężenia prądu płynącego przez próbkę.
5. Wysokooporowy cyfrowy miliwoltomierz do pomiaru napięcia Halla U

H

.

6. Elektromagnes, który tworzą dwie połączone szeregowo cewki umieszczone na wspólnym rdzeniu.
7. Badana, płaskorównoległa próbka germanu o typie przewodnictwa p, umieszczona na płytce zamontowanej w

szczelinie elektromagnesu.

8. Hallotron (H).

Służy do pomiaru wartości indukcji magnetycznej. Umieszczony jest między biegunami elektromagnesu w
pobliżu próbki. Połączony jest z miernikiem indukcji magnetycznej zwanym dalej teslametrem.

ZASILACZ

A V

0 12V~ 0 12V

+

C

~

~

+

_

Wzm.

R

Ω

mV

A

B

C

TESLAMETR

330

N

S

ELEKTROMAGNES

mA

Rys. 2. Schemat układu pomiarowego

Przygotowanie do pomiarów

(wykonuje uprawniony pracownik)
1. Połączyć przyrządy według schematu z rys. 2.
2. Umieścić płytkę z próbką na statywie, umocować.
3. Delikatnie opuścić płytkę pomiędzy nabiegunniki elektromagnesu aż do wyczucia oporu. Umocować sztywno

płytkę na statywie.

4. W przestrzeni pomiędzy próbką a nabiegunnikiem umieścić hallotron.
5. Skręcić pokrętło potencjometru oraz pokrętła prądowe i napięciowe zasilacza maksymalnie w lewą stronę.

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

3

Przebieg pomiarów

I. Badanie zależności napięcia Halla U

H

od natężenia prądu I płynącego przez próbkę umieszczoną w stałym

polu magnetycznym o indukcji B i w stałej temperaturze T

U

H

= f (I)

B,T=const.

1. Pokrętła zasilacza i potencjometru skręcić maksymalnie w lewo.
2. Podłączyć blok zasilający do punktów A i B płytki mieszczącej próbkę, tzn. połączyć punkt A płytki z

amperomierzem a amperomierz z potencjometrem P. Punkt B płytki połączyć z opornikiem o wartości 330

Ω.

3. Wytworzyć pole magnetyczne pomiędzy nabiegunnikami elektromagnesu w następujący sposób:

a) włączyć teslametr i po umieszczeniu sondy w „ekranie” magnetycznym wyzerować go; umocować sondę

na pierwotnym miejscu.

b) włączyć zasilacz i nastawić pokrętło napięciowe zasilacza na 12 V.
c) przekręcać pokrętło prądowe zasilacza w prawo, aż do uzyskania na teslametrze żądanej wartości indukcji

magnetycznej np. 10 mT (lub innej wskazanej przez prowadzącego); zanotować tę wartość.

4. Potencjometrem P regulować wartość prądu przepływającego przez próbkę od 0 do 38 mA z krokiem

pomiarowym np. 2 mA. Dla każdej ustalonej wartości prądu sterującego, odczytywanego na miliampero-
mierzu, notować odpowiadającą mu wartość napięcia Halla U

H

odczytywaną na miliwoltomierzu.

5. Wykonać pomiary wymienione w punkcie 4 dla przeciwnego kierunku prądu przepływającego przez próbkę.

(Aby zmienić kierunek prądu należy zamienić miejscami przewody „+” i „–” wychodzące z kondensatora.)

6. Po zakończeniu pomiarów skręcić potencjometr P maksymalnie w lewo.
7. Wyłączyć pole magnetyczne, nastawiając pokrętła prądowe i napięciowe zasilacza w pozycję „0 ”.
8. Wyłączyć zasilacz wyłącznikiem sieciowym.

II. Badanie zależności napięcia Halla U

H

od indukcji magnetycznej B w stałej temperaturze T

U

H

= f (B)

T=const.

1. Podłączyć blok zasilający do punktów A i C płytki mieszczącej próbkę.
2. Umieścić hallotron w przestrzeni między nabiegunnikami elektromagnesu.
3. Włączyć zasilacz przyciskiem sieciowym.
4. Uwaga! Przy wyłączonym polu magnetycznym napięcie U

H

powinno być równe 0. Jeśli tak nie jest,

doprowadzić je do zera potencjometrem dostrajającym znajdującym się na płytce z próbką (czynność tę
wykonuje uprawniony specjalista ).

5. Potencjometrem P nastawić prąd sterujący próbką na wartość równą w przybliżeniu 20 mA. Zanotować

ustaloną wartość natężenia prądu I.

6. Ustawić pokrętło napięciowe zasilacza na 12 V, a następnie przekręcać pokrętło prądowe w prawo w celu

zmiany wartości indukcji magnetycznej. Zmieniać wartość indukcji od 0 do 10 mT z krokiem pomiarowym
np. 1 mT. Notować wartość indukcji magnetycznej B odczytywaną na teslametrze i odpowiadające jej wartości
napięcia Halla U

H

.

7. Wyłączyć pole magnetyczne skręcając pokrętło prądowe zasilacza do zera.
8. Zmienić kierunek pola magnetycznego zamieniając miejscami przewody w zasilaczu doprowadzającym prąd

do elektromagnesu.

9. Powtórzyć czynności wymienione w punkcie 5.

10. Wyłączyć pole magnetyczne skręcając pokrętła prądowe i napięciowe na zasilaczu w położenia „ 0 ”.
11. Zredukować do zera prąd I sterujący próbką skręcając potencjometr P maksymalnie w lewo.

III. Badanie zmian przewodnictwa germanu w obecności pola magnetycznego.

1. Podłączyć blok zasilający próbkę do punktów A i C.
2. Między punkty A i B podłączyć miliwoltomierz w celu pomiaru spadku napięcia na próbce.
3. Ustawić potencjometr P na maksymalną wartość skręcając go w prawo. Zanotować wartość prądu

przepływającego przez próbkę i spadek napięcia na próbce.

4. Upewnić się czy hallotron znajduje się w przestrzeni między nabiegunnikami elektromagnesu. Włączyć

teslametr.

5. Nastawić pokrętło napięciowe zasilacza na 12 V, a następnie zmieniać indukcję magnetyczną w jak

najszerszym zakresie z określonym krokiem pomiarowym, np. 1 mT, przekręcając pokrętło prądowe zasilacza
w prawo. Notować wartość indukcji magnetycznej B odczytywaną na teslametrze i odpowiadające jej zmiany
spadku napięcia na próbce.
Uwaga! W czasie pomiarów prąd sterujący próbką powinien mieć tę samą wartość. Jeżeli wartość tego
prądu zmienia się wraz ze zmianą indukcji magnetycznej, to należy ją notować.

6. Po skończonych pomiarach należy skręcić maksymalnie w lewą stronę pokrętła prądowe i napięciowe

zasilacza oraz potencjometr P. Wyłączyć z sieci zasilacz i teslametr.

Pracownia Fizyki Współczesnej Instytutu Fizyki PŁ

4

Opracowanie sprawozdania

Uwaga! Wszelkie dane dotyczące rozmiarów próbki, niezbędne do wykonania obliczeń, zamieszczone są na

wywieszce znajdującej się przy stanowisku pomiarowym.

1. Wykreślić zależności napięcia Halla U

H

od natężenia I prądu sterującego próbką.

2. Wykreślić zależności napięcia Halla U

H

od indukcji B. Prostą wyznaczyć stosując metodę najmniejszych

kwadratów, tj. obliczyć jej współczynnik kierunkowy b oraz błąd

∆b tego współczynnika.

3. Obliczyć wartość stałej Halla R

H

, określić jej znak, zidentyfikować rodzaj nośników ładunku w badanym

materiale półprzewodnikowym.

4. Obliczyć koncentrację p nośników prądu.
5. Obliczyć przewodnictwo elektryczne

σ germanu.

6. Obliczyć ruchliwość nośników

µ.

7. Wykreślić względną zmianę przewodnictwa próbki

(

)

( )

B

B

f

=

σ

σ

−

σ

lub jej oporu

(

)

( )

B

R

R

R

B

f

=

−

od

indukcji magnetycznej; (

σ i R są przewodnictwem i oporem przy B = 0, zaś σ

B

i R

B

określają przewodnictwo i

opór w obecności pola magnetycznego).

8. Obliczyć błędy obliczanych wielkości

∆R

H

,

∆σ, ∆p, ∆µ (np. przy wykorzystaniu metody różniczki

zupełnej).

9. Zinterpretować i przedyskutować otrzymane zależności.

Literatura

[1] Ch. Kittel, Wstęp do fizyki ciała stałego, PWN, Warszawa, 1999.
[2] A. Oleś, Metody doświadczalne fizyki ciała stałego, WNT, Warszawa, 1998.
[3] R. Resnick, D. Halliday, Fizyka, t. II, PWN, Warszawa, 1998.

Więcej wiadomości na tematy związane z ćwiczeniem można znaleźć w podręcznikach:

H. Ibach, H. Luth, Fizyka ciała stałego, PWN, Warszawa, 1996.
K. W. Szalimowa, Fizyka półprzewodników, PWN, Warszawa, 1974.

Grubość próbki d = 1·10

−3

m

Długość próbki l = 2·10

−2

m

Szerokość próbki a = 5·10

−3

m

Opór w temperaturze pokojowej R

0

= 57

Ω