05

Cyfrowe Przetwarzanie Sygnałów
Analiza widmowa
dr inż. Jarosław Bułat

2010.03.08

Ćwiczenie 1.

W poniższym programie wykonano analizę częstotliwościową różnymi metodami przebiegu
opisanego następującą zależnością:

x t =cos2  f

1

t0.5cos2  f

2

t ,

gdzie : f

1

=

100Hz , f

2

=

102Hz

•

Która metoda jest właściwa?

•

Powtórz zadanie dla N = 1000 oraz zaprezentuj widmo sygnału dla obu przypadków na
jednym wykresie (oś X wykresu powinna być wyskalowana w częstotliwości unormowanej,

oś Y w dB)

•

Oblicz wartość bezwzględną współczynników transformacji odpowiadających częstotliwościom
f

1

i f

2

i porównaj z wartościami odczytanymi z wykresów.

•

dla f

1

=100Hz, f

2

=102.5Hz i N=1000 wykonaj analizę poniższym programem, wytłumacz

dlaczego wartość maksymalna współczynników odpowiadających f

2

zmniejszyła się chociaż

energia składowej sygnału f

2

pozostała bez zmian (nieznacznie zmieniła się częstotliwość)

clear

all

; close

all

;

fs = 1000; Nx = 1000;
A1 = 1;
A2 = 0.5;
f1 = 100;
f2 = 102;

t = 1/fs*(0:Nx-1);
x = A1*cos( 2*pi*f1*t ) + A2*cos( 2*pi*f2*t );

figure, freqz( x );

% freqz

N = 500;

% FFT

X = fft( x, N );
figure, plot( 20*log10(abs(X(1:end/2+1))) );

fvtool( x );

% fvtool

Ćwiczenie 2.

Dla sygnału z ćw. 1 o parametrach f

1

=100Hz, f

2

=102.5Hz wykonaj analizę częstotliwościową z przy

użyciu transformacji Fouriera interpolując widmo poprzez dodanie zer do sygnału x, w taki sposób
aby cały wektor miał długość 10x większą od oryginalnego. Następnie oblicz transformację Fouriera

DTFT typu ,,lupa'' (patrz ćwiczenie 3 z laboratorium 3) w zakresie f

d

=90Hz, f

g

=120Hz dla 1024

współczynników. Oba wykresy wraz z widmem prostej transformacji FFT (ćw. 1) narysuj na jednym

wykresie (oś X wyskalowana w hercach, oś Y w dB).

Powtórz ćwiczenie stosując różne okna czasowe, tzn. nie analizuj interesujący nas sygnał tylko jego

iloczyn z wybraną funkcją okna (np.: Hanning, Hamming, Blackman, Kaiser, Bartlett, etc...). Zmień
amplitudę drugiej składowej sygnału na 0.0001. Dobierz funkcję okna oraz liczbę próbek sygnału,

zapewniające wymaganą w tym przypadku rozdzielczość częstotliwościową i amplitudową. Obie
składowe mają być w widmie widoczne.

Ćwiczenie 3.

Wyznacz widmo sygnału pseudolosowego n z rozdzielczością 1Hz dla przedziału 0-128Hz (f

s

=1kHz).

clear

all

; close

all

;

Nn = 10000;
randn(

'state'

, 0 );

% inicjalizacja generatora liczb pseudolosowych

n = 0.3*randn( Nn, 1 );

Jakie powinno być widmo sygnału pseudolosowego o rozkładzie normalnym? Dlaczego widmo

takiego sygnału obliczone z jednego okna nie jest takie jakie być powinno? (Jest różne od
teoretycznego). Co należy zrobić aby przybliżyć go do widma teoretycznego? Zastosuj funkcję
spectrum() do wyznaczenia widma tego sygnału. Co ona liczy?
Dodaj ten szum do sygnału z ćw. 1: N=1000, f

1

=100Hz, f

2

=102Hz. Oblicz fft() i spectrum() dla

sygnału sumy. Jakie wnioski można wyciągnąć z tej analizy?

Ćwiczenie 4.

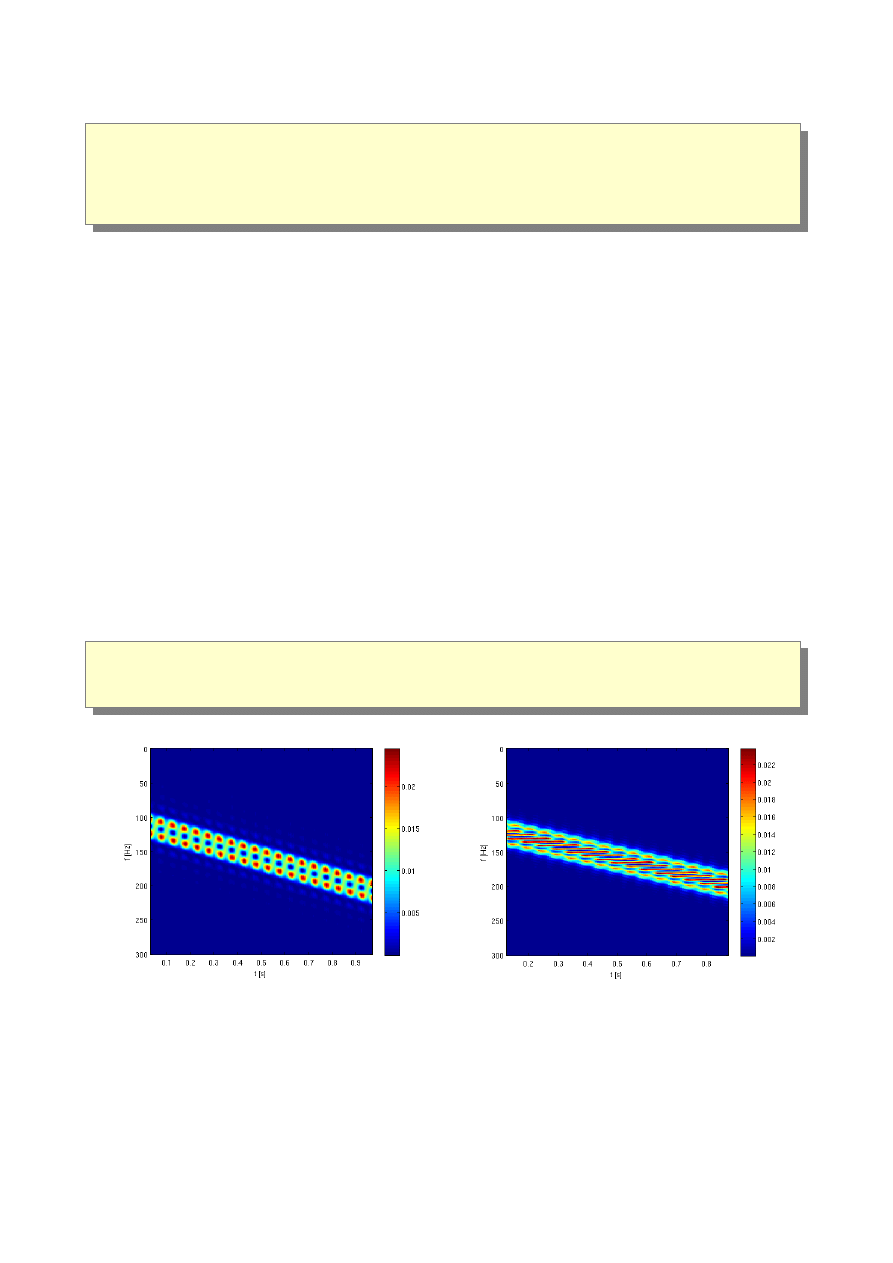
Wygeneruj sygnał spróbkowany częstotliwością f

s

=1000Hz o czasie trwania t=1s opisany

następującą zależnością:

x t =cos2  f t0.5 df t

2



cos2  f  f

0



t0.5 df t

2



, f =100Hz , f

0

=

20Hz , df =100Hz

Następnie wykonaj analizę częstotliwościową jak w ćw. 1 oraz analizę czasowo-częstotliwościową za
pomocą funkcji spectrogram(...). Dobierz długość oraz rodzaj okna analizy w ten sposób aby oba

przebiegi o zmiennej częstotliwości były rozróżnialne. Kosztem czego się ją osiąga? Powtórz analizę
z wykorzystaniem funkcji spectrum(). Poniżej został przedstawiony fragment programu generujący

niewłaściwe wykresy - parametry okna zostały tak dobrane, że nie pozwalają na rozróżnienie obu
składowych sinusoidalnych.

[S,F,T,P] = spectrogram( x, boxcar(64), 60, [0:500], fs );
figure; imagesc( T, F, P ); colormap( jet ); colorbar;
xlabel(

't [s]'

); ylabel(

'f [Hz]'

);

Ćwiczenie 5.

Dla podanego przebiegu, wykonaj analizę częstotliwościową i podaj parametry każdej ze składowych
sygnałów z których został złożony cały sygnał:

•

czas rozpoczęcia i zakończenia każdej składowej

•

częstotliwość początkową i końcową każdej składowej

•

amplituda (w dziedzinie czasu) na początku i końcu każdej składowej

•

poziom szumu w dB

Załóż, że parametry każdej składowej sygnału takiej jak: amplituda, częstotliwość zmieniają się
liniowo w czasie. Przyjmij częstotliwość próbkowania jako: f

s

=1000Hz.