Odwzorowanie wiernokątne Gaussa - Krugera
Najbardziej korzystnym układem z którym mamy do czynienia w geodezji jest układ
współrzędnych prostokątnych (na płaszczyźnie). Taki układ ułatwia rozwiązanie
szeregu zagadnień, gdyż związki zachodzące na płaszczyźnie dają się wyrazić w
sposób prosty.
Rzut Gaussa – Krugera jest wiernokątnym odwzorowaniem walcowym (walec w
położeniu poprzecznym – styczny w południku zwanym południkiem osiowym)
Dal celów geodezyjnych używa się w Polsce trzystopniowych pasów południkowych z
południkami osiowymi:
15°, 18 °, 21 °, 24°
(na wschód od Greenwich)
Przy wyprowadzeniu formuł odwzorowawczych zrobiono następujące założenia:
1. południk osiowy odwzorowuje się w postaci linii prostej, która służy jako oś
odciętych
2. odcięta punktu leżącego na południku osiowym powinna być równa długości łuku
południka liczonego od równika do danego punktu.
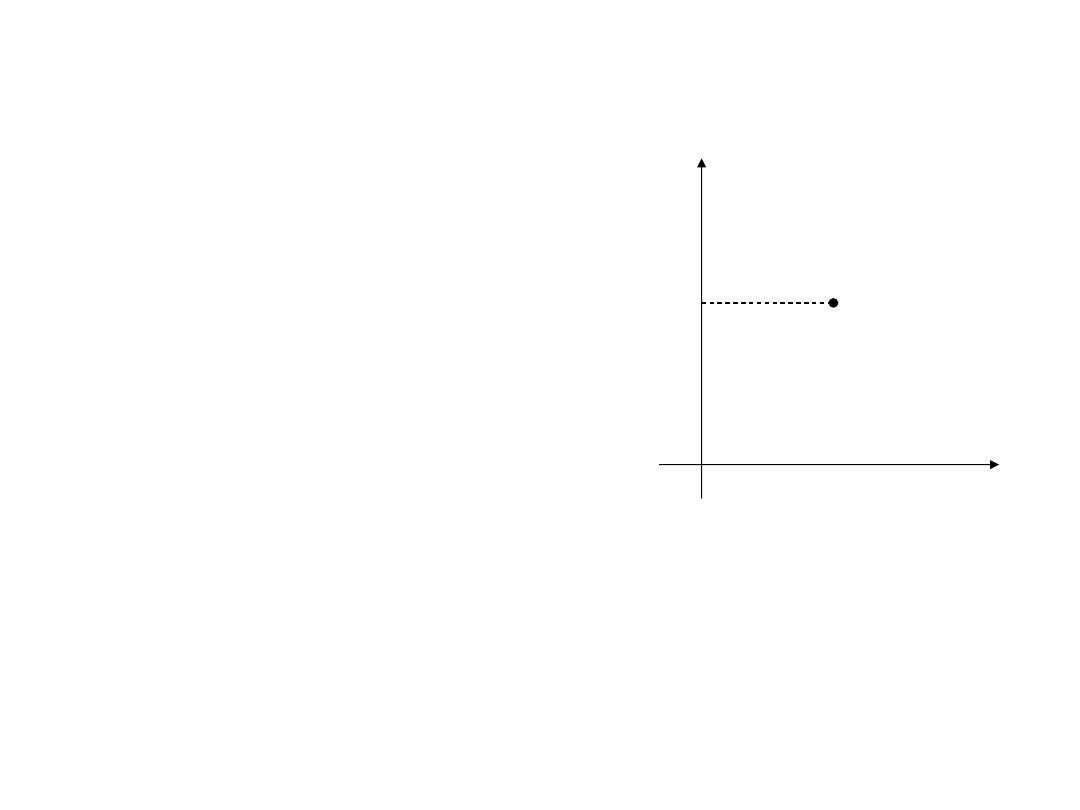
Rzędne w południku są równe zeru, przecięcie południka osiowego z równikiem jest
początkiem układu. Współrzędnymi punktu P są:
P
P
1
P
0
równik
Y
X
połu
dn
ik
osi
owy
X = P
0
P
1
Y = P
1
P
Odcięta X ma zawsze znak dodatni.
Rzędna Y będzie dodatnia jeżeli leży na wschód i
ujemna jeżeli leży na zachód od południka osiowego.
Aby jednak współrzędne punktów miały zawsze
znak dodatni wprowadza się następujący sposób
oznaczenia. Rzędną południka osiowego oblicza się
dzieląc numer południka osiowego przez trzy.
Otrzymana liczba wskazuje ilość tysięcy kilometrów.
Następnie do tej liczby dodaje się 500 km. Np. dla
południka osiowego, którego długość geodezyjna
L = 21°
rzędna wynosi
Y
0
= 7500 km
Jeżeli punkt nie leży w południku osiowym, to jego rzędna będzie wynosić:
Y = Y
0
+ y
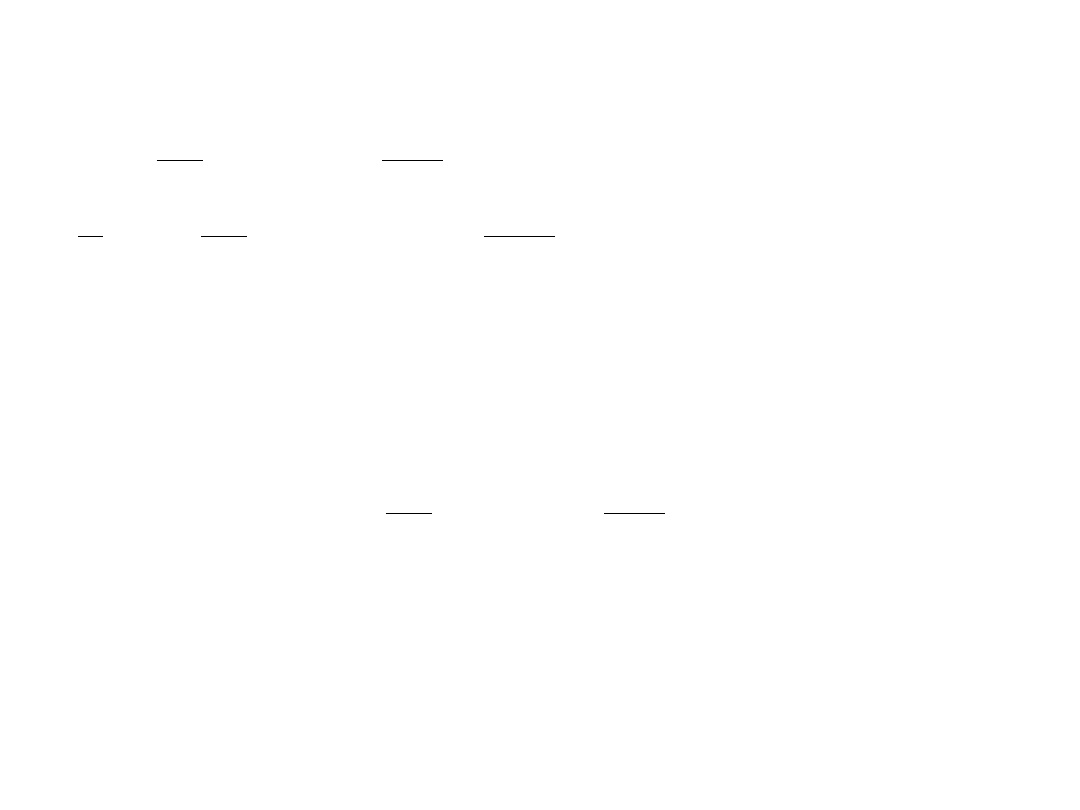
4
2
2
3
4
4
2
2
2
4
9
5
cos
sin
24
cos
sin
2
t
B
B
l
N
B
B
l
N
X
X
poł
2
2
2
4
2
5
5
5
2
2
3
3
3
58
14
18
5
cos
120
1
cos
6
cos
t
t
t
B
l
N
t
B
l
N
B
l
N
Y
Gdzie:
B
e cos
'
B
t
tan
Skala m w tym odwzorowaniu wyraża się wzorem:
2
4
4
4
2
2
2
2
4
5
cos
24
1
cos
2
1
t
B
l
B
l
m
gdzie
X
poł
- długość łuku południka
B
poł
MdB
X
0
l – różnica długości geodezyjnych danego punktu i południka osiowego
(1)
(2)
Para funkcji odwzorowawczych Gaussa-Krugera (odwzorowanie elipsoidy obrotowej na
pobocznice walca) ma następująca postać:
Powyższe wzory można wykorzystywać do obliczenia współrzędnych, zastąpiwszy w
nich Xpoł wyrażeniem długości łuku południka. W tym celu należy
B
B
poł
B
e
dB
e
a
MdB
X
0
0
3
2
2
2
sin
1
1
Jest to całka eliptyczna, nie mająca rozwiązania w dziedzinie funkcji elementarnych.
Obliczamy jej wartość rozwijając wyrażenie podcałkowe według wzory Newtona na
dwumian i całkując następnie ten szereg wyraz po wyrazie. Po rozwinięciu otrzymamy całkę
B
dB
B
A
B
A
B
A
A
e
a
X
0
6
4
2
0
2
...
6
cos
4
cos
2
cos
1
a po scałkowaniu:
...
6
sin
4
cos
2
sin
6
4
2
0
B
A
B
A
B
A
B
A
a
X
(3)
przy czym:
256
5
64
3
4
1
6
4
2
0
e
e
e
A
4
3
256
15
6
4
4
e
e
A
128
15
4
8
3
6
4
2
2
e
e
e
A
3072
35
6
6
e
A
Za pomocą tych wzorów można osiągnąć dokładność obliczeń x,y lepszą niż 1 mm dla l ≤3°
Zamiana współrzędnych prostokątnych x, y na geodezyjne B, L wyraża się wzorami, które
można otrzymać rozwiązując najpierw iteracyjnie równania (1) i (2) względem B i l.
Objaśnimy pokrótce ten proces. Najpierw wyznacza się pierwsze przybliżenie l, biorąc
tylko pierwszy wyraz wzoru (2), tzn.:
B
N
y
l
cos
Po podniesieniu do trzeciej potęgi podstawia się otrzymaną wartość do (2). Z dwóch
pierwszych wyrazów tak przekształconego wzoru wyznacza się l w drugim przybliżeniu.
Kontynuacja takiego postępowania pozwala wprowadzić do wzoru na l kolejne wyrazy.
Otrzymamy:
2
2
2
4
2
5
5
2
2
3
3
38
6
9
2
5
cos
120
1
cos
6
cos
t
t
t
B
N
y
t
B
N
y
B
N
y
l
Po prawej stronie wzoru występują funkcje nieznanego argumentu B, tzn. N, t, η i cosB.
Aby wyliczyć l, trzeba najpierw wyznaczyć B. Wyprowadzenie wzoru na B jest nieco
bardziej złożone. Najpierw należy obliczyć kolejne parzyste potęgi ostatniego wzoru na l.
Otrzymane wyrażenia wprowadza się do wzoru (1). PO przeniesieniu X na lewą stronę
otrzymamy wyrażenie na (x-X) w funkcji y, N, t i η, z którego wyeliminowaliśmy l.
4
2
5
6
4
2
2
3
4
45
30
1
720
4
5
3
1
24
2
t
t
N
t
y
t
N
t
y
N
yt
X
x
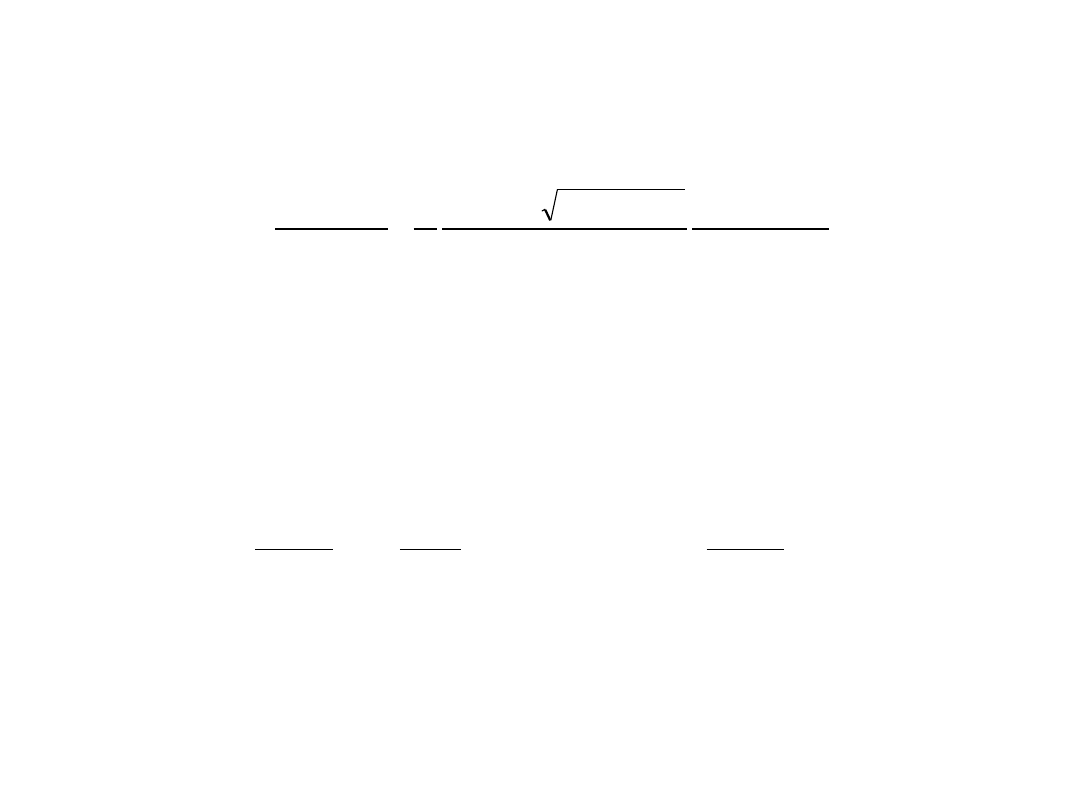
Następnie biorąc X ≡ x, wyznacza się przez postępowanie iteracyjne ze wzoru (3) pewna
wartość szerokości B
1
odpowiadającą kątowi mierze łuku południka o długości x.
Różnica długości łuków południka (x-X) może być wyrażona z dostatecznym
przybiżeniem przez równanie drugiego stopnia względem (B
1
-B)
2
2
2
1
2
2
2
2
2
1
1
sin
1
cos
2
3
M
B
B
e
a
B
e
B
e
t
B
B
M
X
x
Porównanie prawych stron dwóch ostatnich wyrażeń uwolni nas od wartości (x-X).
Rozwiązanie otrzymanego równania względem (B
1
-B) metodą kolejnych przybliżeń daje
wyrażenie na różnicę (B
1
-B). Na koniec rozwinięcie t, η i (MN)
-1
w szeregi względem
małej wartości (B1-B) prowadzi do wzoru, w którym - oprócz y – wszystkie inne wielkości
są zależne od B
1
. Wzór ten przedstawia się następująco:
4
1
2
1
4
1
4
2
1
2
1
2
1
2
1
2
1
2
1
1
1
2
1
45
90
61
360
9
3
5
12
1
2
t
t
N
y
t
t
N
y
t
N
M
y
B
B
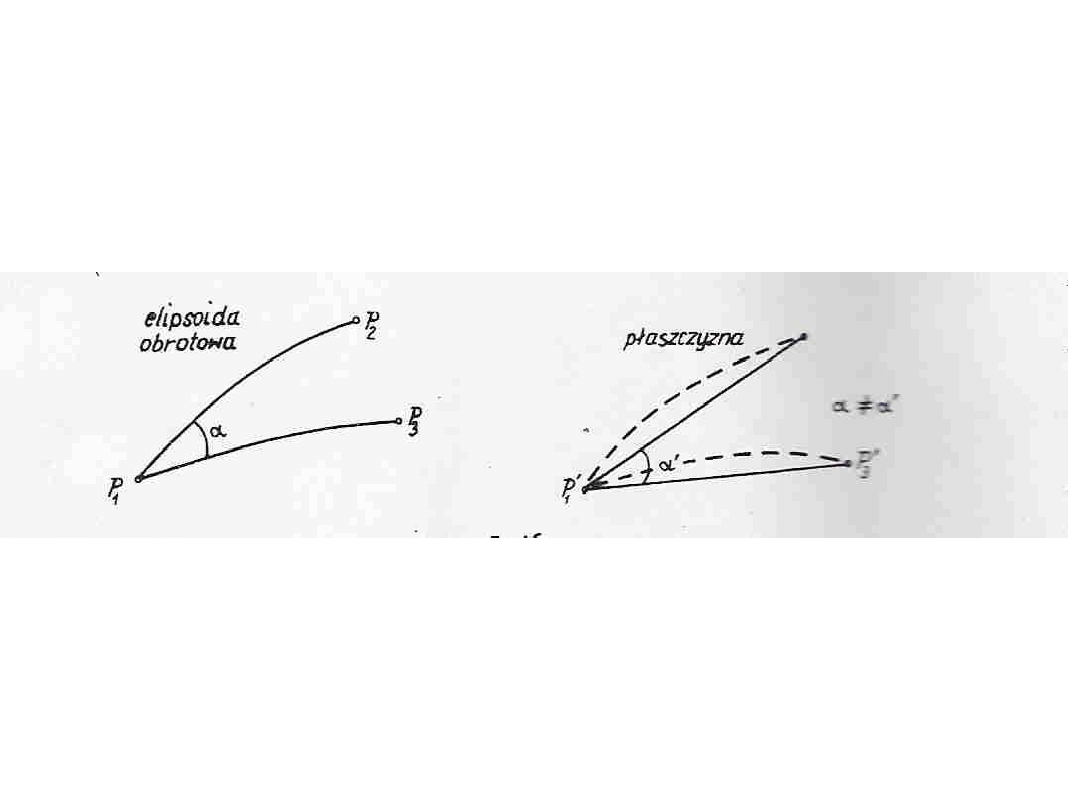
Redukcja kierunków i redukcja boków w odwzorowaniu wiernokątnym Gaussa-Krugera
Wyobraźmy sobie, że na elipsoidzie obrotowej mamy trójkąt P
1
P
2
P
3
. Kąt P
2
P
1
P
3
zawarty
jest między przekrojami normalnymi z punktu P
1
na punkty P
2
i P
3
. W odwzorowaniu na
płaszczyznę (odwzorowanie wiernokątne przekroje są liniami krzywymi). W takim
wypadku zachodzi oczywiście równość katów.
Jeśli odwzorujemy na płaszczyznę punkty P
1
, P
2
i P
3
, a następnie połączymy punkt P
1
’ z
punktami P
2
’ i P
3
’, to otrzymany kąt nie będzie równy katowi na elipsoidzie. W takim
wypadku nastąpi zniekształcenie kątowe i jeżeli chcemy obliczyć wielkość kąta na
płaszczyźnie, to musimy uwzględnić redukcje odwzorowawcze.
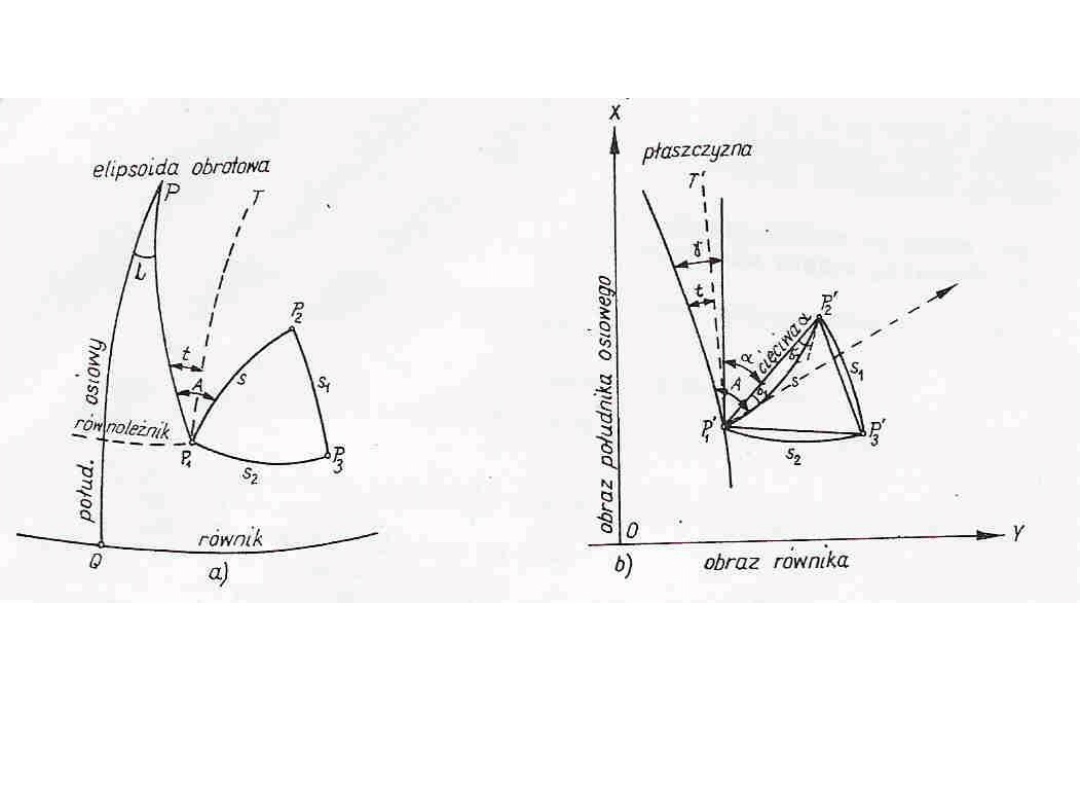
Podstawowe oznaczenia i wielkości stosowane przy odwzorowaniu elipsoidy na
płaszczyznę podamy na przykładzie trójkąta P
1
P
2
P
3
.
QP – osiowy południk danej strefy
P
1
P – południk punktu P
1
P
1
T – krzywa równoległa do południka
osiowego QP (równoleżnik
geodezyjny)
s, s
1
, s
2
– linie geodezyjne
OX – obraz południka osiowego
P
1
’X – południk punktu P
1
’
P
1
’T’ – linia równoległa do południka
osiowego
Wskutek wiernokątności kąty między odpowiednimi liniami będą zachowane. Kąty w
wierzchołkach P
1
P
2
P
3
trójkąta geodezyjnego są równe kątom trójkąta płaskiego P
1
’P
2
’P
3
’
utworzonego przez krzywe – obrazy boków trójkąta na płaszczyźnie. Kat między cięciwą
a linia równoległą do południka osiowego nazywa się kątem kierunkowym na
płaszczyźnie i oznacza się literą
. Kąt γ nazywa się kątem zbieżności południków na
płaszczyźnie. Kąt δ (zawarty między cięciwą i obrazem linii geodezyjnej) nazywa się
redukcją kierunku. Różnica δ – t jest wielkością małą czwartego rzędu:
B
B
l
t
2
2
2
cos
sin
3
2
Kolejność przejścia z elipsoidy na płaszczyznę Gaussa - Krugera
1. Przeliczamy współrzędne geodezyjne B, L na współrzędne płaskie X, Y.
2. Przeliczamy azymut wyjściowy linii geodezyjnej na odpowiadający tej linii kąt
kierunkowy cięciwy
12
1
12
12
A
21
2
21
21
A
...
"
2
3
1
"
cos
sin
3
1
sin
"
"
2
4
2
2
2
l
B
B
B
l
Zazwyczaj w praktyce obliczanie γ” ograniczamy do pierwszego wyrazu zaś
2
1
1
2
2
1
2
2
1
2
12
2
6
"
6
2
"
"
y
y
x
x
R
y
y
y
R
x
x
S
s
S
3. Redukujemy boki i kąty na płaszczyznę Gaussa-Krugera. Redukcje kątowe
wprowadzamy według wzoru:
12
13
"
"
"
gdzie:
6
2
"
"
1
3
2
1
3
13
y
y
y
R
x
x
s
S
6
2
"
"
1
2
2
1
2
12
y
y
y
R
x
x
s
S
Dla obszaru Polski wzór ten można uprościć, przyjmując R
S
(średni promień krzywizny)
odpowiadający szerokości geodezyjnej B = 52°. Otrzymamy wówczas następujący wzór
na redukcję kierunku
2
1
1
2
2
0008439
,
0
"
y
y
x
x
gdzie x i y należy wziąć w kilometrach.
Redukcje boków wyznaczymy ze wzoru:
2
2
2
1
2
1
2
6
1
1
y
y
y
y
R
s
d
S
S
Dla obszaru Polski:
2
2
2
1
2
1
9
0000000040
,
0
1
y
y
y
y
s
d
S
gdzie y należy wziąć w kilometrach.