Pomiary grawimetryczne.

(przyśpieszenia siły ciężkości)

Jednostki: 1 cm· sek

-2

= 1 gal (gal)

10

-3

cm· sek

-2

= 1 mgal (miligal)

10

-6

cm· sek

-2

= 1



gal (mikrogal)

Średnia wartość przyspieszenia ziemskiego

g



981 gal

Rodzaje pomiarów grawimetrycznych

1. Bezwzględne

- wahadło fizyczne

- balistyczne

2. Względne

- wahadłowe

- grawimetr strunowy

- grawimetr statyczny

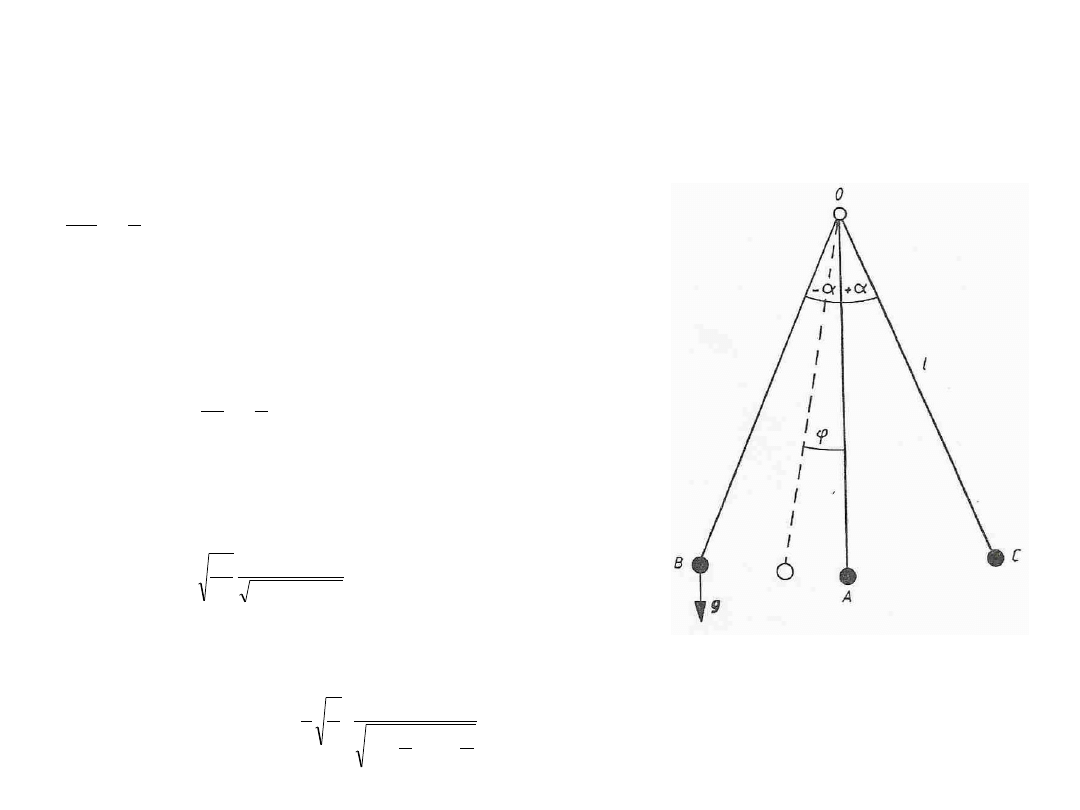
1.Pomiary bezwzględne

a) pomiary bezwzględne z wykorzystaniem wahadła fizycznego

Ruch wahadła matematycznego ujęty jest równaniem różniczkowym





sin

2

2

l

g

dt

d





(2.1)

Przy czym kąt



jest wychyleniem z położenia

równowagi. W położeniu granicznym, gdzie



=



, a

t=0 oraz d



/dt=0, z równania (2.1) wynika, że











cos

cos

2





l

g

dt

d

(2.2)

Przy czym zgodnie z oznaczeniami na rys.,



jest amplitudą drgań wahadła. Dalej

uzyskuje się:







cos

cos

2





d

g

l

dt

(2.3)

Poprzez scałkowanie w granicach od -



do+



znajduje się okres wahadła matematycznego













0

2

2

0

2

sin

2

sin

2

1







d

g

l

dt

T

T

(2.4)

W nowoczesnych aparatach amplituda nie przekracza kilkunastu minut i dlatego













































...

2

sin

64

9

2

sin

2

1

1

4

2







g

l

T

(2.5)

Z błędem nie większym niż10

-10

T

można przyjąć, że półokres wahań











 



2

16

1

1





g

l

T

Wielkość zdefiniowana wzorem Christana Huyghensa (1629-1695):

g

l

T





0

Odpowiada okresowi wahań dla



= 0. Stąd przyspieszenie siły ciężkości

2

0

2

T

l

g





(2.6)

Okres zredukowany wahadła do „zerowej amplitudy” otrzymuje się w myśl wzoru











 



2

0

16

1

1



T

T

(2.7)

Wykorzystywane do pomiarów grawimetrycznych wahadło fizyczne ma w przybliżeniu
taki sam okres wahań, jak wahadło matematyczne o długości

Ma

J

a

l

0





(2.8)

zwanej długością zredukowana wahadła fizycznego. Wielkość a oznacza odległość
środka obrotu wahań od środka ciężkości wahadła fizycznego, a J

0

– moment

bezwładności masy M wahadła względem osi przechodzącej przez jego środek
ciężkości

Metoda swobodnego spadku ciał

Równanie swobodnego spadku ciał można zapisać w znanej z fizyki postaci

2

0

0

2

t

g

t

v

z

z







Równanie to ma swoje źródło w równaniu różniczkowym drugiego rzędu względem czasu
o postaci , wynikającego z równości . Ponieważ g = const., to w wyniku
pierwszego scałkowania otrzymalibyśmy .
A zatem z

0

i v

0

reprezentują stałe całkowania (położenie początkowe z

0

i prędkość

początkowa v

0

w momencie t=0). Dostatecznie precyzyjne pomierzenie tych parametrów

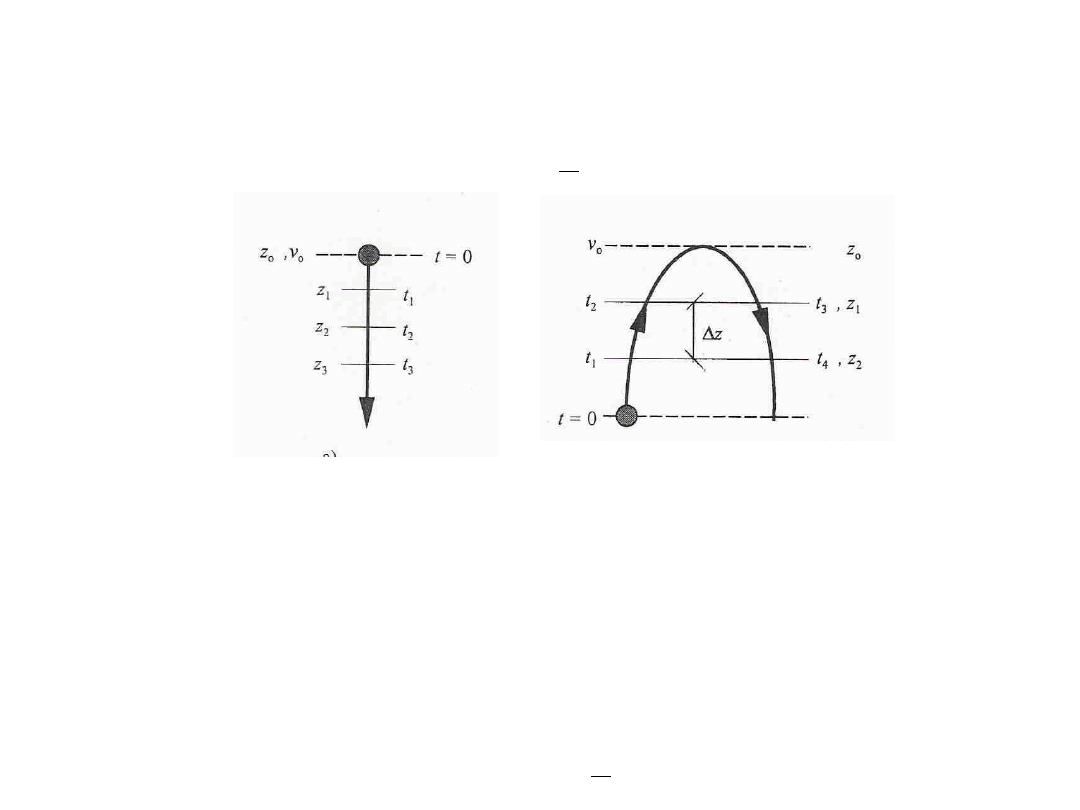
początkowych jest niewykonalne. Z tego powodu drogę i interwały czasu mierzy się
pomiędzy co najmniej trzema punktami na torze spadającego ciała. Można w takim
przypadku napisać dwa równania: jedno dla z

2

– z

1

i drugie dla z

3

– z

1

, lub ogólnie dla

większej liczby interwałów pomiarowych:

g

z







mg

z

m







gt

v

z





0













2

1

1

1

1

2

t

t

g

t

t

v

z

z

i

i

i











Z układu takich równań można albo wyeliminować v

1

, albo potraktować dodatkowo z

1

i v

1

jako niewiadome, gdy rozporządzamy nadliczbowymi obserwacjami z

i

. Przy takim

podejściu należałoby uwzględnić zależność pomiędzy wielkościami obserwowanymi z i t.
W najprostszym przypadku trzech punktów obserwacji wzdłuż drogi spadku
otrzymalibyśmy następujący związek:





 













2

3

1

2

1

3

1

3

1

2

1

2

1

3

2

t

t

t

t

t

t

t

t

z

z

t

t

z

z

g



















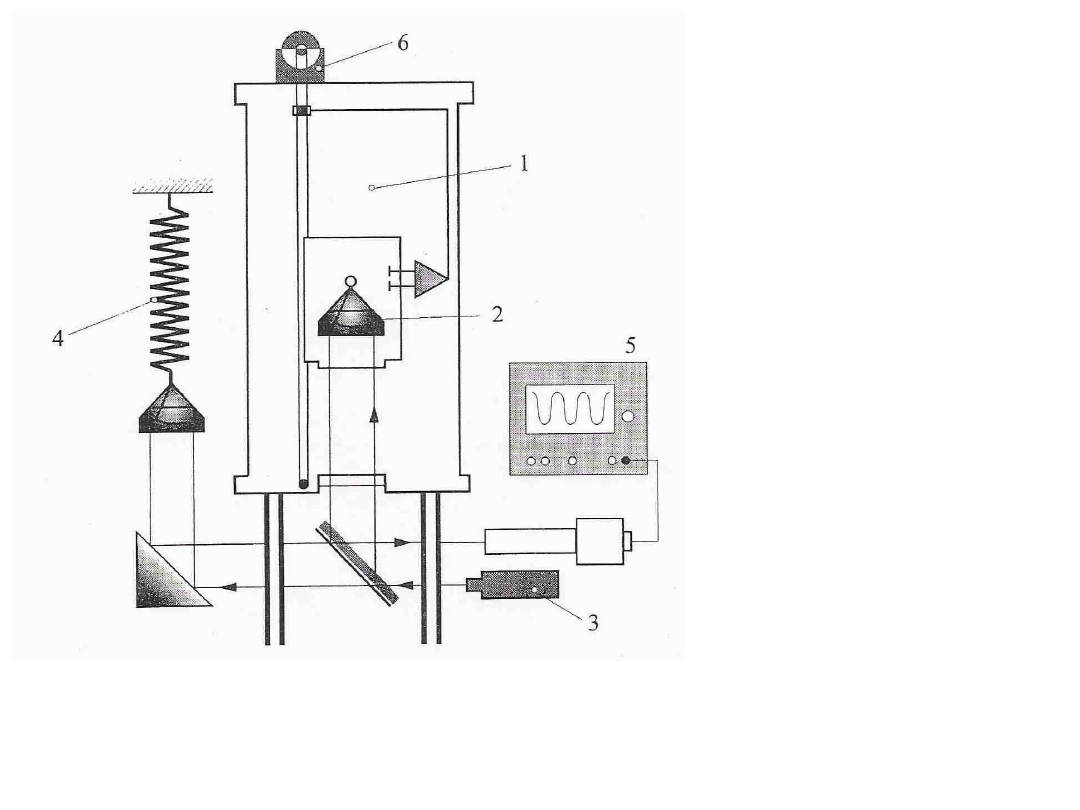
1. – komora próżniowa, 2 – ruchomy pryzmat, 3 – laser, 4 – urządzenie kompensujące

drgania, 5 – licznik lub oscyloskop, 6 – silnik napędzający urządzenie wyrzucające

pryzmat

Dokładność

współczesnych

bezwzględnych

pomiarów

stacjonarnych przyspieszenia siły
ciężkości szacuje się w granicach
jednego

mikrogala.

Pomiary

aparatami przenośnymi są mniej
dokładne. Można ich błędy szacować
na około ±0,002÷0,005 mgala.

Grawimetry statyczne

Do pomiarów względnych przyśpieszenia siły ciężkości stosuje się powszechnie grawimetry
statyczne.

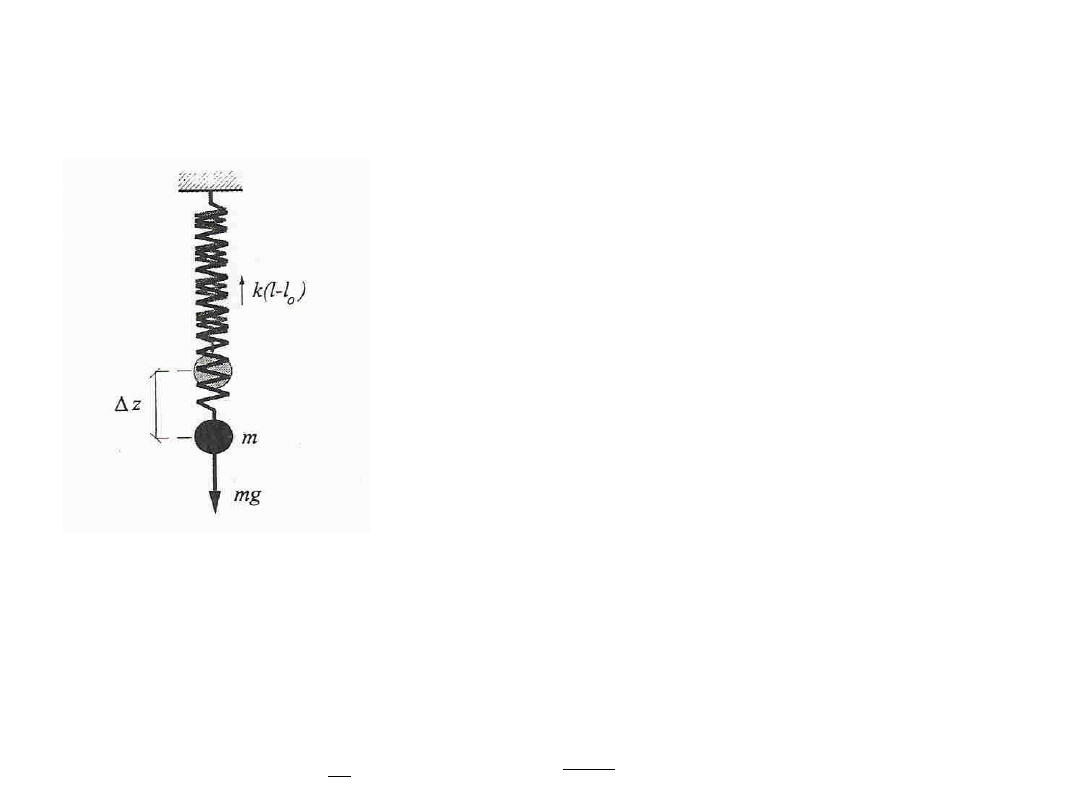
Model grawimetru statycznego

Najprostszy model grawimetru statycznego
stanowić może pionowa sprężyna obciążona
stałą masą. Zmiany przyśpieszenia siły
ciężkości powodują zmienność siły
przykładanej do tej sprężyny i tym samym
zmiany jej długości. W pewnym zakresie
zmiany te będą miały charakter liniowy.
Równanie równowagi statycznej naszego
modelu ma następującą postać:





0

l

l

k

mg





przy czym k jest pewna stałą wartością charakterystyczną dla danej sprężyny, l – to
długość sprężyny obciążonej, zaś l

0

– nie obciążonej. Poprzez różniczkowanie tego

równania można dojść do związku liniowego pomiędzy małą zmianą przyspieszenia



g i

zmianą długości sprężyny



l.

l

m

k

g







l

l

l

g

g





0





albo

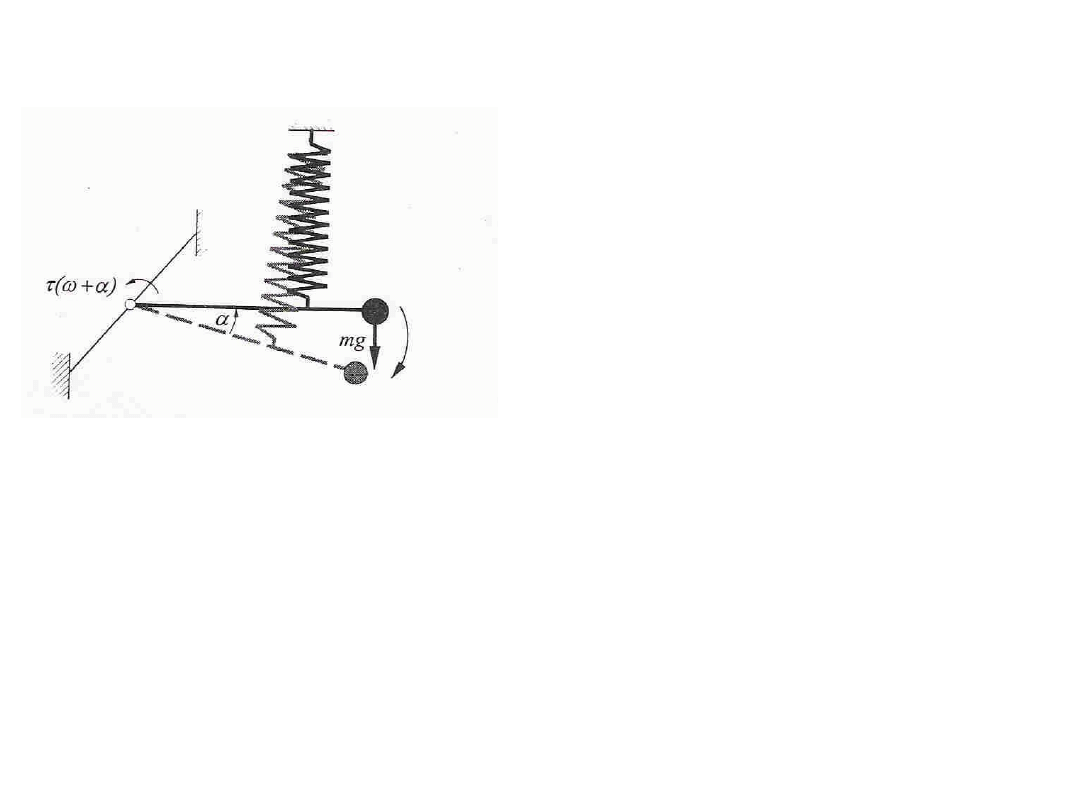
We współczesnych grawimetrach statycznych znalazł zastosowanie inny, bardziej
złożony system pomiarowy

Schemat systemu mierzącego grawimetru

Rysunek przedstawia schemat tego systemu.
Pozioma ‘dźwignia’ o długości a, obciążona
masą m, może się obracać wokół osi O ( z
reguły os tę stanowi pozioma ‘nić torsyjna’).
Na skutek zmiany przyśpieszenia siły
ciężkości dźwignia wykonuje pewien obrót
wokół osi O. Za pomocą sprężyny pomiarowej
można doprowadzić dźwignię do wyjściowego
położenia poziomego. Następuje to w
większości konstrukcji poprzez pochylenie
systemu mierzącego grawimetru.

Śruba mikrometryczna, połączona ze sprężyną pomiarową, umożliwia pomiar przemieszenia
dźwigni, będącego funkcją kata obrotu dźwigni (nachylenie systemu mierzącego). Taka
metoda pomiaru (odczytywania grawimetru), polegająca na doprowadzeniu systemu
mierzącego do pozycji wyjściowej (poziomej) poprzez nachylanie, nosi nazwę odczytu przez
zerowanie (metoda zerowania). Na ogół w pewnym zakresie zmian przyspieszenia istnieje
prawie liniowa zależność pomiędzy katem obrotu dźwigni i zmianą przyspieszenia.
Równanie równowagi statycznej systemu przedstawionego na rysunku ma postać:

















cos

mga

Związek ten wyraża równość momentu siły mg o ramieniu a i momentu skręcającego nici
torsyjnej, przy czym



jest stałym współczynnikiem skręcenia nici torsyjnej,



-

wyjściowym katem skręcenia nici, zaś



to kąt wychylenia dźwigni. Na podstawie tego

równania uzyskuje się związek pomiędzy



g i



, który jest liniowy dla



bliskich zera.











g

a

ma

g





Równania te mają w mniejszym bądź większym stopniu zastosowanie do wszystkich
typów grawimetrów statycznych.

Sprężyny metalowe, zazwyczaj inwarowe, wymagają dobrej izolacji termicznej grawimetru
(±0,001ºC), cechują się małym współczynnikiem termoelastycznym (0÷±0,05x10

-6

/1 ºC),

małą tzw. elastycznością wtórną, natomiast znaczną liniową rozszerzalnością termiczną.
Sprężyny kwarcowe mają duży współczynnik termoelastyczny, zaś bardzo małą liniową
rozszerzalność termiczną, są niemagnetyczne, mają własności higroskopijne, są lekkie mało
podatne na zjawisko histerezy oraz odkształcenia elastyczne na skutek zmian ciśnienia.

W efekcie takich własności grawimetry ze sprężynami metalowymi wymagają, oprócz
termostatów, także szczelnych obudów, chroniących systemy pomiarowe przed zmianami
ciśnienia, a także osłon antymagnetycznych. W związku z tym bywają stosunkowo ciężkie.
Jednakże za ich pomocą osiąga się wysokie dokładności pomiaru, z reguły lepsze niż ±0,02
mgala. Ponadto grawimetry metalowe mają bardzo małe dryfty.

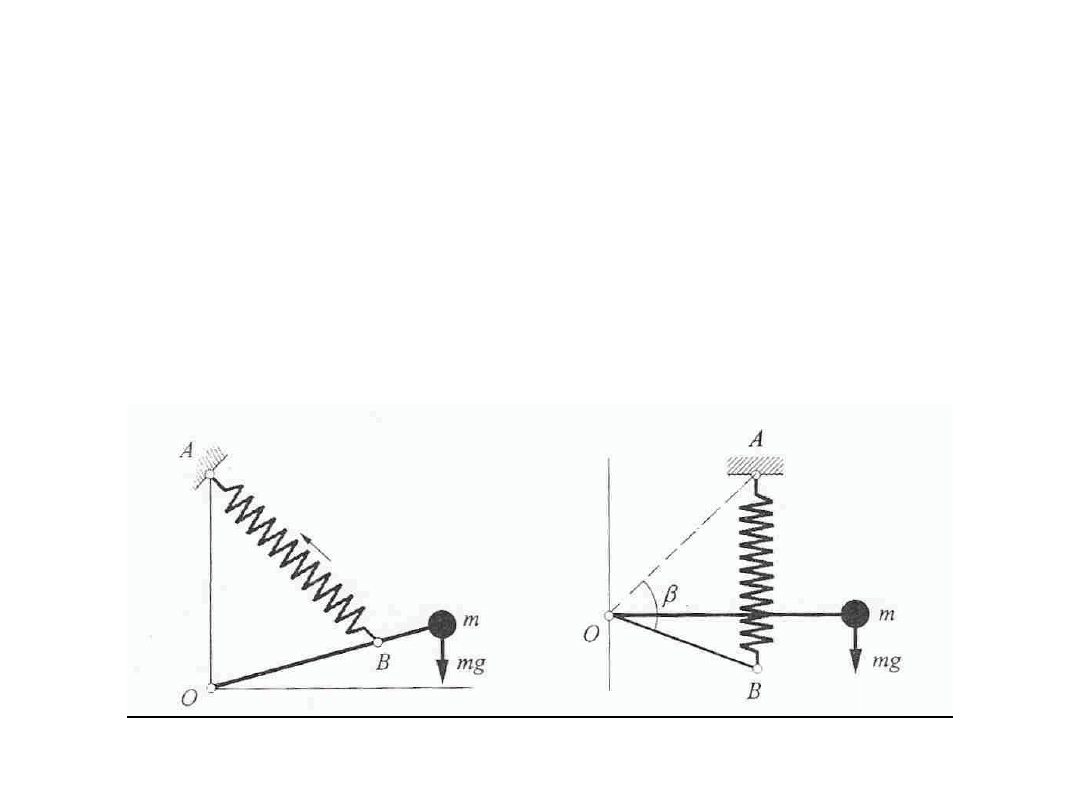
Schemat różnych systemów mierzących grawimetrów

Grawimetry kwarcowe są bardzo lekkie i niewielkiego rozmiaru,a więc wygodne w
użyciu. Niestety charakteryzują się znacznymi wielkościami dryftu, co czyni pomiary
bardziej uciążliwymi. Muszą być bardzo dobrze zabezpieczone przed wpływami
wilgotności. Mniej wrażliwe na wpływy zmian temperatury mogą nie być wyposażone w
termostaty utrzymujące z dużą dokładnością temperaturę wewnętrzną. Są z reguły
wyposażone w bimetaliczne kompensatory temperatury. Zapewniają nieco niższe
dokładności pomiarów niż grawimetry ze sprężynami metalowymi (około ±0,05mgala).

Zasady astatyzacji. Przez astatyzację systemu mierzącego grawimetru rozumie się pewien
mechaniczny zabieg powodujący zwiększenie czułości tego systemu. Reakcja systemu
mierzącego, z poziomą dźwignią o długości a, na zmiany przyśpieszenia jest określona w
równaniu równowagi iloczynem mga z jednej strony, zaś parametrami sprężyny



i



z

drugiej strony.Z wzajemnej relacji tych wielkości wynika określona wielkość reakcji
urządzenia na zmiany przyśpieszenia, czyli czułość grawimetru. Jeśli do układu będącego
w równowadze, zostanie wprowadzony dodatkowy element, np.. w postaci dodatkowego
momentu obrotowego (dodatniego bądź ujemnego), reakcja urządzenia na zmiany
przyspieszenia okaże się zmieniona. W procesie astatyzacji chodzi o takie zakłócenie
pierwotnego stanu równowagi, aby uzyskać możliwie największą czułość urządzenia, nie
doprowadzając go jednakże do stanu równowagi chwiejnej ani obojętnej. I tak na
przykład systemy mierzące z pionową lub ukośna sprężyną i poziomą dźwignią astatyzuje
się poprzez odpowiedni dobór parametrów geometrycznych systemu mierzącego.

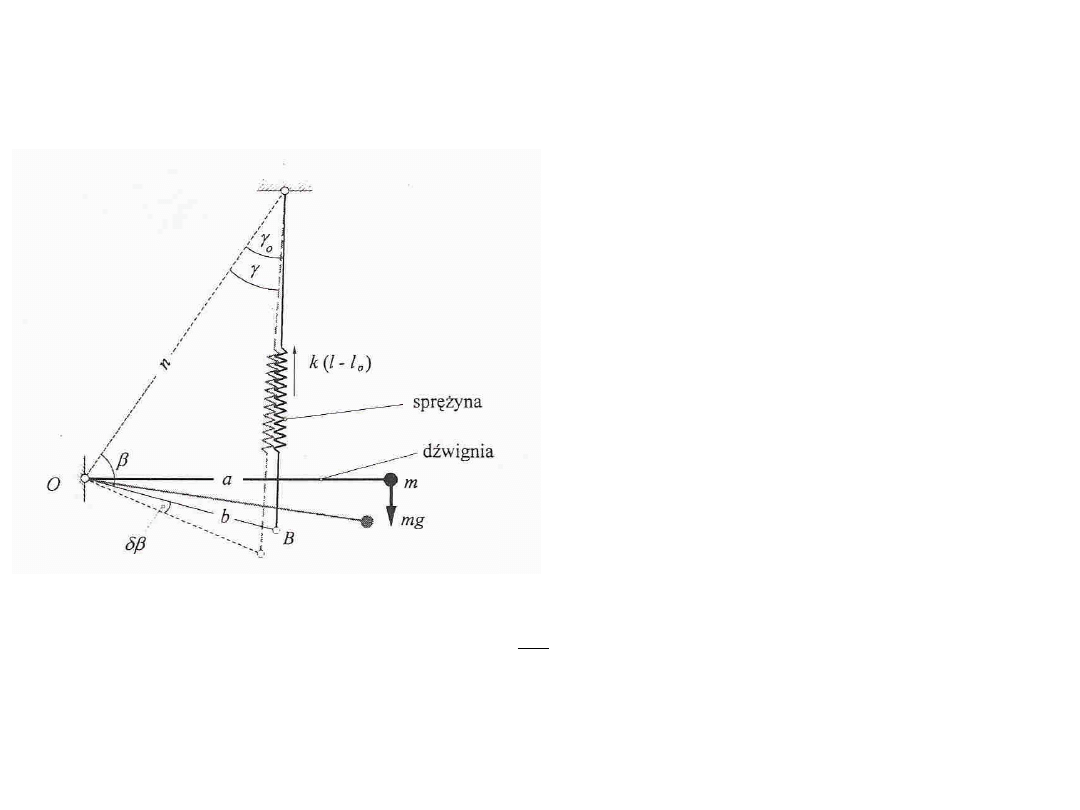
W przypadku systemu przedstawionego schematycznie na rysunku równanie równowagi
przy poziomej dźwigni ma postać:





0

0

sin



n

l

l

k

mga





Wyrażenie nsin



0

to ramię siły k(l-l

0

). Po

wychyleniu dźwigni o kąt



równanie to

zmieni się na









sin

cos

0

n

l

l

k

mga





Zmieniając sin



0

i sin



przez odpowiednie funkcje



i



+



, można łatwo dojść do

następującej relacji





tan

g

dg

d



z której wynika, że największą czułość grawimetru (



max

) osiągniemy, gdy



=90º. Zatem

w konstrukcjach, działających na zasadzie zilustrowanej schematem przedstawionym na
rysunku. Astatyzację można uzyskać poprzez taki dobór punktów zaczepienia sprężyny i
dźwigni, aby kat



był zbliżony do kąta prostego.

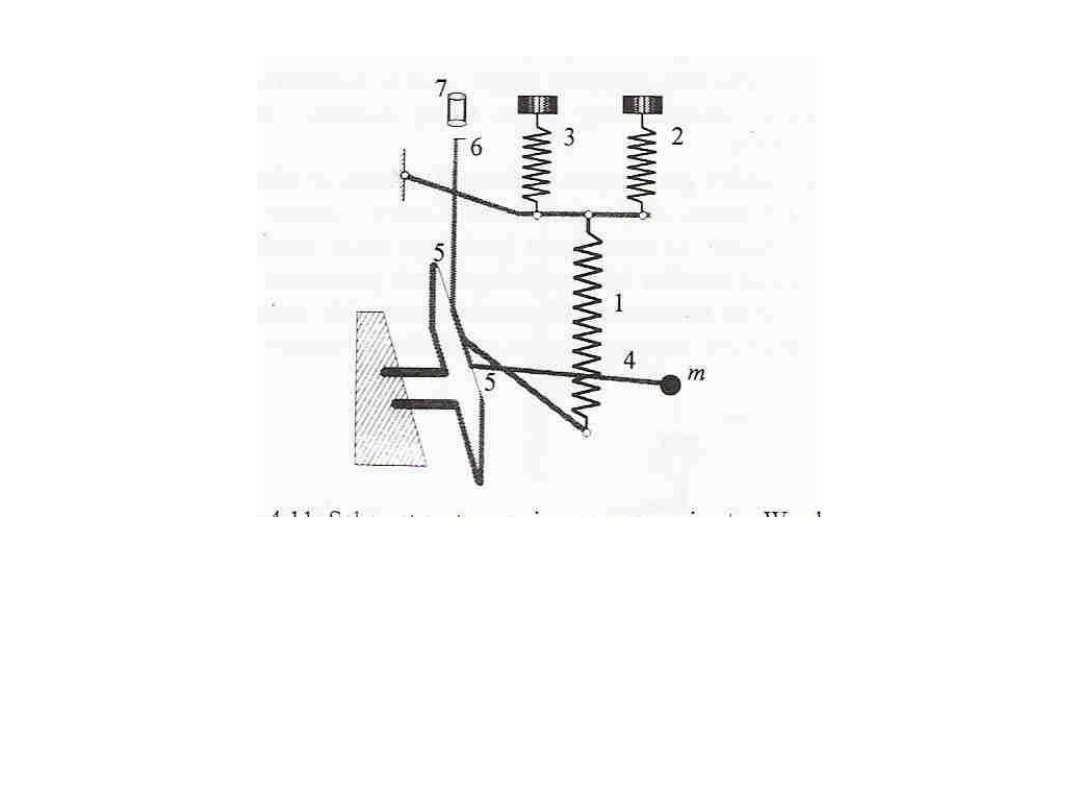
Schemat systemu mierzącego grawimetru Wordena

1. sprężyna pomiarowa (główna), 2 –sprężyna i śruba odczytu,3-sprężyna i śruba zmian

zakresu pomiarowego, 4-dźwignia pozioma obciążona masą, 5-nić torsyjna, 6-wskaźnik

położenia dźwigni, 7-lunetka odczytowa

Relative Spring Gravimeters

Advantages

• Simple To Operate
• Small/Lightweight
• Inexpensive

Problems

• Drifts
• Tares
• Calibration

Cechowanie grawimetrów

Najpowszechniej stosuje się dwie metody cechowania grawimetrów statycznych:
1.) za pomocą baz grawimetrycznych
2.) metoda nachylania

Dryft grawimetrów

działanie grawimetrów statycznych, polegające na odkształceniu elementów
sprężystych, można objaśnić na podstawach teorii elastyczności i reologii. Zjawisko
dryftu systemów mierzących grawimetrów jest efektem nakładania się dwóch efektów:
odstępstwa w zachowaniu się materiału,z którego sporządzono system mierzący, od
zasad teorii Hooka i pewnych zjawisk reologicznych, takich jak pełzanie i płynięcie
materiału.

Wpływ zmiany temperatury na rozszerzalność liniową





t

l

l









1

0

Wpływ mian temperatury na zmianę współczynnika elastyczności sprężyny



(właściwe zjawiska termoelastyczne)





t













1

0

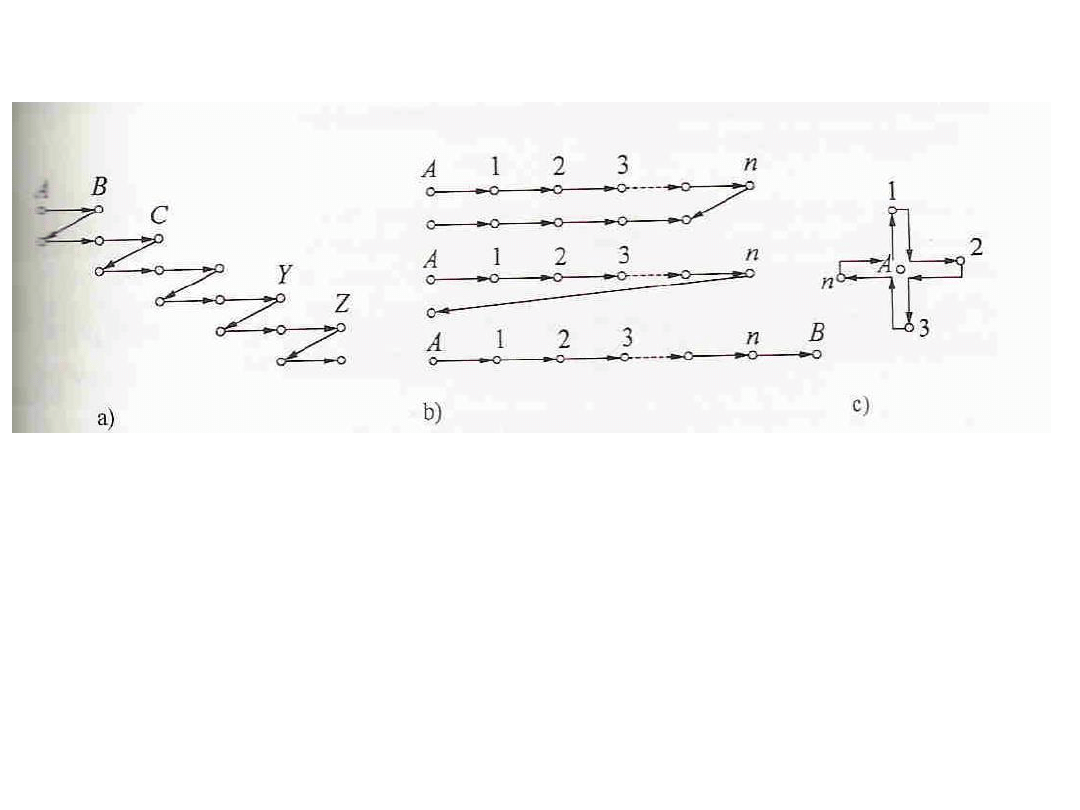
Różne sposoby pomiaru grawimetrami

sposób łańcuchowy

sposób profilowy

sposób gwiazdowy

Poprawki do pomierzonych wartości przyspieszenia siły ciężkości

1. Poprawka ze względu na zmiany przyspieszenia siły ciężkości spowodowana
przyciąganiem Księżyca i Słońca.

Poprawka spowodowana jest zjawiskiem pływów skorupy ziemskiej. Zjawisko pływów i
jego wpływ na pomiary geodezyjne zostaną omówione w dalszej części wykładów.





mgal

z

z

h

k

g

s

k

p































































3

1

2

cos

0379

,

0

3

1

2

cos

0825

,

0

2

3

1

gdzie: Δg

p

– poprawka pływowa do pomierzonej wartości przyspieszenia siły ciężkości

k, h – liczby Love’a
z

k

– topocentryczna odległość zenitalna Księżyca

z

s

– topocentryczna odległość zenitalna Słońca





19

,

1

15

,

1

2

3

1

























h

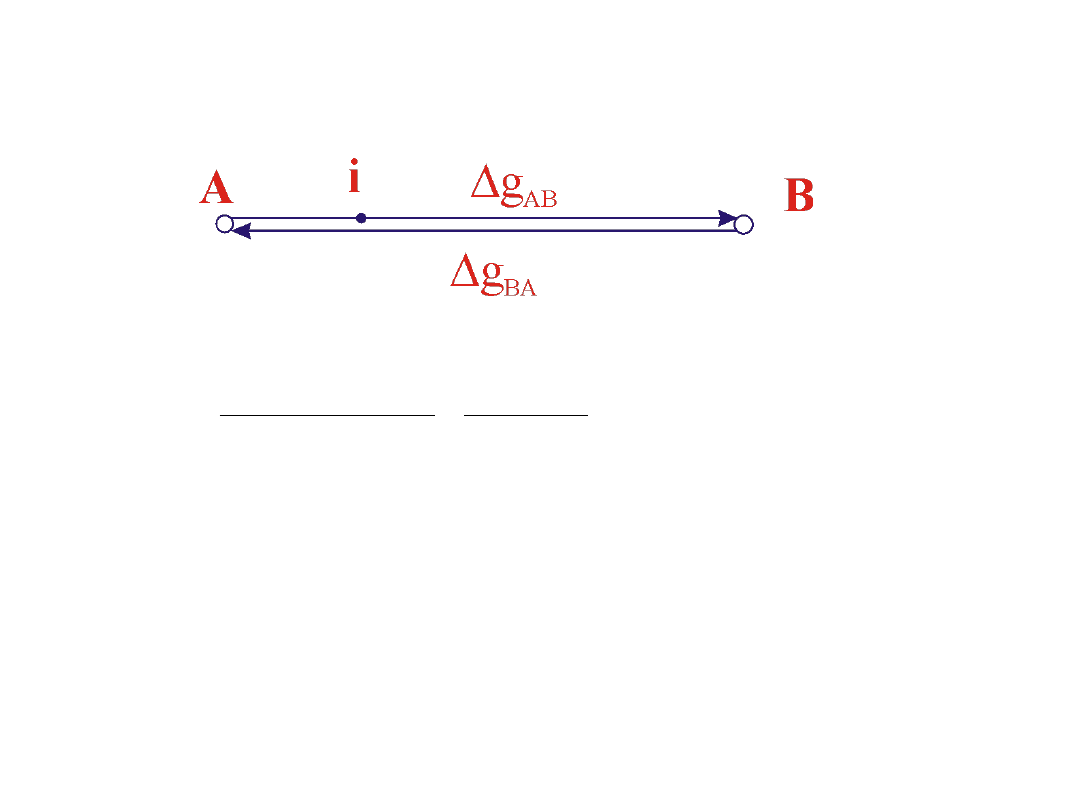
2. Poprawka ze względu na dryft grawimetru

Pomiar grawimetryczny wykonany „tam” i „z powrotem”

BA

AB

g

g

g













Chód:



 



P

AB

t
AB

P

B

P

A

t

A

t

B

t

t

g

T

T

T

T

g

n

























gdzie:

P

BA

P

B

P

A

t
AB

t

A

t

B

t

T

T

t

T

T

















A

i

pom

i

popr

i

T

T

h

g

g







Powyższe dwie poprawki do pomierzonych wartości przyspieszenia są najbardziej istotne.
Przy pomiarach o dokładności rzędu 1μgal wprowadzamy szereg innych poprawek między
innymi spowodowanych zmianami ciśnienia atmosferycznego, zmianami poziomu wody
gruntowej, wilgotności gruntu itp..